尹伯成版西经简明教程课后题答案习题八
- 格式:doc
- 大小:41.00 KB
- 文档页数:7

第八章生产要素价格决定的需求方面1.说明生产要素理论在微观经济学中的地位.解答:要点如下:第一,从商品的角度来看,微观经济学可以分为两个部分,即关于“产品”的理论和关于“要素”的理论.前者讨论产品的价格和数量的决定,后者讨论要素的价格和数量的决定.第二,产品的理论和要素的理论是相互联系的.特别是,产品理论离不开要素理论,否则就不完全.这是因为,首先,产品理论在讨论产品的需求曲线时,假定了消费者的收入水平为既定,但并未说明收入是如何决定的,其次,在推导产品的供给曲线时,假定了生产要素的价格为既定,但并未说明要素的价格是如何决定的.这两点都与要素理论有关.因此,要素理论可以看成是产品理论的自然的延伸和发展. 在西方经济学中,产品理论通常被看成是“价值”理论,要素理论通常被看成是“分配”理论.产品理论加上要素理论,或者,价值理论加上分配理论,构成了整个微观经济学的一个相对完整的体系.2.试述厂商的要素使用原则.解答:要点如下:第一,厂商在使用要素时同样遵循利润最大化原则,即要求使用要素的“边际成本”和“边际收益”相等.第二,在一般情况下,场上使用要素的边际收益是“边际收益产品”(要素的边际产品和产品的边际收益的乘积),边际成本是“边际要素成本”.因此,一般场上使用要素的原则是:边际收益产品等于边际要素成本.第三,在完全竞争条件下,边际收益产品等于“边际产品价值”(要素的边际产品和产品价格的乘积),而边际要素成本等于“要素价格”.于是,完全竞争厂商使用要素的原则是:边际产品价值等于要素价格.3、要素使用原则与利润最大化产量原则有何关系?解答:要点如下:第一,在西方经济学中,利润最大化被假定为是任何厂商的任何活动都必须遵守的原则.因此,无论是产量的决定还是要素使用量的决定,遵守的都是同一个利润最大化原则.该原则意味着,任何厂商的任何活动的“边际收益”和“边际成本”必须相等.第二,在不同的场合,边际收益和边际成本的具体内容并不相同.例如,在产量的决定问题上,边际收益和边际成本是指增加一单位产量增加的收益和成本,而在要素使用量的决定问题上,边际收益和边际成本则是指增加使用一单位要素增加的收益和成本.第三,增加使用一单位要素所增加的收益叫“边际收益产品”,它等于要素的边际产品和产品的边际收益的乘积.因此,增加使用要素的边际收益包括了产品的边际收益.另一方面,要素的边际成本与产品的边际成本的关系则比较复杂.这是因为,要素的边际成本通常仅指增加使用某种特定要素如劳动所引起的成本变化,而产品的边际成本则与多种要素(如劳动和资本)的共同变化有关——产品是由多种要素共同生产出来的.4、在什么情况下,要素的需求曲线不存在?解答:要点如下:第一,要素需求曲线意味着,在一定范围内,对于每一个要素的价格,都有一个唯一的要素需求量与之对应.第二,如果在要素市场上,市场的买方属于完全竞争(卖方则既可以是完全竞争,也可以是不完全竞争),则给定一个要素价格,就有一个唯一的要素需求量与之对应,即存在要素的需求曲线.第三,如果在要素市场上,市场的买方属于不完全竞争(如垄断),则会出现如下情况:对于同一个要素价格,可能会有多个不同的要素需求量与之对应.在这种情况下,就不存在一条确定的要素需求曲线.5、试述厂商及市场在完全竞争和垄断、行业调整存在和不存在等各种情况下的要素需求曲线.解答:要点如下:第一,在完全竞争条件下,厂商对要素的需求曲线向右下方倾斜,即随着要素价格的下降,厂商对要素的需求量将增加.第二,如果不考虑厂商所在行业中其他厂商的调整,则该厂商的要素需求曲线就恰好与其边际产品价值曲线重合.第三,如果考虑厂商所在行业中其他厂商的调整,则该厂商的要素需求曲线将不再与边际产品价值曲线重合.这是因为,随着要素价格的变化,如果整个行业所有厂商都调整自己的要素使用量,从而都改变自己的产量的话,产品的市场价格就会发生变化.产品价格的变化会再反过来使每一个厂商的边际产品价值曲线发生变化.于是,厂商的要素需求曲线将不再等于其边际产品价值曲线.在这种情况下,厂商的要素需求曲线叫做“行业调整曲线”.行业调整曲线仍然向右下方倾斜,但比边际产品价值曲线要陡峭一些.第四,在完全竞争条件下,市场的要素需求曲线等于所有厂商的要素需求曲线(行业调整曲线)的水平相加.第五,不完全竞争的情况比较复杂.在不完全竞争要素市场中,卖方垄断厂商的要素需求曲线向右下方倾斜,即随着要素价格的下降,厂商对要素的需求量将增加,而且,它还与边际收益产品曲线恰好重合. 第六,在不完全竞争要素市场中,如果所有厂商均是卖方垄断者,则它们的要素需求曲线就等于各自的边际收益产品曲线.于是,市场的要素需求曲线就是所有这些厂商的边际收益产品曲线的水平相加.第七,如果在不完全竞争要素市场中,并非所有厂商均是卖方垄断者,则它们的要素需求曲线就是行业调整曲线.于是,市场的要素需求曲线就是所有这些厂商的行业调整曲线的水平相加.买方垄断厂商的要素需求曲线不存在.6、设一厂商使用的可变要素为劳动L,其生产函数为:Q=-0.01L3+L2+38L其中,Q为每日产量,L时每日投入的劳动小时数,所有市场(劳动市场及产品市场)都是完全竞争的,单位产品价格为0.10美元,小时工资为5美元,厂商要求利润最大化.问厂商每天要雇用说少小时劳动?解答:要点如下:已知工资W=5.根据生产函数及产品价格P=0.10,可求得劳动的边际产品价值如下: VMP L =P ×MPP L =P ×dLdQ=0.10×()3801.0(23'++-L L ) =0.01×(-0.03L 2+2L+38)第三,完全竞争厂商的利润最大化要求边际产品价值等于工资,即: 5=0.10×(-0.03L 2+2L+38) 或 0.03L 2-2L+12 第四,解之得: L 1=20/3 L 2=60.第五,当L 1=20/3时,利润为最小(因为6.1=dLdMPP L>0),故略去. 第六,当L 2=60时,利润为最大(6.1-=dLdMPP L<0).故厂商每天要雇佣60小时的劳动.7、已知劳动是唯一的可变要素,生产函数为Q=A+10L-5L 2,产品市场是完全竞争的,劳动价格为W ,试说明: (a )厂商对劳动的需求函数.(b)厂商对劳动的需求量与工资反方向变化. (c)厂商对劳动的需求量与产品价格同方向变化. 解答:(a )因产品市场为完全竞争市场,根据 W=VMP=P ×MPP L =P ×dLdQ即 W=P ×(10-10L )=10P-10PL 得厂商对劳动的需求函数为:L=PW101-(b )因 PW L 101-=∂∂ <0 ,故厂商对劳动的需求量与工资反方向变化.(c )因 210P PP L =∂∂ >0 ,故厂商对劳动的需求量与产品价格同方向变化.8、某完全竞争厂商雇用一个劳动日的价格为10元,其生产情况如下表所示.当产品价格为5元,它应雇用多少个劳动日?解答:由题意可计算得下表:由表中可以看到,当L=7时,边际产品价值与工资恰好相等,均等于10.故厂商应雇佣7个劳动日.9、某产品和要素市场上的完全垄断者的生产函数为Q=4L.如果产品的需求函数为Q=100-P ,工人的劳动供给函数为L=0.5W-20,则为了谋求最大利润,该厂商应当生产多少产量?在该产量下,L ,W ,P 各等于多少?解答:由Q=100-P 即P=100-Q 及Q=4L 得: TR=PQ=(100-Q )×Q=(100-4L )×4L=400L-16L 2dLdTRMRP L ==400-32L 由L=0.5W-20即W=2(L+20)得: TC=WL=2(L+20)L=2L 2+40L MFC L =dLdTC=4L+40 利润最大化要求MRP L =MFC L ,即400-32L=4L+40 于是L=10 Q=4L=4×10=40W=2(20+L )=2(20+10)=60 P=100-Q=100-40=6010、假定一垄断厂商仅使用劳动L 去生产产品.产品按竞争市场中的固定价格2出售.生产函数为q=6L+3L 2-0.02L 3,劳动供函数为W=60+3L.求利润最大化时的L ,q ,W. 解答:由q=6L+3L 2-0.02L 3得:dLdqMPP L ==6+6L-0.06L 2 于是VMP L=P×MPP L=2(6+6L-0.06L2)=12+12L-0.12L2由C L=WL=60L+3L2,得MFC L=60+6L根据VMP L=MFC L有:12+12L-0.12L2=60+6L0.12L2-6L+48=0得L1=10(舍去),L2=40于是,当利润最大化时有:L=40q=6×40+3×402-0.02×403=3760W=60+3×40=180。

习 题 一1. 设λ为的任一特征值,则因 λλ22- 为A =-A 22O 的特征值, 故022=-λλ. 即 λ=0或2.2. A ~B , C ~D 时, 分别存在可逆矩阵P 和Q , 使得 P 1-AP =B , Q1-CQ =D .令T =⎪⎪⎭⎫⎝⎛Q O O P 则 T 是可逆矩阵,且T 1-⎪⎪⎭⎫ ⎝⎛C O O A T =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--Q O O P C O O A Q O O P 11=⎪⎪⎭⎫ ⎝⎛D O O B 3. 设i x 是对应于特征值i λ的特征向量, 则 A i x =i λi x , 用1-A 左乘得 i i i x A x 1-λ=.即i i i x x A 11--λ= 故1-i λ是A 的特征值, i =1,2,, n .4. (1) 可以. A E -λ=)2)(1)(1(-+-λλλ,=P ⎪⎪⎪⎭⎫ ⎝⎛--104003214, ⎪⎪⎪⎭⎫ ⎝⎛-=-2111AP P .(2) 不可以.(3) ⎪⎪⎪⎭⎫ ⎝⎛=110101010P , ⎪⎪⎪⎭⎫⎝⎛=-1221AP P . 5. (1) A 的特征值是0, 1, 2. 故A =-(b -a )2=0. 从而 b =a .又11111-λ----λ----λ=-λa a aa A I =)223(22+---a λλλ 将λ=1, 2 代入上式求得 A =0.(2) P =⎪⎪⎪⎭⎫ ⎝⎛-101010101.6. A I -λ=)1()2(2+-λλ, A 有特征值 2, 2, -1.λ=2所对应的方程组 (2I -A )x =0 有解向量p 1=⎪⎪⎪⎭⎫ ⎝⎛041, p 2=⎪⎪⎪⎭⎫ ⎝⎛401λ=-1所对应的方程组 (I +A )x =0 有解向量p 3=⎪⎪⎪⎭⎫ ⎝⎛001令 P =(p ,1p ,2p 3)=⎪⎪⎪⎭⎫ ⎝⎛140004111, 则 P 1-=⎪⎪⎪⎭⎫ ⎝⎛---4416414030121. 于是有 A 100=P ⎪⎪⎪⎭⎫ ⎝⎛122100100P 1-=⎪⎪⎪⎭⎫ ⎝⎛-⋅-⋅-⋅---12412244023012122431100100100100100100100.7. (1)A I -λ=)1(2+λλ=D 3(λ), λI -A 有2阶子式172111----λ=λ-4λ-4不是D 3(λ)的因子, 所以D 2(λ)=D 1(λ)=1, A 的初等因子为λ-1, 2λ. A 的Jordan 标准形为J =⎪⎪⎪⎭⎫ ⎝⎛-000100001设A 的相似变换矩阵为P =(p 1,p 2,p 3), 则由AP =PJ 得 ⎪⎩⎪⎨⎧==-=23211pAp Ap p Ap 0 解出P =⎪⎪⎪⎭⎫ ⎝⎛-----241231111;(2) 因为),2()1()(23--=λλλD 1)()(12==λλD D ,故A ~J = ⎪⎪⎪⎭⎫ ⎝⎛200010011设变换矩阵为 P = (321,,p p p ), 则⎪⎩⎪⎨⎧=+==33212112p Ap p p Ap p Ap ⇒P =⎪⎪⎪⎭⎫ ⎝⎛---502513803 (3) ),2()1()(23-+=-=λλλλA I D ,1)(2+=λλD 1)(1=λD .A 的不变因子是,11=d ,12+=λd )2)(1(3-+=λλdA ~J =⎪⎪⎪⎭⎫ ⎝⎛--211 因为A 可对角化,可分别求出特征值-1,2所对应的三个线性无关的特征向量: 当λ=-1时,解方程组 ,0)(=+x A I 求得两个线性无关的特征向量,1011⎪⎪⎪⎭⎫ ⎝⎛-=p ⎪⎪⎪⎭⎫ ⎝⎛-=0122p当λ=2时,解方程组 ,0)2(=-x A I 得⎪⎪⎪⎭⎫ ⎝⎛-=1123p , P =⎪⎪⎪⎭⎫ ⎝⎛---101110221 (4) 因⎪⎪⎪⎭⎫ ⎝⎛---+=-41131621λλλλA I ~⎪⎪⎪⎭⎫ ⎝⎛--2)1(11λλ, 故A ~J =⎪⎪⎪⎭⎫⎝⎛10111 设变换矩阵为P =),,(321p p p , 则⎪⎩⎪⎨⎧+===3232211pp Ap p Ap p Ap 21,p p 是线性方程组 0=-x A I )(的解向量,此方程组的一般解形为 p =⎪⎪⎪⎭⎫ ⎝⎛+-t s t s 3 取⎪⎪⎪⎭⎫ ⎝⎛-=0111p , ⎪⎪⎪⎭⎫⎝⎛=1032p为求满足方程 23)(p p A I -=-的解向量3p , 再取 ,2p p = 根据 ⎪⎪⎪⎭⎫ ⎝⎛------t s t s 3113113622~⎪⎪⎪⎭⎫ ⎝⎛----t s t s s 00033000311 由此可得 s =t , 从而向量 T 3213),,(x x x =p 的坐标应满足方程s x x x -=-+3213取 T 3)0,0,1(-=p , 最后得P =⎪⎪⎪⎭⎫ ⎝⎛--010001131 8. 设 f (λ) =4322458-++-λλλλ. A 的最小多项式为 12)(3+-=λλλA m ,作带余除法得 f (λ) = (149542235-+-+λλλλ),)(λA m +1037242+-λλ, 于是f (A )=I A A 1037242+-=⎪⎪⎪⎭⎫ ⎝⎛----346106195026483. 9. A 的最小多项式为 76)(2+-=λλλA m , 设 f (λ)=372919122234+-+-λλλλ,则f (λ)=)()52(2λλA m ++2+λ. 于是 [f (A )]1-=1)2(-+I A .由此求出[f (A )]1-=⎪⎪⎭⎫ ⎝⎛-3217231 10. (1) λI -A =⎪⎪⎪⎭⎫ ⎝⎛---+41131621λλλ标准形⎪⎪⎪⎭⎫ ⎝⎛--2)1(00010001λλ, A 的最小多项式为 2)1(-λ; 2) )1)(1(+-λλ; (3) 2λ.11. 将方程组写成矩阵形式:⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛321321188034011d d d d d d x x x t x t x t x , ⎪⎪⎪⎭⎫ ⎝⎛=321x x x x , ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=t x t x t x t d d d d d d d d 321x , A =⎪⎪⎪⎭⎫ ⎝⎛----188034011 则有J = PA 1-P =⎪⎪⎪⎭⎫ ⎝⎛-100010011, .其中 P =⎪⎪⎪⎭⎫⎝⎛124012001. 令 x =P y , 将原方程组改写成 : ,d d Jy y=t则 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=+==3321211d d d d d d yty y y ty y t y 解此方程组得: y 1=C 1e t+C 2T e t, y 2=C 2e t, y 3=C 3et-. 于是x = P y =⎪⎪⎪⎭⎫ ⎝⎛++++++-t t t tt t t c )t (c c )t (c c t c c e e 24e 4e 12e 2e e 3212121.12. (1) A 是实对称矩阵. A I -λ=2)1)(10(--λλ, A 有特征值 10, 2, 2.当λ=10时. 对应的齐次线性方程组 (10I -A )x = 0的系数矩阵⎪⎪⎪⎭⎫ ⎝⎛--542452228~⎪⎪⎪⎭⎫ ⎝⎛000110102由此求出特征向量p 1=(-1, -2, 2)T, 单位化后得 e 1= (32,32,31--)T . 当λ=1时, 对应的齐次线性方程组 (I -A )x =0的系数矩阵⎪⎪⎪⎭⎫ ⎝⎛-----442442221~⎪⎪⎪⎭⎫ ⎝⎛-000000221 由此求出特征向量 p 2= (-2, 1, 0)T, p 3= (2, 0, 1)T. 单位化后得 e 2=(0,51,52-)T , e 3= (535,534,532)T. 令U =⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---53503253451325325231, 则 U 1-AU =⎪⎪⎪⎭⎫⎝⎛1110. (2) A 是Hermit 矩阵. 同理可求出相似变换矩阵U =⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---2121212i 2i 2i 21210, U 1-AU =⎪⎪⎪⎭⎫ ⎝⎛-22. 13. 若A 是Hermit 正定矩阵, 则由定理1.24可知存在n 阶酉矩阵U , 使得U HAU =⎪⎪⎪⎪⎪⎭⎫⎝⎛n λλλ21, i λ﹥0, i =1, 2, , n . 于是A = U ⎪⎪⎪⎪⎪⎭⎫⎝⎛n λλλ21U H= U ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛n λλλ 21U H U ⎪⎪⎪⎪⎪⎭⎫⎝⎛n λλλ21U H 令B = U ⎪⎪⎪⎪⎪⎭⎫⎝⎛n λλλ21U H 则 A =B 2.反之,当 A =B 2且B 是Hermit 正定矩阵时,则因Hermit 正定矩阵的乘积仍为Hermit 正定矩阵,故A 是Hermit 正定的.14. (1)⇒(2). 因A 是Hermit 矩阵,则存在酉矩阵U,使得U HAU = diag (n λλλ,,,21 )令x =Uy , 其中 y =e k . 则 x ≠0. 于是x H Ax = y H (U HAU ) y =k λ≧0 (k =1, 2,, n ).(2)⇒(3).A =U diag(n λλλ,,,21 )U H=U diag(n λλλ,,,21 )diag(n λλλ,,,21 )U H令 P =diag(n λλλ,,,21 )U H , 则 A =P H P .(3)⇒(1). 任取x ≠0, 有x H Ax = x H P HP x =22Px≧0.习 题 二1. 1x =01i 42i 1+++-++=7+2, 2x =1i)4i(4)2(i)1i)(1(2+-+-+-+=23,∞x =max {}1i 42i 1,,,-+=4.2. 当 x ≠0时, 有 x ﹥0; 当 x ﹦0时, 显然有 x =0. 对任意∈λC , 有x λ=x nk kk nk kk λξωλλξω==∑∑==1212.为证明三角不等式成立, 先证明Minkowski 不等式: 设 1≦p ﹤∞, 则对任意实数 x k ,y k (k =1, 2, , n )有pnk pk k y x 11)(∑=+≦∑∑==+nk ppk nk ppk y x 1111)()(证 当 p =1时,此不等式显然成立. 下设 p ﹥1, 则有∑=+nk pkk y x 1≦∑∑=-=-+++nk p kk k nk p kk k y x y y x x 1111对上式右边的每一个加式分别使用H ölder 不等式, 并由 (p -1)q =p , 得∑=+nk pkky x1≦qnk q p kk pnk pk qnk q p kk pnk p ky x y y x x11)1(1111)1(11)()()()(∑∑∑∑=-==-=+++=qnk p k k pnk pk pn k p ky x y x111111)]()()[(∑∑∑===++再用 qnk p k ky x11)(∑=+ 除上式两边,即得 Minkowski 不等式.现设任意 y =(n ηηη,,,21 )T ∈C n, 则有∑=+=+nk k k ky x 12ηξω=∑=+nk k k k 12)(ηξω≦∑=+nk k k k k 12)(ηωξω≦∑∑==+nk j k nk k k 1212()(ηωξω=y x +.3. (1) 函数的非负性与齐次性是显然的, 我们只证三角不等式.利用最大函数的等价定义:max (A , B ) =)(21b a b a -++ max (),b a y x y x ++≦max (b b a ay x y x ++,)=)(21b b a a b a b a y x y x y y x x --+++++ ≦)(21b a b a b a b a y y x x y y x x -+-++++ =)(21)(21b a b a b a b a y y y y x x x x -+++-++ =max ( b a x x ,)+max ( b a y y ,)(2) 只证三角不等式.k 1a y x ++k 2b y x +≦k 1a x +k 1a y +k 2b x +k 2b y =( k 1a x +k 2b x )+( k 1a y +k 2b y ) . 4. 218132i 453i 11m +=+++++++=A;66132i 453i 1222222F =+++++++=A ; 15m =∞A;=1A 列和范数(最大列模和)=27+;∞A =行和范数(最大行模和)=9 ;5. 非负性: A ≠O 时S1-AS ≠O , 于是 m1ASS A -=>0. A =O 时, 显然 A =0;齐次性: 设λ∈C , 则 λλλ==-m1)(S A S A m1ASS -=λA ;三角不等式: m11m1)(BSS AS S SB A S B A ---+=+=+≦B A BSS ASS +=+--m1m1;相容性: m11m 1)(BSASS S SAB S AB ---==≦m1m1BS S ASS --=A B .6. 因为I n ≠O , 所以n I >0.从而利用矩阵范数的相容性得:n n n I I I =≦n I n I ,即n I ≧1.7. 设 A =(A ij )∈C nn ⨯, x =∈ξξξT 21),,,(n C n, 且 A =ij ji a ,max , 则∑∑=ik kik Ax ξa1≦∑∑ikk ik a ξ=∑∑kiik k a ][ξ≦n A ∑kk ξ=∞mA 1x ;∑∑=ikkik Ax22ξa≦∑∑ikk ika2][ξ=∑∑ikka 22][ξ=n A 2x ≦n A =∞m A2x .8. 非负性与齐次性是显然的, 我们先证三角不等式和相容性成立. A =(a ij ), B =(b ij )∈Cnm ⨯,C =(c st )∈Cln ⨯且 A =ij ji a ,max , B =ij j i a ,max , C =st ts c ,max . 则M B A +=max {m ,n }ij ij ji b a +,max ≦max{m ,n })(max ,ij ij ji b a +≦max{m ,n }(A +B )=max{m ,n }A + max{m ,n }B =MM BA +;MAC= max{m ,l }∑k ktik ti c a,max≦max{m ,n }}{max ,∑kkt ik ti c a≦max{m ,n }}{max 22,∑∑⋅kkt kik ti c a (Minkowski 不等式)= max{m ,n }n AC ≦max{m ,n }max{n ,l }AC =MM C A .下证与相应的向量范数的相容性.设 x =∈ξξξT 21),,,(n C n, d =kmax {k ξ}, 则有∑∑=ikk ik a Ax ξ1≦∑∑i k k ik a ξ=∑∑ki ikka)(ξ≦∑kkna ξ= na∑kkξ≦max{m ,n }A∑kkξ=1Mx A;2Ax =∑∑ikkik a 2ξ≦∑∑ikk ik a 2)(ξ≦∑∑∑ikkk ika )(22ξ (H ölder 不等式)=∑∑∑⋅kk ikik a 22ξ≦mn A 2x≦max{m ,n }A 2x =2Mx A;}{max 1∑=∞=nk k ik iAxξa ≦∑=n k k ik ia 1}{max ξ≦}{max 22∑∑⋅kk kik ia ξ≦}max{22nd na i⋅=n AD ≦max{m ,n }AD =∞xA M .9. 只证范数的相容性公理及与向量2–范数的相容性. 设 A =(a ij )∈C nm ⨯, B =(b st )∈Cln ⨯,x =∈ξξξT 21),,,(n C n且 A =ij ji a ,max , B =st ts b ,max , 则∑=≤≤≤≤=nk kt ik lt m i AB11,1Gmaxb aml ≦}{max ,kt kik ti b a ml ∑≦}{max 22,∑∑⋅kkt kik ti b a ml (Minkowski 不等式)≦ml n ab =))((b nl a mn =GG BA .∑∑===m i nk kik Ax 1212ξa≦∑∑ikk ika2)(ξ≦∑∑∑⋅ikkk ik a )(22ξ (H ölder 不等式)≦∑∑⋅ikkna )(22ξ=mn A 2x=2G x A .10. 利用定理2.12得122H 2===nI UU U.11.A 1-=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---0110211214321 cond 1(A )=225255111=⋅=-AA ; cond ∞(A )=10251=⋅=∞-∞A A . 12.设x 是对应于λ的特征向量, 则A x x m m λ=.又设 v ⋅是C n上与矩阵范数⋅相容的向量范数,那么vm vm v mx A x x ==λλ≦v m x A因 v x >0, 故由上式可得 mλ≦mA ⇒λ≦m mA.习 题 三1. 2c λc λλ))(2(+-=-A I , 当c c 22)(==A ρ﹤1,即 21<c 时, 根据定理3.3, A 为收敛矩阵. 2. 令S)N (=∑=N)(k k A , )(lim N N S +∞→=S , 则 O S S A =-=-+∞→+∞→)(lim lim )1()()(k k k k k .反例: 设 A )(k =⎪⎪⎭⎫ ⎝⎛0001k , 则因 ∑+∞=01k k 发散, 故 ∑+∞=0)(k k A 发散, 但 )(lim k k A +∞→=O .3. 设 A =⎪⎪⎭⎫⎝⎛6.03.07.01.0, 则 )(A ρ≦=∞A 行和范数=0.9<1, 根据定理3.7,∑∞+=⎪⎪⎭⎫ ⎝⎛06.03.07.01.0k k=(I -A )1-=⎪⎪⎭⎫ ⎝⎛937432.4. 我们用两种方法求矩阵函数e A:相似对角化法. 22a λλ+=-A I , a -a i ,i =λ当 =λi a 时, 解方程组 (i a -A )x =0, 得解向量 p 1=(i, 1)T. 当 λ=-i a 时, 解方程组 (i a +A )x =0, 得解向量 p 2=(-i, 1)T.令P =⎪⎪⎭⎫⎝⎛-11i i , 则1-P =⎪⎪⎭⎫ ⎝⎛-i 1i 1i 21, 于是 e A=P ⎪⎪⎭⎫ ⎝⎛a -a i i e 00e 1-P =⎪⎪⎭⎫⎝⎛a a a -a cos sin sin cos . 利用待定系数法. 设e λ=(2λ+a 2)q (λ)+r (λ), 且 r (λ) = b 0+b 1λ, 则由⎩⎨⎧=-=+-aaa b b a b b i 10i 10ei e i ⇒b 0=cos a , b 1=a1sin a .于是e A=b 0I + b 1A =cos a ⎪⎪⎭⎫ ⎝⎛11+a 1sin a ⎪⎪⎭⎫ ⎝⎛-a a =⎪⎪⎭⎫ ⎝⎛-a a a a cos sin sin cos . 后一求法显然比前一种方法更简便, 以后我们多用待定系数法. 设f (λ) = cos λ, 或 sin λ则有⎩⎨⎧=-=+a -a b b aa b b sini i sini i 1010 与 ⎩⎨⎧=-=+a a b b aa b b i cos i i cos i 1010 由此可得⎪⎩⎪⎨⎧-==a a b b sini i 010 与 ⎩⎨⎧==0i cos 10b ab 故(a 2isini a )A =⎪⎪⎭⎫ ⎝⎛-0isini isini 0aa =sin A 与(cosi a )I =⎪⎪⎭⎫⎝⎛a acosi 00cosi =cos A .5. 对A 求得P = ⎪⎪⎪⎭⎫ ⎝⎛--013013111, 1-P =⎪⎪⎪⎭⎫ ⎝⎛-24633011061, 1-P AP =⎪⎪⎪⎭⎫ ⎝⎛-211根据p69方法二,e At =P diag (e t -,e t ,e t 2)1-P =⎪⎪⎪⎭⎫⎝⎛+--++---------tt t t tt t t t t t t t t e 3e 3e 3e 30e 3e 3e 3e 30e e 3e 2e e 3e 4e 661222tsin A =P diag{sin(-1),sin1,sin2}P 1-=⎪⎪⎪⎭⎫ ⎝⎛--01sin 601sin 6001sin 42sin 21sin 22sin 42sin 616. D 3(λ)=101011----λλλ=2)1(-λλ, D 2(λ)=D 1(λ)=1, A ~J =⎪⎪⎪⎭⎫⎝⎛000010011. 现设r (λ,t )=b 0+b 1λ+b 2λ2, 则有⎪⎩⎪⎨⎧==+=++1e 2e 021210b t b b b b b t t ⇒b 0=1, b 1=2e t -t e t -2, b 2= t e t -e t +1. 于是e t A =r (A , t ) = b 0I +b 1A +b 2A 2= I +(2e `t -t e t -2)⎪⎪⎪⎭⎫ ⎝⎛100100011+(t e t -e t+1)⎪⎪⎪⎭⎫⎝⎛100100111=⎪⎪⎪⎭⎫ ⎝⎛-+--tt e 001e 101e e 1e e t t t t t同理,由⎪⎩⎪⎨⎧=-=+=++1sin 2cos 021210b t t b b t b b b ⇒b 0=1, b 1=t sin t +2cos t -2, b 2=1-t sin t -cos t . 将其代入 cos A t =b 0I + b 1A + b 2A 2, 求出cos A t =⎪⎪⎪⎭⎫⎝⎛----t t t t t t t cos 001cos 10cos sin 11cos cos 7. 设 f (A ) =∑+∞=0k kA ka, S N=∑=Nk k A 0k a .则 f (A ) =N N S +∞→lim 并且由于(S N)T=T 0)(∑=Nk k kA a=∑=Nk k k A 0T )(a所以, f (A T )=T)(lim N N S +∞→=f (A )T.8, (1) 对A 求得P =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1111, 1-P =P , J =⎪⎪⎪⎪⎪⎭⎫⎝⎛1111111 则有e tA =P ⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛t t tt t tt ttt t t t t t t e e e e 2e e e 6e 2e 232e1-P =⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛t ttt t t tt te e e 2e 60e e e 200e e 000e 232t t t t t t tsin A t =P ⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---t t t t t t t t t t t t t t t t sin cos sin sin 2cos sin cos 6sin 2cos sin 2321-P =⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---t t t t t t t t t t t t t t t t sin cos sin 2cos 6sin cos sin 2sin cos sin 232cos A t = P ⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----t t t t t t t t t t t t t t t t cos sin cos cos 2sin cos sin 6cos 2sin cos 232P=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----t t t t t t t t t t t t t tt tcos sin cos 2sin 60cos sin cos 200cos sin 000cos 232 (2) 对A 求出P =1-P =⎪⎪⎪⎪⎪⎭⎫⎝⎛0100100000100001, J =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--010212 则有e At=P ⎪⎪⎪⎪⎪⎭⎫⎝⎛---11e e e 222t t tt t1-P =⎪⎪⎪⎪⎪⎭⎫⎝⎛---100010000e 000e e 222t t t t tsin A t =P ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--002sin 2cos 2sin t t t t t P 1-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--0000000002sin 0002cos 2sin t t t t tcos A t =P ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1012cos 2sin 2cos t t t t P 1-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛10000100002cos 0002sin 2cos t t t t 9. (1) sin 2A +cos `2A =[)e (e i 21i i A A --]2=[)(e 21i i A A e -+]2=)e e e (e 41)e e e(e 41i 2i 2i 2i 2OO A A O O A A ++++--+--- =e O=I(2) sin(A +2πI )=sin A cos(2πI )+cos A sin(2πI )=sin A [I -!21(2πI )2+!41(2πI )4-…]+cos A [2πI -!31(2πI )3+!51(2πI )5-…] = sin A [1-!21(2π)2+!41(2π)4-…]I +cos A [2π-!31(2π)3+!51(2π)5-…]I=sin A cos2π+cos A sin2π(3)的证明同上.(4) 因为 A (2πi I )=(2πi I )A ,所以根据定理3.10可得 eIA i π2+=e AeIπi 2=e A[I +(2πI )+!21(2πi I )2+!31(2πi I )3+…] =e A {[1-!21(2π)2+!41(2π)4-…]+i[2π-!31(2π)3+!51(2π)5-…]}I=e A{cos2π+isin2π}I=e A此题还可用下列方法证明:e I A πi 2+=e ⋅A e I i π2=e ⋅AP ⎪⎪⎪⎪⎪⎭⎫⎝⎛i π2iπ2πi 2e e e P 1-=e ⋅A PIP 1-=e A用同样的方法可证: e I A πi 2-=e A e Iπi 2-. 10. A T=-A , 根据第7题的结果得 (e A)T=eTA =eA-, 于是有e A(e A)T=e Ae TA =e AA -=e O=I11. 因A 是Herm(i A )H =-i A H=-i A , 于是有e A i (e A i )H =e A i e A i -=e O =I 12. 根据定理3.13, A1-t t A e d d =e At, 利用定理3.14得 ⎰t A 0d e ττ=⎰-t A A 01d e d d τττ=A 1-τττd e d d 0A t ⎰=A 1-(e -At I ).13. t d dA (t ) =⎪⎪⎭⎫ ⎝⎛---t t t t sin cos cos sin , td d (det A (t ))=t d d (1)=0, det(t d dA (t ))=1, A 1-(t )=⎪⎪⎭⎫ ⎝⎛-t t t t cos sin sin cos , t d d A 1-(t )=⎪⎪⎭⎫ ⎝⎛---t t t t sin cos cos sin14. ⎰t A 0d )(ττ=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎰⎰⎰⎰⎰⎰-00d 30d e 2d e d d e d e 002002002t t t tt t τττττττττττττ=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--+---002301e e1311e e )1(e 212232t t t t t t t t 15. 取 m =2, A (t )=⎪⎪⎭⎫⎝⎛t t t 02, 则 A 2(t )=⎪⎪⎭⎫ ⎝⎛+22340t t t t , t d d (A (t ))2=⎪⎪⎭⎫ ⎝⎛+t t t t 2023423≠2A (t )t d d A (t )=⎪⎪⎭⎫ ⎝⎛+t t t t 2022423. 困为++==--21)]()[(d d )()]()[(d d )]()()([d d )]([d d m m A A A A A A A A A t t tt t t t t t t t t t m +)(d d )]([1t tt A A m - 所以当(t d d A (t ))A (t )=A (t )t d dA (t )时, 有)(d d)]([)(d d )]([)(d d )]([)]([d d 111t tt t t t t t t t t A A A A A A A m m m m ---++= =m [A (t )])(d d 1t tA m - 16. (1) 设B =(ij b )n m ⨯, X =(ij ξ)m n ⨯, 则 BX =(∑=nk kj ik1ξb)m m ⨯,于是有tr(BX )=∑∑∑===++++nk km mk nk kj jk nk k k11111ξξξb b bijBX ξ∂∂)tr(=ji b (i =1,2,…,n ;j =1,2,…,m )⎪⎪⎪⎭⎫ ⎝⎛=mn n m BX X b b b b 1111)(tr(d d=T B 由于 BX 与 TT T )(B X BX =的迹相同,所以T T T ))(tr(d d ))(tr(d d B BX X B X X == (2) 设A =(ij a )n n ⨯,f=tr(AX X T), 则有⎪⎪⎪⎭⎫ ⎝⎛=nm mn X ξξξξ1111T ,AX =⎪⎪⎪⎪⎪⎭⎫⎝⎛∑∑∑∑k km nk kk nk km kkk k ξξξξa a aa1111f =∑∑∑∑∑∑++++lkkm lk lm lkkj lk lj lkk lk l ξξξξξξa a a11)]()([][∑∑∑∑∑∂∂⋅+⋅∂∂=∂∂=∂∂k kj lk lk ij lj kj lk ij lj l k kj lk lj ij ij ξξξξξξξξξξa a a f =∑∑+klj li kkjik ξξa amn ij X ⨯⎪⎪⎭⎫ ⎝⎛∂∂=ξf f d d =X A A X A AX )(T T +=+ 17. 设A = (ij a )m n ⨯, 则 F (x )=(∑∑∑===nk kn k n k k nk k k1211,,,a a a 1k ξξξ),且A d F F F x F nn n n n n n =⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=a a a a a a a a a 21222211121121d d d d d d d ξξξ 18. ()⎪⎪⎪⎭⎫⎝⎛---------=='t t tt t t tt t t t t t t t t tt AtAtA 222222222e 4e 3e 3e 6e 3e 6e 2e e e 4e e 2e 2e e e 2e e 4ee在上式中令t =0, 则有A =⎪⎪⎪⎭⎫ ⎝⎛---=133131113e OA19. A =⎪⎪⎪⎭⎫ ⎝⎛---502613803, x (0)=⎪⎪⎪⎭⎫⎝⎛111, A 的最小多项式为 2)1()(+=λλϕ. 记f (λ)=t λe ,并设 f (λ)=g(λ))(λϕ+)(10λb b +, 则⎩⎨⎧==---tte e 110t b b b ⇒ tt --=+=e ,)1(10t b e t b 于是⎪⎪⎪⎭⎫ ⎝⎛--+=++=---t t t t t t t t 41026138041e e e )1(e t t t AtA I , x (t )=Ate x (0)=⎪⎪⎪⎭⎫ ⎝⎛-++-t t t 6191121e t20. A =⎪⎪⎪⎭⎫ ⎝⎛--101024012, f (t ) =⎪⎪⎪⎭⎫ ⎝⎛-1e 21t , x (0)=⎪⎪⎪⎭⎫⎝⎛-111, =)(λϕdet (λI -A)=23λλ-. 根据O A =)(ϕ,可得; 252423,,A A A A A A ===,….于是23232)!31!21()(!31)(!21)(e A A I A A A I At ++++=++++=t t t t t t=2)1(e A A I t t t --++=⎪⎪⎪⎭⎫⎝⎛---++--t t t e 1e e 210124021t t t t tt x (t )=⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛+=+⎰⎰-t t t t f e )1(11]02111[e ]d 021)0([]d )(e )0([e 0At tAt tA Atx e x ττττ习 题 四(1) Doolite 分解的说明,以3阶矩阵为例:11r 12r 13r 第1框 21l 22r 23r 第2框 31l 32l 33r 第3框计算方法如下:(ⅰ) 先i 框,后i +1框,先r 后l .第1框中行元素为A 的第1行元素;(ⅱ)第2框中的j r 2为A 中的对应元素j a 2减去第1框中同行的21l 与同列的j r 1之积.第3框中的33r 为A 中的对应元素33a 先减去第1框中同行的31l 与同列的13r 之积,再减去第2框中同行的32l 与同列的23r 之积;(ⅲ)第2框中的32l 为A 中的对应元素32a 先减去第1框中同行的31l 与同列的12r 之积,再除以22r . 计算如下:1 3 02 -3 0 2 2 -6A =⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛600030031122012001 (2)Crout 分解的说明,以3阶矩阵为例:11l 12u 13u 第1框 21l 22l 23u 第2框 31l 32l 33l 第3框(ⅰ) 先i 框,后i +1框.每框中先l 后r .第1框中的列元素为A 的第1列的对应元素; (ⅱ) 第2框中的2i l 为A 中对应元素2i a 减去第1框中同行的1i l 与同列的12u 之积;(ⅲ) 第2框中的23u 为A 中的对应元素23a 减去第1框中同行的21l 与同列的13u 之积,再除以22l .第3框中的33l 为A 中的对应元素33a 先减去第1框中同行的31l 与同列的13u 之积,再减去第2框中同行的32l 与同列的23u 之积.计算如下:1 3 02 -3 02 -6 -6A =⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---100010031662032001 2. 先看下三角矩阵的一种写法:⎪⎪⎪⎭⎫⎝⎛333231222111000a a a a a a =⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛33221122321131112100000101001a a a a a a a a a , ii a ≠0 对本题中的矩阵A 求得Crout 分解为A =⎪⎪⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--1002105452115240512005利用下三角矩阵的写法对上面的分解变形可得A =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--10021054521100051000512540152001=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--100210545211000510005100051000512540152001=⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--10052510545251525405152005 3.对A 的第1列向量)1(β, 构造Householder 矩阵1H 使得=)1(1βH 12)1(e β, 31C e ∈⎪⎪⎪⎭⎫ ⎝⎛=010)1(β, ⎪⎪⎪⎭⎫ ⎝⎛-=-01112)1()1(e ββ, u =⎪⎪⎪⎭⎫ ⎝⎛-=--01121212)1()1(12)1()1(e e ββββ⎪⎪⎪⎭⎫ ⎝⎛=-=1000010102T1uu I H , ⎪⎪⎪⎭⎫⎝⎛=2301401111A H , ⎪⎪⎭⎫ ⎝⎛=23141A对1A 的第1列向量⎪⎪⎭⎫⎝⎛=34)2(β, 类似构造Householder 矩阵2H :⎪⎪⎭⎫ ⎝⎛-=--=3110122)2)2(12)2()2ββββe u , 21C e ∈, ⎪⎪⎭⎫ ⎝⎛-=-=4334512T 22uu I H ⎪⎪⎭⎫⎝⎛-=102512A H令12001H H H ⎪⎪⎭⎫⎝⎛=, 则有 ⎪⎪⎪⎭⎫⎝⎛-=100250111HA =R 并且⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛==---1002501115453000153540001001T2T 112111R H H R H H R H A =QR4. 对A 的第1列向量⎪⎪⎪⎭⎫ ⎝⎛=202)1(β, 构造Givens 矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=210210102102113T ,⎪⎪⎪⎪⎭⎫⎝⎛=0022)1(13βT , ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=1132221210220232322A O A T 对1A 的第1列向量⎪⎪⎪⎭⎫⎝⎛-=212)2(β, 构造 ⎪⎪⎪⎪⎭⎫⎝⎛-=3223131322~12T ,⎪⎪⎪⎭⎫ ⎝⎛=023~)2(12βT , ⎪⎪⎪⎪⎭⎫⎝⎛=34023723~112A T 令 ⎪⎪⎭⎫ ⎝⎛=12T12~1T O O T , 则有 ⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==34002372302323221312R A T T . 于是 QR R T T A =⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--==340023723023232232231213123403223121H13H 12 5. 设A =),,(i i 0i 0i 0i 1321ααα=⎪⎪⎪⎭⎫ ⎝⎛----, 对向量组321,,ααα施行正交化, 令⎪⎪⎪⎭⎫ ⎝⎛--==0i 111αβ, ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎪⎭⎫ ⎝⎛=-=i 212i 0i 12i i 0i ],[],[1111222ββββααβ,⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛--=--=323i232i 212i 3i 0i 1211i 0],[],[],[],[222231111333ββββαββββααβ于是⎪⎪⎪⎩⎪⎪⎪⎨⎧++=+-==3213212113i 212i βββαββαβα写成矩阵行式K ),,(1003i 10212i 1),,(),,(321321321ββββββααα=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----=32632316i 203i 612i 316i 21),,(321βββ 最后得A =K ⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----32632316i 203i 612i 316i 21=⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----32006i 630212i 2316i 203i 612i 316i 21=QR 6. 令⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-==10005152********T T 则⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-=011000520550114022011000515*******A T 再令⎪⎪⎪⎪⎪⎭⎫⎝⎛-==305061010610305132T T , ⎪⎪⎪⎪⎪⎭⎫⎝⎛-=3010305000061061612A T T 最后令⎪⎪⎪⎭⎫ ⎝⎛=0101000013T , R A T T T =⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-=0030103050610616123A =⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---=003010305061061603056151302625230161H3H 2H 3R T T T =QR 7.=)1(β(0, 1)T , 12)1(=β, u =2121)1(1)1(=--e e ββ(-1, 1)T, H 1=⎪⎪⎭⎫⎝⎛=-01102T 2uu I , H =⎪⎪⎭⎫ ⎝⎛1001H 则有HAH T=⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛010100001111210121010100001 =⎪⎪⎪⎭⎫ ⎝⎛--120111211, H 是Householder 矩阵. 同理, 对)1(β, 取 c =0, s =1, T 12=⎪⎪⎭⎫⎝⎛-0110, T =⎪⎪⎭⎫⎝⎛12001T , 则 ⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛-=='-0101000011112101210101000011TAT T TA=⎪⎪⎪⎭⎫⎝⎛---120111211, T 是Givens 矩阵. 8. 对 ⎪⎪⎭⎫ ⎝⎛=1612)1(β, 计算u =⎪⎪⎭⎫ ⎝⎛-=--2151202021)1(1)1(e e ββ, H =I -2uu T=⎪⎪⎭⎫ ⎝⎛-344351 令 Q =⎪⎪⎭⎫⎝⎛H 001, 则⎪⎪⎪⎭⎫ ⎝⎛=075075600200200T QAQ同理,对)1(β,为构造Givens 矩阵,令c =53, s =54, ⎪⎪⎪⎪⎭⎫⎝⎛-=5354545312T ,则 当⎪⎪⎭⎫⎝⎛=12001T T 时,='T TA ⎪⎪⎪⎭⎫ ⎝⎛--075075600200200.8. (1) 对A 施行初等行变换⎪⎪⎪⎭⎫ ⎝⎛----100424201011200010321~⎪⎪⎪⎪⎭⎫ ⎝⎛---142000002102121100111201 S=,1420210011⎪⎪⎪⎪⎭⎫ ⎝⎛-- A =⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛-2121101201422021(2) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------10001111010011110010111100011111~⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----110000000011000002102111100210210001 S=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---11000011021021021021, A =⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----1110000111111111 (3)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1000126420100632100101264200016321~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---10100000010100000011000000016321 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=1010010100110001S , ()63212121⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=A 10. (1) ⎪⎪⎪⎭⎫ ⎝⎛=000000005TA A 的特征值是5,0,0. 分别对应特征向量321,,e e e ,从而V=I,),(11p V = ∑=(5), 11AV U =∑1-=⎪⎪⎭⎫ ⎝⎛2151. 令,12512⎪⎪⎭⎫⎝⎛-=U ()21U U U =, 则 I U A ⎪⎪⎭⎫⎝⎛=000005(2)⎪⎪⎭⎫⎝⎛=2112T A A 的特征值是,,1321==λλ对应的特征向量分别为TT11,11⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛.于是 ∑=⎪⎪⎭⎫ ⎝⎛1003, ⎪⎪⎪⎪⎭⎫ ⎝⎛-=21212121V =1V , 11AV U =∑1-=⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-06221612161 取 ⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=3131312U , 构造正交矩阵()21U U U ==⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---31062312161312161 ‘所以,A 的奇异值分解为T 001003V U A ⎪⎪⎪⎪⎭⎫ ⎝⎛=11. 根据第一章定理1.5, A A H的特征值之和为其迹,而由第二章2.7 F -范数的定义A A A A AHH2F)tr(==的特征值之和=∑=ri i 12σ习 题 五1.设x =T 21),,,(n ηηη 为对应于特征值λ的单位特征向量,即(QD )x =λx两边取转置共轭:H H H H x Q D x =与上式左乘得2HH λ=Dx D x即 22222221212n n ηηηd d d λ+++= ,由此立即有2min i id ≤2λ≤2max i id从而 i d i min ≤λ≤i d imax .后一不等式的另一证明:根据定理2.13,λ≤)(QD ρ≤2QD i d im ax 最大特征值的H 22.11定理==D D D2. A 的四个盖尔园是 1G : 9-z ≤6, 2G : 8-z ≤2, 3G : 4-z ≤1, 4G : 1-z ≤1.由于4G 是一个单独的连通区域,故其中必有一个实特征值. 321G G G ⋃⋃是连通区域,其中恰有三个特征值,因而含有一个实特征值 .3. A 的四个盖尔园:1G 1-z ≤2713, :2G 2-z ≤2713, :3G 3-z ≤2713, :4G 4-z ≤2713 是互相隔离的,并且都在右半平面,从而每个盖尔园中恰有一个特征值且为正实数.4.设 =λβαi +为A 的待征值,则有盖尔园k G ,使得k G ∈λ.若α≤0, 则kk a -α≤βαi )(+-kk a ≤k R故 kk a +-)(α≤k R ,即 kk a ≤α+kk R ≤kk R , 这与A 是严格对角占优的条件矛盾.5. (1)当两个盖尔园的交集中含有两个特征值时; (2) 当两个盖尔园相切且切点是A 的单特征值时.6. A 的盖尔园 2:1-z G ≤3, 10:2-z G ≤2, 20:3-z G ≤10. 因1G 是与32G G ⋃分离 的,故1G 中恰有一个实特征值∈1λ[-1, 5].A 的列盖尔园 :'1G 2-z ≤9, 10:'2-z G ≤4, 20:'3-z G ≤2. 因'3G 是与'2'1G G ⋃分离 的,故 '3G 中恰有一个实特征值∈3λ[18, 22].选取 D =diag(1, 1,21), 则 1-DAD 的盖尔园 ''G 1 : 2-z ≤4, :''2G 10-z ≤3, :''3G 20-z ≤5. 这三个盖尔园是相互独立的,故必然有∈1λ[-2, 6], ∈2λ[7, 13], ∈3λ[15, 25]与上面所得的结果对照可知利用Gerschgorin 定理,特征值的最隹估计区间为∈1λ[-1, 5], ∈2λ[7, 13], ∈3λ[18, 22] 7. 因为det(λB -A )=)23)(2(422+-=----λλλλλλ所以广义特征值为1λ=2,2λ=-32.分别求解齐次线性方程组0=-x A B )(1λ , 0=-x A B )(2λ可得对应于1λ与2λ的特征向量分别为⎪⎪⎭⎫⎝⎛121k (01≠k ), ⎪⎪⎭⎫ ⎝⎛-122k (02≠k ) 8. 先证明一个结果:若A 是Hermit 矩阵,n λλ,1分别是A 的最大、最小特征值,则)(max )(max 112x R x R x x =≠==λ, )(max )(max 12x R x R =≠==x x n λ事实上,Ax x x x x Axx x x x Axx x x x x H 1H 22H 220HH 002max 11max max )(max =≠≠≠===x R 下证1λ>1μ,n λ>n μ. 令 Q =A -B , 则)(max max H H 1H 1122Qx x Bx x Ax x x x +====λ>Bx x x H 12max ==1μ( Q 正定,Qx x H>0 )同理可证n λ>n μ.现在设 1<s <n , 则根据定理5.10及上面的结果,有)max(min max min H H H 1021Qx x Bx x Ax x x x P s +====λ>s x x P Bx x μ===H 1021max min9. 显然,A B 1-的特征值就是A 相对于B 的广义特征值. 设为n λλλ,,,21 且j j j Bq Aq λ=, 0≠j q , j =1, 2, …,n其中 n q q q ,,,21 是按B 标准正交的广义特征向量. 当)(1A B -ρ<1时,对任意 x =0≠+++n n q q q c c c 2211)()(2211HH 22H 11H n n n n q q q A q q q Ax x c c c c c c ++++++==))((222111HH 22H 11n n n n n Bq Bq Bq q q q λλλc c c c c c ++++++ =2222211nn c c c λλλ+++≤i iλmax )(22221n c c c ++⋅=Bx x A B H 1)(-ρ<Bx x H反之,若对任意 x ≠0, Ax x H<Bx x H 成立,并且)(1A B -=ρλ, Bq Aq λ=,0≠q ,则取 x=q , 于是有λ=Aq q H <1H =Bq q10. 若λ是BA 的特征值,q 是对应于λ的特征向量,即(BA )q =λq =λIq由此可知,λ是BA 的相对于单位矩阵I 的广义特征值 ,因此BAx x Ix x BAxx x R BA x x I x H 1H H 111222max max )(max )(======λ=)(max H H 12Ax Bxx x x =≤)(max )(max H1H 122Ax x Bx x x x ===)()(11A B λλ同理)(min )(min )(H H 1122Ax Bxx x x R BA x I x n ====λ≥)(min )(min H 1H 122Ax x Bx x x x ===)()(A B n n λλ11. 由于x ≠0时,12)()(==x x R x R ,从而5.24式等价于}0,1)(min{max H 22)(2===-⨯∈x P x x R r n n P r C λ我们约定,下面的最小值都是对12=x来取的. 令x =Qy , 则y y Ax x x R Qy P x P x P ΛH H H2H 2H 2min min )(min 0===== 由于 nr n Q P ⨯-∈)(H 2C, 则在齐次线性方程组 0=Qy P H2中,方程的个数小于未知量的个数,根据 Cramer 法则,它必有非零解. 设),,,,0,,0(~1n r r y ηηη +=,(1~2=y )为满足方程的解(容易证明这种形式的解必存在),则)(min ~min 22112~H ~H 2H 2n n r r r r y Q P y Q P y y ηληληλ ++=++==0Λ≤r λ注意到 ⊆==}1~,~~{2H 2y y Q P y 0}1,{2H 2==y Qy P y 0,从而)(min H 2x R x P 0==)(min H 2y R Qy P 0=≤y y y R y Q P y Q P ΛH ~~~min )~(min H 2H 20===≤r λ 特别地,取),,(12n r q q P +=时,根据定理5.9)(min H 2x R x P r 0==λ故(5.24)式成立.12. 我们约定:以下的最小值是对单位向量来取的,即证},1)(min{max H 22)(20C ===-⨯∈Bx P x x R r n n P r λ成立. 令 x =Qy , 则有y y x R BQy P B Bx P ΛH 0H 2H2min )(min === 设齐次线性方程组 0=BQy P H 2有形如 1~),,,,,0,,0(~21==+y y n r r ηηη 的解(不难证明这样的解一定存在),则因 })({}~)(~{H 2H 200=⊆=y BQ P y y BQ P y所以)(min H 2x R B BxP ≤22112H ~~~min H 2n n r r r r y BQ P y y ηληληλ+++=++= Λ0≤r λ特别地,取 ),,,(21H 2n r r q q q P ++=时,根据定理5.12可得r B Bx P x R λ==)(min H 20由此即知(5.44)成立.习 题 六求广义逆矩阵{1}的一般方法: 1)行变换、列置换法利用行变换矩阵S 和列置换矩阵P , 将矩阵A 化成SAP =⎪⎪⎭⎫⎝⎛O O K I r则S L OO I P A r⎪⎪⎭⎫⎝⎛=)1(, 其中L 可取任意矩阵; 2)标准形法利用行、列的初等变换将A 化成标准形SAT =⎪⎪⎭⎫ ⎝⎛O OO I r 则S L L L I T Ar ⎪⎪⎭⎫⎝⎛=222112)1(, 其中 ij L 为任意适当阶的矩阵. 3) 行变换法利用行变换将A 化成SA =⎪⎪⎭⎫⎝⎛⨯-⨯n r m n r O D )(。

第8课三国至隋唐的文化1.下面是儒家思想在古代的发展情况示意图。
下列对abcd四处出现起伏的原因分析正确的是()A.a处处于低潮受西汉尊崇儒术的影响B.b处处于高潮是受秦朝焚书坑儒的推动C.c处处于低潮是受魏晋南北朝时期佛、道思想的冲击D.d处处于高潮是受明清时期批判思想的推动【答案】C【解析】本题是单类型单项选择题。
据题干设问词,可知这是推断题。
据题干时间信息可知准确时空是封建社会(中国)。
依据材料并结合所学知识可知,c处处于低潮是受魏晋南北朝时期佛、道思想的冲击,C 项正确;a处于低潮受秦朝焚书坑儒的影响,排除A项;b处处于高潮受汉武帝时期罢黜百家,独尊儒术的影响,排除B项;d处处于高潮是受宋明理学的影响,排除D项。
故选C项。
2.东晋南朝时期,社会上逐渐形成了隐逸的文化精神风貌:游离于政治,慕尚隐逸;游离于现世、遁入空门;游离于礼法,注重性情;游离于国家,推崇个体等。
这一状况()A.促使佛道思想成为主流思想B.源于封建统治者的大力提倡C.有利于文学艺术的推陈出新D.反映出南北社会发展差距缩小【答案】C【解析】本题是多类型单项选择题。
据本题题干的提示词,可知这是本质题、原因题、影响题。
据本题时间信息可知准确时空是:魏晋(中国)。
据本题材料信息得出主要结论:魏晋时期的文化发展受到佛道影响,出现一种有别于秦汉文化精神的新风貌,这有利于文学艺术推陈出新,C项正确。
据材料“游离于政治,慕尚隐逸;游离于现世、遁入空门;游离于礼法,注重性情;游离于国家,推崇个体等。
”结合所学可知,魏晋时期佛道盛行,但仍不是主流思想,排除A项;思想的发展源于经济的发展,封建统治者提倡不是根源,排除B项;材料体现的是南朝出现文化精神风貌特点,南北社会发展的差距缩小与材料表述不一致,排除D项。
故选C项。
3.唐高祖以老子出函谷关的传说为基础,认为老子乃陇西李氏先祖,要求全国各地大修老子庙并亲自主持拜祭老子的典礼。
唐太宗也曾以政令、诏书等形式提高道教的地位。

第三单元消费者行为理论1.一个消费者想要一单位X商品的心情甚于想要一单位Y商品,原因是()。
A.商品X的效用与价格相比的性价比要比Y商品的高B.商品X的价格较低C.商品X紧缺D.商品X是满足精神需要的【答案】A【解析】效用就是消费者消费物品或劳务所获得的满足程度,并且这种满足程度纯粹是一种消费者主观心理感觉。
若消费者想要一单位X商品的心情甚于想要一单位Y商品,说明X商品的效用与价格相比的性价比更高。
2.经济学分析的一个假设条件是消费者偏好不变,因此,对在同一地方的同一个消费者来说,同样数量的商品总是提供同量的效用。
()A.正确B.错误C.可能正确也可能错误【答案】A【解析】在消费者偏好不变的前提下,对同一个消费者,同样的商品总能提供同样的效用。
3.总效用曲线达到顶点时,()。
A.边际效用曲线达到最大点B.边际效用为零C.边际效用为正【答案】B【解析】边际效用是总效用曲线的斜率值,当边际效用大于零时,总效用是递增的。
由于边际效用递减,所以,当边际效用为零时,总效用达到最大值。
4.对于一种商品,消费者想要有的数量都已有了,这时,()。
A.边际效用最大B.边际效用为零C.总效用为零【答案】B【解析】消费者不能再通过增加单位商品的消费来增加总效用,所以总效用达到了最大,故此时的边际效用为零。
5.序数效用论认为,商品效用的大小()。
A.取决于它的使用价值B.取决于它的价格C.不可比较D.可以比较【答案】D【解析】序数效用论者认为,效用仅是次序概念而非数量概念。
在分析商品效用时,通过第一、第二、第三等序数来说明各种商品效用的大小,以此作为消费者选择商品的根据,效用大小之间可以比较。
6.无差异曲线的形状取决于()。
A.消费者偏好B.消费者收入C.所购商品的价格D.商品效用水平的大小【答案】A【解析】无差异曲线是表示能给消费者带来同等效用的两种商品的不同组合的曲线,是用来表示消费者偏好相同的两种商品的所有组合的。

厦大经济学考研参考教材介绍文档编制序号:[KK8UY-LL9IO69-TTO6M3-MTOL89-FTT688]2017厦大经济学考研参考教材介绍聚英厦大考研网为同学们整理了经济学考研备考参考教材,让同学们在备考时有的放矢的复习。
简单来说,经济学教材可以分为初级、中级和高级。
大致分类为:初级教材:高鸿业《西方经济学(微观部分)》、尹伯成《微观经济学简明教程》、高鸿业《西方经济学(宏观部分)》、曼昆《经济学原理(宏观经济学分册)》中级教材:平狄克《微观经济学》、范里安《微观经济学:现代观点》、曼昆《宏观经济学》、多恩布什《宏观经济学》高级教材:尼科尔森《微观经济理论基本原理与扩展》、平新乔《微观经济学十八讲》政治经济学两本经典教材:逄锦聚《政治经济学》、宋涛《政治经济学教程》,无所谓初级、中级和高级分类。
当然,除了上述教材外,还有些教材也很经典,但是相对来说,上述几本教材应用特别广。
那么,厦门大学经济学考研具体参考哪些教材呢?同学们可以参考【厦大硕招参考书目】一、微观经济学1.高鸿业《西方经济学(微观部分)》就该书而言,以下几个问题需予以注意:(1)第六版教材于2014年7月出版,预期一些高校依然会将第五版教材(甚至第四版)列为2017年考研参考书目。
复习过程中,适当了解第六版教材变动地方(主要是完全竞争市场的福利),有针对性的复习。
(2)对于跨专业学生,以及专业基础不扎实的学生,即使所报院校未将该书列为参考书目,参考书目为中级微观教材,如范里安《微观经济学:现代观点》,建议在第一轮复习时将该书作为重要参考书目。
(3)该书的难度为中级偏初级,而名校要求达到的层次为中级,甚至有些名校要求难度为中级偏高级,因此复习时,特别是第二轮复习时,应该参考中级微观经济学教材,如范里安《微观经济学:现代观点》或尼科尔森《微观经济理论基本原理与扩展》。
(4)对于各章后面的“结束语”,要点归纳部分一定要看,有些部分甚至容易出考题。

国开(山东)00852《简明中国古代史》形成性考核一复习资
料答案
简明中国古代史-形成性考核一作业资料答案
说明:每学期的课程题目都可能更换,请认真核对是您需要的题目后再下载!
【题目】
【判断题】夏朝最有代表性的手工业是青铜手工业。
对
错
正确的答案是“对”。
【题目】
【判断题】周武王灭商标志了我国古代史上的奴隶制时代基本结束。
对
错
正确的答案是“对”。
【题目】
【判断题】春秋时期首先称霸的诸侯是晋文公。
对
错
正确的答案是“错”。
【题目】
【判断题】商鞅变法是战国时期各国改革中最彻底的改革。
对
错
正确的答案是“对”。
【题目】
【判断题】《诗经》是我国最早的一部诗集。
对
错
正确的答案是“对”。
【题目】
【判断题】刘邦在创建西汉王朝时,就大刀阔斧改革政治制度,以建立他的统治。
对
错
正确的答案是“错”。
【题目】
【判断题】两汉时期,哲学的唯物主义代表人物是西汉的董仲舒。
对
错。

11古代汉语课后习题答案练习二九、下列句子中加点的词或词组,在古代汉语和现代汉语中词性、意义和用法有什么不同?1.儿能骑羊引弓射鸟鼠,少长则射狐菟。
(《汉书·匈奴传》)少:古义为稍,程度副词;今义为少,形容词。
2.子尾多受邑而稍致诸君。
(《左传·昭公十年》)稍:古义为逐渐,时间副词;今义为略微,程度副词。
3.纣贵为天子,死曾不若匹夫。
(《史记·淮南王传》)曾:古义为竟然,情态副词;今义为曾经,时间副词。
4.不可,直不百步耳。
(《孟子·梁惠王上》)直:古义为只、仅,范围副词;今义为不弯曲,形容词。
5.齐因乘胜尽破其军。
(《史记·孙膑》)因:古义为就,副词;今义为因为,连词。
6.骞从月氏至大夏,竟不能得月氏要领。
(《汉书·张骞传》)竟:古义为最终,时间副词;今义为竟然,情态副词。
7.匈奴匿其壮士肥牛马,但见老弱及羸畜。
(《史记·刘敬传》)但:古义为只,范围副词;今义为但是,转折连词。
8.献公说,曰:“璧则犹是也。
虽然,马齿亦益长矣。
”(《韩非子·十过》)虽然:古义为虽然如此,词组;今为让步连词。
按:教材引文误“璧”为“壁”,今正。
十、阅读下面一段短文,说明文中“以”的词性、意义和用法:古代汉语课后习题答案08古代汉语 课后习题答案08 2 2 秦既解邯郸围,而赵王入朝,使赵郝约事于秦,割六县而媾。
虞卿谓赵王曰:“秦之攻王也,倦而归乎?王以其力尚能进,爱王而弗攻乎?”王曰:“秦之攻我也,不遗余力矣,必以倦而归也。
”虞卿曰:“秦以其力攻其所不能取,倦而归,王又以其力之所不能取以送之,是助秦自攻也。
来年秦复攻王,王无救矣。
”王以虞卿之言告赵郝。
赵郝曰:“虞卿诚能尽秦力之所至乎?诚知秦力之所不能进,此弹丸之地弗予,令秦来年复攻王,王得无割其内而媾乎?”(《史记·平原君虞卿列传》)这段文字中共有六个“以”字,分别解释如下:1.王以其力尚能进,爱王而弗攻乎?以,动词,认为,在句中作谓语。

人教版八年级地理下册第八章《西北地区》练习题(含答案)一、选择题浙江是中共一大召开之地,感动中国人物樊锦诗的家乡也在这里。
作为中共党员,她发扬“红船精神”,植根大漠研究石窟艺术,努力打造“数字敦煌”,为保护这一世界文化遗产做出杰出贡献,被誉为“敦煌女儿”。
读下图,完成下面小题。
1.樊锦诗的家乡()A.位于珠江三角洲,地势低平B.为温带季风气候,降水丰富C.河、湖众多,水运十分便利D.土壤肥沃,农耕文明出现晚2.樊锦诗潜心研究的敦煌文物得以长期保存,其自然原因主要是这里()A.气候干旱,风沙掩埋B.山高谷深,地表崎岖C.泥沼密布,难以挖掘D.丝绸古路,人迹罕至3.打造数字敦煌,可以让游客在网上体验莫高窟文物的魅力,实现有效限流。
它的主要好处是()A.促进了红船精神发扬B.保护了世界文化遗产C.提高了文物研究水平D.增加了石窟经济收入4.下图中,山脉两侧地形区景观的描述,与实际情况不相符的是()A.①山的南侧高寒草原上,常见成群的牦牛在觅食B.①山的南侧千里戈壁,沙漠广布C.①山的北侧高原沟壑纵横,黄土广布D.①山的东侧水田连片,秋季稻谷飘香5.“西气东输”工程不经过的区域是:A.西北地区B.北方地区C.南方地区D.青藏地区读中国人均资源占有量与世界平均水平的比较图,完成下列各题。
6.下列资源中,人均占有量最接近世界平均水平的是()A.石油B.水C.耕地D.煤炭7.图中反映我国资源的基本国情是()A.总量丰富B.人均占有量少C.总量缺乏D.人均占有量多地理区域具有整体的相似性和内部的差异性。
读我国北方地区略图,回答下面小题。
8.北方地区突出的自然地理特征是()A.以干旱为主B.以高寒为主C.以旱地为主D.以水田为主9.关于北方地区内部差异的叙述,正确的是()A.①地区位于我国地势的第三级阶梯,地形以平原为主B.②地区黄土广布,水土流失严重C.①③地区相比,传统民居以窑洞为主的是③地区D.②③地区相比,作物熟制为一年一熟的是②地区10.我国西北地区绿洲农业的主要灌溉水源来自()A.高山冰雪融水B.夏季降水C.湖泊水D.河流水内蒙古自治区的库布齐沙漠里,人们在太阳能光伏组件板下饲养动物、种植庄稼,总结出“治沙+种植+养殖+发电+扶贫”五位一体的治沙新模式。

西方经济学》 2007年秋期末B 卷
本试卷需:答题纸 页 草稿纸 页 试卷审核时间: 年 月 日
第 1 页 共 2 页
密
封
线
学校:
专业: 姓名:
学号:
课程考核答卷
考试时间:120分钟 考试方式:闭卷
(提示:答案必须依试题顺序做在答题册上,并标明大、小题号,否则不予计分)
一、填空题(每空1分 共20分)
1、 2、 3、 4、 5、 6、 7、 8、 9、 10、 二、选择题(每小题2分 共20分) 题号 1 2 3 4 5 6 7 8 9 10 答案
三、判断题(每小题1分 共10分) 1、 2、 3、 4、 5、 6、 7、 8、 9、 10、
四、计算题(每小题5分 共10分) 1、 2、
五、简答题(每小题10分 共20分) 1、 2、
五、论述题(每小题10分共20分)
1、
2、
教学单位:重庆工商大学一财教学部出题教师: (签字)教学单位领导:(签字)第2 页共 2 页。

一、填空题1.楚国有亲齐派和亲秦派,屈原属于______派,与他做对的张仪属于诸子百家中的______家。
2.《离骚》中,屈原将怀王比作______,他又将______比作香草。
“美人香草”从此便成为政治的譬喻。
3.《经典常谈》中,认为屈原也是诸子之一,属于______家。
4.大戴是戴德;小戴是______,戴德的侄儿。
他们都是研究“三礼”中的《______》的专家。
5.“四书”中,《______》讲的是古来大学里教学生的方法,《______》则是孔门传授心法的书。
6.“三礼”中,《______》可以说是宗教仪式和风俗习惯的混合物;《______》却是一套理想的政治制度。
7.古代书写文字的方法有契、铸、书和印,其中,甲骨文用的方法是______,金文用的是______,______的书写材料是竹简,______则要用的模子。
1.亲齐纵横2.美人贤臣3.神仙4.戴圣仪礼5.大学中庸6.仪礼周礼7.契铸书印二、选择题1.下列说法有误的一项是( C )A.法家集大成者是韩非子,是儒家代表人物之一的荀子的学生。
B.儒家拥挤旧文化制度,道家反对一切文化制度。
C.清代人普遍认为《汉书》的文学成就高于《史记》。
D.《吕氏春秋》是一部试图统一思想的书,也是我国第一部系统的、完整的书。
【解析】C项,唐代古文运动之前,人们普遍认为《汉书》好于《史记》,之后则《史记》更受推崇。
2.下列说法正确的一项是( C )A.庄子属于道家,与庄子辩论的惠子属于法家。
B.礼治主义和非攻主义都属于儒家学说。
C.春秋时宴会上的赋诗,类似于后世的点戏,常常带有政治意味。
D.《周易》是五经之首,本是辅助卜法的书。
【解析】A项,惠子是辩者,在汉代被称为名家。
B项,非攻主义是墨家学说。
D项,《周易》本是辅助筮法的书。
3.下列说法有误的一项是( B )A.《国语》重在“语”,记事颇简略,又名《春秋外传》。
B.《尚书》是中国最古的记事的史书,《春秋》则是中国第一部通史。
1 -1质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v,t 至(t +Δt)时间内的位移为Δr , 路程为Δs, 位矢大小的变化量为Δr ( 或称Δ|r |),平均速度为v ,平均速率为v .(1) 根据上述情况,则必有()(A) |Δr |= Δs = Δr(B) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= ds ≠ d r(C) |Δr |≠ Δr ≠ Δs,当Δt →0 时有|d r |= dr ≠ d s(D) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= dr = ds(2) 根据上述情况,则必有()(A) |v |= v ,|v |= v (B) |v |≠v ,|v |≠v(C) |v |= v ,|v |≠ v (D) |v |≠v ,|v |= v分析与解(1) 质点在t 至(t +Δt)时间内沿曲线从P 点运动到P ′点,各量关系如图所示, 其中路程Δs =PP ′, 位移大小|Δr |=PP ′,而Δr =|r |-|r |表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′无限趋近P 点,则有|d r |=ds,但却不等于dr .故选(B).(2) 由于|Δr |≠Δs,故t st ΔΔΔΔr ,即|v |≠v .但由于|d r |=ds,故t st d d d d r ,即|v |=v .由此可见,应选(C).1 -2一运动质点在某瞬时位于位矢r (x,y)的端点处,对其速度的大小有四种意见,即(1)t r d d ;(2)t d d r;(3)t s d d ;(4)22d d d d t y t x.下述判断正确的是()(A) 只有(1)(2)正确(B) 只有(2)正确(C) 只有(2)(3)正确(D) 只有(3)(4)正确分析与解t rd d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量;t d d r表示速度矢量;在自然坐标系中速度大小可用公式t sd d v 计算,在直角坐标系中则可由公式22d d d d t yt x v 求解.故选(D).1 -3一个质点在做圆周运动时,则有()(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变分析与解加速度的切向分量a t起改变速度大小的作用,而法向分量a n 起改变速度方向的作用.质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的.至于a t是否改变,则要视质点的速率情况而定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时,a t为一不为零的恒量,当a t改变时,质点则作一般的变速率圆周运动.由此可见,应选(B).1 -4质点的运动方程为23010t t x 和22015t t y ,式中x,y 的单位为m,t 的单位为s。
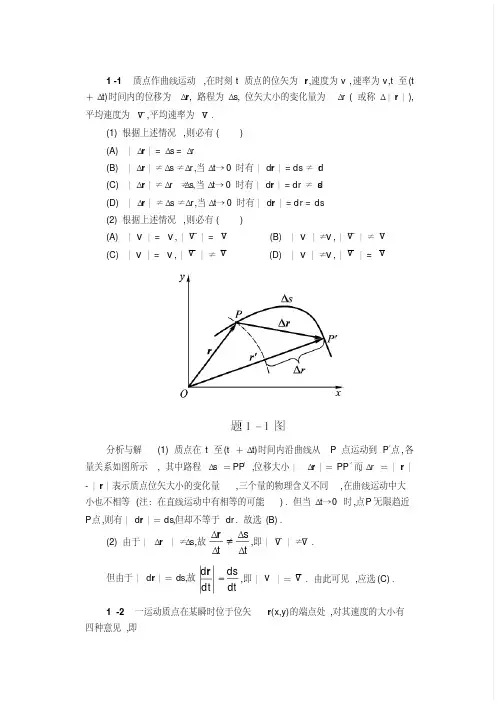
机械原理西⼯⼤版(第⼋版)课后习题答案机械原理西⼯⼤版(第⼋版)课后习题答案第2章2-1 何谓构件?何谓运动副及运动副元素?运动副是如何进⾏分类的?答:参考教材5~7页。
2-2 机构运动简图有何⽤处?它能表⽰出原机构哪些⽅⾯的特征?答:机构运动简图可以表⽰机构的组成和运动传递情况,可进⾏运动分析,⽽且也可⽤来进⾏动⼒分析。
2-3 机构具有确定运动的条件是什么?当机构的原动件数少于或多于机构的⾃由度时,机构的运动将发⽣什么情况?答:参考教材12~13页。
2-4 何谓最⼩阻⼒定律?试举出在机械⼯程中应⽤最⼩阻⼒定律的1、2个实例。
2-5 在计算平⾯机构的⾃由度时,应注意哪些事项?答:参考教材15~17页。
2-6 在图2-20所⽰的机构中,在铰链C、B、D处,被连接的两构件上连接点的轨迹都是重合的,那么能说该机构有三个虚约束吗?为什么?答:不能,因为在铰链C、B、D中任何⼀处,被连接的两构件上连接点的轨迹重合是由于其他两处的作⽤,所以只能算⼀处。
2-7 何谓机构的组成原理?何谓基本杆组?它具有什么特性?如何确定基本杆组的级别及机构的级别?答:参考教材18~19页。
2-8 为何要对平⾯⾼副机构进⾏“⾼副低代"?“⾼副低代”应满⾜的条件是什么?答:参考教材20~21页。
2-9 任选三个你⾝边已有的或能观察到的下列常⽤装置(或其他装置),试画出其机构运动简图,并计算其⾃由度。
1)折叠桌或折叠椅;2)酒瓶软⽊塞开盖器;3)⾐柜上2-11图⽰为⼀简易冲床的初拟设计⽅案。
设计者的思路是:动⼒由齿轮j输⼊,使轴A连续回转;⽽固装在轴^上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的⽬的。
试绘出其机构运动简图(各尺⼨由图上量取),分析是否能实现设计意图,并提出修改⽅案。
1)取⽐例尺绘制机构运动简图2)分析是否能实现设计意图解:f=,可改为f=?-?-=不合理∵03324102-12图⽰机构为⼀凸轮齿轮连杆组合机构,试绘制其机构⽰意简图并计算⾃由度。
研途宝考研/zykzl?fromcode=2014一战教训我毕业于上海的一个二本院校,但当年高考录取分数线在我所在的省是比一本线高8分。
我的成绩还可以,在大学每学期都能拿到学习奖学金,但这并不说明什么,因为大学的考试就是比谁的临时抱佛脚能力强。
很幸运,我这个能力还算强。
大学第一年,我读的是行政管理专业。
大一结束我参加了学校的转专业考试,转到金融学专业。
当时没考虑到未来的打算,转专业只是因为金融学是我校最好的专业。
很幸运,全校五个名额,我转成功了。
可是接下来的三年,我承认自己学业上是荒废了,上课不怎么听,考试临时抱佛脚。
在准备考研复试的时候我才发现,自己的专业知识是多么的差劲,最基本的都不知道。
这里我想强调的是,大学一定要注重专业课的学习。
社会活动可以参加,也有必要参加,但这不是重点,最重要的还是学习。
我大学搞了很多活动,等到毕业之后才发现,这些浪费了我很多的时间,而且搞的自己心静不下来。
准备考研是我进大学就想到的事儿,我认为以后工作的时间有很多,没有必要急着工作,在年轻的时候储备知识,气质在以后会慢慢显现出来。
而且由于本科院校不知名,我一直有个名校情结,想感受下名校的环境和氛围。
也算是对读书时光画个圆满的句号吧。
所以到了大四,我自然而然选择了考研。
具体的大学生活这里我不多说了,总结一下就是,我算是个基础还行的学生,由于高中学习的是物理化学,思维还算灵活,喜欢数学。
在考研的大队伍中,我算是中等水平吧。
毕业那年一月份的研究生考试,我参加了,失败了。
这也是情理中的事儿,如果那样的复习状态我也能考上的话,那这研究生考试也太没有挑战性了。
叙述下失败的过程和背后的原因吧,如果有同学和我当年的状态很像,那赶紧的,调整自己,不能拿自己的前途开玩笑!1、我复习开始的比较晚,我的同学一般大三下学期就开始看书了,看高数的教材、背英文单词、翻翻专业课的书。
而我真正开始复习是大四上学期开学的时候。
考研最佳也是非常重要的时间段是大三的那个暑假,而我完全没有把握住。
西游记第十一章——第二十章一、填空。
1.书中去西天取经的高僧叫_____ 。
2.吃去唐僧白马的三太子是_____ 的儿子。
3.猪八戒又叫_____ ,原为管理天河水兵的_____,获罪下凡,误投猪胎,曾占_____为妖,后经菩萨点化,保唐僧取经,得成正果,封为_____。
4.在护送唐僧去西天取经途中,机智灵活、嫉恶如仇的是______;憨态可掬、好耍小聪明的是______ ,法名是______ ;忠诚老实、勤勤恳恳的是______ 。
5. 唐僧是如来佛祖的弟子_____转世投胎作状元_____之子,出家后法名______ ,修成正果后被封为_______。
6.唐僧骑马西行。
山边城,夜登_______ ,被虎魔王部下生擒。
_______ 搭救了唐僧。
唐僧行至_______ ,忽听喊声如雷:“我师父来也!”叫喊者正是_______ 。
7.唐太宗还魂,登朝宣布大赦天下,严禁毁僧谤佛。
众人推举_______ 主持水陆大会,太宗许之。
8.途经蛇盘山,马匹被_______ 吞食。
观音召出恶龙,将其变为_______ 赐给唐僧当座骑。
二、选择。
1.《西游记》中师徒一共有()人?A. 4B. 5C. 32.唐僧在哪收了猪八戒()?A.高老庄B.流沙河C.五指山3.唐僧在刚收收孙悟空为徒弟时,送他了什么礼物?( )A.鞋和裤子B.虎皮衣 C .金箍圈4.孙悟空被压在哪?( )A.五行山B.五指山C.无影洞5.猪八戒形象的喜剧性及美学意义体现在()。
A、人物形象的不统一B、人物形象言语、行动的矛盾C、猪八戒的性格憨厚老实又爱耍小心眼D、以上都是6.()形象的寓意是心猿,它是七情六欲的主人公。
A、孙悟空B、猪八戒C、沙和尚D、白龙马7.下列关于如来佛祖的说法,错误的是()。
A、如来是西方极乐世界释迦牟尼尊者B、如来在西牛贺洲天竺山灵山鹫峰顶修得丈六金身C、如来是古印度迦吡罗卫国的王子乔达摩·悉达多D、如来创立了大乘佛教8.()照镜子——里外不是人。
第8课 百家争鸣 一、选择题: 1. “祸兮,福之所倚;福兮,祸之所伏”说的是对立的双方能够相互转化。这一观点符合 下列哪一学派思想( ) A.儒家 B.道家 C.法家 D.兵家 2.近年在德国汉堡发现了一本1691年出版的《论语》英译本,该书的前言说:“这位哲学 家的道德是无限辉煌的。”请问这位哲学家的核心思想是( ) A.“无为而治” B.“仁” C.“兼爱”“非攻” D.“法治” 3. 在教育对象问题上,孔子明确提出“无分贵族与平民,不分国界与华夷,只要有心向学, 都可以入学受教”。材料反映孔子的教育主张是( ) A.以“德”教化人 B.有教无类 C.因材施教 D.当仁不让于师 4. 反对战争,珍爱和平是人类的共同追求。我国战国时期,提出“兼爱”“非攻”,反对 各国相互攻伐兼并、残害生命的是( ) A.墨子 B.孟子 C.庄子 D.韩非 5. 下面是几位同学关于孔子的讨论,其中不正确的是( ) A.甲说:他是儒家学派的创始人 B.乙说:他提出了“仁”的学说 C.丙说:他是教育家,对教育贡献很大 D.丁说:他主张实行“仁政”“礼治” 6. 依据所学判断“百家争鸣”局面出现的主要原因是( ) A、社会私学的兴盛 B、诸侯国的兼并战争 C、社会处于大变革时期 D、士人的解放 7.“我无为而民自化,我好静而民自正,我无事而民自富,我无欲而民自朴。”“大小多少,报怨以德。”以上观点反映了诸于百家中哪一学派的思想主张( ) A.墨家 B.道家 C.法家 D.儒家 8. 在人类文明发展的今天,面临着技术进步与战争灾难、经济发展与道德沦丧问题并存。早在1988年,诺贝尔奖获得者汉内斯·阿尔文就宣称:“如果人类要在21世纪生存下去,必须回到2500多年前,去汲取孔子的智慧。”下列选项中,属于孔子的“智慧”的 是( ) A. “仁者爱人” B.“无为而治” C. “兼爱”“非攻” D. 实行“法治” 9. 面对小明同学考砸了的模拟试卷。爸爸暴跳如雷,说要“家法伺候”;妈妈赶紧说:“我们要好好教育孩子,使他进步”;爷爷慢吞吞地说:“这次考差了不全是坏事,知道差在哪儿,坏事也可以变成好事!”其中爸爸的言论最接近下列哪一学派的主张( ) A.儒家 B.法家 C.道家 D.墨家 10. 学习历史有一个基本的结论就是“思想文化是一定现实的反映”。“百家争鸣”学术局面反映的社会现实是( ) A.孔子“有教无类”,使有学问的人增多 B.夏桀暴政,人民怨声四起 C.西周灭商,实行分封制 D.春秋战国时期新旧制度的急剧变化 二.非选择题: 1.请将左边观点与右边对应的人物连接起来: A. “民为贵,社稷次之,君为轻” 孔子 B. “兼爱”“非攻” 老子 C. “仁”“仁者爱人”“己之不欲,勿施于人” 韩非 D. 强调治国要顺应自然和民心 墨子 E. “知彼知己者,百战不殆” 庄子 F. 强调以法治国,建立中央集权专制统治 孙武 G. 世间事物都有对立面,对立的双方能够相互转化 孟子 H. 实行“礼治”,明确尊卑等级,以维系社会秩序 荀子
习 题 8-11.设有一个面薄板(不计其厚度),占有xOy 面上的闭区域D ,薄板上分布有面密度为(,)x y μμ=的电荷,且(,)x y μ在D 上连续,试用二重积分表达该板上的全部电荷Q .解 用一组曲线将D 分成n 个小闭区域i σ∆,其面积也记为(1,2,,)i i n σ∆=.任取一点(,)i i i ξησ∈∆,则i σ∆上分布的电量(,)i i i Q μξησ∆≈∆.通过求和、取极限,便得到该板上的全部电荷为1lim (,)(,)d ,ni i i i DQ x y λμξησμσ→==∆=∑⎰⎰其中1max{i i nλσ≤≤=∆的直径}.2. 设12231()d D I x y σ=+⎰⎰其中1{(,)11,22}D x y x y =-≤≤-≤≤;又22232()d D I x y σ=+⎰⎰其中2{(,)01,02}D x y x y =≤≤≤≤.试利用二重积分的几何意义说明1I 与2I 之间的关系.解 由二重积分的几何意义知,1I 表示底为1D 、顶为曲面223()z x y =+的曲顶柱体1Ω的体积;2I 表示底为2D 、顶为曲面223()z x y =+的曲顶柱体2Ω的体积.由于位于1D 上方的曲面223()z x y =+关于yOz 面和zOx 面均对称,故yOz 面和zOx 面将1Ω分成四个等积的部分,其中位于第一卦限的部分即为2Ω.由此可知124I I =.3. 利用二重积分定义证明: (1) d ()DD σσσ=⎰⎰其中为的面积;(2) (,)d (,)d ()DDkf x y k f x y k σσ=⎰⎰⎰⎰其中为常数;(3)12(,)d (,)d (,)d ,DD D f x y f x y f x y σσσ=+⎰⎰⎰⎰⎰⎰其中12D DD =,1D 、2D 为两个无公共内点的闭区域.证 (1) 由于被积函数(,)1f x y ≡,故由二重积分定义得11d lim (,)lim lim .nniiii i i Df λλλσξησσσσ→→→===∆=∆==∑∑⎰⎰(2) 011(,)d lim (,)lim (,)(,)d .nni i i i i i i i DDkf x y kf k f k f x y λλσξησξησσ→→===∆=∆=∑∑⎰⎰⎰⎰(3) 因为函数(,)f x y 在闭区域D 上可积,故不论把D 怎样分割,积分和的极限总是不变的,因此在分割D 时,可以使1D 和2D 的公共边界永远是一条分割线。
2017厦大经济学考研参考教材介绍聚英厦大考研网为同学们整理了经济学考研备考参考教材,让同学们在备考时有的放矢的复习。
简单来说,经济学教材可以分为初级、中级和高级。
大致分类为:初级教材:高鸿业《西方经济学(微观部分)》、尹伯成《微观经济学简明教程》、高鸿业《西方经济学(宏观部分)》、曼昆《经济学原理(宏观经济学分册)》中级教材:平狄克《微观经济学》、范里安《微观经济学:现代观点》、曼昆《宏观经济学》、多恩布什《宏观经济学》高级教材:尼科尔森《微观经济理论基本原理与扩展》、平新乔《微观经济学十八讲》政治经济学两本经典教材:逄锦聚《政治经济学》、宋涛《政治经济学教程》,无所谓初级、中级和高级分类。
当然,除了上述教材外,还有些教材也很经典,但是相对来说,上述几本教材应用特别广。
那么,厦门大学经济学考研具体参考哪些教材呢?同学们可以参考【厦大硕招参考书目】一、微观经济学1.高鸿业《西方经济学(微观部分)》就该书而言,以下几个问题需予以注意:(1)第六版教材于2014年7月出版,预期一些高校依然会将第五版教材(甚至第四版)列为2017年考研参考书目。
复习过程中,适当了解第六版教材变动地方(主要是完全竞争市场的福利),有针对性的复习。
(2)对于跨专业学生,以及专业基础不扎实的学生,即使所报院校未将该书列为参考书目,参考书目为中级微观教材,如范里安《微观经济学:现代观点》,建议在第一轮复习时将该书作为重要参考书目。
(3)该书的难度为中级偏初级,而名校要求达到的层次为中级,甚至有些名校要求难度为中级偏高级,因此复习时,特别是第二轮复习时,应该参考中级微观经济学教材,如范里安《微观经济学:现代观点》或尼科尔森《微观经济理论基本原理与扩展》。
(4)对于各章后面的“结束语”,要点归纳部分一定要看,有些部分甚至容易出考题。
但是,对于批判性的语句不需要看。
2.尹伯成《微观经济学简明教程》就该书而言,以下几个问题需予以注意:(1)该书有几个版本,如尹伯成《西方经济学简明教程》(第7/8版),各版本差异不大,建议考生选用尹伯成《西方经济学简明教程》,包括微观经济学和宏观经济学两部分内容。
《西方经济学简明教程》参考答案 习题八 第 1 页 共 7 页 习题八
1. 简释下列概念: 要素需求 答:指在一定时期内,对应某一要素的各种价格,厂商愿意并且能够购买的数量,是厂商为了生产和出售产品并从中获益而对要素产生的需求,它是由消费者对消费物品的需求派生出来的,因而是一种派生需求。同时也是一种联合需求。
边际物质产品 答:是指增加一单位某种要素投入所增加的物质产品量。
边际收益产品 答:是指增加一单位某种要素投入所增加的总收益,它等于该要素的边际物质产品与相应产品的边际收益的乘积。
边际产品价值 答:是指增加一单位某种要素投入所增加的产量的销售值,它等于该要素的边际物质产品与相应产品价格的乘积。
边际要素成本 答:是指增加一单位某种要素投入所增加的成本支出。
向后弯曲劳动供给曲线 答:劳动供给曲线表明的是劳动供给量与劳动价格即工资率之间关系的曲线,西方经济学家一般认为个人劳动供给曲线是向后弯曲的,即随着劳动价格即工资率的提高,起初劳动供给量逐渐增加,但当工资率上升到一定程度后,劳动供给量反而会逐渐减少(具体解释可参考下面的习题4),在图形上便呈现为向后弯曲的曲线。但就整个市场而言,劳动供给曲线基本上是向右上倾斜的。 《西方经济学简明教程》参考答案 习题八 第 2 页 共 7 页 洛伦茨曲线 答:由美国统计学家洛伦茨提出的用以衡量一个国家贫富差别程度的收入分配曲线,表示人口累计百分比和收入累计百分比的对应关系,其弯曲程度反映了收入分配的不平等程度。
基尼系数 答:是一种衡量收入不平等程度的标准,由洛伦茨曲线导出,其值由0起最大到1。
2. 厂商利润极大化的条件MC=MR为什么可以重新表达为MFC=MRP?完全竞争条件下出售产品的利润极大化MC=P能否重新表述为MFC=MRP,为什么? 答:从不同的考察角度出发,厂商利润极大化的条件既可以表述为MC=MR,也可以表述为MFC=MRP,这两者都可以保证厂商利润极大化目标的实现。我们知道,为了实现最大限度的利润,厂商需要对投入要素量、产出量作出某种抉择。如果厂商把产量作为选择变量,将总收益、总成本进而总利润视为产量的函数,那么实现最大利润的条件是,厂商把产出量调整到一定数量,使得这一产出量下的最后一个单位的产品所提供的总收益的增加量(即边际收益MR),恰好等于增加这最后一个单位的产品引起的总成本的增加量(即边际成本MC),即使得这一产出量下的MR=MC。 如果厂商把投入的生产要素(如劳动)作为选择变量,将总收益、总成本进而总利润视为投入要素的函数,那么实现最大限度利润的条件就可以表述为MFC=MRP,也就是厂商把雇用的劳动投入量调整到一定数量,使得这一雇用劳动总量下的最后一个单位劳动带来的总收益的增加量(即边际收益产品MRP),恰好等于增加这最后一个单位劳动雇用量引起的总成本的增加量(即边际要素成本MFC)。理由是:假如MRP>MFC,这表示每增加一个单位的劳动投入带来的总收益的增加量超过雇用这个单位劳动引起的总成本的增加量,也就意味着继续增加劳动投入量,增加的每单位劳动投入量都可获得些许利润,从而增加劳动《西方经济学简明教程》参考答案 习题八 第 3 页 共 7 页 投入可使总利润有所增加;反之,假如MRP<MFC,这意味着最后增加雇用的那个单位劳动反而造成损失,从而导致总利润较前减少。所以,如果厂商把投入要素如雇用的劳动量作为选择变量,实现利润极大化的条件便是他雇用的劳动量的MRP=MFC。 事实上,MC=MR和MFC=MRP这两个式子可以相互转换。由于MRP=MPP·MR,因此,MRP/MPP=MR,同样,MFC/MPP=MC。这是因为,MFC表示多使用1单位要素所多支出的成本,MPP表示多使用1单位要素所多生产的产量,因而MFC/MPP就表示多生产1单位产品所多使用的成本,即MC,于是从MRP/MPP=MFC/MPP就得到MC=MR。 假如产品市场是完全竞争,那么利润极大化的条件MC=MR=P就可以表达为MFC=MRP,因为在完全竞争的产品市场上,P=MR。这样,表示增加单位要素投入带来的总收益的增加量的MRP(=MR×MPP)就可以表示为(等同于)VMP(=P×MPP),相应地,利润极大化的条件就可以表达为MFC=MRP。
3. 边际收益产品(MRP)和边际收益(MR)有何区别? 答:边际收益产品(MRP)指增加1单位某种要素投入带来的产量(边际物质产品)的增加的收益,它等于要素的边际物质产品和产品的边际收益之乘积。而边际收益(MR)指增加1单位产品的增加的收益。故二者有别,假定增加1单位产品所增加的收益是5元,而增加1单位要素(如劳动)的增加的产量(边际物质产品,又称边际产量)是3单位,则边际收益产品是15元。
4. 为什么会出现后弯的劳动供给曲线? 答:劳动供给曲线表明的是劳动供给量与劳动价格之间的关系,而劳动供给可看成是闲暇需求的反面。劳动供给增加就是闲暇需求减少,并且劳动价格(工资)就是闲暇的机会成本或价格。从替代效应看,工资上升使得闲暇的机会成本或代价提高,劳动者会愿意用劳动来替代闲暇,即会导致闲暇需求量减少,而劳动供给量增加。但从收入效应看,工资上升时,劳动者越有条件以较少的劳动换得所需要的收入和消费品,从而越不愿意增加劳动供给,而对闲暇需求便会增加。《西方经济学简明教程》参考答案 习题八 第 4 页 共 7 页 一般说来,当工资较低时,替代效应大于收入效应,故闲暇的需求量会随工资上升而下降,即劳动供给量会增加,但工资较高时,则工资上涨引起整个劳动收入增量就很大,收入效应会逐渐大于替代效应,因而劳动供给会减少,使得劳动供给曲线由向右上倾斜转为向左上倾斜,即劳动供给曲线呈后弯状。
5. 形成工资差异的原因有哪些? 答:形成工资差异原因大致有:(1)劳动质量不同,这种差别存在会使劳动者边际生产力不同,并导致工资差异;(2)非货币利益不同,即工作在安全性、辛苦程度、环境、声誉等方面差异而造成劳动心理成本不同,这就要求有工资差异来给予补偿;(3)市场的不完全竞争,使劳动者在不同行业、不同地区和不同单位流动受阻,并形成工资差异;(4)种族、性别、籍贯等不同而造成的歧视。
6. “劣等地上永远不会有级差地祖”这句话对吗?“某块地现在是劣等地,因此它永远不会有级差地租”这个命题正确吗? 答:使用劣等地也必须支付地租,否则,劣等地的所有者绝对不肯出让土地使用权。然而,这种地租不是级差地租,因为级差地租是优等地和中等地所有者所获取的超过劣等地上所获取的地租水平的部分,因此,“劣等地上永远不会有级差地租”这句话是对的。然而,就该块地而言,现在是劣等地,不等于它永远是劣等地。随着社会经济发展,人口增加,人们可能开发了更差的土地,会使本来是劣等地的这块土地变成不是劣等地,从而产生级差地租。可见,题中前一句对,后一句错,二者并不矛盾。
7. 判断下列说法正误,并说明理由: (1) 一个竞争性的厂商,在其最后雇用的那个工人所创造的产值大于其雇用的全部工人的平均产值时,他必定没有实现最大的利润。 答:正确。对竞争性厂商来说,若其最后雇用的那个工人所创造的产值大于其雇用的全部工人的平均产值,即VMPL(=P·MPPL)>VAPL(LTRPQPAPPLL)《西方经济学简明教程》参考答案 习题八 第 5 页 共 7 页 时,则他必定可通过增雇工人使其总利润增加。我们知道,竞争性厂商利润极大化的雇用量为VMPL与MFCL(=W)交点之相应的雇用量,但这个交点必须是处于递减阶段的VMPL曲线(实际上只有这段才被认为等同于厂商对劳动的需求曲线)与MFCL曲线相交之点。即利润极大化的雇用量满足:VMPL=MFCL=W,且0LVMPL。可以证明当VMPL>VAPL时,相应雇用量不可能满足上述条件。
如上图所示,VMPL为劳动的边际产品价值曲线,其递减部分即为竞争性厂商对劳动的需求曲线,VAPL为劳动的平均产品价值曲线,其极大点正好同时位于VMPL曲线上。VMPL与VAPL之间的关系类同于劳动的边际产量(MPPL)与平均产量(APPL)之间的关系,因为前两者分别为不变的产品价格与后两者之乘积:VMPL=P·MPPL,VAPL=P·APPL。 满足VMPL=MFCL=W这一条件的共有两点:A点和B点。在交点A由于VMPL处于递减阶段,故相应的劳动雇用量L1能使厂商实现最大利润,但此时VMPLVAPL但由于VMPL处于递增阶段,此时相应的劳动雇用量L2并没有使厂商达到利润最大,相反地实际上出现了亏损,因为W>VAPL。同时,可以看到,除了B点,当VMPL>VAPL时,相应的雇用量下的VMPL都不可能等于MFCL(=W),因此都没有实现最大限度的利润。实际上,当VMPL>VAPL时,厂商通过增雇工人可使其利润增加。因此竞争性厂商在其最后雇用的那个工人创造的产值(VMPL)大于其雇用的全部工人的平均产值(VAPL)时,他必定没有实现最大利润。
(2) 即使劳动的边际物质产品保持不变,一个垄断厂商对劳动的需求曲线仍《西方经济学简明教程》参考答案 习题八 第 6 页 共 7 页 然是向下倾斜的。 答:正确。因为一个垄断厂商在完全竞争的劳动市场下对劳动的需求曲线即为被雇用劳动的边际收益产品MRP曲线,而边际收益产品等于边际物质产品与边际收益之乘积,即MRP=MPP·MR,因此MRP受MPP与MR两个因素的影响。由于垄断厂商的MR曲线向下倾斜,他对劳动的需求曲线即劳动的边际收益产品曲线也仍然向下倾斜,只是其斜率(此时与MR曲线之斜率等值)比边际物质产品递减时小了些罢了。
(3) 如果一个垄断厂商在完全竞争的劳动市场上同时雇用了熟练劳动力和非熟练劳动力,那么,厂商支付的工资将与他们的边际生产力成比例。 答:正确。熟练劳动力和非熟练劳动力的边际收益产品MRP是不同的。若垄断厂商同时雇用了熟练劳动力和非熟练劳动力,则基于利润极大化的目标他对这两种劳动力的雇用量必定分别为它们各自的边际收益产品等于其市场均衡工资率的这种雇用量。而劳动的边际收益产品即代表了劳动的边际生产力,同时劳动供求平衡时与劳动的边际收益产品等值的工资率等于劳动的边际生产力,因此,若垄断厂商在完全竞争的劳动市场上同时雇用了熟练劳动力和非熟练劳动力,则达到利润极大化时厂商支付给他们的工资必定分别等于其边际生产力,熟练劳动力和非熟练劳动力的工资也就与他们的边际生产力成比例。
(4) 在一个竞争性的劳动市场上,如果最低工资高于均衡工资,必然引起失业。 答:正确。如下图,SL、DL分别为竞争性劳动市场上的劳动供给曲线和劳动需求曲线。它们相交于E点,与E点相应的W*和L*即为均衡工资和均衡就业量。若最低工资WM高于均衡工资W*,即WM>W*,则与最低工资WM相应的劳动供给量为LS,劳动需求量为LD。显然,劳动供给量LS>劳动需求量LD,该竞争性劳动市场将因此出现LSLD(=OLS-OLD)量的失业劳动者。