工程测量观测误差的形成原因及解决方法

建筑工程试验检测结果的误差及控制措施随着建筑工程的不断发展，对建筑材料和结构的质量要求也越来越高。

为了确保建筑工程的安全和稳定，对于建筑材料和结构进行试验检测是非常重要的。

在进行试验检测的过程中，会存在一定的误差，这些误差可能会对试验结果造成影响，甚至对建筑工程的安全构成威胁。

对于建筑工程试验检测结果的误差及其控制措施，需要引起我们的高度重视。

一、建筑工程试验检测结果的误差来源建筑工程试验检测结果的误差主要来自以下几个方面：1. 设备误差：在试验检测过程中使用的设备可能存在精度不足、老化损坏等问题，导致试验结果产生偏差。

2. 操作误差：试验检测人员在进行试验过程中可能存在操作不规范、疏忽大意等情况，导致试验结果出现误差。

3. 环境因素：试验检测的环境因素，如温度、湿度、气压等，都有可能对试验结果产生影响。

4. 样品不均匀性：在进行试验检测时，样品的不均匀性也可能导致试验结果出现误差。

二、建筑工程试验检测结果的控制措施为了降低建筑工程试验检测结果的误差，我们可以采取以下控制措施：1. 设备管理：对试验检测设备进行定期维护和保养，确保设备的精度和可靠性。

2. 人员培训：对试验检测人员进行专业培训，提高其操作技能和规范意识，减少操作误差。

3. 环境监测：对试验检测环境因素进行监测和控制，确保环境条件对试验结果的影响最小化。

4. 样品处理：在进行试验检测时，对样品进行充分混合和均匀处理，降低样品不均匀性对试验结果的影响。

三、建筑工程试验检测结果的误差评定和报告在进行建筑工程试验检测时，我们需要对试验结果的误差进行评定和报告，以便及时发现并解决问题。

对于试验结果的误差评定，我们可以参考以下几个方面：1. 误差分析：对试验结果的误差进行分析，找出误差的来源和影响程度。

2. 误差标定：对试验结果的误差进行标定，确保误差在允许范围内。

3. 误差报告：将试验结果的误差情况进行报告，以便相关部门和人员进行核查和处理。

工程测量中误差产生的原因及规避在建筑工程施工中，工程测量的放样精度对工程质量和进度都有十分重要的影响。

如果工程测量中出现了放样误差，将可能导致开挖、立模、打桩和钢筋捆扎等作业错误施工，带来较大的损失。

1.放样测量中误差产生的原因1.1 人员观测的影响观测人员的测量经验和熟练程度对测量结果也会产生比较大的影响，尤其对于精密工程，仪器操作水平的高低是产生误差的重要来源，甚至可能导致测量误差的产生。

1.2 环境因素的影响测量作业环境对测量放样的影响无处不在，如建筑阻挡视线、大气的折射、卫星星率和磁场对GPS 观测的影响等。

由于精密工程对测量放样的精度较高，因此，某些环境因素所带来的测量误差可能达到或超过工程本身要求的测量精度。

1.3 施测方法的影响不同的施测方法对测量放样结果会产生很大影响。

如全站仪的自由设站后方交会方法测放中线点、改化后的三角高程测量方法等，它们精简了测量环节(如不需对中、不需量取仪器高和棱镜高等)，提高了测量精度。

1.4 仪器因素的影响仪器本身的精度及测量状态对精密工程放样非常重要，如全站仪的测距误差、i 角产生的垂直角测量误差等。

精度高、状况良好的测量设备不仅能够较好地保证放样精度，而且还可大大提高作业效率。

2 .放样测量中误差规避的主要措施工程测量过程中往往会出现一些误差，这些误差有些是被允许的，而有些则会给整个工程的建设质量带来严重的消极影响，必须进行重新测量予以消除，这样就大大降低了工程测量的速度，进而拖慢整个项目的进程。

因此，最大程度避免误差的出现就成了提高测量速度的一个重要环节。

2.1 合理安置测量仪器在安放测量仪器时应选择那些地势平坦、通视效果好的地段，注意避开车流和人流，如果因条件限制确实无法避开，至少要保证地面的坚实。

不要将仪器架设在井盖或过于光滑的地面上，在大风天气要注意将仪器放低，在冬季作业时应预先将附近的积雪清除。

总之，只有将测量仪器平稳、牢固的安置后方可进行工程测量，从而保证测量精度。

测绘工程中的常见误差与校正方法导言测绘工程是现代社会中不可或缺的一项技术，它涉及到土地界址的确定、地图绘制、地形勘测、建筑设计等领域。

然而，在测绘过程中，常常会出现一些误差，这些误差会对工程的精度和可靠性产生重大影响。

因此，了解和校正这些误差成为了测绘工程师的重要任务。

一、仪器误差1. 刻度误差仪器上的刻度通常用来测量长度或角度。

然而，由于制造和使用过程中的种种原因，刻度可能会出现误差。

这种误差通常可以通过对仪器进行校准来消除或减小。

校准包括对刻度进行调整或更换，并使用已知长度或角度进行检验。

2. 指示误差指示误差是指测量仪器指针或显示器的读数与真实值之间的差别。

这种误差可能由仪器的精度不足或指针的漂移引起。

要校正指示误差，需要进行精确的校准，并在测量过程中使用修正因子。

二、环境误差1. 温度误差温度变化会导致仪器和测量对象的体积改变，进而产生测量错误。

为了校正这种误差，可以使用温度补偿装置或者在测量过程中进行温度校正。

2. 大气压力误差地面测量中，大气压力的变化可能导致仪器的读数偏差。

为了校正这种误差，需要进行大气压力的测量，并使用修正因子进行校正。

三、观测误差1. 粗差粗差是指测量结果与实际值相差较大的异常数据，通常是由于人为失误或设备故障引起的。

为了排除这种误差，需要对数据进行检查和重复测量，并排除异常值。

2. 随机误差随机误差是由于各种偶然因素引起的不可预测的误差，它通常呈正态分布。

为了减小随机误差的影响，可以进行多次观测并取平均值，或者使用统计方法进行数据处理。

3. 系统误差系统误差是由于测量仪器、操作方法或环境条件等因素引起的一类相对固定的误差。

为了校正系统误差，可以使用校正模型或修正公式，并根据实际情况进行修正计算。

四、校正方法1. 内部校正内部校正是指在测量过程中使用已知的校正元素进行校正。

例如，在角度测量中，可以使用标准角度进行校准；在距离测量中，可以使用已知的基线长度进行校正。

高程测量中的误差分析与排除方法引言高程测量是工程测量中的重要环节，用于确定地面或物体的垂直位置。

然而，在测量过程中，由于各种因素的影响，会引入一定的误差，影响测量结果的准确性。

因此，误差分析与排除方法的研究对于保证高程测量的精度至关重要。

一、误差来源1.仪器误差：仪器精度、零位偏差等因素会引入误差。

为了减小仪器误差，可以选择精度更高的仪器，并进行校准和调试。

2.观测误差：观测者可能存在主观因素引起的误差，如不稳定的手持姿势、不准确的读数等。

通过培训和规范操作程序，可以提高观测的准确性。

3.大气因素：大气压力、温度、湿度等都会对高程测量结果产生影响。

为了消除大气因素引起的误差，可以进行气压校正和气温修正等工作。

二、误差分析方法1.误差理论：误差理论是一种定量描述误差的方法，通过确定误差类型、计算误差的大小及其传播等，可以评估测量结果的可靠性。

常用的误差理论包括误差传播定律、标准差法等。

2.重复测量法：重复测量法是通过多次测量同一点或同一线段，然后对测量结果进行统计分析，从而获得更准确的测量值。

通过计算平均值、方差等指标，可以估计出测量误差的大小。

3.比较测量法：比较测量法是利用两个或多个测量结果的差异进行测量误差的估计。

例如，在高程测量中，可以选择已知高程的控制点进行比较，通过对比差值来评估测量误差。

三、误差排除方法1.数据处理：在高程测量中，可以运用合理的数据处理方法来减小误差的影响。

例如，利用平差方法对观测数据进行处理，可以消除一部分随机误差。

2.控制环境：为了减小误差的产生，可以采取一定的措施控制测量环境。

例如，在户外测量时，避免测量仪器暴露在直射阳光下，以减少温度变化的影响。

3.质量控制：在高程测量过程中，进行质量控制是保证测量结果准确性的重要手段。

通过建立严格的质量控制体系，对测量仪器、操作流程进行监控，可以有效地排除误差。

结论高程测量中的误差分析与排除方法对于保证测量结果的准确性和可靠性至关重要。

浅谈建筑工程测量误差及应对措施摘要：在建筑工程中测量误差时时刻刻都存在着。

由于受到仪器、人员和外界环境的影响，工程测量误差不容易控制。

如果出现不易发现的错误，致使错误产生导致测量值不准确，直接影响工程施工，造成经济、时间的损失。

为了提高测量值的精度，需要研究影响测量精度的各种误差来源、性质、大小和规律,从而制定出消除或减弱这些误差的原则和方法。

将对影响测量精度和误差产生的原因以及消除或减弱其影响的原因进行分析，并提出了应对措施。

关键词：工程测量，测量误差，应对措施误差的定义:测量值与真实值之差。

当对一个物理量进行多次测量时总会有差异，测量工作是在一定条件下进行的，外界环境的变化、观测者的技术水平和仪器本身构造的不完善等原因，都可能导致测量误差的产生。

测量学上通常把外界环境、测量仪器和观测者的技术水平三个方面综合起来，称为观测条件。

观测条件不理想和不定性，是产生测量误差的根本原因。

通常把观测条件相同的各次观测，称为等精度观测；观测条件不同的各次观测，称为不等精度观测。

误差的来源有很多，概括起来主要分三个方面：1. 仪器误差由于仪器精度上的限制和构造不可能十分完美的缺陷，虽然事前已经校正了仪器但尚有误差未完全消除,仪器误差分为设计原理误差和制造误差。

（1）设计原理误差：仪器在设计时，经常采用近似的实际工作原理来代替理论的工作原理，其所造成的测量误差，称为设计原理误差。

为了减小测量误差，一般在仪器设计时都要求进行修正。

（2）制造误差：测量仪器一般是由多个零部件构成的，在制造和安装中不可避免的存在误差，这种误差即为制造误差。

因此，在测量时，要选择测量误差小的测量器具或带有修正值的测量器具，以减小测量误差。

水准仪在构造上有几个轴线，仪器竖轴、圆水准器轴、视准轴、管水准器轴等。

这些轴线满足一定的几何关系，水准仪才可以正常使用，水准仪在使用或搬运过程中对这些轴线间的关系造成一系列的影响，使仪器不能满足正确的几何关系，产生仪器误差，而这些误差中对测量影响最大的是视准轴与管水准器轴的平行关系被破坏后产生的误差。

工程测量中的误差分析
引言：工程测量中的误差分析是确保测量结果准确性和可靠性
的重要步骤。

本文将探讨工程测量中的误差来源和评估方法，以及
如何减小误差并提高测量结果的可靠性。

主体：
1. 误差来源：
- 仪器误差：包括系统误差和随机误差，可以通过校准和仪器
选用来减小。

- 环境因素：如温度、湿度、大气压等因素对测量结果有影响，需要进行环境补偿和控制。

- 人为因素：操作员技术水平、观测方法等对测量结果有影响，需要培训和规范操作。

- 测量对象本身：如形状、材料等对测量结果存在误差，需要
了解并进行校正。

2. 误差评估方法：
- 系统误差评估：通过测量重复性和准确度指标来评估系统误差，并进行修正。

- 随机误差评估：通过重复测量和统计分析方法来评估随机误差，并计算其标准差和置信区间。

3. 误差减小和可靠性提高方法：
- 选择合适的测量仪器，并进行定期校准和维护。

- 控制环境因素，如保持恒定的温度和湿度。

- 培训测量人员，提高其技术水平和操作规范性。

- 采用多重测量和平均值方法，减小随机误差的影响。

- 结合其他测量方法和技术，如激光测量、摄影测量等来提高测量结果的可靠性。

结论：在工程测量中，误差分析是确保测量准确性和可靠性的关键步骤。

通过了解和评估误差来源，并采取相应的减小和修正措施，可以提高测量结果的可靠性，从而保证工程项目的质量和安全性。

测绘工程中常见的测量误差及其修正技巧引言：在测绘工程中，精确测量是非常重要的，因为精确的测量结果直接影响到后续工作的准确性和可靠性。

然而，由于测量中存在各种各样的误差，我们需要了解这些误差及其修正技巧，以确保测量结果的准确性和可靠性。

一、随机误差在测绘中，随机误差是不可避免的，它主要由观测仪器的精度、观测人员的技能、测量环境的影响等因素引起。

为了修正随机误差，我们可以采取以下技巧：1.重复观测：通过多次观测同一点或同一物体，然后取观测结果的平均值，可以减小随机误差的影响。

2.仪器校准：定期对仪器进行校准，可以提高仪器的精度，减小随机误差的发生。

3.增加观测数量：增加观测数量可以降低随机误差对最终结果的影响，提高测量精度。

二、系统性误差系统性误差是指在一系列测量结果中存在一定的偏差，其主要是由于测量仪器、环境条件等原因导致的。

为了修正系统性误差，我们可以采取以下技巧：1.仪器校正：通过进行仪器校正，可以确定系统性误差的大小和方向，并进行相应的修正。

2.检查环境条件：例如，温度、湿度、大气压力等环境因素可能会对测量结果产生影响，我们需要进行环境条件的检查和调整，以减小系统性误差的发生。

3.标定参照物：在测量中设置标定参照物，并及时校正测量结果，可以有效减小系统性误差。

三、距离测量误差及修正技巧1.仪器误差：距离测量中，仪器的误差是常见的问题。

我们可以通过仪器校准和观测技巧的合理运用来减小仪器误差。

2.地形因素：地形的复杂性可能导致距离测量误差的发生。

在复杂地形中进行测量时，需要考虑地形的影响，并采取相应的措施进行修正，如引入地面因子等。

3.大气折射：大气折射是距离测量中常见的误差来源之一。

为了减小大气折射对测量结果的影响，我们可以使用大气折射修正模型进行修正。

四、方位角测量误差及修正技巧1.仪器误差：方位角测量中，仪器的误差是导致测量误差的一个重要因素。

通过仪器校正和合理的观测技巧，可以减小仪器误差的影响。

测绘技术中的常见误差与误差调整方法测绘技术是一门应用科学，为我们提供了准确的地理空间数据，支持了各种科学研究和工程应用。

然而，在测绘过程中，由于各种原因，常常会产生一定的误差。

了解常见误差及其调整方法对于保证测绘数据的准确性至关重要。

一、角度测量误差角度测量是测绘中最基本的要素之一，然而常常会受到多种因素的干扰而产生误差。

环境的不稳定、仪器的精度限制、人为的操作不准确等，都可能导致角度测量误差。

为了降低误差的影响，我们可以采取一系列的方法。

首先，通过对仪器进行定期校准，可以确保仪器的精度；其次，尽量采用稳定的环境进行测量，减少环境因素的影响；此外，合理的操作方法和技术培训也是减小角度测量误差的关键。

二、距离测量误差在测绘过程中，测量距离是另一个重要的任务。

然而，由于测量仪器的误差、大气条件的变化等原因，距离测量误差也经常存在。

为了减小这种误差，我们可以采取多种方法。

首先，使用精度更高的仪器和测量方法，减少仪器误差对距离测量的影响；其次，采用大气条件修正模型进行修正，消除大气对距离测量的影响；此外，多次测量，并进行平均处理，也可以有效减小距离测量误差。

三、高程测量误差高程测量是测绘中另一个重要的要素，然而也容易受到误差的影响。

地球引力场的不规则分布、大气压力的变化、仪器精度的限制等原因，都可能导致高程测量误差的产生。

为了减小误差，我们可以采取一系列措施。

首先，进行端面标定，提高仪器的精度；其次，进行高程平差，通过多点测量和权衡来消除误差；此外，利用大气压力修正模型进行修正，也是减小高程测量误差的一种常用方法。

四、误差调整方法在测绘实际应用中，误差的调整是不可避免的。

为了综合考虑各种误差，得到更加准确的结果，我们可以采取一系列的误差调整方法。

首先，采用最小二乘法进行数据拟合，通过最小化观测值与估计值之间的差异，得到最优解；其次，采用最小二乘平差法对观测数据进行处理，通过对观测值的权衡和调整，得到更准确的结果；此外，还可以借助控制点的权衡，进行基于控制点的误差调整，提高测绘数据的准确性。

测量误差的分类与误差特性（一）测量误差产生的原因产生测量误差的原因主要有三个方面：（ 1 ）仪器的原因。

每一种测量仪器只具有一定的精度，使测量结果受到影响；（ 2 ）人的原因。

由于观测者的感觉器官的鉴别能力存在局限性，所以对仪器的对中、招平、瞄准、读数等方面都会产生误差；（ 3 ）外界环境的影响。

测量时所处的外界环境中的温度变化、日光照射、大气折光、风力、烟雾等客观情况，使测量结果产生误差。

测量工作中，在一定范围内的误差是不可避免的。

（二）测量误差的分类与处理原则测量误差按其对观测结果影响性质的不同分为系统误差与偶然误差两类。

1 ．系统误差在相同观测条件下，对某一量进行一系列的观测，如果出现的误差在符号和数值上均相同，或按一定的规律变化，这种误差称为系统误差。

例如用名义长度为 30m 而实际长度为 30 . 004m 的钢卷尺量距，每量一尺段就有使距离量短了 0. 004m 的误差，误差的正负号不变，且大小与所量距离的长度成正比。

因此，系统误差具有积累性。

系统误差对观测值的影响具有一定的数学或物理上的规律性，这种规律性如能找到，则系统误差对观测值的影响可以改正，或可用一定的测量方法加以抵消或削弱。

2 ．偶然误差在相同的观测条件下，对某一量进行一系列的观测，若误差出现的符号和数值大小均不一致，从表面上看没有任何规律性，这种误差称为偶然误差，是由人力所不能控制的因素（例如人眼的分辨能力、仪器的极限精度、外界环境的影响等）共同引起的测量误差，其数值的正负、大小纯属偶然。

偶然误差是不可避免的。

在测量工作中，除了上述两种误差以外，还可能发生错误，例如瞄错目标、读错大数等，是由观测者的粗心大意或技术不熟练造成的。

错误是可以避免的，含有错误的观测值应该舍弃，并应重新进行观测。

为了防止错误的发生和提高观测成果的质量，在测量工作中一般要进行多于必要的观测，称为“多余观测”。

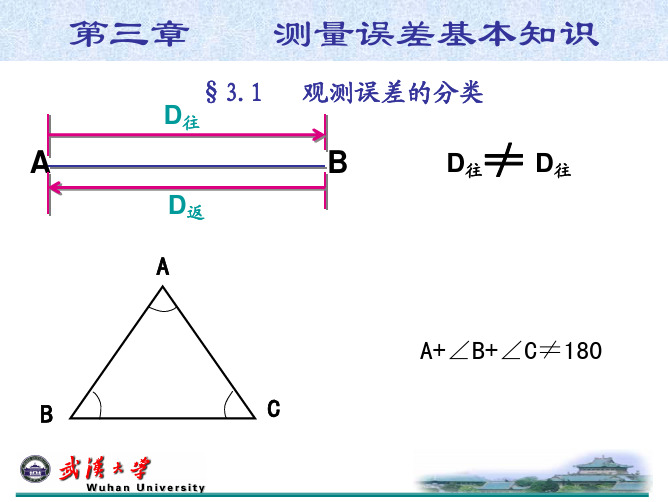
例如一段距离采用往返丈量，往测是属于必要观测，则返测就属于多余观测。

第五节测量误差基础知识一、测量误差概述1．测量误差产生的原因测量时,由于各种因素会造成少许的误差,这些因素必须去了解,并有效的解决,方可使整个测量过程中误差减至最少;实践证明,产生测量误差的原因主要有以下三个方面;1人为因素;由于人为因素所造成的误差,包括观测者的技术水平和感觉器管的鉴别能力有一定的局限性,主要体现在仪器的对中、照准、读数等方面;2测量仪器的原因;由于测量仪器的因素所造成的误差,包括测量仪器在构造上的缺陷、仪器本身的精度、磨耗误差及使用前未经校正等因素;3环境因素;外界观测条件是指野外观测过程中,外界条件的因素,如天气的变化、植被的不同、地面土质松紧的差异、地形的起伏、周围建筑物的状况,以及太阳光线的强弱、照射的角度大小等;测量时受环境或场地之不同,可能造成的误差有热变形误差和随机误差为最显着;热变形误差通常发生于因室温、人体接触及加工后工件温度等情形下,因此必须在温湿度控制下,不可用手接触工件及量具、工件加工后待冷却后才测量;但为了缩短加工时在加工中需实时测量,因此必须考虑各种材料之热胀系数作为补偿,以因应温度材料的热膨胀系数不同所造成的误差;在实际的测量工作中,大量实践表明,当对某一未知量进行多次观测时,不论测量仪器有多精密,观测进行得多么仔细,所得的观测值之间总是不尽相同;这种差异都是由于测量中存在误差的缘故;测量所获得的数值称为观测值;由于观测中误差的存在而往往导致各观测值与其真实值简称为真值之间存在差异,这种差异称为测量误差或观测误差;用L代表观测值,X代表真值,则误差=观测值L—真值X,即∆ 5-1X=L-这种误差通常又称之为真误差;由于任何测量工作都是由观测者使用某种仪器、工具,在一定的外界条件下进行的,所以,观测误差来源于以下三个方面：观测者的视觉鉴别能力和技术水平；仪器、工具的精密程度；观测时外界条件的好坏;通常我们把这三个方面综合起来称为观测条件;观测条件将影响观测成果的精度：若观测条件好,则测量误差小,测量的精度就高；反之,则测量误差大,精度就低；若观测条件相同,则可认为精度相同;在相同观测条件下进行的一系列观测称为等精度观测；在不同观测条件下进行的一系列观测称为不等精度观测;由于在测量的结果中含有误差是不可避免的,因此,研究误差理论的目的不是为了去消灭误差,而是要对误差的来源、性质及其产生和传播的规律进行研究,以便解决测量工作中遇到的一些实际问题;例如：在一系列的观测值中,如何确定观测量的最可靠值；如何来评定测量的精度；以及如何确定误差的限度等;所有这些问题,运用测量误差理论均可得到解决;二、测量误差的分类测量误差按其性质可分为系统误差和偶然误差两类：一系统误差在相同的观测条件下,对某一未知量进行一系列观测,若误差的大小和符号保持不变,或按照一定的规律变化,这种误差称为系统误差;例如水准仪的视准轴与水准管轴不平行而引起的读数误差,与视线的长度成正比且符号不变；经纬仪因视准轴与横轴不垂直而引起的方向误差,随视线竖直角的大小而变化且符号不变；距离测量尺长不准产生的误差随尺段数成比例增加且符号不变;这些误差都属于系统误差;系统误差主要来源于仪器工具上的某些缺陷；来源于观测者的某些习惯的影响,例如有些人习惯地把读数估读得偏大或偏小；也有来源于外界环境的影响,如风力、温度及大气折光等的影响;系统误差的特点是具有累积性,对测量结果影响较大,因此,应尽量设法消除或减弱它对测量成果的影响;方法有两种：一是在观测方法和观测程序上采取一定的措施来消除或减弱系统误差的影响;例如在水准测量中,保持前视和后视距离相等,来消除视准轴与水准管轴不平行所产生的误差；在测水平角时,采取盘左和盘右观测取其平均值,以消除视准轴与横轴不垂直所引起的误差;另一种是找出系统误差产生的原因和规律,对测量结果加以改正;例如在钢尺量距中,可对测量结果加尺长改正和温度改正,以消除钢尺长度的影响;二偶然误差在相同的观测条件下,对某一未知量进行一系列观测,如果观测误差的大小和符号没有明显的规律性,即从表面上看,误差的大小和符号均呈现偶然性,这种误差称为偶然误差;例如在水平角测量中照准目标时,可能稍偏左也可能稍偏右,偏差的大小也不一样；又如在水准测量或钢尺量距中估读毫米数时,可能偏大也可能偏小,其大小也不一样,这些都属于偶然误差;产生偶然误差的原因很多,主要是由于仪器或人的感觉器官能力的限制,如观测者的估读误差、照准误差等,以及环境中不能控制的因素如不断变化着的温度、风力等外界环境所造成;偶然误差在测量过程中是不可避免的,从单个误差来看,其大小和符号没有一定的规律性,但对大量的偶然误差进行统计分析,就能发现在观测值内部却隐藏着一种必然的规律,这给偶然误差的处理提供了可能性;测量成果中除了系统误差和偶然误差以外,还可能出现错误有时也称之为粗差;错误产生的原因较多,可能由作业人员疏忽大意、失职而引起,如大数读错、读数被记录员记错、照错了目标等；也可能是仪器自身或受外界干扰发生故障引起的；还有可能是容许误差取值过小造成的;错误对观测成果的影响极大,所以在测量成果中绝对不允许有错误存在;发现错误的方法是：进行必要的重复观测,通过多余观测条件,进行检核验算；严格按照国家有关部门制定的各种测量规范进行作业等;在测量的成果中,错误可以发现并剔除,系统误差能够加以改正,而偶然误差是不可避免的,它在测量成果中占主导地位,所以测量误差理论主要是处理偶然误差的影响;下面详细分析偶然误差的特性;三、偶然误差的特性偶然误差的特点具有随机性,所以它是一种随机误差;偶然误差就单个而言具有随机性,但在总体上具有一定的统计规律,是服从于正态分布的随机变量;在测量实践中,根据偶然误差的分布,我们可以明显地看出它的统计规律;例如在相同的观测条件下,观测了217个三角形的全部内角;已知三角形内角之和等于180°,这是三内角之和的理论值即真值X,实际观测所得的三内角之和即观测值L;由于各观测值中都含有偶然误差,因此各观测值不一定等于真值,其差即真误差Δ;以下分两种方法来分析：一表格法由5-1式计算可得217个内角和的真误差,按其大小和一定的区间本例为dΔ=3″,分别统计在各区间正负误差出现的个数k及其出现的频率k/nn=217,列于表5-1中;从表5-1中可以看出,该组误差的分布表现出如下规律：小误差出现的个数比大误差多；绝对值相等的正、负误差出现的个数和频率大致相等；最大误差不超过27″;实践证明,对大量测量误差进行统计分析,都可以得出上述同样的规律,且观测的个数越多,这种规律就越明显;表5-1 三角形内角和真误差统计表二直方图法为了更直观地表现误差的分布,可将表5-1的数据用较直观的频率直方图来表示;以真误差的大小为横坐标,以各区间内误差出现的频率k /n 与区间d △的比值为纵坐标,在每一区间上根据相应的纵坐标值画出一矩形,则各矩形的面积等于误差出现在该区间内的频率k /n ;如图5-1中有斜线的矩形面积,表示误差出现在+6″～+9″之间的频率,等于;显然,所有矩形面积的总和等于1;可以设想,如果在相同的条件下,所观测的三角形个数不断增加,则误差出现在各区间的频率就趋向于一个稳定值;当n →∞时,各区间的频率也就趋向于一个完全确定的数值——概率;若无限缩小误差区间,即d △→0,则图5-1各矩形的上部折线,就趋向于一条以纵轴为对称的光滑曲线如图5-2所示,称为误差概率分布曲线,简称误差分布曲线,在数理统计中,它服从于正态分布,该曲线的方程式为式中：Δ为偶然误差；σ＞0为与观测条件有关的一个参数,称为误差分布的标准差,它的大小可以反映观测精度的高低;其定义为：在图5-1中各矩形的面积是频率k /n ;由概率统计原理可知,频率即真误差出现在区间d △上的概率P Δ,记为22221)(σπσ∆-=∆ef 5-2[]nn ∆∆=∞→limσ5-3根据上述分析,可以总结出偶然误差具有如下四个特性：1 有限性：在一定的观测条件下,偶然误差的绝对值不会超过一定的限值；2 集中性：即绝对值较小的误差比绝对值较大的误差出现的概率大；3 对称性：绝对值相等的正误差和负误差出现的概率相同；4 抵偿性：当观测次数无限增多时,偶然误差的算术平均值趋近于零;即[]0lim=∆∞→nn 5-5式中 []∑=∆=∆++∆+∆=∆n i i n 121在数理统计中,也称偶然误差的数学期望为零,用公式表示为E Δ=0; 图5-2中的误差分布曲线,是对应着某一观测条件的,当观测条件不同时,其相应误差分布曲线的形状也将随之改变;例如图5-3中,曲线I 、II 为对应着两组不同观测条件得出的两组误差分布曲线,它们均属于正态分布,但从两曲线的形状中∆∆=∆∆=∆d f d d nk P )(/)(5-4可以看出两组观测的差异;当Δ=0时,πσ21)(11=∆f ,πσ21)(22=∆f ;πσ211、πσ212是这两误差分布曲线的峰值,其中曲线I 的峰值较曲线II 的高,即σ1＜σ2,故第I 组观测小误差出现的概率较第II 组的大;由于误差分布曲线到横坐标轴之间的面积恒等于1,所以当小误差出现的概率较大时,大误差出现的概率必然要小;因此,曲线I 表现为较陡峭,即分布比较集中,或称离散度较小,因而观测精度较高;而曲线II 相对来说较为平缓,即离散度较大,因而观测精度较低;第二节 评定精度的指标研究测量误差理论的主要任务之一,是要评定测量成果的精度;在图5-3中,从两组观测的误差分布曲线可以看出：凡是分布较为密集即离散度较小的,表示该组观测精度较高；而分布较为分散即离散度较大的,则表示该组观测精度较低;用分布曲线或直方图虽然可以比较出观测精度的高低,但这种方法即不方便也不实用;因为在实际测量问题中并不需要求出它的分布情况,而需要有一个数字特征能反映误差分布的离散程度,用它来评定观测成果的精度,就是说需要有评定精度的指标;在测量中评定精度的指标有下列几种：一、 中误差由上节可知5-3式定义的标准差是衡量精度的一种指标,但那是理论上的表达式;在测量实践中观测次数不可能无限多,因此实际应用中,以有限次观测个数n 计算出标准差的估值定义为中误差m ,作为衡量精度的一种标准,计算公式为nm ][ˆ∆∆±=±=σ5-6例5-1有甲、乙两组各自用相同的条件观测了六个三角形的内角,得三角形的闭合差即三角形内角和的真误差分别为：甲：+3″、+1″、-2″、-1″、0″、-3″； 乙：+6″、-5″、+1″、-4″、-3″、+5″; 试分析两组的观测精度; 解用中误差公式5-6计算得：()()()()()3.46534156][0.26301213][222222222222''±=+-+-++-+±=∆∆±=''±=-++-+-++±=∆∆±=）（乙甲nm n m从上述两组结果中可以看出,甲组的中误差较小,所以观测精度高于乙组;而直接从观测误差的分布来看,也可看出甲组观测的小误差比较集中,离散度较小,因而观测精度高于乙组;所以在测量工作中,普遍采用中误差来评定测量成果的精度;注意：在一组同精度的观测值中,尽管各观测值的真误差出现的大小和符号各异,而观测值的中误差却是相同的,因为中误差反映观测的精度,只要观测条件相同,则中误差不变;在公式5-2中,如果令f Δ的二阶导数等于0,可求得曲线拐点的横坐标Δ=±σ≈m ;也就是说,中误差的几何意义即为偶然误差分布曲线两个拐点的横坐标;从图5-3也可看出,两条观测条件不同的误差分布曲线,其拐点的横坐标值也不同：离散度较小的曲线I,其观测精度较高,中误差较小；反之离散度较大的曲线II,其观测精度较低,中误差则较大;二、相对误差真误差和中误差都有符号,并且有与观测值相同的单位,它们被称为“绝对误差”;绝对误差可用于衡量那些诸如角度、方向等其误差与观测值大小无关的观测值的精度;但在某些测量工作中,绝对误差不能完全反映出观测的质量;例如,用钢尺丈量长度分别为100 m 和200 m 的两段距离,若观测值的中误差都是±2 cm,不能认为两者的精度相等,显然后者要比前者的精度高,这时采用相对误差就比较合理;相对误差K 等于误差的绝对值与相应观测值的比值;它是一个不名数,常用分子为1的分式表示,即T1==观测值误差的绝对值相对误差式中当误差的绝对值为中误差m 的绝对值时,K 称为相对中误差;mD Dm K 1==5-7在上例中用相对误差来衡量,则两段距离的相对误差分别为1/5000和1/10000,后者精度较高;在距离测量中还常用往返测量结果的相对较差来进行检核;相对较差定义为DD D D D D D ∆=∆=-平均平均平均返往1 5-8相对较差是真误差的相对误差,它反映的只是往返测的符合程度,显然,相对较差愈小,观测结果愈可靠;三、极限误差和容许误差 一极限误差由偶然误差的特性一可知,在一定的观测条件下,偶然误差的绝对值不会超过一定的限值;这个限值就是极限误差;在一组等精度观测值中,绝对值大于m 中误差的偶然误差,其出现的概率为%；绝对值大于2m 的偶然误差,其出现的概率为%；绝对值大于3m 的偶然误差,出现的概率仅为%;根据式5-2和式5-4有上式表示真误差出现在区间-σ,+σ内的概率等于,或者说误差出现在该区间外的概率为;同法可得上列三式的概率含义是：在一组等精度观测值中,绝对值大于σ的偶然误差,其出现的概率为%；绝对值大于2σ的偶然误差,其出现的概率为%；绝对值大于3()955.021)(222222222≈∆=∆∆=<∆<-⎰⎰+-∆-+-σσσσσπσσσd ed f P ()997.021)(333323322≈∆=∆∆=<∆<-⎰⎰+-∆-+-σσσσσπσσσd e d f P ()683.021)(222≈∆=∆∆=<∆<-⎰⎰+-∆-+-σσσσσπσσσd ed f Pσ的偶然误差,出现的概率仅为%;在测量工作中,要求对观测误差有一定的限值;若以m 作为观测误差的限值,则将有近32%的观测会超过限值而被认为不合格,显然这样要求过分苛刻;而大于3m 的误差出现的机会只有3‰,在有限的观测次数中,实际上不大可能出现;所以可取3m 作为偶然误差的极限值,称极限误差,m 3=∆极;二容许误差在实际工作中,测量规范要求观测中不容许存在较大的误差,可由极限误差来确定测量误差的容许值,称为容许误差,即m 3=∆容当要求严格时,也可取两倍的中误差作为容许误差,即m 2=∆容如果观测值中出现了大于所规定的容许误差的偶然误差,则认为该观测值不可靠,应舍去不用或重测;第三节 误差传播定律前面已经叙述了评定观测值的精度指标,并指出在测量工作中一般采用中误差作为评定精度的指标;但在实际测量工作中,往往会碰到有些未知量是不可能或者是不便于直接观测的,而由一些可以直接观测的量,通过函数关系间接计算得出,这些量称为间接观测量;例如用水准仪测量两点间的高差h ,通过后视读数a 和前视读数b 来求得的,h =a －b ;由于直接观测值中都带有误差,因此未知量也必然受到影响而产生误差;说明观测值的中误差与其函数的中误差之间关系的定律,叫做误差传播定律,它在测量学中有着广泛的用途;一、 误差传播定律设Z 是独立观测量x 1,x 2,…,x n 的函数,即 )(21n x x x f Z ，，， = a式中：x 1,x 2,…,x n 为直接观测量,它们相应观测值的中误差分别为m 1,m 2,…,m n ,欲求观测值的函数Z 的中误差m Z ;设各独立变量x i i =1,2,…,n 相应的观测值为L i ,真误差分别为Δx i ,相应函数Z 的真误差为ΔZ ;则因真误差Δx i 均为微小的量,故可将上式按泰勒级数展开,并舍去二次及以上的各项,得:a 减去b 式,得上式即为函数Z 的真误差与独立观测值L i 的真误差之间的关系式;式中ix f∂∂为函数Z 分别对各变量x i 的偏导数,并将观测值x i =L i 代入偏导数后的值,故均为常数;若对各独立观测量都观测了k 次,则可写出k 个类似于c 式的关系式将以上各式等号两边平方后再相加,得上式两端各除以k ,因各变量x i 的观测值L i 均为彼此独立的观测,则Δx i Δx j 当i ≠j 时,亦为偶然)(2211n n x x x x x x f Z Z ∆+∆+∆+=∆+，，， )()(221121n nn x x fx x f x x f x x x f Z Z ∆∂∂++∆∂∂+∆∂∂+=∆+ ，，， 2211n nx x f x x f x x f Z ∆∂∂++∆∂∂+∆∂∂=∆ ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧∆∂∂++∆∂∂+∆∂∂=∆∆∂∂++∆∂∂+∆∂∂=∆∆∂∂++∆∂∂+∆∂∂=∆)()(22)(11)()2()2(22)2(11)2()1()1(22)1(11)1( k n n k k k n n n n x x f x x f x x f Z x x f x x f x x f Z x x f x x f x x f Z [][][][][]j i nji j i j i n n x x xf x f x x f x x f x x f Z ∆∆⎪⎪⎭⎫⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂+∆⎪⎪⎭⎫ ⎝⎛∂∂++∆⎪⎪⎭⎫ ⎝⎛∂∂+∆⎪⎪⎭⎫ ⎝⎛∂∂=∆∑≠=1,22222221212 [][][][][]k x x x f x fk x x fkx x fkx x fkZ j i n ji j i j inn ∆∆⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂+∆⎪⎪⎭⎫⎝⎛∂∂++∆⎪⎪⎭⎫⎝⎛∂∂+∆⎪⎪⎭⎫⎝⎛∂∂=∆∑≠=1,22222221212][lim=∆∆∞→kx x j i k b误差;根据偶然误差的第四个特性可知,上式的末项当k →∞时趋近于0,即故上式可写为 根据中误差的定义,上式可写成当k 为有限值时,即22222221212n n z m xf m x f m x f m ⎪⎪⎭⎫⎝⎛∂∂++⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂= 5-9 或2222222121n nz m xf m x f m x f m ⎪⎪⎭⎫⎝⎛∂∂++⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂±= 5-10式中ix f∂∂为函数Z 分别对各变量x i 的偏导数,并将观测值x i =L i 代入偏导数后的值,故均为常数;公式5-9或5-10即为计算函数中误差的一般形式;从公式的推导过程,可以总结出求任意函数中误差的方法和步骤如下： 1．列出独立观测量的函数式：)(21n x x x f Z ，，， = 2．求出真误差关系式;对函数式进行全微分,得n ndx x fdx x f dx x f dZ ∂∂++∂∂+∂∂=2211 因dZ 、dx 1、dx 2、…都是微小的变量,可看成是相应的真误差ΔZ 、Δx 1、Δx 2、…,因此上式就相当于真误差关系式,系数ix f∂∂均为常数; 3．求出中误差关系式;只要把真误差换成中误差的平方,系数也平方,即可直接写出中误差关系式：[][][][]⎪⎪⎭⎫ ⎝⎛∆⎪⎪⎭⎫⎝⎛∂∂++∆⎪⎪⎭⎫⎝⎛∂∂+∆⎪⎪⎭⎫⎝⎛∂∂=∆∞→∞→kx x fkx x fkx x f kZ nn k k 22222221212lim lim 22222221212n nz xf x f x f σσσσ⎪⎪⎭⎫ ⎝⎛∂∂++⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂=22222221212n nzm xf m x f m x f m ⎪⎪⎭⎫⎝⎛∂∂++⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂= 按上述方法可导出几种常用的简单函数中误差的公式,如表5-2所列,计算时可直接应用;表5-2 常用函数的中误差公式二、 应用举例误差传播定律在测绘领域应用十分广泛,利用它不仅可以求得观测值函数的中误差,而且还可以研究确定容许误差值;下面举例说明其应用方法;例5-2在比例尺为1：500的地形图上,量得两点的长度为d = mm,其中误差m d =± mm,求该两点的实际距离D 及其中误差m D ;解：函数关系式为D =Md ,属倍数函数,M =500是地形图比例尺分母;mmm Mm m m mm Md D d D 1.0100)2.0(5007.11117004.23500±=±=±⨯====⨯==两点的实际距离结果可写为 m ± m;例5-3水准测量中,已知后视读数a = m,前视读数b = m,中误差分别为m a =± m,m b =± m,试求两点的高差及其中误差;解：函数关系式为h =a -b ,属和差函数,得mm m m mb a h b a h 004.0003.0002.0258.1476.0734.12222±=+±=+±==-=-=两点的高差结果可写为 m ± m;例5-4在斜坡上丈量距离,其斜距为L = m,中误差m L =± m,并测得倾斜角α=10°34′,其中误差m α=±3′,求水平距离D 及其中误差m D ;解：首先列出函数式αcos L D = 水平距离m D 303.243'3410cos 50.247=︒⨯=这是一个非线性函数,所以对函数式进行全微分,先求出各偏导值如下：864 3.45'3410sin 50.247'3410sin 830 9.0'3410cos -=︒⨯-=︒⋅-=∂∂=︒=∂∂L DLDα写成中误差形式mm D m L D m L D 06.0'3438'3)3864.45(05.09830.0 22222222±=⎪⎭⎫⎝⎛⨯-+⨯±=⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂±=αα故得D = m ± m;例5-5图根水准测量中,已知每次读水准尺的中误差为m i =±2 mm,假定视距平均长度为50 m,若以3倍中误差为容许误差,试求在测段长度为L km 的水准路线上,图根水准测量往返测所得高差闭合差的容许值;解：已知每站观测高差为：b a h -=则每站观测高差的中误差为：mm 222±==i h m m因视距平均长度为50 m,则每公里可观测10个测站,L 公里共观测10L 个测站,L 公里高差之和为：L h h h h 1021+++=∑L 公里高差和的中误差为：mm 5410L m L m h ±==∑往返高差的较差即高差闭合差为：返往h h f h ∑+∑= 高差闭合差的中误差为：mm 1042L m m h f ==∑以3倍中误差为容许误差,则高差闭合差的容许值为：mm 3810123L L m f h f h ≈±==容在前面水准测量的学习中,我们取L f h 40±=容mm 作为闭合差的容许值是考虑了除读数误差以外的其它误差的影响如外界环境的影响、仪器的i 角误差等;三、 注意事项应用误差传播定律应注意以下两点： 一要正确列出函数式例：用长30 m 的钢尺丈量了10个尺段,若每尺段的中误差为m l =±5 mm,求全长D 及其中误差m D ;全长m 300301010=⨯==l D ,l D 10=为倍乘函数;但实际上全长应是10个尺段之和,故函数式应为1021l l l D +++= 为和差函数;用和差函数式求全长中误差,因各段中误差均相等,故得全长中误差为mm 1610±==l D m m若按倍数函数式求全长中误差,将得出mm 5010±==l D m m按实际情况分析用和差公式是正确的,而用倍数公式则是错误的; 二在函数式中各个观测值必须相互独立,即互不相关;如有函数式1221++=y y z a 22321+==x y x y ； b若已知x 的中误差为m x ,求Z 的中误差m z ; 若直接用公式计算,由a 式得：21224y y z m m m +±= c而 x y x y m m m m 2321==， 将以上两式代入c 式得x x x z m m m m 5)2(4)3(22=+±=但上面所得的结果是错误的;因为y 1和y 2都是x 的函数,它们不是互相独立的观测值,因此在a 式的基础上不能应用误差传播定律;正确的做法是先把b 式代入a式,再把同类项合并,然后用误差传播定律计算;x m x x z 7m 57x 1)22(23z =⇒+=+++=第四节 等精度直接观测平差当测定一个角度、一点高程或一段距离的值时,按理说观测一次就可以获得;但仅有一个观测值,测的对错与否,精确与否,都无从知道;如果进行多余观测,就可以有效地解决上述问题,它可以提高观测成果的质量,也可以发现和消除错误;重复观测形成了多余观测,也就产生了观测值之间互不相等这样的矛盾;如何由这些互不相等的观测值求出观测值的最佳估值,同时对观测质量进行评估,即是“测量平差”所研究的内容;对一个未知量的直接观测值进行平差,称为直接观测平差;根据观测条件,有等精度直接观测平差和不等精度直接观测平差;平差的结果是得到未知量最可靠的估值,它最接近真值,平差中一般称这个最接近真值的估值为“最或然值”,或“最可靠值”,有时也称“最或是值”,一般用x 表示;本节将讨论如何求等精度直接观测值的最或然值及其精度的评定;一、等精度直接观测值的最或然值等精度直接观测值的最或然值即是各观测值的算术平均值;用误差理论证明如下：设对某未知量进行了一组等精度观测,其观测值分别为L 1、L 2、…L n ,该量的真值设为X ,各观测值的真误差为Δ1、Δ2、…、Δn ,则Δi =L i -Xi =1,2,…,n ,将各式取和再除以次数n ,得X nL n -=∆][][ 即X nn L +∆=][][根据偶然误差的第四个特性有X nL n =∞→][lim 所以0][lim=∆∞→n n 由此可见,当观测次数n 趋近于无穷大时,算术平均值就趋向于未知量的真值;当n 为有限值时,算术平均值最接近于真值,因此在实际测量工作中,将算术平均值作为观测的最后结果,增加观测次数则可提高观测结果的精度;二、评定精度 一 观测值的中误差 1．由真误差来计算当观测量的真值已知时,可根据中误差的定义即nm ][∆∆±= 由观测值的真误差来计算其中误差; 2．由改正数来计算在实际工作中,观测量的真值除少数情况外一般是不易求得的;因此在多数情况下,我们只能按观测值的最或然值来求观测值的中误差;1改正数及其特征最或然值x 与各观测值L i 之差称为观测值的改正数,其表达式为n)2,1( ，， =-=i L x v i i 5-11在等精度直接观测中,最或然值x 即是各观测值的算术平均值;即nL x ][=显然0][)(][1=-=-=∑=L nx L x v ni i 5-12上式是改正数的一个重要特征,在检核计算中有用; 2公式推导已知X L i i -=∆,将此式与式5-8相加,得X x v i i -=∆+ a令δ=-X x ,则δ+-=∆i i v b对上面各式两端取平方,再求和2][2][][δδn v vv +-=∆∆。

工程测量观测误差的形成原因及解决方法摘要：通过对工程测量观测误差成因的分析，得出了造成观测误差的主要原因是仪器误差、观测误差和外部环境的影响。

文章结合有关资料，从仪器设备的日常维护、观察技能、观察人员与观察工作的态度等方面，归纳出了如何控制这些误差。

关键词：工程测量；观测误差；形成原因；仪器误差前言：随着我国社会的迅速发展，我国的工程建设工程越来越多，而工程测量是其中的一个重要方面，它直接关系到工程的质量和安全性[1]。

在施工中，由于工程的计量错误，将会对项目的整体质量产生直接的影响。

故对对工程测量中存在的误差来源和控制对策进行分析具有重要的重要的指导作用。

一、工程测量误差形成原因（一）仪器误差在实际应用中，观测员依靠测量仪器(图一）来获得观测资料，但由于各测量仪具有特定的精度和应用需求，因此也会对观测结果产生影响[2]。

按测试的技术需求，选用各种类型的仪表，而较低档的仪表难以胜任较高的测试工作。

如果使用6英寸精密的全站仪作控制线，其结果远没有6英寸精密仪表来得精确。

又比如，水平仪的基本要求是水平仪，即采用了水平线上的泡沫点的居中。

气泡是否处于中心，需要肉眼来观测，因为受生物力学的制约，无法准确分辨出气泡的中心。

水平管中流体与管道表面的摩擦和粘着，称为水平管的泡心偏差。

其尺寸与水平管内壁弯度相关。

对比两者，前者占主导地位。

另外，还要配备相应的测量仪。

比如，在测量时，由于水平尺的雕刻问题，都会对测量的结果造成一定的影响。

随着现代电子学的发展，各类高精度的测控设备层出不穷，经纬仪和电磁波测距已经逐步被数字水准仪和电子全站仪所代替。

但是，再先进的仪器也只是使它的精确性得到改善，而它自身的错误是无法避免的。

我们只有在实际操作中进行控制。

图一工程测量仪（二）自然条件的影响在观察时，由于地形、温度、湿度、风力、大气折射、交通条件等，这些都会对测量结果产生不同程度的影响[3]。

而且，由于各种因素的变动，会对观察的结果造成一定的影响，从而导致测量的结果出现偏差。

《建筑工程测量》5测量误差在建筑工程领域，测量工作是至关重要的一环。

准确的测量数据为工程的设计、施工和质量控制提供了可靠的依据。

然而，在测量过程中，误差的存在是不可避免的。

了解测量误差的来源、性质和处理方法，对于提高测量精度、保证工程质量具有重要意义。

一、测量误差的定义和分类测量误差，简单来说，就是测量值与真实值之间的差异。

根据误差的性质和产生原因，可以将其分为系统误差、偶然误差和粗差三大类。

系统误差是在相同观测条件下，对某一量进行一系列观测，误差的大小和符号保持不变或按一定规律变化的误差。

例如，测量仪器的刻度不准确、测量方法的不完善等都可能导致系统误差的产生。

系统误差具有累积性，会对测量结果产生较大的影响，因此在测量工作中需要采取一定的措施来消除或减小系统误差。

偶然误差则是在相同观测条件下，对某一量进行一系列观测，误差的大小和符号没有明显的规律，但从总体上服从一定的统计规律的误差。

例如，观测者的读数误差、外界环境的微小变化等都可能引起偶然误差。

偶然误差不能通过某种方法消除，但可以通过增加观测次数、采用合理的测量方法等手段来减小其对测量结果的影响。

粗差是一种明显超出规定条件下预期的误差，通常是由于观测者的粗心大意、仪器故障等原因造成的。

粗差会严重影响测量结果的可靠性，在数据处理中需要及时发现并剔除。

二、测量误差的来源测量误差的来源是多方面的，主要包括以下几个方面：1、测量仪器误差测量仪器本身的精度和性能会对测量结果产生影响。

例如，仪器的制造误差、校准误差、老化磨损等都会导致测量结果的偏差。

2、观测者误差观测者的技术水平、操作习惯、工作态度等都会引入误差。

例如，观测者的读数不准确、记录错误、对测量方法的理解偏差等。

3、外界环境误差测量工作通常在外界环境中进行，外界环境的变化会对测量结果产生影响。

例如，温度、湿度、风力、大气折光等因素的变化都会导致测量误差的产生。

4、测量方法误差测量方法的选择不当或不完善也可能导致误差的产生。

1 工程测量常见错误及产生的原因1.1 测量人员流动性大，仪器管理混乱。

建筑工程施工测量人员是施工生产一线生产工人，野外作业时间长、风险责任大、条件艰苦，从测量建筑工程师至测量员，有条件的干一段时间可能就调离或是转行，如三亚洞库项目到完工，测量工作几次易人，有时还出现断档，使整个项目的测量工作没有到位。

测量仪器使用、保养、标定不能按规定规程进行，损坏、丢失严重，往往是出现明显错误的测量数据时才采取措施甚至有些施工企业把测量仪器设备划归物资部门管理，保管不合规程、记录不清，一套仪器再使用时已支离破碎。

1.2 测量人员素质及能力参差不齐。

部分建筑施工企业没有专职的施工测量人员，在施工过程中基本上都是由其他技术员(施工员)兼职，主要聘用测量工、学校刚毕业出来的人员担任测量负责人，无独立工作经验，这些缺乏专门训练的业余人员，对常规测量仪器的性能、操作及测量方法都一知半解，根本不能胜任施工测量工作，也就无法保证施工测量的质量。

1.3 测量仪器的操作不当，且日常保修不到位。

一般来说，测量所用的仪器都属于精密仪器，在使用过程中，由于测量人员的水平有限，没有严格按照正确的使用方法操作，导致测量仪器的灵敏度降低。

1.4 测量的质量监管与控制不到位。

对建筑工程质量的监控，现有的体制是政府监理和社会监理共同参与，有条件的建设单位，还有自己的建筑工程监督部门，可谓三管齐下。

但是，在实际的建筑工程质量监控和建筑工程竣工验收时，都只注重其他施工质量的检查与控制，而忽视施工测量质量的检验。

1.5 测量人员与设计、技术部分沟通协调不畅。

随着大型建筑工程项目的不断涌现，工程测量在先进仪器使用、精度要求上日益专业化，技术建筑工程师已不能完成施工放样、模板安装位置检查、隧道断面测量等工作，需要测量建筑工程师的全程参与测控。

2 工程测量中应注意的一些事项2.1 施测前，所用仪器和水准尺等器具必须经检校。

2.2 仪器要调平。

仪器不平时，望远镜绕横轴扫出的为一个斜面，读数时水准管泡要居中。

测绘技术中的常见测量误差及其处理方法测绘技术作为一门重要的地理信息科学与技术，广泛应用于城市规划、土地管理、工程建设等领域。

然而，由于测绘作业的复杂性和人为操作的不可避免性，常常会引入一些测量误差。

本文将讨论测绘技术中的常见测量误差及其处理方法，以帮助读者更好地理解和应用测绘技术。

一、数据采集误差数据采集是测绘技术的基础，而数据采集误差是最常见的误差类型之一。

数据采集误差包括人为操作误差、仪器精度误差和环境因素等。

为了降低数据采集误差，我们可以采取以下措施：1. 通过培训提高操作人员的专业水平，提高其对仪器的掌握程度；2. 使用高精度仪器进行测量，减小仪器精度误差；3. 在数据采集前，测量场地的环境因素，如气温、湿度等，并进行相应的纠正。

二、大地控制网误差大地控制网是测绘工程中至关重要的控制点系统，它的精度直接影响整个工程的测量结果。

大地控制网误差主要包括基线误差和观测角误差。

为了处理大地控制网误差，可以采用以下方法：1. 对基线进行精确观测，并使用精度较高的测量仪器；2. 在观测过程中，使用相同的仪器和观测方法，以减小观测角误差。

三、平差误差平差是一种常见的误差校正方法，可以通过对测量数据进行分析和处理，获得更准确的测量结果。

平差误差的主要类型包括观测误差、数据传输误差和计算误差。

以下是常用的平差处理方法：1. 最小二乘法平差：通过最小化观测值与平差值之间的差异来优化测量结果；2. 合理权值赋值：对不同测量数据赋予合理的权值，减小异常数据对平差结果的影响；3. 检查测量数据的合理性，排除错误数据。

四、引起图件误差的因素图件误差是指由于绘图过程中引入的误差，如绘图仪器的精度、绘制过程中的绘图误差等。

为了降低图件误差：1. 使用精度较高的绘图仪器，如CAD等；2. 在绘制过程中，注意操作规范，减小绘图误差；3. 对绘图过程进行审核，确保图件的准确性。

总结测绘技术中常见的测量误差包括数据采集误差、大地控制网误差、平差误差和图件误差。