第二章 湿空气的性质与冷却塔的热力计算

冷却塔计算公式与单位冷却塔是一种用于回收工业废热的设备，它通过将水与空气进行热量交换的方式来冷却热水。

冷却塔的性能通常使用一些计算公式和单位来评估，以下是一些与冷却塔相关的常见计算公式和单位。

1.计算湿球温度：湿球温度通常用于检测空气中的湿度，可通过以下公式计算：Tw = Tdb - (Tdb - Tdp) × RH/100其中，Tw表示湿球温度，Tdb表示干球温度，Tdp表示露点温度，RH 表示相对湿度。

2.计算露点温度：露点温度是一个表示空气中饱和水蒸汽开始凝结的温度值，可通过以下公式计算：Tdp = (243.12 × (17.62 × Tdb + 243.12) / (17.62 - Tdb)) / (log(RH/100) + ((17.62 × Tdb) / (243.12 + Tdb - (17.62 × Tdb))))其中，Tdb表示干球温度，Tdp表示露点温度，RH表示相对湿度。

3.计算湿度比：湿度比是空气中单位质量的水蒸汽含量，可以通过以下公式计算：W=(0.622×e)/(P-e)其中，W表示湿度比，e表示饱和水蒸汽压力，P表示空气压力。

4.计算冷却效能：冷却效能是衡量冷却塔性能的重要指标之一，可通过以下公式计算：E = (Tin - Tout) / (Tin - Twb)其中，E表示冷却效能，Tin表示进水温度，Tout表示出水温度，Twb表示湿球温度。

5.计算冷却水量：冷却水量是指单位时间内通过冷却塔的水量，可以通过以下公式计算：Q = m × Cp × (Tin - Tout)其中，Q表示冷却水量，m表示水的质量流率，Cp表示水的比热容，Tin表示进水温度，Tout表示出水温度。

6.计算空气流量：空气流量是指单位时间内通过冷却塔的空气量，可以通过以下公式计算：Qa=ρa×Va其中，Qa表示空气流量，ρa表示空气密度，Va表示空气流速。

冷却塔的热力计算冷却塔的任务是将一定水量Q ，从水温t 1冷却到t 2，或者冷却△t ＝t 1－t 2。

因此，要设计出规格合适的冷却塔，或核算已有冷却塔的冷却能力，我们必须做冷却塔的热力计算。

为了便于计算，我们对冷却塔中的热力过程作如下简化假设：（1）散热系数α，散质系数v β，以及湿空气的比热c ，在整个冷却过程被看作是常量，不随空气温度及水温变化。

(2) 在冷却塔内由于水蒸气的分压力很小，对塔内压力变化影响也很小，所以计算中压力取平均大气压力值。

（3）认为水膜或水滴的表面温度与内部温度一致，也就是不考虑水侧的热阻。

(4) 在热平衡计算中，由于蒸发水量不大，也可以将蒸发水量忽略不计。

(5) 在水温变化不大的范围内，可将饱和水蒸汽分压力及饱和空气与水温的关系假定为线性关系。

冷却塔的热力计算方法有焓差法、湿差法和压差法等，其中最常用的是麦克尔提出的焓差法，以下简要介绍冷却塔的焓差法热力计算。

麦克尔提出的焓差法把过去由温度差和浓度差为动力的传热公式，统一为一个以焓差为动力的传热公式。

在方程式中，麦克尔引进入刘易斯关系式，导出了以焓差为动力的散热方程式。

()dV h h dH t xv q 0"-=β （1）式中：q dH —— 水散出热量；xv β —— 以含湿差为基准的容积散质系数()[]kg kg s m kg //3⋅⋅ ；"t h —— 温度为水温t 时饱和空气比焓 (kg kJ /)； 0h —— 空气比焓 (kg kJ /)。

将式（1）代入冷却塔内热平衡方程：n w w q tdQ c Qdt c dH += （2）式中：q dH —— 水散出热量；w c —— 水的比热()[]C /J o ⋅kg k ；Q —— 冷却水量 (s /g k )； u Q —— 蒸发水量 (s /g k ) t —— 水温度 （℃）并引入系数K ：m w u m u w r tc Q r t Q c K 2211-=-=式中 m r ——塔内平均汽化热（kg kJ /）经整理，并积分后，可得冷却塔热力计算的基本方程式：⎰-=120"t t t wxv h h dt c Q vK β （3） 上式的左端表示在一定淋水填料及格型下冷却塔所具有的冷却能力，它与淋水填料的特性、构造、几何尺寸、冷却水量有关，称冷却塔的特性数，以符号愿'Ω表示，即：Q VK xv β=Ω'（3）式的右端表示冷却任务的大小，与气象条件有关，而与冷却塔的构造无关，称为冷却数(或交换数)，以符号'Ω表示，也即：⎰-=Ω120"t t t w h h dt c由于水温不是空气焓的直接函数，直接积分有困难，所以，在求解冷却数的时候，一般均采用近似积分方法。

冷却塔的热力计算冷却塔的任务是将一定水量Q ，从水温t 1冷却到t 2，或者冷却△t ＝t 1－t 2。

因此，要设计出规格合适的冷却塔，或核算已有冷却塔的冷却能力，我们必须做冷却塔的热力计算。

为了便于计算，我们对冷却塔中的热力过程作如下简化假设：（1）散热系数α，散质系数v β，以及湿空气的比热c ，在整个冷却过程被看作是常量，不随空气温度及水温变化。

(2) 在冷却塔内由于水蒸气的分压力很小，对塔内压力变化影响也很小，所以计算中压力取平均大气压力值。

（3）认为水膜或水滴的表面温度与内部温度一致，也就是不考虑水侧的热阻。

(4) 在热平衡计算中，由于蒸发水量不大，也可以将蒸发水量忽略不计。

(5) 在水温变化不大的范围内，可将饱和水蒸汽分压力及饱和空气与水温的关系假定为线性关系。

冷却塔的热力计算方法有焓差法、湿差法和压差法等，其中最常用的是麦克尔提出的焓差法，以下简要介绍冷却塔的焓差法热力计算。

麦克尔提出的焓差法把过去由温度差和浓度差为动力的传热公式，统一为一个以焓差为动力的传热公式。

在方程式中，麦克尔引进入刘易斯关系式，导出了以焓差为动力的散热方程式。

()dV h h dH t xv q 0"-=β （1） 式中：q dH —— 水散出热量；xv β —— 以含湿差为基准的容积散质系数()[]kg kg s m kg //3⋅⋅ ；"t h —— 温度为水温t 时饱和空气比焓 (kg kJ /)； 0h —— 空气比焓 (kg kJ /)。

将式（1）代入冷却塔内热平衡方程：n w w q tdQ c Qdt c dH += （2）式中：q dH —— 水散出热量；w c —— 水的比热()[]C /J o ⋅kg k ；Q —— 冷却水量 (s /g k )；u Q —— 蒸发水量 (s /g k )t —— 水温度 （℃） 并引入系数K ：式中 m r ——塔内平均汽化热（kg kJ /）经整理，并积分后，可得冷却塔热力计算的基本方程式：⎰-=120"t t t w xv h h dt c Q v K β （3） 上式的左端表示在一定淋水填料及格型下冷却塔所具有的冷却能力，它与淋水填料的特性、构造、几何尺寸、冷却水量有关，称冷却塔的特性数，以符号愿'Ω表示，即：（3）式的右端表示冷却任务的大小，与气象条件有关，而与冷却塔的构造无关，称为冷却数(或交换数)，以符号'Ω表示，也即：由于水温不是空气焓的直接函数，直接积分有困难，所以，在求解冷却数的时候，一般均采用近似积分方法。

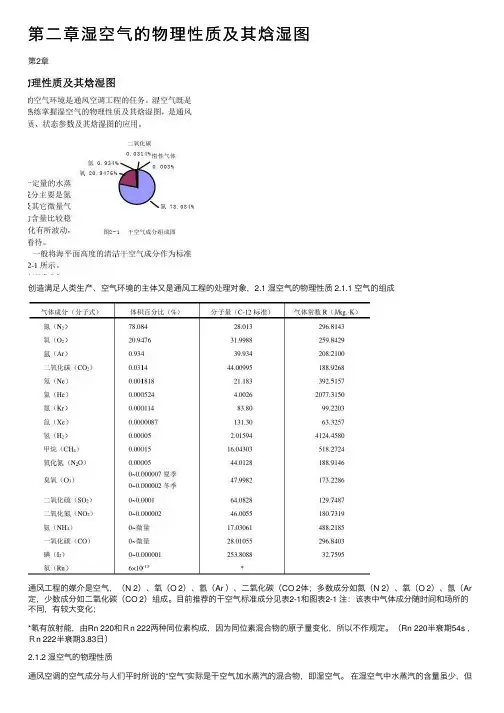
第⼆章湿空⽓的物理性质及其焓湿图第2章创造满⾜⼈类⽣产、空⽓环境的主体⼜是通风⼯程的处理对象，2.1 湿空⽓的物理性质 2.1.1 空⽓的组成通风⼯程的媒介是空⽓，（N 2）、氧（O 2）、氩（Ar ）、⼆氧化碳（CO 2体；多数成分如氮（N 2）、氧（O 2）、氩（Ar 定，少数成分如⼆氧化碳（CO 2）组成。

⽬前推荐的⼲空⽓标准成分见表2-1和图表2-1 注：该表中⽓体成分随时间和场所的不同，有较⼤变化；*氡有放射能，由Rn 220和Ｒn 222两种同位素构成，因为同位素混合物的原⼦量变化，所以不作规定。

（Rn 220半衰期54s ，Ｒn 222半衰期3.83⽇）2.1.2 湿空⽓的物理性质通风空调的空⽓成分与⼈们平时所说的“空⽓”实际是⼲空⽓加⽔蒸汽的混合物，即湿空⽓。

在湿空⽓中⽔蒸汽的含量虽少，但其变化却对空⽓环境的⼲燥和潮湿程度产⽣重要影响，且使湿空⽓的物理性质随之改变[4]。

因此研究湿空⽓中⽔蒸汽含量的调节在通风空调中占有重要地位。

地球表⾯的湿空⽓中，尚有悬浮尘埃、烟雾、微⽣物及化学排放物等，由于这些物质并不影响湿空⽓的热⼒学特性，因此本章不涉及这些内容。

1、压⼒空⽓分⼦永不停息、⽆规则的热运动对容器壁⾯产⽣的压强，习惯叫做空⽓的绝对静压，是⽓体状态的基本参量之⼀。

海平⾯的标准⼤⽓压为101325Pa 。

压⼒的单位有Pa 、mbar 等，⼤⽓压⼒各单位之间的换算见表2-2。

⼤⽓压⼒随海拔⾼度⽽变化，可由以下经验公式计算：2559.550)105577.21(H P P ??-=-，Pa （2-1）式中 P 0——海平⾯⼤⽓压⼒，Pa ；H ——海拔⾼度，m 。

当海平⾯P 0=101325Pa 时，可作出海拔⾼度和⼤⽓压⼒变化关系的曲线，⼤⽓压⼒随海拔⾼度的变化如图2-2所⽰。

⼤⽓压⼒值⼀般在⼠5%范围内波动。

-112345678405060708090100110⼤⽓压 P /k P a海拔⾼度 /km图2-2 ⼤⽓压与海拔⾼度的关系湿空⽓各组分⽓体的分压⼒遵循道尔顿定律。

冷却塔的热力计算冷却塔是一种用于降低流体温度的设备，广泛应用于石油化工、电力、空调等行业。

其基本原理是通过风和水的热交换来降低水的温度，以实现对流体的冷却。

首先，进行冷却塔热力计算时需要确定进出口流体的温度差，即冷却塔进口水温和出口水温的差值。

该温度差是衡量冷却效果的主要指标之一、通常情况下，冷却塔的设计师会根据具体需求和设备参数来确定这个温度差。

其次，需要确定进出口流体的流量。

流量是冷却效果的另一个重要指标，它直接影响到热负荷的大小。

通常情况下，冷却塔的设计师会根据设备和系统的需求来确定流量。

接下来，需要确定冷却塔的换热特性。

冷却塔的换热特性是指冷却塔的热传导效果。

在冷却塔的设计中，通常会采用一些换热器，如填料、喷淋装置等，来提高冷却效果。

根据填料的形状、材料和布置方式等因素，可以计算出冷却塔的换热特性。

在进行热力计算时，还需要考虑环境因素。

冷却塔通常通过与周围环境空气的接触来实现热交换。

因此，环境温度、湿度和风速等因素都会对冷却效果产生影响。

一般情况下，冷却塔的设计师会通过考虑这些因素来确定冷却塔的热力计算参数。

最后，通过以上参数的计算，可以得到冷却塔的热力计算结果。

这些结果包括冷却塔的热效率、冷却塔的工作量和冷却塔的能效比等。

根据这些结果，可以评估冷却塔的工作状态和性能，并进行必要的调整和优化。

冷却塔的热力计算是冷却塔设计和使用过程中的重要环节。

只有正确地进行热力计算，才能确保冷却塔的正常运行和达到预期的效果。

在实际应用中，还需要结合其他因素，如材料选择、环保要求等，进行综合考虑，以满足具体需求。

总之，冷却塔的热力计算是一项复杂而重要的任务。

合理的热力计算结果可以有效地指导冷却塔的设计和使用，提高冷却效果，降低能耗，并确保冷却塔的安全运行。

冷却塔的热力计算冷却塔的热力计算冷却塔的任务是将一定水量Q ，从水温t 1冷却到t 2，或者冷却△t ＝t 1－t 2。

因此，要设计出规格合适的冷却塔，或核算已有冷却塔的冷却能力，我们必须做冷却塔的热力计算。

为了便于计算，我们对冷却塔中的热力过程作如下简化假设：（1）散热系数α，散质系数v β，以及湿空气的比热c ，在整个冷却过程被看作是常量，不随空气温度及水温变化。

(2) 在冷却塔内由于水蒸气的分压力很小，对塔内压力变化影响也很小，所以计算中压力取平均大气压力值。

（3）认为水膜或水滴的表面温度与内部温度一致，也就是不考虑水侧的热阻。

(4) 在热平衡计算中，由于蒸发水量不大，也可以将蒸发水量忽略不计。

(5) 在水温变化不大的范围内，可将饱和水蒸汽分压力及饱和空气与水温的关系假定为线性关系。

冷却塔的热力计算方法有焓差法、湿差法和压差法等，其中最常用的是麦克尔提出的焓差法，以下简要介绍冷却塔的焓差法热力计算。

麦克尔提出的焓差法把过去由温度差和浓度差为动力的传热公式，统一为一个以焓差为动力的传热公式。

在方程式中，麦克尔引进入刘易斯关系式，导出了以焓差为动力的散热方程式。

()dV h h dH t xv q 0"-=β （1） 式中：q dH —— 水散出热量；xv β —— 以含湿差为基准的容积散质系数()[]kg kg s m kg //3⋅⋅ ；"t h —— 温度为水温t 时饱和空气比焓 (kg kJ /)； 0h —— 空气比焓 (kg kJ /)。

将式（1）代入冷却塔内热平衡方程：n w w q tdQ c Qdt c dH += （2）式中：q dH —— 水散出热量；w c —— 水的比热()[]C /J o ⋅kg k ；Q —— 冷却水量 (s /g k )； u Q —— 蒸发水量 (s /g k ) t —— 水温度 （℃）并引入系数K ：mw u m u w r tc Q r t Q c K 2211-=-=式中 m r ——塔内平均汽化热（kg kJ /）经整理，并积分后，可得冷却塔热力计算的基本方程式：⎰-=120"t t t w xv h h dt c Q vK β （3） 上式的左端表示在一定淋水填料及格型下冷却塔所具有的冷却能力，它与淋水填料的特性、构造、几何尺寸、冷却水量有关，称冷却塔的特性数，以符号愿'Ω表示，即：Q VK xv β=Ω'（3）式的右端表示冷却任务的大小，与气象条件有关，而与冷却塔的构造无关，称为冷却数(或交换数)，以符号'Ω表示，也即：⎰-=Ω120"t t t w h h dt c由于水温不是空气焓的直接函数，直接积分有困难，所以，在求解冷却数的时候，一般均采用近似积分方法。

冷却塔的热力计算冷却塔的任务是将一定水量Q ，从水温t 1冷却到t 2，或者冷却△t ＝t 1－t 2。

因此，要设计出规格合适的冷却塔，或核算已有冷却塔的冷却能力，我们必须做冷却塔的热力计算。

为了便于计算，我们对冷却塔中的热力过程作如下简化假设：（1）散热系数α，散质系数v β，以及湿空气的比热c ，在整个冷却过程被看作是常量，不随空气温度及水温变化。

(2) 在冷却塔内由于水蒸气的分压力很小，对塔内压力变化影响也很小，所以计算中压力取平均大气压力值。

（3）认为水膜或水滴的表面温度与内部温度一致，也就是不考虑水侧的热阻。

(4) 在热平衡计算中，由于蒸发水量不大，也可以将蒸发水量忽略不计。

(5) 在水温变化不大的范围内，可将饱和水蒸汽分压力及饱和空气与水温的关系假定为线性关系。

冷却塔的热力计算方法有焓差法、湿差法和压差法等，其中最常用的是麦克尔提出的焓差法，以下简要介绍冷却塔的焓差法热力计算。

麦克尔提出的焓差法把过去由温度差和浓度差为动力的传热公式，统一为一个以焓差为动力的传热公式。

在方程式中，麦克尔引进入刘易斯关系式，导出了以焓差为动力的散热方程式。

()dV h h dH t xv q 0"-=β （1）式中：q dH —— 水散出热量；xv β —— 以含湿差为基准的容积散质系数()[]kg kg s m kg //3⋅⋅ ；"t h —— 温度为水温t 时饱和空气比焓 (kg kJ /)；0h —— 空气比焓 (kg kJ /)。

将式（1）代入冷却塔内热平衡方程：n w w q tdQ c Qdt c dH += （2）式中：q dH —— 水散出热量；w c —— 水的比热()[]C /J o ⋅kg k ；Q —— 冷却水量 (s /g k )； u Q —— 蒸发水量 (s /g k ) t —— 水温度 （℃）并引入系数K ：mw u m u w r tc Q r t Q c K 2211-=-=式中 m r ——塔内平均汽化热（kg kJ /）经整理，并积分后，可得冷却塔热力计算的基本方程式：⎰-=120"t t t w xv h h dt c Q vK β （3） 上式的左端表示在一定淋水填料及格型下冷却塔所具有的冷却能力，它与淋水填料的特性、构造、几何尺寸、冷却水量有关，称冷却塔的特性数，以符号愿'Ω表示，即：Q VK xv β=Ω'（3）式的右端表示冷却任务的大小，与气象条件有关，而与冷却塔的构造无关，称为冷却数(或交换数)，以符号'Ω表示，也即：⎰-=Ω120"t t t w h h dt c由于水温不是空气焓的直接函数，直接积分有困难，所以，在求解冷却数的时候，一般均采用近似积分方法。

工艺设计计算书1． 热力性能计算 1．1 热力性能计算方法工艺设计采用CTI 颁布的权威软件“CTIToolkit ”进行设计，并按GB7190.2 ―1997《大型玻璃纤维增强塑料冷却塔》进行校核，用焓差法计算，积分计算采用辛普逊20段近似积分计算公式。

计算公式逆流冷却塔热力计算基本方程式：⎰-''=12t t w ii dtC N （1） 式中：t 1、t 2―进、出塔水温 ℃i ―冷却塔淋水装置中对应于某点温度的空气比焓 kJ/kg i ″ ―与i 对应的饱和空气焓 kJ/kg K ―蒸发水量带走的热量系数 )20(56.0585122---=t t K （2）20段近似积分计算公式：⎥⎦⎤⎢⎣⎡∆++∆+∆+∆++∆+∆+∆+∆⋅∆⋅=)111(2)111(4116018421931200i i i i i i i i t C N w（3） 式中：C w ―水的比热 4.1868 kJ/（kg ·℃） Δt ―进出水温差 ℃ Δt= t 1- t 2Δi 0，Δi 1，Δi 2，······Δi 19，Δi 20 ―分别表示对应于t 2，t 2+Δt/20，t 2+2Δt/20······t 2+19Δt/20，t 1时的焓差，即i ″- i kJ/kg 空气的焓按下式计算：““θθθθP P P C r C i q g ⋅Φ-⋅Φ++=00)(622.0 （4）式中：C g ―干空气的比热 1.005 kJ/kgC q ―水蒸气的比热 1.842 kJ/kgr 0 ―温度为0度时水的汽化热 2500.8kJ/kg θ ―空气干球温度 ℃ Φ ―相对湿度P 0 ―进塔空气大气压 kPaP “θ―空气温度为t 时的饱和水蒸气分压力 kPa 如取Φ=1，可将（4）改写为温度t 时的饱和湿空气焓计算式：““ttq g tP P P t C r t C i -++=00")(622.0 （5） 饱和水蒸气分压力及相对湿度按下式计算：)16.373(0024804.0)16.373lg(2.8)16.37311(305.31420141966.0T TT E -⋅-⋅+-⋅-=E t P 100665.98"⨯= （6） 式中：T ―绝对温度 K T=273.16+t"0")(000662.0θττθP P P --=Φ （7）式中：τ ―空气湿球温度，由机械通风干湿表测得 ℃ P “τ―空气温度为τ时的饱和水蒸气分压力 kPa将进塔空气干球温度θ1、湿球温度τ1及大气压P 0代入以上各式，即可求得进塔空气的相对湿度Φ和焓值i 1。

湿空气冷却计算示例湿空气冷却计算示例●湿空气冷却湿空气冷却时，存在两种情况：一种是冷却后温度高于湿空气的露点温度，此时湿空气冷却前后湿空气质量不变，湿空气中水蒸气分压力不变，湿空气中湿含量不变，湿空气的相对湿度变大。

另一种是冷却后温度低于湿空气的露点温度，此时湿空气冷却过程中会水蒸气凝结成液滴析出，冷却前后湿空气中干空气质量不变，水蒸气质量减少，湿空气中水蒸气分压力降低，湿空气中湿含量降低，湿空气的相对湿度变大且达到100%。

●冷却后温度高于露点温度时设湿空气质量为m aw，由温度t1冷却到t2，则冷却过程放热量为：Q c=m aw C paw-aw (t1-t2)式中，Q c为冷却过程中放热量，J；m aw为湿空气质量，kg；C paw-aw为基于湿空气质量的湿空气定压比热容，J/(K.kg(湿空气))；t1为冷却前湿空气的温度，℃；t2为冷却后湿空气的温度，℃。

计算示例：湿空气质量3kg，温度35℃，相对湿度60%，当冷却到30℃时，确定放热量和冷却后相对湿度。

35℃时，相应的纯水饱和蒸气压为5624 Pa，则湿空气中水蒸气的分压力为：p w=0.6×5624=3374 Pa由p w，可得湿空气的露点温度为26℃（湿空气冷却后温度高于其露点温度）。

设湿空气总压力（即大气压力）为101325Pa，则湿空气的湿含量为：d aw=0.622p w/(p aw-p w)=0.622×3374/(101325-3374)=0.0214g(水蒸气)/g(干空气)35℃时干空气的定压比热容C pa=1005J/(K.kg), 水蒸气的定压比热容C pw=1925J/(K.kg)，基于湿空气质量的湿空气定压比热容为：C paw-aw=C pa/(1+d aw)+d aw C pw/(1+d aw)=1005/(1+0.0214)+0.0214×1925/(1+0.0214)=1024J/(K.kg(湿空气))湿空气冷却过程放热量为：Q c=m aw C paw-aw (t1-t2)=3×1024×(35-30)=15360 J30℃时纯水的饱和蒸气压为4246Pa，冷却过程中水蒸气分压力不变，则冷却后湿空气相对湿度为：φ= p w /p s=3374/4246=79%说明：计算湿空气冷却或加热过程中放出或吸收的热量时，当冷却或加热前后温度变化不大时，可近似采用初始温度时湿空气的定压比热容；当温度变化较大时，宜采用冷却或加热前后平均温度下湿空气的定压比热容。

冷却塔的热力计算冷却塔的任务是将一定水量Q ，从水温t 1冷却到t 2，或者冷却△t ＝t 1－t 2。

因此，要设计出规格合适的冷却塔，或核算已有冷却塔的冷却能力，我们必须做冷却塔的热力计算。

为了便于计算，我们对冷却塔中的热力过程作如下简化假设：（1）散热系数α，散质系数v β，以及湿空气的比热c ，在整个冷却过程被看作是常量，不随空气温度及水温变化。

(2) 在冷却塔内由于水蒸气的分压力很小，对塔内压力变化影响也很小，所以计算中压力取平均大气压力值。

（3）认为水膜或水滴的表面温度与内部温度一致，也就是不考虑水侧的热阻。

(4) 在热平衡计算中，由于蒸发水量不大，也可以将蒸发水量忽略不计。

(5) 在水温变化不大的范围内，可将饱和水蒸汽分压力及饱和空气与水温的关系假定为线性关系。

冷却塔的热力计算方法有焓差法、湿差法和压差法等，其中最常用的是麦克尔提出的焓差法，以下简要介绍冷却塔的焓差法热力计算。

麦克尔提出的焓差法把过去由温度差和浓度差为动力的传热公式，统一为一个以焓差为动力的传热公式。

在方程式中，麦克尔引进入刘易斯关系式，导出了以焓差为动力的散热方程式。

()dV h h dH t xv q 0"-=β （1）式中：q dH —— 水散出热量；xv β —— 以含湿差为基准的容积散质系数()[]kg kg s m kg //3⋅⋅ ；"t h —— 温度为水温t 时饱和空气比焓 (kg kJ /)； 0h —— 空气比焓 (kg kJ /)。

将式（1）代入冷却塔内热平衡方程：n w w q tdQ c Qdt c dH += （2）式中：q dH —— 水散出热量；w c —— 水的比热()[]C /J o ⋅kg k ；Q —— 冷却水量 (s /g k )； u Q —— 蒸发水量 (s /g k ) t —— 水温度 （℃）并引入系数K ：m w u m u w r tc Q r t Q c K 2211-=-=式中 m r ——塔内平均汽化热（kg kJ /）经整理，并积分后，可得冷却塔热力计算的基本方程式：⎰-=120"t t t wxv h h dt c Q vK β （3） 上式的左端表示在一定淋水填料及格型下冷却塔所具有的冷却能力，它与淋水填料的特性、构造、几何尺寸、冷却水量有关，称冷却塔的特性数，以符号愿'Ω表示，即：Q VK xv β=Ω'（3）式的右端表示冷却任务的大小，与气象条件有关，而与冷却塔的构造无关，称为冷却数(或交换数)，以符号'Ω表示，也即：⎰-=Ω120"t t t w h h dt c由于水温不是空气焓的直接函数，直接积分有困难，所以，在求解冷却数的时候，一般均采用近似积分方法。