梁在简单载荷作用下变形的

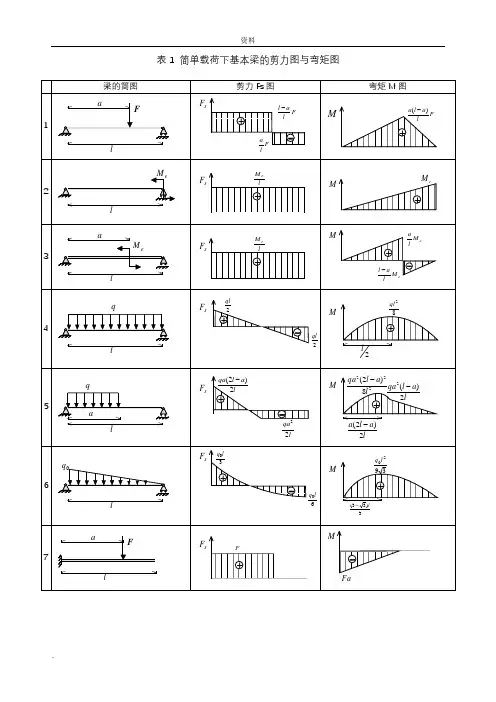
表1 简单载荷下基本梁的剪力图与弯矩图注：外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件常用截面几何与力学特征表表2-5 .......资料.注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰•=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：maxy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EI w 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

2）三跨等跨梁的内力和挠度系数 表2-12注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

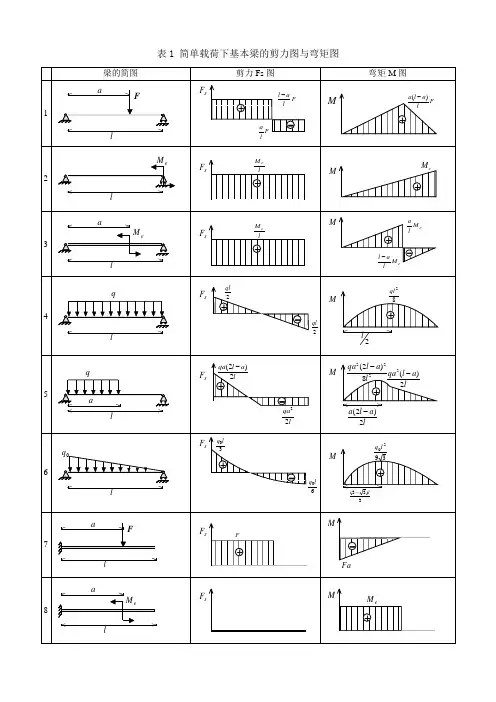
表1 简单载荷下基本梁的剪力图与弯矩图表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注：力边界条件即剪力图、弯矩图在该约束处的特征。

常用截面几何与力学特征表表2-5注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰•=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：m axy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

2）三跨等跨梁的内力和挠度系数 表2-12注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

东北农业大学网络教育学院建筑力学作业题（一）一、单项选择题（将正确答案字母序号填入括号里，每小题1分，共5分）1、平面力系向点1简化时，主矢F R ＝0，主矩M 1≠0，如将该力系向另一点2简化，则（ ）。

A ：F R ≠0，M 2≠0；B ：F R ＝0，M 2≠M 1；C ：F R ＝0，M 2＝M 1；D ：F R ≠0，M 2＝M 1。

2. 大小相等的四个力，作用在同一平面上且力的作用线交于一点C ，试比较四个力对平面上点O 的力矩，哪个力对O 点之矩最大（ ）A ．力P 1B ．力P 2C ．力P 3D ．力P 4 3. 两端铰支的等直压杆，其横截面如图所示。

试问压杆失稳时，压杆将绕横截面上哪一根轴转动？( ) Py 1Z 1yZA. Z 轴B. Y 轴C. Z 1轴D. Y 1轴4. 如图所示矩形截面，判断与形心轴z 平行的各轴中，截面对哪根轴的惯性距最小以下结论哪个正确？（ ）A. 截面对Z 1 轴的惯性矩最小B. 截面对Z 2 轴的惯性矩最小C. 截面对与Z 轴距离最远的轴之惯性矩最小D. 截面对Z 轴惯性矩最小5. 指出以下应力分布图中哪些是正确的（ ）• ·C P 1 P 2 P 3A. 图(a)(b) 正确B. 图(b)(c) 正确C. 图(c)(d) 正确D. 图(b) (d) 正确二、判断题（每小题1分，共5分）1. 作用在一个物体上有三个力，当这三个力的作用线汇交于一点时，此力系必然平衡。

（ ）2. 一空间力系，若各力作用线平行某一固定平面，则其独立的平衡方程只有3个。

（ ）3. 压缩与弯曲的组合变形，在进行强度计算时，如考虑附加弯矩的影响，结果是偏于安全的。

（ ）4. 下图为几何不变体系且无多余约束。

（ ）5. 矩形截面梁受横向力作用而弯曲时，其横截面上最大剪应力的大小是平均剪应力的3倍。

（ ）三、填空题（每空1分；共15分。

）1. 横截面面积A=10cm 2的拉杆，P=40KN ，当α=60°斜面上的σ = ，σα= ，τα= 。

y Fl 3 EI
§8-6 提高梁的刚度的措施
影响梁弯曲变形的因素不仅与梁的支承和载荷情况有关,而且还与梁 的材料、截面尺寸、形状和梁的跨度有关。所以,要想提高弯曲刚度,就应 从上述各种因素入手： 一、调整加载方式 二、减小跨度或增加支座 三、选择合理截面 四、合理选用材料
§8-6 提高梁的刚度的措施 一、合理安排梁的约束与加载方式
矩形木梁的合理高宽比 ( h/b= ) 1.5
b
英(T.Young)于1807年著«自然哲学与机械技术讲义 »一书中指出: 矩形木梁的合理高宽比 为
h 2 时,强 度 最 大; h 3 时,刚 度 最 大.
b
b
§8-6 提高梁的刚度的措施
三、选择合理截面
bh2 Wz 6
h2 d 2 b2
Wz
机械加工，镗孔，尾架，减少挠度。
§8-6 提高梁的刚度的措施
跨度为l 的简支梁，承受均布载荷q作用，如果将梁两端的铰支座各向 内移动 l/4，最大挠度将仅为前者的8.75%。
§8-6 提高梁的刚度的措施 三、选择合理截面
§8-6 提高梁的刚度的措施 三、选择合理截面
矩形木梁的合理高宽比
h 北宋李诫于1100年著«营造法式 »一书中指出:
b 6
(d 2
b2 )
d 2b b3 6
ቤተ መጻሕፍቲ ባይዱ
dW 0 db
d 2 3b2 0
b d 3
h d 2 b2 d 2 d 2 2d 33
h b
2d
3 d
23 2
3
h
b
§8-6 提高梁的刚度的措施 四、合理选用材料
各种材料的弹性模量E差别不大。 选用高强度材料，只能提高许用应力 同类的材料，“E”值相差不多，故换用同类材料只能提高强度，不能提高 刚度。

B
查表，得
y
C

y
4
Cq

y
Cm
l
q
A
2 5ql ml 384EI 16 EI
()
Bq
θA θAq θAm
3 ml ql 24 EI 3EI
Aq
m
A
C y cq
(
)
Bm
Am
C ycm
θB θBq θBm
3 ml ql 24 EI 6 EI
(
2
3
ml 16 EI
ml 3EI ml 3EI 一、梁的刚度条件
w
max
L
w L
max


1 1 w (对土建工程: ( ~ )) 250 1000 L
其中[]称为许用转角；[w/L]称为许用挠跨比。通常依此 条件进行如下三种刚度计算： 、校核刚度：
梁的变形及刚度计算 一、基本概念（挠度、转角、挠曲线） 取梁的左端点为坐标原点，梁变形前的轴线为 x 轴 ，横截面的铅垂对称轴为 y 轴 ， x y 平面为纵 向对称平面
x
A
y
B
一、基本概念（挠度、转角、挠曲线）
度量梁变形后横截面位移的两个基本量 1、挠度（ y）: 横截面形心 C (即轴线上的点)在垂直于 x
例题求图示梁截面B的挠度
q A EIz
a C
B
L
解法1：为了利用附录IV表中的结果，可将原荷载视 为图(1)和图(2)两种情况的叠加
q A EIz
a C
B
L L c q (2) B
q A c L (1) B A
a
q

(e) 结果（转角和挠度方程）。 AC段
ቤተ መጻሕፍቲ ባይዱ
Pb 2 2 EIv1 ' EI 1 (l b 2 3x1 ) 6l (0 x1 a) EIv Pb (l 2 b 2 x 2 ) 1 1 6l
CB段
Pb 2 2 3l 2 2 EIv2 ' EI 2 6l l b 3x b x 2 a (a x 2 l ) EIv Pb l 2 b 2 x 2 x l x a 3 2 2 2 6l b
例9-4。图示杆系中，AB和CD梁的抗弯为EI，BD杆的拉压刚度是EA，不计剪切变形的影响，求BD
杆的内力。
A
B l/2
解(a) 确定静不定梁的基本结构 取D为多余约束
A
R'D
B
C
l
D
D (1)
RD
C
(2)
D
(b) 求变形几何关系
vD1 vD2
(c) 求物理关系
l 3 RD l 2 R l l D 3EI EA 3EI 2 EA R' D l 3 ql 4 8 EI 3EI
第 9 章
梁的变形与刚度设计
DESIGN OF BEAMS FOR BENDING DEFLECTIONS
一。 弯曲变形概念
y
θ
P
受载荷作用后，梁的轴线将弯曲成为一条光滑的连续曲线 在平面弯曲的情况下，这是一条位于载荷所在平面内的平 面曲线。梁弯曲后的轴线称为挠曲线。
x
O
v
梁截面有沿垂直方向的线位移v，称为挠度；相对于原截面转过的角位移θ，称为转角 挠曲线是一条连续光滑平面曲线，其方程是

再积分一次，可以得到挠曲线方程
y 1 EI z [ ( M ( x ) dx ) dx Cx D )




【例 10.1】简支梁受均布荷载q作用，如图10.3所示，EI为常数。 试求此梁的转角和挠曲线方程，以及此梁的最大挠度ymax(通常用 符号f表示)和两端截面的转角θA和θB。 【解】(1) 列出挠曲线的近似微分方程 RA=RB= ql/2 M(x)= qlx/2 - qx2/2 EId2y/dx2 =-M(x)=- qlx/2 +qx2/2 (2) 积分 将上式连续积分两次，可以得到 EI dy/dx =EIθ=- qlx2/4 + qx3/6 +C EIy=- qlx3/12 + qx4/24 +Cx+D




(3) 确定积分常数 为了确定积分出现的四个积分常数，除了要利用边界条件外， 还要利用相邻两段梁在交接外变形的连续条件。 边界条件： x1=0，y1=0 x2=l，y2=0 连续条件： x1=x2=a，θ1=θ2y1=y2 将以上条件代入式(a)、(b)、(c)、(d)，联立求解，可得积分 常数 D1=D2=0C1=C2= Pb/6l (l2-b2)



【例11.5】一简支梁由18号工字钢制成，受均布荷载q的作用，如 图10.7所示。已知材料的E=210GPa，［σ］=150MPa，［f/l］ =1/400。试校核梁的强度和刚度。 【解】(1) 由型钢表查得18号工字钢 Wz=185cm3=185×103mm3 Iz=1660cm4=1660×104mm4 (2) 强度校核 Mmax= ql2/8 = 24×32/8kN· m=27kN· m σmax= Mmax/Wz = 27×106/185×103MPa=146MPa<［σ］

2 2
dvM dxEI ( z x)
θ ( x) = = ∫
⎛ M ( x) ⎞ v( x) = ∫ dxEI ⎜∫ z
dx + C
dx ⎟dx + Cx + D C,D 为积分常数，由梁的位移约束条件确定。 ⎝ EI z⎠ 挠曲线近似微分方程通解的积分常数确定以后，就得 到了挠曲线方程和转角方程，这种求梁变形的方法称为积 分法。
本章小结
挠曲线、挠度、转角、挠曲线方程、转角方程
v = f ( x)
θ = θ ( x)
挠曲线微分方程
dv θ ≈ tgθ = dx
dv ±
2
2
dx dv 2 ⎤⎡ 1+ ( ) ⎥⎢ dx ⎦⎣
将b处约束去掉基本静定系静定基相当系统加上q及约束力变形协调条件marblqlvbeirb39梁的位移计算本章小结挠曲线挠度转角挠曲线方程转角方程dx挠曲线微分方程dxdv40梁的位移计算积分法求梁的位移边界条件和连续条件dvmdxdx叠加法求梁的位移梁的刚度条件4041梁的位移计算提高梁的刚度的主要措施增大截面惯性矩
23
梁的位移计算
24
梁的位移计算
25
梁的位移计算
思考：
应用叠加法求梁的位移，必须满足的条件是什么？ 答：小变形，材料符合胡克定律。
26
梁的位移计算
4 3
已知图1B点的挠度和转角分别为 ql / 8 EI ， ql / 6 EI ， 图2C截面的转角为多少？
q
A
l
B
ql / 8 EI
3
q
A B
3
16
例
３
求简支梁最大挠度，Ｆ已知，EI为常数。
解
１、建立挠曲线微分方程

§8-3
用叠加法计算梁的变形及 梁的刚度计算
一、用叠加法计算梁的变形——简捷方法 叠加法应用的条件 在材料服从胡克定律、且变形很小的前 提下,载荷与它所引起的变形成线性关系。 即挠度、转角与载荷（如P、q、M）均为一次线性关系 计算梁变形时须记住梁在简单荷载作用下 的变形——转角、挠度计算公式（见附录Ⅳ）。
3 3
pl 7 pl 3 pl wc wc1 wc 2 24 EI 48EI 16 EI

B
c
c
p
这种分析方法叫做梁的逐段刚化法。
例题2 用叠加法求AB梁上E处的挠度 E
p
p
p
wE 2
wE 1
B
wE = wE 1+ wE 2 = wE 1+ wB/ 2
wB=?
P
机械：1/5000~1/10000,
土木：1/250~1/1000 机械：0.005~0.001rad
[w]、[θ]是构件的许可挠度和转角，它们决定于构 件正常工作时的要求。 [例8-8]图示工字钢梁，l =8m，Iz=2370cm4,Wz=237cm3 ，[ w/l ]= 1／500，E=200GPa，[σ]=100MPa。试根据梁 的刚度条件，确定梁的许可载荷 [P]，并校核强度。
例题 2
按叠加原理得
wC wC 1 wC 2
5ql 4 5ql 4 0 768EI 768EI
ql 3 ql 3 3ql 3 A A1 A2 48EI 384EI 128EI ql 3 ql 3 7ql 3 B B1 B 2 48EI 384EI 384EI
c
c
A
P M =Pl/2 B C B

跳板，木板横截面尺寸b=500 mm，h=50 mm，木板材料的许 用应力［σ］=6 MPa 。 试求：
(1) 一体重为700 N (2) 要求两名体重均为700 N的工人抬着1500 N的货物安全 走过，木板的宽度不变，重新设计木板厚度h。
第6章 弯 曲
解 (1) 计算弯矩的最大值Ｍmax。当工人行走到跳板中央
(2) 横截面上的弯矩在数值上等于该截面左侧(或右侧）所 有外力对该截面形心的力矩的代数和。
第6章 弯 曲
为了使所求得的剪力与弯矩符合前面的符号规定，按此 规律计算剪力时，截面左侧梁上外力向上取正值，向下取负 值，截面右侧梁上外力向下取正值，向上取负值；计算弯矩 时，截面左侧梁上外力对该截面形心的力矩顺时针转向取正 值，逆时针转向取负值，截面右侧外力对该截面形心的力矩 逆时针转向取正值，顺时针转向取负值。可以将这个规则归 纳为一个简单的口诀：左上右下，剪力为正；左顺右逆，弯 矩为正。
第6章 弯 曲 图 6.10
第6章 弯 曲 解 设截面m-m与B端之间的距离为x，取m-m截面的右段
为研究对象，画出受力图，如图6.10(b)所示。 根据平衡条件：
由Fs=qx可绘出剪力图，如图6.10(c)所示；由 描点可绘出弯矩图，如图6.10(d)
第6章 弯 曲
6.3 弯曲时的正应力与强度计算
m，材料的许用应力[σ]=150 MPa， 求此悬臂梁的许可载荷。
图 6.15
第6章 弯 曲 解 绘出悬臂梁的弯矩图，如图6.15(b)所示。 图中，Mmax=Fl=4000F 梁的横截面抗弯截面系数为
由梁的弯曲正应力强度条件得
因此, 悬臂梁的许可载荷为F=25 000 N。
第6章 弯 曲 【例6.5】 某建筑工地上, 用长l=3 m的矩形截面木板做

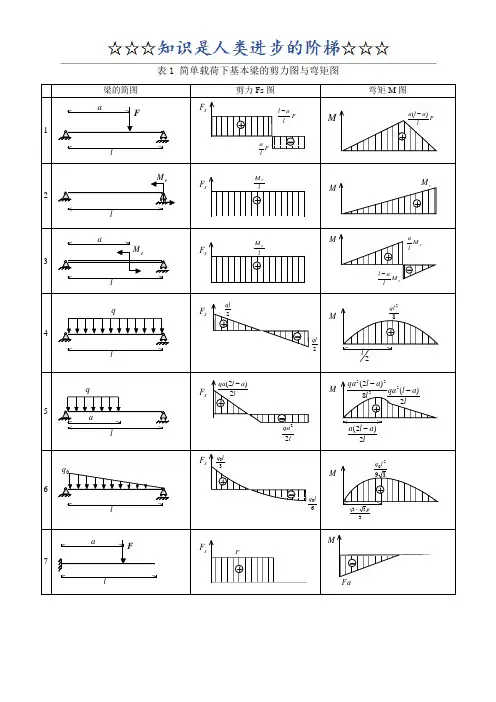
表1 简单载荷下基本梁的剪力图与弯矩图梁的简图剪力Fs 图弯矩M 图1laFsF F la F l al -+-F la l a )(-+M2l eMsF lM e +MeM +3laeMsF lM e +Me M lal -e M la +-4lqsF +-2ql 2qlM82ql +2l5lq asF +-la l qa 2)2(-lqa 22M2228)2(l a l qa -+la l qa 2)(2-la l a 2)2(-6lqsF +-30l q 60l qM3920l q +3)33(l-7aFlsF F+Fa-M8aleMsF+eM M9lqs F ql+M22ql -10lqsF 2l q +M620l q -表2 各种载荷下剪力图与弯矩图的特征某一段梁上的外力情况 剪力图的特征弯矩图的特征无载荷水平直线斜直线或集中力 F突变 F 转折或或集中力偶eM 无变化 突变e M均布载荷q斜直线抛物线 或零点极值表3 各种约束类型对应的边界条件约束类型 位移边界条件力边界条件（约束端无集中载荷）固定端0=w ,0=θ —简支端0=w0=M自由端 —0=M ,0=S F常用截面几何与力学特征表表2-5注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰•=AdA y I 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：max y IW =3．i 称截面回转半径（mm ），其基本计算公式如下：AI i = 4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EI w 100ql 表中系数4⨯=。

第二节
剪力和弯矩
图5-8 外伸梁
解1)求支座反力： 取整梁为研究对象，设FA、ＦB方向向上，列 平衡方程
第二节
剪力和弯矩
2)求各截面的剪力和弯矩：1-1截面左侧(图5-8b)，得 二、剪力图和弯矩图 (1)绘制梁内力图的基本方法和步骤 1)求支座反力。
第二节
剪力和弯矩
5M9.t作用处，以及分布载荷 的分布规律变化处(对均布载荷而言，
5M18.tif
3.组合截面惯性矩、平行移轴公式
第三节
(1)平行移轴公式
梁弯曲时横截面上的应力
工程上，梁常用的横截面形状，除了有简单的矩
形、圆形截面外，还有一些比较复杂的形状,这些截面可以看成由简 单截面组合而成。 (2)组合截面惯性矩的计算 由惯性矩定义可知，组合截面对某轴的
惯性矩等于各简单形状截面对同一轴惯性矩之和。
第四节
梁弯曲时的强度计算
图5-26 改善载荷的布置
2.选择合理的截面形状
(1)根据抗弯截面系数与截面面积的比值Wz/A选择截面
梁的承载能
力与抗弯截面系数Wz成正比，而用料的多少又与截面面积A成正比， 所以合理的截面形状应该是在截面积相同的情况下具有较大的抗弯 截面系数。
第四节
梁弯曲时的强度计算
表5-2 /A比值
第四节
梁弯曲时的强度计算
5M22.tif
解1)作弯矩图(图5-22b)。截面B有最大的负弯矩值，截面C有最大 正弯矩值。
第四节
3)校核强度。
梁弯曲时的强度计算
2)计算截面形心的位置及对中性轴的惯性矩。
二、提高梁弯曲强度的措施 1.降低最大弯矩值M (1)合理布置梁的支座 以简支梁受均布载荷作用为例(图5-23a),跨中

Fl
3

ql
4
3 EI
2
8 EI
3
B BF Bq
Fl

ql
2 EI
6 EI
§8-4 用叠加法求挠度和转角
F q
A
C a a B
按叠加原理求A点转角和C点挠度.
解:（a）载荷分解如图 （b）由梁的简单载荷变形表,
F
A
=
B
查简单载荷引起的变形.
( A ) F Fa
2
q
5qa
F
A
3 EI
24 EI
=
B
（c）叠加
A ( A )F ( A )q
a
2
(3 F 4qa )
+
q
A B
12 EI
yc ( yc ) F ( yc ) q
( 5qa
4

Fa
3
)
24 EI
6 EI
1
M
2
M
3
一、前提条件：弹性、小变形。 二、叠加原理：各荷载同时作用下，梁任一截面的挠度或转角，等于各荷 载分别单独作用下同一梁同一截面挠度或转角的代数和。
B ( F1 , F 2 , , F n ) B 1 ( F1 ) B 2 ( F 2 ) Bn ( F n )
§8-4 用叠加法求挠度和转角
解：集中力 F在B端产生的挠度和转角
y BF
Fl
3
3 EI
BF
Fl
2
2 EI
§8-4 用叠加法求挠度和转角
均布载荷q在B端产生的挠度和转角

10.3 叠加法求梁的转角和挠度
从上节几个例题可以看出, 梁的转角方程和挠度方程是梁上载荷的线性齐次函 数, 这是由于梁的变形通常很小, 梁变形后, 仍可按原始尺寸进行计算, 而且梁 的材料符合胡克定律。 在此情况下, 当梁上同时有几个载荷作用时, 由每一个 载荷所引起的转角和挠度不受其他载荷的影响。 这样, 就可应用叠加法。 用叠 加法求梁的转角和挠度的过程是: 先分别计算每个载荷单独作用下所引起的转 角和挠度, 然后分别求它们的代数和, 即得这些载荷共同作用时梁的转角和挠度。 叠加法虽然不是一个独立的方法, 但它对于计算几个载荷作用下梁指定截面的 转角或指定点的挠度是比较简便的。 为了便于应用, 表10-1中节录了简单载荷 作用下梁的转角和挠度。
现在讨论式(d)中正、 负号的选择问题。 式中的
的正、 负号应根据弯矩
正、 负号规定与选定的坐标系来确定。 由图10-3a可见, 当弯矩为正值时, 挠
曲线为凹向, 其二阶微分 亦为正值; 由图10-3b可见, 当弯矩为负值时, 挠
曲线为凸向, 其二阶微分为
负值。 由此可见, 对于所选定的坐标系, M
第10章 弯曲变形与简单超静定梁
10.1 梁的变形和位移
梁在载荷作用下, 即使具有足够的强度, 如果其变形过大, 也可能影响梁的正 常工作。 例如: 齿轮传动轴的变形过大, 会影响齿轮的啮合(图10-1); 起重 机大梁的变形过大, 会在起重机行驶时发生剧烈的振动等。 因此, 对梁的变 形有时需要加以限制, 使它满足刚度的要求。 与上述情况相反, 有时则要利用梁的变形来达到一定的目的。 有些机械零件, 例如车辆上的叠板弹簧, 就是利用它的变形来减轻撞击和振动的影响的。 此外, 在求解超静定梁时, 必须考虑梁的已知变形条件才能求解。 为了解决上述问题, 需要研究梁的变形。

表1 简单载荷下基本梁的剪力图与弯矩图注：外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注：力边界条件即剪力图、弯矩图在该约束处的特征。

电厂分散控制系统故障分析与处理作者：单位：摘要：归纳、分析了电厂DCS系统出现的故障原因，对故障处理的过程及注意事项进行了说明。

为提高分散控制系统可靠性，从管理角度提出了一些预防措施建议，供参考。

关键词：DCS故障统计分析预防措施随着机组增多、容量增加和老机组自动化化改造的完成，分散控制系统以其系统和网络结构的先进性、控制软件功能的灵活性、人机接口系统的直观性、工程设计和维护的方便性以及通讯系统的开放性等特点，在电力生产过程中得到了广泛应用，其功能在DAS、MCS、BMS、SCS、DEH系统成功应用的基础上，正逐步向MEH、BPC、ETS和ECS方向扩展。

但与此同时，分散控制系统对机组安全经济运行的影响也在逐渐增加；因此如何提高分散控制系统的可靠性和故障后迅速判断原因的能力，对机组的安全经济运行至关重要。

本文通过对浙江电网机组分散控制系统运行中发生的几个比较典型故障案例的分析处理，归纳出提高分散系统的可靠性的几点建议，供同行参考。

1考核故障统计浙江省电力行业所属机组，目前在线运行的分散控制系统，有TELEPERM-ME、MOD300，INFI-90，NETWORK-6000，MACSⅠ和MACS-Ⅱ，XDPS-400，A/I。

DEH有TOSAMAP-GS/C800，DEH-IIIA等系统。

笔者根据各电厂安全简报记载，将近几年因分散控制系统异常而引起的机组故障次数及定性统计于表1表1热工考核故障定性统计2热工考核故障原因分析与处理根据表1统计，结合笔者参加现场事故原因分析查找过程了解到的情况，下面将分散控制系统异常（浙江省电力行业范围内）而引起上述机组设备二类及以上故障中的典型案例分类浅析如下：2.1测量模件故障典型案例分析测量模件“异常”引起的机组跳炉、跳机故障占故障比例较高，但相对来讲故障原因的分析查找和处理比较容易，根据故障现象、故障首出信号和SOE记录，通过分析判断和试验，通常能较快的查出“异常”模件。

精品资料表1 简单载荷下基本梁的剪力图与弯矩图梁的简图剪力Fs 图弯矩M 图1laFsF F l a F l al -+-F la l a )(-+M2l eMsF lM e +MeM +3laeMsF lM e +Me M lal -e M la +-4lqsF +-2ql 2qlM82ql +2l5lqasF +-la l qa 2)2(-lqa 22M2228)2(l a l qa -+la l qa 2)(2-la l a 2)2(-6lqsF +-30l q 60l qM3920l q +3)33(l-7aFlsF F+Fa-M精品资料8aleMsF+eM M9lqs F ql+M22ql -10lqsF 2l q +M620l q -注：外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征某一段梁上的外力情况 剪力图的特征弯矩图的特征无载荷水平直线斜直线或集中力 F突变 F 转折或或集中力偶eM 无变化 突变e M均布载荷q斜直线抛物线或零点极值表3 各种约束类型对应的边界条件约束类型位移边界条件力边界条件精品资料（约束端无集中载荷）固定端0=w ,0=θ —简支端0=w0=M 自由端—0=M ,0=S F注：力边界条件即剪力图、弯矩图在该约束处的特征。

常用截面几何与力学特征表表2-5精品资料精品资料精品资料精品资料精品资料精品资料精品资料______________________________________________________________________________________________________________精品资料注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰∙=A dA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：max y IW =3．i 称截面回转半径（mm ），其基本计算公式如下：AI i = 4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

表 1 简单载荷下基本梁的剪力图与弯矩图注：外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁2．单跨梁的内力及变形表（表2-6~表2-10）1）简支梁的反力、剪力、弯矩、挠度表2-62）悬臂梁的反力、剪力、弯矩和挠度表2-73）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-84）两端固定梁的反力、剪力、弯矩和挠度表2-95 ）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14 ）1）二跨等跨梁的内力和挠度系数表2-11均布荷载 q ＝11.76kN/m ，每跨各有一集中荷载 F ＝29.4kN ，求中间支座的最大弯矩和剪力。

M B 支＝（－0.125×11.76×52）＋（－ 0.188×29.4×5）＝（－ 36.75）＋（ -27.64）＝－ 64.39kN ·mV B 左＝（－0.625×11.76×5）＋（－ 0.688×29.4）＝（－ 36.75）＋（－ 20.23）＝－ 56.98kN[例 2] 已知三跨等跨梁 l ＝ 6m ，均布荷载 q ＝11.76kN/m ，求边跨最大跨中弯矩 [解 ] M1 ＝ 0.080×11.76×62＝33.87kN ·m 。

2）三跨等跨梁的内力和挠度系数 表 2-12注： 1．在均布荷载作用下： M ＝表中系数×4ql 2；V ＝表中系数× ql ； w 表中系数ql。

100EI Fl 3Fl ；V ＝表中系数× F ； w 表中系数 Fl。

100EI2．在集中荷载作用下： M ＝表中系数×[例 1] 已知二跨等跨梁 l ＝5m ，［解］f ⅜ 跨内帰大 支座弯矩 弯矩荷載图VCXAflM 2-0.5500 -O I OSo-O (O 5Q0.4500.550(Jf≡¾-0,050 -0.500 D.0751-0.050 -0.050 -0,0500,5000.050UHiD跨度中点挠度-0.45(J 0,990 -0.625 0.990L A 4-L073L054-0÷117-0.033 0.383D-0.C67 0.0170.433f t J÷175 -0.150一(L 1500.350-0,075 -0.0750.425ΓJ⅛3.175 -0.075-0.075-0,07S0.050-0.3131 0,677 -0.313λ1620.1370 + 175-o r osα 0,325-0.617-0.4170*033 0.5β3 0.033-0.5670.0830.5730.365 -0.208-O.on-0,017 0.885 -0.313 0.104-0.650 0.500"-W0.650-0,5750 0.575-0.425E146 1.6150.208 1.146- 0,075- 0,50C 0.5000.0750.075-0Λ69-0.9371U46L 615-0.469-0,675-0.375 0,6250.0500.0500.9900.677 L 0.3124 注：1．在均布荷载作用下：M ＝表中系数× ql2；V＝表中系数× ql；w表中系数ql 100EI2．在集中荷载作用下：M ＝表中系数× Fl；V＝表中系数× F；w 表中系数Fl。