南京邮电大学2011-12研究生最优化试题标准答案[1]

（3） min z 2x1 3x2 x3 x1 4x2 2x3 8
s.t.3x1 2x2 6 x1, x2 , x3 0
解：引入剩余变量 x 4 , x5 和人工变量 x6 , x7 ,利用两阶段法得到辅助线性规划 max w x6 x7 max z' 2x1 3x2 x3
400 件，售货 600 件，五月份进货 500 件，售货 600 件，六月份进货 600 件售货 600 件时， 最大利润为 6100 元。
1.6 设市场上可买到 n 种不同的食品，第 j 种食品的单位售价为 c j ，每种食品含有 m 种基本 营养成分，第 j 种食品每一个单位含第 i 种营养成分为 aij ，每人每天对第 i 种营养成分的需 要量不少于 bi ，试确定在保持营养成分要求条件下的最经济食谱。
⑤因为 p2 , p4 线性相关， x 2 , x 4 不能构成基变量；
⑥因为 p3, p4 线性无关，可得基解 x(6) (0,0,1,1) ， z6 3 ；
所以 x(2) , x(4) , x(6) 是原问题的基可行解， x(6) 是最优解，最优值是 z 3 。
（2） max z x1 x2 2x3 x4 x5
x1
x2
x3
x4
x5
x6
x7
z'
5
0
1
4
2
w
5
0
-1
2
x2
1 4
1
1 2
x7
5 2
0
-1
3
0
4
3
0
4
1
-1
3
0
2
2
-1
0
1
0
2
4

min f g T p
p
s.t.
1 T p Bp 2 , 1 p 2 , p span g B g ,
1 1 其中 是信任域的半径， 而 p span g, B g 意味着 p g B g ( 和 为
两个实数)， g f ， B 是一个对称实矩阵。解决下面的问题：
为一个面积为 1 的正方形（如下图所示） 。
y 1 (xi, yj)
o
1
x
现在要求解满足下面两个条件的函数 z ( x, y ) ：
(i) z ( x, y ) 在定义域 S 上的曲面积分 A z x, y 最小； (ii) z x, y 在定义域 S 的边界上的点 x, y 的取值为给定值。
学时 50 学分 2.5 成绩
自动化工程学院 （学生填写）
学 院
1. (10 分)对于下面的线性规划问题：
min 5 x1 x2 s.t. 2x1 1 / 2 x2 8 x1 , x2 0 x1 x2 5
，
(a) 把上面问题改写为标准型(3 分)。 (b) 采用单纯形方法算法或者单纯形表计算本问题的最小值和对应的最小解
2
定义域 S 内部的点 xr , y s 所对应的函数值 z xr , ys ，满足上面的条件(i). 解决下面的问题： (a) 写出符合题意要求的优化问题的具体形式。
共
10
页，第 8
页
6. (20 分)二维子空间最小化(2-dimensional subspace minimization)是一种信任域 方法，其问题可以描述为：
1
共
10
页，第 2
页

信源解码3 S3 (t )
解密3
信道解码3 解扩器3 解扰器3 射频解调器3
信源解码4 S4 (t)
解密4
信道解码4 解扩器4 解扰器4 射频解调器4
4. 二进制的最佳接收机有两类：相关型最佳接收机和由匹配滤波器构成的最佳
接收机。相关型最佳接收机见书 P303 ，图 10-2 为不等概情况，图 10-3 为等
Si Ni
1 a2 =r= 2
n0 BBPF
1 ×10−6
=
2×
2 4 ×10−14
×
2×
2 ×106
= 1.56
3）非相干解调误码率为 Pe
=
1
−
e
1 2
r
2
=
1 e −0.78 2
=
0.23
八．1）
⎡0 0 1 1 0 0 0⎤
H
= ⎢⎢1 ⎢1
11
0
1
0
0
⎥ ⎥
1 0 0 0 1 0⎥
⎢⎣1 0 1 0 0 0 1⎥⎦
S3 (t)
信道
信源编码3 加密3 信道编码3 扩频器3 加扰器3 射频调制器3
S4 (t) 信源编码4 加密4 信道编码4 扩频器4 加扰器4 射频调制器4
信源解码1 S1 (t )
解密1
信道解码1 解扩器1 解扰器1 射频解调器1
信源解码2 解密2 信道解码2 解扩器2 解扰器2 射频解调器2 S2 (t)
2) Α = [1 0 0] • G = (1 0 0 0 1 1 1)
3) 可写出全部码组，计算每个码组的码重，最小的码重就是最小汉明距离
或者直接由生成矩阵可以看出最小汉明距离为 d0 = 3

mi 1 m *m j * g j (x*) 0最优化理论、方法及应用试题一、(30 分)1、针对二次函数f(x) 1x T Qx b T x c，其中Q是正定矩阵，试写出最速下降算法的详细步骤，并简要说明其优缺点？答：求解目标函数的梯度为g(x) Qx b，g k g(x k) Qx k b，搜索方向：从X k出发，沿g k作直线搜索以确定x k 1。

Stepl:选定X。

,计算f o,g oStep2:做一维搜索，f k i min f X k tg k , x k 1 X k tg k.Step3 :判别，若满足精度要求，则停止；否则，置 k=k+1,转步2优缺点：最速下降法在初始点收敛快，收敛速度慢。

算法简单，在最优点附近有锯齿现象,2、有约束优化问题min f (x)g i(x) 0,i 1,2,L ,ms.th j (x) 0,j 1,2,L ,l最优解的必要条件是什么？答：假设x*是极小值点。

必要条件是f，g，h函数连续可微，而且极小值点的所有起作用约束的梯度h(x*)(i 1,2丄，1)和g j(x*)( j 1,2,L ,m)线性无关，则* * * *存在1 , 2丄，I, 1, 2丄，m,使得lf(x*) i* h i(x*)i 1j*g j(x*) 0,j 1,2,L* * * * *1 ,2 ,L , l , 1 , 2 ,L ,*0, j 03、什么是起作用约束？什么是可行方向？什么是下降方向？什么是可行下降方向？针对上述有约束优化问题，如果应用可行方向法，其可行的下降方向怎样确定？答：起作用约束：若g j(x0) 0，这时点x0处于该约束条件形成的可行域边界上,它对x0的摄动起到某种限制作用可行方向：x0是可行点，某方向 p，若存在实数0 0,使得它对任意2、应用共轭梯度方法求解无约束优化问题 min X 28X |，初始点为X 0 1 1 丁 。

答：假设误差范围是0.001。

南京邮电大学2010/2011学年第二学期《高等数学A 》(下）期末试卷A 答案及评分标准 一、选择题（本大题分5小题，每题3分，共15分）1、交换二次积分⎰⎰x e dy y x f dx ln 01),(的积分次序为（c ）(A ) ⎰⎰x e dx y x f dy ln 01),( (B )⎰⎰1),(dx y x f dy e e y(C )⎰⎰eeydx y x f dy ),(10(D )⎰⎰ex dx y x f dy 1ln 0),(2、锥面22y x z +=在柱面x y x 222≤+内的那部分面积为 （D ）(A )⎰⎰-θππρρθcos 2022d d (B )⎰⎰-θππρρθcos 20222d d(C )⎰⎰-θππρρθcos 202222d d (D )⎰⎰-θππρρθcos 20222d d3、若级数∑∞=-1)2(n nn x a 在2-=x 处收敛，则级数∑∞=--11)2(n n n x na 在5=x （B ） (A ) 条件收敛 (B ) 绝对收敛 (C ) 发散(D ) 收敛性不确定 4、下列级数中收敛的级数为 （A ）(A ) ∑∞=-1)13(n nn n (B )∑∞=+121n n n (C ) ∑∞=+111sin n n (D )∑∞=13!n n n 5、若函数)()2()(2222x axy y i xy y x z f -+++-=在复平面上处处解析，则实常数a 的值 为 （c ）(A ) 0 (B ) 1 (C ) 2 (D ) -2二、填空题（本大题分5小题，每题4分，共20分）1、曲面122-+=y x z 在点)4,1,2(处的切平面方程为624=-+z y x2、已知)0(:222>=+a a y x L ，则=-+⎰Lds xy y x )]sin([22 32 a π 3、Ω是由曲面22y x z +=及平面)0(>=R R z 所围成的闭区域，在柱面坐标下化三重积分⎰⎰⎰+Ωdxdydz y x f )(22为三次积分为⎰⎰⎰RR dz f d d ρπρρρθ)(20204、函数x x f =)()0(π≤≤x 展开成以2π为周期的正弦级数为nx nx n n sin )1(211+∞=-=∑，收敛区间为π<≤x 05、=+-)1(i Ln2,1,0),243(2ln ±±=++k k i ππ=-]0,[Re 2zz e s z1-三、(本题8分）设),()(22xy y xg y x f z ++=，其中函数)(t f 二阶可导，),(v u g 具有二阶连续偏导数，求y x z x z ∂∂∂∂∂2,解：2112yg g y f x x z ++'=∂∂ … 3分=∂∂∂yx z2f xy ''4113122221g y x g y xyg g --++ 5分四、(本题8分）在已知的椭球面134222=++z y x 内一切内接的长方体（各边分别平行坐标轴）中，求最大的内接长方体体积。

《最优化方法》（研究生）期末考试练习题答案二.简答题1．;0, ,843 ,2 2-,3 34 s.t. ,95- min 2121212121≤=--≥+≥++y y y y y y y y y y 2．,065 6143≥+x x （以1x 为源行生成的割平面方程） 注意：在1x 为整数的情况下，因为3x ,04≥x ，该方程自然满足，这是割平面的退化情形,2141 41 43≥+x x （以2x 为源行生成的割平面方程）3．6648.31854.1*2)854.1()(2131.01146.1*2)146.1()(854.13*618.00)(618.0146.13*382.00)(382.03,031311111111111=+-==+-==+=-+==+=-+===μϕλϕμλa b a a b a b a 0.927.21.8540]1.8540[854.1,0)()(,*2211=+===≤x b a 近似的最优解：。

，初始的保留区间为即：。

所以，不经计算也可以看出事实上μϕλϕ4．令1.01.0)(4.04.0)(11)(7.27.2)(222222221)2(*111)1(*111)0(*121)1(*11-=-=-=-=-=-=-=-=-------x x x x x x x e x e x x f ex ex x f x e x x f e x e x x f拟合问题等价于求解下列最小二乘问题：∑=412))((mini ix f三.计算题1．分别用最速下降方法和修正的牛顿法求解无约束问题 22214)(min x x x f +=。

取初始点()()Tx 2,21=，.1.0=ε()().1641642,2821121⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫⎝⎛=∇=⎪⎪⎭⎫⎝⎛=∇d f x x x f T方向为：从而最速下降法的搜索，在初始点，解：()()()()直至满足精度。

继续迭代方向为：从而最速下降法的搜索，，在从而求解得到：其中满足最优步长,.48/6565/19248/65-65/19265/6,65/96)65/6,65/96((-4,-16)*130/172,2 130,/17.)162(4)42()162,42()()(min )(122221)1(1)1(1*)1(*⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛=∇-=-=+==-+-=--=++=+d f x x f d x f d x f d x f TTT Tλλλλλλλλλλ()()2-2- 1648/1002/1 8/1002/1,8002 2,21111⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=∇-=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛==--f G d G G x T索方向为：从而修正的牛顿法的搜，在初始点()()()()即为所求的极小点。

2
2006 五、画图题
2、 H (z)
1 z1 1 0.81z2
z
z(z 1)
0.9 jz
0.9
j
，幅频相应曲线为“双峰”，图略。
七、简单计算题
3、本人认为该题条件关系式 y(n) x2 (n) 可能是笔误，应该改为 y(n) x2 (2n) ，所以 y(n)
是对 x2 (n) 的偶数点抽取，且此时未被 y(n)抽取到的 x2 (n) 的奇数点样值全为零，再参考邓
2008 年 六、说明题
1、基本解题思路如下：（图来自西电高西全 DSP 教材，注意图中 k 的取值范围有印刷错误！）
2、栅栏效应
2009 年 一、填空题 2、参考邓书第 13 页 二、选择题 2、
四、证明题 1、见吴镇扬书第 136 页
五、分析题 1、
2010 年 2、1250，2500 考点：DFT 的频率选择性。
5、{2，1，0，0，4，3} 考点：循环移位定理 二、选择题 4、A 方法一：求出零极点，几何法画出幅频相应曲线；方法二：通过计算关键频率点的
响应值来估计，当 w=0 即 z=1 时，H(1) 0；当 w=pi 即 z=-1 时，H(-1)=0，故为低通。
五、设计题 2、（2）
3、
六、综合计算题
响应曲线右移 得到 HP DF 的幅频响应曲线，类似可得， z 2 对应于 e j2w ，即把 LP DF 的幅
频响应曲线横向压缩为原来的一半得到 BS DF 的幅频响应曲线。ps：今年复试重考了本题！ （6）能够分辨的两个频率分量的最小间隔 （12）半径稍小于 1 的圆上（参考张书 177 页） 3、简答题 （1）时不变：本人对该题答案所作出的时不变结论持怀疑态度，欢迎大家讨论！

南京邮电大学经济与管理学院数据结构1999——2006编译原理2000——2002，2004——2005操作系统2000——2001企业管理2000，2003——2005微观经济学2004——2006，2010（2010为回忆版）经济学原理2003通信与信息工程学院通信系统原理1998——2009（1999——2000，2007——2009有答案）数字信号处理1999——2006信号与系统2003——2006信号与线性系统1997，1999——2002微机原理及应用1999——2006（注：1999——2000年试卷名称为“微机原理”；2000年试卷共7页，缺第1页）电磁场理论1998——2004数字电路1999——2000电路分析1997，1999——2004计算机学院通信系统原理1998——2009（1999——2000，2007——2009有答案）微机原理及应用1999——2006（注：1999——2000年试卷名称为“微机原理”；2000年试卷共7页，缺第1页）数据结构1999——2006编译原理2000——2002，2004——2005操作系统2000——2001光电学院通信系统原理1998——2009（1999——2000，2007——2009有答案）光学2003——2004微机原理及应用1999——2006（注：1999——2000年试卷名称为“微机原理”；2000年试卷共7页，缺第1页）信号与系统2003——2006信号与线性系统1997，1999——2002电磁场理论1998——2004数字电路1999——2000电路分析1997，1999——2004自动化学院通信系统原理1998——2009（1999——2000，2007——2009有答案）信号与系统2003——2006信号与线性系统1997，1999——2002数字信号处理1999——2006电磁场理论1998——2004数字电路1999——2000电子测量原理2004电路分析1997，1999——2004数理学院（无此试卷）传媒技术学院教育学专业基础综合（全国统考试卷）2007——2009信息网络技术研究所通信系统原理1998——2009（1999——2000，2007——2009有答案）微机原理及应用1999——2006（注：1999——2000年试卷名称为“微机原理”；2000年试卷共7页，缺第1页）数据结构1999——2006编译原理2000——2002，2004——2005操作系统2000——2001电磁场理论1998——2004数字电路1999——2000电路分析1997，1999——2004。

最优化方法定义可行方案：如果一个方案能达到预定目的，则该方案就叫可行方案。

最优方案：可行方案中最好的方案叫最有方案，它能达到最优化效果。

最优化M题：如何从可行方案中找出最优方案就叫最优化M题。

最优化方法：求解最优化闷题的数学方法叫最优化方法。

最优化方法解决实际问题的一般步骤：1提出最优化问题，叙述目标是什么？约束条件是什么？求什么变量？即确定变量，列出目标函数及约束表达式，建立最优化问题的数学模型。

2分析模型，选择合适的求解方法。

3编制计算机程序，上机求最优解。

对算法的收敛性，通用性，简便性，效率及误差等作出评价。

系统：由相互联系的若干部分构成的具有一定功能的整体。

系统的基本特征：1系统巾若干部分组成，每一部分具有其特定的功能。

2系统屮的各个要素之间相互制约，联系和作用。

3系统是具有一定功能的整体，系统的总功能不等于各个部分功能的简单迭加，系统的功能大于各部分的功能之和。

4系统存在于一定的环境之中，系统与环境之间存在相互作川，系统与环境的划分是相对的，对于一个系统是环境，而对于另一个系统而言可能是其中的一部分。

系统分析法：1确定所研宄系统的范M及其所处的环境。

2确定系统的组成部分，结构，功能，目的，各部分的功能和闪部规律。

3明确系统各个部分之间的联系，及整个系统与环境之间的联系。

4在上述分析的基础上，确记问题的决策变量及评价方案优劣的指标。

决策变量：决定方案优劣的变量。

数学模型：用字母，数字，各种符号，图像，逻辑框图描述实际系统的特征和内在联系的模型。

数学模型的组成：1常数，指在所研究的问题中保持相对固定或变化不大的呈。

2参数由具体系统的内外部条件确定的量。

3变量，指在模型中待确定的量。

4函数关系描述模型中常数，参数，变量之间相互关系的方程式或不等式。

独立变量：彼此独立的变量。

相关变量：其值可由独立变量确定的量。

工程优化问题：最优准则包括系统性能准则和经济准则。

系统性能准则是指使系统的某些性能指标达到最大或最小。

2000年试题参考答案一、填空1、)(log 2i x p - ∑∞=-12)(log )(i i i x p x p p(x i )=n1i=1,2,3… 2、)2)(ex p(21)(22σσπa x x f --=ak 0(a H t E •=)0()]([ξ) π2020h w n k (输出噪声功率谱密度H o w w k n w p ≤=20)()3、恒参信道 随参信道 恒参信道4、接收信号中除当前码元以外的所有码元在抽样时刻的总和si ss T w T T i w H ππ22)4(≤=+∑+∞-∞= 部分响应系统 滚降系统（均衡） 5、相位连续 幅度恒定（能量集中） 带宽最小 6、2，17、h c c w w w w H w w H ≤=-++常数)()( 相干二、1、信息熵H=－p(x 1)2log p(x 1)－p(x 0)2log p(x 0)= bit/符号 信息速率Rb=1000×s=970 bit/s2、接收端收到0的概率p(0)=×+×=(全概率公式) 接收端收到1的概率p(1)=1－p(0)=平均丢失信息量H(x/y)= －p(0)[p(0/0)2log p(0/0)－p(1)2log p(1/0)] －p(1)[p(0/1)2log p(0/1)－p(1)2log p(1/1)]=[2log 2log 2log 2log bit/符号 信息传输速率R=1000(H －H(x/y))bit/s=810 bit/s三、1、mm f f w A k m =11022/1044=⨯===f m m f m radw vA srad k ππ2、)]102sin(102cos[)(46t t A t m s ⨯+⨯=ππ3、khz B m khzf m f B f f 40110)1(2===+=4、调制制度增益6)1(32=+=f f m m G 接收机输出信噪比3106161⨯==o o i i N S N S 噪声功率w k B n N i7120108401010222--⨯=⨯⨯⨯=⨯⨯= 接收机输入信号功率w N S i i 4310341061-⨯=⨯⨯=平均发射功率w S S i 3400106=⨯=四、1、等效带宽0041221ττππ=⨯=B 奈奎斯特传输速率baud R B 00max 21412ττ=⨯= 2、系统实际带宽0002121ττππ=⨯=B 最高频带利用率hz baud B R B /10max ==η3、s bit R R B b /238log 02max τ=⨯= 4、s bit R s bit R b b /23/340max 0ττ=<=但由于,2,1230=≠k kR b τ因此存在码间干扰（无码间干扰传输要求⋅⋅⋅==,2,1,max n nR R B B ） 五、发送”1”错判为”0”的概率2)1()1()(201011-=-+=-=⎰⎰+-+-A dV A V dV A V f Pe A A发送”0”错判为”1”的概率2)1()1()(210100-=--=-=⎰⎰--A dV A V dV A V f Pe AA系统误码率2)1(2121201-=+=A Pe Pe Pe （对双极性信号，最佳判决门限为Vd *=0）六、1、用π相位表示”1”，用0相位表示 ”0”，2PSK 波形如图1 1 0 0 1 1 0 02、baud k R s bit k R B b 2048/2048== 信号频率khz f s 2048=带宽khz f B s 40962== 频带利用率hz baud BR B/5.0==η 3、 框图如下图 (反向抽判)各点波形如下图参考”0” 1 1 0 0 1 1 0 0abcd七、1、输出信噪比N o M q S 222==，由题意7,102,10,40lg 10424≥≥≥≥N qSq S N o o 即 2、抽样频率m 2f f s ≥，码元周期s T s μ2=，码元速率Mbaud T R sB 5.01==，时分复用时，hz f R f m B s 3571,710≤≤⨯⨯3、为保证不过载，要求m s m s m m f f A f f A πσπ200,01.02≥=≤• 八、1、1),()(=-=k t T ks t h 一般情况2、3、最佳判决时刻取20T t =，02max 20max 2A ,41,2n Tr T A E n E r ===故 九、1、当输入为时，)(t δ系统冲激响应为)2()()(s T t t t h --=δδ，wTs j e w H 21)(--=2、易知该系统为第Ⅳ类部分响应系统，因此12-=r C r2001年试题参考答案一、填空 1、M 2logM s T 2log 1 s T 2 M 2log 212、R(∞) R(0) R(0)-R(∞)3、接收信号中除当前码元以外的所有码元在抽样时刻的总和si s sT w T T i w H ππ≤=+∑+∞-∞=)2( 部分响应系统 滚降系统（均衡） 4、552khz 96khz （为余数为最大整数，，k n kB nB f nkB f h s 22),1(2+=+=）5、最大似然比准则 -1 2psk6、最大输出信噪比准则 )()(*d jwt t t kS e W kS d --二、1、22/105.0)()()(322B f f B f hzw k f H f P f P c c i o +≤≤-⨯==- wB k df k df f P N Bf B f o o c c 32223210105.02)(-+--∞+∞-⨯=⨯⨯==⎰⎰（系数2是由于双边功率谱密度）2、）310)(5.0)(-⨯=τδτi R (注：）（频域，时域频域）（（时域w t πδδ211↔↔))]()([105.0)(32c B c B o f f g f f g k f P ++-⨯=-（选用f 作变量时，无系数2π）t f j c B t f j c B c c e Bt BSa f f g e Bt BSa f f g ππππ22)()(,)()(-↔+↔-（频域平移，c c f w π2=）32223210)2cos()(])()([105.0)(---⨯=+⨯=τπτπππτππc t f j t f j o f B BSa k e Bt BSa e Bt BSa k R c c 三、1、5=mmf W A k rad w v A v rad k m m f 33102,10,/10⨯===ππ,)102sin(10)(3t t m ⨯=π2、5==mm f f W A k m3、khz m f B f 126102)1(23=⨯⨯=+=,载频hz f c 610=4、输入信号功率w v S i 50002)100(2==输入噪声功率w B f Pn N i 4.2)(2== 调制制度增益450)1(32=+=f f m m G310375.94.25000450⨯=⨯=o o N S 四、信息码 1 0 1 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0差分码0 1 1 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 HDB3 +1 0 -1 0 +1 -1 +1 -1 +1 -1 0 0 0 –V +B 0 0 +V 0 0 五、1、抽样频率khz f s 8= 编码位数38log 2==N 带宽khz khz B 2408310=⨯⨯=2、khz B B 480)1('=+=α 六、 发送”1”错判为”0”的概率=--=-=⎰⎰∞-∞-dx A x dx A x f Pe Vd nnVd ]2)(exp[21)(221σσπ发送”0”错判为”1”的概率dx A x dx A x f Pe Vdn nVd⎰⎰∞-+-=+=]2)(exp[21)(2200σσπ系统误码率为dxA x p dx A x p Pe p Pe p Pe VdnnVdnn⎰⎰∞-∞-+-+--=+=]2)(exp[21)0(]2)(exp[21)1()0()1(222201σσπσσπ最佳判决门限设为*d V ，应使系统误码率最小。

南京邮电大学2011/2012学年第二学期《高等数学A 》期末试卷（A ）参考答案院(系) 班级 学号 姓名一、选择题（每小题3分，共15分）1、设L 是圆周=>=-+⎰Lyds a a a y x ，则)0()(222( D )22232)(4)(2)()(a D a C a B a A πππ2、积分⎰⎰=θπρρθρθρθcos 020)sin ,cos (d f d I 可以写成（ D ）(A )⎰⎰-2010),(y y dx y x f dy(B )⎰⎰-21010),(y dx y x f dy(C )⎰⎰1010),(dy y x f dx(D ) ⎰⎰-2010),(x x dy y x f dx3、若级数∑∞=--11)2(n n n x na 在2-=x 处收敛，则级数∑∞=+-+11)2(1n n nx n a 在5=x （ B ）(A )条件收敛 (B )绝对收敛 (C )发散 (D )收敛性不确定4、二元函数处在点)0,0()0,0(),(,0)0,0(),(,),(22M y x y x y x xyy x f ⎪⎩⎪⎨⎧=≠+= （ C ）(A ) 连续，偏导数存在 (B ) 连续，偏导数不存在 (C ) 不连续，偏导数存在 (D ) 不连续，偏导数不存在 5、i z =是函数)1)(1(2z e z zπ++的 （ C ）(A )本性奇点 (B )一级极点 (C )二级极点 (D )三级极点二、填空题（每小题3分，共15分）1、设2222:a z y x =++∑，则=+⎰⎰∑dS y x )2(22 44a π。

2、向量场]0),cos (),sin [(z y x y z A -+=的旋度为），，（011。

3、设⎪⎩⎪⎨⎧<<≤≤=ππππx x xx f 220)(，∑∞==1sin )(n nnx bx s ，其中⎰=ππsin )(2nxdx x f b n ,则=-)25(πS π43-。

来源于网络南京邮电大学2010/2011学年第二学期《高等数学A 》(下）期末试卷A 答案及评分标准 一、选择题（本大题分5小题，每题3分，共15分） 1、交换二次积分⎰⎰x e dy y x f dx ln 01),(的积分次序为 （c ）x e ln 1e (2积为 ((35=x(4、下列级数中收敛的级数为 （A ）(A ) ∑∞=-113(n nn n (B )∑∞=+121n n n (C ) ∑∞=+111sin n n (D )∑∞=13!n n n来源于网络5、若函数)()2()(2222x axy y i xy y x z f -+++-=在复平面上处处解析，则实常数a 的值 为 （c）(A ) 0 (B ) 1 (C ) 2 (D ) -2来源于网络二、填空题（本大题分5小题，每题4分，共20分）1、曲面122-+=y x z 在点)4,1,2(处的切平面=+-)1(i Ln2,1,0),243(2ln ±±=++k k i ππ=-]0,[Re 2zz e s z1-来源于网络三、(本题8分）设),()(22xy y xg y x f z ++=，其中函数)(t f 二阶可导，),(v u g 具有二阶连续偏导2028),,(=+=x yz z y x F x λ，来源于网络028),,(=+=y xz z y x F y λ，解得：1,31,32===z y x ， (3)分，证明：yx ∂∂，所以曲线积分与路径无关….3分….5分装 订 线内 不 要 答 题自觉遵 守 考 试规 则，诚 信 考 试，绝 不 作 弊七、(本题8分）计算⎰⎰++∑dxdy z dzdx y dydz x 333，其中?为上半球面221y x z --=的上侧。

来源于网络设,ln )(xxx f =2ln 1)(x x x f -='当e x >时单调递减，2、沿指定曲线的正向计算下列复积分⎰=-2||2)1(z zdz z z e来源于网络解：原式 =)]1),((Re )0),(([Re 2z f s z f s i +π…2分zz 解：++220)1)(1(y n y x 1)4(11++=n n π……2 分来源于网络∑∑∞=+∞=+=010)4(11n n n n nn x n x a π，,4π=R 收敛域：)4,4[-……2 分,0)0()0(='=f f 又)(x f 的二阶导数)(x f ''在]1,1[-内连续，所以K x f ≤''|)(|,!2)()0()0()(2x f x f f x f ξ''+'+= ξ在0与x 之间来源于网络|1(|n f ,22n K ≤ 所以∑∞=1n |)1(|n f 收敛，同理∑∞=1n |11(|+n f 也收敛……5 分 由于|1)11(|||||n f b b +≤|1)11(||1)1(|||n f n f b +≤|1)11(|||+≤n f b。

二、判断题（并作简要解释）1、OFDM 系统在发方使用FFT 进行多载波调制，在收方使用IFFT 调制。

2、有线信道属于恒参信道，又称时不变信道。

3、GSM 属于时分多址，3G 属于码分多址。

4、标准调幅AM 信号的包络调制解调属于线性解调方式。

5、部分响应改变了信号的谱特性，付出的代价是输出电平的增多，属于牺牲信噪比换取带宽。

6、一般来说数字信号通信中只有知道信号状态，信息接收机才能进行均衡。

7、在线路编码中，HDB 3的编码效率为1/2。

8、矩形脉冲由于频谱功率泄露到旁瓣较多，故不适合天线通信系统。

9、无线移动通信信道中运动的速度越大和波长越大，引入的多普勒效应就越大。

10、如果符号的间隔小于无线信道的相干时间，则该信道属于时间选择信道。

三、1、什么事二进制编码信道？画出示意图并写出误码率公式。

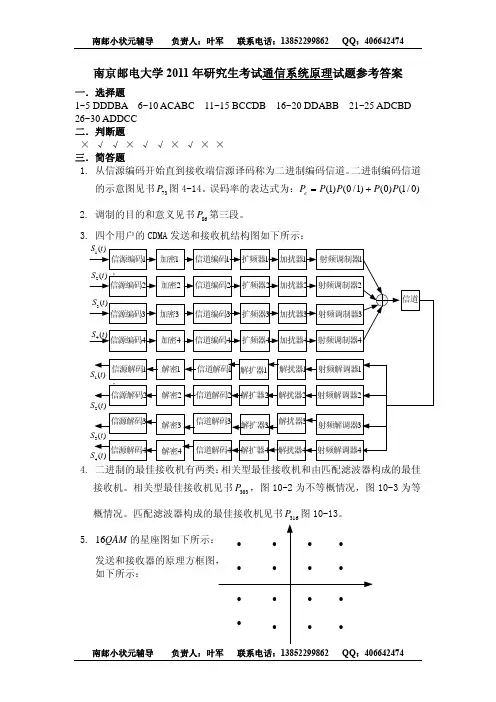
2、数字调制的目的和意义？3、四个用户的CDMA 发送与接收机构图，并做适当解释。

4、二进制最佳接收机原理框图，分等概和不等概，并作适当解释。

5、画出16QAM 的星座图，发送与接收器原理图，并作适当解释。

四、已知()[()]cos AM c S t A m t tω=+i 1）求总功率P AM ；2）指出载波功率P C 及边带功率P S ；3）求出信号的频谱并画图。

五、广义平稳的随机过程X （t ）通过下图所示线性时不变系统，已知X （t ）的自相关函数为R X （τ），功率谱密度为P X （f ），H （f ）是带宽为1/（2Ts ）的理想低通滤波器。

试求：1）写出系统的总体传递函数；2）Y （t ）的功率谱密度；3）画出Y （t ）的功率谱（假设输入带宽为宽带白噪声，单边功率谱密度为n 0）。

六、10路带宽为5KHz 的模拟基带信号数字化，然后进行时分复用传输。

采用256级均匀量化编码。

1）试画出该时分复用系统的帧结构（标明帧长时隙宽度）；2）求信号的传码率；3）求无码间串扰时所需最小系统带宽。

南京邮电大学2011/2012学年第 二 学期《通信原理B 》期末试卷（A ）院（系） ___________ 班级_________ 学号 _____________ 姓名 _____________ 题号 -一一 -二二四五六七八九总分得分得百一、选择题（2分X 10）：（答案写入框内，否则不得分）1、 下列选项中 —不是数字通信系统的优点。

A ）抗干扰性强B ）传输带宽大C ）差错可控制D ）易于加密2、 下列选项中不属于通信系统可靠性指标的是 _____ 。

A ）误码率B ）误信率C ）频带利用率D ）输出信噪比3、 香农公式指出，信道容量与下列 __________ 三个因素有关。

A ）频率、码元速率、信号幅度 B ）带宽、信号功率、噪声功率密度谱 C ）频率特性、信号分布、噪声分布D ）带宽、码元速率、信噪比4、 ____________________________________________________ 窄带高斯噪声的相位服从—分布，同相分量服从 _____________________________________________ 分布。

A ）均匀，正态 B ）瑞利，均匀C ）均匀，瑞利D ）不确定5、 下列系统中存在门限效应的是。

A ）相干 AMB ） DSBC ） FMD ） VSB6、 AM 信号一般采用 ___________ 解调，DSB 和SSB 信号采用 ________ 解调。

A ）包络，同步B ）鉴频器，同步C ）相干，差分相干D ）同步，包络 7、 数字基带信号的功率谱密度由 _______ 和 ______ 两部分组成。

A ）离散谱，线谱 B ）广义谱，谱线 C ）离散谱，连续谱 D ）连续谱，光谱 8 二进制数字调制系统中，性能最差， 占用频带最宽。

A ）ASK, PSK B ）FSK, PSKC ）DPSK, ASKD ）ASK, FSK9、 对频率在（6〜10）kHz 的信号，最小抽样频率是 ____________ 。

《最优化方法》1一、填空题：1．最优化问题的数学模型一般为：____________________________，其中 ___________称为目标函数，___________称为约束函数，可行域D 可以表示 为_____________________________，若______________________________， 称*x 为问题的局部最优解，若_____________________________________，称*x 为问题的全局最优解。

2．设f(x)= 212121522x x x x x +-+，则其梯度为___________，海色矩阵___________,令,)0,1(,)2,1(T T d x ==则f(x)在x 处沿方向d 的一阶方向导数为___________，几何意义为___________________________________,二阶 方向导数为___________________，几何意义为_________________________ ___________________________________。

3．设严格凸二次规划形式为：则其对偶规划为___________________________________________。

4．求解无约束最优化问题：n R x x f ∈),(min ，设k x 是不满足最优性条件的第k 步迭代点，则：用最速下降法求解时，搜索方向k d =___________用Newton 法求解时，搜索方向k d =___________用共轭梯度法求解时，搜索方向k d =___________________________________________________________________________。

二．（10分）简答题：试设计求解无约束优化问题的一般下降算法。

三．（25分）计算题1． （10分）用一阶必要和充分条件求解如下无约束优化问题的最优解：)1(632)(m in 21212131----=x x x x x x x f .2． （15分）用约束问题局部解的一阶必要条件和二阶充分条件求约束问题： 的最优解和相应的乘子。

三、计算题(10分)
则
(3分)
(4分)
相量图(3分)
四、计算题(10分)
去耦等效电路图(3分)
(3分)
(2分)
(2分)
五、计算题(10分)
相量模型图(2分)
(2分)
(3分)
(3分)
六、计算题(10分)
运算模型图(3分)
Hale Waihona Puke (4分)(3分)七、计算题(10分)
八、计算题(10分)
先将原电路等效后或直接列写方程可求得
09.若网络函数 ，则其零点为，极点为。
10.二端口的对称有电气对称和两种对称形式，对于对称二端口的 参数或 参数，只有个是独立的。
二、选择题(每题2分，共20分)
01.电感线圈等效电路如图1所示,对基波的阻抗为 则对二次谐波的阻抗为（）。
A. B. C. D.
02.电路如图2所示, ，则单口网络相量模型的等效阻抗等于（）。
A. B. C. D.
03.电路如图3所示，二端网络“消耗”的无功功率为（）。
A. B.
C. D.
04.正弦稳态电路如图4所示， ,则电流 等于（）。
A. B.
C. D.
05.正弦稳态电路如图5所示，已知 ,则比值 =()。
A. B. C. D.
06.对称三相三线制电路如图6所示，负载为 形联结，线电压 ，若因故障 相断路（相当于 打开），则电压表读数（有效值）为（）。
01， ， ；02，初相位,一一对应；03, ，感性负载；04， ， ；
05，1, ；06，110，300；07， ， ；08， ， ；09， ；10，结构对称；2。
二、选择题(每题2分，共20分)
01,D；02,C；03,B；04,A；05,A；06,B；07,C；08,D；09,B；10,AC。

一、（3％×8）（1）线性规划,0 153 22 ..3 min 21212121≤≥-=--≤+-x x x x x x t s x x 的对偶规划为自由变量21212121 ,0 15 332 ..2-ax y y y y y y t s y y m ≤-≥-≤+-。

（2）在三维空间3R 中，集合},1|),,{(222z x y z y x z y x +≥≤++的极点构成的集合为 },1|),,{(222z x y z y x z y x +≥=++ 。

（3）用黄金分割法求解某个函数在区间[-1,3]上的极小点，若要求缩短后的区间的长度不大于原始区间的0.08，则需要迭代的次数为 6（4）函数65722),,(32121232221321++--+++=x x x x ax x x x x x x f 为严格凸函数，则常数a 的取值范围是 22||<a（5）在最速下降法，Newton 法，FR 方法，PRP 方法，DFP 方法，BFGS 方法中不具备二次终止性的算法为 最速下降法（6）求函数2221212),(x x x x f +=的极小点，取Tx )1,0()0(=，用最速下降法一步得到的下一迭代点(1)x= T )0,0(（7）对于无约束优化问题min 212122216432x x x x x x ---+，(1,)Tp a =为目标函数在点(0,1)T 的下降方向，则a 的取值范围是 27->a（8）用内罚函数法（对数罚函数）求解0x 01.. min 212221≥≤-+x t s x x ，其增广目标函数为 212221ln )1ln(x r x r x x ---+二、（10％）()f x 为凸集nD R ⊂上的函数，令(){(,)|,,()}epi f x y x D y R y f x =∈∈≥，证明()f x 为凸函数的充要条件是()epi f 为凸集。