Solutions to Exercises(DBMS)

外文原文：Database1.1Database conceptThe database concept has evolved since the 1960s to ease increasing difficulties in designing, building, and maintaining complex information systems (typically with many concurrent end-users, and with a large amount of diverse data). It has evolved together with database management systems which enable the effective handling of databases. Though the terms database and DBMS define different entities, they are inseparable: a database's properties are determined by its supporting DBMS and vice-versa. The Oxford English dictionary cites[citation needed] a 1962 technical report as the first to use the term "data-base." With the progress in technology in the areas of processors, computer memory, computer storage and computer networks, the sizes, capabilities, and performance of databases and their respective DBMSs have grown in orders of magnitudes. For decades it has been unlikely that a complex information system can be built effectively without a proper database supported by a DBMS. The utilization of databases is now spread to such a wide degree that virtually every technology and product relies on databases and DBMSs for its development and commercialization, or even may have such embedded in it. Also, organizations and companies, from small to large, heavily depend on databases for their operations.No widely accepted exact definition exists for DBMS. However, a system needs to provide considerable functionality to qualify as a DBMS. Accordingly its supported data collection needs to meet respective usability requirements (broadly defined by the requirements below) to qualify as a database. Thus, a database and its supporting DBMS are defined here by a set of general requirements listed below. Virtually all existing mature DBMS products meet these requirements to a great extent, while less mature either meet them or converge to meet them.1.2Evolution of database and DBMS technologyThe introduction of the term database coincided with the availability of direct-access storage (disks and drums) from the mid-1960s onwards. The term represented a contrast with the tape-based systems of the past, allowing shared interactive use rather than daily batch processing.In the earliest database systems, efficiency was perhaps the primary concern, but it was already recognized that there were other important objectives. One of the key aims was to make the data independent of the logic of application programs, so that the same data could be made available to different applications.The first generation of database systems were navigational,[2] applications typically accessed data by following pointers from one record to another. The two main data models at this time were the hierarchical model, epitomized by IBM's IMS system, and the Codasyl model (Network model), implemented in a number ofproducts such as IDMS.The Relational model, first proposed in 1970 by Edgar F. Codd, departed from this tradition by insisting that applications should search for data by content, rather than by following links. This was considered necessary to allow the content of the database to evolve without constant rewriting of applications. Relational systems placed heavy demands on processing resources, and it was not until the mid 1980s that computing hardware became powerful enough to allow them to be widely deployed. By the early 1990s, however, relational systems were dominant for all large-scale data processing applications, and they remain dominant today (2012) except in niche areas. The dominant database language is the standard SQL for the Relational model, which has influenced database languages also for other data models.Because the relational model emphasizes search rather than navigation, it does not make relationships between different entities explicit in the form of pointers, but represents them rather using primary keys and foreign keys. While this is a good basis for a query language, it is less well suited as a modeling language. For this reason a different model, the Entity-relationship model which emerged shortly later (1976), gained popularity for database design.In the period since the 1970s database technology has kept pace with the increasing resources becoming available from the computing platform: notably the rapid increase in the capacity and speed (and reduction in price) of disk storage, and the increasing capacity of main memory. This has enabled ever larger databases and higher throughputs to be achieved.The rigidity of the relational model, in which all data is held in tables with a fixed structure of rows and columns, has increasingly been seen as a limitation when handling information that is richer or more varied in structure than the traditional 'ledger-book' data of corporate information systems: for example, document databases, engineering databases, multimedia databases, or databases used in the molecular sciences. Various attempts have been made to address this problem, many of them gathering under banners such as post-relational or NoSQL. Two developments of note are the Object database and the XML database. The vendors of relational databases have fought off competition from these newer models by extending the capabilities of their own products to support a wider variety of data types.1.3General-purpose DBMSA DBMS has evolved into a complex software system and its development typically requires thousands of person-years of development effort.[citation needed] Some general-purpose DBMSs, like Oracle, Microsoft SQL Server, and IBM DB2, have been undergoing upgrades for thirty years or more. General-purpose DBMSs aim to satisfy as many applications as possible, which typically makes them even more complex than special-purpose databases. However, the fact that they can be used "off the shelf", as well as their amortized cost over many applications and instances, makes them an attractive alternative (Vsone-time development) whenever they meet an application's requirements.Though attractive in many cases, a general-purpose DBMS is not always the optimal solution: When certain applications are pervasive with many operating instances, each with many users, a general-purpose DBMS may introduce unnecessary overhead and too large "footprint" (too large amount of unnecessary, unutilized software code). Such applications usually justify dedicated development.Typical examples are email systems, though they need to possess certain DBMS properties: email systems are built in a way that optimizes email messages handling and managing, and do not need significant portions of a general-purpose DBMS functionality.1.4Database machines and appliancesIn the 1970s and 1980s attempts were made to build database systems with integrated hardware and software. The underlying philosophy was that such integration would provide higher performance at lower cost. Examples were IBM System/38, the early offering of Teradata, and the Britton Lee, Inc. database machine. Another approach to hardware support for database management was ICL's CAFS accelerator, a hardware disk controller with programmable search capabilities. In the long term these efforts were generally unsuccessful because specialized database machines could not keep pace with the rapid development and progress of general-purpose computers. Thus most database systems nowadays are software systems running on general-purpose hardware, using general-purpose computer data storage. However this idea is still pursued for certain applications by some companies like Netezza and Oracle (Exadata).1.5Database researchDatabase research has been an active and diverse area, with many specializations, carried out since the early days of dealing with the database concept in the 1960s. It has strong ties with database technology and DBMS products. Database research has taken place at research and development groups of companies (e.g., notably at IBM Research, who contributed technologies and ideas virtually to any DBMS existing today), research institutes, and Academia. Research has been done both through Theory and Prototypes. The interaction between research and database related product development has been very productive to the database area, and many related key concepts and technologies emerged from it. Notable are the Relational and the Entity-relationship models, the Atomic transaction concept and related Concurrency control techniques, Query languages and Query optimization methods, RAID, and more. Research has provided deep insight to virtually all aspects of databases, though not always has been pragmatic, effective (and cannot and should not always be: research is exploratory in nature, and not always leads to accepted or useful ideas). Ultimately market forces and real needs determine the selection of problem solutions and related technologies, also among those proposed by research. However, occasionally, not the best and most elegant solution wins (e.g., SQL). Along their history DBMSs and respective databases, to a great extent, have been the outcome of such research, while real product requirements and challenges triggered database research directions and sub-areas.The database research area has several notable dedicated academic journals (e.g., ACM Transactions on Database Systems-TODS, Data and Knowledge Engineering-DKE, and more) and annual conferences (e.g., ACM SIGMOD, ACM PODS, VLDB, IEEE ICDE, and more), as well as an active and quite heterogeneous (subject-wise) research community all over the world.1.6Database architectureDatabase architecture (to be distinguished from DBMS architecture; see below) may be viewed, to some extent, as an extension of Data modeling. It is used to conveniently answer requirements of different end-users from a same database, as well as for other benefits. For example, a financial department of a company needs the payment details of all employees as part of the company's expenses, but not other many details about employees, that are the interest of the human resources department. Thus different departments need different views of the company's database, that both include the employees' payments, possibly in a different level of detail (and presented in different visual forms). To meet such requirement effectively database architecture consists of three levels: external, conceptual and internal. Clearly separating the three levels was a major feature of the relational database model implementations that dominate 21st century databases.[13]The external level defines how each end-user type understands the organization of its respective relevant data in the database, i.e., the different needed end-user views.A single database can have any number of views at the external level.The conceptual level unifies the various external views into a coherent whole, global view.[13] It provides the common-denominator of all the external views. It comprises all the end-user needed generic data, i.e., all the data from which any view may be derived/computed. It is provided in the simplest possible way of such generic data, and comprises the back-bone of the database. It is out of the scope of the various database end-users, and serves database application developers and defined by database administrators that build the database.The Internal level (or Physical level) is as a matter of fact part of the database implementation inside a DBMS (see Implementation section below). It is concerned with cost, performance, scalability and other operational matters. It deals with storage layout of the conceptual level, provides supporting storage-structures like indexes, to enhance performance, and occasionally stores data of individual views (materialized views), computed from generic data, if performance justification exists for such redundancy. It balances all the external views' performance requirements, possibly conflicting, in attempt to optimize the overall database usage by all its end-uses according to the database goals and priorities.All the three levels are maintained and updated according to changing needs by database administrators who often also participate in the database design.The above three-level database architecture also relates to and being motivated by the concept of data independence which has been described for long time as a desired database property and was one of the major initial driving forces of the Relational model. In the context of the above architecture it means that changes made at a certain level do not affect definitions and software developed with higher level interfaces, and are being incorporated at the higher level automatically. For example, changes in the internal level do not affect application programs written using conceptual level interfaces, which saves substantial change work that would be needed otherwise.In summary, the conceptual is a level of indirection between internal and external. On one hand it provides a common view of the database, independent of different external view structures, and on the other hand it is uncomplicated by details of how the data is stored or managed (internal level). In principle every level, and even every external view, can be presented by a different data model. In practice usually a given DBMS uses the same data model for both the external and the conceptual levels (e.g., relational model). The internal level, which is hidden inside the DBMS and depends on its implementation (see Implementation section below), requires a different levelof detail and uses its own data structure types, typically different in nature from the structures of the external and conceptual levels which are exposed to DBMS users (e.g., the data models above): While the external and conceptual levels are focused on and serve DBMS users, the concern of the internal level is effective implementation details.中文译文：数据库1.1 数据库的概念数据库的概念已经演变自1960年以来，以缓解日益困难，在设计，建设，维护复杂的信息系统（通常与许多并发的最终用户，并用大量不同的数据）。

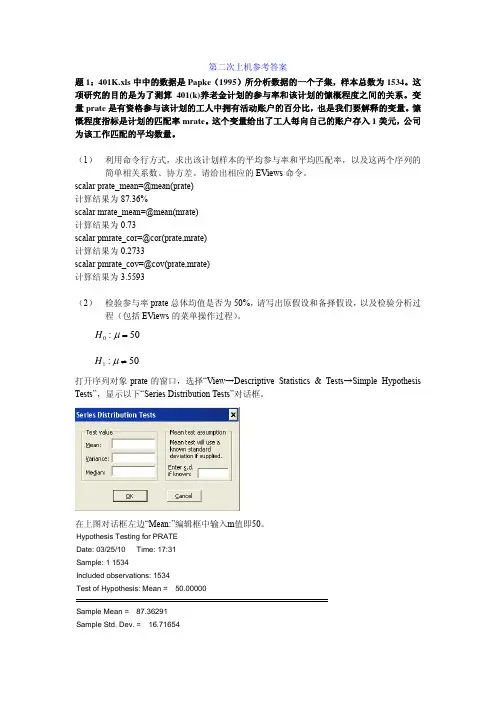
第二次上机参考答案题1：401K.xls 中中的数据是Papke （1995）所分析数据的一个子集，样本总数为1534。

这项研究的目的是为了测算401(k)养老金计划的参与率和该计划的慷概程度之间的关系。

变量prate 是有资格参与该计划的工人中拥有活动账户的百分比，也是我们要解释的变量。

慷慨程度指标是计划的匹配率mrate 。

这个变量给出了工人每向自己的账户存入1美元，公司为该工作匹配的平均数量。

（1） 利用命令行方式，求出该计划样本的平均参与率和平均匹配率，以及这两个序列的简单相关系数、协方差。

请给出相应的EViews 命令。

scalar prate_mean=@mean(prate) 计算结果为87.36%scalar mrate_mean=@mean(mrate) 计算结果为0.73scalar pmrate_cor=@cor(prate,mrate) 计算结果为0.2733scalar pmrate_cov=@cov(prate,mrate) 计算结果为3.5593（2） 检验参与率prate 总体均值是否为50%，请写出原假设和备择假设，以及检验分析过程（包括EViews 的菜单操作过程）。

50:0=μH50:1≠μH打开序列对象prate 的窗口，选择“View →Descriptive Statistics & Tests →Simple HypothesisTests”，显示以下“Series Distribution Tests”对话框。

在上图对话框左边“Mean:”编辑框中输入m 值即50。

Hypothesis Testing for PRATE Date: 03/25/10 Time: 17:31 Sample: 1 1534Included observations: 1534Test of Hypothesis: Mean = 50.00000 Sample Mean = 87.36291 Sample Std. Dev. = 16.71654Method Value Probabilityt-statistic 87.540100.0000由t 统计量的相伴概率判断，在99%置信水平上拒绝原假设。

_______________________________ 少年易学老难成，一寸光阴不可轻-百度文库一Chapter 1 Data Structures and Algorithms: Instructor's CD questions1.The primary purpose of most computer programs isa)to perform a mathematical calculation.*b) to store and retrieve information.c)to sort a collection of records.d)all of the above.e)none of the above.2.An integer is aa)) simple typeb)aggregate typec)composite typed)a and be)none of the above3.A payroll records is aa)simple typeb)aggregate typec)composite type*d) a and b e) none of the above4.Which of the following should NOT be viewed as an ADT?a)listb)integerc)array*d) none of the above5.A mathematical function is most like a*a) Problemb)Algorithmc)Program6.An algorithm must be or do all of the following EXCEPT:a)correctb)composed of concrete steps*c) ambiguousd)composed of a finite number of stepse)terminate7.A solution is efficient ifa.it solves a problem within the require resource constraints.b.it solves a problem within human reaction time.1_______________________________ 少年易学老难成，一寸光阴不可轻-百度文库_______ c.it solves a problem faster than other known solutions.d.a and b.*e. a and c.f. b and c.8.An array isa)A contiguous block of memory locations where each memory location storesa fixed-length data item.b)An ADT composed of a homogeneous collection of data items, each data item identified by a particular number.c)a set of integer values.*d) a and b.e)a and c.f)b and c.9.Order the following steps to selecting a data structure to solve a problem.(1)Determine the basic operations to be supported.(2)Quantify the resource constraints for each operation.(3)Select the data structure that best meets these requirements.(4)Analyze the problem to determine the resource constraints that anysolution must meet.a)(1, 2, 3, 4)b)(2, 3, 1, 4)c)(2, 1, 3, 4)*d) (1, 2, 4, 3)e) (1, 4, 3, 2)10.Searching for all those records in a database with key value between 10 and 100 is known as:a) An exact match query.*b) A range query.c)A sequential search.d)A binary search.Chapter 2 Mathematical Preliminaries: Instructor's CD questions1.A set has the following properties:a)May have duplicates, element have a position.b)May have duplicates, elements do not have a position.c)May not have duplicates, elements have a position.*d) May not have duplicates, elements do not have a position._______________________________ 少年易学老难成，一寸光阴不可轻-百度文库2.A sequence has the following properties:a)) May have duplicates, element have a position.b)May have duplicates, elements do not have a position.c)May not have duplicates, elements have a position.d)May not have duplicates, elements do not have a position.3.For set F, the notation |P| indicatesa)) The number of elements in Pb)The inverse of Pc)The powerset of F.d)None of the above.4.Assume that P contains n elements. The number of sets in the powerset of P isa)nb)n A2*c) 2A nd)2A n - 1e) 2A n + 15.If a sequence has n values, then the number of permutations for that sequence will bea)nb)n A2c)n A2 - 1d)2A n*e) n!6.If R is a binary relation over set S, then R is reflexive if*a) aRa for all a in S.b)whenever aRb, then bRa, for all a, b in S.c)whenever aRb and bRa, then a = b, for all a, b in S.d)whenever aRb and aRc, then aRc, for all a, b, c in S.7.If R is a binary relation over set S, then R is transitive ifa)aRa for all a in S.b)whenever aRb, then bRa, for all a, b in S.c)whenever aRb and bRa, then a = b, for all a, b in S.*d) whenever aRb and aRc, then aRc, for all a, b, c in S.8.R is an equivalence relation on set S if it isa)) reflexive, symmetric, transitive.b)reflexive, antisymmetric, transitive.c)symmetric, transitive.少年易学老难成，一寸光阴不可轻-百度文库d)antisymmetric, transitive.e)irreflexive, symmetric, transitive.f)irreflexive, antisymmetric, transitive.9.For the powerset of integers, the subset operation defines *a) a partial order.b)a total order.c)a transitive order.d)none of the above.10.log nm is equal toa) n + m*b) log n + log mc)m log nd)log n - log m11.A close-form solution isa) an analysis for a program.*b) an equation that directly computes the value of a summation.c) a complete solution for a problem.12.Mathematical induction is most likea) iteration.*b) recursion.c)branching.d)divide and conquer.13.A recurrence relation is often used to model programs witha)for loops.b)branch control like "if" statements.*c) recursive calls.d) function calls.14.Which of the following is not a good proof technique.a) proof by contradiction.*b) proof by example.c) proof by mathematical induction.15.We can use mathematical induction to:a) Find a closed-form solution for a summation.*b) Verify a proposed closed-form solution for a summation.c) Both find and verify a closed-form solution for a summation._______________________________ 少年易学老难成，一寸光阴不可轻-百度文库一Chapter 3 Algorithm Analysis: Instructor's CD questions1.A growth rate applies to:a)the time taken by an algorithm in the average case.b)the time taken by an algorithm as the input size grows.c)the space taken by an algorithm in the average case.d)the space taken by an algorithm as the input size grows.e)any resource you wish to measure for an algorithm in the average case.*f) any resource you wish to measure for an algorithm as the input size grows.2.Pick the growth rate that corresponds to the most efficient algorithm as n gets large:a) 5n*b) 20 log nc)2nA2d)2A n3.Pick the growth rate that corresponds to the most efficient algorithm when n =4.a)5nb)20 log nc)2nA2*d)2A n4.Pick the quadratic growth rate.a)5nb)20 log n*c) 2nA2d) 2An5.Asymptotic analysis refers to:a) The cost of an algorithm in its best, worst, or average case.*b) The growth in cost of an algorithm as the input size grows towards infinity.c)The size of a data structure.d)The cost of an algorithm for small input sizes6.For an air traffic control system, the most important metric is:a)The best-case upper bound.b)The average-case upper bound.c)) The worst-case upper bound.d)The best-case lower bound._______________________________ 少年易学老难成，一寸光阴不可轻-百度文库__________e)The average-case lower bound.f)The worst-case lower bound.7.When we wish to describe the upper bound for a problem we use:a)) The upper bound of the best algorithm we know.b)The lower bound of the best algorithm we know.c)We can't talk about the upper bound of a problem because there can alwaysbe an arbitrarily slow algorithm.8.When we describe the lower bound for a problem we use:a)The upper bound for the best algorithm we know.b)the lower bound for the best algorithm we know.c)The smallest upper bound that we can prove for the best algorithm that could possibly exist.*d) The greatest lower bound that we can prove for the best algorithm that could possibly exist.9.When the upper and lower bounds for an algorithm are the same, we use:a)big-Oh notation.b)big-Omega notation.*c) Theta notation.d)asymptotic analysis.e)Average case analysis.f)Worst case analysis.10. When performing asymptotic analysis, we can ignore constants and low order terms because:*a) We are measuring the growth rate as the input size gets large.b)We are only interested in small input sizes.c)We are studying the worst case behavior.d)We only need an approximation.11.The best case for an algorithm refers to:a) The smallest possible input size.*b) The specific input instance of a given size that gives the lowest cost.c)The largest possible input size that meets the required growth rate.d)The specific input instance of a given size that gives the greatest cost.12.For any algorithm:a)) The upper and lower bounds always meet, but we might not know what they are.少年易学老难成，一寸光阴不可轻-百度文库b)The upper and lower bounds might or might not meet.c)We can always determine the upper bound, but might not be able to determine the lower bound.d)We can always determine the lower bound, but might not be able to determine the upper bound.13.If an algorithm is Theta(f(n)) in the average case, then it is: a) Omega(f(n)) in the best case.*b) Omega(f(n)) in the worst case.c) O(f(n)) in the worst case.14.For the purpose of performing algorithm analysis, an important property ofa basic operation is that:a)It be fast.b)It be slow enough to measure.c)Its cost does depend on the value of its operands.*d) Its cost does not depend on the value of its operands.15.For sequential search,a) The best, average, and worst cases are asymptotically the same.*b) The best case is asymptotically better than the average and worst cases.c)The best and average cases are asymptotically better than the worst case.d)The best case is asymptotically better than the average case, and the average case is asymptotically better than the worst case.Chapter 4 Lists, Stacks and Queues: Instructor's CD questions1.An ordered list is one in which:a) The element values are in sorted order.*b) Each element a position within the list.2.An ordered list is most like a:a)set.b)bag.c)) sequence.3.As compared to the linked list implementation for lists, the array-based listimplementation requires:a)More spaceb)Less space*c) More or less space depending on how many elements are in the list._______________________________ 少年易学老难成，一寸光阴不可轻-百度文库4.Here is a series of C++ statements using the list ADT in the book.L1.append(10);L1.append(20);L1.append(15);If these statements are applied to an empty list, the result will look like:a)< 10 20 15 >*b) < | 10 20 15 >c)< 10 20 15 | >d)< 15 20 10 >e)< | 15 20 10 >f)< 15 20 10 | >5.When comparing the array-based and linked implementations, the array-based implementation has:a)) faster direct access to elements by position, but slower insert/delete from the current position.b)slower direct access to elements by position, but faster insert/delete from the current position.c)both faster direct access to elements by position, and faster insert/delete from the current position.d)both slower direct access to elements by position, and slower insert/delete from the current position.6.For a list of length n, the linked-list implementation's prev function requiresworst-case time:a)O(1).b)O(log n).*c) O(n).d) O(n A2).7.Finding the element in an array-based list with a given key value requiresworst case time:a)O(1).b)O(log n).*c) O(n).d) O(n A2).8.In the linked-list implementation presented in the book, a header node isused:*a) To simplify special cases._______________________________ 少年易学老难成，一寸光阴不可轻-百度文库一b)Because the insert and delete routines won't work correctly without it.c)Because there would be no other way to make the current pointer indicatethe first element on the list.9.When a pointer requires 4 bytes and a data element requires 4 bytes, thelinked list implementation requires less space than the array-based list implementation when the array would be:a)less than 1/4 full.b)less than 1/3 full.*c) less than half full.d)less than 第full.e)less than 34 fullf)never.10.When a pointer requires 4 bytes and a data element requires 12 bytes, thelinked list implementation requires less space than the array-based list implementation when the array would be:a)) less than 1/4 full.b)less than 1/3 full.c)less than half full.d)less than 2/3 full.e)less than 34 fullf)never.11.When we say that a list implementation enforces homogeneity, we meanthat:a) All list elements have the same size.*b) All list elements have the same type.c) All list elements appear in sort order.12.When comparing the doubly and singly linked list implementations, we findthat the doubly linked list implementation*a) Saves time on some operations at the expense of additional space.b)Saves neither time nor space, but is easier to implement.c)Saves neither time nor space, and is also harder to implement.13. We use a comparator function in the Dictionary class ADT:a)to simplify implementation.*b) to increase the opportunity for code reuse.c) to improve asymptotic efficiency of some functions.14.All operations on a stack can be implemented in constant time except:少年易学老难成，一寸光阴不可轻-百度文库a) Pushb)Popc)The implementor's choice of push or pop (they cannot both be implementedin constant time).*d) None of the above.15.Recursion is generally implemented usinga) A sorted list.*b) A stack.c) A queue.Chapter 5 Binary Trees: Instructor's CD questions1.The height of a binary tree is:a)The height of the deepest node.b)The depth of the deepest node.*c) One more than the depth of the deepest node.2.A full binary tree is one in which:*a) Every internal node has two non-empty children.b) all of the levels, except possibly the bottom level, are filled.3.The relationship between a full and a complete binary tree is:a)Every complete binary tree is full.b)Every full binary tree is complete.*c) None of the above.4.The Full Binary Tree Theorem states that:a)) The number of leaves in a non-empty full binary tree is one more than the number of internal nodes.b)The number of leaves in a non-empty full binary tree is one less than the number of internal nodes.c)The number of leaves in a non-empty full binary tree is one half of the number of internal nodes.d)The number of internal nodes in a non-empty full binary tree is one half of the number of leaves.5.The correct traversal to use on a BST to visit the nodes in sorted order is:a) Preorder traversal.*b) Inorder traversal.c) Postorder traversal.6. When every node of a full binary tree stores a 4-byte data field,10少年易学老难成，一寸光阴不可轻-百度文库two 4-byte child pointers, and a 4-byte parent pointer, theoverhead fraction is approximately:a)one quarter.b)one third.c)one half.d)two thirds.*e) three quarters.f) none of the above.7.When every node of a full binary tree stores an 8-byte data field and two 4-byte child pointers, the overhead fraction is approximately:a)one quarter.b)one third.*c) one half.d)two thirds.e)three quarters.f)none of the above.8.When every node of a full binary tree stores a 4-byte data field and theinternal nodes store two 4-byte child pointers, the overhead fraction is approximately:a)one quarter.b)one third.*c) one half.d)two thirds.e)three quarters.f)none of the above.9.If a node is at position r in the array implementation for a complete binarytree, then its parent is at:a)) (r - 1)/2 if r > 0b)2r + 1 if (2r + 1) < nc)2r + 2 if (2r + 2) < nd)r - 1 if r is evene)r + 1 if r is odd.10.If a node is at position r in the array implementation for a complete binarytree, then its right child is at:a)(r - 1)/2 if r > 0b)2r + 1 if (2r + 1) < n*c) 2r + 2 if (2r + 2) < nd)r - 1 if r is evene)r + 1 if r is odd.11_______________________________ 少年易学老难成，一寸光阴不可轻-百度文库—11.Assume a BST is implemented so that all nodes in the left subtree of agiven node have values less than that node, and all nodes in the rightsubtree have values greater than or equal to that node. Whenimplementing the delete routine, we must select as its replacement:a) The greatest value from the left subtree.*b) The least value from the right subtree.c) Either of the above.12.Which of the following is a true statement:a)In a BST, the left child of any node is less than the right child, and in a heap, the left child of any node is less than the right child.*b) In a BST, the left child of any node is less than the right child, but in a heap, the left child of any node could be less than or greater than the right child.c)In a BST, the left child of any node could be less or greater than the right child, but in a heap, the left child of any node must be less than the right child.d)In both a BST and a heap, the left child of any node could be either less than or greater than the right child.13.When implementing heaps and BSTs, which is the best answer?a)The time to build a BST of n nodes is O(n log n), and the time to build a heap of n nodes is O(n log n).b)The time to build a BST of n nodes is O(n), and the time to build a heap of n nodes is O(n log n).*c) The time to build a BST of n nodes is O(n log n), and the time to build a heap of n nodes is O(n).d) The time to build a BST of n nodes is O(n), and the time to build a heap of n nodes is O(n).14.The Huffman coding tree works best when the frequencies for letters area) Roughly the same for all letters.*b) Skewed so that there is a great difference in relative frequencies for various letters.15.Huffman coding provides the optimal coding when:a)The messages are in English.b)The messages are binary numbers.*c) The frequency of occurrence for a letter is independent of its context within the message.d) Never.12_______________________________ 少年易学老难成，一寸光阴不可轻-百度文库一Chapter 6 Binary Trees: Instructor's CD questions1.The primary ADT access functions used to traverse a general tree are: a) left child and right siblingb) left child and right child*c) leftmost child and right siblingd) leftmost child and next child2.The tree traversal that makes the least sense for a general treeis:a) preorder traversal*b) inorder traversalc) postorder traversal3.The primary access function used to navigate the general tree when performing UNION/FIND is:a)left childb)leftmost childc)right childd)right sibling*e) parent4.When using the weighted union rule for merging disjoint sets, the maximum depth for any node in a tree of size n will be:a) nearly constant*b) log nc)nd)n log ne)n A25.We use the parent pointer representation for general trees to solve which problem?a)Shortest pathsb)General tree traversal*c) Equivalence classesd) Exact-match query6. When using path compression along with the weighted union rule for merging disjoint sets, the average cost for any UNION or FIND operation in a tree of size n will be:*a) nearly constantb)log nc)nd)n log n13_______________________________ 少年易学老难成，一寸光阴不可轻-百度文库一7.The most space efficient representation for general trees will typically be:a) List of children*b) Left-child/right siblingc) A K-ary tree.8.The easiest way to represent a general tree is to:a) convert to a list.*b) convert to a binary tree.c) convert to a graph.9.As K gets bigger, the ratio of internal nodes to leaf nodes:a)) Gets smaller.b)Stays the same.c)Gets bigger.d)Cannot be determined, since it depends on the particular configuration of the tree.10.A sequential tree representation is best used for:*a) Archiving the tree to disk.b)Use in dynamic in-memory applications.c)Encryption algorithms.d)It is never better than a dynamic representation.Chapter 7 Internal Sorting: Instructor's CD questions1.A sorting algorithm is stable if it:a) Works for all inputs.*b) Does not change the relative ordering of records with identical key values.c) Always sorts in the same amount of time (within a constant factor) for a given input size.2.Which sorting algorithm does not have any practical use?a) Insertion sort.*b) Bubble sort.c)Quicksort.d)Radix Sort.e)a and b.3.When sorting n records, Insertion sort has best-case cost:a)O(log n).14_______________________________ 少年易学老难成，一寸光阴不可轻-百度文库*b) O(n).c)O(n log n).e)O(n!)f)None of the above.4.When sorting n records, Insertion sort has worst-case cost:a)O(log n).b)O(n).c)O(n log n).*d) O(n A2)e)O(n!)f)None of the above.5.When sorting n records, Quicksort has worst-case cost:a)O(log n).b)O(n).c)O(n log n).*d) O(n A2)e)O(n!)f)None of the above.6.When sorting n records, Quicksort has average-case cost:a)O(log n).b)O(n).c)) O(n log n).d)O(n A2)e)O(n!)f)None of the above.7.When sorting n records, Mergesort has worst-case cost:a)O(log n).b)O(n).*c) O(n log n).d)O(n A2)e)O(n!)f)None of the above.8.When sorting n records, Radix sort has worst-case cost:a)O(log n).b)O(n).c)O(n log n).d)O(n A2)e)O(n!)15少年易学老难成，一寸光阴不可轻-百度文库*f) None of the above.9.When sorting n records with distinct keys, Radix sort has a lower bound of:a)Omega(log n).b)Omega(n).*c) Omega(n log n).d)Omega(n A2)e)Omega(n!)f)None of the above.10.Any sort that can only swap adjacent records as an average case lower bound of:a)Omega(log n).b)Omega(n).c)Omega(n log n).*d) Omega(n A2)e)Omega(n!)f)None of the above.11.The number of permutations of size n is:a)O(log n).b)O(n).c)O(n log n).d)O(n A2)*e) O(n!)f)None of the above.12.When sorting n records, Selection sort will perform how many swaps in the worst case?a) O(log n).*b) O(n).c)O(n log n).d)O(n A2)e)O(n!)f)None of the above.13.Shellsort takes advantage of the best-case behavior of which sort?*a) Insertion sortb)Bubble sortc)Selection sortd)Shellsorte)Quicksortf)Radix sort16_______________________________ 少年易学老难成，一寸光阴不可轻-百度文库_______________14.A poor result from which step causes the worst-case behavior for Quicksort?*a) Selecting the pivotb)Partitioning the listc)The recursive call15.In the worst case, the very best that a sorting algorithm can do when sorting n records is:a)O(log n).b)O(n).*c) O(n log n).d)O(n A2)e)O(n!)f)None of the above.Chapter 8 File Processing and External Sorting: Instructor's CD questions1.As compared to the time required to access one unit of data frommain memory, accessing one unit of data from disk is:a)10 times faster.b)1000 times faster.c)1,000,000 time faster.d)10 times slower.e)1000 times slower.*f) 1,000,000 times slower.2.The most effective way to reduce the time required by a disk-based program is to:a) Improve the basic operations.*b) Minimize the number of disk accesses.c)Eliminate the recursive calls.d)Reduce main memory use.3.The basic unit of I/O when accessing a disk drive is:a)A byte.*b) A sector.c)A cluster.d)A track.e)An extent.4.The basic unit for disk allocation under DOS or Windows is:a)A byte.b)A sector.*c) A cluster.17少年易学老难成，一寸光阴不可轻-百度文库d) A track.e) An extent.5.The most time-consuming part of a random access to disk is usually: *a) The seek.b)The rotational delay.c)The time for the data to move under the I/O head.6.The simplest and most commonly used buffer pool replacement strategy is:a)First in/First out.b)Least Frequently Used.*c) Least Recently Used.7.The C++ programmer's view of a disk file is most like:a)) An array.b)A list.c)A tree.d)A heap.8.In external sorting, a run is:a)) A sorted sub-section for a list of records.b)One pass through a file being sorted.c)The external sorting process itself.9.The sorting algorithm used as a model for most external sorting algorithms is:a)Insertion sort.b)Quicksort.*c) Mergesort.d) Radix Sort.10.Assume that we wish to sort ten million records each 10 bytes long (for a total file size of 100MB of space). We have working memory of size 1MB, broken into 1024 1K blocks. Using replacement selection and multiway merging, we can expect to sort this file using how many passes through the file?a)About 26 or 27 (that is, log n).b)About 10.c)4.*d) 2.Chapter 9 Searching: Instructor's CD questions18少年易学老难成，一寸光阴不可轻-百度文库1.Which is generally more expensive?a) A successful search.*b) An unsuccessful search.2.When properly implemented, which search method is generally the most efficient for exact-match queries?a)Sequential search.b)Binary search.c)Dictionary search.d)Search in self-organizing lists*e) Hashing3.Self-organizing lists attempt to keep the list sorted by:a) value*b) frequency of record accessc) size of record4.The 80/20 rule indicates that:a) 80% of searches in typical databases are successful and 20% are not.*b) 80% of the searches in typical databases are to 20% of the records.c) 80% of records in typical databases are of value, 20% are not.5.Which of the following is often implemented using a self-organizing list? *a) Buffer pool.b)Linked list.c)Priority queue.6.A hash function must:a)) Return a valid position within the hash table.b)Give equal probability for selecting an slot in the hash table.c)Return an empty slot in the hash table.7.A good hash function will:a)Use the high-order bits of the key value.b)Use the middle bits of the key value.c)Use the low-order bits of the key value.*d) Make use of all bits in the key value.8.A collision resolution technique that places all records directlyinto the hash table is called:a)Open hashing.b)Separate chaining.*c) Closed hashing.d) Probe function.19少年易学老难成，一寸光阴不可轻-百度文库9.Hashing is most appropriate for:a)In-memory applications.b)Disk-based applications.*c) Either in-memory or disk-based applications.10.Hashing is most appropriate for:a)) Range queries.b)Exact-match queries.c)Minimum/maximium value queries.11.In hashing, the operation that will likely require more record accesses is: *a) insertb) deleteChapter 10 Indexing: Instructor's CD questions1.An entry-sequenced file stores records sorted by:a)Primary key value.b)Secondary key value.*c) Order of arrival.d) Frequency of access.2.Indexing is:a) Random access to an array.*b) The process of associating a key with the location of a corresponding data record.c) Using a hash table.3.The primary key is:a)) A unique identifier for a record.b)The main search key used by users of the database.c)The first key in the index.4.Linear indexing is good for all EXCEPT:a)Range queries.b)Exact match queries.*c) Insertion/Deletion.d)In-memory applications.e)Disk-based applications.5.An inverted list provides access to a data record from its:a) Primary key.20______________________________ 少年易学老难成，一寸光阴不可轻-百度文库*b) Secondary key.c) Search key.6.ISAM degrades over time because:a) Delete operations empty out some cylinders.*b) Insert operations cause some cylinders to overflow.c) Searches disrupt the data structure.7.Tree indexing methods are meant to overcome what deficiency in hashing? *a) Inability to handle range queries.。

Oracle CODASYL DBMSOracle CODASYL DBMS provides a powerful and reliable database environment for mission-critical applications running under the Digital VAX and Alpha OpenVMS operating systems,including large-scale applications such as insurance claim processing, power plant operation,and shop floor control systems. With comprehensive system management capabilities and afull range of features, Oracle CODASYL DBMS optimizes system performance, enhancesuser productivity, and provides a stable foundation for the deployment of new technologies.Proven Stability, Performance, and CODASYL-ComplianceFor years, Digital Equipment Corporation’s DBMS databasesystem provided the id eal foundation for programmers, analysts,or administrators who used conventional, non-relational plan-ning and coding techniques to design, build, and maintainapplications for long-term corporat e use. Its stable architecturewas especially preferred for large-scale, mission-critical appli-cations that did not map well to a relational database model.T oday Oracle continues the tradition of DBMS reliability andperformance with Oracle CODASYL DBMS, a multiuser,CODASYL-compliant database management system for theDigital V AX and Alpha OpenVMS operating systems.CODASYL DBMS is designed for databases of all levels ofcomplexity, ranging from simple hierarchies to sophisticatednetworks with multilevel relationships, and engineered formultiuser environments, supporting full concurrent accesswithout compromising the integrity and security of theuser’s database. For application environments where stability,high availability, and throughput are essential, CODASYLDBMS provides a reliable operating platform and a soliddevelopment base.Multiversioning Support for Continual UptimeOracle CODASYL DBMS brings additional power, performance,and system management features to the Digital environment.New to CODASYL DBMS is multiversioning support, whichfacilitates upgrades in production environments by allowingyou to install and test CODASYL DBMS while you continueto run older versions in production. This eliminates the down-time usually associated with database upgrades, and allowsyou to perform “rolling upgrades” to your CODASYL DBMSenvironment. It also allows you to transition to newer versionsof CODASYL DBMS as they become available, withoutcompromising user productivity.®Enabling the Information AgeComprehensive Management CapabilitiesNew capabilities in CODAS YL DBMS give you greater control over your database, and enables you to fine tune for better performance. A new option to the database verification opera-tion (DBO/VERIFY) enables CODASYL DBMS to run five to 10 times faster than previous versions, and provides a more thorough verification and an enhanced list of corruption diagnostics for facilitating repair tasks. An enhanced database statistics package also provides you with detailed information about the real-time usage of your database resources. In addi-tion, CODASYL DBMS’s RELOAD AREA utility can prevent sluggish I/O performance by efficiently scanning stored records and moving them closer to their optimal target pages. When using RELO AD AREA, you can specify a reload sequence or use the default provided. Y ou can also perform the RELOAD operation while the database is online. This allows you to avoid unnecessary database downtime.Support for Large and Growing DatabasesCODASYL DBMS is tuned for the information management needs of growing enterprises. For example, CODASYL DBMS gives you the ability to utilize V ery Large Memory configurations —configurations with more than four gigabytes of RAM—on your 64-bit Alpha systems. CODASYL DBMS’s V ery Large Memory support allows you to store a larger portion of your database in memory, so less time is spent moving data to and from disk, and more users can access more data from your database faster. In addition, CODASYL DBMS’s after image journaling (AIJ) features prevent AIJ files from consuming vast amounts of disk space. Even if your database is growing rapidly, CODASYL DBMS provides automatic backup of full AIJ files without DBA intervention, and helps maintain optimal performance.Oracle CODASYL DBMSDiscrete Disaster RecoveryT o protect your enterprise against data and productivity losses resulting from a node or cluster failure, CODASYL DBMS’s Hot Standby option allows you to completely duplicate a data-base and its environment. In the event of a failure, you can use the replicated database as the master database, with minimal interruption of database users and application processing. The Hot Standby option automatically performs coordinated database synchronization and verification with minimal impact on system resources—the only manual step the administrator must perform is to start the replication services. An additional, optional component—called the Replication Governor—coordinates the database replication and ensures complete synchronization between the master and standby databases.Y ou can implement master and standby databases on systems running OpenVMS V AX, OpenVMS Alpha, or both. Reliable Database ControlsCODASYL DBMS gives you comprehensive database manage-ment controls that help you to optimize your Digital V AX and Alpha OpenVMS environment. Its incremental backup capabilities speed routine maintenance, while its three-phase recovery-by-page feature determines exactly which pages are corrupt and allows you to restore only those pages. Y ou also gain additional locking control with CODASYL DBMS’s two-phase locking option, which allows you to lock individual pages as well as individual records. Fewer locks are especially useful in high-throughput, low-contention environments, such as OLTP environments.Oracle CODASYL DBMS Key FeaturesHardware and Software RequirementsOracle CODASYL DBMS runs on any valid Digital Alpha or VAX configuration running the OpenVMS operating system.Oracle Corporation World Headquarters 500 Oracle ParkwayRedwood Shores, CA 94065USAWorldwide Inquiries:415.506.7000Fax 415.506.7200/To offer our customers the most complete and effective informationmanagement solutions, Oracle Corporation offers its products, along with support, education, and consulting, in more than 90 countries.Oracle is a registered trademark, and Enabling the Information Age and Oracle CODASYL DBMS are trademarks of Oracle Corporation.All other company and product names mentioned are used for identification purposes only, and may be trademarks of their respective owners.Copyright © Oracle Corporation 1995All Rights Reserved Printed in the USA 9680.1295.5K Part #: A24170Performance and AvailabilityRELOAD area utilityAfter-Image Journaling (AIJ) management:circular AIJ, AIJ Backup Server, and AIJ Log ServerIncremental backups Recovery by page Two-phase lockingFull concurrent access capabilities(storage, retrieval, update, and deletion) in a multi-user environment Record locking and journalingAutomatic transaction and verb rollback Multiple database support (one or more databases per process)Two Phase Commit capability automatically commits or rolls back updates across multiple databases in one transaction Full VMScluster support, including automatic recovery upon node failure Integration with CDD/Repository for OpenVMSSecurity and LanguagesSchema, Subschema, Storage Schema, and Security Schema Data Definition Languages (DDLs)Security audit logging of database and Security Schema accessFORTRAN Data Manipulation Language (FDML)Generic DML preprocessor for C, Pascal,and DEC AdaCallable interpretive interface for any OpenVMS Alpha language that adheres to the OpenVMS calling standardAutomatic subschema definition extraction from the CDD/Repository for DEC C,MACRO, DEC Pascal, and DEC Ada when using the high-level call interface or generic DML preprocessorDatabase ManagementEasy-to-use utility command language (DBO)Database Restructuring Utility (DRU)provides the ability to change manydatabase characteristics without unloading and reloading the databaseInitial Load utility; Unload utility for data extraction; functionality for database restructuring with Unload/LoadSimple restructuring, including adding AREAS and initializing AREAS, without unloading and reloading a databaseInteractive Database Query utility (DBQ)with video display of subschema structure diagrams on VT100, VT200, or VT300compatible terminalsVerification and BackupOnline and incremental database verification including verification by setFull and incremental database backup with or without concurrent database users Full and incremental database restore of the entire database or individual areas Ability to redo a sequence of committed transactions (roll forward)Database Tuning and OptimizationBATCH RETRIEVAL ready mode (data-base snapshots) for increased concurrency in large retrieval applicationsSpace Area Management (SPAM) pages which improve database free-space search performanceBoolean record selection expression with index optimization on FIND and FETCH DML statementsData compression of data items and database key (DBKey) pointersDirect record access through database key (DBKey) pointersAutomatic expansion of large records across multiple database pagesSorted sets implemented with B-trees or simple chains; prefix and suffix compression for sort keys with the B-tree implementation DECnet database access for full remote read/write access to non-redundantdistributed databasesPrinted on recycled paper with soy-based inks®Enabling the Information Age。

数据库管理系统原理实践报告Database Management System (DBMS) is a crucial component in the world of computer science. Database Management System（DBMS）是计算机科学世界中至关重要的一个组成部分。

It is essential for the organization and management of data in a systematic and efficient manner. 它对数据的组织和管理以系统化和高效的方式非常重要。

A fundamental aspect of DBMS lies in its ability to provide a structured approach for accessing, managing, and updating data. DBMS的一个基本方面在于它提供了一个结构化的方法来访问、管理和更新数据。

With the exponential growth of data in today's digital age, the significance of database management systems has become increasingly evident. 随着当今数字化时代数据呈指数级增长，数据库管理系统的重要性变得日益明显。

One of the key benefits of a DBMS is its ability to ensure data integrity and security. DBMS的一个关键好处在于它确保了数据的完整性和安全性。

By implementing various security measures such as user authentication and access control, DBMS can prevent unauthorized access and ensure that only authorized users can manipulate the data. 通过实施各种安全措施，如用户认证和访问控制，DBMS可以防止未经授权的访问，并确保只有授权用户可以操纵数据。

Economics 2020a / HBS 4010 / HKS API-111FALL 2010Solutions to Practice Problems for Lectures 1 to 41.1. Quantity Discounts and the Budget Constraint(a) The only distinction between the budget line with a quantity discount and an ordinary budget line is the change in price for purchases of x beyond Q* units. This change in price induces a change in slope of the budget line.Therefore, the budget line is piecewise linear with(1)slope = -p / q = -1 if 0 < x < Q*.(2)slope = -p’ / q = -1/4 if 0 > Q*.We now need to identify the y-intercept and point of change of slope to fully describe the budget constraint.y-interceptIf the consumer purchases only good y, she can purchase W / q = 32 / 4 = 8 units. So, one boundary point for the budget constraint is point A = (0, 8).Change of slopeThe slope of the budget constraint changes at x = Q*.At x = Q*, the consumer spends 4Q* on good x and has wealth W – 4Q* to spend on good y – corresponding to a total of (W – 4Q*) / q = 8 – Q* units of y given that W = 32 and q = 4.That is, the point on the budget line where the price of x (and thus the slope of the budget line) changes is B = (Q*, 8 – Q*).Piecewise Linear Budget ConstraintThe equation for the first (of two) linear segment of the budget constraint is y= y-intercept + slope * x,which in this case yields the equationy = 8 – x.We can solve for the second linear segment of the budget constraint by using the equation y = constant + slope * x.We know that the slope of this second segment of the budget constraint is -1/4 and the and that it starts at the point B = (Q*, 8-Q*). This gives the equation8-Q* =constant – ¼ * Q*OR constant = 8 – (3/4) Q*Thus, the second component of the budget constraint is given byy = 8 – (3/4) Q* - (1/4) x.With this as background, we can now substitute the appropriate values of Q* to find the budget constraints in (a1), (a2), (a3).(a1) Component 1: Straight line y = 8 – x between A = (0, 8) and B = (5, 3).Component 2: Straight line y = (17 – x ) / 4 between B = (5, 3) and C = (17, 0).(a2) Component 1: Straight line y = 8 – x between A = (0, 8) and B’ = (16/3, 3).Component 2: Straight line y = 4 – x /4 between B’ = (16/3, 8/3) and C = (16, 0).(a3) Component 1: Straight line y = 8 – x between A = (0, 8) and B’’ = (6, 2).Component 2: Straight line y = (14 - x ) / 4 between B’’ = (6, 2) and C = (14, 0).The graph below illustrates the budget set with Q* = 6. The boundary of the budget set is in bold. The dotted line indicates the convex combination of the intercepts of the budget set (0, 8) and (14, 0), showing that the budget set is not convex.Problem 1.1: Budget Set if Q* = 6246810121416Good 1G o o d 2(b) The quantity discount affects the budget constraint if the point (Q*, 0) lies within the budget constraint – i.e. if the consumer can afford to purchase enough units of good x to reach the quantity discount: p Q* < W, or Q* < w / p .(c) The budget set is not convex for any positive value of Q* that influences the budget constraint – i.e. Q* < W / p .It is straightforward to see this in a graph. The line between any point on the budget constraint with x < Q* and any other point on the budget constraint with x > Q* is entirely outside the budget set. The quantity discount expands the budget constraint, and thereby expands the set of points included in convex combinations of the budget constraints – including many points that remain outside the budget set.To make the same point algebraically, suppose that Q* = 6 and consider the straight line between the x-intercept (32 – 3Q*, 0) = (14, 0) and the y-intercept (0, W / q) = (0, 8) of the budget set. (It is also possible to make this same argument without assuming a specific value of Q*, but then the notation may make the exposition rather unwieldy.)A convex combination of these two points takes the form [14 α, 8(1- α)]. For α = ½, this convex combination produces the bundle [7, 4], which has associated value 41 (10 units at original prices 4 per unit and one unit of x purchased at quantity discount), and is not affordable with budget 32.Intuitively, each convex combination of points on the boundary of the budget set would be in the budget set based on the average prices of those goods. At (14, 0), the average price of x is 32 / 14, while at (0, 8) the average price of y is 4. Thus, the bundle (7, 4) would be affordable at average price 32/14 for x and average price 4 for y. But with the quantity discount, the average price of x declines with the number of units purchased – exactly the opposite of what would be required for convex combinations to remain in the budget set.1.2. Discounts on Initial Units and the Budget Constraint(a) As in Problem 1.1, The only distinction between the budget line with a quantity discount and an ordinary budget line is the change in price for purchases of x beyond Q* units. This change in price induces a change in slope of the budget line.Therefore, the budget line is piecewise linear withslope = -p / q = -1/2 if 0 < x < Q*.slope = -p’ / q = -1 if 0 > Q*.We now need to identify the y-intercept and point of change of slope to fully describe the budget constraint.y-interceptIf the consumer purchases only good y, she can purchase W / q = 24 / 4 = 6 units. So, one boundary point for the budget constraint is point A = (0, 6).Change of slopeThe slope of the budget constraint changes at x = Q*.At x = Q*, the consumer spends 2Q* on good x and has wealth W – 2Q* to spend on good y – corresponding to a total of (W – 2Q*) / q = 8 – Q* / 2 units of y given thatW = 24 and q = 4.That is, the point on the budget line where the price of x (and thus the slope of the budget line) changes is B = (Q*, 6 – Q* / 2).Piecewise Linear Budget ConstraintThe equation for the first (of two) linear segment of the budget constraint is y= y-intercept + slope * x,which in this case yields the equationy = 6 – x / 2.We can solve for the second linear segment of the budget constraint by using the equation y = constant + slope * x.Using slope = -1 and the values (Q*, 6- Q*/2), we can solve for the constant and identify the constant on the second piece of the budget constraint: y = c onstant + slope * x:6 - Q* / 2=constant – Q*6 + Q* / 2 = constant,Thus, the second component of the budget constraint is given byQ* / 2 – x.y = 6+With this as background, we can now substitute the appropriate values of Q* to find the budget constraints in (a1), (a2), (a3).(a1)Component 1: Straight line y = 6 – x / 2 between A = (0, 6) and B = (2, 5).Component 2: Straight line y = 7 - x between B = (2, 5) and C = (7, 0).(a2)Component 1: Straight line y = 6 – x / 2 between A = (0, 6) and B’ = (4, 4).Component 2: Straight line y = 8 –x between B’ = (4, 4) and C = (8, 0).(a3)Component 1: Straight line y = 6 – x / 2 between A = (0, 6) and B’’ = (6, 3).Component 2: Straight line y = 9 - x between B’’ = (6, 3) and C = (9, 0).Problem 1-2: Budget Set with Q* = 42468G o o d 2The graph below illustrates the budget set with Q* = 6. By contrast to the graph for Problem 1.1 above, it is apparent from inspection that this budget set is convex.(b) The budget set is convex for every positive value of Q*,It is straightforward to see this in a graph. The line between any point on the budget constraint with x < Q* and any other point on the budget constraint with x > Q* is always inside the budget set. By comparison to a pricing rule that maintains the same (lower initial) price for all units of good y , the price increase for later units of y causes the budget constraint to contract in a way that ensures that all convex combinations of points on the boundary of the budget set are still contained in the budget set.1.3.Revealed Preference and Transitivity (Problem 1 on Problem Set 1)Solution will be included with Problem Set 1 Solutions1.4.(Not) The Subsidy Principle (Problem 2 on Problem Set 1)Solution will be included with Problem Set 1 Solutions1.5 Revealed Preference and Compensated Demand(a) Suppose that the new bundle chosen by the consumer is (x*, y*). The Law of Compensated Demand says that (x* - 5)(8 – 10) + (y* - 5)(12 – 10) < 0 for the first case where prices change to p1 = 8 and p2 = 12 and wealth stays at 100. This simplifies to the equation 2 (y* - 5) – 2(x* - 5) < 0, or x* > y*. The original bundle (5, 5) is still available under these conditions. So, the Law of Compensated Demand rules out all bundles with x* < 5.Similarly, The Law of Compensated Demand says that(x* - 5)(16 – 10) + (y* - 5)(24 – 10) < 0for the second case where prices change to p1 = 16 and p2 = 24 and wealth increases to 200. This simplifies to the equation 6x* + 14y* - 100 < 0. The budget constraint is given by 16 x* + 24 y* = 200 since the consumer spends all money on goods. Rearranging terms to isolate y*, we find y* = 25 / 3 – 2x* / 3. Substituting back into the inequality, we find6 x* - 14 (2/3) x* + 14 * 25 / 3 – 100 < 0,which simplifies to x* > 5. Once again, the Law of Compensated Demand rules out all bundles with x* < 5. In fact, these two cases correspond to the budget line, since prices and wealth simply double from the first case to the second.(b) Let (x*, y*, z*) be the bundle chosen under the new conditions. By the Law of Compensated Demand,(x* - 5)(8 – 10) + (y* - 10) (10 – 10) + (z* - 10) (12 – 10) < 0,which simplifies to x* > z*.But it is possible for demand for any individual good to increase or decrease. For example, the bundle (2, 13.4, 0) satisfies this inequality with demand for good x falling despite its drop in price, while demand for good 2 increases and demand for good z falls. Similarly, the bundle (11, 0, 31/6) satisfies this inequality with demand for goods x and z increasing while demand for good 2 falls.Note that (2, 13.4, 0) and (11, 0, 31/6) were not available at the original prices, so WARP does not rule out the possibility of choosing either of them over (5, 5, 5), the bundle selected at the original prices.While we cannot conclude that demand for any one particular good must increase or fall, we can rule out some combinations of changes. If demand for good z rises, then demand for good x must rise even more, while if demand for good x falls, then demand for good 3 must fall even more. It seems natural that demand for good x would rise and demand for good z would fall, since the price of good x declined while the price of good z increased, but this need not be the case.OPTIONAL PROBLEM FROM MWG4. MWG 2.D.4:You should be able to identify the non-convexity of this budget set immediately: if you were to draw a line connecting the points (24,0) and (a , M), the points on this line would lie outside the budget set. What this means in practical terms is that the individual can choose to have 24 hours of leisure (no work) and no consumption, or a hours of leisure and M consumption, but if the individual were to choose an amount of leisure exactly ½ of the way between a and 24, they would get less than ½ M in consumption. [The same is true if you pick any other fraction.] This makes it unlikely that individuals will choose (leisure, consumption) bundles that place them on the non-convex portion of a budget set. Try drawing some indifference curves and you will see that depending on how steep or flat these curves are, people will tend to locate either at (24,0) or (a ,M). Moreover, two people with very similar indifference curves might end up choosing very different bundles because of this non-convexity.To demonstrate this non-convexity mathematically, the strategy is to find the slope of the line connecting (24,0) and (a ,M), and then show that at the point on this line whereleisure=16 (or alternatively, work=8 hours), you get a consumption level above the point on the budget set (16,b ). Thus, the first helpful step is to find the values for a and b .The point (16,b ) is attained with 8 hours of labor at a wage rate of s per hour, so b =8s. The value of a indicates how much leisure you will have left, if you work enough hours to consume M. You can consume M by working 8 hours at wage rate s and (16-a ) hours at wage rate s’:'81616'8')16(8s s M a a s s M s a s M −−=−=−−+=If we work 8 hours (leisure=16), where would this put us on the line between (24,0) and (a ,M)? If we calculate the slope of the line with respect to work hours instead of withrespect to leisure hours, we get rise/run = (M-0)/(24-a ). Working 8 hours would thus give consumption of: '888s s M M −+ And then we need only show that this quantity is larger than 8s. There are many ways to do this; the most elegant is to notice that if we changed s’ to s in the above expression: s s M M s s M M 88888==−+ Since we know from the problem that s’>s, s s M M s s M M s s M M 88888'888==−+>−+ This demonstrates that the line is outside the budget set. NOTE: A full mathematical proof is ideal, but not necessary. Instead, a descriptive answer showing a clear understanding of the mathematical meaning of convexity as well as its practical interpretation in this problem, along with an appropriate graphical illustration, would be sufficient. 2.1 Transformations of Utility Functions (a) When x = y , u(x , y ) = xy = x 2. The desired transformation function f solves the equation f (u (x ,y )) = x when x = y OR f (x 2) = x , which can be solved by inspection: f (z ) = SQRT(z ). Then v (x , y ) = f (u (x , y )) = SQRT(xy ) = x 1/2 y 1/2Next compute the Marginal Rate of Substitution for u and for v .∂u / ∂x = y∂u / ∂y = x ,so(∂u / ∂y) / (∂u / ∂x) = x / y .∂v / ∂x = 1/2 x -1/2 y 1/2 ∂v / ∂y = 1/2 x 1/2 y -1/2so (∂v / ∂y) / (∂v / ∂x) = x / y.(b) When x = y, u(x, y) = 2x + y2= 2x + x2.The desired transformation function solves the equationf(u(x, y)) = x when x = yOR f(2x + x2) = x.This indicates that f(x) is the inverse function to g(x) = 2x + x2To invert this function, solve the equationx2z=2x+z + 1 = 2x + x2 + 1z + 1 = (x+1)2SQRT (z + 1) = x + 1SQRT(z + 1) – 1 = xSo if g(x) = 2x + x2, then g -1(x) = SQRT(x+1) – 1 – i.e. f(x) = SQRT(x+1) – 1. Then, v(x, y) = f(u(x,y)) = SQRT(2x + y2 – 1) – 1.Next compute the Marginal Rate of Substitution for u and for v.∂u / ∂x = 2 ∂u / ∂y = 2y,so (∂u / ∂y) / (∂u / ∂x)= y..∂v / ∂x = (2x + y2 – 1) -1/2∂v / ∂y = y (2x + y2 – 1) -1/2so (∂v / ∂y) / (∂v / ∂x)= y.2.2 Convex Preferences and Quasiconcave Utility FunctionsConsider the utility functions u1(x, y) = xy, u2(x, y) = x + y,u3(x, y) = x + SQRT(y).(a) As shown in the graph, these three utility functions produce indifference curves with qualitatively distinct properties. For indifference curves corresponding to u1, convex combinations of bundles on an indifference curve lie above the indifference curve. For indifference curves corresponding to u2, convex combinations of bundles on an indifference curve lie exactly on the indifference curve. For indifference curves corresponding to u3, convex combinations of bundles on an indifference curve lie below the indifference curve. That is, u1 appears to be strictly quasiconcave, u2 appears to be weakly quasiconcave and u3 does not appear to be quasiconcave.Problem 2.1 Graph102030(b) Taking partial derivatives:∂u 1 / ∂x = y ∂u 1 / ∂y = x;∂u 2 / ∂x = 1 ∂u 2 / ∂y = 1;∂u 3 / ∂x = 1∂u 3 / ∂y = 2y.MRS 1 = (∂u 1 / ∂x) / (∂u 1 / ∂y)= y / x.MRS 2 = (∂u 1 / ∂x) / (∂u 1 / ∂y)= 1.MRS 1 = (∂u 1 / ∂x) / (∂u 1 / ∂y)= 1 / 2y.Along an indifference curve as x increases and y decreases, MRS 1 is decreasing, MRS 2 is constant, and MRS 3 is increasing. This indicates that u 1 is strictly quasiconcave, u 2 is weakly quasiconcave, and u 3 is not quasiconcave.2.3 Skiing & Violins(a)Graph for Problem 2.32468101214161820(b) As shown in the graph, a convex combination of two points on the same indifference curve lies below the indifference curve, indicating that with these indifference curves, the consumer strictly prefers the weighted average of utilities of two different bundles to the convex combination of those bundles. Thus, the preferences represented by these utility functions are not convex.(c) The lowest indifference curve is tangent to the budget line at B = (10, 10). The second indifference curve intersects with the budget line at A = (0, 15) and at (20, 5). The third indifference curve intersects with the budget line only at the boundary pointC = (30, 0). Comparing these points and indifference curves, the optimal bundle on the budget line is at C = (30, 0). All other bundles on the budget line lie below the last indifference curve and therefore C = (30, 0) is strictly preferred to all other options on the given budget line.(d) The nonconvexity of preferences induces a choice of bundle that specializes in consumption of a single good. In essence, once we knew that the preferences were nonconvex as shown (with indifference curves that are mirror images of those for convex preferences) then it was almost certain that the optimal bundle would be at one of the ends of the budget line at A = (0, 15) or C = (30, 0).2.4 Piecewise Linear Indifference Curves and Optimal Bundles(a) First equate each bundle to a different bundle with x = y and then use transitivity to compare the bundles. The consumer is indifferent between bundle (x 1, y 1) and bundle (k 1, k 1) where k 1 = (x 1 + 2 y 1) / 3. The consumer is indifferent between bundle (x 2, y 2) and bundle (k 2, k 2) where k 2 = (2 x 2 + y 2) / 3.The consumer’s preference between the bundles can be identified from the comparison between k 1 and k 2. If k 1 > k 2, i.e. (x 1 + 2 y 1) / 3 > (2 x 2 + y 2) / 3, then the consumer strictly prefers (x 1, y 1) to (x 2, y 2). Similarly, if k 2 > k 1, i.e. (x 2 + 2 y 2) / 3 > (2 x 1 + y 1) / 3, then the consumer strictly prefers (x 2, y 2) to (x 1, y 1). Finally, if k 1 = k 2, i.e. (x 1 + 2 y 1) / 3 > (2 x 2 + y 2) / 3, then the consumer is indifferent between (x 1, y 1) and (x 2, y 2).(b) On a graph, show this consumer’s indifference curves through (4, 4) and (8, 8).Graph for Problem 2.4(b)24681012(c) As shown in the graph below, the bundle (4, 4) lies on the budget line and is the optimal choice.Graph for Problem 2.4(c)12345678optimal choice. Graph for Problem 2.4(d)24681012With equal prices, as in (c), the consumer will naturally choose a bundle with equal amounts of each good. However, if the price of one good is much larger than the other (as in (d), when p > 2q) then the degree of the consumer’s preference for equal consumption is outweighed by the difference in prices and the consumer will specialize consumption to just one good.2.5 Perfect ComplementsSolution will be included with Problem Set 1 Solutions3.1 Cobb-Douglas Utility(a) Start by writing the Lagrangian:L(x, y) = xα y1-α– λ (px + qy - W)Taking partial derivatives gives the first-order conditions∂L / ∂x = α xα-1 y1-α– λp =α (x / y) α-1– λp = 0; (1)∂L / ∂y = (1-α) xα y –α – λq =(1-α) (x / y)α – λq =0; (2) ∂L / ∂λ = W – px – qy = 0. (3) Rearrange and solve for x and y however you like. For example, you could start by solving (1) and (2) for λ, then using those two equalities to solve for y as a function of x.λ= α (x / y)α-1 / pq;λ= (1-α) (x / y)α/Setting these equal,α (x / y)α-1 / p = (1-α) (x / y)α / q;OR α (y / x) / p = (1-α) / q;OR y = (1-α) px / αq. (4) Finally, we can solve for the optimal bundle by substituting (4) into (3) – which is simply the budget constraint.First rewrite (3) asx = (W – qy) / p (5) then substitute (5) into (4):y = (1- α) (W – qy) / αqα) W / αq - (1- α) y / αy =(1-ORα) W / q - (1- α) yOR αy =(1-α) W / q. (6) ORy =(1-This is the formula for the choice of y in the optimal bundle. Substituting (6) into (5) yields the formula the choice of x in the optimal bundle.α) W) / p(1-x =(W-OR x = αW/ p. (7)(b) Use the same FOCs as above to solve for the Lagrange multiplier:q;λ= (1-α) (x / y)α/From (6) and (7),x / y = αq / (1-α) p,implying λ= (1-α) (αq / (1-α) p)α/ q,which can be simplified slightly toλ= (α / p)α[(1-α) / q)1-α.(c) Returning to the results from (a), the optimal choice of x is linear in W, αand 1 / p,and similarly the optimal choice of y is linear in W, 1-αand 1 / q. One property of these results is that total expenditure on x is equal to px*(p, W) = αW, while total expenditureon y is equal to qx*(p, W) = (1-α)W. That is, the parameter αdetermines the proportionof wealth spent on each good, then the prices p and q, translate that proportional expenditure into particular quantities of x and y.(d) Optimal BundleWith transformed utility function v(x, y) = α ln x + (1-α) ln y,L(x, y) = α ln x + (1-α) ln y – λ (px + qy - W)Taking partial derivatives gives the first-order conditions∂L / ∂x = α / x– λp = 0; (1’)∂L / ∂y = (1-α) / y – λq=0; (2’) ∂L / ∂λ = W – px – qy = 0. (3’) Solving (1) and (2) for λ,λ= α / px;λ= (1-α) / qy;Setting these equal,α / px = (1-α) / qyOR y= (1-α) px / αq,which is identical to (4). Thus, the optimal bundle is unchanged by the transformation of the utility function .Lagrange MultiplierNow solving λ = (1-α) / qy for λgivesλ= (1-α) / q[(1- α) W / q]ORλ= 1 / W .Using the interpretation of λas the “shadow price of the budget constraint”, the number of utility units achieved per additional unit of money varies with the form of the utility function. Therefore, since the transformation of the utility function changed the definition of one unit of utility, the Lagrange multiplier must also change as a result of this transformation.3.2. Skiing & Violins revisited(a) This is a separable utility function with associated first-order condition (MRS form)(∂u / ∂x) / p = (∂u / ∂y) / qOR 10 / p= 2y / q.With p = 10 and q = 20, the first-order condition is given by10 / 10 = 2y / 20 OR y = 10.(b) From 2.3, we know that the utility function is not quasiconcave – so that preferences are not convex and in fact, the first-order condition identifies a global minimum (i.e. minimum utility available on the budget constraint) rather than a maximum.(c) When the first-order conditions identify a minimum rather than a maximum, then the optimal bundle must be at one of the endpoints of the budget line, in this case (30, 0) and (0, 15). Computing u(30, 0) = 300 and u(0, 15) = 225, we conclude that the optimal bundle is (30, 0), since this gives higher utility in the comparison of the endpoints.3.3 Comparative Statics with One Good (Problem 3 on Problem Set 2)Solution will be included with Problem Set 2 Solutions3.4 Comparative Statics and the Marginal Rate of Substitution (Problem 1 on Problem Set 2)Solution will be included with Problem Set 2 Solutions3.5 Utility Maximization with Quantity Discount (Problem 2 on Problem Set 2)Solution will be included with Problem Set 2 Solutions3.6. Utility Maximization with Discounts on Initial Units(a) The budget constraint is piecewise linear, with slope -1/2 between the pointA = (0, 6) and pointB = (2, 5) (the point where the quantity discount applies). The budget constraint is “kinked” at point B, with slope changing to -1 betweenB = (2, 5) andC = (7, 0).The natural method for solving this problem is to find the optimal bundle on each separate linear portion of the budget line, and then compare these two bundles(a1) Between A = (0, 6) and B = (2, 5)On this part of the budget line, p = 2, q = 4 and the first-order condition is given by (∂u / ∂x) / (∂u / ∂y)) = p / q OR y = x / 2.The equation for the line between A and B is y = 6 – x / 2. Substituting the first-order condition into the budget line equation gives the solution x = 6, corresponding to a point beyond the end of the line between A and B. This indicates that the first-order conditions for a maximum cannot be satisfied on the line between A and B and instead that the optimal bundle on this line must be at either A or B. Since A yields utility 0, the optimal bundle on this line must be at B.TECHNICAL COMMENT: The first-order condition identifies the optimal bundle for a budget line from (0, 6) to (12, 0) – the budget line that applies with no increase in the price of x for x > Q*. Under these conditions, the optimal bundle would be (6, 3), producing utility 18. When the first-order condition is not satisfied on the line between A and B, the utility function must be strictly increasing (or strictly decreasing) on that line. In this case, the utility function starts at 0 at point A and is strictly increasing in x untilreaching point B where x = 2. Therefore, the maximum value of the utility function on the line between A and B occurs at the boundary, point B.(a2). Between B = (2, 5) and C = (7, 0),On this part of the budget line, p = 4, q = 4 and the first-order condition is given by (∂u / ∂x) / (∂u / ∂y)) = p / q OR y = x.The equation for the line between B and C is y = 7 – x. Substituting the first-order condition into the budget line equation gives the condition 2x = 7, which yields the solution x = 3.5, corresponding to the bundle (3.5. 3.5). This is the unique point on the line between B and C that satisfies the first-order condition.(a3) Comparing the candidate solutions.We have two candidate bundles for the consumer’s optimum. Bundle (2, 5) yields utility 10 and is the optimal choice on the budget line between A and B. By comparison, bundle (3.5, 3.5) yields utility 49/4 and is the optimal choice on the budget line between B and C. Since 49/4 > 10, bundle (7/2, 7/2) is the global optimum.(b) The solution follows the same method as in (a), but with slightly different budget equations throughout the analysis. As before, the budget constraint is piecewise linear, with slope -1/2 between the point A = (0, 6) and point B’ = (4, 4) (the point where the quantity discount applies) and separate slope -1 between B’ = (4, 4) and C = (8, 0).(b1) Between A = (0, 6) and B’ = (4, 4),On this part of the budget line, p = 2, q = 4 and the first-order condition is given by (∂u / ∂x) / (∂u / ∂y)) = p / q OR y = x / 2.As in (a1), the first-order condition identifies a bundle beyond the end of the line between A and B’. so the optimal bundle on this part of the budget line is at a boundary point, in this case at B’ = (4, 4).(b2) Between B’ = (4, 4) and C = (8, 0),On this part of the budget line, p = 4, q = 4 and the first-order condition is given by (∂u / ∂x) / (∂u / ∂y)) = p / q OR y = x.The equation for the line between B’ and C is y = 8 – x. Substituting the first-order condition into the budget line equation gives 2x = 8, which yields the solutionx = 4, corresponding to the bundle (4. 4). This is the unique point on the line between B’ and C’ that satisfies the first-order condition.(b3) Comparing the candidate solutions.We’ve identified the same bundle (4, 4) as the optimal bundle on each separate component of the budget constraint. Therefore, the bundle, which lies exactly at the boundary between the two parts of the budget constraint, must be the global optimum.(c) The solution follows the same method as above, but with again slightly different budget equations throughout the analysis. As before, the budget constraint is piecewise linear, with slope -1/2 between the point A = (0, 6) and point B’’ = (6, 3) (the point where the quantity discount applies) and separate slope -1 between B’’ = (6, 3) and C = (9, 0).(c1) Between A = (0, 6) and B’ = (6, 3)On this part of the budget line, p = 2, q = 4 and the first-order condition is given by(∂u / ∂x) / (∂u / ∂y)) = p / q OR y = x / 2.identifying a bundle (6, 3) that lies at the boundary of the line between A and B’’.(c2) Between B’’ = (6, 3) and C’’ = (9, 0),On this part of the budget line, p = 4, q = 4 and the first-order condition is given by(∂u / ∂x) / (∂u / ∂y)) = p / q OR y = x.The equation for the line between B’’ and C’’ is y = 9 – x. Substituting the first-order condition into the budget line equation gives 2x = 9, which corresponds to a bundle with x = 4.5 that does not lie on the line between B’’ and C’’. The optimal bundle on this line must be at one of the boundaries and in this case is at point B’’ = (6, 3).(c3) Comparing the candidate solutions.We’ve identified the same bundle (6, 3) as the optimal bundle on each separate component of the budget constraint. Therefore, the bundle, which lies exactly at the boundary between the two parts of the budget constraint, must be the global optimum. (d) For purchases of good x beyond Q* units, the prices of the two goods are equal, so with the given utility function, the consumer would then want to set the quantities of these two goods equal. However, if Q* is relatively large by comparison to W, the consumer has reason to consume more of x than y (setting x = 2y if possible) in order to take advantage of the reduced price for x on initial purchases.In (a) and (b), when Q* is low, the consumer simply sets x = y and the value of Q* only affects the total number of units of each good that the consumer can choose.。

2021年陕西省榆林市全国计算机等级考试数据库技术模拟考试(含答案) 学校:________ 班级:________ 姓名:________ 考号:________一、1.选择题(10题)1. 下面不属于DBMS的数据操纵方面的程序模块的是A.DDL翻译程序模块B.查询处理程序模块C.数据更新程序模块D.嵌入式查询程序模块2. 由实例管理器、模式管理器、安全管理器、存储管理器、备份管理器、恢复管理器、数据管理器和SQL工作表单组成的Oracle数据库管理工具是A.Oracle Developer/2000B.Oracle Enterprise ManagerC.Oracle Designer/2000D.Oracle Discoverer/20003.数据独立性是指（）。

A.数据依赖于程序B.数据库系统C.数据库管理系统D.数据不依赖于程序4. 下面有关模式分解的叙述中，不正确的是______。

A.若一个模式分解保持函数依赖，则该分解一定具有无损连接性B.若要求分解保持函数依赖，那么模式分解可以达到3NF，但不一定能达到BCNFC.若要求分解既具有无损连接性，又保持函数依赖，则模式分解可以达到3NF，但不一定能达到BCNFD.若要求分解具有无损连接性，那么模式分解一定可以达到BCNF5. 下面说法中错误的是______。

A.子类具有继承性B.子类的键是其超类的键C.子类继承超类上定义的全部属性，其本身不可包含另外的属性D.同一实体类型的若干子类之间可相交也可不相交6. 在一个单链表中，若要删除p节点的后续节点，则执行A.p↑.next：=p↑.next↑.next；B.p：=p↑.next；p↑.next：=p↑.next↑.next；C.flee(p↑.next)；D.p：=p↑.next↑.next；7. 进程是______。

A.与程序等效的概念B.行进中的程序C.一个系统软件D.存放在内存中的程序8. 下列哪一个描述是Internet比较恰当的定义? ( )A.一组协议集B.一个由许多个网络组成的网络C.OSI模型的下三层D.一种内部网络结构9. 下面不正确的说法是A.关键字是关系中能够用来唯一标识元组的属性B.在一个关系中，关键字的值不能为空C.一个关系中的所有候选关键字均可以被指定为主关键字D.关键字只能由单个的属性组成10. 在以下所列的条目中，______是数据库管理员(DBA)的职责。

2021年江苏省南通市全国计算机等级考试数据库技术预测试题(含答案) 学校:________ 班级:________ 姓名:________ 考号:________一、1.选择题(10题)1.多年来，人们习惯于从计算机主机所使用的主要元器件把计算机的发展进行分代，所谓第4代计算机使用的主要元器件是（）。

A.电子管B.晶体管C.中小规模集成电路D.大规模和超大规模集成电路2. 在DB2中，( )是数据库管理器根据查询条件从一个或多个基表中选取的元组的集合。

A.查询表B.模式C.索引D.结果表3. 数据库管理系统DBMS中用来定义模式、内模式和外模式的语言是______。

A.DMLB.CC.DDLD.Basic4. 下列属于特权指令的有Ⅰ．设置时钟Ⅰ．启动设备执行I/O操作Ⅰ．逻辑运算指令Ⅰ．访管指令A.Ⅰ，Ⅰ和ⅠB.Ⅰ和ⅠC.Ⅰ和ⅠD.Ⅰ和Ⅰ5. 下面列出的条目中，关于数据仓库基本特征的叙述不正确的是?A.数据仓库是面向主题的B.数据仓库的数据是集成的C.数据仓库的数据是相对稳定的D.数据仓库的数据是当前的，确保最新6. 关系数据库中，下列说法不正确的是A.每一个关系模型中，属性的个数是固定的B.在关系中元组的顺序(行的顺序)是无关紧要的C.在关系中属性的顺序(列的顺序)是无关紧要的D.关系中可以有重复的元组7. 规范化理论是关系数据库进行逻辑设计的理论依据。

根据这个理论，关系数据库的关系必须满足：其中每一属性都是A.互不相关的B.互不分解的C.长度可变的D.互相关联的8. 存储管理的目的是实现______。

A.提高计算机资源的利用率B.扩充主存容量，并提高主存利用效率C.有效使用和分配外存空间D.提高CPU的执行效率9. 在数据库中可以创建和删除表、视图、索引，可以修改表。

这是因为数据库管理系统捉供了A.数据定义功能B.数据操纵功能C.数据维护功能D.数据控制功能10. 设有栈S和队列Q，其初始状态为空，元素a1、a2、a3、a4、a5、a6依次入栈，出栈的元素则进入队列Q，若6个元素出列的顺序是a2、a4、a3、a6、a5、a1，则栈的容量至少是多大?A.6B.4C.3D.2二、填空题(10题)11. 设散列表的地址空间为0到18，散列函数为h(k)＝kmod 19，用线性探查法解决碰撞。