固体地球物理学概论第四章-01分解

《固体地球物理学概论》第一章：引言1、地球物理学的定义。

解：地球物理学是以地球为研究对象的一门应用物理学。

2、地球物理学组成及研究内容。

解：组成包括：理论地球物理、应用地球物理A. 理论地球物理学着眼于基础理论方面的研究，研究的主要内容有：（1）研究地球形状与重力分布的重力学；（2）研究地震及弹性波在地球内部传播规律的地震学；（3）研究地球磁现象的地磁学；（4）研究地球电性质的地电学；（5）研究地球内部热过程和热状态的地热学；（6）深部探测和地球动力学等。

B. 应用地球物理学是解决勘察石油、金属、非金属矿或其它地质问题的。

3、地球物理学的基本特点。

解：1、入地的窗口：根据地面或空中的资料和信息，了解地球深部情况；2、地球物理方法反演的多解性：正演问题、反演问题、精度问题3、地球物理方法的间接性问题4、建模与简化：就是以数学公式或数值形式表征地球某种性质或规律，它是对复杂研究客体的合理抽象和简化，从而更能反映客体的内在本质。

5、地球物理学初值和边值的约束作用：现在的地球为地球演化提供了一个作为初值（终值）的时间条件，而地面观测又为地球内部的物理过程提供了一个边界条件。

6、对地球物理学结论的可靠性估计（1）可靠性高的：牛顿万有引力定律，球谐分析理论、地球形状、地球自转周期；（2）可靠性较高：GPS、地球的速度分层结构；（3）可靠性具中的：地球的年龄、地球的分层结构（4）可靠性差的：大陆漂移和板块构造、地球内部的温度分布、地震预报；（5）可靠性最差的：地幔对流假说、地球起源假说、地磁场起源假说第二章：地球的起源1、戴文赛新星云假说的要点。

解：行星的形成要经过“原始星云→星云盘→尘层→星子→行星”这样几个步骤。

（1）原始星云的形成：原始星云是由一块星际云块塌缩并瓦解而成的。

根据维里定理，星际云质量比太阳现质量大三个数量级，它才会塌缩。

（2）星云盘的形成：原始星云盘继续塌缩，半径逐渐减小，因角动量守恒，造成自转速度增大。

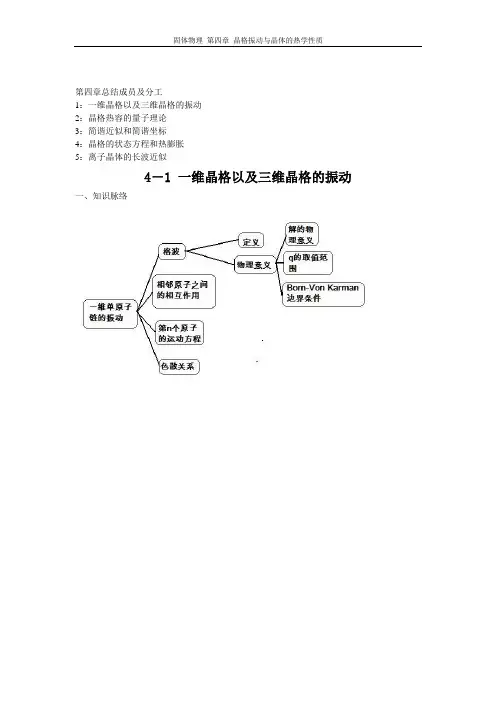
第四章总结成员及分工1：一维晶格以及三维晶格的振动2：晶格热容的量子理论3：简谐近似和简谐坐标4：晶格的状态方程和热膨胀5：离子晶体的长波近似4－1 一维晶格以及三维晶格的振动一、知识脉络二、重点1.格波的概念和“格波”解的物理意义(1)定义：晶格原子在平衡位置附近作振动时，将以前进波的形式在晶体中传播，这种波称为格波。

(2)物理意义：一个格波解表示所有原子同时做频率为ω的振动，不同原子之间有位相差。

相邻原子之间的位相差为aq 。

(3) q 的取值范围：－(π/a)<q ≤(π／a)这个范围以外的值，不能提供其它不同的波。

q 的取值及范围常称为布里渊区（Brillouin zones ）。

(4) Born-Von Karman 边界条件: 1)(=-Naq i e h Naq ⨯=π22.一维单原子链的色散关系22241[1cos ]sin ()2aq aq m m ββω=-=把 ω 与q 之间的关系称为色散关系(disperse relation)，也称为振动频谱或振动谱。

3.一维单原子链的运动方程相邻原子之间的相互作用βδδ-≈-=d dvF ad v d ⎪⎪⎭⎫ ⎝⎛=22δβ 第n 个原子的运动方程11()(2)n n n n i t naq nq m Ae ωμβμμμμ∙∙+--=+-=4.一维双原子链中两种原子的运动方程及其解（1）运动方程( equation))2(2221212n n n n M μμμβμ---=+++∙∙ )2(2221212n n n n M μμμβμ---=+++∙∙（2）方程的解(solution)])2([2q na t i n Ae -=ωμ ])12([12aq n t i n Be +-+=ωμ5.声学波与光学波的概念与物理意义（1）声学波与光学波的定义}]sin )(41[1{2/1222aq M m mM mM M m +-++=+βω }]sin )(41[1{2/1222aq M m mMmM M m +--+=-βω ω＋对应的格波称为光学波（optic wave ）或光学支（optic branch) ；ω－对应的格波称为声学波(acoustic wave)或声学支（acoustic branch ）（2）两种格波的振幅比aq m A B cos 222ββω--=⎪⎭⎫⎝⎛++aq m A B cos 222ββω--=⎪⎭⎫⎝⎛--（3）ω＋ 与ω－ 都是q 的周期函数)()(q aq --=+ωπω)()(q aq ++=+ωπω其中aq a22ππ≤〈-6.对色散关系的讨论（1）一维单原子链与一维双原子链的格波解的差异一维单原子链只有一支格波（一个波矢对应一个格波）— 声学波；而一维双原子链则有两支格波（一个波矢对应两个格波）— 声学波和光学波，两支格波的频率各有一定的范围：0)0()(min ==--ωω Maβπωω2)2()(max ==-- m aβπωω2)2()(min ==++ mMM m )(2)0()(max +==++βωω 在ω-max 与ω+min 之间有一频率间隙，说明这种频率的格波不能被激发。

第四章 晶格振动和晶体的热学性质● 晶格振动：晶体中的原子在格点附近作热振动● 原子的振动以波的形式在晶体传播（原子的振动波称为格波） ● 晶格振动对晶体的性质有重要影响 主要内容● 晶格动力学（经典理论，1912年由波恩和卡门建立）晶格振动的模式数量（有多少种基本的波动解） 晶格振动的色散关系（波动的频率和波数的关系）● 晶格振动的量子理论 ● 固体的热容量 4.1 一维单原子链的振动原子链共有N 个原胞，每个原胞只有一个原子,每个原子具有相同的质量m,平衡时原子间距等于晶格常数a,原子沿链方向运动,第n 个原子离开平衡位置的位移用x n 表示,第n 个原子和第n+1个原子间的相对位移为 一维单原子链原子振动时，相邻两个原子之间的间距: 基本假设● 平衡时原子位于Bravais 格点上 ● 原子围绕平衡位置作微振动●简谐近似：原子间的相互作用势能只考虑到平方项 微振动时：简谐近似：势能展开式保留到二次项微振动：原子离开平衡位置的位移与原子间距相比是小量。

晶体中原子的平衡位置由原子结合能（势）决定。

任何一种晶体，原子间的相互作用势能可以表述成原子之间距离的函数。

n n x x -=+1δδ+=a x ()()⋅⋅⋅+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛+=+=222 21 )(δδδa ax d U d x d U d a U a U x U把qa改变一个2π的整数倍，原子的振动相同，因此可以把qa限制负pi和正pi之间，此范围以外的q值，并不提供新的物理内容.群速度是指波包的传播速度，dw/dq,也就是能量在介质中的传播速度。

在布里渊区的边界上，群速度为零，波是一个驻波。

4.2 一维双原子链的振动q趋于0时，w也趋于零，称为声学波4.3 三维晶格的振动(略) 一个原胞中有n 个原子晶格基矢： 原胞数目： 原子的质量： 对于一个波矢q,有3n 个ω（即有3n 支色散曲线） 在3n 支色散关系中，当q→0时（长波）：有三支ω →0，且各原子的振幅趋于相同，这三支为声学波。