1-1周期现象

①太阳每天东升西落。
②某教师每天上课的时间。
（ ）
（ ）
③抛掷硬币正反面交替变化。
④一年二十四节气的变化。
（ ）
（ ）
畅言教育
北京师范大学出版社｜必修四
【解题探究】1、题(1)中月球到太阳的距离是固定不变的吗？ 2、题(2)中教师每天上课的时间是固定的吗？ 【探究提示】 1、因为太阳与月球都是在不停地运动，所以月球到太阳 的距离不是固定不变的，但是在某个时间点，月球到太阳 的距离是确定不变的。 2、教师每天上课的时间不是固定的，如数学教师今天是
畅言教育
北京师范大学出版社｜必修四
【解析】地球每24小时自转一周；①为周期现象。某中
学历年来高一(二)班的学生数是不固定的，且无规律；②
不是周期现象。③中的数虽有规律，但不重复出现，故不
是周期现象。十字路口的红绿灯的闪烁是有规律地重复出 现的，④是周期现象。 答案：①④
畅言教育
北京师范大学出版社｜必修四
畅言教育
北京师范大学出版社｜必修四
新知练习
1、判一判(正确的打“√”，错误的打“×”)
(1)每天晚上的新闻联播是周期现象。( )
(2)中国社会福利彩票中奖是周期现象。( )
(3)某中学每天上第一节课的时间是周期现象。( )
畅言教育
北京师范大学出版社｜必修四
【解析】(1)正确。每天晚上的新闻联播都是19:00播出。 (2)错误。中国社会福利彩票中奖无规律可循，故 不是周期现象。 (3)正确。每天上第一节课的时间是固定的。 答案：(1)√ (2)× (3)√
畅言教育
北京师范大学出版社｜必修四
2、做一做(请把正确的答案写在横线上) (1)观察“2，0，1，5，2，0，1，5，2，0，1，5，…”寻找 规律，则第25个数字是________。 (2)今天是星期一，那么再过100天是_______。 (3)我们知道2012年伦敦奥运会是第30届，那么第36届奥运会 是______年。

2.经历数据分析及观察散点图特征，感受周期现
象对实际工作的意义;(重点)
3.能熟练地判断简单的实际问题的周期.（难点）
探究点1 对周期现象的理解
当潮汐发生时，水的深度会产生周期性变化，
为了研究水深的变化规律，我们可以构造一个函
数.例如，确定一个位置，考察该处水深H和时间t
的关系，那么H就是t的函数.下表1-1是某港口在
( B )年
A.2018 举办一次. 【解析】选B.2014+8=2022. B.2022 C.2026 D.2030
【解题关键】冬奥会和夏季奥运会一样,都是每隔4年
3.某齿轮转动装备如图,大齿轮有44个齿,小齿轮有22 个齿,当大齿轮转动10周时,小齿轮转动 A.10周 B.5周 C.15周 ( D ) D.20周
某一天水深与时间的对应关系表，通过表中数据， 我们来研究H(t)这个函数.
表1-1 时刻 1:00 2:00 3:00 4:00 5:00 6:00 7:00 8:00 水深 /m 5.0 6.2 7.5 7.3 6.2 5.3 4.1 3.1 时刻 9:00 10:00 11:00 12:00 13:00 14:00 15:00 16:00 水深 /m 2.5 2.7 3.5 4.4 5.0 6.2 7.5 7.3 时刻 17:00 18:00 19:00 20:00 21:00 22:00 23:00 24:00 水深 /m 6.2 5.3 4.1 3.1 2.5 2.7 3.5 4.4
【即时训练】
下列现象不是周期现象的是( A.四季交替现象 C.每年春节联欢晚会 B )
B.暴风雪的发生 D.物理中的简谐振动
【解析】A，C，D中的现象都符合周期现象的特征，
而B中暴风雪的发生是一种随机现象.

周期现象使用说明：1.阅读探究课本53 p 页的基础知识，自主高效预习，提升自己的阅读理解能力；2.完成教材助读设置的问题，然后结合课本的基础知识和例题，完成本学案内容。

【学习目标】1.通过实例了解自然界存在着丰富的周期现象，并能从数据或图形中，读出周期规律。

2.通过本节的学习，使学生对周期现象有一个初步的认识，感受生活中处处有数学。

3.培养学生学好数学的信心，学会运用联系的观点认识事物。

【重点难点】重点：感受周期现象的存在，会判断是否为周期现象。

难点：周期现象的深刻理解以及简单的应用。

一、知识链接我们已经知道，潮汐、钟表都是一种周期现象，钱塘江潮波浪每隔一段时间会重复出现，这也是一种周期现象。

请你再举出生活中存在周期现象的例子。

二.教材助读我们怎样从数学的角度研究周期现象呢？请同学们自主学习课本P3—P4的相关内容，并思考回答下列问题：①如何理解“散点图”？②图1-1中横坐标和纵坐标分别表示什么？③如何理解图1-1中的“H/m ”和“t/h ”？④对于周期函数的定义，你的理解是怎样？总结：周期函数定义的理解要掌握三个条件，即存在不为0的常数T ；x 必须是定义域内的任意值；f(x ＋T)＝f(x)。

三、预习自测1．下列现象是周期现象的是 ( ) ①日出日落 ②潮汐 ③海啸 ④地震A. ①②B. ①②③C. ①②④D. ③④2．设钟摆每经过1.8s 回到原来的位置。

在图中钟摆达到最高位置时开始计时， 经过1min 后，请你估计钟摆在铅垂线的左边还是右边。

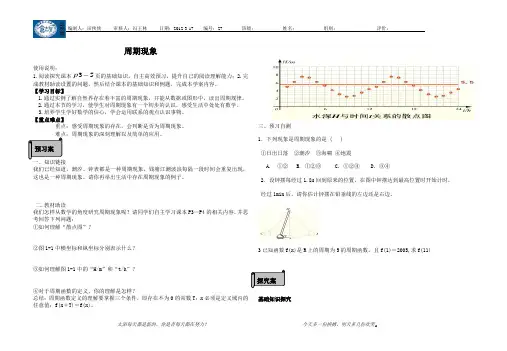
3已知函数f(x)是R 上的周期为5的周期函数，且f(1)＝2005,求f(11)基础知识探究预习案 探究案1.地球围绕着太阳转，地球到太阳的距离y是时间t的函数吗？如果是，这个函数y＝f(t)是不是周期函数？2.图1-3（见课本）是钟摆的示意图，摆心A到铅垂线MN的距离记为y，钟摆离铅垂线MN 的角记为θ，根据物理知识判断，y与θ是否是时间t的周期函数？综合应用探究图1-4（见课本）是水车的示意图，水车上A点到水面的距离为y，假设水车5min转一圈，那么y随时间的变化规律是否具有周期性？【当堂检测】1.（1）地球上一年春、夏、秋、冬四季的变化是周期现象吗？（2）钟表的分针每小时转一圈，它的运行是周期现象吗？（3）连续抛一枚硬币，面值朝上我们记为0，面值朝下我们记为1，数字0和1是否会周期性的重复出现？2.今天是星期三那么7k(k∈Z)天后的那一天是星期几?7k(k∈Z)天前的那一天是星期几?100天后的那一天是星期几?100天前的那一天是星期几？我的收获。

136.6
P/mmHg 93.35 136.65 115 93.35
115
5
(1)请根据上表提供的数据，在坐标系中作出血压P与时间 t的对应关系的散点图. (2)血压随时间的变化的现象是周期现象吗？ 【解题指南】通过散点图的变化趋势研究周期现象.
【解析】(1)作出血压P与时间t的散点图.如下：
(2)由散点图可以看出，每经过15 s，血压就重复出现相 同的数值，因此血压随时间的变化的现象是周期现象.
【方法技巧】应用周期现象解决实际问题的两个要点
【变式训练】今天是星期五，则168天后是_______，170 天后是_______. 【解题指南】一星期是7天，一个循环. 【解析】因为168=7×24，,170=7×24+2，所以168天 后仍是星期五，170天后是星期天. 答案：星期五 星期天
依据规定，当海浪高于1米时才对冲浪爱好者开放，依据 上表可以判断，一天内的8:00至20:00时之间，有多少时 间可以供冲浪者运动？
【解题探究】1.从图像观察，函数值有没有重复出现？ 2.对题(2)中的数据如何提取有效信息？ 【探究提示】1.有，当x分别在[0,2],[3,5],[6,8]取值时， 对应的y值会重复出现. 2.将实际问题中的数据转化为散点图，利用散点图解决实 际问题.
【微思考】 (1)重复出现的现象是周期现象吗？ 提示：不一定，重复出现，还要有规律. (2)有规律可循的现象是周期现象吗？ 提示：不一定，有规律可循，还要重复出现.
【即时练】 下列现象不是周期现象的是_________(填序号). ①挂在弹簧下方上下震动的小球； ②游乐场中摩天轮的运行； ③抛一枚骰子，向上的数字是奇数； ④每四年出现1个闰年. 【解析】①②④都有规律可循，而抛一枚骰子，向上的数 字可能是奇数，也可能是偶数,无规律可循.故③不是周期 现象. 答案：③

7.50
A B C D
5.00 2.50
xA = 0.3848 xB = 5.6152 xC = 12.3848 xD = 17.6152
21 24
0
3
6
9
与水面的距离) 5.一条货船的吃水深度（船底与水面的距离)为4米，安全条例 一条货船的吃水深度 规定至少要有1.5米的安全间隙 船底与洋底的距离）， 米的安全间隙（ ），该船 规定至少要有1.5米的安全间隙（船底与洋底的距离），该船 何时能进入港口？在港口能呆多久？ 何时能进入港口？在港口能呆多久？A
21：00 18 ： 15 2.5
24：00 ： 5.0
水深/米
1.大约什么时间港口的水最深？深度约是多少？ 1.大约什么时间港口的水最深？深度约是多少？大约什 大约什么时间港口的水最深 么时间港口的水最浅？深度约是多少？ 么时间港口的水最浅？深度约是多少？ 2.在什么时间范围内，港口的水深增长？ 2.在什么时间范围内，港口的水深增长？在什么时间 在什么时间范围内 范围内，港口的水深减少？ 范围内，港口的水深减少？ 3.试着用图形描述这个港口从 时到24 试着用图形描述这个港口从0 24时水深的变化情 3.试着用图形描述这个港口从0时到24时水深的变化情 。（作出这些数据的散点图 作出这些数据的散点图） 况。（作出这些数据的散点图） 4.用一个函数来近似描述这个港口的水深与时间的函 4.用一个函数来近似描述这个港口的水深与时间的函 数关系. 数关系.
在日常生活中， 在日常生活中，有一些现象 是按照一定的规律周而复始， 是按照一定的规律周而复始，不断 重复出现。比如：一年有12个月， 12个月 重复出现。比如：一年有12个月， 从一月开始到十二月； 从一月开始到十二月；我们把这种特殊的 规律问题称为周期问题。 规律问题称为周期问题。

为简”、“化无限为有限”的目的. (2)只要确定好周期现象中重复出现的“基本单位”就可以 把问题转化到一个周期内来解决.
【例2】水车上装有16个盛水槽，每个盛水槽最多盛水10升， 假设水车5分钟转一圈，计算1小时内最多盛水多少升？ 【审题指导】由于水车每隔5分钟转一圈，所以要计算1小 时内最多盛水多少升，关键是确定1小时内水车转多少圈.
(C)11点处
(D)12点处
【解析】选B.由题意得，60分钟后分针恰好指在2点处,所以
再过40分钟，分针指在10点处.
3.若葡萄与苹果如下图所示排列,则第2 012个水果是______.
【解析】因为2 012=402×5+2结合图形可知第2 012个水果 是苹果. 答案:苹果
4.一列数，2、0、1、1、2、0、1、1、„„共2 011个，则 最后一个数字是______，其中有______个2，______个0，_
1.下列变化中不是周期现象的是( (A)“春去春又回” (B)钟表的分针每小时转一圈 (C)“哈雷彗星”的运行时间 (D)射击运动员射击时射中的环数
)
【解析】选D.射击运动员射击时射中的环数是随机数，不是
周期性出现的.
2.钟表分针的运行是一个周期现象，其周期为60分钟，现在 分针恰好指在2点处，100分钟后分针指在( (A)8点处 (B)10点处 )
(3)经过7.2秒，小球在平衡位置的左边还是右边？
【审题指导】解答本题要注意以下两点:⑴小球的运动规律
为M-O-N-O-M.⑵从M到O，从O到N，从N到O，从O到M时间相同.
【规范解答】(1)由题意知小球依M-O-N-O-M作周期性运动从 M到达O所用时间为0.5秒,„„„„„„„„„„„„2分 所以小球第三次经过平衡位置O的时间为0.5×5=2.5(秒)； „„„„„„„„„„„„„„„„„„„„„„„4分

若钟摆的高度h(mm) 例2 若钟摆的高度 与时间t(s)之间的函数关系如 与时间 之间的函数关系如 图所示． 图所示． (1)求该函数的周期； 求该函数的周期； 求该函数的周期 (2)求t＝10s时钟摆的高度． 时钟摆的高度． 求 ＝ 时钟摆的高度 由图像可知， 解:(1)由图像可知，该函数的得周期 由图像可知 该函数的得周期T=1.5s (2)设h=f(t), 设 ∵T=1.5s × ∴ f(10) =f(1+6×1.5) =f(1) =20 时钟摆的高度为20mm． 故t＝10s时钟摆的高度为 ＝ 时钟摆的高度为 ．
已知函数y=f(x),x∈R图像如图所示： 图像如图所示： 例1 已知函数 ∈ 图像如图所示 y (0)= 0 ； f(1)= 0 ；
…… …… -2 -1 0 1 2 3 4 …… x
f( n )= 0 ； …… (2)f(-1.5)= 0.5； f(0.5)= 0.5； f( 0.5+n )= 0.5 问题1： 问题 ：你能用数学语言描述这个函数的特征 吗？ f(x+1)=f(x) f(x+n)=f(x)
北师大版必修4课件
§1 周期现象
日出日落、月缺月圆、 日出日落、月缺月圆、寒来暑 自然界中有许多“ 往……自然界中有许多“按一定规 自然界中有许多 律周而复始”的现象， 律周而复始”的现象，这种按一定 规律不断重复出现的现象称为周期 现象。再比如人自出生之日起， 现象。再比如人自出生之日起，人 的情绪、体力、智力等心理、 的情绪、体力、智力等心理、生理 状况也呈周期变化（ 状况也呈周期变化（称为生物节 ）．另外 另外， 律）．另外，物理学中也大量存在 周期性运动变化， 周期性运动变化，例如匀速圆周运 动位置变化的周期性、 动位置变化的周期性、简谐振动位 移变化的周期性、 移变化的周期性、交变电流变化的 周期性，等等． 周期性，等等．那么数学中是如何 刻画这种变化规律呢？ 刻画这种变化规律呢？

高一年级数学学科编号：22 班级： 学生姓名： 设计人：史旭龙 审核人：安仓娃课题：§1周期现象【学习目标】(1)了解周期现象在现实中的广泛存在;(2)经历数据分析以及观察散点图特征的学习过程,受周期现象对实际工作的意义; (3)能熟练判断简单的实际问题的周期. (4)能利用周期函数定义进行简单运用。

【学习重点】感受周期现象的存在，会判断是否为周期函 数.【学习难点】对周期现象的理解以及周期函数概念的理解，以及简单的应用.第一部分【自主学习】1、周期现象：每经过相同时间间隔T ，某种现象就 出现一次，这种现象称为周期现象.2、周期函数：已知函数f(x)满足对定义域内的任意x ，均存在非零常数 ，使得f(x ＋T)＝f(x)第二部分【合作探究】1、某港口在某季节每天的水深()y m 与时间()x h 的观测数据及其关系如下表：请根据表中的给出的数据，作出散点图，并判断这个港口的水深是否具有周期现象.2、地球围绕着太阳转，地球到太阳的距离y 是时间t 的函数吗？如果是，这个函数y ＝f(t)是不是周期函数？/t h0 3 6 9 12 15 18 21 24 /y m10131071013107103、已知函数f(x)是R上的周期为5的周期函数，且f(1)＝2005,求f(11)第三部分【课堂练习】1、判断下列现象是否周期现象：（1）地球上一年四季春、夏、秋、冬的变化；（2）钟表的分针的运动；（3）连续抛一枚硬币，出现正面向上；（4）国庆节到了，街上多处悬挂着红、蓝、绿相间的彩灯.2、地球同步卫星绕地球公转的周期是（）A一年B一个月 C 24小时 D 12小时3、已知奇函数f(x)是R上的函数，且f(1)＝2，f(x＋3)＝f(x)，求f(8).第四部分【课后反思】请学生回顾本节课所学过的知识内容有哪些？所涉及到的主要数学思想方法有那些？。

各种现象------长短周期现象、拖带现象、钩拢现象长短周期现象、拖带现象、钩拢现象与等频现象-1、长短周期现象；是一些室早易出现在长心动周期后.并由它引起的长代偿间歇又促使下一个室早发生.如此重复形成二联律.这种遵守二联律法则的室性早搏与某些恶性室性心律失常密切相关.称为长短周期现象。

这种现象诱发的室性心律失常大多是多形性室速.尖端扭转型室速.室颤的发生与此现象有关。

2、拖带现象；各种心动过速.适时的外界提前冲动或刺激可以提前进人心动过速的起博点或折返环.使..心动过速的节律重整.心动过速并未被终止.并随超速刺激.出现节律连续重整.心速增至超速刺激频率.一旦停止刺激.心动过速频率逐渐恢复至被刺激前频率.这种现象称为心动过速的拖带现象。

3、钩拢现象与等频现象；在频率完全相等或接近相等的双重心律所互相形成的干扰性和阻滞性脱节中.双重心律的心搏几乎同时或同时出现的现象称钩拢现象。

钩拢现象中的双重心律由于频率完全相等或接近相等而互相形成干扰性和阻滞性脱节.双重心律的等频程度同时也反映了两重心律的钩拢重度。

根据这两种心律的不同钩拢现象可分为不完全性（指干扰性或阻滞性脱节中的双重心律的频率相等.两种心律先后出现.但差距不大.基本钩拢在一起. ）和完全性.（指双重心律在干扰性或阻滞性脱节中频率完全相等且心搏是同时出现.两种心博完全钩拢在一起.）。

心电图；1 不完全性钩拢现象；双重心律频率相等但钩拢程度较差， P--R间距长。

表现为；⑴ P—R固定.但P与QRS无关系；⑵心室率快时心电图显示类似伴干扰性房室传导延缓的窦性心动过速或房性心动过速图形，但一旦心室率减慢，呈现完全性房室脱节现象。

2 完全性钩拢现象；双重心律完全等频，又同时出现。

主要表现为；⑴一系列P波埋在QRS波群中，是QRS波群与P波同时出现相互重叠所致；⑵一系列房性融合波或室性融合波。

等频现象；指任何原因引起的两种心律在互相干扰性和阻滞性脱节中表现为频率近乎相等的现象，如果双重心律的频率完全相等则称为完全等频现象，钩拢现象中的双重心律均为等频现象。

§1周期现象§2角的概念的推广学习目标：1.了解现实生活中的周期现象.2.了解任意角的概念，理解象限角的概念．(重点)3.掌握终边相同角的含义及其表示．(难点)4.会用集合表示象限角．(易错点)[自主预习·探新知]1．周期现象(1)以相同间隔重复出现的现象叫作周期现象．(2)要判断一种现象是否为周期现象，关键是看每隔一段时间，这种现象是否会重复出现，若出现，则为周期现象；否则，不是周期现象．思考1：“钟表上的时针每经过12小时运行一周，分针每经过1小时运行一周，秒针每经过1分钟运行一周．”这样的现象，具有怎样的特征？提示：周而复始，重复出现．2．角的概念(1)角的有关概念(2)角的概念的推广思考2：如果一个角的始边与终边重合，那么这个角一定是零角吗？提示：不一定，若角的终边未作旋转，则这个角是零角．若角的终边作了旋转，则这个角就不是零角．3．象限角的概念(1)前提条件①角的顶点与原点重合．②角的始边与x轴的非负半轴重合．(2)结论角的终边(除端点外)在第几象限，我们就说这个角是第几象限角．(3)终边相同的角及其表示所有与角α终边相同的角，连同角α在内，可构成一个集合：S＝{β|β＝α＋k×360°，k∈Z}．如图1-2-1所示：图1-2-1注意以下几点：①k是整数，这个条件不能漏掉．②α是任意角．③k·360°与α之间用“＋”号连接，如k·360°－30°应看成k·360°＋(－30°)(k∈Z)．④终边相同的角不一定相等，但相等的角终边一定相同，终边相同的角有无数个，它们相差周角的整数倍．思考3：假设60°的终边是OB，那么－660°，420°的终边与60°的终边有什么关系，它们与60°分别相差多少？提示：它们的终边相同．－660°＝60°－2×360°，420°＝60°＋360°，故它们与60°分别相隔了2个周角的和及1个周角．[基础自测]1．判断(正确的打“√”，错误的打“×”)(1)某同学每天上学的时间是周期现象．()(2)第三象限角一定比钝角大．()(3)始边相同，终边不同的角一定不相等．()(4)始边相同，终边也相同的角一定相等．()[答案](1)×(2)×(3)√(4)×2．下列说法正确的是()A．三角形的内角一定是第一、二象限角B．钝角不一定是第二象限角C．相差180°整数倍的角为终边相同的角D．钟表的时针旋转而成的角是负角D[A错，如90°既不是第一象限角，也不是第二象限角；B错，钝角在90°到180°之间，是第二象限角；C错，终边相同的角之间相差360°的整数倍；D正确，钟表的时针是顺时针旋转，故是负角．]3．－378°是第________象限角．()A．一B．二C．三D．四D[－378°＝－360°－18°，因为－18°是第四象限角，所以－378°是第四象限角．]4．把－936°化为α＋k·360°(0°≤α<360°，k∈Z)的形式为________.【导学号：64012019】[解析]－936°＝－3×360°＋144°，故－936°化为α＋k·360°(0°≤α<360°，k∈Z)的形式为144°＋(－3)×360°.[答案]144°＋(－3)×360°[合作探究·攻重难](1)下列变化中不是周期现象的是()A．“春去春又回”B．钟表的分针每小时转一圈C．天干地支表示年、月、日的时间顺序D．某交通路口每次绿灯通过的车辆数(2)水车上装有16个盛水槽，每个盛水槽最多盛水10升，假设水车5分钟转一圈，计算1小时内最多盛水多少升．(1)D[由周期现象的概念易知，某交通路口每次绿灯通过的车辆数不是周期现象．故选D.](2)因为1小时＝60分钟＝12×5分钟，且水车5分钟转一圈，所以1小时内水车转12圈．又因为水车上装有16个盛水槽，每个盛水槽最多盛水10升，所以每转一圈，最多盛水16×10＝160(升)，所以水车1小时内最多盛水160×12＝1 920(升)．1．如图1-2-2所示是某人的心电图，根据这个心电图，请你判断其心脏跳动是否正常．图1-2-2[解]观察图像可知，此人的心电图是周期性变化的，因此心脏跳动正常．下列结论：①锐角都是第一象限角；②第二象限角是钝角；③小于180 °的角是钝角、直角或锐角．其中，正确结论的序号为______.【导学号：64012019】[思路探究]根据任意角、象限角的概念进行判断，正确区分第一象限角、锐角和小于90°的角．[解析]①锐角是大于0°且小于90°的角，终边落在第一象限，故是第一象限角，所以①正确；②480°角是第二象限角，但它不是钝角，所以②不正确；③0°角小于180°，但它既不是钝角，也不是直角或锐角，所以③不正确．[答案]①2．下列说法正确的是()A．终边相同的角一定相等B．钝角一定是第二象限角C．第一象限角一定不是负角D．小于90°的角都是锐角B[终边相同的角不一定相等，故A不正确；钝角一定是第二象限角，故B 正确；因－330°是第一象限角，所以C不正确；－45°<90°，但它不是锐角，所以D不正确．]1．任意角都是象限角吗？为什么？提示：不是．一些特殊角终边可能落在坐标轴上．如果角的终边在坐标轴上，这个角就不是象限角．2．象限角的表示．提示：已知α为第二象限角，问2α，α2分别为第几象限的角？[思路探究] 由角α为第二象限角，可以写出α的范围：90°＋k ·360°<α<180°＋k ·360°(k ∈Z )，在此基础上可以判断2α，α2的范围，进而可以判断出它们所在的象限．[解] ∵α是第二象限角，∴90°＋k ·360°<α<180°＋k ·360°(k ∈Z )． ∴180°＋2k ·360°<2α<360°＋2k ·360°(k ∈Z )．∴2α是第三或第四象限角，以及终边落在y 轴的负半轴上的角． 同理，45°＋k 2·360°<α2<90°＋k2·360°(k ∈Z )． ①当k 为偶数时，令k ＝2n (n ∈Z )． 则45°＋n ·360°<α2<90°＋n ·360°(k ∈Z )， 此时α2为第一象限角；②当k 为奇数时，令k ＝2n ＋1(n ∈Z )． 则225°＋n ·360°<α2<270°＋n ·360°(n ∈Z )． 此时α2为第三象限角．综上可知，α2为第一或第三象限角． 母题探究1．(变设问)在本例条件下，求角2α的终边的位置． [解] ∵α是第二象限角，∴k ·360°＋90°<α<k ·360°＋180°(k ∈Z )． ∴k ·720°＋180°<2α<k ·720°＋360°(k ∈Z )．∴角2α的终边在第三或第四象限或在y 轴的非正半轴上． 2．(变条件)若角α变为第三象限角，则角α2是第几象限角？[解] 如图所示，先将各象限分成2等份，再从x 轴正半轴的上方起，按逆时针方向，依次将各区域标上一、二、三、四，则标有“三”的区域即为角α2的终边所在的区域，故角α2为第二或第四象限角．[规律方法]倍角、分角所在象限的判定思路(1)已知角α终边所在的象限，确定nα终边所在的象限，可依据角α的范围求出nα的范围，再直接转化为终边相同的角即可．注意不要漏掉nα的终边在坐标轴上的情况．(2)已知角α终边所在的象限，确定αn终边所在的象限，分类讨论法要对k的取值分以下几种情况进行讨论：k被n整除；k被n除余1；k被n除余2，…，k 被n除余n－1.然后方可下结论．几何法依据数形结合思想，简单直观．终边相同的角3．在同一坐标系中作出390°，－330°，30°的角并观察这三个角终边之间的位置关系，角的大小关系．提示：如图所示，三个角终边相同，相差360°的整数倍．4．对于任意一个角α，与它终边相同的角的集合应如何表示？提示：所有与角α终边相同的角连同α在内，可以构成一个集合，S＝{β|β＝α＋k·360°，k∈Z}，即任何一个与角α终边相同的角，都可以表示成角α与周角整数倍的和．已知α＝－1 910°.(1)把α写成β＋k·360°(k∈Z,0°≤β<360°)的形式，并指出它是第几象限角；(2)求θ，使θ与α的终边相同，且－720°≤θ<0°.【导学号：64012019】[思路探究]利用终边相同的角的关系α＝β＋k·360°，k∈Z.求解．[解](1)－1 910°＝250°－6×360°，其中β＝250°，从而α＝250°＋(－6)×360°，它是第三象限的角．(2)令θ＝250°＋k·360°(k∈Z)，取k＝－1，－2就得到满足－720°≤θ<0°的角，即250°－360°＝－110°，250°－720°＝－470°.所以θ为－110°，－470°.母题探究1. (变条件)若将例题改为如图1-2-3所示的图形，那么阴影部分(包括边界)表示的终边相同的角的集合如何表示？图1-2-31．下列变化是周期现象的是() A．地球自转引起的昼夜交替变化B．随机数表中数的排列C．某交通路口每小时通过的车辆数D．某同学每天打电话的时间A[由周期现象的概念知A为周期现象．]2．与－265°终边相同的角为()A．95°B．－95°C．85°D．－85°A[因为－265°＝－360°＋95°，所以－265°与95°终边相同．]3．25°的角的始边与x轴的非负半轴重合，把终边按顺时针方向旋转2.5周所得的角是________.【导学号：64012019】[解析]由题意，所得的角为25°＋360°×(－2.5)＝－875°.[答案]－875°4．终边在直线y＝－x上的角的集合S＝________.[解析]由于直线y＝－x是第二、四象限的角平分线，在0°～360°间所对应的两个角分别是135°和315°，从而S＝{α|α＝k·360°＋135°，k∈Z}∪{α|α＝k·360°＋315°，k∈Z}＝{α|α＝2k·180°＋135°，k∈Z}∪{α|α＝(2k＋1)·180°＋135°，k∈Z}＝{α|α＝n·180°＋135°，n∈Z}．[答案]{α|α＝n·180°＋135°，n∈Z}5．已知，如图1-2-5所示．图1-2-5(1)写出终边落在射线OA，OB上的角的集合；(2)写出终边落在阴影部分(包括边界)的角的集合．[解](1)终边落在射线OA上的角的集合是{α|α＝k·360°＋210°，k∈Z}．终边落在射线OB上的角的集合是{α|α＝k·360°＋300°，k∈Z}．(2)终边落在阴影部分(含边界)角的集合是{α|k·360°＋210°≤α≤k·360°＋300°，k∈Z}．。

【复习回顾】
1.角的定义是什么？ 2.角的范围是什么？
定义1 ：由一个顶点出发的两条射线所组成的图形。 定义2:平面内一条射线绕着端点从一个位置旋转到 另一个位置所成的图形叫做角。
锐角；钝角；直角；平角；周角；角的范围是(0°，360°)
【思考】
如果你的手表慢了5分钟，你是怎样将它校准 的？如果你的手表快了1.25小时，你应当如何将它 校准？当时间校准后，分针旋转了多少度？
【象限角】
第二象限角 y
【坐标轴上的角】
第一象限角 如果角的终边落在 了坐标轴上，就认 角α终边 为这个角不属于任 何象限。
第四象限角 0
α
x
0
角α始边
第三象限角
平面直角坐标系
定义：我们使角的顶点与原点重合，角的 始边与X轴的非负半轴重合。那么，角的 终边在第几象限，我们就说这个角是第几 象限角。
【例1】在0°～360°范围内，找出与950°12′角终边相同的角，并判定它是第几 象限角。 解：-950°12′=129°48′－3×360°， 所以在0°~360°范围内，与-950°12′ 角终边相同的角是129°48′，它是第二象限 角。
【例2】写出终边在y轴上的角的集合。
解：终边落在ｙ轴正半轴上的角的集合为
分析问题
我们知道，海水会发生潮汐现象。但潮汐发生
时，水的深度会产生周期性的变化。为了研究水
深的变化规律，我们可以构造一个函数。如：确
定一个位置，考察该处水深H和时间t的关系， 那么H就是t的函数。 教材P4图1-1
例1 地球围绕着太阳转，地球到太阳 的距离y随时间的变化是周期性的吗？
解：在任何一个确定的时刻，地球与太阳的 距离y是唯一确定的，每经过一年地球围绕着 太阳转一周。无论哪个时刻t算起，经过一年 时间，地球又回到原来的位置，所以，地球与 太阳的距离是周期变化的。

数学周期现象知识点总结数学周期现象是数学中一个非常重要的概念，它在许多不同的数学领域中都有着广泛的应用。

周期现象可以在代数、几何、微积分、概率统计等领域中找到，并且在实际生活中也有着许多的应用。

了解周期现象的基本概念和性质，对于理解数学问题和解决实际问题都是非常有帮助的。

1. 周期现象的基本概念周期现象指的是一种在某个区间内重复出现的规律性现象。

这种现象在数学中广泛存在，其中最为典型的就是正弦函数和余弦函数。

这两个函数都是以2π为周期来重复的函数，因此它们在周期现象的研究中具有着非常重要的地位。

对于一个周期现象，可以用函数的图像来进行描述。

在图像中，可以看到函数在某一段区间内重复进行，形成周期性的波动。

而在数学上，可以用函数的性质和周期函数的定义来进一步描述周期现象。

2. 周期函数的性质周期函数是指在某一段区间内具有重复规律的函数。

其中，最为典型的周期函数就是正弦函数和余弦函数。

这两个函数在周期性上有着非常明显的特点，即它们在2π的整数倍上具有相同的函数值。

这也是周期函数的最基本性质之一。

另外，周期函数的另一个重要性质是其在周期区间内具有对称性。

这是因为周期函数在周期区间内的函数值是重复的，因此可以通过对称轴来完成函数值的对称。

这个对称性在周期函数的图像中可以很清楚地看到，因此对于周期函数的性质研究中具有着重要的作用。

另外，周期函数还具有相位差和振幅的性质。

其中，相位差指的是函数图像在周期内的偏移量，而振幅则是函数图像在周期内的最大偏移量。

这两个性质在周期函数的图像中可以很直观地看到，因此对于周期函数的性质研究也是非常重要的。

3. 周期函数的应用周期函数在数学中有着广泛的应用。

其中，最为典型的就是在物理学和工程学中的应用。

在这两个领域中，周期函数可以用来描述许多自然现象和工程问题，因此在解决实际问题时有着重要的作用。

在物理学中，周期函数被广泛用来描述振动现象。

其中，最典型的就是弹簧振子和单摆的运动。

— 25 —
— 返回 —
随堂巩固验收
03
高中新教材同步导学案•BS•数学•必修第二册
— 返回 —
1．下列现象是周期现象的有( D ) ①太阳的东升西落；②月亮的圆缺；③太阳表面的太阳黑子活动；④心脏的收缩与舒 张． A．1 个 B．2 个 C．3 个 D．4 个
[解析] 由周期现象的描述知①②③④均为周期现象．
— 10 —
— 返回 —
课堂互动探究
02
高中新教材同步导学案•BS•数学•必修第二册
— 返回 —
题型一 生活中的周期现象 【典例 1】 (1)我国农历用鼠牛虎兔龙蛇马羊猴鸡狗猪这 12 种动物按顺序轮流代表 各年的年号，2016 年是猴年，那么 1949 年是( A ) A．牛年 B．虎年 C．兔年 D．龙年 (2)受日月的引力，海水会发生涨落，这种现象叫做潮汐．已知某海滨浴场的海浪高 度 y(米)是时间 t(0≤t≤24，单位：时)的函数，记作 y＝f(t)，下表是某日各时的浪高数据：
2．周期函数的定义 一般地，对于函数 y＝f(x)，x∈A，如果存在一个非零常数 T，使得对任意的 x∈A， 都有 x＋T∈A 且满足 f(x＋T)＝f(x) ，那么函数 y＝f(x)称作周期函数，非零常数 T 称这个 函数的周期．
— 5—
高中新教材同步导学案•BS•数学•必修第二册
— 返回 —
[温馨提示](1)周期函数的定义是对定义域中的每一个值来说的．如果只有个别的 x 值 满足 f(x＋T)＝f(x)，那么 T 是不能称为 f(x)的周期的．
— 返回 —
— 8—
高中新教材同步导学案•BS•数学•必修第二册
2．若 f(x)的最小正周期 T＝1，则下列选项不是 f(x)的周期是( B ) A．－1 B．0 C．2 D．－2

元素周期表中的周期性规律与趋势元素周期表是化学中最重要的工具之一，它对于研究元素的性质和化学反应具有深远的意义。

在元素周期表中，元素的排列遵循一定的规律和趋势，这些规律和趋势对于我们理解元素的性质和预测其化学行为至关重要。

周期性规律是指元素周期表中元素性质的重复变化规律。

这些规律可以总结为周期表的水平行和垂直列。

首先，我们来看一下周期表的水平行，也就是元素周期数的变化。

在元素周期表中，水平行代表着元素的周期数，周期数从左到右递增。

这意味着同一周期内的元素具有相似的化学性质，因为它们的电子结构是相似的。

例如，第一周期的元素都只有一个能级，它们都是单质，具有相似的反应性和物理性质。

另一个周期性规律是元素周期表中的垂直列，也被称为族。

元素周期表中的族数从上到下递增，而同一族的元素具有相似的化学性质。

这是因为同一族的元素具有相似的外层电子配置。

有些族的元素非常活泼，在与其他元素发生化学反应时往往能释放出大量的能量。

比如，第一族的碱金属元素（钠、钾等）都是非常活泼的金属，与水反应时能产生剧烈的氢气和碱溶液。

而第十八族的气体元素（氦、氖等）则是非常稳定的，几乎不与其他元素反应。

除了周期性规律外，元素周期表还展现了一些趋势。

这些趋势可以帮助我们理解元素的性质和预测其反应性。

下面我们来看几个常见的周期表趋势。

首先是电离能的趋势。

电离能指的是将一个电子从原子轨道中移除所需的能量。

一般来说，原子半径越小，电离能越大。

这是因为较小的原子有更强的核吸引力，更难将电子移除。

相反，较大的原子有较小的核吸引力，因此更容易丧失电子。

其次是电负性的趋势。

电负性是指原子对电子的亲和力，即吸引和保持电子的能力。

一般来说，原子的电负性随着周期数的增加而增加，因为更多的电子会导致更强的电子排斥效应。

而电负性随着族数的增加而减小，因为电子外层的屏蔽效应会减弱核对电子的吸引力。

最后是原子半径的趋势。

原子半径指的是原子的大小。

一般来说，原子半径随着周期数的增加而减小，因为随着原子核电荷数的增加，核对电子的吸引力增强，使得电子更加靠近原子核。

y．假设水车每５min转一圈，那么y的值每经过５min就会 重复出现，因此，距离y随时间的变化规律也具有周期性．
A
y
由上面的例子，我们可以看到在自 然界中存在着大量的周期现象。
(3)由散点图，可以估计出，在3:00和15:00，水深
取得最大值为7.5m，即浪最高，所以，在3:00和
15:00观潮比较合适。
(4)由给定条件，知水深至少为5.5m时才能保证需要货船安全
驶入港口。作一条H= 5.5m的水平直线。
8 6 4 2 0 0
H/m
t/h
8
16
24
由图可知，安全时间段为1：30~5：40, 13：30~17：40.
7:00
8:00
4.1
3.1
15:00
16:00
7.5
ቤተ መጻሕፍቲ ባይዱ7.3
23:00
24:00
3.5
4.4
水深H与时间t关系的散点图
8 6 4 2 0 0 8 16 24
t/h H/m
8
H/m
6
4
2
0 0 3 89 15 16 21 24
t/h
每经过相同的时间间隔T（12h），水深就重复出现相同的数 值，即H（t+T）= H（t），水深基本上是随着时间周期性变 化的。
从散点图可以看出，每经过相同的时间间 隔，水深就重复出现相同的数值。因此，水 深是周期性变化的。这样的周期现象在我们 身边还有很多，下面我们再分析几个例子。
例１ 地球围绕着太阳转，地球到太阳的距离y随时间的变化
是周期性的吗？ 解: 根据物理学知识,我们知道在任何一个确定的时刻,地
球与太阳的距离y是唯一确定的，每经过一年地球围绕太阳

在日常生活中，有一些现象 是按照一定的规律周而复始，不断 重复出现。比如：一年有12个月， 从一月开始到十二月；我们把这种特殊的 规律问题称为周期问题。
问题1
如果现在是早上9点钟,问你:24小时以后是几点钟?
你会毫不犹豫地回答:还是早 上9点钟。因为你很清楚,0 点、1点、2点、3点……23 点,每隔24小时就重复出现 一次。
小结：
回顾这节课所学过的内容有那些？
问题2
如果今天是星期一,问 你:7天以后是星期几?
抽象概括
相同的间隔而重复出现的现象称为周期现象,如 “24小时1天”、“7天1星期”、“365天1年” 就是我们所熟悉的周期现象。
自然界中有很多周期现象。 大家能在举些例 子吗？ 如日出日落、月圆月缺、四季交替,等等。
感受钱塘江潮
海水受日月的引力，在一定的时候发生涨落的现象叫潮。 一般地，早潮叫潮，晚潮叫汐。
4.是不是函数图像？
课堂练习题 1.地球围绕太阳转（如图 1 ），地 球到太阳的距离y是时间t的函数吗？ 如果是，这个函数y=f(t) 是不是周 期变化？
太阳 地球
图1
2.地球上一年春、夏、秋、冬四季的变 化是周期现象吗？ 3.钟表的分针每小时转一圈，它的运行 是周期现象？ 4.连续抛一枚硬币，面值朝上我们记为 0 ，面值朝下我们记为 1 ，数字 0 和 1 是否会周期性地重复出现？
圣米切尔山
涨潮
落潮
生物中也有很多周期现象,
1.如人的脉搏大约每隔0.85秒跳一跳,眼 睛大约每隔4秒眨一眨。 2.科学家发现,人的体力从弱到强又从 强到弱存在着23天的变化周期, 3.人的智力则存在着33天的变化周期。
某港口在某季节每天的时间与水深关系表：
时刻 0：00 5.0 9：00 2.5

12:00 13:00 14:00 15:00 16:00
2.5 2.7 3.5 4.4 5.0 6.2 7.5 7.3
17:00 18:00 19:00 20:00 21:00 22:00 23:00 24:00
6.2 5.3 4.1 3.1 2.5 2.7 3.5 4.4
根据上表提供的数据在坐标纸做出水深H与时间t 关系的散点图。
函数f(x)满足对定义域内的任意x，均存在非零常数T使得
f(x+T)=f(x)
我们称f(x)是周期函数，T称为这个函数的周期.
习题1—1
思考 1.“东升西落照苍穹，影短影长角不同” 是周期现象吗？ 2.今天星期五，那么150天之后是星期几？
另见书本思考交流
作业
习题1—1 写在作业本上课代表统一上塘江潮
波浪每隔一段时间会重复出现，这种现象就叫作 周期现象。 周期现象：
走路时，手臂自然地随步伐周期性的摆动；
太阳东升西落重复出现的周期就是“一日”； 月亮由圆变缺，又由缺变圆，就是“一月”； 冬去春来，循环往复就是“一年”。
规律技巧：判断某种现象是否为 周期现象，关键要看该现象是否 每隔一段时间就重复出现一次
在任何确定的时间，地球与太阳距离y是唯一确定的，每经 过一年地球围绕着太阳转一周。 无论从哪个时间t算起，经过一年时间(T=365天），地球又回到 原来的位置，所以地球与太阳的距离是周期变化的。
y=f(t+365)=f(t)
举 例
例2 钟摆问题 摆心A到铅垂线MN的距离记为y，钟摆偏离铅垂线的角度记 为θ。无论从哪个时间t算起，经过一段时间，钟摆又回到了原 来的位置，角度又变成了θ，所以y与θ都随时间的变化而周期 性变化。
有什么结论？