专题：质心系概论

大学物理力学第六章质心运动定理（一）引言概述：
大学物理力学第六章质心运动定理（一）是研究质点系运动的基本定理之一。

它提供了描述质点系运动的质心运动定理，通过质心的位置和速度来刻画整个质点系的运动状态。

本文将从质心的定义、质心运动的基本性质、运动定理的表达形式、定理的证明过程以及实际应用等五个大点来详细阐述质心运动定理的相关内容。

正文：
一、质心的定义
1. 质心的概念及其物理意义
2. 如何计算质心的位置坐标
二、质心运动的基本性质
1. 质心的速度与质点的速度之间的关系
2. 质心的加速度与质点的加速度之间的关系
3. 质心运动的平稳性及其相关说明
三、质心运动定理的表达形式
1. 质心运动定理的基本公式
2. 质心运动定理的向量形式
3. 质心运动定理的微分形式
四、质心运动定理的证明过程
1. 利用质心的定义和质点系的微分元素进行推导
2. 推导过程中的重要假设和简化处理
3. 将推导结果与实际情况进行对比验证
五、质心运动定理的实际应用
1. 航天器的姿态控制与稳定
2. 运动物体的动量变化分析
3. 天文学中的质心运动定理应用
总结：
本文从质心的定义、质心运动的基本性质、运动定理的表达形式、定理的证明过程以及实际应用等五个大点全面阐述了大学物理力学第六章质心运动定理（一）的相关内容。

这一定理的正确应用，不仅能够帮助我们更好地理解质点系的运动规律，还在实际生活中有着广泛的应用前景，对于提高物体运动控制、动量变化分析、航天器姿态控制等方面都具有重要意义。

通过深入学习和理解质心运动定理，我们能够更好地应用物理学知识解决实际问题，推动科学技术的发展。

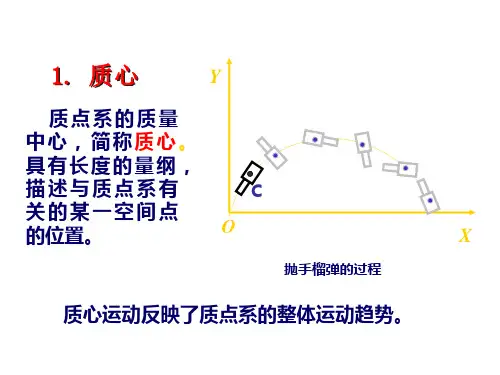
质心知识点总结归纳质心（Center of Mass）是物体集中质量的平均位置。

在物理学中，质心是描述物体运动的重要概念，对于研究物体的运动、碰撞、转动等现象都有重要的意义。

同时，质心在工程、航天航空等领域也有着广泛的应用。

质心的计算方法有多种，可以通过物体的密度分布、几何形状和其他条件来进行计算。

而质心的运动规律也可以通过牛顿定律和动量定律来描述。

本文将从质心的概念、计算方法、运动规律以及工程应用等方面对质心的知识点进行总结和归纳。

一、质心的概念1. 定义质心是物体所有质点的集中位置，也可以看作是物体的平衡点。

在质心系中，物体的总动量和总角动量相对于质心系均为零。

2. 特点（1）质心不一定位于物体内部，可以位于物体的外部；（2）质心的运动不一定与物体的其他点相同；（3）质心的位置与物体的形状和质量分布有关；（4）质心具有跟随物体运动的特点。

二、质心的计算方法1. 特殊形状物体的质心计算（1）均匀杆对于一根均匀杆，质心位于杆的中点处。

（2）均匀圆环对于一个均匀圆环，质心位于环的中心处。

2. 连续体的质心计算对于连续分布的质量分布，可以通过积分的方法来计算质心。

一般来说可以使用以下公式来计算：\[ x_{cm} = \frac{1}{M} \int x\;dm \]\[ y_{cm} = \frac{1}{M} \int y\;dm \]\[ z_{cm} = \frac{1}{M} \int z\;dm \]其中，\( x_{cm} \)、\( y_{cm} \)、\( z_{cm} \) 分别表示质心在 x、y、z 方向上的位置，M 表示物体的总质量。

三、质心的运动规律1. 质心的运动状态质心的运动状态可以通过牛顿定律和动量定律描述。

在外力作用下，质心会产生加速度，并且质心的加速度与物体的质量成反比。

2. 刚体的平动运动对于刚体的平动运动，可以通过质心的运动来描述整个刚体的运动状态。

刚体的平动运动可以看作是质心的平动运动。

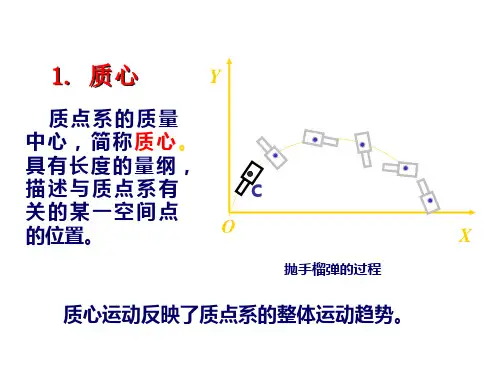
第五章质心刚体质心运动定理ca m F v v =合外质点系的质心加速度由合外力确定，与内力无关。

牛顿定律的独特性质：如果它在某一小尺度范围内是正确的，那么在大尺度范围内也将是正确的。

特殊的质点系——刚体m1l5.1.2 质点系动力学量的分解质心参考系：随质心一起运动的平动参考系，简称质心系。

在质心系中质心静止==c c v r v v常矢量质心系中的运动图象各质点从质心四面散开，或向质心八方汇聚。

质心成为一个运动中心，运动时时刻刻是“各向同性的”。

质点系的动量质点系的动量等于质心的动量c p p v v =质点系相对质心的动量总是为零0=′=′∑ii i v m p vv 质点系中各质点m i 相对质心的运动),(i i v r ′′v v m iO Ci r ′v ir v Cr v 在任一参考系中质点系的动量、动能和角动量与质心运动的关系核反应中的资用能质点系的角动量i c i i c i v v v r r r ′+=′+=v v v v v v ,∑×=iii i v m r L v v v ∑∑∑∑′×′+×⎟⎠⎞⎜⎝⎛′+⎟⎠⎞⎜⎝⎛′×+⎟⎠⎞⎜⎝⎛×=i i i i c i i i i i i c c i i c v m r v r m v m r v m r L v v v v v v v v v ∑′×′=′×=′+=ii i i c c c c v m r L v m r L L L L vv v v v v v v v , ,质点系的角动量可分解成质心角动量与质点系相对质心的角动量之和同一参考点质心为参考点m iOCi r ′v ir v Cr v 其中5.1.3 质心参考系质心系一般是非惯性系，引入平移惯性力ci a m v −在质心系中质点系的动能定理和角动量定理质心系中质点系的动量恒为零，质点系的动量定理不必考虑。

动力学中的质心系变换理论动力学（Dynamics）是自然科学的一个分支，主要研究物体运动的规律以及其与力、能量和作用的关系。

质心系变换理论（Center of mass frame transformation）是其中一个非常重要的概念，在动力学的研究中起到了重要的作用。

本文将对质心系变换理论的概念、意义和应用进行探讨。

一、质心的概念质心（Center of mass）是物理学中一个非常重要的概念。

在二维或三维空间中，质心就是表示物体所占据的空间中心的点。

在物理学中，常用以下公式来计算质心。

其中，m表示物体的质量，r表示物体所占据的空间坐标。

质心在动力学研究中的作用非常重要，因为它可以用来描述物体的运动和旋转。

二、质心系的定义质心系（Center of mass system）一般指的是一个虚拟的坐标系，它可以在不同恒定的坐标系下进行移动和旋转，并且保持物体的质心不动。

这里要强调的是，质心系的移动和旋转并不影响物体的运动，所以它被称为“惯性参考系”。

三、质心系变换理论的概念质心系变换理论是动力学中一个非常重要的概念。

它主要指的是，在不同的参考系下，物体在质心系中的运动方程式是相同的。

换句话说，无论物体在哪一个静止的参考系下运动，只要我们找到了它的质心系，那么物体在质心系下的运动方程式就是相同的。

这一点可以用数学公式来表示。

设在坐标系A下，物体动量为P，质心位置为r；在坐标系B下，物体动量为P'，质心位置为r'。

那么有以下关系式：P=P'+Mvr=r'+ut其中，M表示物体的总质量，v表示静止参考系B相对于A的速度矢量，u表示静止参考系B相对于A的位移矢量。

四、质心系变换理论的应用质心系变换理论在动力学研究中有着广泛的应用。

以下是一些常见的例子。

1、可以将静止参考系转化成质心系。

由于质心系是惯性参考系，所以质心系中的运动方程是相对简单的。

这种转化方法特别适用于研究质点的统计性质，如质点输运定理等。

理解质心坐标系质心坐标系是研究物体运动和平衡的重要工具。

它是基于质点运动的原理，通过将整个物体简化为一个质点，从而简化了问题的复杂性。

理解质心坐标系对于研究力学和物体运动十分关键。

一、什么是质心坐标系质心坐标系是一种以质点（物体的质量集中在其中的一个点）作为参考点的坐标系。

在质心坐标系中，质点的位置被定义为原点，而物体的其它部分则围绕着质点进行运动。

质心坐标系的特点在于简化了物体运动问题的计算。

通过将物体看作质点，我们可以忽略物体内部各部分之间的相互作用，并且可以将复杂的运动问题转化为简单的质点运动问题。

二、质心的计算方法为了确定质心坐标系，我们需要计算出物体的质心位置。

质心的位置可以通过求质心坐标的平均值来确定。

对于连续分布的物体，质心的计算公式如下：x_c = (m1x1 + m2x2 + … + mnxn) / (m1 + m2 + … + mn)y_c = (m1y1 + m2y2 + … + mnyn) / (m1 + m2 + … + mn)z_c = (m1z1 + m2z2 + … + mnzn) / (m1 + m2 + … + mn)其中，(x1, y1, z1)、(x2, y2, z2)、…、(xn, yn, zn)是物体上各质点的坐标，m1、m2、…、mn是它们的质量。

三、质心坐标系的应用质心坐标系在力学和物体运动的研究中有广泛的应用。

它可以简化复杂的物体运动问题，使得我们可以更容易地分析和计算运动的参数。

例如，在静力学中，质心坐标系可以帮助我们确定物体的平衡条件。

如果一个物体在质心坐标系中保持静止，那么我们可以推断该物体受到的合力和合力矩均为零。

这使得我们可以通过简单的计算，确定物体是否处于平衡状态。

在动力学中，质心坐标系对于研究物体的运动轨迹和动量变化也非常有用。

通过将物体看作质点，我们可以将复杂的运动问题转化为质点运动问题，从而更容易地分析和预测物体的运动情况。

四、总结理解质心坐标系对于研究力学和物体运动具有重要意义。

质心系前面我们回顾了Newton 定律以及由它导出的一些重要的推论，主要有由于Newton 定律只在惯性系中才是成立的，因此作为其推论，这些定理的成立的前提当然也要求所涉及的量都是相对于某个惯性系测量或计算出的。

但是，存在一个可能是非惯性系的特殊参考系，这些推论在其中也都是成立的，其中一些，譬如动量定理，其形式来的还要更加简单。

这个特殊的参考系就是质心系，也就是以质心为原点并随质心一起平动的参考系。

如果我们用表示粒子在某个惯性系中的位矢，而a r K a a r ′K 则表示它在质心系中的位矢，它们之间有如下关系：CM a r R r a ′=+K K K (1) 在质心系中质心当然始终是位于原点的，因此0a a am r ′=∑K (2)另一方面，体系的总动量就是质心的动量，因此，体系在质心系中的总动量就该为零。

当然，上式两边对时间求微商也就得到了同样的结论。

， 0a a a a a ad p m r m r dt ′′==∑∑K K ′=K (3) 这个方程其地位就相当于在一般惯性系中的质心运动定理。

利用这些关系，你会发现描述体系状态的那些量——如角动量以及动能——都可以表示为两部分之和：一部分描述质心的运动，另一部分则描述体系相对于质心的运动。

如角动量()()CM CM CM CM CM a a a a a a a a a a a aa a a a a L L r p R r m R r R m R r m r R m r a′′==×=+×+⎛⎞′′=×+×⎜⎟⎝⎠′+×∑∑∑∑∑∑K K K K K K K K K K K K K K a a a m r ′+∑K CM R ⎛⎞×⎜⎟⎜⎟⎝⎠K (4) 其中第一项正是质心的角动量，而最后一项则是体系相对于质心的角动量： CM CM CM , a a aL R P L r m ar ′′=×=×′∑K K K K K K (5) 而中间两项则显然是等于零的，因此CM L L L ′=+K K K (6) 角动量变化的原因，即力矩，也可以作类似的分解，一部分对质心的运动负责，另一部分则负责相对于质心的运动：()CM CM CM CM CM with and a a a a a a a a a a aa a a aa r F R r F R F r F R F r F ττττττ′==×=+×′=×+×′′=+=×=×∑∑∑∑∑∑K K K K KK K K K K K ′K K K K K K K K (7)由于总的外力，第一项正是质心角动量的变化率，而我们又知道CMF MP =K K Lτ=K K ，由此L τ′′=K K (8) 即不管质心系是否是惯性参考系（也就是说，不管体系是否受到外力的作用），在质心系中角动量定理依然成立。

质心系中的功能原理质心系（又称质心参考系）是一种研究物体运动的参考系，它是相对于一个物体或者一组物体的质心（重心）而言的。

在质心系中，质心的坐标保持不变，物体的运动变得相对简单起来。

我们可以通过了解质心系的功能原理，来深入理解质心系的作用和重要性。

首先，我们先来介绍一下质心的概念。

质心是一个物体或一组物体的集中力量的中心点，可以看作是物体的平均位置。

在一个简单的情况下，物体的质心就是物体的几何中心。

而在一个复杂的情况下，物体的质心就是根据物体的质量分布来计算的一个位置。

质心系的功能原理基于以下两个主要观点：1. 质心系是一个惯性系：在一个惯性系中，牛顿力学定律成立，即物体上的力等于质量乘以加速度。

在质心系中，质心保持静止或以恒定速度直线运动，可以看作是一个惯性系，物体上的力等于质量乘以相对于质心系的加速度。

2. 质心系的加速度可以简化计算：在质心系中，质心的坐标保持不变，物体的运动相对于质心系变得相对简单起来。

我们可以选择质心系作为研究物体运动的参考系，以便更容易计算物体的加速度和运动状态。

基于以上观点，我们可以总结出质心系的功能原理如下：1. 简化系统的描述：通过选择质心系，我们可以简化描述物体运动的方程，更容易计算物体的加速度和运动状态。

例如，在质心系中，如果物体相对质心系保持静止，那么它不会受到合外力的作用；如果物体相对质心系做匀速直线运动，那么它的加速度为零。

2. 独立性原理：根据独立性原理，我们可以将一个由多个物体组成的系统看作是由多个独立的质点组成的。

在质心系中，我们可以将物体的运动分解为质点的运动，每个质点受到的力等于质量乘以相对于质心系的加速度。

这样，我们可以分别分析每个质点的运动，然后将它们的运动合成为整个系统的运动。

3. 简化受力分析：在质心系中，物体上的力等于质量乘以相对于质心系的加速度。

通过选择质心系，我们可以简化受力分析，只需考虑作用在质心上的力，而不需要考虑其他复杂的力。

第六章质心质点组的运动比较复杂，采用两种眼光来处理二、着眼于把握质点组的总体运动，再分析各个质点之间的相对运动。

即将质点组的复杂运动分解为这两种运动的叠加，这是一种新的途径，可将力学理论推向一个新的境界。

一、着眼于每个质点，平等地对待每个质点，将相互作用分为内部的外部的，分析了内部相互作用的若干特点之后，确定了质点组的动量变化定理及其守恒条件，机械能变化定理及其守恒条件，和角动量变化定理及其守恒条件，成功地解决了一批典型的力学问题，诸如：–两体碰撞–火箭推进速度–三种宇宙速度–有心运动这标志着我们把牛顿力学理论推进到一个新的阶段。

是否存在这样一种运动，它反映了质点组总体运动的宏观特点？θθ2λ2Rm说明(1)质心相对于质点组的位置与坐标系无关，质心的位置完全由质点组的质量分布决定(2)对于密度均匀，形状对称的物体，其质心在物体的几何中心处对于一般物体，质心不一定在物体上例如圆环的质心在圆环的轴心上锥体上滚②物体若有某种对称性，质心就位于对称的位置。

它与牛顿第二定律在形式上完全相同，相应于系统的质量全部集中于系统的质心，在合外力的作用下，质心以加速度a c 运动∑==N i iC F a M 1凡是由牛顿第二定律直接导出的定理，如质点动量变化定理，机械能变化定理，质点角动量变化定理，均适用于质心。

只需将质点的质量改换为质点组的总质量，力改换为合外力系统内力不会影响质心的运动定向爆破质心参考系质心参考系：随质心一起运动的平动参考系，简称质心系。

质心系以可以是惯性系，也可以是非惯性系。

在质心系中质心静止c v i r cr icr COi质心系中所有质点相对于质心的动量之和为零.若选质心为参考点,则质心的坐标始终为零。

质点组整体随质心的运动+各质点相对于质心的运动质点组的复杂运动通常可分解为：核反应中的资用能高能粒子碰静止靶粒子能量利用率低，采用对撞质心动能定理质心系中质点组动能定理的微分形式kdE dW dW dW =++惯外内()()()0i c i c i i c c iidW m a dr a d m r a d Mr =-⋅=-⋅=-⋅=∑∑惯kk E W W dE dW dW ∆=+=+外内外内 ,质心系中质点组动能定理的微分形式和积分形式与惯性系完全相同，机械能定理也相同。