厦门市重点名校2019-2020学年高二下学期期末质量检测地理试题含解析

2019－2020学年度厦门市第一学期高一年级质量检测数学试题满分为150分，考试时间120分钟.注意事项：1.答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.全部答案答在答题卡上，答在本试卷上无效。

一、选择题：本大题共8个小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合，B＝{x|lg（2x﹣2）＞0}，则A∩B＝（）A.{x|﹣3＜x＜﹣}B.{x|1＜x≤2}C.D.{x|x≤﹣1}2.已知f（lnx）＝x＋1，则f（x）＝（）A.e x＋1B.e x﹣1C.x＋1D.x2＋13.《九章算术》是我国古代内容极为丰富的数学名著，卷一《方田》[三三]：“今有宛田，下周六步，径四步问为田几何？”译成现代汉语其意思为：有一块扇形的田，弧长6步，其所在圆的直径是4步，问这块田的面积是（）平方步？A.6B.3C.12D.94.的值为（）A. B. C. D.5.已知a＝log1.60.6，b＝0.60.6，c＝1.60.6，则a，b，c的大小关系为（）A.a＞b＞cB.c＞a＞bC.c＞b＞aD.b＞c＞a6.函数f（x）＝ln|x|＋|cos x|（且x≠0）的图象大致是（）A. B.C. D.7.函数y＝sin（ωx＋φ）与y＝cos（ωx＋φ）（其中ω＞0，|φ|＜）在x∈[0，]的图象恰有三个不同的交点P，M，N，△PMN为直角三角形，则φ的取值范围是（）A.[﹣，]B.（﹣，]C.[﹣，）D.[0，]8.函数的最大值是（）A. B. C. D.二、多选题：本大题共2个小题，每小题5分，共10分。

在每小题给出的四个选项中，有多项符合题目要求。

全部选对的得5分，选对但不全的得3分，有选错的得0分.9.设P是一个数集，且至少含有两个数，若对任意a、b∈P，都有a＋b、a﹣b、ab、∈P（除数b≠0）则称P是一个数域，例如有理数集Q是数域，下列命题中正确的是（）A.数域必含有0，1两个数B.整数集是数域C.若有理数集Q⊆M，则数集M必为数域D.数域必为无限集10.已知不恒为零的函数f（x）在定义域[0，1]上的图象连续不间断，满足条件f（0）＝f（1）＝0，且对任意x1，x2∈[0，1]都有|f（x1）﹣f（x2）|≤|x1﹣x2|，下列四个结论中正确的有（）A.若f（1﹣x）＝f（x）且0≤x≤时，f（x）＝x（x﹣），则当＜x≤1时，f（x）＝（1﹣x）（﹣x）B.若对∀x∈[0，1]都有f（1﹣x）＝﹣f（x），则y＝f（x）至少有3个零点C.对∀x∈[0，1]，|f（x）|≤恒成立D.对∀x1，x2∈[0，1]，|f（x1）﹣f（x2）|≤恒成立三、填空题：本大题共6小题，每小题5分，共30分.在答题卡上的相应题目的答题区域内作答.11.已知集合A＝{1，2，3，4}，那么A的真子集的个数是.12.在△ABC中，向量＝，P是BN上一点，若向量＝λ＋，则λ＝.13.设函数f（x）＝A sin（ωx＋φ）（A＞0，ω＞0，﹣＜φ＜，x∈R）的部分图象如图所示.则函数y＝f（x）的解析式为.14.已知θ是钝角，且，则的值为.15.已知函数，g（x）＝x2﹣2mx＋5m﹣2（m∈R），对于任意的x1∈[﹣2，2]，总存在x2∈[﹣2，2]，使得f（x1）＝g（x2）成立，则实数m的取值范围是.16.已知函数f（x）＝，若对任意a，b，c∈（0，＋∞）都有f（a）＋f（b）＞f（c）成立，则m的取值范围是三、解答题：本大题共6小题，共70分，解答题应写出文字说明，证明过程或演算步骤，在答题卡上相应题目的答题区域内作答.17.（本小题满分10分）已知向量＝（1，2sin x），＝（1，cos x﹣sin x），f（x）＝（1）求函数f（x）最小正周期；（2）求函数f（x）的单调递增区间；（3）当x∈[0，]时，若方程|f（x）|＝m有两个不等的实数根，求m的取值范围.已知函数f（x）为定义在R上的奇函数，当x＞0时，f（x）＝x﹣.（1）求f（﹣2）的值；（2）用函数单调性的定义证明：函数f（x）在（0，＋∞）上单调递增；（3）求函数f（x）在x∈R上的解析式.如图，已知△OAB中，点C是点B关于A的对称点，点D是线段OB的一个靠近B的三等分点，DC和OA交于E，设＝，＝（1）用向量与表示向量；（2）若＝，求实数λ的值.图为大型观览车主架示意图.点O为轮轴中心，距地面高为32m（即OM＝32m）.巨轮半径为30m，点P为吊舱与轮的连结点，吊舱高2m（即PM＝2m），巨轮转动一周需15min.某游人从点M进入吊舱后，巨轮开始按逆时针方向匀速转动3周后停止，记转动过程中该游人所乘吊舱的底部为点M'.（1）试建立点M'距地面的高度h（m）关于转动时间t（min）的函数关系，并写出定义域；（2）求转动过程中点M'超过地面45m的总时长.今年入秋以来，某市多有雾霾天气，空气污染较为严重.市环保研究所对近期每天的空气污染情况进行调査研究后发现，每一天中空气污染指数与f（x）时刻x（时）的函数关系为f（x）＝|log25（x＋1）﹣a|＋2a＋1，x∈[0，24]，其中a为空气治理调节参数，且a∈（0，1）.（1）若a＝，求一天中哪个时刻该市的空气污染指数最低；（2）规定每天中f（x）的最大值作为当天的空气污染指数，要使该市每天的空气污染指数不超过3，则调节参数a应控制在什么范围内？设函数f（x）＝，其中k＜﹣2.（1）求函数f（x）的定义域D（用区间表示）；（2）讨论函数f（x）在D上的单调性；（3）若k＜﹣6，求D上满足条件f（x）＞f（1）的x的集合（用区间表示）.2020年厦门市高一年期末考试模拟3数学试题参考答案一.选择题（共8小题）1.【解答】解：由得，或，解得x≤﹣1或0＜x≤2，∴A＝{x|x≤﹣1或0＜x≤2}，且，∴.故选：C.2.【解答】解：已知f（lnx）＝x＋1，设lnx＝t，则x＝e t，所以f（t）＝e t＋1，故f（x）＝e x＋1.故选：A.3.【解答】解：∵弧长6步，其所在圆的直径是4步，∴由题意可得：S＝×2×6＝6（平方步），故选：A.4.【解答】解：＝cos45°cos15°﹣sin45°sin（180°＋15°）＝cos45°cos15°＋sin45°sin15°＝cos（45°﹣15°）＝cos30°＝，故选：A.5.【解答】解：∵a＝log1.60.6＜log1.61＝0，0＜b＝0.60.6＜0.60＝1，c＝1.60.6＞1.60＝1.∴c＞b＞a.故选：C.6.【解答】解：∵函数f（x）＝ln|x|＋|cos x|，（且x≠0），∴f（﹣x）＝f（x），∴f（x）为偶函数，故排除A.∵且x≠0，当x＝时，f（）＝ln＞0，故排除C，当x＞0时，f（x）＝lnx＋cos x，可得：f′（x）＝﹣sin x，令﹣sin x＝0，作出y＝与y＝sin x图象如图可知两个函数有一个交点，就是函数有一个极值点，故选：D.7.【解答】解：图象恰有三个不同的交点P，M，N，△PMN为直角三角形，可知直角三角形△PMN的高为，且是等腰直角三角形，可得斜边长为2，即周期T＝2.∴，那么ω＝.∵x∈[0，]上，∴ωx＋φ∈[φ，＋φ]上，根据正余弦函数的图象性质，可得：φ，且＋φ.又∵|φ|＜，∴φ.故选：A.8.【解答】解：函数，则f（x）≥0，∴f2（x）＝，令g（x）＝f2（x），g′（x）＝[2（sin x＋1）•cos x（3＋2cos x＋sin x）﹣（sin x＋1）2•（﹣2sin x＋cos x）]＝（sin x＋1）（cos x＋2）（sin x＋2cos x＋1），令g′（x）＝0，得sin x＋1＝0或sin x＋2cos x＋1＝0；当sin x＝﹣1，f（x）＝0，为最小值，当sin x＋2cos x＝﹣1时，设方程的根为m，则导数在x＝m处附近左正右负，为极大值点，也为最大值点.此时sin m＋2cos m＝sin（m＋φ）＝﹣1，其中tanφ＝2，则tan（m＋φ）＝，tan m＝tan（m＋φ﹣φ）＝，则cos m＝﹣即有f（m）＝＝﹣cos m＝，故选：D.二.多选题（共2小题）9.【解答】解：当a＝b时，a﹣b＝0、＝1∈P，故可知A正确.当a＝1，b＝2，∉Z不满足条件，故可知B不正确.当M中多一个元素i则会出现1＋i∉M所以它也不是一个数域；故可知C不正确.根据数据的性质易得数域有无限多个元素，必为无限集，故可知D正确.故选：AD.10.【解答】解：由f（1﹣x）＝f（x）得函数f（x）图象关于直线x＝对称，若0≤x≤时，f（x）＝x（x﹣），则当＜x≤1时，f（x）＝（1﹣x）（﹣x），故A正确；∵f（1﹣x）＝﹣f（x），故函数图象关于（，0）对称，又由f（0）＝f（1）＝0，故函数f（x）至少有3个零点0，，1.故B正确；∵当0≤x≤时，|f（x）|≤x≤；当＜x≤1时，则1﹣x≤，|f（x）|＝|f（x）﹣f（1）|≤（1﹣x）≤＝.∴∀x∈[0，1]，|f（x）|≤恒成立，故C正确，设∀x1，x2∈[0，1]，当|x1﹣x2|≤时，|f（x1）﹣f（x2）|≤|x1﹣x2|≤，当|x1﹣x2|＞时，|f（x1）﹣f（x2）|＝|f（x1）﹣f（0）＋f（1）﹣f（x2）|≤|f（x1）﹣f（0）|＋|f（1）﹣f（x2）|≤|x1﹣0|＋|1﹣x2|＝×1＋（1﹣x2）＝﹣（x2﹣x1）≤﹣×＝.故D正确故选：ABCD.三.填空题（共6小题）11.【解答】解：集合A＝{1，2，3，4}的真子集有：∅，{1}，{2}，{3}，{1，2}，…，{2，3，4}共15个.故答案为：1512.【解答】解：如图.设＝x，＝＝＝＝＝＝（1﹣x）∵＝λ＋，∴得解得：故答案为：13.【解答】（本题满分为8分）解：由图象知，A＝2，…（2分）又＝﹣＝，ω＞0，所以T＝2π＝，得ω＝1.…（4分）所以f（x）＝2sin（x＋φ），将点（，2）代入，得＋φ＝2kπ＋（k∈Z），即φ＝＋2kπ（k∈Z），又﹣＜φ＜，所以，φ＝.…（6分）所以f（x）＝2sin（x＋）.故答案为：.…（8分）14.【解答】解：∵θ是钝角，且，∴cosθ＝﹣＝﹣，∴＝﹣2sinθcosθ＝﹣2××（﹣）＝.故答案是：.15.【解答】解：（1）∵函数f（x）＝2﹣x＝2﹣（x＋2）＋2＝3﹣，∴当x∈[﹣2，2]时，2≤f（x）≤3，∴f（x）的值域是[2，3]；（2）又当x∈[﹣2，2]时，①若m＜﹣2，则g（x）＝x2﹣2mx＋5m﹣2在[﹣2，2]上是增函数，最小值g（﹣2）＝9m＋2，最大值g（2）＝m＋2；∴g（x）的值域是[9m＋2，m＋2]，∴[2，3]⊆[9m＋2，m＋2]，即，解得﹣1≤m≤0，此时无解；②若m＞2，则g（x）＝x2﹣2mx＋5m﹣2在[﹣2，2]上是减函数，最小值g（2）＝m＋2，最大值g（﹣2）＝9m＋2；∴g（x）的值域是[m＋2，9m＋2]，∴[2，3]⊆[m＋2，9m＋2]，即，解得﹣≤m≤0，此时无解；③若﹣2≤m≤2，则g（x）＝x2﹣2mx＋5m﹣2在[﹣2，2]上是先减后增的函数，最小值是g（m）＝﹣m2＋5m﹣2，最大值是max{g（﹣2），g（2）}＝max{9m＋2，3m ＋2}；∴当m≥0时，g（x）的值域是[﹣m2＋5m﹣2，9m＋2]，∴[2，3]⊆[﹣m2＋5m﹣2，9m＋2]，即，解得≤m≤1，或m≥4（不符合条件，舍去）；则取≤m≤1；当m＜0时，g（x）的值域是[﹣m2＋5m﹣2，m＋2]，∴[2，3]⊆[﹣m2＋5m﹣2，m＋2]，即；解得m＝1，或m≥4，不符合条件，舍去；综上知，实数m的取值范围是：[，1].故答案为：[，1].16.【解答】解：依题意，设f（x）在（0，＋∞）上的最小值和最大值分别为f（x）min和f（x）max，f（x）＝＝1＋，①当m＝1时，f（x）＝1，所以满足f（a）＋f（b）＝2＞1＝f（c）；②当m＞1时，f（x）为（0，＋∞）上的减函数，且当x→＋∞时，f（x）→1＋，所以f（0）＞f（x）max＞f（x）min＞1，要使任意a，b，c∈（0，＋∞）都有f（a）＋f（b）＞f（c）成立，只需2f（x）min＞f（x）max，只需2×1≥f（0）＝m，所以1＜m≤2；③当m＜1时，f（x）为（0，＋∞）上的增函数，且当x→＋∞时，f（x）→1﹣，所以f（0）＜f（x）min＜f（x）max＜1，要使任意a，b，c∈（0，＋∞）都有f（a）＋f（b）＞f（c）成立，只需2f（x）min＞f（x）max，即2m≥1，解得m，所以；综上m∈[，2]，故答案为：[，2].四.解答题（共6小题）17.【解答】解：（1）由已知得f（x）＝•＝1＋2sin x（cos x﹣sin x）＝sin（2x＋），故f（x）的最小正周期T＝＝π；（2）令﹣＋2kπ≤2x＋≤＋2kπ，k∈z，交点：﹣＋kπ≤x≤＋kπ，故f（x）的递增区间是[﹣＋kπ，＋kπ]，（k∈z）；（3）画出函数y＝|f（x）|在[0，]上的简图如下所示：，当m∈（0，1）∪（1，）时，直线y＝m和y＝|f（x）|的图象在[0，]上有2个不同的交点，故方程|f（x）|＝m有2个不同的实数根，故m的范围是（0，1）∪（1，）.18.【解答】解：（1）根据题意，当x＞0时，f（x）＝x﹣，则f（2）＝2﹣＝，又由f（x）为奇函数，则f（﹣2）＝﹣f（2）＝﹣，（2）证明：设0＜x1＜x2，f（x1）﹣f（x2）＝（x1﹣）﹣（x2﹣）＝（x1﹣x2）﹣（﹣）＝（x1﹣x2）（1＋），又由0＜x1＜x2，则x1﹣x2＜0，则f（x1）﹣f（x2）＜0，即函数f（x）在（0，＋∞）上单调递增；（3）函数f（x）为定义在R上的奇函数，则f（0）＝0，设x＜0，则﹣x＞0，即f（﹣x）＝﹣x﹣，又由f（x）为奇函数，则f（x）＝﹣f（﹣x）＝x＋，故f（x）＝.19.【解答】解：（1）△OAB中，∵点C是点B关于A的对称点，∴＝＝，∴＝﹣，∴＝＋＝﹣＋（﹣）＝﹣﹣；又∵＝2＝2，点D是线段OB的一个靠近B的三等分点，∴＝；又∵＝＋＝﹣＋，∴＝＋＝2＋（﹣＋）＝＋；（2）∵＝＋，设＝＋＝＋x，＝y，x、y∈R；∴＋＝y＋xy，即，解得y＝，x＝；∴＝，＝；∴当＝时，λ＝.20.【解答】解：（1）如图所示，以O为坐标原点，建立平面直角坐标系xOy，设以Ox为始边，按逆时针方向经过时间t（min）转动至终边OP′所形成的角为t﹣，则点P′的纵坐标为30sin（t﹣），所以M′点距地面的高度为h＝30sin（t﹣）＋32﹣2＝30（1﹣cos t），t∈[0，45]；（2）当点M′超过地面45m时，h＝30（1﹣cos t）＞45，即cos t＜﹣，所以＋2kπ＜t＜＋2kπ，k∈Z，即5＋15k＜t＜10＋15k，k∈Z；因为t∈[0，45]，所以t∈（5，10）∪（20，25）∪（35，40），所以总时长为15分钟，即点M′超过地面45m的总时长为15分钟.21.【解答】解：（1）a＝时，f（x）＝|log25（x＋1）﹣|＋2，x∈[0，24]，令|log25（x＋1）﹣|＝0，解得x＝4，因此：一天中第4个时刻该市的空气污染指数最低.（2）令f（x）＝|log25（x＋1）﹣a|＋2a＋1＝，当x∈（0，25a﹣1]时，f（x）＝3a＋1﹣log25（x＋1）单调递减，∴f（x）＜f（0）＝3a ＋1.当x∈[25a﹣1，24）时，f（x）＝a＋1＋log25（x＋1）单调递增，∴f（x）≤f（24）＝a＋1＋1.联立，解得0＜a≤.可得a∈.因此调节参数a应控制在范围.22.【解答】解：（1）设t＝x2＋2x＋k，则f（x）等价为y＝g（t）＝，要使函数有意义，则t2＋2t﹣3＞0，解得t＞1或t＜﹣3，即x2＋2x＋k＞1或x2＋2x＋k＜﹣3，则（x＋1）2＞2﹣k，①或（x＋1）2＜﹣2﹣k，②，∵k＜﹣2，∴2﹣k＞﹣2﹣k，由①解得x＋1＞或x＋1，即x＞﹣1或x，由②解得﹣＜x＋1＜，即﹣1﹣＜x＜﹣1＋，综上函数的定义域为（﹣1，＋∞）∪（﹣∞，﹣1﹣）∪（﹣1﹣，﹣1＋）.（2）f′（x）＝＝＝﹣，由f'（x）＞0，即2（x2＋2x＋k＋1）（x＋1）＜0，则（x＋1＋）（x＋1﹣）（x＋1）＜0解得x＜﹣1﹣或﹣1＜x＜﹣1＋，结合定义域知，x＜﹣1﹣或﹣1＜x＜﹣1＋，即函数的单调递增区间为：（﹣∞，﹣1﹣），（﹣1，﹣1＋），同理解得单调递减区间为：（﹣1﹣，﹣1），（﹣1＋，＋∞）.（3）由f（x）＝f（1）得（x2＋2x＋k）2＋2（x2＋2x＋k）﹣3＝（3＋k）2＋2（3＋k）﹣3，则[（x2＋2x＋k）2﹣（3＋k）2]＋2[（x2＋2x＋k）﹣（3＋k）]＝0，∴（x2＋2x＋2k＋5）（x2＋2x﹣3）＝0即（x＋1＋）（x＋1﹣）（x＋3）（x﹣1）＝0，∴x＝﹣1﹣或x＝﹣1＋或x＝﹣3或x＝1，∵k＜﹣6，∴1∈（﹣1，﹣1＋），﹣3∈（﹣1﹣，﹣1），∵f（﹣3）＝f（1）＝f（﹣1﹣）＝f（﹣1＋），且满足﹣1﹣∈（﹣∞，﹣1﹣），﹣1＋∈（﹣1＋，＋∞），由（2）可知函数f（x）在上述四个区间内均单调递增或递减，结合图象，要使f（x）＞f（1）的集合为：（）∪（﹣1﹣，﹣3）∪（1，﹣1＋）∪（﹣1＋，﹣1＋）.。

2019-2020学年福建省厦门市高一下学期期末考试英语试题及答案第一部分听力（共两节,满分30分）第Ⅰ卷第一节（共5小题；每小题1.5分,满分7.5分）听下面5段对话。

每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。

听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例：How much is the shirt?A.£19.15.B.£9.18.C.£9.15.答案是C。

1.How does the man feel?A.Delighted.B.Worried.C.Nervous.2.Where does the conversation probably take place?A.At a museum.B.In a shop.C.At a stadium.3.What will the weather be like next Monday?A.Cloudy.B.Rainy.C.Sunny.4.When does George ask the woman to do?A.Put up a tent.B.Go camping together.C.Read the instructions.5.Why did the man sleep poorly last night?A.It was too cold.B.It was too bright.C.It was too noisy.第二节（共15小题,每小题1.5分,满分22.5分）听下面5段对话或独白。

每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。

听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟；听完后,各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料,回答第6、7题。

6.Whose birthday party are the speakers going to attend?A.Mike’s.B.Shelly’s.C.Karl’s.7.What does Karl look like?A.He is very thin.B.He wears a beard.C.He has black hair.听第7段材料,回答第8至9题。

试卷类型：A高二年级考试地理试题2024.07注意事项：1.答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共 15 小题，每小题3 分，共45 分。

每小题只有一个选项符合题目要求。

山东某中学地理学习小组进行了影子日变化观测活动。

下图示意该小组测得的某日一天当中太阳和影子变化示意图(图示时间为北京时间)。

据此完成 1~3 题。

1.推测该小组测量当天的日期是A.3 月21 日B.6 月22 日C.9 月23 日D.12 月22 日2.推算当地的经度是A.116 °EB.120 °EC.124 °ED.128 °E高二地理试题第 1 页(共8 页)3.已知甲、乙两个时刻竿影等长，甲时刻为北京时间 13：34，则乙时刻对应的地方时为A.10:10B.10:26C.10:42D.10:58每年 3 月下旬至4 月初，果树抗寒能力急剧下降，极易发生冻害。

为了减轻霜冻对果树的影响，农业上会使用无人机搅动近地面气流，提高下层空气温度。

下图为我国某地使用无人机对近地面气流进行干扰前，不同高度气温随时间的变化。

据此完成4~5 题。

4.该地最可能位于A.新疆B.云南C.河北D.黑龙江5.采用无人机干扰，进行防冻的最佳时间是A.4:00—6:00B.18:00—20:00C.20:00—22:00D.22:00—24:00冰川侵蚀产生的大量松散岩屑和由山坡上崩落下来的碎屑，进入冰川体后，随冰川运动向下游搬运，这些被搬运的岩屑叫冰碛物。

出露在冰川表面的叫表碛，夹在冰内的叫内碛，位于冰川底部的叫底碛。

下图为 1990 年与2019 年贡嘎山典型冰川表碛厚度随海拔高度变化情况。

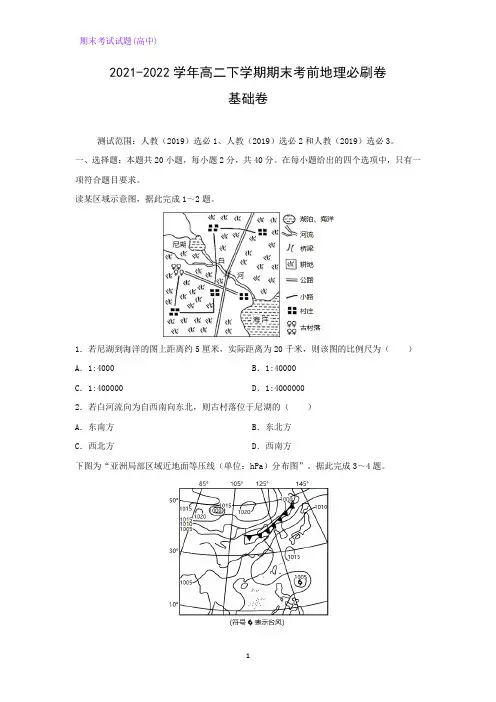
2021-2022学年高二下学期期末考前地理必刷卷基础卷测试范围：人教（2019）选必1、人教（2019）选必2和人教（2019）选必3。

一、选择题：本题共20小题，每小题2分，共40分。

在每小题给出的四个选项中，只有一项符合题目要求。

读某区域示意图，据此完成1～2题。

1．若尼湖到海洋的图上距离约5厘米，实际距离为20千米，则该图的比例尺为（）A．1:4000 B．1:40000C．1:400000 D．1:40000002．若白河流向为自西南向东北，则古村落位于尼湖的（）A．东南方B．东北方C．西北方D．西南方下图为“亚洲局部区域近地面等压线（单位：hPa）分布图”。

据此完成3～4题。

3．下图中沿ab一线所作的天气系统示意图正确的是（）A．B．C．D．4．当图示台风中心运行到上海东侧洋面时，上海的风向为（）A．西北风B．东北风C．东南风D．西南风近年来，我国外来物种数量大增。

下图为我国各省外来入侵植物种数分布图。

据此完成5～6题。

5．外来入侵植物的危害主要是使当地（）A．水土流失多发B．河流水量锐减C．生物多样性减少D．洪涝灾害多发6．云南是外来入侵植物种数最多的省份之一，也是我国的“植物王国”。

下列自然带不易在云南发现的是（）A．高寒荒漠带B．亚热带常绿阔叶林带C．亚热带常绿硬叶林带D．热带季雨林带根据中国地震台网测定：北京时间2021年05月21日21时48分在云南省大理州漾濞县苍山西镇发生6.4级地震，震源深度8千米，之后又发生了多次余震。

据此完成7～8题。

7．该地震发生时，纽约（西五区）时间为（）A．22日24时48分B．22日10时48分C．21日18时48分D．21日8时48分8．该地震发生时，太阳直射点大致在（）A．0°～23.5°N之间B．0°～23.5°S之间C．23.5°N～66.5°N之间D．23.5°S～66.5°S之间。

长沙市2023—2024学年度高二第二学期第二次阶段性检测地理（答案在最后）本试题卷分选择题和非选择题两部分，共8页。

时量75分钟，满分100分。

第Ⅰ卷选择题（共48分）一、选择题（本题共16小题，每小题3分，共48分。

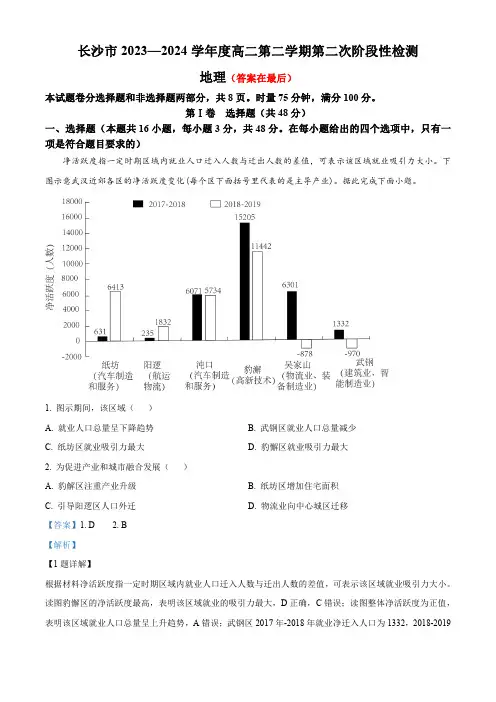
在每小题给出的四个选项中，只有一项是符合题目要求的）净活跃度指一定时期区域内就业人口迁入人数与迁出人数的差值，可表示该区域就业吸引力大小。

下图示意武汉近郊各区的净活跃度变化(每个区下面括号里代表的是主导产业)。

据此完成下面小题。

1.图示期间，该区域（）A.就业人口总量呈下降趋势B.武钢区就业人口总量减少C.纸坊区就业吸引力最大D.豹懈区就业吸引力最大2.为促进产业和城市融合发展（）A.豹解区注重产业升级B.纸坊区增加住宅面积C.引导阳逻区人口外迁D.物流业向中心城区迁移【答案】1.D 2.B【解析】【1题详解】根据材料净活跃度指一定时期区域内就业人口迁入人数与迁出人数的差值，可表示该区域就业吸引力大小。

读图豹懈区的净活跃度最高，表明该区域就业的吸引力最大，D正确，C错误；读图整体净活跃度为正值，表明该区域就业人口总量呈上升趋势，A错误；武钢区2017年-2018年就业净迁入人口为1332，2018-2019年净迁出为970人，该时间段总体就业以迁入为主，B错误，该题选D。

【2题详解】读图豹懈区产业以高新技术产业为主导产业，综合效益较高，产业和城市融合度较高，不需要产业升级，A 错误；纸坊区以汽车制造和服务为主，需要大量劳动力，且该时期就业净迁入人口增多，需要增加住宅面积满足新迁入人口的需要，B正确；阳逻区主导产业为航运和物流，需要劳动力，且图示时间段就业人口迁入较少，仍需要大量劳动力，不应引导人口外迁，C错误；中心城区地价较高，物流中心占地面积较大，应向郊区交通便利的地区迁移，D错误，该题选B。

【点睛】影响城市功能区的因素：自然地理条件、历史文化因素、经济发展水平、交通运输状况等，但诸方面因素往往是相互交错、相互制约的,不能截然分开。

2019～2020学年度高一下学期期中考试地理试题一、选择题: 本题共30小题，每小题2分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

下图示意我国人口数据统计（部分），读图回答1~2题。

1.图示信息可以直接推测出我国城市化特征是A．城市人口比重提高 B．城市等级不断提升 C．城市交通更加通畅 D．城市环境不断改善2.图示信息反映了我国人口变化特点有A．人口增长速度加快 B．老龄化日益突出 C．乡村人口比重上升 D．出现人口负增长下图为“某国2017年人口年龄结构金字塔图”。

读下图回答3~4题。

3．导致该国青壮年性别比严重失衡的因素是A．政局动荡 B．生育观念 C．产业结构 D．自然灾害4．该国最可能位于A．北美 B．西亚 C．西欧 D．南美春运，指春节前后一段时间的运输业务，表现为全国性的交通运输高峰。

“反向春运”是指年轻人将老家的父母和孩子接到自己工作的城市过年，节后再返乡。

据此完成5~6题。

5．导致春运期间人口流动量大的最主要因素是A．经济因素 B．国家政策 C．交通运输 D．家庭因素6．下列城市可能属于“反向春运”热门目的地的是A．成都 B．重庆 C．上海 D．西安下列左图为“甲、乙、丙、丁四国人口增长状况图”，右图为“不同阶段人口发展模式图”。

读图完成7~8题。

7．左图中四个国家人口增长特点与右图人口增长阶段对应正确的是A．甲—① B．乙—② C．丙—③ D．丁—④8．影响丙国人口增长模式的主要原因有①经济发展水平较高②人口受教育程度较低③人们的生育意愿较低④医疗卫生水平较低A．①② B．③④ C．②④ D．①③下图为2010年我国东部地区甲、乙两城市常住人口密度和商务楼相对高度（楼高）分布图。

完成9~10题。

9．与甲城市相比，乙城市A．职能种类较少 B．服务范围较大 C．等级较高 D．规模较大10．关于甲城市功能区分布的推断，最有可能的是①M处为中心商务区②N处中心商务区③P处为卫星城④Q处为卫星城A．①③ B．①④ C．②③ D．②④下图为“我国某城市空间结构形态演变过程示意图”，读图回答11~12题。

三明市2019-2020学年第二学期普通高中期末质量检测高二地理试题(考试时间:2020年7月22日下午3:00~5:00满分:100分)注意事项1.试卷分第I卷(选择题部分)和第Ⅱ卷(综合题部分)2.所有答案请答在答题卡上。

请用2B铅笔将选择题答案填涂在答题卡上,综合題答案请用黑色水笔写在相应的答题卡上,不得超出答题扫描区作答第|卷(选择题共计46分)一、单项选择题(共23小题,每小题2分,共计46分。

在每小题列出的四个选项中,只有项最符合题目要求)地摊经济由来已久,是指通过摆地摊获得收入来源形成的一种经济形式。

是人类最原始也是最有生命力的商业活动之一。

据此完成1-3题1.地摊经济的特点()A.商户运营成本高B.从业人员技术水平高C.创业投资门槛低D.商品种类齐全2.疫情防控期间,地摊经济深受百姓欢迎的原因()A.商品价格低B.商场较封闭C.商品质量优D.商场货源不足3.地摊经济的意义不包括()A.缓解了就业问题B.增加了经济收入C.改善了环境问题D.促进地方经济繁荣图1为甲、乙两个区域,读图完成4-5题图甲孟买地理位置示意图图乙洛杉观地理位置示意图图14.下列有关孟买和洛杉矶气候的叙述,正确的是()A.孟买夏季炎热干燥B.洛杉矶夏季高温多雨C.孟买冬季高温多雨D.洛杉矶冬季温和湿润5.孟买位于洛杉矶的_______方向()A.西南B.东南C.西北D.东北日本大城市一房难求,农村却到处是空置的“鬼屋”,近几年,日本一些村镇开始免费向民众发放房子,还赠送修缮补贴,但要求住房人必须长期居住,同时对住房人的基本条件也提出了一系列要求。

据此完成6-7小题6.日本“鬼屋”日益增多的根本原因是()A.严重的人口老龄化B.农村房价过高C.社会负担逐渐减轻D.房屋修缮成本高7.日本部分村镇对免费住房人的要求,最可能是()A.技术B.性别C.学历D.年龄开平市地处珠江三角洲西南部(粤西地区),是著名的华侨之乡,世界文化遗产开平碉楼多兴建于明末至民国时期,多依山而建,现存1800多座,为多层建筑,墙体厚实坚国。

2019-2020年高二下学期期末数学试卷（理科）含解析一、选择题（本大题共12个小题，每小题5分，在每小题中，只有一项是符合题目要求的）1．已知集合A={x∈R||x|≤2}，B={x∈R|x≤1}，则A∩B=（）A．（﹣∞，2]B．[1，2]C．[﹣2，2] D．[﹣2，1]2．已知复数=i，则实数a=（）A．﹣1 B．﹣2 C．1 D．23．将点M的极坐标（4，）化成直角坐标为（）A．（2，2）B．C．D．（﹣2，2）4．在同一平面的直角坐标系中，直线x﹣2y=2经过伸缩变换后，得到的直线方程为（）A．2x′+y′=4 B．2x′﹣y′=4 C．x′+2y′=4 D．x′﹣2y′=45．如图，曲线f（x）=x2和g（x）=2x围成几何图形的面积是（）A．B．C．D．46．10件产品中有3件次品，不放回的抽取2件，每次抽1件，在已知第1次抽出的是次品的条件下，第2次抽到仍为次品的概率为（）A．B．C．D．7．下列说法中，正确说法的个数是（）①命题“若x2﹣3x+2=0，则x=1”的逆否命题为：“若x≠1，则x2﹣3x+2≠0”；②“x＞1”是“|x|＞1”的充分不必要条件；③集合A={1}，B={x|ax﹣1=0}，若B⊆A，则实数a的所有可能取值构成的集合为{1}．A．0 B．1 C．2 D．38．设某批产品合格率为，不合格率为，现对该产品进行测试，设第ε次首次取到正品，则P（ε=3）等于（）A．C32（）2×（）B．C32（）2×（）C．（）2×（）D．（）2×（）9．在10件产品中，有3件一等品，7件二等品，从这10件产品中任取3件，则取出的3件产品中一等品件数多于二等品件数的概率（）A． B．C．D．10．函数f（x）=e﹣x+ax存在与直线2x﹣y=0平行的切线，则实数a的取值范围是（）A．（﹣∞，2]B．（﹣∞，2）C．（2，+∞）D．[2，+∞）11．函数y=e sinx（﹣π≤x≤π）的大致图象为（）A．B． C． D．12．已知曲线C1：y=e x上一点A（x1，y1），曲线C2：y=1+ln（x﹣m）（m＞0）上一点B（x2，y2），当y1=y2时，对于任意x1，x2，都有|AB|≥e恒成立，则m的最小值为（）A．1 B．C．e﹣1 D．e+1二、填空题（本大题共4个小题，每小题5分，共20分）13．已知随机变量X服从正态分布X～N（2，σ2），P（X＞4）=0.3，则P（X＜0）的值为．14．若函数f（x）=x2﹣alnx在x=1处取极值，则a=．15．如图的三角形数阵中，满足：（1）第1行的数为1；（2）第n（n≥2）行首尾两数均为n，其余的数都等于它肩上的两个数相加．则第10行中第2个数是．16．在平面直角坐标系xOy中，直线1与曲线y=x2（x＞0）和y=x3（x＞0）均相切，切点分别为A（x1，y1）和B（x2，y2），则的值为．三、解答题（本大题共6小题，共70分，解答应写出必要的文字说明、证明过程及演算步骤）17．在平面直角坐标系xOy中，圆C的参数方程为（φ为参数），直线l过点（0，2）且倾斜角为．（Ⅰ）求圆C的普通方程及直线l的参数方程；（Ⅱ）设直线l与圆C交于A，B两点，求弦|AB|的长．18．在直角坐标系xOy中，已知直线l：（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C：ρ2（1+sin2θ）=2．（Ⅰ）写出直线l的普通方程和曲线C的直角坐标方程；（Ⅱ）设点M的直角坐标为（1，2），直线l与曲线C 的交点为A、B，求|MA|•|MB|的值．19．生产甲乙两种元件，其质量按检测指标划分为：指标大于或者等于82为正品，小于82为次品，现随机抽取这两种元件各100件进行检测，检测结果统计如表：测试指标[70，76）[76，82）[82，88）[88，94）[94，100）元件甲8 12 40 32 8元件乙7 18 40 29 6（Ⅰ）试分别估计元件甲，乙为正品的概率；（Ⅱ）在（Ⅰ）的前提下，记X为生产1件甲和1件乙所得的正品数，求随机变量X的分布列和数学期望．20．设函数f（x）=x3﹣+6x．（Ⅰ）当a=1时，求函数f（x）的单调区间；（Ⅱ）若对∀x∈[1，4]都有f（x）＞0成立，求a的取值范围．21．为了研究家用轿车在高速公路上的车速情况，交通部门对100名家用轿车驾驶员进行调查，得到其在高速公路上行驶时的平均车速情况为：在55名男性驾驶员中，平均车速超过100km/h的有40人，不超过100km/h的有15人．在45名女性驾驶员中，平均车速超过100km/h 的有20人，不超过100km/h的有25人．（Ⅰ）完成下面的列联表，并判断是否有99.5%的把握认为平均车速超过100km/h的人与性别有关．平均车速超过100km/h人数平均车速不超过100km/h人数合计男性驾驶员人数女性驾驶员人数合计（Ⅱ）以上述数据样本来估计总体，现从高速公路上行驶的大量家用轿车中随机抽取3辆，记这3辆车中驾驶员为男性且车速超过100km/h的车辆数为X，若每次抽取的结果是相互独立的，求X的分布列和数学期望．参考公式与数据：Χ2=，其中n=a+b+c+dP（Χ2≥k0）0.150 0.100 0.050 0.025 0.010 0.005 0.001 k0 2.072 2.706 3.841 5.024 6.635 7.879 10.82822．已知函数f（x）=﹣alnx+1（a∈R）．（1）若函数f（x）在[1，2]上是单调递增函数，求实数a的取值范围；（2）若﹣2≤a＜0，对任意x1，x2∈[1，2]，不等式|f（x1）﹣f（x2）|≤m||恒成立，求m的最小值．2015-2016学年吉林省东北师大附中净月校区高二（下）期末数学试卷（理科）参考答案与试题解析一、选择题（本大题共12个小题，每小题5分，在每小题中，只有一项是符合题目要求的）1．已知集合A={x∈R||x|≤2}，B={x∈R|x≤1}，则A∩B=（）A．（﹣∞，2]B．[1，2]C．[﹣2，2] D．[﹣2，1]【考点】交集及其运算．【分析】先化简集合A，解绝对值不等式可求出集合A，然后根据交集的定义求出A∩B即可．【解答】解：∵A={x||x|≤2}={x|﹣2≤x≤2}∴A∩B={x|﹣2≤x≤2}∩{x|x≤1，x∈R}={x|﹣2≤x≤1}故选D．2．已知复数=i，则实数a=（）A．﹣1 B．﹣2 C．1 D．2【考点】复数代数形式的乘除运算．【分析】直接由复数代数形式的乘除运算化简复数，再根据复数相等的充要条件列出方程组，求解即可得答案．【解答】解：===i，则，解得：a=1．故选：C．3．将点M的极坐标（4，）化成直角坐标为（）A．（2，2）B．C．D．（﹣2，2）【考点】简单曲线的极坐标方程．【分析】利用x=ρcosθ，y=ρsinθ即可得出直角坐标．【解答】解：点M的极坐标（4，）化成直角坐标为，即．故选：B．4．在同一平面的直角坐标系中，直线x﹣2y=2经过伸缩变换后，得到的直线方程为（）A．2x′+y′=4 B．2x′﹣y′=4 C．x′+2y′=4 D．x′﹣2y′=4【考点】伸缩变换．【分析】把伸缩变换的式子变为用x′，y′表示x，y，再代入原方程即可求出．【解答】解：由得，代入直线x﹣2y=2得，即2x′﹣y′=4．故选B．5．如图，曲线f（x）=x2和g（x）=2x围成几何图形的面积是（）A．B．C．D．4【考点】定积分在求面积中的应用．【分析】利用积分的几何意义即可得到结论．【解答】解：由题意，S===4﹣=，故选：C．6．10件产品中有3件次品，不放回的抽取2件，每次抽1件，在已知第1次抽出的是次品的条件下，第2次抽到仍为次品的概率为（）A．B．C．D．【考点】条件概率与独立事件．【分析】根据题意，易得在第一次抽到次品后，有2件次品，7件正品，由概率计算公式，计算可得答案．【解答】解：根据题意，在第一次抽到次品后，有2件次品，7件正品；则第二次抽到次品的概率为故选：C．7．下列说法中，正确说法的个数是（）①命题“若x2﹣3x+2=0，则x=1”的逆否命题为：“若x≠1，则x2﹣3x+2≠0”；②“x＞1”是“|x|＞1”的充分不必要条件；③集合A={1}，B={x|ax﹣1=0}，若B⊆A，则实数a的所有可能取值构成的集合为{1}．A．0 B．1 C．2 D．3【考点】命题的真假判断与应用．【分析】①根据逆否命题的定义进行判断②根据充分条件和必要条件的定义进行判断，③根据集合关系进行判断．【解答】解：①命题“若x2﹣3x+2=0，则x=1”的逆否命题为：“若x≠1，则x2﹣3x+2≠0”正确，故①正确，②由|x|＞1得x＞1或x＜﹣1，则“x＞1”是“|x|＞1”的充分不必要条件；故②正确，③集合A={1}，B={x|ax﹣1=0}，若B⊆A，当a=0时，B=∅，也满足B⊆A，当a≠0时，B={}，由=1，得a=1，则实数a的所有可能取值构成的集合为{0，1}．故③错误，故正确的是①②，故选：C8．设某批产品合格率为，不合格率为，现对该产品进行测试，设第ε次首次取到正品，则P（ε=3）等于（）A．C32（）2×（）B．C32（）2×（）C．（）2×（）D．（）2×（）【考点】n次独立重复试验中恰好发生k次的概率．【分析】根据题意，P（ε=3）即第3次首次取到正品的概率，若第3次首次取到正品，即前两次取到的都是次品，第3次取到正品，由相互独立事件的概率计算可得答案．【解答】解：根据题意，P（ε=3）即第3次首次取到正品的概率；若第3次首次取到正品，即前两次取到的都是次品，第3次取到正品，则P（ε=3）=（）2×（）；故选C．9．在10件产品中，有3件一等品，7件二等品，从这10件产品中任取3件，则取出的3件产品中一等品件数多于二等品件数的概率（）A． B．C．D．【考点】古典概型及其概率计算公式．【分析】先求出基本事件总数，再求出取出的3件产品中一等品件数多于二等品件数包含的基本事件个数，由此能求出取出的3件产品中一等品件数多于二等品件数的概率．【解答】解：∵在10件产品中，有3件一等品，7件二等品，从这10件产品中任取3件，基本事件总数n==120，取出的3件产品中一等品件数多于二等品件数包含的基本事件个数m==22，∴取出的3件产品中一等品件数多于二等品件数的概率p===．故选：C．10．函数f（x）=e﹣x+ax存在与直线2x﹣y=0平行的切线，则实数a的取值范围是（）A．（﹣∞，2]B．（﹣∞，2）C．（2，+∞）D．[2，+∞）【考点】利用导数研究曲线上某点切线方程．【分析】利用在切点处的导数值是切线的斜率，令f′（x）=2有解；利用有解问题即求函数的值域问题，求出值域即a的范围．【解答】解：f′（x）=﹣e﹣x+a据题意知﹣e﹣x+a=2有解即a=e﹣x+2有解∵e﹣x+2＞2∴a＞2故选C11．函数y=e sinx（﹣π≤x≤π）的大致图象为（）A．B． C． D．【考点】抽象函数及其应用．【分析】先研究函数的奇偶性知它是非奇非偶函数，从而排除A、D两个选项，再看此函数的最值情况，即可作出正确的判断．【解答】解：由于f（x）=e sinx，∴f（﹣x）=e sin（﹣x）=e﹣sinx∴f（﹣x）≠f（x），且f（﹣x）≠﹣f（x），故此函数是非奇非偶函数，排除A，D；又当x=时，y=e sinx取得最大值，排除B；故选：C．12．已知曲线C1：y=e x上一点A（x1，y1），曲线C2：y=1+ln（x﹣m）（m＞0）上一点B（x2，y2），当y1=y2时，对于任意x1，x2，都有|AB|≥e恒成立，则m的最小值为（）A．1 B．C．e﹣1 D．e+1【考点】利用导数求闭区间上函数的最值．【分析】当y1=y2时，对于任意x1，x2，都有|AB|≥e恒成立，可得：=1+ln（x2﹣m），x2﹣x1≥e，一方面0＜1+ln（x2﹣m）≤，．利用lnx≤x﹣1（x≥1），考虑x2﹣m≥1时．可得1+ln（x2﹣m）≤x2﹣m，令x2﹣m≤，可得m≥x﹣e x﹣e，利用导数求其最大值即可得出．【解答】解：当y1=y2时，对于任意x1，x2，都有|AB|≥e恒成立，可得：=1+ln（x2﹣m），x2﹣x1≥e，∴0＜1+ln（x2﹣m）≤，∴．∵lnx≤x﹣1（x≥1），考虑x2﹣m≥1时．∴1+ln（x2﹣m）≤x2﹣m，令x2﹣m≤，化为m≥x﹣e x﹣e，x＞m+．令f（x）=x﹣e x﹣e，则f′（x）=1﹣e x﹣e，可得x=e时，f（x）取得最大值．∴m≥e﹣1．故选：C．二、填空题（本大题共4个小题，每小题5分，共20分）13．已知随机变量X服从正态分布X～N（2，σ2），P（X＞4）=0.3，则P（X＜0）的值为0.3．【考点】正态分布曲线的特点及曲线所表示的意义．【分析】根据随机变量X服从正态分布，可知正态曲线的对称轴，利用对称性，即可求得P （X＜0）．【解答】解：∵随机变量X服从正态分布N（2，o2），∴正态曲线的对称轴是x=2∵P（X＞4）=0.3，∴P（X＜0）=P（X＞4）=0.3．故答案为：0.3．14．若函数f（x）=x2﹣alnx在x=1处取极值，则a=2．【考点】利用导数研究函数的极值．【分析】求出函数的导数，得到f′（1）=0，得到关于a的方程，解出即可．【解答】解：∵f（x）=x2﹣alnx，x＞0，∴f′（x）=2x﹣=，若函数f（x）在x=1处取极值，则f′（1）=2﹣a=0，解得：a=2，经检验，a=2符合题意，故答案为：2．15．如图的三角形数阵中，满足：（1）第1行的数为1；（2）第n（n≥2）行首尾两数均为n，其余的数都等于它肩上的两个数相加．则第10行中第2个数是46．【考点】归纳推理．【分析】由三角形阵可知，上一行第二个数与下一行第二个数满足等式a n +1=a n +n ，利用累加法可求．【解答】解：设第一行的第二个数为a 1=1，由此可得上一行第二个数与下一行第二个数满足等式a n +1=a n +n ，即a 2﹣a 1=1，a 3﹣a 2=2，a 4﹣a 3=3，…a n ﹣1﹣a n ﹣2=n ﹣2，a n ﹣a n ﹣1=n ﹣1， ∴a n =（a n ﹣a n ﹣1）+（a n ﹣1﹣a n ﹣2）+…+（a 4﹣a 3）+（a 3﹣a 2）+（a 2﹣a 1）+a 1 =（n ﹣1）+（n ﹣2）+…+3+2+1+1 =+1=，∴a 10==46．故答案为：46．16．在平面直角坐标系xOy 中，直线1与曲线y=x 2（x ＞0）和y=x 3（x ＞0）均相切，切点分别为A （x 1，y 1）和B （x 2，y 2），则的值为．【考点】抛物线的简单性质．【分析】求出导数得出切线方程，即可得出结论．【解答】解：由y=x 2，得y ′=2x ，切线方程为y ﹣x 12=2x 1（x ﹣x 1），即y=2x 1x ﹣x 12， 由y=x 3，得y ′=3x 2，切线方程为y ﹣x 23=3x 22（x ﹣x 2），即y=3x 22x ﹣2x 23， ∴2x 1=3x 22，x 12=2x 23， 两式相除，可得=．故答案为：．三、解答题（本大题共6小题，共70分，解答应写出必要的文字说明、证明过程及演算步骤） 17．在平面直角坐标系xOy 中，圆C 的参数方程为（φ为参数），直线l 过点（0，2）且倾斜角为．（Ⅰ）求圆C 的普通方程及直线l 的参数方程；（Ⅱ）设直线l 与圆C 交于A ，B 两点，求弦|AB |的长． 【考点】参数方程化成普通方程． 【分析】（Ⅰ）圆C 的参数方程为（φ为参数），利用cos 2φ+sin 2φ=1消去参数可得圆C 的普通方程．由题意可得：直线l 的参数方程为．（Ⅱ）依题意，直线l的直角坐标方程为，圆心C到直线l的距离d，利用|AB|=2即可得出．【解答】解：（Ⅰ）圆C的参数方程为（φ为参数），消去参数可得：圆C的普通方程为x2+y2=4．由题意可得：直线l的参数方程为．（Ⅱ）依题意，直线l的直角坐标方程为，圆心C到直线l的距离，∴|AB|=2=2．18．在直角坐标系xOy中，已知直线l：（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C：ρ2（1+sin2θ）=2．（Ⅰ）写出直线l的普通方程和曲线C的直角坐标方程；（Ⅱ）设点M的直角坐标为（1，2），直线l与曲线C 的交点为A、B，求|MA|•|MB|的值．【考点】简单曲线的极坐标方程；参数方程化成普通方程．【分析】（Ⅰ）直线l：（t为参数），消去参数t可得普通方程．曲线C：ρ2（1+sin2θ）=2，可得ρ2+（ρsinθ）2=2，把ρ2=x2+y2，y=ρsinθ代入可得直角坐标方程．（Ⅱ）把代入椭圆方程中，整理得，设A，B对应的参数分别为t1，t2，由t得几何意义可知|MA||MB|=|t1t2|．【解答】解：（Ⅰ）直线l：（t为参数），消去参数t可得普通方程：l：x﹣y+1=0．曲线C：ρ2（1+sin2θ）=2，可得ρ2+（ρsinθ）2=2，可得直角坐标方程：x2+y2+y2=2，即．（Ⅱ）把代入中，整理得，设A，B对应的参数分别为t1，t2，∴，由t得几何意义可知，．19．生产甲乙两种元件，其质量按检测指标划分为：指标大于或者等于82为正品，小于82为次品，现随机抽取这两种元件各100件进行检测，检测结果统计如表：测试指标[70，76）[76，82）[82，88）[88，94）[94，100）元件甲8 12 40 32 8元件乙7 18 40 29 6（Ⅰ）试分别估计元件甲，乙为正品的概率；（Ⅱ）在（Ⅰ）的前提下，记X为生产1件甲和1件乙所得的正品数，求随机变量X的分布列和数学期望．【考点】离散型随机变量的期望与方差；古典概型及其概率计算公式；离散型随机变量及其分布列．【分析】（Ⅰ）利用等可能事件概率计算公式能求出元件甲，乙为正品的概率．（Ⅱ）随机变量X的所有取值为0，1，2，分别求出相应的概率，由此能求出随机变量X的分布列和数学期望．【解答】解：（Ⅰ）元件甲为正品的概率约为：，元件乙为正品的概率约为：．（Ⅱ）随机变量X的所有取值为0，1，2，，，，所以随机变量X的分布列为：X 0 1 2P所以：．20．设函数f（x）=x3﹣+6x．（Ⅰ）当a=1时，求函数f（x）的单调区间；（Ⅱ）若对∀x∈[1，4]都有f（x）＞0成立，求a的取值范围．【考点】利用导数求闭区间上函数的最值；利用导数研究函数的单调性．【分析】（Ⅰ）求出函数的导数，解关于导函数的不等式，求出函数的单调区间即可；（Ⅱ）问题转化为在区间[1，4]上恒成立，令，根据函数的单调性求出a的范围即可．【解答】解：（Ⅰ）函数的定义域为R，当a=1时，f（x）=x3﹣x2+6x，f′（x）=3（x﹣1）（x﹣2），当x＜1时，f′（x）＞0；当1＜x＜2时，f′（x）＜0；当x＞2时，f′（x）＞0，∴f（x）的单调增区间为（﹣∞，1），（2，+∞），单调减区间为（1，2）．（Ⅱ）即在区间[1，4]上恒成立，令，故当时，g（x）单调递减，当时，g（x）单调递增，时，∴，即．21．为了研究家用轿车在高速公路上的车速情况，交通部门对100名家用轿车驾驶员进行调查，得到其在高速公路上行驶时的平均车速情况为：在55名男性驾驶员中，平均车速超过100km/h的有40人，不超过100km/h的有15人．在45名女性驾驶员中，平均车速超过100km/h 的有20人，不超过100km/h的有25人．（Ⅰ）完成下面的列联表，并判断是否有99.5%的把握认为平均车速超过100km/h的人与性别有关．平均车速超过100km/h人数平均车速不超过100km/h人数合计男性驾驶员人数401555女性驾驶员人数202545合计6040100（Ⅱ）以上述数据样本来估计总体，现从高速公路上行驶的大量家用轿车中随机抽取3辆，记这3辆车中驾驶员为男性且车速超过100km/h的车辆数为X，若每次抽取的结果是相互独立的，求X的分布列和数学期望．参考公式与数据：Χ2=，其中n=a+b+c+dP（Χ2≥k0）0.150 0.100 0.050 0.025 0.010 0.005 0.001 k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828【考点】离散型随机变量的期望与方差；独立性检验；离散型随机变量及其分布列．【分析】（Ⅰ）完成下面的列联表，并判断是否有99.5%的把握认为平均车速超过100km/h的人与性别有关．求出Χ2，即可判断是否有99.5%的把握认为平均车速超过100km/h的人与性别有关．（Ⅱ）根据样本估计总体的思想，从高速公路上行驶的大量家用轿车中随机抽取1辆，驾驶员为男性且车速超过100km/h的车辆的概率，X可取值是0，1，2，3，，求出概率得到分布列，然后求解期望即可．【解答】解：（Ⅰ）平均车速超过100km/h人数平均车速不超过100km/h人数合计男性驾驶员人数40 15 55女性驾驶员人数20 25 45合计60 40 100因为，所以有99.5%的把握认为平均车速超过100km/h与性别有关．…（Ⅱ）根据样本估计总体的思想，从高速公路上行驶的大量家用轿车中随机抽取1辆，驾驶员为男性且车速超过100km/h的车辆的概率为．X可取值是0，1，2，3，，有：，，，，分布列为X 0 1 2 3P．…22．已知函数f（x）=﹣alnx+1（a∈R）．（1）若函数f（x）在[1，2]上是单调递增函数，求实数a的取值范围；（2）若﹣2≤a＜0，对任意x1，x2∈[1，2]，不等式|f（x1）﹣f（x2）|≤m||恒成立，求m的最小值．【考点】利用导数求闭区间上函数的最值；利用导数研究函数的单调性．【分析】（1）求出函数的导数，问题转化为a≤x2，求出a的范围即可；（2）问题可化为，设，求出函数的导数，问题等价于m≥x3﹣ax在[1，2]上恒成立，求出m的最小值即可．【解答】解：（1）∵在[1，2]上是增函数，∴恒成立，…所以a≤x2…只需a≤（x2）min=1…（2）因为﹣2≤a＜0，由（1）知，函数f（x）在[1，2]上单调递增，…不妨设1≤x1≤x2≤2，则，可化为，设，则h（x1）≥h（x2）．所以h（x）为[1，2]上的减函数，即在[1，2]上恒成立，等价于m≥x3﹣ax在[1，2]上恒成立，…设g（x）=x3﹣ax，所以m≥g（x）max，因﹣2≤a＜0，所以g'（x）=3x2﹣a＞0，所以函数g（x）在[1，2]上是增函数，所以g（x）max=g（2）=8﹣2a≤12（当且仅当a=﹣2时等号成立）．所以m≥12．即m的最小值为12．…2016年10月17日。

福建省厦门市2019-2020学年中考第三次质量检测地理试题一、选择题（本题包括25个小题，每小题2分，共50分．在每个小题给出的四个选项中，只有一项是符合题目要求的。

）1．我国各地出产不同的水果，如辽宁、山东的苹果、梨，湖南、江西的柑橘，广东、海南的芒果、香蕉，新疆的葡萄、哈密瓜等。

这说明我国（）A．气候复杂多样，适宜大多数植物生长B．夏季普遍高温，热量丰富C．全国降水丰富D．季风气候显著【答案】A【解析】【详解】我国各地出产不同的水果以及其他农作物，这充分说明了我国气候复杂多样，使许多植物在我国能找到适合生长的地区，故选A。

【点睛】本题考查我国气候复杂多样的有利方面。

2．亚洲南部、北部的海洋分别是（）A．大西洋北冰洋B．印度洋北冰洋C．太平洋北冰洋D．北冰洋印度洋【答案】B【解析】【分析】【详解】从海陆位置上看，亚洲位于亚欧大陆东部，亚洲东临太平洋，南临印度洋，北临北冰洋，故选B。

【点睛】本题主要考查了亚洲周围的海洋。

3．对欧洲西部地理位置特征的描述，正确的是( )①主要位于北温带②有北回归线穿过③西临太平洋④位于亚欧大陆西部A．①③B．②④C．①④D．②③【答案】C【解析】【分析】【详解】欧洲西部有北极圈穿过，②错；欧洲西部西临大西洋，③错；欧洲西部主要位于北温带，位于亚欧大陆西部，①④正确；故C符合题意，选C。

4．以下东南亚国家与中国陆上接壤的有①越南②老挝③缅甸④柬埔寨⑤泰国⑥新加坡⑦马来西亚⑧菲律宾A．①②③B．③④⑥C．⑥⑦⑧D．①③⑦【答案】A【解析】【分析】【详解】我国的陆上国界漫长，达2万多千米，接壤的国家有14个，分别是：朝鲜、蒙古、俄罗斯、哈萨克斯坦、吉尔吉斯斯坦、塔吉克斯坦、阿富汗、巴基斯坦、印度、尼泊尔、不丹、缅甸、老挝、越南。

东南亚位于亚洲的东南部，主要国家有越南、老挝、柬埔寨、泰国、缅甸、马来西亚、新加坡、菲律宾、印度尼西亚和文莱。

因此东南亚各国中与我国陆上接壤的有缅甸、老挝和越南。