第5章自相关性资料讲解
- 格式：ppt
- 大小：812.00 KB
- 文档页数：60
下载文档原格式
合集下载
计量经济学第五章
• 首先估计出一般方程 • View/Coefficient Tests/Redundant
Variables-Likelihood Ratio • 出现对话框时,写入删除变量名--OK • 对比删除前后的AIC与SC信息值,信息
值小的结论是应采纳的。
9
用Eviews的误设定检验3
• 第一,估计出简单(单纯)方程 • 第二,在命令窗口上写入genr v_hat=resid 或者 Procs/Generate Series中 v_hat=resid 发现 v_hat • 第三,估计出新的回归方程
无约束模型(U)
有约束模型(K) (general to simple)
计算统计量F
F=(RSSK-RSSu)/J RSSu/(n-k-1)
~F(J, n-k)
J 为表示约束条件数, K 为表示自变量数 或者 应估计的参数数, n 为表示样本数(obs)
4
2. LM检验(Lagrange Multiplier
多重共线性多出现在横截面资料上。
16
三、异方差性的检验及对策
Var(ℇi)≠Var(ℇj) (i≠j)时, ℇi中存在异方差性(Herteroskedasticity)。 即随机项中包含着对因变量的影响因素。 异方差性多发生在横截面资料上。
17
异方差性的检验
1.图示检验法 如模型为Yi=0+1X1i+2X2i+…+ℇi 时,
7
用Eviews的误设定检验1
• 首先估计出简单(单纯)方程 • View/Coefficient Tests/Omitted
Variables-Likelihood Ratio • 出现对话框时,写入新变量名 OK • 检验结果出现在上端,如果P值很小时, 拒
Variables-Likelihood Ratio • 出现对话框时,写入删除变量名--OK • 对比删除前后的AIC与SC信息值,信息
值小的结论是应采纳的。
9
用Eviews的误设定检验3
• 第一,估计出简单(单纯)方程 • 第二,在命令窗口上写入genr v_hat=resid 或者 Procs/Generate Series中 v_hat=resid 发现 v_hat • 第三,估计出新的回归方程
无约束模型(U)
有约束模型(K) (general to simple)
计算统计量F
F=(RSSK-RSSu)/J RSSu/(n-k-1)
~F(J, n-k)
J 为表示约束条件数, K 为表示自变量数 或者 应估计的参数数, n 为表示样本数(obs)
4
2. LM检验(Lagrange Multiplier
多重共线性多出现在横截面资料上。
16
三、异方差性的检验及对策
Var(ℇi)≠Var(ℇj) (i≠j)时, ℇi中存在异方差性(Herteroskedasticity)。 即随机项中包含着对因变量的影响因素。 异方差性多发生在横截面资料上。
17
异方差性的检验
1.图示检验法 如模型为Yi=0+1X1i+2X2i+…+ℇi 时,
7
用Eviews的误设定检验1
• 首先估计出简单(单纯)方程 • View/Coefficient Tests/Omitted
Variables-Likelihood Ratio • 出现对话框时,写入新变量名 OK • 检验结果出现在上端,如果P值很小时, 拒
随机振动--第5章-相关函数
15
自相关函数的性质：
⑴ 自相关函数是偶函数
Rx E X t X t E X t X t Rx
16
自相关函数的性质：
⑵ 周期平稳过程的自相关函数也是周期函数， 其周期与过程的周期相同。
Rx T E X t X t T E X t X t Rx
x
2
9
相关函数的定义
既然相关系数能够表示两个随机过程之间的相 关性，且 E[ X (t1)Y (t1 )] E[ X (t1) X (t1 )] 与相关 系数之间具有线性函数关系，必然也具有相同 的作用，即也能描述相关性！！！ 定义：
自相关函数R ( ) E[ X (t ) X (t )] xx 互相关函数Rxy ( ) E[ X (t )Y (t )] R yx ( ) E[Y (t ) X (t )]
17
自相关函数的性质：
⑶τ=0时的自相关函数就是均方值
Rx E X t X t
2 Rx 0 E X t X t x
18
lim Rx ⑷ 如果随机过程不是周期过程，则：
2 x
25
定义：
Rxy t1 , t2 E X t1 Y t2 x1 y2 p x1 , t1；y2 , t2 dx1dy2
为X t 和Y t 的互相关函数。
描述：两个随机过程之间的线性依赖关系。
Ryx t1 , t2 E Y t1 X t2 y1 x2 p y1 , t1；x2 , t2 dx2 dy1
自相关函数的性质：
⑴ 自相关函数是偶函数
Rx E X t X t E X t X t Rx
16
自相关函数的性质：
⑵ 周期平稳过程的自相关函数也是周期函数， 其周期与过程的周期相同。
Rx T E X t X t T E X t X t Rx
x
2
9
相关函数的定义
既然相关系数能够表示两个随机过程之间的相 关性，且 E[ X (t1)Y (t1 )] E[ X (t1) X (t1 )] 与相关 系数之间具有线性函数关系，必然也具有相同 的作用，即也能描述相关性！！！ 定义：
自相关函数R ( ) E[ X (t ) X (t )] xx 互相关函数Rxy ( ) E[ X (t )Y (t )] R yx ( ) E[Y (t ) X (t )]
17
自相关函数的性质：
⑶τ=0时的自相关函数就是均方值
Rx E X t X t
2 Rx 0 E X t X t x
18
lim Rx ⑷ 如果随机过程不是周期过程，则：
2 x
25
定义：
Rxy t1 , t2 E X t1 Y t2 x1 y2 p x1 , t1；y2 , t2 dx1dy2
为X t 和Y t 的互相关函数。
描述：两个随机过程之间的线性依赖关系。
Ryx t1 , t2 E Y t1 X t2 y1 x2 p y1 , t1；x2 , t2 dx2 dy1
自相关(序列相关)
高阶序列相关的广义差分法
如果原模型存在：
i 1 i 1 2 i 2 l i l i
(2.5.11)
可以将原模型变换为：
Yi 1Yi 1 l Yi l 0 (1 1 l ) 1 ( X i 1 X i 1 l X i l ) i
yt 0 1x1t 2 x2t k xkt yt 1 ut
（4）回归含有截距项； （5）没有缺落数据。
一阶自相关的Dubin-watson检验
自相关存在时，有 ut ut 1 v，vt无自相关。 t Covut , ut 1 相关系数： ，
三、序列相关性的后果
1、参数估计量无偏但非有效 ； 2、变量的显著性检验失去意义 ； 3、模型的预测失效 ；
1、参数估计量无偏但非有效
OLS参数估计量仍具无偏性
OLS估计量不具有有效性
在大样本情况下，参数估计量仍然不具有渐近有效 性，这就是说参数估计量不具有一致性
2、变量的显著性检验失去意义
i 1 l ,2 l , , n
(2.5.12) 模型(2.5.12)为广义差分模型，该模型不存在序列相 关问题。采用OLS法估计可以得到原模型参数的无偏、 有效的估计量。 广义差分法可以克服所有类型的序列相关带来的问题， 一阶差分法是它的一个特例。
随机误差项相关系数的估计
应用广义差分法，必须已知不同样本点之间随机误差 项的相关系数1, 2,…, l 。实际上，人们并不知道它 们的具体数值，所以必须首先对它们进行估计。
Euiu j 0, i j
i
如果仅是Eut ut 1 0 ，称有一阶自相关 二、实际经济问题中的序列相关性
计量经济学(2010)(第五章 自相关)
年份
xi
3.3 3.3
y
i
i
0.0543 0.2543
1990 1991
6.2 7.8
1998 1999
2.5 2.7
1992
1993 1994 1995 1996
5.8
5.7 5.0 4.0 3.2
1.4
1.4 1.5 1.9 2.6
-0.3423
-0.3704 -0.4674 -0.3488 0.1262
残 差 图 1
.2 .0 -.2 -.4 -.6 1990 1992 1994 1996
1998 2000 2002 2004
( t 1 , t ) 图形
.6 .4
残 差 图 2
.2
RESID
.0 -.2 -.4 -.6 -.5 -.4 -.3 -.2 -.1 .0 .1 .2 .3 .4 .5 RESID(-1)
思考题与练习题
书上 P109 : 1，2，3 ，同时完成以下补充题：
补充题：在研究劳动力在价值增值中所占份额（即劳动力份额 Y ） 的时间 t 趋势变化中，根据1949~1964年间美国的数据， 得到如下回归结果： 模型A: t=
t21
ˆ ) 2(1 )
（4）根据DW检验临界值 (a) 当
dL , dU ，进行推断：
，则
0 d dL
u
t
存在正自相关；
(b) 当
(c) 当
dU d 4 dU
，则
，则
ut
不存在自相关。
存在负自相关。
4 dL d 4
u
t
DW检验应用说明
1、D-W检验仅适用于一阶线性自相关，对高阶自相关或 非线性自相关均不适用；也不适用于自回归模型。
第5章自相关性-精品文档
2 1n 2 n1
2 2
Ω I
自相关性的分类
如果仅存在 E(t t-1)0
Y X u t 0 1 t t
t=1,2, …,n
称为一阶自相关，或自相关（autocorrelation） 自相关往往可写成如下一阶自回归形式：
二阶自相关系数
如果式中的随机误差项
v t 不是经典误差项，即
t-2
其中包含有 u t 的成份，如包含有 u t 2 则需将 u 显含在回归模型中，即为
u u + u + v t= 1 t 1 2 t 2 t
其中， 1 为一阶自相关系数， 2 为二阶自相关系
数，v t 是经典误差项。此式称为二阶自回归模式，
t
v
E ( u 0 。 vt 的假定，与 ut-s不相关，即 tv t s)
可得出如下结论：
Cov ( u ( u [( u v u t ,u t 1) E tu t 1) E t 1 t) t 1]
2 E ( u u v t 1 t 1 t) 2 E ( u ( u v t 1)E t 1 t) 2
一阶自回归形式的性质
对于一元线性回归模型:
Y = + X + u 1 2
假定随机误差项 u 存在一阶自相关:
u u v t = t1+ t
其中， u t 为现期随机误差， u t - 1 为前期随机误差。 是经典误差项，满足零均值 E(vt ) = 0 ，同方 2 ，无自相关 差 V E ( v v ) 0( t s ) a r(v )= t s t v
二、自相关性的原因
1、经济变量固有的惯性
自相关(序列相关)
常用的方法有： （1）科克伦-奥科特（Cochrane-Orcutt）迭代法。 （2）杜宾（durbin）两步法
附：杜宾（durbin）两步法
该方法仍是先估计1，2，，L，再对差分 模型进行估计。
第一步，变换差分模型为下列形式：
Yi 1Yi 1 l Yi l 0 (1 1 l ) 1 ( X i 1 X i 1 l X i l ) i
利用
ut ut 1 vt
有
ut 1 ut 2 vt 1,, ut m1 ut m vt m1
ut mut m m1vt ( m1) m2vt ( m2) vt 1 vt
1 2 Cov N , N u n 1
i 1 l ,2 l , , n
（2.5.13）
采用 OLS 法估计该方程，得各Y j ( j i 1, i 2, i l ) 前的
ˆ1 , ˆ 2 , , ˆl 。 系数 1 , 2 , , l 的估计值
ˆ1 , ˆ 2 ,, ˆ l 代入差分模型 第二步，将估计的
i
对各方程估计并进行显著性检验，如果存在某 一种函数形式，使得方程显著成立，则说明原模 型存在序列相关性。
具体应用时需要反复试算。 回归检验法的优点是：
一旦确定了模型存在序列相关性，也就同时知 道了相关的形式；
它适用于任何类型的序列相关性问题的检验。
（2）杜宾-瓦森（Durbin-Watson）检验法
三、序列相关性的后果
1、参数估计量无偏但非有效 ； 2、变量的显著性检验失去意义 ； 3、模型的预测失效 ；
第五讲 自相关
第五讲、自相关1、自相关的概念：古典线性回归中假设扰动项u i中不存在自相关，即E(u i u j)=0, i≠j这表明任一观察值的扰动项不受其他观察值的扰动项的影响。
但是如果存在E(u i u j) ≠0, i≠j表明存在自相关问题。
自相关通常与时间序列数据有关，但截面数据中也可能产生自相关的问题（空间相关），例如，某一家庭消费支出的增加可能影响不愿比别人逊色的另一家庭消费支出的影响。
图a-d表明扰动项u存在可辨别的模式（可能存在自相关），而图e则表明不存在系统模式（可能不存在自相关）。
2、导致自相关的因素：（1）在涉及时间序列数据的回归方程中，大多数经济时间序列数据的一个显著特征是“惯性”或“延迟性”。
如GDP、就业、货币供给等时间序列都呈现周期性，连续的观察值之间很可能存在相互依赖或是相关的。
（2）模型设定错误：应该包括在模型中的重要变量未包括进模型（过低设定）或模型选择了错误的函数形式，这时残差会呈现出系统模式。
（3）蛛网现象：即解释变量是时间滞后变量，即具有时间滞后效应。
如农产品供给模型中价格对供给的影响存在蛛网现象（滞后效应）。
这种情况下的扰动项不是随机的。
（4）数据加工：在实证研究中，通常原数据是要经过加工的。
例如季度数据的时间序列回归中，数据通常是由月度数据按季相加再平均得到，而这种“平滑”过程的本身可能导致扰动项的系统模式，从而产生自相关。
3、自相关的后果：（1）虽然最小二乘估计仍然是线性和无偏的，但不是有效的，即最小二乘估计量(OLS)不是最优线性无偏估计量(BLUE)。
（2）OLS估计量的方差是有偏的，计算OLS估计量的方差或标准差的公式可能严重低估真实的方差或标准差，从而导致常用的t检验和F检验是不可靠的。
（3）通常计算的R2也是不可靠的。
4、自相关的诊断自相关的诊断存在异方差诊断中的类似问题，即ui是无法观察的，而且也不知道其产生机制：我们通过OLS估计，仅仅得到的是ei，通过对ei的讨论来“了解”自相关是否存在。
计量经济学课件05-自相关
缺点：计算量大。
et et et 检验每种估计式是否显著 e t et
e t 1 vt
et21 vt 1et 1 2 et 2 vt et 1 vt
et 1
vt
自相关检验3——偏相关系数检验
2
4、统计检验（t检验和F检验）失效
自相关性的检验
按时间先后顺序绘制残差图et-t
正自相关
负自相关
由于经济的惯性，通常不会出现负自相关的形式
绘制et-et-1散点图
正自相关
负自相关
自相关检验1——DW检验
DW检验(德宾-沃森检验)
特点： (1).解释变量是非随机的 (2).只适用于检验一阶自相关（一元和多元回归都适用） (3).当模型中出现被解释变量的滞后期，DW检验失效 即方程中不能出现yt=β0+β1xt+ β2yt-1+ut
Yt -1= 0 + 1 X t -1 + ut-1
相减，得：Yt-Yt -1 = 0 (1-) + 1 (Xt - Xt-1) + ut - ut-1 作广义差分变换： Yt* = Yt - Yt -1 ;
0* = 0 (1- ) ； X t* = X t - Xt-1；
在多个变量的之间如果只考虑之间的相关关系其他变量固定不变这种相关性称为偏相关用来衡量片相关的指标叫做是对残差做相关性检验得到相关图看图判断偏自相关偏相关系数系数的类型具体的操作而应介绍房内空调开关及棉被加枕的位置
第5章 自相关性
本章内容
5.1 5.2 5.3 5.4 自相关性及产生原因 自相关性的影响 自相关性的检验 自相关性的解决方法
第五章-时间序列的模型识别汇总
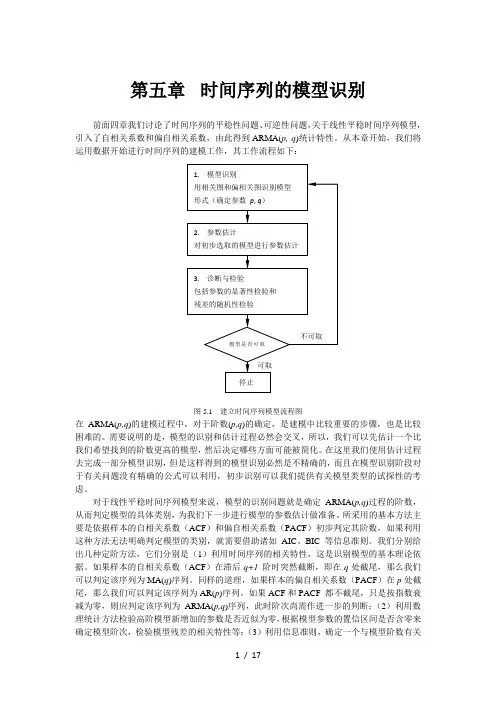
第五章时间序列的模型识别前面四章我们讨论了时间序列的平稳性问题、可逆性问题，关于线性平稳时间序列模型，引入了自相关系数和偏自相关系数，由此得到ARMA(p, q)统计特性。
从本章开始，我们将运用数据开始进行时间序列的建模工作，其工作流程如下：图5.1 建立时间序列模型流程图在ARMA(p,q)的建模过程中，对于阶数(p,q)的确定，是建模中比较重要的步骤，也是比较困难的。
需要说明的是，模型的识别和估计过程必然会交叉，所以，我们可以先估计一个比我们希望找到的阶数更高的模型，然后决定哪些方面可能被简化。
在这里我们使用估计过程去完成一部分模型识别，但是这样得到的模型识别必然是不精确的，而且在模型识别阶段对于有关问题没有精确的公式可以利用，初步识别可以我们提供有关模型类型的试探性的考虑。
对于线性平稳时间序列模型来说，模型的识别问题就是确定ARMA(p,q)过程的阶数，从而判定模型的具体类别，为我们下一步进行模型的参数估计做准备。
所采用的基本方法主要是依据样本的自相关系数（ACF）和偏自相关系数（PACF）初步判定其阶数，如果利用这种方法无法明确判定模型的类别，就需要借助诸如AIC、BIC 等信息准则。
我们分别给出几种定阶方法，它们分别是（1）利用时间序列的相关特性，这是识别模型的基本理论依据。
如果样本的自相关系数（ACF）在滞后q+1阶时突然截断，即在q处截尾，那么我们可以判定该序列为MA(q)序列。
同样的道理，如果样本的偏自相关系数（PACF）在p处截尾，那么我们可以判定该序列为AR(p)序列。
如果ACF和PACF 都不截尾，只是按指数衰减为零，则应判定该序列为ARMA(p,q)序列，此时阶次尚需作进一步的判断；（2）利用数理统计方法检验高阶模型新增加的参数是否近似为零，根据模型参数的置信区间是否含零来确定模型阶次，检验模型残差的相关特性等；（3）利用信息准则，确定一个与模型阶数有关的准则函数，既考虑模型对原始观测值的接近程度，又考虑模型中所含待定参数的个数，最终选取使该函数达到最小值的阶数，常用的该类准则有AIC 、BIC 、FPE 等。
06- 自相关性.
3、DW检验的缺陷
我们当然期望有一张能够给出相应的 n 、 k 和 α 值下各 种DW临界值的表（就象t检验，F检验一样），使得我们可以 按常规假设检验那样根据临界值作出判断。 DW统计量的分布依赖于解释变量的具体观测值。因此不 象t、F检验那样，有一张能够给出DW临界值的表。为解决这 一问题，德宾和沃森证明， DW 统计量的真实分布位于两个 极限分布之间，这两个分布分别称为下分布和上分布。 德宾和沃森据此导出了一个下界dL和一个上界du来检验自 相关，dL和du仅依赖于的数目n、解释变量k，以及显著性水 平α ，而不依赖于解释变量所取的值。 无结论区的存在是DW法的最大缺陷。
一个观测值。具体补法为：
（3、广义差分变换同样可以推广应用到多元线性回归模型
中。
（4、广义差分变换还可以推广到高阶自相关的模型中。 （5、如果广义变换后，模型还存在自相关性，可以继续使 用广义差分变换，直到自相关性消除为止。
25
2018/12/15
5.4.2、自相关系数的估计 1、直接ρ =1。注意广义变换后的模型是没有常数项的（截 距项）
29
2018/12/15
年份 1989 1990 1991 1992 1993
国内生产总值 GDP 16992.3 18667.8 21781.5 26923.5 35333.9
进口总额 IM 2199.9 2574.3 3398.7 4443.3 5986.2
年份 1998 1999 2000 2001 2002
2018/12/15
Durbin两步估计法
27
2018/12/15
28
2018/12/15
5.5
案例分析——中国商品进口模型
对进口国来说，其经济发展水平决定商品进口情况。根据我
第五讲 自相关性
第5章 自相关性5.1 自相关性及其产生的原因5.1.1 什么是自相关性对于模型：t kt k t t t u x b x b x b b y +++++= 22110 (5.1.1)如果随机误差项的各期值之间存在着相关关系，即协方差0)())())(((),cov(≠=--=s t s s t t s t u u E u E u u E u E u u （s t ≠，k s t ,2,1,=）这时，称随机误差项之间存在自相关性或序列相关(Autocorrelation or serial correlation)。
随机误差项的自相关性可以有多种形式，其中最常见的类型是随机误差项之间存在一阶自相关性或一阶序列相关：0)(),cov(11≠=--t t t t u u E u u ，或者：)(1-=t t u f u 。
一阶自相关性可以表示为t t t v u u +⋅=-1ρ (5.1.2)其中ρ是t u 与1-t u 的一阶自相关系数，t v 是满足回归模型基本假定的随机误差项。
因为在大样本情况下，根据OLS 原理，ρ的OLS 估计式为：∑∑--=211ˆt t tuuu ρ（0)(=t u E ）而t u 和1-t u 之间的相关系数r 为：∑∑∑--=2121t tt t uu u u r ≈ρˆ211=∑∑--t t tuu u （在大样本情况下，∑∑-≈212t t u u ） 因此，可以认为ρ是t u 与1-t u 的一阶自相关系数。
1≤ρ，1=ρ表示完全正自相关，t t t v u u +=-1；10〈〈ρ表示正自相关；0=ρ表示不存在自相关，t t v u =；01〈〈-ρ表示负自相关；1-=ρ表示完全负自相关，t t t v u u +-=-1。
自相关性的一般形式可以表示成：),,,(21p t t t t u u u f u ---= ，或者：t p t p t t t v u u u u ++++=---ρρρ 2211 (5.1.3)称之为p 阶自回归形式，或模型存在p 阶自相关。
自相关系数‘-概述说明以及解释
自相关系数‘-概述说明以及解释1.引言1.1 概述概述:自相关系数是用于衡量时间序列数据中各个数据点之间的相关性程度的统计指标。
在时间序列分析中，了解数据点之间的关联性可以帮助我们预测未来的趋势和波动。
自相关系数可以告诉我们当前数据点与之前数据点之间的相关性强弱，进而帮助我们做出更准确的预测。
本文将介绍自相关系数的定义、计算方法及其在实际应用中的领域。
通过深入理解和掌握自相关系数的概念，我们可以更好地分析时间序列数据，从而提高预测的准确性和可靠性。
1.2 文章结构本文分为引言、正文和结论三部分。
在引言部分，我们将介绍本文的概述、文章结构和目的。
在正文部分，我们将详细讨论什么是自相关系数、自相关系数的计算方法以及自相关系数的应用领域。
最后，在结论部分，我们将总结自相关系数的重要性，讨论自相关系数的局限性，并展望未来可能的研究方向。
通过这样的结构安排，读者可以系统地了解和掌握自相关系数的相关知识，深入理解其在实际应用中的意义和价值。
1.3 目的自相关系数作为统计学中重要的概念，其在时间序列分析、信号处理、经济学和金融等领域都有广泛的应用。
因此，本文的目的是深入探讨自相关系数的概念、计算方法以及在不同领域中的应用，希望读者能够通过阅读本文，全面了解和掌握自相关系数的相关知识，进一步拓展对其应用的认识，为实际问题的分析和解决提供理论支持和参考。
同时，本文也将探讨自相关系数的局限性，引领读者思考如何克服这些局限性，并提出未来研究的方向，为自相关系数的进一步研究和应用提供启示。
通过本文的阐述，希望能够增进读者对自相关系数的理解，为其在实际应用中发挥更大的作用提供帮助。
2.正文2.1 什么是自相关系数：自相关系数是统计学中一种用来衡量时间序列数据中自相关性程度的指标。
在时间序列分析中，自相关性指的是同一个变量在不同时间点上的相关性。
自相关系数用来表示数据之间的相关性程度，如果两个数据在时间上相关，那么它们之间的自相关系数将会是一个非零的值，反之则为零。
第5章自相关性-文档资料45页
30
•自相关图。在STATA中输入ac resid 图形中包括95%置信区间的阴影区域标注。 在这一区域之外的那些相关都是个体显著的。本例中，
residt和residt-1之间的相关是显著的。
-0.40 -0.20 0.00 0.20 0.40 0.60
0
5
10
15
20
31
Lag
Bartlett's formula for MA(q) 95% confidence bands
5.2 自相关性的后果
5.2.1 模型参数估计值不具有最优性 1．参数估计值仍具有无偏性
2．参数估计值不再具有最小方差性
5.2.2 低估随机误差项的方差
5.2.3 模型的统计检验失效
实际意义。
5.2.4 区间估计和预测区间的精度降低
5.3 自相关性检验
5.3.1 图示法
1．按时间顺序绘制残差图
图5.3.1 正自相关
图5.3.2 负自相关
t
图5.3.3 正自相关
图5.3.4 负自相关
5.3.2 德宾一沃森(Durbin-Watson)检验
DW检验的假定； 第五，统计数据比较完整，无缺失项。
DW检验的基本原理和步骤为
STATA中命令：dwstat
例：通货膨胀和赤字对利率的影响
利用INTDEF.RAW数据集，做i3对inf和def的回归。 导出残差。对残差项进行自相关分析。LAG是时滞； AC是自相关；PAC是偏自相关。比如residt和residt-2 之间的相关系数为0.1605，相应的偏自相关为-0.1801 。
Q统计量(Box-Pierce混合法)的原假设是所有各种时滞 的自相关都是0。这里绝大多数的P值都低于0.05，因此 能够拒绝原假设，即残差项存在显著的自相关。
•自相关图。在STATA中输入ac resid 图形中包括95%置信区间的阴影区域标注。 在这一区域之外的那些相关都是个体显著的。本例中，
residt和residt-1之间的相关是显著的。
-0.40 -0.20 0.00 0.20 0.40 0.60
0
5
10
15
20
31
Lag
Bartlett's formula for MA(q) 95% confidence bands
5.2 自相关性的后果
5.2.1 模型参数估计值不具有最优性 1．参数估计值仍具有无偏性
2．参数估计值不再具有最小方差性
5.2.2 低估随机误差项的方差
5.2.3 模型的统计检验失效
实际意义。
5.2.4 区间估计和预测区间的精度降低
5.3 自相关性检验
5.3.1 图示法
1．按时间顺序绘制残差图
图5.3.1 正自相关
图5.3.2 负自相关
t
图5.3.3 正自相关
图5.3.4 负自相关
5.3.2 德宾一沃森(Durbin-Watson)检验
DW检验的假定； 第五，统计数据比较完整，无缺失项。
DW检验的基本原理和步骤为
STATA中命令：dwstat
例：通货膨胀和赤字对利率的影响
利用INTDEF.RAW数据集，做i3对inf和def的回归。 导出残差。对残差项进行自相关分析。LAG是时滞； AC是自相关；PAC是偏自相关。比如residt和residt-2 之间的相关系数为0.1605，相应的偏自相关为-0.1801 。
Q统计量(Box-Pierce混合法)的原假设是所有各种时滞 的自相关都是0。这里绝大多数的P值都低于0.05，因此 能够拒绝原假设，即残差项存在显著的自相关。
第五章 自相关
第七章自相关让我们回忆古典线性回归假设中对扰动项u i的要求: 总体回归函数的扰动项u i无序列相关或无自相关。
但在实际研究中，误差项常常不满足上述假定。
本章要讨论以下问题：1.自相关性质是什么？2.自相关的理论与实际结果是什么？3.如何诊断自相关？4.如果发现比较严重的自相关，如何采取补救措施？§7.1 自相关的性质自相关就是指总体回归方程的误差项u i之间存在着相关，即：在时间（如在时间序列数据中）或空间（如在截面数据中）按顺序所列观察值序列的各成员间存在着相关。
正如异方差的产生常常与截面数据有关，自相关问题通常与时间序列数据有关。
但截面数据中也可能产生自相关问题。
古典线性回归模型中扰动项u i中不存在自相关可表示为：E(u i u j) = 0, i≠j (7.1)其含义为两个不同误差项u i和u j的乘积的期望是零，即，任一观察值的扰动项不受其他观察值扰动项的影响。
例如，在分析消费支出与家庭收入的时序数据时，本期家庭收入的增加，只影响本期消费支出，对以后的消费支出没有影响。
如果不同误差项之间存在着依赖关系，即u i存在自相关，则可表示为：E(u i u j) ≠ 0, i≠j (7.2)这种情况下，本期家庭收入的增加，可能会影响下一期或以后几期的消费支出。
由于我们无法观察到总体扰动项u i，我们只能通过样本扰动项e i来判断u i的行为。
如果u i或e i呈现出图7.1中a ~ d的形式，则表示u i自相关，如果u i或e i呈现图7.1 中e的形式，则表示u i不存在自相关。
§7.2 自相关产生的原因§7.2.1 惯性多数经济时间序列都存在惯性。
如国民生产总值、就业、货币供给、价格指数、消费、投资等，都呈现周期波动。
当经济复苏时，由萧条的底部开始，大多数经济序列向上移动，在向上移动的过程中，序列某一点的值会大于其前期值。
这种向上的“动力”存在，直到经济开始衰退。
序列自相关课件
第3节
序列相关性的检验
二、回归检验法 2.步骤： （2）对残差序列et , (t = 1 ,2 ,… , T ) 用普通最小二 乘法进行不同形式的回归拟合。如 et = ρ et – 1 + vt et = ρ1 et – 1 + ρ2 et – 2 + vt et = ρ et- 12 + v t et = ρ e t − 1 + vt （3）对上述各种拟合形式进行显著性检验，从而 确定误差项ut存在哪一种形式的自相关。
2011年11月29日 28 贺炎林 第5章序列相关性
第3节
序列相关性的检验
三、杜宾—瓦森（Durbin-Watson）检验法 4．步骤:
（1）计算DW值 （2）给定α，由n和k的大小查DW分布表，得临界值dL和dU （3）比较、判断
2011年11月29日 6 贺炎林 第5章序列相关性
二、序列相关产生的原因
1.经济变量固有的惯性 大多数经济时间数据都有一个明显的特点:惯性， 表现为较高的经济增长率会持续一段时间，较高的失业 率也会持续一段时间。 例如，绝对收入假设下居民总消费函数模型： Ct=β0+β1Yt+μt t=1,2,…,T 由于消费习惯的影响被包含在随机误差项中，则可能 出现序列相关性（往往是正相关 ）。
26
贺炎林 第5章序列相关性
第3节
序列相关性的检验
三、杜宾—瓦森（Durbin-Watson）检验法 3．D.W.统计量: 因为ρ的取值范围是[-1,1]，所以DW统计量的取 值范围是 [0, 4]。ρ 与DW值的对应关系见表
ρ
DW DW = 2 DW = 0 DW = 4 0 < DW < 2 2 < DW < 4
中级计量经济学-自相关
ut = 1ut-1 + 2ut-2 + ... + mut-m + vt
其中 为自相关系数， 为经典误差项，即
12
一阶自回归（AR(1)）展开
2 V 2 12
12 2
1n 2n
2
1 v
1 2
1n 2n
2
1
1
2
n
1
n2
n1
n2
1
13
第二节 自相关的后果
本节基本内容:
2 u
低估了随机扰动项的 方差
16
三、对模型检验的影响
^
^
若忽视自相关， t
2
^
SE( 2 ) ˆu
2
1
xi2
u
1 xi2
低估了真实方差
ˆu
et2
n 2
低估了 u
t值被高估，相应的F检验与可 决系数检验也变得不可靠。
17
四、对模型预测的影响
考 虑 对 个 别
值的预测
YF YˆF
误差项 u1,u2 ,..., un 间存在 正相关
不能判定是否有自相关
误差项 u1,u2 ,..., un 间 无自相关
4 - dU DW 4 - dL
4 - dL DW 4
不能判定是否有自相关
误差项 u1,u2 ,..., un 间存在 负相关
31
用坐标图更直观表示DW检验规则：
f (DW)
35
一、 已知时的GLS
假设
其中，
， 为经典误差项，可以推导：
36
对于一元线性回归模型
将模型滞后一期可得
Yt-1 = 0 + β1Xt-1 + ut-1
其中 为自相关系数， 为经典误差项，即
12
一阶自回归（AR(1)）展开
2 V 2 12
12 2
1n 2n
2
1 v
1 2
1n 2n
2
1
1
2
n
1
n2
n1
n2
1
13
第二节 自相关的后果
本节基本内容:
2 u
低估了随机扰动项的 方差
16
三、对模型检验的影响
^
^
若忽视自相关， t
2
^
SE( 2 ) ˆu
2
1
xi2
u
1 xi2
低估了真实方差
ˆu
et2
n 2
低估了 u
t值被高估，相应的F检验与可 决系数检验也变得不可靠。
17
四、对模型预测的影响
考 虑 对 个 别
值的预测
YF YˆF
误差项 u1,u2 ,..., un 间存在 正相关
不能判定是否有自相关
误差项 u1,u2 ,..., un 间 无自相关
4 - dU DW 4 - dL
4 - dL DW 4
不能判定是否有自相关
误差项 u1,u2 ,..., un 间存在 负相关
31
用坐标图更直观表示DW检验规则：
f (DW)
35
一、 已知时的GLS
假设
其中，
， 为经典误差项，可以推导：
36
对于一元线性回归模型
将模型滞后一期可得
Yt-1 = 0 + β1Xt-1 + ut-1
第五章 自相关
15
= σ 2/∑xt2 [1 +2ρ r +2ρ 2 r2 + 2ρ 3 r3+ ……] = σ 2/∑xt2 (1 +ρ r )/ (1 -ρ r ) 如果不考虑自相关,估计值的方差为 Var(βhatLs) =σ 2/∑xt2 =Var(βhat) = σ 2/∑xt2 (1 +ρ r )/ (1 -ρ r ) = Var(βhatLs) (1 +ρ r )/ (1 -ρ r ) Var(βhatLs)= Var(βhat) (1 -ρ r )/ (1 +ρ r )
第五章
自相关
1
第一节自相关定义及D-W检验
一,自相关的定义 当误差项不再是相互独立的,即 cov(ij) ≠0,就产生了自相关(Autocorrelation),也叫序列相关(serial correlation). 即t,t-1 t-2……是相关的. t ,t-k被称为k阶自相关 t , t-1被称为1阶自相关 t ,t-2被称2为阶自相关 ……以此类推.
=0.7921
RDlevel2 < R12
23
此外,哈韦(Harvey)给出下面的定义: RDlevel2 =1-RSS0/RSS1(1- R12) 不考虑自由度和方差的调整. 同样是上面的例题 RDlevel2 =1-0.0434/0.0278(1-0.8405) =0.7510
24
二, ρ未知时的处理方法. 首先要寻找并确定ρ.有两类方法 第一,循环查找法 1,科克伦-欧卡特方法(Cochran-Orucutt Procedure) 第一步,估计模型 yt=α +βxt +t, 得到t和RSS,定义RSS=RSS旧
6
DW检验的局限性
= σ 2/∑xt2 [1 +2ρ r +2ρ 2 r2 + 2ρ 3 r3+ ……] = σ 2/∑xt2 (1 +ρ r )/ (1 -ρ r ) 如果不考虑自相关,估计值的方差为 Var(βhatLs) =σ 2/∑xt2 =Var(βhat) = σ 2/∑xt2 (1 +ρ r )/ (1 -ρ r ) = Var(βhatLs) (1 +ρ r )/ (1 -ρ r ) Var(βhatLs)= Var(βhat) (1 -ρ r )/ (1 +ρ r )
第五章
自相关
1
第一节自相关定义及D-W检验
一,自相关的定义 当误差项不再是相互独立的,即 cov(ij) ≠0,就产生了自相关(Autocorrelation),也叫序列相关(serial correlation). 即t,t-1 t-2……是相关的. t ,t-k被称为k阶自相关 t , t-1被称为1阶自相关 t ,t-2被称2为阶自相关 ……以此类推.
=0.7921
RDlevel2 < R12
23
此外,哈韦(Harvey)给出下面的定义: RDlevel2 =1-RSS0/RSS1(1- R12) 不考虑自由度和方差的调整. 同样是上面的例题 RDlevel2 =1-0.0434/0.0278(1-0.8405) =0.7510
24
二, ρ未知时的处理方法. 首先要寻找并确定ρ.有两类方法 第一,循环查找法 1,科克伦-欧卡特方法(Cochran-Orucutt Procedure) 第一步,估计模型 yt=α +βxt +t, 得到t和RSS,定义RSS=RSS旧
6
DW检验的局限性
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ˆ1
ut ut 1 ut12
r
tn1(Yt Y)(Xt X)
tn1(Yt Y)2
tn1(Xt X)2
根据相关系数的定义，u t 和u t1 之间的相关系数 为：
utut1
ut2
u2 t1
utut1
ut2
u2 t1
uuttu1 t 21ˆ1
式中 u t 是u t -1 滞后一期的随机误差项。因此，计算
自相关往往可写成如下一阶自回归形式：
t=β1t-1+vt
-1<<1
记 为 AR(1) ， 称 β1 为 自 回 归 系 数 （ coefficient of AutoRegression）
vi是满足以下标准的OLS假定的随机干扰项：
一阶自相关系数
根据普通最小二乘法原理，模型中 1的OLS估计式
为：
还有生产企业当期的产出水平要受到上期产出水 平的影响。
2、模型设定不当
主要表现在模型中丢掉了重要的解释变量或模型函 数形式有偏误。 1）模型中略去了具有自相关性的解释变量
例如，本来应该估计的模型为
Yt=0+1X1t+ 2X2t + t， 其中Yt为需求，X1为猪肉价格，X2为消费者收入 水平，ut是无自相关的。 但在模型设定中做了下述回归：
如果忽略了消费支出变量的滞后作用，把模型设定为 ：
Y t01 X 1 t2 X 2 t v t
而被解释变量和随机扰动又有着相同的分布，这样，上述这 些被解释变量的自相关，很可能引起随机扰动项的自相关。
3、数据处理造成的相关
在实际经济问题中，有些数据是通过已知数据 生成的。因此，新生成的数据与原数据间就有了 内在的联系，表现出序列相关性。 例如：季度数据来自月度数据的简单平均，这 种平均的计算减弱了每月数据的波动性，使季度 数据具有平滑性，从而使随机干扰项出现序列相 关。
3）由被解释变量本身的自相关性所决定
例如：消费支出Yt不仅和收入X1，价格X2有关， 而且与前期消费支出有关，由于心理，习惯，环 境等方面的原因，消费者在收入下降或者价格上 升时也要保持原有的消费水平，所以，本期的消 费支出Yt与前期消费支出Yt-1有关，正确模型设
定应该是 Y t 0 1 X 1 t 2 X 2 t 3 Y t 1 u i
Yt=0+1X1t+ vt 因此， vt=2X2t + t，如果X2确实影响Y，则出现 自相关。
2）模型的函数形式不适当
例如：如果真实的边际成本回归模型应为：
Yt= 0+1Xt+2Xt2+t
其中：Y=边际成本，X=产出， 但建模时设立了如下模型：
Yt= 0+1Xt+vt 因此，由于vt= 2Xt2+t, ，包含了产出的平方对 随机项的系统性影响，随机项也呈现自相关性。
ij, i,j=1,2, …,n
如果对于不同的样本点，随机误差项之间不再
是不相关的，而是存在某种相关性，则认为出现 了自相关性（auto correlation） 。
序列相关
序列相关指的是两个（或更多）不同变量之间 的关系，自相关性是序列相关的一种特殊情况
。它是指同一变量的逐次项之间的关系，因此 ,自相关较多地表现在时间序列数据中，由于 序列相关性经常出现在以时间序列为样本的模 型中，因此，本节将用下标t代表i。
自相关也是相关的一种，即指一随机变量在时
间上与其滞后项之间的相关。这里是指回归模
型中随机误差项ut与其滞后项的相关关系。
即
C ( u to ,u t i) v 0 ,i 1 ,2 , ,t.
自相关性的分类
Yt 01Xtut
如果仅存在 E(t t-1)0
t=1,2, …,n
称为一阶自相关，或自相关（autocorrelation）
Co (utv,uts)s2
二、自相关性的原因
1、经济变量固有的惯性 大多数经济时间数据都有一个明显的特点:惯性， 表现在时间序列不同时间的前后关联上。
例如，绝对收入假设下居民总消费函数模型：
Ct=0+1Yt+t t=1,2,…,n 由于消费习惯的影响被包含在随机误差项中，则 可能出现序列相关性（往往是正相关 ）。
§第5章 自相关性
Serial Corre关性概念 二、自相关性的来源 三、自相关性的后果 四、自相关性的检验 五、自相关性的解决办法 六、案例
一、自相关性概念
对于模型
Yi=0+1X1i+2X2i+…+kXki+i
i=1,2, …,n
随机项互不相关的基本假设表现为
Cov(i , j)=0
在经济计量分析中，通常采用一阶自回归形式，
即假定自回归形式为一阶自回归 A R (1 ) 。
一阶自回归形式的性质
对于一元线性回归模型:
Y=1+2X+u
假定随机误差项 u 存在一阶自相关:
ut =ut-1+vt
其中，u t 为现期随机误差，u t - 1 为前期随机误差。
v t 是经典误差项，满足零均值 E(vt ) = 0 ，同方
的自相关系数 称为一阶自相关系数。对于大样本 显然有 ˆ1 ，一阶自回归形式可表示为：
ut = ut-1 + vt.
二阶自相关系数
如果式中的随机误差项 v t 不是经典误差项，即
其中包含有 u t 的成份，如包含有 u t 2 则需将 u t - 2 显含在回归模型中，即为
ut =1ut-1+2ut-2+vt
其中， 1 为一阶自相关系数， 2 为二阶自相关系 数，v t 是经典误差项。此式称为二阶自回归模式，
记为 A 。R (2 )
高阶自相关系数
一般地，如果 u1,u2 ,...,ut 之间的关系为
u t= 1 u t- 1 + 2 u t- 2 + ...+ m u t- m + v t
其中， v t 为经典误差项。则称此式为 m 阶自回 归模式，记为 AR (m ) 。
差 Var(vt)=v2 ，无自相关 E(vtvs)0(ts)
的假定v，t 与 ut-s不相关，即E(utvts)0 。
可得出如下结论：
Co(vut,ut1)E(utut1)E[(ut1 vt )ut1] E(ut21 ut1vt ) E(ut21)E(ut1vt ) 2
类似地， 一般地，
C ov(ut,ut 2)E (utut 2)E [ut 1 ut 2vtut 2] E (ut 1,ut 2)2 2
ut ut 1 ut12
r
tn1(Yt Y)(Xt X)
tn1(Yt Y)2
tn1(Xt X)2
根据相关系数的定义，u t 和u t1 之间的相关系数 为：
utut1
ut2
u2 t1
utut1
ut2
u2 t1
uuttu1 t 21ˆ1
式中 u t 是u t -1 滞后一期的随机误差项。因此，计算
自相关往往可写成如下一阶自回归形式：
t=β1t-1+vt
-1<<1
记 为 AR(1) ， 称 β1 为 自 回 归 系 数 （ coefficient of AutoRegression）
vi是满足以下标准的OLS假定的随机干扰项：
一阶自相关系数
根据普通最小二乘法原理，模型中 1的OLS估计式
为：
还有生产企业当期的产出水平要受到上期产出水 平的影响。
2、模型设定不当
主要表现在模型中丢掉了重要的解释变量或模型函 数形式有偏误。 1）模型中略去了具有自相关性的解释变量
例如，本来应该估计的模型为
Yt=0+1X1t+ 2X2t + t， 其中Yt为需求，X1为猪肉价格，X2为消费者收入 水平，ut是无自相关的。 但在模型设定中做了下述回归：
如果忽略了消费支出变量的滞后作用，把模型设定为 ：
Y t01 X 1 t2 X 2 t v t
而被解释变量和随机扰动又有着相同的分布，这样，上述这 些被解释变量的自相关，很可能引起随机扰动项的自相关。
3、数据处理造成的相关
在实际经济问题中，有些数据是通过已知数据 生成的。因此，新生成的数据与原数据间就有了 内在的联系，表现出序列相关性。 例如：季度数据来自月度数据的简单平均，这 种平均的计算减弱了每月数据的波动性，使季度 数据具有平滑性，从而使随机干扰项出现序列相 关。
3）由被解释变量本身的自相关性所决定
例如：消费支出Yt不仅和收入X1，价格X2有关， 而且与前期消费支出有关，由于心理，习惯，环 境等方面的原因，消费者在收入下降或者价格上 升时也要保持原有的消费水平，所以，本期的消 费支出Yt与前期消费支出Yt-1有关，正确模型设
定应该是 Y t 0 1 X 1 t 2 X 2 t 3 Y t 1 u i
Yt=0+1X1t+ vt 因此， vt=2X2t + t，如果X2确实影响Y，则出现 自相关。
2）模型的函数形式不适当
例如：如果真实的边际成本回归模型应为：
Yt= 0+1Xt+2Xt2+t
其中：Y=边际成本，X=产出， 但建模时设立了如下模型：
Yt= 0+1Xt+vt 因此，由于vt= 2Xt2+t, ，包含了产出的平方对 随机项的系统性影响，随机项也呈现自相关性。
ij, i,j=1,2, …,n
如果对于不同的样本点，随机误差项之间不再
是不相关的，而是存在某种相关性，则认为出现 了自相关性（auto correlation） 。
序列相关
序列相关指的是两个（或更多）不同变量之间 的关系，自相关性是序列相关的一种特殊情况
。它是指同一变量的逐次项之间的关系，因此 ,自相关较多地表现在时间序列数据中，由于 序列相关性经常出现在以时间序列为样本的模 型中，因此，本节将用下标t代表i。
自相关也是相关的一种，即指一随机变量在时
间上与其滞后项之间的相关。这里是指回归模
型中随机误差项ut与其滞后项的相关关系。
即
C ( u to ,u t i) v 0 ,i 1 ,2 , ,t.
自相关性的分类
Yt 01Xtut
如果仅存在 E(t t-1)0
t=1,2, …,n
称为一阶自相关，或自相关（autocorrelation）
Co (utv,uts)s2
二、自相关性的原因
1、经济变量固有的惯性 大多数经济时间数据都有一个明显的特点:惯性， 表现在时间序列不同时间的前后关联上。
例如，绝对收入假设下居民总消费函数模型：
Ct=0+1Yt+t t=1,2,…,n 由于消费习惯的影响被包含在随机误差项中，则 可能出现序列相关性（往往是正相关 ）。
§第5章 自相关性
Serial Corre关性概念 二、自相关性的来源 三、自相关性的后果 四、自相关性的检验 五、自相关性的解决办法 六、案例
一、自相关性概念
对于模型
Yi=0+1X1i+2X2i+…+kXki+i
i=1,2, …,n
随机项互不相关的基本假设表现为
Cov(i , j)=0
在经济计量分析中，通常采用一阶自回归形式，
即假定自回归形式为一阶自回归 A R (1 ) 。
一阶自回归形式的性质
对于一元线性回归模型:
Y=1+2X+u
假定随机误差项 u 存在一阶自相关:
ut =ut-1+vt
其中，u t 为现期随机误差，u t - 1 为前期随机误差。
v t 是经典误差项，满足零均值 E(vt ) = 0 ，同方
的自相关系数 称为一阶自相关系数。对于大样本 显然有 ˆ1 ，一阶自回归形式可表示为：
ut = ut-1 + vt.
二阶自相关系数
如果式中的随机误差项 v t 不是经典误差项，即
其中包含有 u t 的成份，如包含有 u t 2 则需将 u t - 2 显含在回归模型中，即为
ut =1ut-1+2ut-2+vt
其中， 1 为一阶自相关系数， 2 为二阶自相关系 数，v t 是经典误差项。此式称为二阶自回归模式，
记为 A 。R (2 )
高阶自相关系数
一般地，如果 u1,u2 ,...,ut 之间的关系为
u t= 1 u t- 1 + 2 u t- 2 + ...+ m u t- m + v t
其中， v t 为经典误差项。则称此式为 m 阶自回 归模式，记为 AR (m ) 。
差 Var(vt)=v2 ，无自相关 E(vtvs)0(ts)
的假定v，t 与 ut-s不相关，即E(utvts)0 。
可得出如下结论：
Co(vut,ut1)E(utut1)E[(ut1 vt )ut1] E(ut21 ut1vt ) E(ut21)E(ut1vt ) 2
类似地， 一般地，
C ov(ut,ut 2)E (utut 2)E [ut 1 ut 2vtut 2] E (ut 1,ut 2)2 2