函数及其图形解读

函数及其图形知识点总结引言在数学中，函数是一种描述自变量和因变量之间关系的工具。

它是一种非常重要的数学工具，可以用来描述各种各样的现象，包括物理、化学、经济、生物等领域中的问题。

在本文中，我将总结关于函数及其图形的重要知识点，包括函数的定义、性质、图像、分类以及一些相关的概念。

我将从基本概念开始，逐步深入，希望对读者有所帮助。

一、函数的定义函数是一种映射关系，它将一个集合中的元素映射到另一个集合中的元素。

通常情况下，我们用f(x)来表示函数，其中x是自变量，f(x)是因变量。

函数的定义包括以下几个要点：1. 定义域：函数的自变量的取值范围。

2. 值域：函数的因变量的取值范围。

3. 对应关系：自变量和因变量之间的对应关系。

4. 映射规则：描述自变量和因变量之间的映射关系的规则。

函数可以用各种形式表示，包括公式、图表、表格等。

在实际应用中，函数通常用符号、字母、数字、等式等来表示。

函数的定义对于理解和应用函数非常重要，因为它决定了函数的性质和特点。

二、函数的性质1. 有界性：函数的定义域和值域都可能是有界的或无界的。

有界性是函数性质的重要特点之一，对于函数的图像有着重要的意义。

2. 单调性：函数在定义域内可能是单调递增的、单调递减的或者不单调。

单调性是函数图像的一个关键特征，可以通过函数的导数来进行分析。

3. 周期性：某些函数具有周期性，即在一定的区间内具有重复的规律性。

正弦函数和余弦函数就是典型的周期函数的例子。

4. 奇偶性：函数的奇偶性描述了函数图像关于原点的对称性。

奇函数具有关于原点对称，偶函数具有关于y轴对称。

5. 渐近线：函数图像可能有水平渐近线、垂直渐近线或者斜渐近线。

这些渐近线在分析函数图像的特点时非常有用。

三、函数的图像函数的图像是函数性质与特点的重要体现。

数学中有很多种函数图像，每种函数图像都有其独特的特点。

以下是几种常见的图像：1. 直线的图像：表示成y = kx + b的线性函数具有直线的图像，直线的斜率决定了线的倾斜程度，截距决定了直线与坐标轴的交点位置。

五、基本初等函数及其性质和图形1.幂函数函数称为幂函数。

如，，，都是幂函数。

没有统一的定义域，定义域由值确定。

如,。

但在总是有定义的，且都经过（1,1）点。

当时，函数在上是单调增加的，当时，函数在内是单调减少的。

下面给出几个常用的幂函数：的图形，如图1-1-2、图1-1-3。

图1-1-2图1-1-32.指数函数函数称为指数函数，定义域，值域；当时函数为单调增加的；当时为单调减少的，曲线过点。

高等数学中常用的指数函数是时，即。

以与为例绘出图形，如图1-1-4。

图1-1-43.对数函数函数称为对数函数，其定义域，值域。

当时单调增加，当时单调减少，曲线过（1，0）点，都在右半平面内。

与互为反函数。

当时的对数函数称为自然对数，当时，称为常用对数。

以为例绘出图形，如图1-1-5。

图1-1-54.三角函数有，它们都是周期函数。

对三角函数作简要的叙述：（１）正弦函数与余弦函数：与定义域都是，值域都是。

它们都是有界函数，周期都是，为奇函数，为偶函数。

图形为图1-1-6、图1-1-7。

图1-1-6正弦函数图形图1-1-7余弦函数图形（２）正切函数，定义域，值域为。

周期，在其定义域内单调增加的奇函数，图形为图1-1-8图1-1-8（３）余切函数，定义域，值域为，周期。

在定义域内是单调减少的奇函数，图形如图1-1-9。

图1-1-9（４）正割函数，定义域，值域为，为无界函数，周期的偶函数，图形如图1-1-10。

图1-1-10（５）余割函数，定义域，值域为，为无界函数，周期在定义域为奇函数，图形如图1-1-11。

图1-1-115.反三角函数反正弦函数，定义域，值域，为有界函数，在其定义域内是单调增加的奇函数，图形如图1-1-12；图1-1-12，为有界函数，在其定义域内为单调减少的非奇非偶函数，图形如图1-1-13；图1-1-13反正切函数，定义域，值域为，为有界函数，在定义域内是单调增加的奇函数，图形如图1-1-14；图1-1-14为有界函数，在其定义域内单调减少的非奇非偶函数。

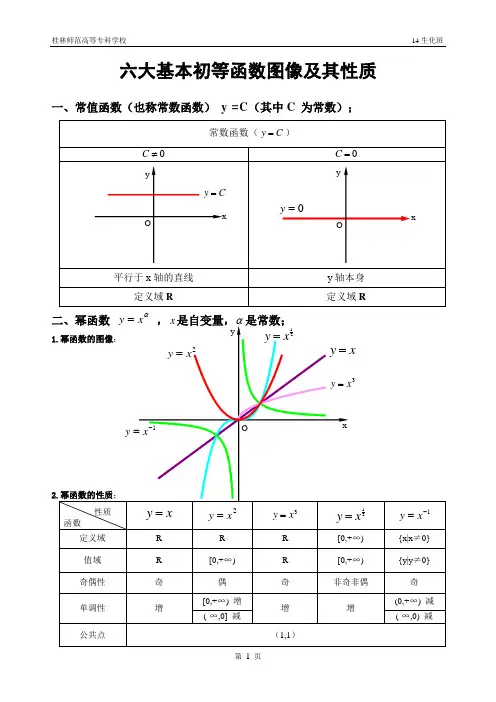
六大基本初等函数图像及其性质一、常值函数（也称常数函数）y =C（其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

1(3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。

b.1.当1>a 时，a 值越大，xa y =的图像越靠近y 轴；b.2.当10<<a 时，a 值越大，x a y =的图像越远离y 轴。

4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。

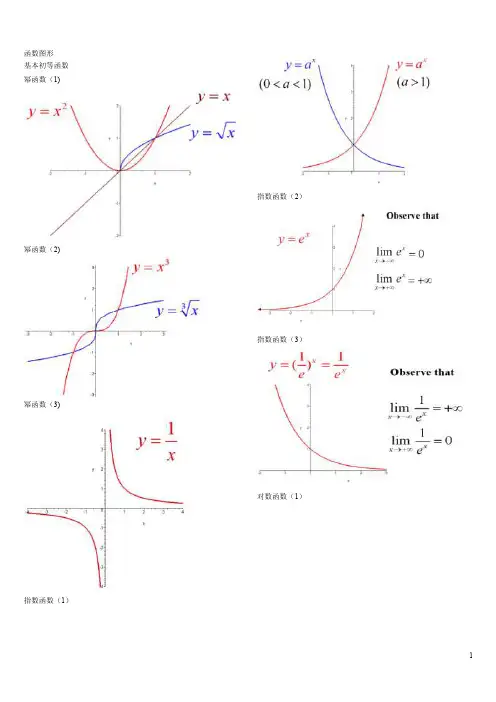
函数图形基本初等函数幂函数（1)幂函数（2)幂函数（3)指数函数（1）指数函数（2）指数函数（3）对数函数（1）对数函数（2）三角函数（1）三角函数（2）三角函数（3）三角函数（4）三角函数（5）反三角函数（1）反三角函数（2）反三角函数（3）反三角函数（4）反三角函数（5）反三角函数（6）反三角函数（7）反三角函数（8）双曲函数（1）双曲函数（2）双曲函数（3）双曲函数（4）双曲函数（5）双曲函数（6）双曲函数（7）反双曲函数（1）反双曲函数（2）反双曲函数（3）反双曲函数（4）反双曲函数（5）反双曲函数（6）y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1) 极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性) 极限的性质(3) (不等式性质) 极限的性质(4) (局部有界性) 极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)等价无穷小(x->0)sinx等价于xarcsinx等价于x tanx等价于x arctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2)数列的夹逼性(1) 数列的夹逼性(2) pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了文案编辑词条B 添加义项?文案，原指放书的桌子，后来指在桌子上写字的人。

函数图像总结函数图像是指函数在直角坐标系中的图形表示。

通过观察函数图像，可以了解函数的基本特征和性质。

下面我将对常见的函数图像进行总结。

一、一次函数图像：一次函数的一般形式为y = kx + b，其中k为斜率，b为截距。

当k>0时，函数图像呈现正斜率，向右上方倾斜；当k<0时，函数图像呈现负斜率，向右下方倾斜；当k=0时，函数图像为水平直线；当b>0时，函数图像在y轴上方截距b的位置；当b<0时，函数图像在y轴下方截距-b的位置。

二、二次函数图像：二次函数的一般形式为y = ax^2 + bx + c，其中a决定了函数的开口方向和开口大小，b决定了函数图像的对称轴位置，c决定了函数图像与y轴的交点。

当a>0时，函数图像向上开口；当a<0时，函数图像向下开口；当b=0时，函数图像的对称轴为y轴；当b>0时，函数图像的对称轴在原点的右侧；当b<0时，函数图像的对称轴在原点的左侧。

三、指数函数图像：指数函数的一般形式为y = a^x，其中a为底数。

当底数a>1时，函数图像呈现增长趋势，向上凸起；当0<a<1时，函数图像呈现递减趋势，向下凹陷；当a=1时，函数图像为水平直线。

四、对数函数图像：对数函数的一般形式为y = loga(x)，其中a为底数。

当底数a>1时，函数图像呈现增长趋势，向右上方倾斜；当0<a<1时，函数图像呈现递减趋势，向右下方倾斜；当a=1时，函数图像为y轴。

五、三角函数图像：常见的三角函数包括正弦函数、余弦函数、正切函数等。

正弦函数的图像呈现周期性的波形，振动范围在[-1,1]之间；余弦函数的图像也呈现周期性的波形，振动范围也在[-1,1]之间；正切函数的图像在某些点上发生突变，振动范围在整个坐标轴上。

总结以上几种函数图像，可以根据函数的数学表达式和特点来推测图像的形状和性质，进而帮助解决与函数相关的问题。

五大基本初等函数性质及其图像五、基本初等函数及其性质和图形1.幂函数函数称为幂函数。

如，，，都是幂函数。

没有统一的定义域，定义域由值确定。

如,。

但在内总是有定义的，且都经过（1,1）点。

当时，函数在上是单调增加的，当时，函数在内是单调减少的。

下面给出几个常用的幂函数：的图形，如图1-1-2、图1-1-3。

图1-1-2图1-1-32.指数函数函数称为指数函数，定义域，值域；当时函数为单调增加的；当时为单调减少的，曲线过点。

高等数学中常用的指数函数是时，即。

以与为例绘出图形，如图1-1-4。

图1-1-43.对数函数函数称为对数函数，其定义域，值域。

当时单调增加，当时单调减少，曲线过（1，0）点，都在右半平面内。

与互为反函数。

当时的对数函数称为自然对数，当时，称为常用对数。

以为例绘出图形，如图1-1-5。

图1-1-54.三角函数有，它们都是周期函数。

对三角函数作简要的叙述：（１）正弦函数与余弦函数：与定义域都是，值域都是。

它们都是有界函数，周期都是，为奇函数，为偶函数。

图形为图1-1-6、图1-1-7。

图1-1-6正弦函数图形图1-1-7余弦函数图形（２）正切函数，定义域，值域为。

周期，在其定义域内单调增加的奇函数，图形为图1-1-8图1-1-8（３）余切函数，定义域，值域为，周期。

在定义域内是单调减少的奇函数，图形如图1-1-9。

图1-1-9（４）正割函数，定义域，值域为，为无界函数，周期的偶函数，图形如图1-1-10。

图1-1-10（５）余割函数，定义域，值域为，为无界函数，周期在定义域为奇函数，图形如图1-1-11。

图1-1-115.反三角函数反正弦函数，定义域，值域，为有界函数，在其定义域内是单调增加的奇函数，图形如图1-1-12；图1-1-12反余弦函数，定义域为[-1，1]，值域为，为有界函数，在其定义域内为单调减少的非奇非偶函数，图形如图1-1-13；图1-1-13反正切函数，定义域，值域为，为有界函数，在定义域内是单调增加的奇函数，图形如图1-1-14；图1-1-14反余切函数，定义域为，值域，为有界函数，在其定义域内单调减少的非奇非偶函数。

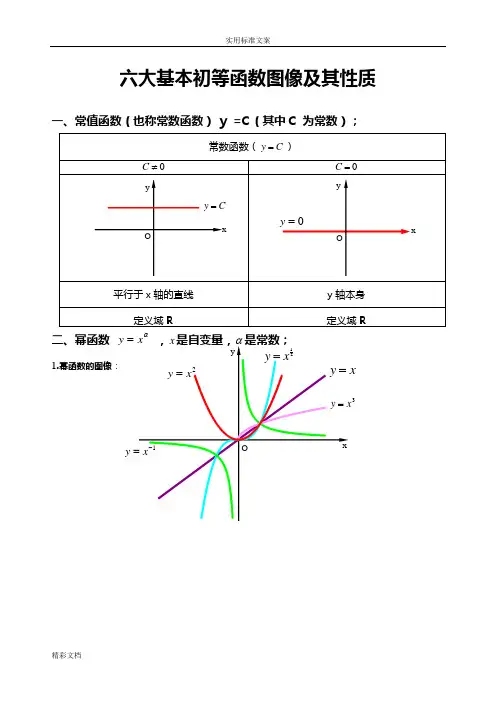
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；二、幂函数 αy =1.幂函数的图像：3y2.幂函数的性质；1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数yxx a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。

b.1.当1>a 时，a 值越大，x a y =的图像越靠近y 轴；b.2.当10<<a 时，a 值越大，xay =的图像越远离y 轴。

4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) nm n m a a a +=⋅ (2) n m n m a a a -=÷(3)()()mn nmnm aaa ==(4)()n n n b a ab =b.根式的性质；f xxxx g ⎪⎫ ⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。

经典数学函数图像(大全)1. 一次函数图像一次函数图像是一条直线，其一般形式为 y = mx + b，其中 m是斜率，b 是 y 轴截距。

当 m > 0 时，直线向上倾斜；当 m < 0 时，直线向下倾斜。

2. 二次函数图像二次函数图像是一个抛物线，其一般形式为 y = ax^2 + bx + c，其中 a、b、c 是常数。

当 a > 0 时，抛物线开口向上；当 a < 0 时，抛物线开口向下。

3. 三角函数图像三角函数图像包括正弦函数、余弦函数和正切函数。

正弦函数图像是一条波动曲线，余弦函数图像与正弦函数图像相似，但相位差为π/2。

正切函数图像是一条周期性振荡的曲线。

4. 指数函数图像指数函数图像是一条上升或下降的曲线，其一般形式为 y = a^x，其中 a 是底数，x 是指数。

当 a > 1 时，曲线上升；当 0 < a < 1 时，曲线下降。

5. 对数函数图像对数函数图像是一条上升或下降的曲线，其一般形式为 y =log_a(x)，其中 a 是底数，x 是真数。

当 a > 1 时，曲线上升；当0 < a < 1 时，曲线下降。

6. 双曲函数图像双曲函数图像包括双曲正弦函数、双曲余弦函数和双曲正切函数。

双曲正弦函数和双曲余弦函数图像都是上升或下降的曲线，而双曲正切函数图像是一条周期性振荡的曲线。

7. 幂函数图像幂函数图像是一条上升或下降的曲线，其一般形式为 y = x^n，其中 n 是指数。

当 n > 0 时，曲线上升；当 n < 0 时，曲线下降。

8. 反比例函数图像反比例函数图像是一条双曲线，其一般形式为 y = k/x，其中 k是常数。

当 k > 0 时，曲线位于第一和第三象限；当 k < 0 时，曲线位于第二和第四象限。

经典数学函数图像(大全)3. 反三角函数图像反三角函数是三角函数的反函数，包括反正弦函数、反余弦函数和反正切函数。

高中数学-函数图像详解基本初等函数的图像1. 一次函数性质：一次函数图像是直线，当k>0时，函数单调递增；当k<0时，函数单调递减2. 二次函数性质：二次函数图像是抛物线，a决定函数图像的开口方向，判别式b^2-4ac 决定了函数图像与x轴的交点，对称轴两边函数的单调性不同。

3. 反比例函数性质：反比例函数图像是双曲线，当k>0时，图像经过一、三象限；当k<0时，图像经过二、四象限。

要注意表述函数单调性时，不能说在定义域上单调，而应该说在（-∞，0），（0，∞）上单调。

4.指数函数当0<a<b<1<c<d时，指数函数的图像如下图< span>不同底的指数函数图像在同一个坐标系中时，一般可以做直线x=1，与各函数的交点，根据交点纵坐标的大小，即可比较底数的大小。

5.对数函数当底数不同时，对数函数的图像是这样变换的6. 幂函数y=x^a性质：先看第一象限，即x>0时，当a>1时，函数越增越快；当0<a<1时，函数越增越慢；当a<0时，函数单调递减；然后当x<0时，根据函数的定义域与奇偶性判断函数图像即可。

< span>7. 对勾函数对于函数y=x+k/x，当k>0时，才是对勾函数，可以利用均值定理找到函数的最值。

函数图形的变换注意：对于函数图像的变换，有的时候，看到解析式，可能会有两种以上的变换，尤其是针对x轴上的，那么此时，一定要根据上面的规则，判断好顺序，否则顺序错了，可能就没办法经过变换得到了！例如：画出函数y=ln|2-x|的图像通过研究这个函数解析式，我们知道此函数是由基本初等函数y=lnx通过变换而来，那么这个函数经过了几步变换呢？变换的顺序又是如何？下面我们一起来看一看。

通过解析式x上附加的东西，我们会发现，会有对称变换，x前面加了负号，还有翻折变换，x上面还有绝对值，还有平移变换，前面加了一个2，既然有3种变换，那么顺序如何呢？牢记住一点：针对x轴上的变换，那就一定要看x这个符号有啥变化。

函数及其图像分析详解函数是高中数学中非常重要的一个概念，它可以描述两个变量之间的关系，或者将一个自变量的值映射到一个因变量的值上。

在实际应用中，各种函数及其图像都有着非常重要的作用，本文将对常见的函数及其图像进行详细的分析。

一、常见的函数类型1.线性函数线性函数是最简单的一类函数，它的定义域为全体实数集合R，表达式为：y=kx+b（其中k和b为常数）。

直线y=kx+b就是它的图像，这条直线在坐标系中的位置由直线的斜率和截距决定。

斜率表示函数在一定区间内自变量变化时因变量的变化幅度，截距表示函数与y轴的交点。

2.二次函数二次函数是一类带有平方项的函数，也是非常常见的函数类型。

它的定义域为全体实数集合R，表达式为：y=ax^2+bx+c（其中a,b,c为常数）。

二次函数的图像是一个抛物线，抛物线开口的方向由a的正负号决定。

当a>0时，抛物线开口朝上，当a<0时，抛物线开口朝下。

3.指数函数指数函数是一类用x的幂作为自变量的函数，自变量为x，因变量为y，通式为y=a^x，其中a为大于0且不等于1的常数。

指数函数的图像是一条右侧开口的曲线，曲线在x轴上向右无限延伸，当x趋近于负无穷大时，曲线趋近于y轴。

4.对数函数对数函数是指数函数的反函数，它的定义域为(0,+∞)，值域为全体实数集合R，通式为y=loga x，其中a为大于0且不等于1的常数。

对数函数的图像是一条带左侧开口的曲线，曲线在y轴上向上无限延伸，当x趋近于正无穷大时，曲线趋近于x轴。

5.三角函数三角函数是用角度作为自变量的函数，它是解决几何问题中经常使用的函数。

常见的三角函数包括正弦函数、余弦函数、正切函数等，它们的定义域为全体实数集合R，值域为[-1,1]。

三角函数的图像是一条在[-1,1]区间内振荡的波形，波形周期的长度由函数的周期决定。

二、函数图像分析的相关概念1.函数的极值函数的极值是函数在定义域内的最大值和最小值。

在一段区间内，如果函数的导数在该区间内始终大于0，则该函数在这段区间内单调递增，在这段区间内的最大值即为函数的极大值。

函数及其图像总结知识点函数的图像是函数表示的一种形式，它是函数在坐标系中的图形表示。

函数的图像可以帮助我们更直观地理解函数的特点和性质。

在学习函数的过程中，函数的图像是一个非常重要的知识点。

本文将总结函数的相关知识点，以帮助读者更好地掌握这一重要的数学概念。

一、函数的定义在数学中，函数是一种特殊的关系。

如果存在一种依赖关系，使得除了x以外，对每个x都只有唯一的y和y唯一对应某个x，那么就称这种依赖关系为函数。

函数的符号表示通常是f(x)或者y=f(x)，其中x为自变量，y为因变量。

函数的定义域是自变量的取值范围，值域是函数的输出范围。

二、常见函数1. 线性函数：y=ax+b，其中a和b为常数。

线性函数的图像是一条直线，斜率a决定了直线的斜率，常数b决定了直线的截距。

线性函数是最简单的函数之一，它们在数学建模中有着广泛的应用。

2. 二次函数：y=ax^2+bx+c，其中a、b和c为常数且a不等于0。

二次函数的图像是一条抛物线，开口向上或向下取决于a的正负。

二次函数在物理学、工程学等领域有着重要的应用。

3. 指数函数：y=a^x，其中a为正实数且不等于1。

指数函数的图像是一条逐渐增长或逐渐减小的曲线。

指数函数在自然科学和经济学中有着广泛的应用。

4. 对数函数：y=loga(x)，其中a为正实数且不等于1。

对数函数的图像是一条渐进线，对数函数能够将指数函数的性质转化为更容易理解的形式。

5. 三角函数：包括正弦函数、余弦函数、正切函数等。

三角函数在物理学、工程学和天文学中有着重要应用。

以上函数是常见的、在数学教育中重点研究的函数。

这些函数具有各自的特点和性质，通过学习这些函数，我们可以更好地理解数学中的各种问题，并且为进一步学习高等数学课程打下扎实的基础。

三、函数的性质1. 奇函数和偶函数：奇函数满足f(-x)=-f(x)，偶函数满足f(-x)=f(x)。

通过奇偶函数的性质，我们可以推导出一系列关于函数图像的对称性质，以及某些函数值的简化表示。

函数及图像的知识点总结函数是数学中的一个重要概念，也是数学分析和高等代数的基础内容。

在数学中，函数是一种对应关系，可以简单的理解为一种特殊的映射关系，将一个变量的取值映射到另一个变量的取值。

在数学中，通常用f(x)来表示一个函数，其中x是自变量，f(x)是函数的因变量。

函数的定义：在数学中，函数是一个对应关系，它将一个或多个输入值映射到一个输出值。

函数通常用一个算式或图形来表示。

函数可以用以下的方式表示：f：A→B其中，A是函数的定义域，B是函数的值域。

定义域表示函数的输入值的集合，值域表示函数的输出值的集合。

函数的定义域和值域决定了函数的有效输入和输出的范围。

函数的图像：函数的图像是函数在平面直角坐标系中的图形，通常用函数的定义域和值域的点来表示。

函数的图像可以用直线、曲线或点来表示。

通过函数的图像可以直观地看出函数的性质和特点。

常见的函数类型：1. 线性函数：线性函数是指函数的图像是一条直线。

线性函数的一般形式为f(x) = ax + b，其中a和b为常数，a称为斜率，b称为截距。

线性函数的图像是一条斜率为a，截距为b的直线。

2. 二次函数：二次函数是指函数的图像是一条抛物线。

二次函数的一般形式为f(x) = ax^2 + bx + c，其中a、b和c为常数。

二次函数的图像是一条开口的抛物线，开口的方向由二次项的系数a的正负决定。

3. 指数函数：指数函数是指函数的自变量为指数的函数。

指数函数的一般形式为f(x) =a^x，其中a为常数且a>0，a不等于1。

指数函数的图像是一条递增或递减的曲线，曲线的斜率由底数a的大小和正负决定。

4. 对数函数：对数函数是指函数的自变量为对数的函数。

对数函数的一般形式为f(x) =log_a(x)，其中a为常数且a>0，a不等于1。

对数函数的图像是一条递增或递减的曲线，曲线的斜率由底数a的大小和正负决定。

函数的性质：1. 定义域和值域：函数的定义域和值域决定了函数的有效输入和输出的范围。

函数与其图像知识点总结函数与其图像是数学中常见的概念，对于理解数学问题和解决实际问题具有重要意义。

在高中阶段，学生已经接触到了函数与其图像的相关知识，下面将从函数的定义、性质、图像绘制及应用等方面进行总结。

一、函数的定义1. 自变量和因变量函数是一个映射关系，它描述了自变量和因变量之间的对应关系。

通常情况下，自变量用x表示，因变量用y表示。

在函数中，自变量的取值范围我们称之为定义域，因变量的取值范围称之为值域。

2. 函数的定义函数的定义包括了自变量的定义域和因变量的值域，以及自变量和因变量之间的对应关系。

一般情况下，我们用符号y=f(x)表示函数的定义，其中f表示函数名称，x表示自变量，y表示因变量。

3. 函数的表示函数可以用表达式、图像、数据表等形式进行表示。

常见的函数表示形式包括解析式表示、图像表示、数据表示等。

二、函数的性质1. 奇偶性函数的奇偶性是指当自变量x的取值变化时，因变量y的取值是否满足某种对称性。

若对于任意x∈D，都有f(-x) = f(x)，则函数f(x)是偶函数；若对于任意x∈D，都有f(-x) = -f(x)，则函数f(x)是奇函数。

2. 单调性函数的单调性是指当自变量x的取值增大时，因变量y的取值是单调递增还是单调递减。

若对于任意x1 > x2，有f(x1) > f(x2)，则函数f(x)是递增函数；若对于任意x1 > x2，有f(x1) < f(x2)，则函数f(x)是递减函数。

3. 周期性函数的周期性是指函数在一定范围内具有重复性。

若存在正数T，使得对于任意x∈D，有f(x+T) = f(x)，则函数f(x)是周期函数，其中T称为函数的周期。

4. 上下界函数的上下界是指函数在定义域内取值的最大值和最小值。

若存在常数M，使得对于任意x∈D，都有f(x) ≤ M，则M称为函数f(x)的上界；若存在常数m，使得对于任意x∈D，都有f(x) ≥ m，则m称为函数f(x)的下界。

六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；二、幂函数 αy =1.幂函数的图像：2.幂函数的性质；3y1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1(1）当1>a 时函数为单调增,当10<<a 时函数为单调减；2）不论x 为何值,y总是正的,图形在x 轴上方；3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫⎝⎛=1)(的函数图像关于y 轴对称。

b.1.当1>a 时，a 值越大，x a y =的图像越靠近y 轴；b.2.当10<<a 时，a 值越大，xay =的图像越远离y 轴。

4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) n m n m a a a +=⋅ (2) n m n m a a a -=÷(3)()()mn nmnm aaa ==(4)()nn n b a ab =yxf x xxx g ⎪⎫ ⎛=1)(b.根式的性质；(1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a an m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。