- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.2 离散无记忆信道
4.2.1离散信道数学模型
信道描述
信道可以引用三组变量来描述: 信道输入:X=(X1, X2 … Xi,… ), Xi ∈{a1 … an} 信道输出:Y= (Y1, Y2 … Yj,…), Yj ∈{b1 … bm} 信道概率转移矩阵:
p{y/x}=p(y1y2..yn|x1x2…xn)
–输入变量取值离散而输出变量取值连续 –输入变量取值连续而输出变量取值离散
时间离散的连续信道: 信道输入和输出是连续的时间序列
波形信道: 输入和输出都是时间的实函数x(t), y(t)
两端信道
多端信道
恒参信道:参数不随时间变化
随参信道:参数随时间变化
无记忆信道和有记忆信道
对称信道和非对称信道
多元接入信道 广播信道 无损信道 确定信道 无噪信道
转移矩阵
P
p 0
1 p 1 q
0 q
1
p
1-p
0
2
1-q
q
1
4.2.3二元对称消失信道
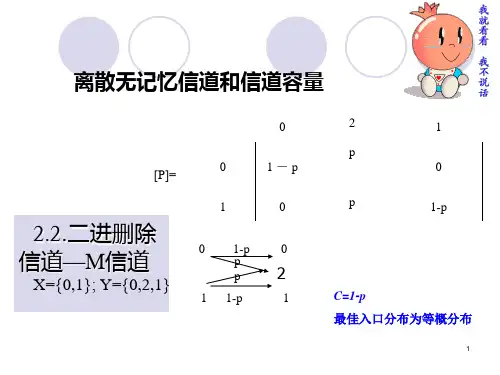
二元删除信道BEC
– 输入符号X取值{0,1};0 – 输出符号Y取值{0,1,2}
1-p-q
q
p
0
转移矩阵
pq
x
1 p q q
p 1 1 - p - q1
P
p
q 1 p q
先验概率:
信源发出消息ai的概率p(ai)=P(X= ai)
3、有干扰有记忆信道
4.2.2单符号离散信道
X={a1,a2,……ar} P(Y/X)={p(bj/ai)} (i=1,2,……r;j=1,2,……s) Y={b1,b2,……bs} 0≤p(bj/ai)≤1
信道的传递概率又称为转移概率
矩阵[P]称为转移矩阵或信道矩阵;表示为:
b1
b2
…
… a1 p(b1/a1) p(b2/a1)
即:{ X p(y|x) Y }
定义4.2.1若离散信道对任意N长的输入、输 N
出序列有p( y | x) p( yn则| xn称) 它为离散无记忆信道 n 1
DMC。其信源模型为{X p(yn|xn) Y} 任何时刻信道的输出至于此时刻信道的输入有 关,而与以前的输入无关。
定义4.2.2对任意n和m,i∈A,j∈B,若离散无 记忆信道还满足 P( yn j | xn i) P( ym j | xm i)
则称此信道为平稳的或恒参的。
1、无扰(无噪)信道
–信道的输出信号Y与输入信号X之间有
确定的关系Y=f (X),已知X后就确知Y
–转移概率:
p(Y
|
X
)
1, 0,
Y f(X) Y f(X)
2、有干扰无记忆信道
信道的输出信号Y与输入信号X之间没有确定y1 | x1) p( y2 | x2) p( yL | xL )
i
j
p(xi y j ) log
•很重要的一种特殊信道 •信道转移概率:
1-p
0
0
p
p
1
1
1-p
01
P
1
p
p
p 1 p
0 1
• p(0|0) = 1-p p(1|1) = 1-p
• p(0|1) = p p(1|0) = p
4.2.2二元删除信道BEC
二元删除信道BEC – 输入符号X取值{0,1};0
– 输出符号Y取值{0,1,2}
bs p(bs/a1)
…
[P]= a2 p(b1/a2) p(b2/a2)
p(bs/a2)
……
…
…
… ar p(b1/ar) p(b2/ar)
… p(bs/ar)
[P]矩阵为一个r×s矩阵,其每行元素之和等于1
3、图示法描述
例4.2.1:二元对称信道
•二元对称信道BSC
–输入符号X取值{0,1}; –输出符号Y取值{0,1}
联合概率:
p=(pa(ia|bi)j)p=(bPji (|1Xap=i)(aa=iip,/Yb(=bj )j)bpj)(i a1i
p(bj)
| bj)
1
前向概率:(及信道传递概率)
p(bj | ai)=P(Y= bj | X= ai)
r
输出符号概率:
p(bj)=P(Y=
bj)p(b j
)
i 1
p(ai
3〉研究信道的目的 在通信系统中研究信道,主要是为了描述、
度量、分析不同类型信道,计算其容量,即极 限传输能力,并分析其特性。
输入量X (随机过程)
p(Y|X) 信道
输出量Y (随机过程)
•按输入/输出信号在幅度和时间上的取值: •离散信道:
–输入和输出的随机序列取值都是离散的信道 •连续信道:
–输入和输出的随机序列取值都是连续的信道 •半离散(半连续)信道:
4.2.4平均互信息
定义4.2.4原始信源熵与信道疑义度之差称 为平均互信息。
I(X;Y) H(X) H(X |Y)
Y未知,X 的不确定度为H(X) Y已知,X 的不确定度变为H(X |Y)
信息= 先验不确定性-后验不确定性 = 不确定性减少的量
平均互信息
通信系统中,若发端的符号为X ,收端的符号为Y – 如果是一一对应信道,接收到Y后,对X的不确定 性将完全消除:H(X|Y) = 0 – 一般情况: H(X |Y) <H(X),即了解Y后对X的不 确定度的将减少
)
p(b j
|
ai )
( j 1,2,...,s)
4.2.3信道疑义度
定义4.2.3称输入空间X对输入空间Y的条件熵
H (X | Y ) E[H (X | y j )] p(xi , y j ) log p(xi | y j )
ij
可疑度,它表示接收者收到Y后,对信源X仍 然存在的平均不确定度。对于接收者来说, 条件熵H(X/Y)称为疑义度,对X尚存在的平 均不确定度是由于干扰(噪声)引起的
通过信道传输消除了一些不确定性,获得了一定的
信息。 0 I ( X ;Y ) H ( X )
信源X
有扰信道
信宿Y
干扰源
平均互信息的另一种定义方法:
I (X ;Y )
i
j
p(xi y j ) log
p(xi | y j ) p(xi )
i
j
p(xi y j ) log
p(xi y j ) p(xi ) p( y j )
p(ai | bj )
(i=p(1a,i 2) p,…(bj,r|)ai )
r
后验概率:
p(ai ) p(bj | ai )
i 1
信宿收到bj 后推测信源发出 (i 1,2,...,r)
ai的概率
( j 1,2,...,s)
r
p(ai|bj)=P(X= ai |Y= bj) r
p(ai, bj)