实验一 牛顿环 实验讲义

牛顿环〔实验目的〕1、观察牛顿环干涉现象及特点；2、掌握用牛顿环测量透镜球面的曲率半径的方法；3、熟悉读数显微镜的使用。

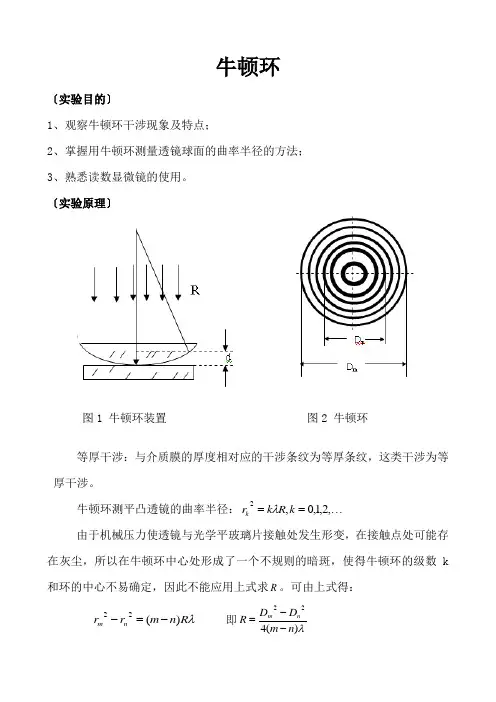
〔实验原理〕图1 牛顿环装置 图2 牛顿环等厚干涉：与介质膜的厚度相对应的干涉条纹为等厚条纹，这类干涉为等厚干涉。

牛顿环测平凸透镜的曲率半径：⋯==,2,1,0,2k R k r k λ由于机械压力使透镜与光学平玻璃片接触处发生形变，在接触点处可能存在灰尘，所以在牛顿环中心处形成了一个不规则的暗斑，使得牛顿环的级数k 和环的中心不易确定，因此不能应用上式求R 。

可由上式得：λR n m r r nm )(22-=- 即λ)(422n m D D R nm --=[实验内容及步骤] 1、调节仪器（1）将仪器摆放好，点亮钠光灯，调节牛顿环仪使干涉条纹约处于中央位置，然后将其放在测量显微镜工作平台的中央处。

（2）使钠光灯通过凸透镜平行入射透光反射镜，调整工作平台和支架的高度。

（3）聚焦。

转动聚焦手轮，使镜筒缓慢移动，当物镜距牛顿环仪上表面约３.5c ｍ左右时，叉丝和干涉条纹均可看清楚了。

（4）分别转动x,y 轴上的测微器，使其示数分别为2.5cm 和0.65cm ，使物镜对准工作平台中心，在目镜视场中让叉丝交点与牛顿环中央大致重合，并使叉丝分别与x,y 轴平行。

2、测量干涉圆环直径m n D D 、。

[注意事项]１、调节读数显微镜筒向下运动时应缓慢、稳当，勿使其下端的45度反射镜架碰到牛顿环仪的透镜上。

２、测牛顿环时，级数不能查错。

３、测量显微镜的测微鼓轮在每一次测量过程中只能向一个方向旋转，中途不能反转，以避免测微螺距间隙引起的回程误差。

Ｐ图3 牛顿环仪器位置简图。

实验一 牛顿环测透镜曲率半径“牛顿环”是一种分振幅等厚干涉现象，它在光学加工中有着广泛的应用，例如测量光学元件的曲率半径等。

这种方法是光学法的一种，适用于测量大的曲率半径。

一、实验目的1、学会用牛顿环测量透镜的曲率半径的原理和方法。

2、学会读数显微镜的调整和使用。

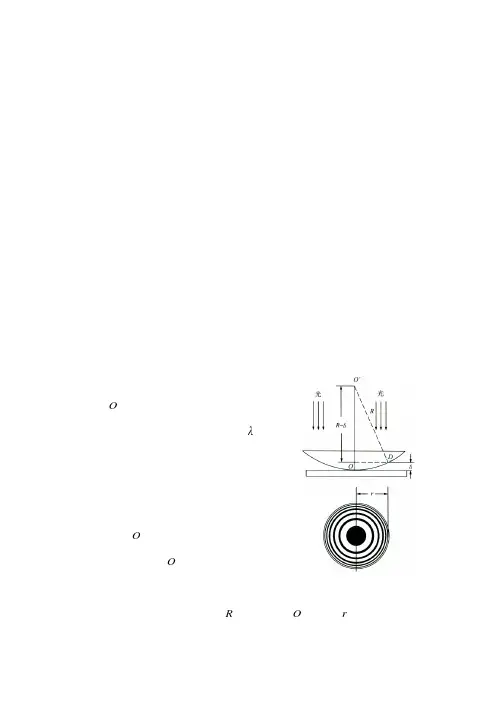
二、实验仪器读数显微镜（JCD 3型）、牛顿环装置、钠光灯、升降台三、实验原理用一块曲率半径很大的平凸透镜，将其凸面放在另一块光学平板玻璃上即构成牛顿环装置（如图1）这时在透镜凸面和平板玻璃之间形成从中心向四周逐渐增厚的空气层。

当一束单色光垂直入射到平凸透镜上，入射光经空气层上下表面反射的两相干光束存在光程差，在透镜凸面上相遇而发生干涩折。

由于光程差取决于空气层的厚度，所以厚度相同处呈现同一干涉条纹，显然这些干涉条纹是以接触点为中心的一系列明暗相间的同心圆环，称为牛顿环（如图2），是等厚干涉条纹。

如图1所示，在P 点处两相干光的光程差为：图1 牛顿环装置图 图2 牛顿环22λδ+=d （1）式中d 为P 处空气层厚度，2λ是光波在平面玻璃界面反射时产生半波损失而带来的附加光程差。

设R 为平凸透镜球面的曲率半径，r 为P 点所在环的半径，它们与厚度d 之间的几何关系为()2222222r d Rd R r d R R ++-=+-= （2）因为R »d，所以2d «2Rd，略去2d 项，（2）式变为Rr d 22≈ （3）若P 处恰为暗环，则δ必满足下式： ()212λδ+=k （k=0，1，2，3，…） （4）式中，k 为干涉条纹的级次。

综合式（1），（3），（4），得到第k 级暗环半径为 λkR r k =（5）由（5）知，只要入射光波长λ已知，测出第k 级暗环半径k r 即可得出R 值。

但是利用此测量关系式时往往误差很大，这是因为透镜凸面和平板玻璃平面不可能是理想的点接触，接触压力会引起弹性形变，使接触处变为一个圆面；或者，由于灰尘存在使平凸透镜凸面和平面玻璃之间有间隙，从而引起附加光程差，中央的暗斑可变成亮斑或半明半暗。

一、实验目的1. 理解牛顿环的原理及其形成条件。

2. 通过观察牛顿环的干涉条纹，测量平凸透镜的曲率半径。

3. 熟悉光学仪器和实验操作方法。

二、实验原理牛顿环是由平凸透镜与平板玻璃之间形成的空气薄层引起的等厚干涉现象。

当光线垂直照射到平凸透镜和平板玻璃的接触面时，部分光线在接触面发生反射，部分光线穿过空气薄层后再发生反射。

这两束反射光相互干涉，形成明暗相间的干涉条纹。

根据干涉条件，明纹处的光程差为半个波长，即Δl = (m + 1/2)λ，其中m为干涉级数，λ为光的波长。

对于牛顿环，空气薄层的厚度h与干涉级数m之间的关系为：h = (m + 1/2)λR其中R为平凸透镜的曲率半径。

通过测量干涉条纹的级数，可以计算出平凸透镜的曲率半径。

三、实验仪器与设备1. 平凸透镜2. 平板玻璃3. 平行光源4. 凸透镜支架5. 米尺6. 干涉条纹观察仪7. 记录纸8. 镜子9. 光具座四、实验步骤1. 将平板玻璃放在光具座上，将平凸透镜放在平板玻璃上，调整使其与平板玻璃接触良好。

2. 将平行光源照射到平凸透镜和平板玻璃的接触面，调整光源方向，使光线垂直照射。

3. 将干涉条纹观察仪放置在光具座上，调整使其与平行光源和透镜平行。

4. 观察干涉条纹，记录明纹和暗纹的位置，用米尺测量条纹间距。

5. 根据干涉级数m和条纹间距，计算平凸透镜的曲率半径R。

五、实验结果与分析1. 通过观察干涉条纹，记录了10个明纹和暗纹的位置，计算出干涉级数m。

2. 根据干涉级数m和条纹间距，计算平凸透镜的曲率半径R。

实验数据如下：m = 5d = 0.5 mmR = (m + 1/2)λ/d = (5 + 1/2)×600 nm/0.5 mm = 3.6 m六、实验总结1. 通过牛顿环法实验，成功测量了平凸透镜的曲率半径。

2. 实验过程中，注意了光线的垂直照射和干涉条纹的观察，保证了实验结果的准确性。

3. 通过实验，加深了对牛顿环原理和等厚干涉现象的理解。

实验09 用牛顿环测曲率半径光的干涉现象证实了光在传播过程中具有波动性;光的干涉现象在工程技术和科学研究方面有着广泛的应用;获得相干光的方法有两种：分波阵面法例如杨氏双缝干涉、菲涅尔双棱镜干涉等和分振幅法例如牛顿环等厚干涉、迈克尔逊干涉仪干涉等;本实验主要研究光的等厚干涉中的两个典型干涉现象,即牛顿环和劈尖干涉,它们都是用分振幅方法产生的干涉,其特点是同一条干涉条纹处两反射面间的厚度相等,故牛顿环和劈尖都属于等厚干涉;在实际工作中,通常利用牛顿环来测量光波波长,检查光学元件表面的光洁度、平整度和加工精度,利用劈尖来测量微小长度、薄膜的厚度和固体的热膨胀系数等;实验目的22λδ+=K K d 8-1式中2λ是因为光线由光疏媒质空气进入光密媒质玻璃在交界面反射时有一位相π的突变而引起的附加光程差半波损失;由图8-1所示的几何关系,有： 因为K d R >>,故可略去2K d 项而得：Rr d KK 22= 8-2根据干涉条件,两束相干光当光程差为波长的整数倍时互相加强,光程差为半波长的奇数倍时互相抵消,因此,第K 级明环和暗环的形成条件是：λδK = 为明环 8-32)12(λδ+=K 为暗环 8-4由公式8-1、8-2、8-3、8-4可求得第K 级明环和暗环的半径为： 明环： 2)12(λR K r K -= ,3,2,1=K 8-5暗环： λKR r K =,2,1,0=K 8-6从公式8-5、8-6可知,在平凸透镜凸面与平面玻璃的接触点即0=K r 处,干涉圆环为暗环,实际观察到的是一个暗圆斑;2. 透镜曲率半径R 的测量方法及系统误差的处理方法如果已知入射光波长λ,则只要设法测得明环或是暗环的半径K r ,就可以由8-5、8-6式求得平凸透镜的曲率半径R 值,反之,当曲率半径R 已知时,则可求得波长λ值;但是,由于玻璃的弹性形变及接触处不干净等原因,使接触处不可能是一个几何点,即中心点的半径不为零,这使得在环心处平凸透镜与平面玻璃之间有一附加厚度其符号可正可负,环心的干涉结果会是一个较大的暗斑,这种情况均导致每环半径K r 发生变化,这时如果仍用8-5、8-6式进行计算,就势必造成较大的系统误差;改用下述方法进行测量,就能消除这个系统误差;假设用暗环进行测量,测出第m 级和n 级的暗环半径m r 和n r ,设这些数据带有上述系统误差,但我们可以认为：r 是测准了的,误差主要是在级数m 和n 上,由于加上了一个附加厚度,使得在理想的点接触时,本该是第x m +环之处,我们现在看到的是第m 环,本该是第x n +环之处,我们现在看到的是第n 环;按8-5、8-6式本该有：上面两式是准确的,把它们平方后相减可得即 λ)(22n m r r R n m --=若用环的直径来表示,则上式可写为λ)(422n m D D R nm --= 8-78-7式只涉及两环级数之差,而不决定于级数本身,从而消除了因级数不准带来的系统误差;另一方面,由8-7式可以发现,只要级数差)(n m -一定,则暗环的直径平方差也是一定值,例如=-=-=-)()()(212222211221210220D D D D D D ,这样,在测量中,可测量多个暗环的m D 和n D 值,然后用逐差法求出多个)(22n m D D -,以平均值)(22n m D D -代进8-7式计算R ,可以进一步减小测量误差,从而有利于进一步提高R 的测量结果的精确度;上面的讨论对于明条纹也有同样的结果; 3. 劈尖干涉玻璃板,包线,这样,二光束相遇时,2δ=nd 要形成暗条纹,则 d =由上式可知,当此时d 总数;在N 不太多的情况下可以直接数出来;但一般情况N 数目很大,故先测出单位长度上的暗条纹数0N ,再测出两玻璃板交接线至待测物间的距离L ,则L N N 0=,于是nL N d 20λ= 8-8 如劈尖间的媒质为空气,则1=n ;仪器介绍JCD 2-A 型读数显微镜 1. 读数显微镜概述读数显微镜即为测量显微镜;显微镜通常起放大物体的作用,而读数显微镜除放大物体外,还能测量物体的大小;读数显微镜的规格型号很多,但基本结构是相同的;本实验使用的是JCD 2-A 型读数显微镜,测量范围为0~50mm,最小分度值为0.01mm 与螺旋测微计相同,可估读到0.001mm;读数显微镜的优点是既有螺旋测微计的测量精度,又不会使被测物体变形、受损,还兼有低倍率显微镜的作用; 2. JCD 2-A 型读数显微镜的外型结构手轮10可使反射镜11的方向适当即目镜视场中背景光亮度适当；显微镜的高度和水平位置均可调节,松开锁紧手轮13和16,显微镜可在竖直方向和水平方向移动；测得数可从标尺18和测微手轮17读得：从标尺上读得的mm位读数加上从测微手轮上读得的数即为最后的测得数,测微手轮的结构与读数方法与螺旋测微计类似,测微手轮每转动一周,显微镜就横移1mm的距离,测微手轮的圆周等分为100小格,因此每一小格表示0.01mm,加上估读的一位,测微手轮可读到0.001mm,因此最后结果可读出五位有效数字;实验内容与要求能通过牛顿环的中心,并依次与各暗环相切;（4）开始测量;由于接近牛顿环中心处的圆环宽度变化很大,不易测准,故可以从10=K 开始测量;又因为暗环较易对准,所以实验时是测量暗环直径D ;选择牛顿环的测量范围为29~10=K 共20个环,为了消除空程差螺距差,注意只能往一个方向进行测量,这时可安排测量顺序如下：转动测微手轮使十字叉丝向左移动到第32环以外,然后倒回到第29环,使十字叉丝与暗环的左侧或右侧相切,对准并读数,记为左29x ,然后缓慢移动十字叉丝至第28环,读出左28x ,逐条依次测量i x ,直至测读出左10x ；继续向原方向转动测微手轮,越过牛顿环的中心区域至第10环,读出右10x ,至第11环,读出右11x ,逐条依次测量i x ,直至测读出右29x ,将全部测量数据填入下面的数据表格中;（5n m 22nm D D -、R σ,并求相对误差r E ;（6）根据实验室给定的牛顿环曲率半径标称值1.855=标R mm,按照0-30式计算百分差r δ; 2. 用劈尖干涉法测量微小物体的厚度（1）将劈尖取代牛顿环放置在读数显微镜的玻璃平台上,在目镜视场中找到干涉条纹,调节调焦手轮,使条纹清晰;移动劈尖,使干涉条纹和叉丝竖线平行;（2）旋转测微手轮,使十字叉丝沿某一方向移动,测出21条干涉暗条纹之间的总长度0L ,在不同位置分别测量4次;（3）计算单位长度的暗条纹数0N 001L n N -=,测4次求平均值0N ; （4）测出由劈尖的顶端开始0=K 至待测物的总长度L ,连续测4次,求平均值L ; （5）按8-8式计算待测物的厚度d ; （6）计算误差;注意事项1. 测量时,只能往一个方向缓慢转动读数显微镜的测微手轮,中途切不可反转,以免带来空程差螺距差;2. 测量中途,如眼睛感到疲劳,可稍作休息再行读数,以保证测量数据的准确性;3. 爱护仪器,各光学镜面不得用手或其它物体触摸;4. 牛顿环装置上的三个压紧螺丝不可拧得太紧,以防压碎镜片;5. 本实验所使用的钠灯光源是冷光源,点亮之后不要轻易关掉它,关掉之后也不能马上再启动,必须先拿开灯罩冷却几分钟后才能再次启动;思考问题课前预习题1. 牛顿环与劈尖干涉有什么相同与不同之处2. 为什么牛顿环的各环宽度不等试解释牛顿环内疏外密的现象;3. 如果本实验观测到的牛顿环中心不是暗斑而是亮斑,试分析其可能性;这种情况对测量R 有没有影响课后思考题4. 牛顿环是非等间隔的干涉环,为什么在实验中仍用逐差法处理数据5. 在牛顿环实验中,假如平玻璃板上有微小的凸起,则凸起处空气薄层的厚度减小,导致等厚干涉条纹发生畸变;试问这时的牛顿环暗环将局部内凹还是局部外凸为什么6. 怎样利用劈尖干涉现象测表面平整度。

牛顿环实验引言牛顿环实验是一种基于光波干涉现象的实验，由英国物理学家爱萨克·牛顿于17世纪发现和描述。

这个实验通过使用一块凸透镜和与其接触的一块平面玻璃板来观察干涉现象。

在实验中，光在透镜和玻璃板之间反射和折射，形成了圆形的干涉环。

这些干涉环的直径和强度可以用来计算透镜和玻璃板的特性以及光的波长。

牛顿环实验为研究光学干涉提供了重要的实验基础。

实验原理牛顿环实验依赖于光的干涉现象。

当光通过透明介质表面并发生反射或折射时，会发生干涉现象。

牛顿环实验中的凸透镜和平面玻璃板之间形成的空气薄膜就是干涉的介质。

当平行入射的光通过透镜时，由于光线朝向法线的度数不同，光线将发生不同程度的折射。

这些折射光线相遇并发生干涉，形成一系列明暗相间的圆环。

这些圆环被称为“牛顿环”。

实验步骤进行牛顿环实验的步骤如下：1. 准备实验装置：将一块凸透镜放在平坦的台座上，然后将一块平面玻璃板放在透镜上。

确保透镜和玻璃板之间有足够的接触以形成空气薄膜。

2. 照明实验装置：使用光源照明实验装置，确保光线垂直于透镜和玻璃板表面。

这可以通过调整光源和装置之间的距离来实现。

3. 观察牛顿环：通过透镜观察干涉环。

透镜的中心将显示最亮的环，然后环的亮度将逐渐减弱直到消失。

这些环的直径的变化可以用来计算透镜和玻璃板的特性。

实验结果分析牛顿环实验中观察到的干涉环的直径可以用来计算玻璃板的厚度。

根据光的干涉理论，当光由高折射率介质（透镜）射向低折射率介质（玻璃板）时，从中心到第N个圆环的半径R可以通过以下公式计算：R = sqrt(N * λ * R / (2 * n))其中，N是干涉环的数量，λ是光的波长，n是玻璃的折射率。

利用实验测得的干涉环半径和已知的波长，可以推算出玻璃的折射率。

实验结果的精度将取决于实验仪器的精确度和实验者的技巧。

应用领域牛顿环实验在科学和工程领域具有广泛的应用。

这个实验可以用来测量透镜的曲率半径、表面形状和折射率，以及透明材料的性质。

牛　顿　环 【实验目的】　（１）观察干涉现象，并用以测定平凸透镜的曲率半径　（２）掌握利用牛顿环光波波长的方法　（３）熟悉读数显微镜的结构，掌握其使用方法　【实验仪器】　读数显微镜，牛顿环，钠光灯　【实验原理】　如图１所示，将一块曲率半径较大的平凸透镜的凸面放在一平面玻璃板上，就组成了一个牛顿环装置，在透镜的凸表面与平面玻璃板的上表面之间，形成了一个空气薄层，在以接触点O为中心的任一圆周上，空气层的厚度都相等．这样，如果有以波长为λ的单色光垂直入射时，则空气薄层的上边缘面所反射的光和下边缘面所反射的光之间就有了光程差，因此发生干涉现象．光程差相等的地方就是以O点为中心的同心圆，因此干涉条纹也就是一组以O点为中心的同心圆，称为牛顿环． 图１　设平凸透镜的曲率半径为R，距接触点O半径为r的圆周上一点D 处的空气层厚度为δ ，对应于D 点产生的干涉所形成的暗条纹的条件为 2)12(22λλδ+=+k ， K ＝０、１、２　… （１）　由图１的几何关系可看出 2222222)(δδδ+−+=−+=R R r R r R （２）　由于δ>>R ，上式中δ２　略去，故　R r 22=δ （３）　将δ值代入式（１），化简　R k r λ=2 （４）　由式（４）可知，如果已知单色光的波长λ，又能测出各暗条纹的半径r ，就可算出曲率半径R ．反之，如果知道R ，测出r ，亦可算出单色光的波长λ．　 在实际测量时，由于牛顿环的级数K 和中心不易确定，可将式（４）变为如下形式 图２　λm D D R mm k 422−=+ （５）　式中，D k +m 和D m 分别为k+m 级和k 级暗环的直径（如图２），从式（５）可知，只要求出所测各环的环数差m ，而无须确定各环的级数，不必确定圆环的中心，避免了实验中圆心不易确定的困难． 【实验步骤】　１　调整实验装置 ⑴　调节牛顿环仪上的三个螺钉，用眼睛直接观察，使干涉条纹成圆形并处在牛顿环仪的中心．注意平凸透镜和玻璃板不能挤压过紧，以免损坏牛顿环仪．　⑵　将牛顿环仪置于显微镜筒下方（如图３），开启钠光灯源，调节显微镜座 架的高度，使套在显微镜镜头上４５°的反射镜M 与钠光灯等高．　⑶　调节目镜，使十字叉丝清晰，调节反射镜M ，使显微镜下视场黄光均匀． 图３　⑷　调节调焦旋钮对牛顿环聚焦，使干涉条纹清晰．调节时，显微镜筒应自下而上缓慢移动，直到在目镜中看清干涉条纹止（不要自上而下调，以免损坏仪器），并适当移动牛顿环仪，使牛顿环圆心处在视场中央．　２　观察干涉条纹的分布特征　观察牛顿环条纹的粗细和形状，间距是否相等，并从理论上做出解释，观察牛顿环中心是亮斑还是暗斑．　３　测量平凸透镜的曲率半径 １、目镜；２、镜筒；３、调焦手轮；４、柱；　５、横杆；６、测微刻度轮；７、物镜；　⑴　调节目镜镜筒，使一根十字 叉丝与显微镜移动方向垂直，保持这条叉 丝与干涉条纹相切，另一根水平叉丝则和　显微镜移动方向一致，以便观察和测量条纹的直径．　⑵　旋转显微镜的鼓轮，使十字叉丝由牛顿环中央缓慢向左移动到４５环，然后单方向向右移动，测出显微镜的叉丝与各条纹相切的读数d 45 ，d 40 ，d 35，d 15，d 10，d 5的读数．然后继续向右移动，经过环的中心，到另一边继续向右测出d 5′，d 10′，d 15′，d 35′，d 40′，ｄ４５′则第ｎ级条纹的直径'nn n d d D −=　（d n ′指环中心另一边的读数），测量时应注意回程差．　⑶　用逐差法，将D k 值分为两组，一组为k+m ，另一组为k ，将数据填入表１中　【数据记录与处理】（ｐｓ：下面的表格是一个表格，同志们不要画成两个）　表１　m ＝３０ nm 2.03.589±=λ　+m k =−=+λm D D R k mk 422 （mm ）　。

1312 牛 顿 环（实验讲义P205 实验二十四）【实验目的】（1）观察干涉现象，并用以测定平凸透镜的曲率半径 （2）掌握利用牛顿环光波波长的方法（3）熟悉读数显微镜的结构，掌握其使用方法 【实验仪器】读数显微镜，牛顿环，钠光灯 【实验原理】如图1所示，将一块曲率半径较大的平凸透镜的凸面放在一平面玻璃板上，就组成了一个牛顿环装置，在透镜的凸表面与平面玻璃板的上表面之间，形成了一个空气薄层，在以接触点O 为中心的任一圆周上，空气层的厚度都相等．这样，如果有以波长为λ的单色光垂直入射时，则空气薄层的上边缘面所反射的光和下边缘面所反射的光之间就有了光程差，因此发生干涉现象．光程差相等的地方就是以O 点为中心的同心圆，因此干涉条纹也就是一组以O 点为中心的同心圆，称为牛顿环．设平凸透镜的曲率半径为R ，距接触点O 半径为r 的圆周上一点D 处的空气层厚度为δ ，对应于D 点产生的干涉所形成的暗条纹的条件为2)12(22λλδ+=+k ， K ＝0、1、2 (1)由图1的几何关系可看出2222222)(δδδ+-+=-+=R R r R r R （2）由于δ>>R ，上式中δ 2略去，故Rr 22=δ （3）将δ值代入式（1），化简R k r λ=2 （4） 图1由式（4）可知，如果已知单色光的波长λ，又能测出各暗条纹的半径r ，就可算出曲率半径R ．反之，如果知道R ，测出r ，亦可算出单色光的波长λ．在实际测量时，由于牛顿环的级数K 和中心不易确定，可将式（4）变为如下形式λm D D R mm k 422-=+ （5）式中，D k +m 和D m 分别为k+m 级和k 级暗环的直径（如图2），从式（5）可知，只要求出所测各环的环数差m ,而无须确定各环的级数，不必确定圆环的中心，避免了实验中圆心不易确定的困难． 图2 【实验内容】1 调整实验装置⑴ 调节牛顿环仪上的三个螺钉，用眼睛直接观察，使干涉条纹成圆形并处在牛顿环仪的中心．注意平凸透镜和玻璃板不能挤压过紧，以免损坏牛顿环仪．⑵ 将牛顿环仪置于显微镜筒下方(如图3),开启钠光灯源，调节显微镜座架的高度，使套在显微镜镜头上45°的反射镜M 与钠光灯等高．⑶ 调节目镜，使十字叉丝清晰，调节反射镜M ，使显微镜下视场黄光均匀．⑷ 调节调焦旋钮对牛顿环聚焦，使干涉条纹清晰．调节时，显微镜筒应自下而上缓慢移动，直到在目镜中看清干涉条纹止(不要自上而下调，以免损坏仪器)，并适当移动牛顿环仪，使牛顿环圆心处在视场中央．2 观察干涉条纹的分布特征观察牛顿环条纹的粗细和形状，间距是否相等，并从理论上做出解释，观察牛顿环中心是亮斑还是暗斑．1、目镜；2、镜筒；3、调焦手轮；3 测量平凸透镜的曲率半径 4、柱； 5、横杆；6、测微刻度轮； ⑴ 调节目镜镜筒，使一根十字 7、物镜；叉丝与显微镜移动方向垂直，保持这条叉 图3 丝与干涉条纹相切，另一根水平叉丝则和显微镜移动方向一致，以便观察和测量条纹的直径．⑵ 旋转显微镜的鼓轮，使十字叉丝由牛顿环中央缓慢向左移动到32环，然后单方向向右移动，测出显微镜的叉丝与各条纹相切的读数d 30 ，d 29 ，……，d 12，d 11，的读数．然后继续向右移动，经过环的中心，到另一边继续向右测出d 11′，d 12′，……，d 29′，d 30′，则第n级条纹的直径'n n n d d D -= (d n ′指环中心另一边的读数)，测量时应注意回程差．⑶ 用逐差法，将D k 值分为两组，一组为k+m ，另一组为k ，将数据填入表1中 【数据记录与处理】nm 3.589==-+22k D D m k (mm 2) =-∆+)(22k D D m k (mm 2)=-=+λm D D R km k 422(mm)=-∆=∆+λm D D R k m k 4)(22 (mm)实验结果：±=∆±=R R R (mm)【注意事项】⑴ 使用读数显微镜进行测量时，手轮必须向一个方向旋转，中途不可倒退． ⑵ 读数显微镜镜筒必须自下而上移动，切莫让镜筒与牛顿环装置碰撞．⑶ 光学仪器光学面在实验时不要用手去摸或与其他东西相接触，因为这样极易磨损 精致的光学表面，这点在实验中千万小心，若有不洁需用专门的擦镜纸擦试．【思考题】(1) 什么是光的干涉？产生光的干涉现象的条件是什么？(2) 观察牛顿环为什么选用钠光灯作光源？若用白光照射将如何？(3) 本实验处理数据时，为什么要用逐差法？用算术平均法行吗？为什么？(4) 使用读数显微镜进行测量时，手轮为什么必须向一个方向旋转，中途不可倒退？ (5) 使用读数显微镜进行测量时，为什么读数显微镜镜筒必须自下而上移动？。

牛顿环一、实验目的1、掌握用牛顿环测定透镜曲率半径的方式。

2、通过实验加深对等厚干涉原理的理解。

3、熟悉读数显微镜的使用方法。

二、实验原理1、等厚干涉如图，光线11’和22’的光程差为&=2h + λ/2 .光程差只与厚度h有关，式中λ/2是因为光线由光疏介质射到光密介质且在aa界面反射时有一相位突变引起的附加误差。

产生第m级暗条纹的条件是：2h + λ/2 =（2m+1）* λ/2 (m=0,1,2……) 即h = mλ/2产生第m级亮条纹的条件是：2h + λ/2 =2m* λ/2 （m=1,2,……）即h = (m-1)/2 * λ/2因此在空气厚度相同处产生连续的干涉条纹，厚度不同处，产生不同级的干涉条纹。

2、用牛顿环测透镜的曲率半径牛顿环是用分振幅方法产生的等厚干涉条纹，可用于测量透镜的曲率半径，也可用于检查物体表面的光洁度和平面度。

如图，∆PFC中，R2 = r k2 + （R - &）2 R k表示第k级暗纹半径，&表示P点处空气膜层厚度，PP’= &，r k2 = - &2 + 2&R ≈2&R光在P处空气膜上、下界面所反射两束光的程差为∆= 2& + λ/2当∆= （2k+1）* λ/2时，得到干涉暗条纹，所以2& + λ/2 = （2k+1）* λ/2 ，即& = kλ/2所以，r k2 = kRλ实际测量时，空气层厚度为&+&0 ，得r k2 = kRλ- 2R&0测出k=m, k=n的梁换半径r m与r n ,得=r m - r n = （m-n）Rλ………………消除2R&的影响所以，R = （r m 2- r n 2）/ 20λ三、实验仪器读数显微镜，钠光灯，牛顿环仪等四、实验步骤1、开启钠光灯，调节旋转手轮，使反光镜不向上反光；2、调节牛顿环仪的三个螺钉，使小干涉圆环位于其中心，且干涉冤魂越小越好，越细越好；3、旋转测微鼓轮，使显微镜筒位于标尺中部（即25mm处），将牛顿环仪置于台面玻璃上，使干涉圆环的中心正对显微镜光轴，调节使目镜的视场全部被照亮；4、显微镜的调节，先调目镜，使叉丝最清晰，视场明亮，将镜筒聚焦于牛顿环，移动牛顿环，使圆环中心正对叉丝中心；5、测量环直径时，使一根叉丝与镜筒横向移动方向平行，另一根叉丝与暗环相切，镜筒应始终沿一个方向移动，读取数据。

大学物理牛顿环实验一、实验目的1、观察牛顿环的干涉现象2、研究干涉现象与光波的波动性质3、学习使用分光仪、读数显微镜的方法二、实验原理牛顿环是一种典型的干涉现象，它是由一束光分成两束相干光，在空间叠加而成。

当一束光照射在玻璃表面时，会产生反射和透射两种现象。

反射光会在玻璃表面形成亮斑，而透射光则会继续传播。

当透射光再次照射到玻璃表面时，会再次产生反射和透射，形成一系列的反射和透射光。

这些反射和透射光会相互干涉，形成明暗相间的条纹，这就是牛顿环。

三、实验步骤1、调整分光仪，使一束光通过玻璃棱镜，分成两束相干光，并在空间叠加。

2、调整分光仪的望远镜，观察到清晰的牛顿环。

3、使用读数显微镜测量牛顿环的直径，并记录下来。

4、改变分光仪的棱镜角度，观察干涉条纹的变化，并记录下来。

5、分析实验数据，得出结论。

四、实验结果与分析1、实验结果在实验中，我们观察到了清晰的牛顿环干涉现象，并且使用读数显微镜测量了牛顿环的直径。

随着分光仪棱镜角度的变化，干涉条纹也会发生变化。

2、结果分析通过实验数据，我们可以得出以下（1）牛顿环是由两束相干光在空间叠加而形成的干涉现象。

（2）干涉条纹的明暗交替是由于两束光的相位差引起的。

（3）通过测量牛顿环的直径，我们可以计算出光波的波长。

（4）随着分光仪棱镜角度的变化，干涉条纹会发生变化，这是因为光的波长和入射角发生了变化。

五、结论通过本次实验，我们深入了解了干涉现象与光波的波动性质，学习了使用分光仪、读数显微镜的方法。

这对于我们今后在光学领域的研究具有重要意义。

大学物理牛顿环实验一、实验目的1、观察牛顿环的干涉现象2、研究干涉现象与光波的波动性质3、学习使用分光仪、读数显微镜的方法二、实验原理牛顿环是一种典型的干涉现象，它是由一束光分成两束相干光，在空间叠加而成。

当一束光照射在玻璃表面时，会产生反射和透射两种现象。

反射光会在玻璃表面形成亮斑，而透射光则会继续传播。

当透射光再次照射到玻璃表面时，会再次产生反射和透射，形成一系列的反射和透射光。

第1篇一、实验背景牛顿环实验是光学中的一个经典实验，通过观察和分析牛顿环现象，可以深入了解光的干涉原理，并应用于测量透镜的曲率半径等实际应用中。

牛顿环实验的核心原理是等厚干涉现象，即在薄膜层厚度相同的位置，光波发生干涉，形成明暗相间的条纹。

二、实验原理1. 牛顿环的形成牛顿环实验装置主要由一块曲率半径较大的平凸透镜和一块光学玻璃平板组成。

当平凸透镜的凸面与平板接触时，在接触点附近形成一层空气膜。

当平行单色光垂直照射到牛顿环装置上时，光在空气膜的上、下表面反射，形成两束光波。

这两束光波在空气膜上表面相遇，产生干涉现象。

2. 等厚干涉现象在牛顿环装置中，空气膜的厚度从中心到边缘逐渐增加。

由于空气膜厚度相同的位置对应于同一干涉条纹，因此这种现象称为等厚干涉。

根据等厚干涉原理，厚度相同的位置，光程差也相同，从而形成明暗相间的干涉条纹。

3. 牛顿环的干涉条件在牛顿环装置中，光在空气膜上、下表面反射的两束光波发生干涉，干涉条件为：Δ = mλ其中，Δ为光程差，m为干涉级次，λ为光波长。

4. 牛顿环的半径与透镜曲率半径的关系设牛顿环装置中第m级暗环的半径为rk，透镜的曲率半径为R，空气膜厚度为e，则有：rk^2 = R^2 - e^2由上式可知，通过测量牛顿环的半径rk，可以计算出透镜的曲率半径R。

三、实验步骤1. 准备实验装置，包括牛顿环仪、钠光灯、凸透镜、平板玻璃等。

2. 将牛顿环仪放置在实验台上，调整透镜与平板玻璃之间的距离，使牛顿环清晰可见。

3. 打开钠光灯，调整显微镜的焦距，使牛顿环图像清晰。

4. 测量第m级暗环的半径rk，重复多次测量，求平均值。

5. 根据测量结果，利用上述公式计算透镜的曲率半径R。

四、实验结果与分析通过实验测量，可以得到一系列牛顿环的半径rk。

根据实验原理，可以计算出透镜的曲率半径R。

通过对比实际值与测量值，可以分析实验误差，并探讨提高实验精度的方法。

五、实验结论牛顿环实验是一种经典的干涉实验，通过观察和分析牛顿环现象，可以深入了解光的干涉原理，并应用于测量透镜的曲率半径等实际应用中。

实验报告--牛顿环实验报告：牛顿环一、实验目的1.学习和掌握牛顿环的原理和实验方法。

2.观察和分析牛顿环的干涉现象。

3.通过实验数据分析，得出环的直径与条纹间距之间的关系。

4.学习使用逐差法处理实验数据。

二、实验原理牛顿环是一种利用光的干涉现象来测量表面曲率或者验证光学元件表面的形状和光学原理的实验方法。

其基本原理是当光从两种不同介质（如空气和玻璃）的界面反射时，会产生相干光束，它们之间会发生干涉现象，从而形成明暗交替的环状条纹。

根据干涉理论，若光程差等于波长的整数倍，则出现亮条纹；若光程差等于半波长的奇数倍，则出现暗条纹。

因此，通过测量亮条纹或暗条纹的位置，可以计算出光的波长以及被测表面的曲率。

三、实验步骤1.搭建实验装置：将牛顿环装置放置在显微镜上，使牛顿环能被显微镜清晰观察到。

2.调节显微镜：通过显微镜观察牛顿环，调整显微镜的倍数和位置，使条纹清晰可见。

3.测量直径：使用测量显微镜中的标尺，测量牛顿环的直径（如D）。

4.测量条纹间距：在显微镜下，测量相邻亮条纹（或暗条纹）之间的距离（如d）。

5.改变光源波长：更换不同颜色的光源（如红光、绿光、紫光等），重复步骤1至4，记录数据。

6.数据处理与分析：利用所得数据，分析环的直径与条纹间距之间的关系。

四、实验数据分析根据实验数据，我们可以得出以下结论：1.随着光源波长的增加，牛顿环的直径（D）也相应增加。

这符合光的干涉理论，因为波长越长的光，其干涉条纹的间距也越大。

2.相邻亮条纹间距（d）与光源波长（λ）之间存在近似线性关系。

通过线性拟合，我们可以得出d与λ之间的关系式为d = kλ，其中k为常数。

这个关系式可以用作计算被测表面曲率的基础。

通过本实验，我们学习到了牛顿环的原理和实验方法，并观察到了光的干涉现象。

通过测量和分析牛顿环的直径和条纹间距，我们得出了它们与光源波长之间的关系。

这些知识对于我们理解和掌握光学原理，以及进行相关应用研究具有重要意义。

牛 顿 环（实验讲义P205 实验二十四）【实验目的】（1）观察干涉现象，并用以测定平凸透镜的曲率半径 （2）掌握利用牛顿环光波波长的方法（3）熟悉读数显微镜的结构，掌握其使用方法 【实验仪器】读数显微镜，牛顿环，钠光灯 【实验原理】如图1所示，将一块曲率半径较大的平凸透镜的凸面放在一平面玻璃板上，就组成了一个牛顿环装置，在透镜的凸表面与平面玻璃板的上表面之间，形成了一个空气薄层，在以接触点O 为中心的任一圆周上，空气层的厚度都相等．这样，如果有以波长为λ的单色光垂直入射时，则空气薄层的上边缘面所反射的光和下边缘面所反射的光之间就有了光程差，因此发生干涉现象．光程差相等的地方就是以O 点为中心的同心圆，因此干涉条纹也就是一组以O 点为中心的同心圆，称为牛顿环．设平凸透镜的曲率半径为R ，距接触点O 半径为r 的圆周上一点D 处的空气层厚度为δ ，对应于D 点产生的干涉所形成的暗条纹的条件为2)12(22λλδ+=+k ， K ＝0、1、2 (1)由图1的几何关系可看出2222222)(δδδ+-+=-+=R R r R r R （2）由于δ>>R ，上式中δ 2略去，故Rr 22=δ （3）将δ值代入式（1），化简R k r λ=2 （4） 图1由式（4）可知，如果已知单色光的波长λ，又能测出各暗条纹的半径r ，就可算出曲率半径R ．反之，如果知道R ，测出r ，亦可算出单色光的波长λ．在实际测量时，由于牛顿环的级数K 和中心不易确定，可将式（4）变为如下形式λm D D R mm k 422-=+ （5）式中，D k +m 和D m 分别为k+m 级和k 级暗环的直径（如图2），从式（5）可知，只要求出所测各环的环数差m ,而无须确定各环的级数，不必确定圆环的中心，避免了实验中圆心不易确定的困难． 图2 【实验内容】1 调整实验装置⑴ 调节牛顿环仪上的三个螺钉，用眼睛直接观察，使干涉条纹成圆形并处在牛顿环仪的中心．注意平凸透镜和玻璃板不能挤压过紧，以免损坏牛顿环仪．⑵ 将牛顿环仪置于显微镜筒下方(如图3),开启钠光灯源，调节显微镜座架的高度，使套在显微镜镜头上45°的反射镜M 与钠光灯等高．⑶ 调节目镜，使十字叉丝清晰，调节反射镜M ，使显微镜下视场黄光均匀．⑷ 调节调焦旋钮对牛顿环聚焦，使干涉条纹清晰．调节时，显微镜筒应自下而上缓慢移动，直到在目镜中看清干涉条纹止(不要自上而下调，以免损坏仪器)，并适当移动牛顿环仪，使牛顿环圆心处在视场中央．2 观察干涉条纹的分布特征观察牛顿环条纹的粗细和形状，间距是否相等，并从理论上做出解释，观察牛顿环中心是亮斑还是暗斑．1、目镜；2、镜筒；3、调焦手轮；3 测量平凸透镜的曲率半径 4、柱； 5、横杆；6、测微刻度轮； ⑴ 调节目镜镜筒，使一根十字 7、物镜；叉丝与显微镜移动方向垂直，保持这条叉 图3 丝与干涉条纹相切，另一根水平叉丝则和显微镜移动方向一致，以便观察和测量条纹的直径．⑵ 旋转显微镜的鼓轮，使十字叉丝由牛顿环中央缓慢向左移动到32环，然后单方向向右移动，测出显微镜的叉丝与各条纹相切的读数d 30 ，d 29 ，……，d 12，d 11，的读数．然后继续向右移动，经过环的中心，到另一边继续向右测出d 11′，d 12′，……，d 29′，d 30′，则第n级条纹的直径'n n n d d D -= (d n ′指环中心另一边的读数)，测量时应注意回程差．⑶ 用逐差法，将D k 值分为两组，一组为k+m ，另一组为k ，将数据填入表1中 【数据记录与处理】=-+22k D D m k (mm 2) =-∆+)(22k D D m k (mm 2)=-=+λm D D R km k 422(mm)=-∆=∆+λm D D R k m k 4)(22 (mm)实验结果：±=∆±=R R R (mm)【注意事项】⑴ 使用读数显微镜进行测量时，手轮必须向一个方向旋转，中途不可倒退． ⑵ 读数显微镜镜筒必须自下而上移动，切莫让镜筒与牛顿环装置碰撞．⑶ 光学仪器光学面在实验时不要用手去摸或与其他东西相接触，因为这样极易磨损 精致的光学表面，这点在实验中千万小心，若有不洁需用专门的擦镜纸擦试．【思考题】(1) 什么是光的干涉？产生光的干涉现象的条件是什么？(2) 观察牛顿环为什么选用钠光灯作光源？若用白光照射将如何？(3) 本实验处理数据时，为什么要用逐差法？用算术平均法行吗？为什么？(4) 使用读数显微镜进行测量时，手轮为什么必须向一个方向旋转，中途不可倒退？ (5) 使用读数显微镜进行测量时，为什么读数显微镜镜筒必须自下而上移动？。

牛顿环-劈尖若将同一点光源发出的光分成两束，让它们各经不同路径后再相会在一起，当光程差小于光源的相干长度，一般就会产生干涉现象。

如测量光波的波长，精确地测量长度、厚度和角度，检验试件表面的光洁度，研究机械零件内应力的分布以及在半导体技术中测量硅片上氧化层的厚度等。

牛顿环、劈尖是其中十分典型的例子，它们属于用分振幅的方法产生的干涉现象，也是典型的等厚干涉条纹。

【实验目的】1.观察和研究等厚干涉现象和特点。

2.学习用等厚干涉法测量平凸透镜曲率半径和薄膜厚度。

3.熟练使用读数显微镜；学习用逐差法处理实验数据的方法。

【实验仪器】测量显微镜，钠光光源，牛顿环仪，牛顿环和劈尖装置。

图1 实验仪器实物图【实验原理】1.牛顿环“牛顿环”是一种用分振幅方法实现的等厚干涉现象，最早为牛顿所发现。

为了研究薄膜的颜色，牛顿曾经仔细研究过凸透镜和平面玻璃组成的实验装置。

他的最有价值的成果是发现通过测量同心圆的半径就可算出凸透镜和平面玻璃板之间对应位置空气层的厚度；对应于亮环的空气层厚度与1、3、5…成比例，对应于暗环的空气层厚度与0、2、4…成比例。

牛顿环装置是由一块曲率半径较大的平凸玻璃透镜，将其凸面放在一块光学玻璃平板（平晶）上构成的，如图2所示。

平凸透镜的凸面与玻璃平板之间形成一层空气薄膜，其厚度从中心接触点到边缘逐渐增加。

若以平行单色光垂直照射到牛顿环上，则经空气层上、下表面反射的二光束存在光程差，它们在平凸透镜的凸面相遇后，将发生干涉。

其干涉图样是以玻璃接触点为中心的一系列明暗相间的同心圆环（如图3所示），称为牛顿环。

由于同一干涉环上各处的空气层厚度是相同的，因此称为等厚干涉。

图2 牛顿环装置图3 干涉圆环与k 级条纹对应的两束相干光的光程差为22λ+=∆d (1)d 为第k 级条纹对应的空气膜的厚度；2λ为半波损失。

由干涉条件可知，当∆=(２ｋ＋１) 2λ（ｋ＝0，1，2，3，...） 时，干涉条纹为暗条纹，即2)12(22λλ+=+k d得λ2kd =（2） 设透镜的曲率半径为Ｒ，与接触点Ｏ相距为ｒ处空气层的厚度为ｄ，由图2所示几何关系可得222)(r d R R +-=2222r d Rd R ++-=由于Ｒ>>ｄ，则 d 2可以略去Rr d 22= （3）由(2)和(3)式可得第ｋ级暗环的半径为：•• λλkR kR Rd r k =⋅==2222(4) 由(4)式可知，如果单色光源的波长λ已知，只需测出第k 级暗环的半径ｒm ，即可算出平凸透镜的曲率半径Ｒ；反之，如果Ｒ已知，测出ｒm 后，就可计算出入射单色光波的波长λ。