基本体及其截断53页PPT

（a）
（b）
图 3-17 平面体的截交线
如图 3-17b 立体图为正六棱柱被一平面截切，得到截交线
ABCDEF 为六边形，因截平面与正投影面(V 面)垂直，截交线 A BCDEF 在正面上的投影积聚为一条斜线 a’d’，且点 B 与 F 、C 与 E 的正面投影重合，见主视图；截交线的水平投影为一 正六边形(abcdef)且与正六棱柱下底面的水平投影重合，见俯
长方体。首先切和出三视图相对应的线 两块切则去再，修制改成模型，直至
长方体。 条，初步确定其将要 模型。所切的模型完全与三
切去的是 A、B 两块。
视图一一对应。
图 3-29 看图制作模型
感谢下 载
作圆锥截交线的方法：当圆锥截交线为圆和直线时，其投影可 截交线为椭圆、抛物线或双曲线时，需采用辅助素线法和辅助平面
按表 3-2 图例，分别画前两种情况下，截交线在三个视图中的投影。
实际机件常由几个回转体组成为组合体，这样，截交线就由几 3-27 所示为螺钉头、铣床顶尖的截交线。
a) 螺钉头的截交线
（a）平面立体
（b）曲面立体
图 3-15 基本体的截交线
立体被平面截切，被截切后的部分称为截切体，用来截切立体 平面，平面与立体表面的交线称为截交线。
（a）方形斜槽
（b）顶尖
图 3-16 截切体与相贯体的实例
一、平面体的截交线
1 平面体的截交线
平面立体的截交线是一个封闭的平面多边形(图 a) ，它的边是 立体表面的交线，它的顶点是截平面与平面立体棱线的交点。
（a）
（b）
（c）
图 3-25 圆球的截交线
示例 3-6 求作开槽半球体的截交线，图 3-26a 所示。

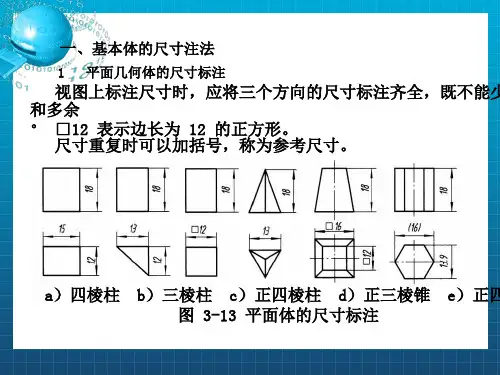
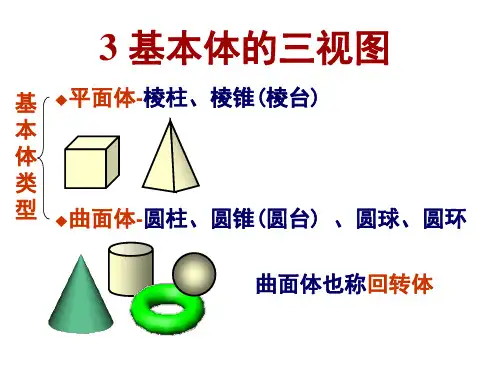
（1）多面体: 若干个平面多边形围成的几何体 面----围成多面体的各个多边形
棱
棱----相邻两个面的公共边
顶点-----棱与棱的公共点
（2）旋转体: 由一条平面曲线（包括直线）绕它 轴
所在的平面内的一条定直线旋转所形成的曲面叫做
旋转面,封闭的旋转面围成的几何体叫做旋转体,
这条定直线叫做旋转体的轴。
答：不一定是
问题3：长方体按如图截去一角后所得的两部分还是棱柱吗？
D'
C'
A' B'
D C
A
B
它们都符合棱柱的定义，是棱柱
探究三、 棱锥及其结构 思考5：观察下列多面体,有什么相同点？
(1)
(3)
(5)
(8)
（1）主要结构特征：
①有一个面是多边形；
②其余各面都是有一个公共顶点的三角形；
（3）棱锥的分类 ①按棱锥底面边数分类: 三棱锥，四棱锥，五棱锥......；
顶点 S
底面：多边形面； 侧面：有公共顶点 的各三角形面；
侧棱：相邻侧面的公共边； 顶点：各侧面 的公共顶点.
D 侧棱
A
表示：棱椎用表示顶点和底面各顶点的字母表示.
侧面
C 底面
B
棱锥的表示：棱锥S—ABCD
【练习2】判断正误 (1).棱锥的侧面均为三角形( √ ) (2).有一个面是多边形，其余各面都是三角形的几何体叫棱锥(× ) 【练习3】下面几何体是棱锥吗？
四棱柱：底面是四边形的棱柱. 直四棱柱：侧棱与底面垂直的四棱柱. 长方体：底面是矩形的直四棱柱. 正四棱柱：底面是正方形的长方体.
正方体：所有棱长都相等的正四棱柱.
全集U={四棱柱}

点叫做棱柱的顶点． (2)棱柱的分类及表示：根据底面多边形的 边数 分为三棱柱(底面是三角形)、四棱柱
(底面是四边形)……，例如底面是五边形的棱柱可表示为五棱柱 ABCDE-A′B′C′D′E′.
必修第一册·人教数学B版
(3)特殊的棱柱： 直棱柱：侧棱 垂直 于底面的棱柱； 斜棱柱：侧棱 不垂直 于底面的棱柱； 正棱柱：底面是 正多边形 的 直 棱柱； 平行六面体：底面是 平行四边形 的四棱柱．
必修第一册·人教数学B版
返回导航 上页 下页
8．1 基本立体图形 第一课时 棱柱、棱锥、棱台的结构特征
必修第一册·人教数学B版
返回导航 上页 下页
内容标准
学科素养
1.了解空间几何体的分类及其相关概念． 2.理解棱柱、棱锥、棱台的定义，知道这三种几何体的结构特 征，能够识别和区分这些几何体.
数学抽象 直观想象
必修第一册·人教数学B版
课前 • 自主探究
返回导航 上页 下页
课堂 • 互动探究
课后 • 素养培优
课时 • 跟踪训练
必修第一册·人教数学B版
返回导航 上页 下页
[教材提炼] 知识点一 空间几何体 预习教材，思考问题 (1)观察纸箱、金字塔、茶叶盒、水晶石等有什么相同的特点？ [提示] 围成它们的每个面都是平面图形，并且都是平面多边形． (2)观察纸杯、奶粉罐、腰鼓、篮球等几何体有什么相同的特点？ [提示] 围成它们的面不全是平面图形，有些面是曲面．
(底面是四边形)……，其中三棱锥又叫四面体．
棱锥用表示顶点和底面各顶点的字母来表示，例如三棱锥可表示为：三棱锥 S-ABC.
(3)特殊的棱锥 正棱锥：底面是 正多边形 ，并且顶点与底面中心的连线 垂直 于底面的棱锥．

作图： 1)求特殊点。从图3-10(a)可看出，点A和点C分别是截交线的最低、最高 点，点B和点D分别是截交线的最前、最后点，它们也是椭圆长短轴的端 点。它们的V面、H面投影可利用积聚性直接求得，然后根据V面投影a′、 c′和b′、d′以及H面投影a、c和b、d求得W面投影a"、c"和b"、d"。由 于b"d"和a"c"互相垂直，且b"d">a"c"，所以截交线的W面投影中以b"d" 为长轴，a"c"为短轴。 2)求一般位置点。为使作图准确，还须作出若干一般点。如图3-10(b)所 示，先在H面投影上取对称于水平中心线的点e、f，在V面投影上即可得 到e′、f′，再求出e"、f"。用同样方法还可作出其他若干点。 3)依次光滑连接a"、e"、b" ……，即得截交线的W面投影。 此题也可根据椭圆长、短轴用四心圆法近似画出椭圆。
例3-3：试画出图3-9所示四棱柱被P、Q两平面切去一角后的三面投影图。 作图: 1）画出四棱柱的三面投影图； 2）根据Ｐ、Ｑ两截平面的位置，画出它们的V面投影。标出截交线上各点的V投影 1′、2′、3′、4′、5′、6′、7′； 3）由于四棱柱的各棱面均为侧垂面，可由截交线上各点的V面投影，直接求出它们的W投影1"、2"、3"、4"、5"、6"、7"； 4）由截交线上各点的V、W面投影，可求出H面投影1、2、3、4、5、6、7； 5）依次连接各点的同面投影，得到截交线的投影。截交线的H、W面投影均可见，画成粗实线。描粗加深全图。 注意：在H面投影上，棱线的一段虚线不要漏画。

请点击鼠标左键显示后面内容
例7. 画圆锥体及其表面上各点的三视图。 画圆锥体及其表面上各点的三视图。
k
A
B
S
k’
k ’’
a’
(c’) )
(a”) )
c”
1’
பைடு நூலகம்
b’
b”
(C)
作图步骤： 画各视图的轴线; （1）画各视图的轴线; （2）画俯视图的底圆轮廓; 画俯视图的底圆轮廓; 画主视图的轮廓素线; （3）画主视图的轮廓素线; （4）根据投影规律求第三投影; 根据投影规律求第三投影; 点的三投影; (5) 用素线法求 A 点的三投影; （6）根据B点的特殊位置求其三投影; 根据B点的特殊位置求其三投影; (7) 用辅助平面法求C点的三投影。 用辅助平面法求C点的三投影。
1、圆柱体
圆柱体表面由圆柱面和上、下两个平面组成。圆柱面由直 线AB绕与它平行的轴线等距旋转而成。
Z
O
素线
A V a' d' c' B
b' B A
母线
O
C
X 最左轮 廓素线
Y 最前轮 廓素线
（1）圆柱的投影图
a' b'
c'
d'
分析圆柱轮廓素线的投影
V面投影 轮廓素线
圆柱轮廓 素线(转向 轮廓线）
e
f
请点击鼠标左键显示后面内容
例4. 画正三棱锥及表面上各点的三视图。 画正三棱锥及表面上各点的三视图。
K
k’ k
k” k
D
P
A
作图步骤：
E
S
P
C
e’
b’ b
d’
(d”) )

上一页 下一页 退 出
案例3 绘制斜割圆柱体上的截交线 案例绘制
1．绘制截割前圆柱的左视 图，找出椭圆的四个特殊位置点的 正面投影和水平投影，求出其侧面 投影
2．在俯视图适当位置找四 个一般点的水平投影，按投影 规律找出其正面投影，求出其 侧面投影
3．光滑连接各点的 侧面投影
4．擦去被切部分的轮廓线， 按线型描深图线
上一页 下一页 退 出
案例2 绘制四棱锥截交线 案例绘制
1．绘制截平面与四 棱锥棱线交点的水平投 影和侧面投影
2．绘制正垂面截 切后的水平投影和侧 面投影
3．擦去切割部分的轮廓 线及辅助线，按线型描深 图线，完成水平投影和侧 面投影
上一页 下一页 退 出
案例3 绘制斜割圆柱体上的截交线
案例绘制
绘制如图所示平面斜切圆柱体的截交线，已知该切
课题4 绘制圆锥的三视图
案例出示
如图所示，绘制其三视图，并分析投影特性。
案例分析
如图所示，圆锥体由一个圆锥面和圆形的底面围成。圆锥面可 看成是一条与轴线相交的直线（母线）绕轴线旋转一周形成的。该圆 锥的底面为水平面，圆锥面的轴线垂直于水平投影面。
想一想，绘制圆锥的三视图时，应该先绘制哪个视图？圆锥面的 水平投影有何特性？
案例5 绘制球的三视图 知识拓展
如图a)，求出圆球表面上A点的另两投影，A点的位置分析如图所示。 1.判断A点在球体表面上的位置 A点在上半球、在后半球、在左半球 2.在圆球表面上求作点的方法：（如图e） 由于球面的投影没有积聚性，因此要借助于球体表面上的辅助圆来求点。 辅助圆法—过点在球面上作一辅助圆，作出该圆的各投影后再将点对应 到圆的投影上。 作图步骤如下，如图d),即为所求点的三面投影。
案例绘制

5.2 曲面立体
本节讨论基本曲面立体，如圆柱、圆锥、球和圆环等的 形成方法、投影图及其表面取点、线的作图等问题。由于 它们是以一直线或曲线为母线绕一定直线为轴旋转而成的 立体，故又称为回转体。上述基本曲面立体为常见的回转 体。
一、常见的回转体 二、复合回转体
一、常见的回转体
曲面的几个基本概念：
曲面的种类－规则曲面与非规则曲面
1)投影分析
由于环面的旋转轴线垂直于H面，其H面投影是两个同心圆，即赤道圆 和喉圆的H面投影。其V、W面的投影形状相同，都是由两个圆和与它们上 下相切的两段水平轮廓线组成。V面投影中的两个圆分别是环面上平行于V 面的最左、最右两个母线圆A和B的反映实形的投影。它们中均有半个圆被 部分环面遮住而画成虚线。环面的三面投影均是各投影面的转向线，即该面 投影可见与不可见的分界线。
显然m''可见，而n''
()
1( )
为不可见。
1( )
2.棱锥体
棱锥体由底面和棱面所围成，其各棱线汇交于锥顶。
正三棱锥的三视图及 其表面上取点
1)投影分析
正三棱锥底面为水平面， 其水平投影反映实形，正 面、侧面投影积聚为横线 段；棱面SAB和SAC为一 般位置平面，其三个投影 均为类似形。
2)视图画法
d'' m''
c'd'
M Ba'('b'') c''
Ad
C b
a mc
Y
已知圆锥表面的点M的正面投影m',求出M点的其它投影。
s'
s''
m'
a' 1' c'(d') d

（3）在平面体投影图中的点，一种是棱线交点的投影； 另一种是棱线的积聚投影。投影图中的线，一种是面与面 的交线即棱线的投影；另一种是面的积聚投影。凡投影图 中用实线表示的线是形体上可见线的投影或可见面的积聚 投影；用虚线表示的线是不可见线的投影或不可见面的积 聚投影，但用实线表示的线也可能是形体上可见线与不可 见线投影的重合。投影图中每个封闭的线框在一般情况下 表示一个面的投影，但也可能是几个面投影的重合或孔洞 的投影，要对照其他几个投影图分析后才能确定。
北京四合院：分前后两院，居中的正房体制最为尊崇，是举行家庭礼仪、接见尊贵宾客 的地方，各幢房屋朝向院内，以游廊相连接。 规整式住宅是中国汉族地区传统民居的主流，以采取中轴对称式布局的北京四合院为典 型代表。四合院，是华北、东北地区民用住宅中的一种组合式建筑，是一种四四方方或 者是长方形的院落。北京四合院虽是中国封建社会宗法观念和家庭制度在居住建筑上的 具体表现，但庭院方阔，尺度合宜，宁静亲切，花木井然，是十分理想的室外生活空间。 四合院的走向一般是坐北向南，四合院中，有正房，即北房，这是院中的主房，东西两 侧，为东西厢房。东西厢房比较对称，建筑格式也大体相同或相似。南面建有南房，与 北房相对应。整个四合院，大都按照中国传统的习惯，采用对称的办法建筑成。
蒙古包分为固定式与游动式两种样式。半农半牧区大多 建造固定式的蒙古包，周围墙壁用土砌成，上面用苇草 搭盖；游牧区以游动式的蒙古包较多，一种可拆卸的蒙 古包以牲畜驮运来迁移，另一种不可拆卸的蒙古包靠牛 车或马车拉运来迁移。
生活在西双版纳的傣族人民都是以干栏式竹楼为传统住宅。傣 族的竹楼分为上下二层，上层住人，下层离地面约2米左右， 主要堆放杂物或饲养牲畜。 一防潮湿；二散热通风；三可避虫兽侵袭，四可避洪水冲击， 因为这里每年雨量集中，常发洪水，楼下架空，墙又为多空隙 的竹篾，所以很利于洪水的通过；五是建盖竹楼的材料来源方 便，就地取材，比较经济。 傣族竹楼量随着社会的进步发展而有新变化。最主要变化 是在建筑材料方面，由干栏式竹楼逐步向木楼、砖木结构以及 钢混结构发展变化。但由于傣族喜爱自己民族传统的建筑形式， 除少部份傣族民居向现代化建筑改变外，而大多数傣族民居仍 然保持着干栏式的建筑结构和造型。

17
第二节 截交线的画法
• 二、平面截切平面基本体
一类参考
18
第二节 截交线的画法
• 二、平面截切平面基本体
截交线是一个由直线组成的封闭的平面多边形。
截交线的每条边是截平面与棱面的交线。
⒈ 求截交线的两种方法：
★ 求各棱线与截平面的交点→棱线法。
★ 求各棱面与截平面的交线→棱面法。
⒉ 求截交线的步骤：
找出截交线的已知投影一类，参考预见未知投影。
30
第二节 截交线的画法
• 三、平面截切回转体
画出截交线的投影
当截交线的投影为非圆曲线时，其作图步骤为： ☆ 先找特殊点，再补充中间点。 ☆ 将各点光滑地连接起来，并判断截交线的可
见性。
一类参考
31
第二节 截交线的画法
• 三、平面截切回转体 圆柱的截交线
★找中间点
★光滑连接各点
★分析转向轮廓线的投影
一类参考
34
椭圆的长、 短轴随截平面与 圆柱轴线夹角的 变化而改变。
45°
什么情况下
截投平影面为与圆圆呢柱？轴 线成45°时。
一类参考
35
例例：：求求左左视视图图
一类参考
36
第二节 截交线的画法
• 三、平面截切回转体
例：圆柱被一个截平面斜切，已知其两个视图，求作第三视图。
a (b)
点的可见性规定点：
b
若点所在的平面的投影可见， 点的投影也可见；若平面的投影 a
积聚成直线，点的投影也可一类见参考 。
a

b
4
第一节 基本体的三视图
• 一、平面基本体的三视图
【例3－1】根据已知条件，补画第三视图，并求作形体 表面A、B、C三点的三面投影。