初一数学上册计算题天天练(强烈推荐)37

初一数学上册计算题（400道题）时间：2021.03.01 创作：欧阳语（1）= （2）= （3） = （4） = （5）= （6）=（7）= （8） = （9）= （10）=（11）（12）（13）（14）（15）（16）（17）（18）（19）（20）；（21）；（22）；（23）；（24）；（25）；（26）.（27）（28）（29）（30）（31）（32）（33）（34）（35）（36）（37）（38）如果，求的值（39）已知与互为相反数，求的值。

（40）（41）（42）（43）（44）（45）（46）（47）（48）（49）（50）100（51）（52）（53）（54）（55）（56）（57）（58）（59）若，，求a + b的值．（60）已知│a+1│与│b－2│互为相反数，求a－b的值．（61）(-12)÷4×(-6)÷2; ;（62）（62）（63）;（64）;（64）;（67）;（68）(－5)×(－7)－5×（－6）（69）.（72）（73）;（75）;（76）（－5）×（－8）×0×（－10）×（－15）；（77）（－3）×（－4）×（－5）+（－5）×（－7）（78）（－0.1）×（－1）×（－100）－0.•01×（1000）．（79）2×（－1）×（－）×（－）；（80）－ + －－）×（－20）；（81）（－3）×（－0.12）×（－2）×33；（82）（－ + －）×（－36）．（83）－×（12－2－0.6）（84）（+）×|－|×2×（－5）；（85）（－1）×3（－）×（－1）（86）（87）（－2）×（－）= （88）0×（－13.52）= （89）（－1）×a =（90）（－3.25）×（+）=（91）（－185.8）×（－36）×0×（－25）=（92）（93）（94）（－）×0.125×（－2）×（－8）；97）（98）（－0.25）×0.5×（－4）×4；（99）（－4）×（－18.36）×2.5；（100）（－）×（－18）+（－）×（－3）×2；（101）（－47.65）×2+（－37.15）×（－2）+10.5×（－7）．（102）[（－2）×（－4）+（－5）]×[－3－（－2）×（－3）]．（103）（104）（105）（106）（107）（－23）+7+（－152）+65 （108）|+（－）|（109）（－）+|―|（112）38+（－22）+（+62）+（－78）（113）（－8）+（－10）+2+（－1）（114）（－）+0+（+）+（－）+（－）（115）（－8）+47+18+（－27）（116）（－5）+21+（－95）+29 （117）（－8.25）+8.25+（－0.25）+（－5.75）+（－7.5）（118） 6+（－7）+（9）+2 （119）72+65+（-105）+（－28）（120）（－23）+|－63|+|－37|+（－77）（121）19+（－195）+47 （122）（+18）+（－32）+（－16）+（+26）（122）(－3)－5（123）（－0.8）+（－1.2）+（－0.6）+（－2.4）（124）（－8）+（－3）+2+（－）+12（125）5+（－5）+4+（－）（126）（-6.37）+（－3）+6.37+2.75（127）(－12.5)－(－7.5) （128）(－26)―(－12)―12―18（129）―1―(－)―(+) （130）(－20)－(+5)－(－5)－(－12)（131）(－23)―(－59)―(－3.5) （132）|－32|―(－12)―72―(－5)（133）(－)―（－）―（134）（+）―（－）―（－）―（135）（－）―3―（－3.2）―7 （136）（+）―（－）―（137）（+6.1）―（－4.3）―（－2.1）―5.1 （138）（－）―(－1)―(－1)―(+1.75)（139）(－3)―(－2)―(－1)―(－1.75) （140）－8－5＋4－3（141）－4++(－)―（142）0.5+（－）－（－2.75）+（143）（+4.3）－（－4）+（－2.3）－（+4）（144）（－0.5）－（－3）＋6.75－5（145）（－9）×（146）（－）×（－0.26）（147）（－2）×31×（－0.5）（148）×（－5）＋×（－13）（149）（－4）×（－10）×0.5×（－3）（150）（－）××（－1.8）（151）（－0.25）×（－）×4×（－7）（152）（－）×（－）×（－）（153）（－8）×4×（－）×（－0.75）（154）4×（－96）×（－0.25）×（155）（－1+）×56（156）（――）×36 （157）（－36）×（＋－）（158）（－）×（8－－0.4）（159）（－66）×〔1－（－）＋（－）〕（160）25×－（－25）×＋25×（161）（+－＋）×72（162）×(2－)×(－)×(－) （163）18÷（－3）（164）（－24）÷6（165）（－57）÷（－3）（166）（－）÷（167）（－42）÷（－6）（168）（+）÷（－）（169）（－）÷9 （170）0.25÷（－）（171）－36÷（－1）÷（－）（172）（－1）÷（－4）÷（173）3÷（－）×(－) （174）0÷［(－3)×(－7)］（175）－3÷（－）（176）（－24）÷（－6）（177） 2÷（5－18）×（178）1÷（－3）×（－）（179）－×（－）÷（－）（180）（－）÷（－）（181）（－+）÷（－）（182）－3.5 ×（－0.5）×÷（183）－1÷（－1）×1×（－7）（184）×（－－）÷（185）÷（－2）－×－÷4（186）0.8×+4.8×（－）－2.2÷+0.8×（187）2÷（－）×÷（－5）（188）（－）×（－15×4）（189）（－2.4）（190）［15－（1÷1＋3］÷（－1）（191）×（－5）÷（－）×5（192）－（－+－）÷（－）（193）－13×－0.34×+×（－13）－×0.34（194） 8－（－25）÷（－5）（195）（－13）×（－134）××（－）（196）（－4）－（－5）+（－4）－3（197）（－16－50+3）÷（－2）（198）（－0.5）－（－3）+6.75－5（199）178－87.21+43+53－12.79（200）（－6）×(－4)+(－32)÷(－8)－3 （201）－－(－)+|－1|（202）（－9）×(－4)+ (－60)÷12 （203）[(－)－1+]÷(－)（204）－|－3|÷10－（－15）×（205）－1×（－）÷2（206）（2－3+1）÷（－1）×（－7）（207）－×（8－2－0.04）（208）－2×（ 209）－－（210）－（211）－2×（212）÷（213）×（214）＋（215）××（216）×－（217）＋＋（218）－×－（219）+（220）0－÷3×（221）×÷（222）－×－÷（223）×(－＋1) ×0 （224）6+×（225）－10+8÷－4×3 （226）－－（227）－（1－0.5）×（228）××（229）4×+6 （230）×××（231）－+2×+（－6）÷（232）÷（-8）－×（-）（233）×（）×（234）－2［－3×］÷（235）÷9÷（236）36×（237）－｛｝（238）－+（1－0.5）××［2×］（239）－4×+（240）－－+×÷（241）（-5.3）-（+4.8）+（-3.2）-（-2.5）；（242）（243）-10+8÷（-2）2-3×（-4）-15；（244）-14-（1-0.5）××[2-（-3）2]．（245）（246）（247）（248）（249）（250）（251）（252）（253）; （254）(x＋1)－3(x－1)=1－3x; （255）(x－2)－2(4x－1)=3(1－x).（256）（257）；（258）（259）（260）（261）（262）（263）（264）（265）（266）（267）（268）（269）（270）（271）（272）（273）（274）（275）（276）（277）错误！未找到引用源。

初一上册的有理数计算题。

初一上册的有理数计算题包括以下几种类型：
1.加法：同号的两数相加，并把绝对值相加，取相同的符号；异号且绝对值不
相等的两数相加，进行抵消后，取绝对值较大的数的符号；互为相反数的两个数相加，结果为零；任何有理数与零相加，仍得这个数。

2.减法：减去一个数相当于加上这个数的相反数。

3.乘法：两数相乘同号得正，异号得负，然后将两数的绝对值相乘，得出结果；
任何数与0相乘，结果都得0。

4.除法：除以一个不等于0的数，等于乘以这个数的倒数；两数相除，同号得
正，异号得负；0除以任何一个不等于0的数，得数都是0。

下面是一些具体的初一上册的有理数计算题示例：
1. 2 + 3 - 4 × 5 ÷ 6
2.( - 3) + ( - 2) - ( - 5)× ( - 6) ÷ ( - 12)
3.-4 + 2×(-3) -6÷0.25
4.(-5)÷[1.85-(2-1.75)×7]
5.18÷{1-[0.4+ (1-0.4)]×0.4}
6.1÷(-2/3)×7
7.-3-[4-(4-3.5×2)]×[-2+(-3)]
8.8+(-1/4)-5-(-0.25)
9.99×26
10.(3.5-7.75-4.25)÷1.1
请注意，这些题仅供参考，可以结合实际的教材内容进行选择。

初一数学上册计算题（400道题）（1）()22--= （2）3112⎛⎫⎪⎝⎭－=（3）()91- = （4）()42-- =（5）()20031-= （6）()2332-+-=（7）()33131-⨯--= （8）()2233-÷- =（9）)2()3(32-⨯-= （10）22)21(3-÷-=（11）()()3322222+-+-- （12）235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭（13）()34255414-÷-⎪⎭⎫ ⎝⎛-÷ （14）()⎪⎭⎫ ⎝⎛-÷----721322246（15）()()()33220132-⨯+-÷--- （16） []24)3(2611--⨯--（17）])3(2[)]215.01(1[2--⨯⨯-- （18）（19）()()()33220132-⨯+-÷--- （20）22)2(3---；（21）]2)33()4[()10(222⨯+--+-； （22）])2(2[31)5.01()1(24--⨯⨯---；332222()(3)(3)33÷--+-（23）94)211(42415.0322⨯-----+-； （24）20022003)2()2(-+-；（25）)2()3(]2)4[(3)2(223-÷--+-⨯--； （26）200420094)25.0(⨯-.（27）()0252423132.⨯--÷-⎛⎝ ⎫⎭⎪+⎡⎣⎢⎢⎤⎦⎥⎥ （28）()()----⨯-221410222（29）()()()-⨯÷-+-⎛⎝ ⎫⎭⎪⨯-÷-3120313312232325.. （30）()()()-⎛⎝ ⎫⎭⎪⨯-⨯-⨯-212052832.（31） （32）(56)(79)---（33）(3)(9)(8)(5)-⨯---⨯- （34）3515()26÷-+（35）5231591736342--+- （36）()()22431)4(2-+-⨯---（37）411)8()54()4()125.0(25⨯-⨯-⨯-⨯-⨯33182(4)8-÷--（38）如果0)2(12=-++b a ，求20112010()-3ab a b a a ++-（）的值（39）已知|1|a +与|4|b -互为相反数，求b a 的值。

－4.5 ,－2.25 ,8 ,4.5 ,8二、－11的绝对值是( ),－3.8的相反数是( )。

三、－16的绝对值是( ),7.2的相反数是( )，－5.5的倒数是( )。

四、|42.5|=( )，（－1)4=( )。

五、计算。

2 1(－—)－(－—)＋(－6) 3×[(－4)3÷(－1)]7 73 1 1—＋(－—)＋(－—）17－(－26)－9－(－15)4 6 51(－0.8)×—×(－9) (－1)3＋52(－1)101861 1 1(－—)÷(－—－—)×0 8－[(－4)3＋(－3]9 4 9(—－—)＋(－—) 14＋(－26)＋9－(－16)8 2 89 1(—＋—)×(－70) (－4)4＋52(－1)17258 8(－7)＋(－16) 6×(－10) －11.5＋(－8)1 1(－—)×(－—) －12＋[5＋(－15＋8)] (－5)2＋125 4－40＋10＋(－17)－(－21) 8.6－(－5.4)－(－4.5)＋4.22 1 134 9 (—－—)＋(—＋—) 8.3－(－—)－(－4.9)－—5 7 4 7 5 5－4 ,－4.25 ,3 ,－3 ,－2二、3.5的绝对值是( ),6.9的相反数是( )。

三、－22的绝对值是( ),4的相反数是( )，6的倒数是( )。

四、|28|=( )，（－2)4=( )。

五、计算。

2 6(－—)－(－—)＋(－9) 25＋[(－3)3×(－5)]7 76 1 6—－(－—)＋(－—）3＋(－13)＋10－(－10)7 6 51(－0.1)×—×(－200) (－4)3＋23(－1)124491 1 1(－—)÷(－—＋—)×0 10＋[(－1)2－(－4]9 9 8(—＋—)÷(－—) 10－(－25)＋9＋(－17)6 2 71 1(—＋—)×(－10) (－3)2－33(－1)15626 6(－8)÷(－19) 1÷(－7) 2＋(－11)1 1(－—)－(－—) －2＋[－4＋(－17－6)] (－5)2－426 330＋13－(－6)＋(－21) 3.5＋(－9)－(－1.7)＋42 1 1 1 6 7 (—－—)－(—－—) 7.4＋(－—)－(－1.5)－—9 6 7 5 5 5－3 ,－1 ,5 ,3.5 ,－7二、20.5的绝对值是( ),－6.6的相反数是( )。

七年级上册数学计算题专练一、有理数运算类。

1. 计算：(-3)+5 - (-2)- 解析：- 根据有理数加减法法则，减去一个数等于加上这个数的相反数。

- 所以(-3)+5 - (-2)=(-3)+5 + 2。

- 先计算(-3)+5 = 2，再计算2+2 = 4。

2. 计算：-2×(-3)÷(1)/(2)- 解析：- 根据有理数乘除法法则，先算乘法-2×(-3)=6。

- 再算除法6÷(1)/(2)=6×2 = 12。

3. 计算：(-2)^3+(-3)×[(-4)^2 - 2]- 解析：- 先计算指数运算，(-2)^3=-8，(-4)^2 = 16。

- 然后计算括号内的式子(-4)^2-2 = 16 - 2=14。

- 接着计算乘法-3×14=-42。

- 最后计算加法-8+(-42)=-8 - 42=-50。

二、整式加减类。

4. 化简：3a + 2b-5a - b- 解析：- 合并同类项，对于a的同类项3a-5a=(3 - 5)a=-2a。

- 对于b的同类项2b - b=(2 - 1)b = b。

- 所以化简结果为-2a + b。

5. 计算：(2x^2 - 3x + 1)-(3x^2 - 5x - 2)- 解析：- 去括号，得到2x^2-3x + 1-3x^2 + 5x+2。

- 合并同类项，2x^2-3x^2=(2 - 3)x^2=-x^2，-3x+5x=( - 3+5)x = 2x，1 + 2=3。

- 所以结果为-x^2+2x + 3。

三、一元一次方程类。

6. 解方程：2x+3 = 5x - 1- 解析：- 移项，将含x的项移到一边，常数项移到另一边，得到2x-5x=-1 - 3。

- 合并同类项-3x=-4。

- 系数化为1，x=(4)/(3)。

7. 解方程：(x+1)/(2)-(2x - 1)/(3)=1- 解析：- 先去分母，等式两边同时乘以6，得到3(x + 1)-2(2x - 1)=6。

初一数学上册计算题（400道题）（1）()22--= （2）3112⎛⎫⎪⎝⎭－=（3）()91- = （4）()42-- =（5）()20031-= （6）()2332-+-=（7）()33131-⨯--= （8）()2233-÷- =（9）)2()3(32-⨯-= （10）22)21(3-÷-=（11）()()3322222+-+-- （12）235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭（13）()34255414-÷-⎪⎭⎫ ⎝⎛-÷ （14）()⎪⎭⎫ ⎝⎛-÷----721322246（15）()()()33220132-⨯+-÷--- （16） []24)3(2611--⨯--（17）])3(2[)]215.01(1[2--⨯⨯-- （18）（19）()()()33220132-⨯+-÷--- （20）22)2(3---；（21）]2)33()4[()10(222⨯+--+-； （22）])2(2[31)5.01()1(24--⨯⨯---；332222()(3)(3)33÷--+-（23）94)211(42415.0322⨯-----+-； （24）20022003)2()2(-+-；（25）)2()3(]2)4[(3)2(223-÷--+-⨯--； （26）200420094)25.0(⨯-.（27）()0252423132.⨯--÷-⎛⎝ ⎫⎭⎪+⎡⎣⎢⎢⎤⎦⎥⎥ （28）()()----⨯-221410222（29）()()()-⨯÷-+-⎛⎝ ⎫⎭⎪⨯-÷-3120313312232325.. （30）()()()-⎛⎝ ⎫⎭⎪⨯-⨯-⨯-212052832.（31） （32）(56)(79)---（33）(3)(9)(8)(5)-⨯---⨯- （34）3515()26÷-+（35）5231591736342--+- （36）()()22431)4(2-+-⨯---（37）411)8()54()4()125.0(25⨯-⨯-⨯-⨯-⨯33182(4)8-÷--（38）如果0)2(12=-++b a ，求20112010()-3ab a b a a ++-（）的值（39）已知|1|a +与|4|b -互为相反数，求b a 的值。

七年级数学上册综合算式专项练习题多项式的加减法运算数学是一门需要思考和解决问题的学科，而多项式的加减法运算是数学中一个基础且重要的概念。

加减法运算是我们在日常生活中最常见的运算之一，掌握多项式的加减法运算方法对我们的数学学习和解决实际问题都非常有帮助。

本文将为大家介绍七年级数学上册综合算式专项练习题——多项式的加减法运算。

一、多项式的加法运算多项式的加法运算是指对两个或多个多项式进行相加的操作。

在进行多项式的加法运算时，需要考虑同类项的合并，即将同类项的系数相加，而同类项的组成要素包括变量和指数。

例如，我们有两个多项式：3x² + 2x + 5 和 2x² + 4x + 1，要求将它们相加。

首先，我们可以按照同类项进行合并，即将同类项的系数相加。

合并后的多项式为 (3x² + 2x + 5) + (2x² + 4x + 1) = 5x² + 6x + 6。

在实际的加法运算中，可能会涉及到更多的多项式。

同样的原则，我们需要将所有的同类项进行合并，合并后得到的多项式即为最终的结果。

二、多项式的减法运算多项式的减法运算是指对两个多项式进行相减的操作。

在进行多项式的减法运算时，需要考虑同类项的合并，即将同类项的系数相减，而同类项的组成要素包括变量和指数。

例如，我们有两个多项式：5x² + 3x + 7 和 2x² + x + 3，要求将它们相减。

同样地，首先，我们可以按照同类项进行合并，即将同类项的系数相减。

合并后的多项式为 (5x² + 3x + 7) - (2x² + x + 3) = 3x² + 2x + 4。

同样地，在实际的减法运算中，可能会涉及到更多的多项式。

我们需要将所有的同类项进行合并，合并后得到的多项式即为最终的结果。

三、综合算式专项练习题为了巩固多项式的加减法运算，我们来做一些综合算式专项练习题。

七年级数学上册综合算式专项练习题平均数的计算练习本文旨在为七年级数学上册的综合算式专项练习题提供平均数的计算练习。

以下是一系列练习题，可以帮助学生巩固平均数的概念，并提供一些实际应用的练习。

练习题一：一家餐馆连续7天的日销售额（单位：元）分别为1200，1500，800，1300，1000，1100，900。

求这7天的平均日销售额。

解答：将这7天的日销售额相加：1200 + 1500 + 800 + 1300 + 1000 + 1100 + 900 = 6900。

然后将总销售额除以天数：6900 ÷ 7 = 985.71（保留两位小数）。

所以这7天的平均日销售额为985.71元。

练习题二：某班级的学生身高（单位：厘米）如下：150，155，158，160，165，168，170，175，178，180。

求这些学生的平均身高。

解答：将这些学生的身高相加：150 + 155 + 158 + 160 + 165 + 168 + 170 + 175 + 178 + 180 = 1599。

然后将总身高除以学生人数：1599 ÷10 = 159.9（保留一位小数）。

所以这些学生的平均身高为159.9厘米。

练习题三：某商品在1月~10月的每月销量（单位：件）如下：100，150，80，120，90，110，130，70，95，105。

求这10个月的平均月销量。

解答：将这10个月的销量相加：100 + 150 + 80 + 120 + 90 + 110 + 130 +70 + 95 + 105 = 1050。

然后将总销量除以月数：1050 ÷ 10 = 105。

所以这10个月的平均月销量为105件。

练习题四：某家庭的每月用电量（单位：千瓦时）如下：200，150，180，220，250，190，210。

求这7个月的平均月用电量。

解答：将这7个月的用电量相加：200 + 150 + 180 + 220 + 250 + 190 + 210= 1400。

七年级数学上册天天练试题姓名 出题人：陈老师•、选择题。

（3X 5=15分）1、已知一个正方体的每一表面都填有唯一一个数字 的数互为倒数，若这个正方体的表面展开图如图所示RTA ABC 绕直角边 AC 旋转一周，所得几何体的主视4、 一个长方体的截面不可能是（ A 、三角形 B 、梯形5、 若3个不相等的有理数的和为 A 、3个加数全为0）OC 、五边形D 、七边形 则下列结论正确的是（ ）是（ )O1 1 1A 、一 ，B 、— ,13 231C 、一,T D,1,T 2 33 2、如图是某一立体图形的三视图，则这个三体图形是（ △主视图A 、正三棱柱左视图B 、三棱锥 俯视图C 、圆柱D 、圆锥，且各相对表面所填3、将如图所示的B、最少有两个加数是负数C、至少有一个加数是负数D、最少有两个加数是正数二、填空题。

（3X5=15分）1、圆锥的侧面和底面相交成条线，这条线, 线（填“直” 或“曲”）O2、n边形从一个顶点出发的对角线有，这些对角线把n边形分成个三角形。

3、如果海平面的高度记为Om, 一潜水艇在海面下方30m 深处，记作，一飞机在海面上空1000m的高度记作o111114、1,-一7■，―，-，一•；——，则第9、10个数分别是 q，猜2 3 4 5 6想第2004个数是，如果这一列数无限排下去，越来越接近。

5、与原点距离为3个单位的点有个，它们分别表示有理数和O三、计算题。

（4X 5=20分）1、试计算：1 41 1 11 + 1 -- 11+ 11 11 一+…+ | —一1 的值。

32 4 35 4 10 92000 9 # A 19991999D1998，试比较A与B的大小。

20012000200019993）3、4、如图，在数轴上有三个点A、B、C。

回答下列问题:AB C-5 -4 -3 -2 -1 0 1 2 3 4 5（1）将点B向左移动2个单位长后，三个点表示的数哪个最小？是多少?（2）将点A向右移动7个单位长后，三个点表示的数哪个最大？是多少？（3）将点C向左移动7个单位长后，点B表示的数比点C表示的数大多少？（4）怎样移动A、B、C中的两个点，才能使三个点表示的数相同，有几种移动方法大山教育试题（二）姓名出题人：陈老师、选择题。

初一数学上册计算题天天练第1天一、有理数口算（直接写出得数）1、)8()16(-+-=2、122+- =3、 )85(78-+ =4、)15()14(+-- =5、)16(4--=6、)6()4(-⨯-=7、)31(84-⨯=8、3)48(÷- =9、⎪⎭⎫ ⎝⎛-÷-316)( = 10、)2(3--= 11、42- = 12、42)(- = 13、20121)(- = 14、20131)(- = 15、20121- 16、 =二、整式的加减——去括号、合并同类型（1）)(2)(2b a b a a +-++ （2）)32(2[)3(1yz x x xy +-+--]三、整式的加减——先化简、再求值233(4333)(4),2;a a a a a a +----+=-其中四、解一元一次方程（1）2x+5=5x-7 (2) 4-3(2-x)=5x()32--一、有理数混合运算1、31277⎛⎫÷- ⎪⎝⎭85513)64(⨯÷-⨯2、22128(2)2⎛⎫-⨯-+÷- ⎪⎝⎭3、 9181739⨯⎪⎭⎫ ⎝⎛-二、整式的加减——去括号、合并同类型（3）)32(3)23(4)(5b a b a b a -+--+； （4）)377()5(322222a b ab b ab a a ---+--三、整式的加减——先化简、再求值 22222222(22)[(33)(33)],1, 2.x y xy x y x y x y xy x y ---++-=-=其中四、解一元一次方程（3）3（x-2）=2-5(x-2) (4) 2(x+3)－5(1－x)=3(x －1)一、有理数混合运算4、⎪⎭⎫ ⎝⎛-++-÷41312112415、()31-6612131⨯⎪⎭⎫ ⎝⎛+-- 6、)43(411)43()411(-------二、整式的加减——去括号、合并同类型（5） )45()54(3223--++-x x x x （6）)324(2)132(422+--+-x x x x三、整式的加减——先化简、再求值 ()()()2222223224b ab a ab b a b ab a +-+-+---- 其中4.0,41=-=b a四、解一元一次方程(5) 3(1)2(2)23x x x +-+=+ (6) 3(2)1(21)x x x -+=--一、有理数混合运算7、⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+--318216315414 8、173115321176.0324-⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-+÷+⨯-二、整式的加减——去括号、合并同类型（7）)69()3(522x x x +--++-. （8）)35()2143(3232a a a a a a ++--++-三、整式的加减——先化简、再求值 2(a 2b ＋2b 3－ab 3)＋3a 3－(2ba 2－3ab 2＋3a 3)－4b 3，其中a ＝－3，b ＝2四、解一元一次方程(7)2x =3x-1 (8) 2x －13 =x+22 +1一、有理数混合运算9、108524835)16(+⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛-+- 10、()()631)2(42+--⨯--+-二、整式的加减——去括号、合并同类型（9）)(4)(2)(2n m n m n m -++-+ （10）]2)34(7[522x x x x ----三、整式的加减——先化简、再求值21x 2－2212- (x + y )2⎡⎤⎢⎥⎣⎦－23(－32x 2＋31y 2)，其中x ＝－2， y ＝－34四、解一元一次方程(9)12131=--x (10) x x -=+38一、有理数混合运算11、20112012)2(21-⨯⎪⎭⎫ ⎝⎛- 12、⎪⎭⎫ ⎝⎛-+-127659521()36-⨯ 13、()1-⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-÷3114310二、整式的加减——去括号、合并同类型（1）(2)(3)x y y x --- （2）()()()b a b a b a 4227523---+-三、整式的加减——先化简、再求值21x －2(x －31y 2)＋(－23x ＋31y 2)，其中x ＝－2，y ＝－32．四、解一元一次方程(11) 12542.13-=-x x (12 ) 310.40.342x x -=+一、有理数混合运算14、()2332-÷-()2-⨯ 15、81)4(2033--÷- 16、100()()222---÷⎪⎭⎫ ⎝⎛-÷32二、整式的加减——去括号、合并同类型（3）()[]22222223ab b a ab b a --- (4) 2213[5(3)2]42a a a a ---++三、整式的加减——先化简、再求值 x x x x x x 5)64(213223312323-++-⎪⎭⎫ ⎝⎛--- 其中x ＝－121四、解一元一次方程(13) 1111248x x x x -=++ (14) 3142125x x -+=-一、有理数混合运算17、）（）（32312115--+--- 18、）（）（）（846592-÷---⨯+-二、整式的加减——去括号、合并同类型(5) 2x －(3x －2y ＋3)－(5y －2)； (6) －(3a ＋2b )＋(4a －3b ＋1)－(2a －b －3)三、整式的加减——先化简、再求值21x 2－2⎪⎭⎫ ⎝⎛+--⎪⎭⎫ ⎝⎛-222231322331y x y x ，其中x ＝－2，y ＝－34四、解一元一次方程1512 (15)=-+x x 312121 (16)-=-x x一、有理数混合运算19、100512161004----÷+）（ 20、()()()201321111-+-+-二、整式的加减——去括号、合并同类型(1)(8xy －x 2＋y 2)＋(－y 2＋x 2－8xy )； (2)(2x 2－21＋3x )－4(x －x 2＋21)三、整式的加减——先化简、再求值 x x x x x x 5)64(213223312323-++-⎪⎭⎫ ⎝⎛--- 其中x ＝－121；四、解一元一次方程 (17) 31257243y y +-=- (18) 576132x x -=-+一、有理数混合运算 21、)43(65)531(42-⨯--÷- 22、4)28.0(5)2(43÷--⨯-+ 23、2)6543187(36-+-⨯-二、整式的加减——去括号、合并同类型（3）()[]22222223ab b a ab b a --- (4) 2213[5(3)2]42a a a a ---++三、整式的加减——先化简、再求值21x 2－2⎪⎭⎫ ⎝⎛+--⎪⎭⎫ ⎝⎛-222231322331y x y x ，其中x ＝－2，y ＝－34四、解一元一次方程(19)143321=---m m (20) 52221+-=--y y y一、有理数混合运算24、419932(4)(1416)41313⎡⎤--⨯-÷-⎢⎥⎣⎦)22- 25、()⎪⎭⎫⎝⎛-⨯÷-++-31324323二、整式的加减——去括号、合并同类型 (5)()()()xy yx xy yxy x -+---+-22222322 (6) 3x 2－［7x －(4x －3)－2x 2］．三、整式的加减——先化简、再求值2(a 2b ＋2b 3－ab 3)＋3a 3－(2ba 2－3ab 2＋3a 3)－4b 3，其中a ＝－3，b ＝2四、解一元一次方程 (21)12136x x x -+-=- (22) 38123x x ---=一、有理数混合运算24、⎪⎪⎭⎫ ⎝⎛--⨯+-2323221)21(2 25、()⎥⎦⎤⎢⎣⎡-÷⎪⎭⎫ ⎝⎛⨯-+---2512.01452二、整式的加减——去括号、合并同类型(3) 2x －(3x －2y ＋3)－2(5y －2)； (4) －2(3a ＋2b )＋(4a －3b ＋1)－(2a －b －3)三、整式的加减——先化简、再求值已知2-a ＋(b ＋1)2＝0，求5ab 2－[2a 2b －(4ab 2－2a 2b )]的值四、解一元一次方程 (23) 12(x-3)=2-12(x-3) (24)35.012.02=+--x x一、实数混合运算二、解一元一次不等式（组）1、 136155-+x x ＞2、⎩⎨⎧++-x x xx 423215三、解方程组1、503217x y x y -=⎧⎨+=⎩ 2、四、先化简、再求值：)31(6)31(322y x y x x +-+--，其中2-=x ，1-=y)512(5)1-)313(3)2-一、实数混合运算二、 解一元一次不等式（组）1、 x x 4923+≥-2、⎩⎨⎧-≤+>+145321x x xx三、解方程组1、 2、四、先化简、再求值:3x 2y ﹣[2xy ﹣2（xy ﹣x 2y ）+x 2y 2]，其中x=3，y=﹣33271816)3-+--31433)4---⨯一、实数混合运算二、解一元一次不等式（组）1、)1(5)32(2+<+x x2、⎪⎩⎪⎨⎧--≤--x x x x 14214)23(三、解二元一次方程组1、 2、四、先化简、再求值: )3(2)52(4222xy x y xy x xy ++-+-其中 x =-2，y =133364271)6-+---2)3(223)5-----π()()()9-214-4-2-23323⎪⎭⎫ ⎝⎛⨯+⨯一、实数混合运算1、()22-错误!未找到引用源。

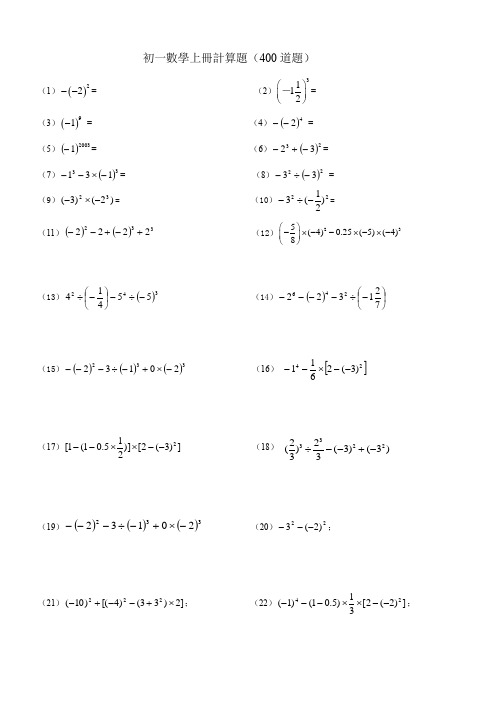
初一數學上冊計算題（400道題）（1）()22--= （2）3112⎛⎫⎪⎝⎭－=（3）()91- = （4）()42-- =（5）()20031-= （6）()2332-+-=（7）()33131-⨯--= （8）()2233-÷- =（9）)2()3(32-⨯-= （10）22)21(3-÷-=（11）()()3322222+-+-- （12）235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭（13）()34255414-÷-⎪⎭⎫ ⎝⎛-÷ （14）()⎪⎭⎫ ⎝⎛-÷----721322246（15）()()()33220132-⨯+-÷--- （16） []24)3(2611--⨯--（17）])3(2[)]215.01(1[2--⨯⨯-- （18） （19）()()()33220132-⨯+-÷--- （20）22)2(3---；（21）]2)33()4[()10(222⨯+--+-； （22）])2(2[31)5.01()1(24--⨯⨯---； 332222()(3)(3)33÷--+-（23）94)211(42415.0322⨯-----+-； （24）20022003)2()2(-+-；（25）)2()3(]2)4[(3)2(223-÷--+-⨯--； （26）200420094)25.0(⨯-.（27）()0252423132.⨯--÷-⎛⎝ ⎫⎭⎪+⎡⎣⎢⎢⎤⎦⎥⎥ （28）()()----⨯-221410222（29）()()()-⨯÷-+-⎛⎝ ⎫⎭⎪⨯-÷-3120313312232325.. （30）()()()-⎛⎝ ⎫⎭⎪⨯-⨯-⨯-212052832.（31） （32）(56)(79)---（33）(3)(9)(8)(5)-⨯---⨯- （34）3515()26÷-+（35）5231591736342--+- （36）（37）411)8()54()4()125.0(25⨯-⨯-⨯-⨯-⨯ ()()22431)4(2-+-⨯---33182(4)8-÷--（38）如果0)2(12=-++b a ，求20112010()-3ab a b a a ++-（）の值（39）已知|1|a +與|4|b -互為相反數，求b a の值。

3－4—, －2.5 ,0 ,－3.252、写出下列各数的相反数。

1－—, －22 ,－15 ,－1.263、写出下列各数的绝对值。

24—, －4.6 ,6 , 0.5674、比较下列各组数的大小。

(1)－15与8 (2)－2.5与－0.75 (3)|－9.9|与|－1.5|(4)－—与－—(5)－10与－|－5| (6)|－39.8|与|－2.5|7 35、计算。

5 71－—＋—14×(－17)－30×(－17)9 157 1 1(－－－)÷－(－66)÷12÷(－27)8 5 63 1 1－(—－—＋—)×128 7×[19＋(－5)2]4 8 423—, 1 ,0 , 452、写出下列各数的相反数。

1—, 16.5 ,－20 ,－5.293、写出下列各数的绝对值。

2－9—, －3.55 ,－10 , 0.2474、比较下列各组数的大小。

(1)－15与9 (2)－4与－0.5 (3)|－4.2|与|－0.8|(4)－—与－—(5)－10与－|－3| (6)|－77|与|－2|4 55、计算。

7 12－—＋—30×(－19)＋13×(－19)9 151 4 1(－－－)÷－(－120)×6÷(－21)5 5 61 1 6－(—＋—＋—)×105 8×[1－(－3)3]3 5 72－4—, －4 ,0 , 1.652、写出下列各数的相反数。

1—, －12 ,1 ,－5.563、写出下列各数的绝对值。

41—, 0.95 ,9 ,－0.474、比较下列各组数的大小。

(1)－12与5 (2)－3与1.75 (3)|－9|与|－3.4|(4)－—与－—(5)－16与－|－8| (6)|－48.2|与|－7|8 55、计算。

5 132－—＋—5×(－20)－12×(－20)6 157 1 1(－＋－)×－(－102)×12÷(－12)8 3 71 8 1－(—－—＋—)×168 8×[12－(－2)3]4 7 63－1—, 4.5 ,0 , 3.252、写出下列各数的相反数。

七上几何计算题专项练习
本文档为七年级上学期几何计算题专项练，在这里你将能够巩固和提高你的几何计算能力。

以下是一些练题供你参考：
1. 长方形的面积计算
问题：一个长方形的长为5米，宽为3米，求其面积。

解答：
面积计算公式为：面积 = 长 ×宽
所以，该长方形的面积为 5米 × 3米 = 15平方米
2. 三角形的周长计算
问题：一个三角形的三边长分别为6厘米、8厘米和10厘米，求其周长。

解答：
周长计算公式为：周长 = 边1长 + 边2长 + 边3长
所以，该三角形的周长为 6厘米 + 8厘米 + 10厘米 = 24厘米
3. 圆的周长和面积计算
问题：一个圆的半径为2米，求其周长和面积。

解答：
圆的周长计算公式为：周长= 2πr （其中π取3.14）
所以，该圆的周长为 2 × 3.14 × 2米 = 12.56米
圆的面积计算公式为：面积= πr²
所以，该圆的面积为 3.14 × 2米 × 2米 = 12.56平方米
4. 平行四边形的面积计算
问题：一个平行四边形的底边长为8厘米，高度为5厘米，求其面积。

解答：
平行四边形的面积计算公式为：面积 = 底边长 ×高度
所以，该平行四边形的面积为 8厘米 × 5厘米 = 40平方厘米
希望以上练习题能够帮助你加深对几何计算的理解和应用。

继续努力，你会越来越擅长几何计算！。