热力学习题及答案ppt课件

热力学习题答案Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】第9章热力学基础一. 基本要求1. 理解平衡态、准静态过程的概念。

2. 掌握内能、功和热量的概念。

3. 掌握热力学第一定律，能熟练地分析、计算理想气体在各等值过程中及绝热过程中的功、热量和内能的改变量。

4. 掌握循环及卡诺循环的概念，能熟练地计算循环及卡诺循环的效率。

5. 了解可逆过程与不可逆过程的概念。

6. 解热力学第二定律的两种表述，了解两种表述的等价性。

7. 理解熵的概念，了解热力学第二定律的统计意义及无序性。

二. 内容提要1. 内能功热量内能从热力学观点来看，内能是系统的态函数，它由系统的态参量单值决定。

对于理想气体，其内能E仅为温度T的函数，即当温度变化ΔT时，内能的变化功热学中的功与力学中的功在概念上没有差别，但热学中的作功过程必有系统边界的移动。

在热学中，功是过程量，在过程初、末状态相同的情况下，过程不同，系统作的功A也不相同。

系统膨胀作功的一般算式为在p—V图上，系统对外作的功与过程曲线下方的面积等值。

热量热量是系统在热传递过程中传递能量的量度。

热量也是过程量，其大小不仅与过程、的初、末状态有关，而且也与系统所经历的过程有关。

2. 热力学第一定律系统从外界吸收的热量，一部分用于增加内能，一部分用于对外作功，即热力学第一定律的微分式为3. 热力学第一定律的应用——几种过程的A、Q、ΔE的计算公式（1）等体过程体积不变的过程，其特征是体积V =常量；其过程方程为在等体过程中，系统不对外作功，即0A。

等体过程中系统吸收的热量与系统内V能的增量相等，即(2) 等压过程压强不变的过程，其特点是压强p =常量；过程方程为在等压过程中，系统对外做的功系统吸收的热量 )(12T T C M MQ P mol P -=式中R C C V P +=为等压摩尔热容。

（3）等温过程 温度不变的过程，其特点是温度T =常量；其过程方程为pV =常量在等温过程中，系统内能无变化，即（4）绝热过程 不与外界交换热量的过程，其特点是dQ=0，其过程方程pV γ=常量在绝热过程中，系统对外做的功等于系统内能的减少，即7. 循环过程 系统从某一状态出发，经过一系列状态变化后又回到了初始状态的整个变化过程。

第2章化学热力学初步（习题解）第二章化学热力学初步1. 热力学第一定律?U?Q?W,由于U为状态函数，所以Q和W也是状态函数，对吗？为什么？答：不对。

Q和W只有在能量交换的时候才会有具体的数值，并且随途径不同，共和热的数值都会有变化，所以不是状态函数。

2. 解释下列名词 (1) 体系与环境 (2) 热（Q） (3) 功（W）(4) 焓（H）和焓变（?H） (5) 热力学能U(6) 恒容反应热（QV）和恒压反应热（Qp）答：(1) 热力学中称研究的对象为体系，称体系以外的部分为环境。

(2) 体系在变化过程中吸收的热量为Q。

(3) 体系对环境所做的功。

(4) H＝U+PV当泛指一个过程的时候，其热力学函数的改变量为焓变。

(5) 体系内一切能量的总和叫热力学能。

(6) 在恒容过程中完成的化学反应，其热效应称为恒容反应热。

在恒压过程中完成的化学反应，其热效应称为恒压反应热。

3. 什么叫状态函数？它具有何特性？答：藉以确定体系状态的物理量称为体系的状态函数。

它具有加和性。

4. 何谓热效应？测量方法有哪两种？答：化学反应的热效应为当生成物和反应物的温度相同时，化学反应过程中的吸收或放出的热量。

可以选择恒压和恒容两种条件下测量。

5. 什么叫热化学方程式？书写热化学方程式要注意哪几点？答：表示出反应热效应的化学方程式叫做热化学方程式。

书写化学方程式时要注意一下几点：(1)写热化学方式式，要注意反应的温度和压强条件，如果反应是在298K和1.013×105Pa下进行时，习惯上不予注明。

（2）要注明物质的聚集状态和晶形。

（3）方程式中的配平系数只是表示计量数，不表示分子数。

但计量数不同时，同一反应的反应热数值也不同。

6. ①无机化学中常用的反应热有哪几种？反应热的实质是什么？什么类型的化学反应QV＝Qp？等摩尔的NaOH和NH3・H2O溶液分别与过量的HCl溶液中和所放热量是否相等？为什么？②反应2N2（g）＋O2（g）＝2N2O（g）在298K时，ΔrHm?=164KJ・mol-1, 求反应的ΔU?答：①无机化学中常用的反应热有恒压反应热和恒容反应热。

材料热力学习题1、阐述焓H 、内能U 、自由能F 以及吉布斯自由能G 之间的关系，并推导麦克斯韦方程之一：T P PST V )()(∂∂-=∂∂。

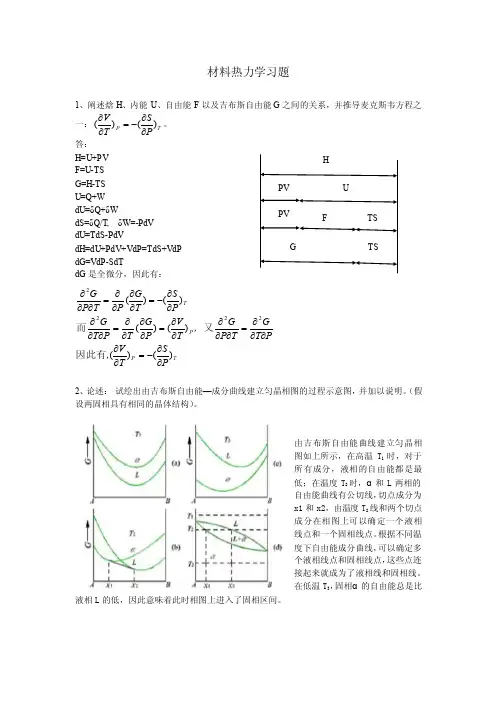
答： H=U+PV F=U-TS G=H-TS U=Q+W dU=δQ+δWdS=δQ/T, δW=-PdV dU=TdS-PdVdH=dU+PdV+VdP=TdS+VdP dG=VdP-SdTdG 是全微分，因此有：TP P TP ST V ，PT G T P G ，T V P G T P T G P S T G P T P G )()()()()()(2222∂∂-=∂∂∂∂∂=∂∂∂∂∂=∂∂∂∂=∂∂∂∂∂-=∂∂∂∂=∂∂∂因此有又而2、论述： 试绘出由吉布斯自由能—成分曲线建立匀晶相图的过程示意图，并加以说明。

（假设两固相具有相同的晶体结构）。

由吉布斯自由能曲线建立匀晶相图如上所示，在高温T 1时，对于所有成分，液相的自由能都是最低；在温度T 2时，α和L 两相的自由能曲线有公切线，切点成分为x1和x2，由温度T 2线和两个切点成分在相图上可以确定一个液相线点和一个固相线点。

根据不同温度下自由能成分曲线，可以确定多个液相线点和固相线点，这些点连接起来就成为了液相线和固相线。

在低温T 3，固相α的自由能总是比液相L 的低，因此意味着此时相图上进入了固相区间。

3、论述：通过吉布斯自由能成分曲线阐述脱溶分解中由母相析出第二相的过程。

第二相析出：从过饱和固溶体α中(x0)析出另一种结构的β相(xβ)，母相的浓度变为xα. 即：α→β+ α1α→β+ α1 的相变驱动力ΔGm的计算为ΔGm=Gm(D)-Gm(C)，即图b中的CD段。

图b中EF是指在母相中出现较大为xβ的成分起伏时，由母相α析出第二相的驱动力。

4、根据Boltzman方程S=kLnW，计算高熵合金FeCoNiCuCrAl和FeCoNiCuCrAlTi0.1（即FeCoNiCuCrAl各为1mol，Ti为0.1mol）的摩尔组态熵。

目录第一章 (1)第二章 (18)第三章 (258)第一章 温 度1-1 在什么温度下,下列一对温标给出相同的读数：（1）华氏温标和摄氏温标；（2）华氏温标和热力学温标；（3）摄氏温标和热力学温标？ 解：（1）Q 9325F t t =+∴当F t t =时，即可由9325t t =+，解得325404t ⨯=-=- 故在40c -o 时 F t t =（2）又Q 273.15T t =+ ∴当F T t =时 则即9273.15325t t +=+ 解得：241.155301.444t ⨯== ∴273.15301.44574.59T K =+= 故在574.59T K =时，F T t =（3）Q 273.15T t =+ ∴若T t = 则有273.15t t += 显而易见此方程无解，因此不存在T t =的情况。

1-2 定容气体温度计的测温泡浸在水的三相点槽内时，其中气体的压强为50mmHg 。

（1）用温度计测量300K 的温度时，气体的压强是多少？ （2）当气体的压强为68mmHg 时，待测温度是多少？ 解：对于定容气体温度计可知：()273.15trPT P K P = (1) 115030055273.16273.16tr P T P mmHg ⨯===(2) 2268273.16273.1637250tr P T KK K P === 1-3 用定容气体温度计测得冰点的理想气体温度为273.15K ，试求温度计内的气体在冰点时的压强与水的三相点时压强之比的极限值。

题1-4图解：根据00lim ()273.16limtr tr P P trP T T P K P →→==已知 冰点273.15T K =你∴0273.15lim0.99996273.16273.16tr P trP T KP K K →==。

1-4 用定容气体温度计测量某种物质的沸点。

原来测温泡在水的三相点时，其中气体的压强500tr P mmHg =；当测温泡浸入待测物质中时，测得的压强值为734P mmHg =,当从测温泡中抽出一些气体,使tr P 减为200mmHg 时,重新测得293.4P mmHg =,当再抽出一些气体使tr P 减为100mmHg 时,测得146.68P mmHg =.试确定待测沸点的理想气体温度.解：根据273.16trPT K P =333146.68273.16273.16400.67100tr P T KK K P === 从理想气体温标的定义：0273.16limtr P trPT K P →=依以上两次所测数据,作T-P 图看趋势得出0tr P →时,T 约为400.5K 亦即沸点为400.5K. 1-5 铂电阻温度计的测量泡浸在水的三相点槽内时，铂电阻的阻值为90.35欧姆。

第1章 《热力学》习题解答1-1若一打足气的自行车内胎在7.0C 时轮胎中空气压强为54.010Pa ⨯，则在温度变为37.0C 时，轮胎内空气压强为多少？（设内胎容积不变）[解]：轮胎内的定质量空气做等容变化状态1 Pa P K T 511100.4,280⨯== 状态2：?,28022==P K T 由查理定律得Pa Pa P T T P T T P P 55112212121043.4100.4280310⨯=⨯⨯==⇒= 1-2 氧气瓶的容积为233.210m -⨯，其中氧气的压强为71.310Pa ⨯，氧气厂规定压强降到61.010Pa ⨯时，就应重新充气，以免经常洗瓶. 某小型吹玻璃车间平均每天用去30.40m 在51.0110Pa ⨯压强下的氧气，问一瓶氧气能用多少天？（设使用过程中温度不变）[解]：设氧气瓶的容积为320102.3m V -⨯=，使用过程的温度T 保持不变使用前氧气瓶中，氧气的压强为Pa P 71103.1,⨯= 根据克拉帕龙方程nRT PV =得： 使用前氧气瓶中，氧气的摩尔数为RTV P n 011,=氧气压强降到Pa P 62100.1,⨯=时，氧气瓶中，氧气的摩尔数为RTV P n 022,=所以能用的氧气摩尔数为()21021,P P RTV n n n -=-=∆ 平均每天用去氧气的摩尔数RTV P n 333,=故一瓶氧气能用的天数为()()5.91001.140.010113102.3,562332103=⨯⨯⨯-⨯=-=∆=-P V P P V n n N 1-3在湖面下50.0m 深处（温度为4.0C ），有一个体积为531.010m -⨯的空气泡升到湖面上来. 若湖面的温度为17.0C ，求气泡到达湖面的体积.（取大气压为50 1.01310Pa p =⨯）[解]：空气泡在湖面下50.0m 深处时，3511100.1,277m V K T -⨯==Pa P gh P 5530110013.610013.15010100.1⨯=⨯+⨯⨯⨯=+=ρ气泡到达湖面时，Pa P K T 522100.1,290⨯==由理想气体状态方程222111T V P T V P =得： 35351122121029.6100.12772900.1013.6m m V T T P P V --⨯=⨯⨯⨯=⋅=1-4如图所示，一定量的空气开始时在状态为A ，压力为2atm ，体积为l 2, 沿直线AB 变化到状态B 后，压力变为1 atm ，体积变为l 3. 求在此过程中气体所作的功。

第一章 热力学基本定律习题及答案§ 1. 1 （P10）1.“任何系统无体积变化的过程就一定不做功。

”这句话对吗？为什么？解：不对。

体系和环境之间以功的形式交换的能量有多种，除体积功之外还有非体积功，如电功、表面功等。

2. “凡是系统的温度下降就一定放热给环境，而温度不变时则系统既不吸热也不放热。

”这结论正确吗？举例说明。

答：“凡是系统的温度下降就一定放热给环境”不对：体系温度下降可使内能降低而不放热，但能量可以多种方式和环境交换，除传热以外，还可对外做功，例如，绝热容器中理想气体的膨胀过程，温度下降释放的能量，没有传给环境，而是转换为对外做的体积功。

“温度不变时则系统既不吸热也不放热”也不对：等温等压相变过程，温度不变，但需要吸热(或放热), 如P Ө、373.15K 下，水变成同温同压的水蒸气的汽化过程，温度不变，但需要吸热。

3. 在一绝热容器中，其中浸有电热丝，通电加热。

将不同对象看作系统，则上述加热过程的Q 或W 大于、小于还是等于零？（讲解时配以图示） 解：（1）以电热丝为系统：Q<0，W>0（2）以水为系统：Q>0，W=0（忽略水的体积变化） （3）以容器内所有物质为系统：Q=0，W>0（4）以容器内物质及一切有影响部分为系统：Q=0，W=0（视为孤立系统）4. 在等压的条件下，将1mol 理想气体加热使其温度升高1K ，试证明所做功的数值为R 。

解：理想气体等压过程：W = p(V -V ) = pV -PV = RT -RT = R(T -T ) = R5. 1mol 理想气体，初态体积为25dm , 温度为373.2K ，试计算分别通过下列四个不同过程，等温膨胀到终态体积100dm 时，系统对环境作的体积功。

（1）向真空膨胀。

（2）可逆膨胀。

（3）先在外压等于体积50 dm 时气体的平衡压力下，使气体膨胀到50 dm ，然后再在外压等于体积为100dm 时气体的平衡压力下，使气体膨胀到终态。