六年级下册M2U5第一课时

六年级下册数学教案第五单元第一课时鸽巢问题人教版教学内容：本课时为六年级下册数学第五单元《鸽巢问题》的第一课时，涉及的主要内容是理解鸽巢原理，并能够应用这一原理解决实际问题。

通过本课时的学习，学生将掌握如何利用鸽巢原理进行数量关系的推断，培养逻辑思维能力和问题解决能力。

教学目标：1. 理解并掌握鸽巢原理的基本概念。

2. 能够运用鸽巢原理解决具体的数学问题。

3. 培养学生的逻辑思维能力和数学应用意识。

4. 激发学生对数学学习的兴趣，提高解决实际问题的能力。

教学难点：1. 鸽巢原理的理解和运用。

2. 如何将实际问题抽象为鸽巢问题模型。

3. 解决问题时逻辑推理的严密性。

教具学具准备：1. 教学PPT或黑板，用于展示问题和原理。

2. 准备相关的练习题目和实例，用于课堂练习和讨论。

3. 学生需准备笔记本和文具，用于记录重点和解题过程。

教学过程：1. 导入：通过生活中的实例引入鸽巢原理，如分配糖果、排座位等，引发学生兴趣。

2. 新知讲解：介绍鸽巢原理的定义，通过具体例子讲解原理的应用。

3. 案例分析：分析几个典型问题，让学生理解鸽巢原理的应用方法和逻辑推理过程。

4. 小组讨论：学生分组讨论，解决教师提出的实际问题，加深对鸽巢原理的理解。

5. 巩固练习：进行课堂练习，让学生独立解决相关问题，教师巡回指导。

板书设计：1. 鸽巢原理的定义。

2. 鸽巢原理的应用步骤。

3. 典型例题及其解答过程。

4. 学生练习题。

作业设计：1. 基础练习：布置一些基础的鸽巢问题，巩固学生对原理的理解。

2. 提高练习：设计一些稍有难度的实际问题，让学生尝试解决。

3. 拓展阅读：推荐相关的数学阅读材料，鼓励学生了解更多数学故事和背景。

课后反思：1. 学生对鸽巢原理的理解程度。

2. 教学过程中学生的参与度和积极性。

3. 学生在解决问题时遇到的困难和常见错误。

4. 教学方法的适用性和改进空间。

本课时结束后，教师应针对学生的掌握情况进行适当的辅导和补充，确保每位学生都能够理解并能够运用鸽巢原理解决实际问题。

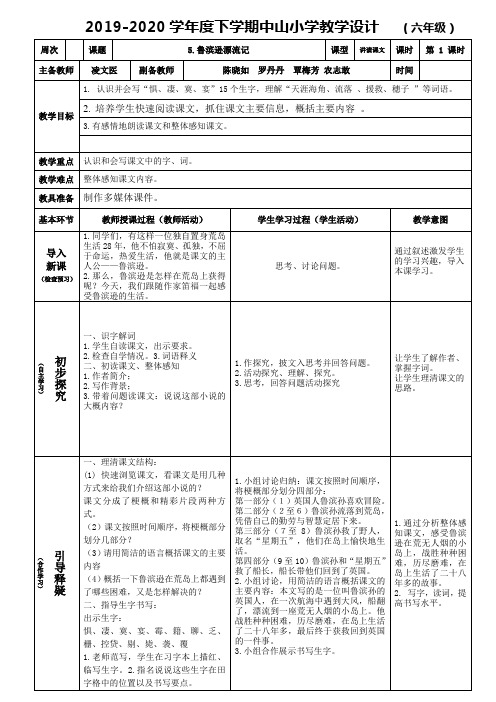
2019-2020学年度下学期中山小学教学设计 （六年级）周次课题 5.鲁滨逊漂流记课型讲读课文课时 第 1 课时 主备教师 凌文医副备教师陈晓如 罗丹丹 覃梅芳 农志敢时间教学目标1. 认识并会写“惧、凄、寞、宴”15个生字，理解“天涯海角、流落 、援救、穗子 ”等词语。

2. 培养学生快速阅读课文，抓住课文主要信息，概括主要内容 。

3.有感情地朗读课文和整体感知课文。

教学重点 认识和会写课文中的字、词。

教学难点 整体感知课文内容。

教具准备 制作多媒体课件。

基本环节教师授课过程（教师活动）学生学习过程（学生活动）教学意图导入 新课 （检查预习） 1.同学们，有这样一位独自置身荒岛生活28年，他不怕寂寞、孤独，不屈于命运，热爱生活，他就是课文的主人公——鲁滨逊。

2.那么，鲁滨逊是怎样在荒岛上获得呢？今天，我们跟随作家笛福一起感受鲁滨逊的生活。

思考、讨论问题。

通过叙述激发学生的学习兴趣，导入本课学习。

初步探究（自主学习）一、识字解词1.学生自读课文，出示要求。

2.检查自学情况。

3.词语释义二、初读课文、整体感知 1.作者简介； 2.写作背景； 3.带着问题读课文：说说这部小说的大概内容？1.作探究，披文入思考并回答问题。

2.活动探究、理解、探究。

3.思考，回答问题活动探究让学生了解作者、掌握字词。

让学生理清课文的思路。

引导释疑（合作学习）一、理清课文结构：(1) 快速浏览课文，看课文是用几种方式来给我们介绍这部小说的？ 课文分成了梗概和精彩片段两种方式。

（2）课文按照时间顺序，将梗概部分划分几部分？ （3）请用简洁的语言概括课文的主要内容 （4）概括一下鲁滨逊在荒岛上都遇到了哪些困难，又是怎样解决的？ 二、指导生字书写： 出示生字：惧、凄、寞、宴、霉、籍、聊、乏、栅、控贷、剔、毙、袭、覆1.老师范写，学生在习字本上描红、临写生字。

2.指名说说这些生字在田字格中的位置以及书写要点。

1.小组讨论归纳：课文按照时间顺序，将梗概部分划分四部分：第一部分（１）英国人鲁滨孙喜欢冒险。

“1351”课改集体备课教案
学段：高段学科：数学（六）年级下册
（四）学生通过“假设分析法→归纳总结”的学习过程来解决问题二。

（1）用假设法分析。

8÷3=2（本）......2（本），剩下2本，分别放进其中2个抽屉中，使其中2个抽屉都变成3本，因此把8本书放进3个抽屉中，不管怎么放，总有1个抽屉里至少放进3本书。

10÷3=3（本）......1（本），把10本书放进3个抽屉中，不管怎么放，总有1个抽屉里至少放进4本书。

3、交流提升
归纳总结：
综合上面两种情况，要把a本书放进3个抽屉里，如果a
÷3=b（本）......1（本）或a÷3=b（本）......2（本），那么一定有1个抽屉里至少放进（b+1）本书。

鸽巢原理（二）：如果把多于kn个的物体任意分别放进n个空抽屉（k是正整数，n是非0的自然数），那么一定有一个抽屉中至少放进了（k+1)个物体。

五、达标检测
完成教材第68-69页的“做一做”。

学生独立思考解答问题，集体交流、纠正。

六、总结反馈
谈谈这节课的收获和体会。

七、作业布置：
做练习册上的相关练习。