下载文档原格式
. . kszl 正方体的十一种侧面展开图 我上立体几何课时，为了激发学生的兴趣，让学生手工制作立方体，然后总结研究它的侧面展开图有多少种情形，现总结如下：
1. 141型，中间一行4个作侧面，上下两个各作为上下底面，共有六种基本图形
2. 132型，中间3个作侧面，共3中基本图形
3. 222型，两行只能有1个正方形相连 . . kszl 4. 33型，两行只能有一个正方形相连 5 正方体的十一种平面展开图可记忆成下面口诀： 一三二，一四一，一在同层可任意，两个三，日状连，三个二，成阶梯，相邻必有日，整体没有田。 .
. kszl 七年级下册数学动点题！急需，3题以上的啊！ 七年级下册几何动点！ 2010-7-20 09:56 最佳答案 1.矩形ABCD中，AB=6,BC=8,P是边AD上的动点，PE⊥AC于点E，PF⊥BD于点F，PE+PF的值是多少？ 解：4.8 2.在正方形ABCD中，P为BC边上一点，Q为CD边上一点。若PQ=BP+DQ，求角PAQ的度数 解：方法一：延长QD至E,使DE=BP,易知△ABP≌△ADE,则AP=AE,所以△APQ≌△AEQ,因为角PAE=90度,所以角PAQ=45度. 方法二：作三角形APQ中PQ边上的高，交PQ于E点。因QD垂直与AD，QE垂直于AE，所以AQ是角DAE的平分线，同理，AP是角BAE的平分线。因此得角PAB+角QAD＝角PAE+角QAE＝1/2角BAD＝45度 如图，直线y=-(3分之根号3)x+1与x轴y轴分别交于B、A两点，以AB为直角边的等腰直角三角形ABC的顶点C在第一象限且∠ABC=90度 （1）求A、B点坐标 （这问不用做，答案是A(0，1)B(根号3，0)） （2）将△ABC以每秒1个单位长度的速度延x轴平行移动，移动时间为t(秒)平移后三角形记作△AtBtCt，设平移过程中△AtBtCt与四边形AOBC重叠部分面积为S。试探究S与t的关系式并写出自变量t的取值范围（有三种情况）
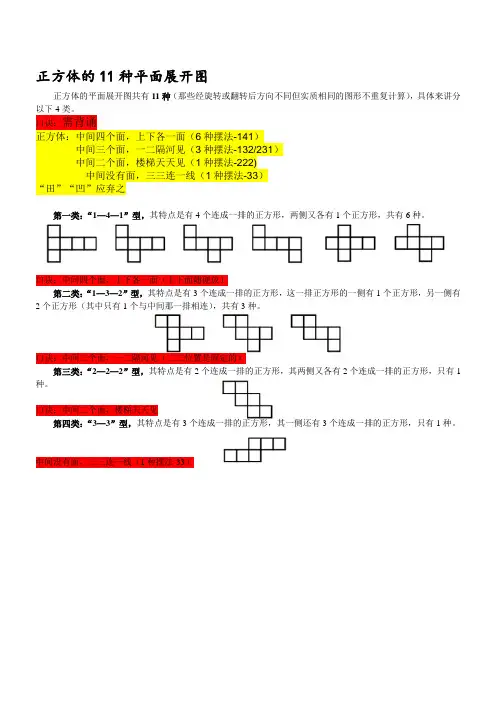
正方体的11种平面展开图
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。
口诀：需背诵
正方体：中间四个面，上下各一面（6种摆法-141）
中间三个面，一二隔河见（3种摆法-132/231）
中间二个面，楼梯天天见（1种摆法-222)
中间没有面，三三连一线（1种摆法-33）
“田”“凹”应弃之
第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。
口诀：中间四个面，上下各一面（上下面随便放）
第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。
口诀：中间三个面，一二隔河见（二三位置是固定的）
第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。
口诀：中间二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。
中间没有面，三三连一线（1种摆法-33）。
