球总数为5÷0.1=50(个),得红球数为50-5=45(个).
【想一想】 连续10次抛掷一枚均匀的硬币,正面朝上的次数为8次,这 与计算的概率0.5相差很大,这是为什么? 提示:通过试验的方法估计正面朝上的概率,只有试验的次 数足够多,事件发生的频率才可以接近概率值.
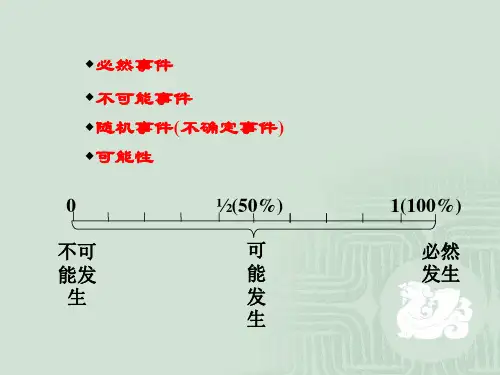
【微点拨】频率与概率的区别
25.3用频率估计概率
1.频率 在一个试验中,_事__件__发__生__的次数与_试__验__的__总__次__数__的比值叫做 事件发生的频率. 2.频率的特性 对一般的随机事件,在做大量重复试验时,随着试验次数的增加, 一个事件出现的频率,显示出一定的_稳__定__性.
3.频率与概率的关系
在大量重复试验中,如果事件A发生的频率
【解题探究】
(1)根据表格中的频率,可以发现这些数值在哪个 数据上下波动? 提示:0.9. (2)在移植的4万棵幼树中,成活的数量与哪个数值 有关? 提示:幼树成活的概率. (3)要保证有9万棵成活的幼树,大约需要移植多少 棵? 提示:10万.
【尝试解答】(1)观察表格发现,这种幼树成活的 概率是0.9. (2)4×0.9=3.6(万). (3)9÷0.9=10(万),10-4=6(万).
知识点一 频率与概率的关系
【示范题1】(2013·青岛中考)一个不透明的口袋装有除颜色外都相同
的五个白球和若干个红球,在不允许将球倒出来数的情况下,小亮为了
估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋里随
机摸出一球,记下颜色,然后把它放回口袋中.不断重复上述过程.小亮
共摸了100次,其中有10次摸到白球.因此小亮估计口袋中的红球大约
知识点二 频率与概率关系的应用
【示范题2】某林业部门统计某种幼树在一定条件下的移