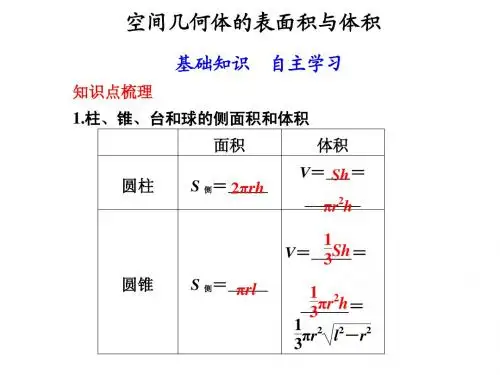
第一章空间几何体复习课.ppt
- 格式：ppt
- 大小：530.50 KB
- 文档页数：28
下载文档原格式
合集下载
1复习课(45张PPT)
圆锥
四棱柱 五棱柱
三棱锥 四棱锥 五棱锥
②按“围成图形的面”分
棱柱 平面
棱锥 圆柱 曲面 圆锥
球
球
◇长方体：有8个顶点，12条棱，6个面，且各面都 是长方形（正方形是特殊的长方形）；正方体是特 殊的长方体。
◇棱柱：上下两个面称为棱柱的底面，其它各面称 为侧面，长方体是四棱柱。
◇圆柱：有上下两个底面和一个侧面，两个底面是 半径相等的圆。
21
左画三个，右画两个
俯视图
左视图
例7、如图所示，是由几个小立方体搭成的几何体 的俯视图，小正方形中的数字表示在该位置上的小 立方体的个数。请画出几何体的主视图和左视图。
1 2 3 12
3 41 12
主视图 左视图
2.用小立方体搭成的几何体的主视图和俯视 图如图，问，这样的几何体是否只有一种？ 它最少需多少个小立方体？它最多需多少个 小立方体？请画出最多与最少时的左视图。
主视图
俯视图
用小立方块搭一个几何体，使得从正面、 上面看它得到的形状图如图所示. 这样的几 何体只有一种吗？它最少需要多少个小立方 块？最多需要多少个小立方块？
从正面看
从上面看
6、正多面体的顶点数、面数、棱数之间的关系
名称
各面形状 面数f 棱数e 顶点数v f+v-e
正四面体 正三角形 4
6
4
2
一、由五个正方形组连成的
“五子连”形
如
二、由五个正方形组成的
“7字”形
如
三、由五个正方形组成的
“凹字”形
如
四、由四个正方形组成的
“田字”形
如
例3、下图中是正方体的展开图的有（ ）
A、2个 B、3个 C、4个 D、5个
四棱柱 五棱柱
三棱锥 四棱锥 五棱锥
②按“围成图形的面”分
棱柱 平面
棱锥 圆柱 曲面 圆锥
球
球
◇长方体：有8个顶点，12条棱，6个面，且各面都 是长方形（正方形是特殊的长方形）；正方体是特 殊的长方体。
◇棱柱：上下两个面称为棱柱的底面，其它各面称 为侧面，长方体是四棱柱。
◇圆柱：有上下两个底面和一个侧面，两个底面是 半径相等的圆。
21
左画三个，右画两个
俯视图
左视图
例7、如图所示，是由几个小立方体搭成的几何体 的俯视图，小正方形中的数字表示在该位置上的小 立方体的个数。请画出几何体的主视图和左视图。
1 2 3 12
3 41 12
主视图 左视图
2.用小立方体搭成的几何体的主视图和俯视 图如图，问，这样的几何体是否只有一种？ 它最少需多少个小立方体？它最多需多少个 小立方体？请画出最多与最少时的左视图。
主视图
俯视图
用小立方块搭一个几何体，使得从正面、 上面看它得到的形状图如图所示. 这样的几 何体只有一种吗？它最少需要多少个小立方 块？最多需要多少个小立方块？
从正面看
从上面看
6、正多面体的顶点数、面数、棱数之间的关系
名称
各面形状 面数f 棱数e 顶点数v f+v-e
正四面体 正三角形 4
6
4
2
一、由五个正方形组连成的
“五子连”形
如
二、由五个正方形组成的
“7字”形
如
三、由五个正方形组成的
“凹字”形
如
四、由四个正方形组成的
“田字”形
如
例3、下图中是正方体的展开图的有（ ）
A、2个 B、3个 C、4个 D、5个
立体几何复习课 ppt课件
一个平面平行，则这两个平面平行。
•
符号表示：a ,b ,a b P ,a /, / b // //
•
（2）性质定理：如果两个平行平面同时和第三个
平面相交，那么它们的交线平行。
符号表示： // , a , b a /b /。
立体几何复习课
13
5.直线、平面垂直的判定与性质
• 直线与平面垂直
• （2）直线与平面相交--有且只有一个公共点
• （3）直线与平面平行----没有公共点
立体几何复习课
11
平面与平面之间的位置关系
• （1）两个平面平行---没有公共点 • （2）两个平面相交---有一条公共直线
立体几何复习课
12
4.直线、平面平行的判定与性质
(1)直线与平面平行
•
（1)判定定理：平面外一条直线与此平面内的一条
• ①证明 BC⊥侧面 PAB； • ②证明侧面PAD⊥侧面PAB； • ③求侧棱PC与底面ABCD所成角的大小；
• ④求平面 PAB与平面 PCD所成二面角余弦值
立体几何复习课
19
如图8，在矩形ABCD中，AB=2,AD=1，E是 CD边上的中点，以AE为折痕将 △DAE向上折起， 使D为D
• （1）求证：AD⊥ EB；
D． 1 2
立体几何复习课
6
• 例2. 一水平放置的平面图形，用斜二测 画法画出了它的直观图，此直观图恰好是 一个边长为2的正方形，如图3则原平面图 形的面积为（ ）
• A．4 3 • B．4 2 • C．8 3
• D．8 2
立体几何复习课
7
体积与表面积
立体几何复习课
8
3.点、线、面之间的位置关系
必修2第一章空间几何体单元复习课件人教新课标
3. 棱台、圆台可看作是棱锥、圆 锥由平面截去一部分所得，所以棱台、 圆台的问题常转化为棱锥、圆锥.
4. 画空间几何体的三视图时注意 长对正,高平齐,宽相等.
5. 画空间几何体的直观图时注意 x,y轴相交成45°，平行x轴的线段的长 度保持不变.平行y轴的线段的长度变为 本来的一半.
要点总结
1.1空间几何体的结构
1、画轴 2、画底面
3、画侧棱 4、成图
确定平行线段 确定线段长度
1.3空间几何体的表面积与体积
1.3.1柱体、椎体、台体、球体的 表面积与体积
r O
r ' O
l r’＝r
l r’＝0
l
O
r 上底扩大
O
r 上底缩小
O
S柱 2r(r l) S台 (r2 r 2 rl rl ) S锥 r(r l)
侧棱 D' A'
D
A
C' 上底面
B' 侧面 C
下底面
B
棱锥特点： 1.可看作用一个平行于棱锥 底面的平面去截棱锥.
O'
轴
母线
侧面
O
底面
母线 S 轴
侧面
底面
O
圆柱特点： 1.以矩形的一边所在直线为 旋转轴，其余三边旋转形成 的面所围成的旋转体.
圆锥特点： 1.以直角三角形的一条直角 边所在直线为旋转轴，其余 两边旋转形成的面所围成的 旋转体.
轴
母线 O'
侧面
O
底面
圆台特点： 1.用平行于圆锥底面的平面 去截圆锥，底面与截面之间 的部分.
球体特点：
半径 1.以半圆的直径所在直线为
O
球心 旋转轴，半圆面旋转一周形
4. 画空间几何体的三视图时注意 长对正,高平齐,宽相等.
5. 画空间几何体的直观图时注意 x,y轴相交成45°，平行x轴的线段的长 度保持不变.平行y轴的线段的长度变为 本来的一半.
要点总结
1.1空间几何体的结构
1、画轴 2、画底面
3、画侧棱 4、成图
确定平行线段 确定线段长度
1.3空间几何体的表面积与体积
1.3.1柱体、椎体、台体、球体的 表面积与体积
r O
r ' O
l r’＝r
l r’＝0
l
O
r 上底扩大
O
r 上底缩小
O
S柱 2r(r l) S台 (r2 r 2 rl rl ) S锥 r(r l)
侧棱 D' A'
D
A
C' 上底面
B' 侧面 C
下底面
B
棱锥特点： 1.可看作用一个平行于棱锥 底面的平面去截棱锥.
O'
轴
母线
侧面
O
底面
母线 S 轴
侧面
底面
O
圆柱特点： 1.以矩形的一边所在直线为 旋转轴，其余三边旋转形成 的面所围成的旋转体.
圆锥特点： 1.以直角三角形的一条直角 边所在直线为旋转轴，其余 两边旋转形成的面所围成的 旋转体.
轴
母线 O'
侧面
O
底面
圆台特点： 1.用平行于圆锥底面的平面 去截圆锥，底面与截面之间 的部分.
球体特点：
半径 1.以半圆的直径所在直线为
O
球心 旋转轴，半圆面旋转一周形
《新课程标准高中数学必修②复习讲义》第一、二章-立体几何
一、立体几何知识点归纳 第一章 空间几何体（一)空间几何体的结构特征（1）多面体——由若干个平面多边形围成的几何体.围成多面体的各个多边形叫叫做多面体的面，相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做顶点.旋转体--把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其中,这条定直线称为旋转体的轴。
（2）柱，锥,台，球的结构特征 1。
棱柱1。
1棱柱—-有两个面互相平行，其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱。
1。
2相关棱柱几何体系列(棱柱、斜棱柱、直棱柱、正棱柱）的关系： ①⎧⎪⎧−−−−−→⎨⎪−−−−−→⎨⎪⎪⎩底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱 底面为矩形侧棱与底面边长相等1.3①侧棱都相等,侧面是平行四边形;②两个底面与平行于底面的截面是全等的多边形； ③过不相邻的两条侧棱的截面是平行四边形；④直棱柱的侧棱长与高相等，侧面与对角面是矩形。
1。
4长方体的性质：①长方体一条对角线长的平方等于一个顶点上三条棱的平方和；【如图】222211AC AB AD AA =++②（了解)长方体的一条对角线1AC 与过顶点A 的三条棱所成的角分别是αβγ，，，那么222cos cos cos 1αβγ++=，222sin sin sin 2αβγ++=；③（了解）长方体的一条对角线1AC 与过顶点A 的相邻三个面所成的角分别是αβγ，，,则，222sin sin sin 1αβγ++=222cos cos cos 2αβγ++=.1.5侧面展开图:正n 棱柱的侧面展开图是由n 个全等矩形组成的以底面周长和侧棱长为邻边的矩形. 1.6面积、体积公式：2S c hS c h S S h=⋅=⋅+=⋅直棱柱侧直棱柱全底棱柱底，V （其中c 为底面周长,h 为棱柱的高)2.圆柱2。
1圆柱—-以矩形的一边所在的直线为旋转轴，其余各边旋转而形成的曲面所围成的几何体叫圆柱.2.2圆柱的性质：上、下底及平行于底面的截面都是等圆;过轴的母线截面（轴截面）是全等的矩形.2。
第一章空间几何体小结复习
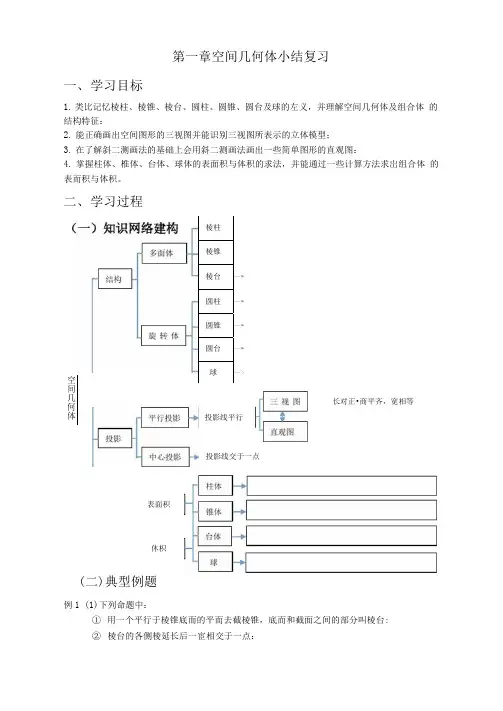
第一章空间几何体小结复习一、 学习目标1. 类比记忆棱柱、棱锥、棱台、圆柱、圆锥、圆台及球的左义，并理解空间几何体及组合体 的结构特征：2. 能正确画出空间图形的三视图并能识别三视图所表示的立体模型；3. 在了解斜二测画法的基础上会用斜二测画法画出一些简单图形的直观图：4. 掌握柱体、椎体、台体、球体的表面积与体积的求法，并能通过一些计算方法求岀组合体 的表而积与体积。
二、 学习过程(二)典型例题例1 (1)下列命题中：① 用一个平行于棱锥底而的平而去截棱锥，底而和截面之间的部分叫棱台:② 棱台的各侧棱延长后一宦相交于一点： 空间几何体 棱柱棱锥棱台—► 圆柱—► 圆锥—► 圆台—► 球—> 长对正•商平齐，宽相等 投影线交于一点 投影线平行休枳 表面积③ 圆台可以看做直角梯形以托垂直于底边的腰所在的直线为旋转轴，其余三边旋转形 成的曲而围成的几何体：④ __________________________________________________________________ 以半圆所在直径为旋转轴，半圆旋转一周形成球。
正确命题的序号是 ______________________ O（2） 一棱锥的侧棱都相等，所有的侧而上的髙也相等，则这个棱锥的底面是（） A.直角三角形 B.菱形 C.正多边形 D.矩形8000 B. 3D. 4000 例3圆柱内有一个内接长方体AC [t 长方体对角线长是10JN 协，圆柱的侧面展开图为矩 形，此矩形的而积是IOO^VH 2,求圆柱的体积。
例4 一个直角梯形的两底长为2和5,高为4,将英绕较长的底旋转一周，求所得旋转体的 侧面积。
三、 总结提升1•对于空间几何体的结构特征，一是要类比记忆棱柱、棱锥、棱台等多而体的概念性质：二 是圆柱、圆锥、圆台及球都是旋转体，轴截面是解决这四类几何体问题的关键。
2. 对于简单的空间几何体，要能正确画出三视图，同样要由三视图想象出空间几何体的模型; 对于斜二测画法，不仅要理解画法规则，还要能将三视图和宜观图进行相互的转换，而且还 能进行相关的计算。
人教版高中数学必修立体几何复习课件(共102张PPT)
1 1
1
11.已知某个几何体的三视图如图2，根据图中标出的尺寸 （单位：cm），可得这个几何体的体积是_____8_0__0.0 cm 3
3
2 0 20
主视图
10
10
2 俯0视图
2 侧0视图
第二章 点、直线、平面之间的位置关系
• 四个公理
直线与直线位置关系 • 三类关系 直线与平面位置关系
平面与平面位置关系
（3）
a a
// b
b
（较常用）；
（4）
a
//
a
；
（5）
a a
b
a
（面面垂直 线面垂直）
a b
4.面面垂直
向的侧视图（或称左视图）为（
A
A
H
G
Q
B
C
侧视 B
）A
C
I
P
E
图1
F
B
D
E
D
图2
F
B
B
B
E A．
E B．ቤተ መጻሕፍቲ ባይዱ
E C．
E D．
练习10：(1)如图是一个空间几何体的三
视图，如果直角三角形的直角边长均为
正视图 侧视图
1，那么几何体的体积为( ) C
A．1 B．1 C． 1 D．1
俯视图
2
3
6
V1 3S底 h1 31111 3
②判定定理：如果一个平面内的两条相交直线都平行于 另一个平面，那么两个平面互相平行；
符号表述： a,b , a b O, a //,b // //
//
③面面平行的性质定理：
a
a
//
人教A版高中数学必修二课件：第一章 空间几何体阶段复习课(共43张PPT)
的时光。 永不言败，是成功者的最佳品格。 生命太过短暂，今天放弃了明天不一定能得到。 自卑是剪了双翼的飞鸟，难上青天，这两者都是成才的大忌。 如果我不坚强，那就等着别人来嘲笑。 有人将你从高处推下的时候恰恰是你展翅高飞的最佳时机。 自己选择的路，跪着也要把它走完。 一个今天胜过两个明天。 我们的人生必须励志，不励志就仿佛没有灵魂。 快乐要懂得分享，才能加倍的快乐。 宁可失败在你喜欢的事情上，也不要成功在你所憎恶的事情上。 命是弱者的借口，运是强者的谦辞，辉煌肯定有，就看怎么走。 生活中若没有朋友，就像生活中没有阳光一样。 生命力的意义在于拚搏，因为世界本身就是一个竞技场。 只有坚持才能获得最后的成功。 鸟欲高飞先振翅，人求上进先读书。 过错是暂时的遗憾，而错过则是永远的遗憾！ 尽管社会是这样的现实和残酷，但我们还是必须往下走。 人生如棋，走一步看一步是庸者，走一步算三步是常者，走一步定十步是智者。 能够摄取必要营养的人要比吃得很多的人更健康，同样地，真正的学者往往不是读了很多书的人，而是读了有用的书的人。
空间几何体的结构及其三视图和直观图复习课课件
变式训练 2 将正三棱柱截去三个 角(如图 1 所示 A，B，C 分别是 △GHI 三边的中点)得到几何体如 图 2，则该几何体按图 2 所示方向 的侧视图为选项图中的 ( A )
解析
解题时在图 2 的右边放扇墙 ( 心中有
墙)，可得答案 A.
题型三
几何体的直观图
例 3 已知△ABC 的直观图 A′B′C′是边长为 a 的正三角形，求原△ABC 的面积. 思维启迪：按照直观图的画法，建立适当的坐
答案
①④
探究提高 解决该类题目需准确理解几何体的 定义，要真正把握几何体的结构特征，并且学 会通过反例对概念进行辨析，即要说明一个命 题是错误的，设法举出一个反例即可.
变式训练 1 以下命题： ①以直角三角形的一边为轴旋转一周所得 的旋转体是圆锥； ②以直角梯形的一腰为轴旋转一周所得的 旋转体是圆台； ③圆柱、圆锥、圆台的底面都是圆； ④一个平面截圆锥，得到一个圆锥和一个圆 台. 其中正确命题的个数为( A.0 B.1 ) C.2 D.3
标系将三角形 A′ B′ C′ 还原， 并利用平面几 何的知识求出相应的线段、角，求解时要注意 线段和角的变化规律.
解 建立如图所示的坐标系 xOy′，△A′B′C′的顶点 C′在 y′ 轴上，A′B′边在 x 轴上，
把 y′轴绕原点逆时针旋转 45° 得 y 轴，在 y 轴上取点 C 使 OC＝2OC′，A、B 点即为 A′、 B′点，长度不变. 已知 A′B′＝A′C′＝a，在△OA′C′中， OC′ A′C′ 由正弦定理得 ＝ ， sin 45° sin∠OA′C′ sin 120° 6 所以 OC′＝ a＝ a， sin 45° 2 所以原三角形 ABC 的高 OC＝ 6a， 1 6 2 所以 S△ABC＝ × a× 6a＝ a . 2 2
复习课(一) 空间几何体及点、线、面的位置关系
(3)该几何体由一个长、宽、高分别为 2,1,1 的长方体和两个底 面半径为 1，高为 1 的四分之一圆柱体构成，
∴V＝2×1×1＋2×41×π×12×1＝2＋π2. [答案] (1)A (2)① (3)2＋π2
首页
上一页
下一页
末页
结束
[类题通法] (1)紧扣结构特征是判断的关键，熟悉空间几何体的结构特征， 依据条件构建几何模型，在条件不变的情况下，变换模型中的线 面关系或增加线、面等基本元素，然后再依据题意判定． (2)求不规则几何体的表面积时，通常将所给几何体分割成基 本的柱、锥、台体，先求这些柱、锥、台体的表面积，再通过求 和或作差求得几何体的表面积．
(3)侧、俯视图都反映了物体的宽度——“宽相等”．
2．表面积
(1)多面体的表面积：多面体的各个面都是平面，表面积是各
面面积之和．
(2)旋转体的表面积：
①S圆柱＝2πrl＋2πr2；
②S圆锥＝πrl＋πr2；
③S圆台＝π(R＋r)l＋πr2＋πR2.
首页
上一页
下一页
末页
结束
3．体积
(1)柱体：V柱体＝Sh(S为底面面积，h为高)．
首页
上一页
下一页
末页
[类题通法] 1．平行、垂直关系的相互转化
结束
2．证明空间线面平行或垂直需注意三点 (1)由已知想性质，由求证想判定． (2)适当添加辅助线(或面)是解题的常用方法之一． (3)用定理时要先明确条件，再由定理得出相应结论．
3 2 π.
(2)由正视图知，三棱柱的底面边长为2，高为1，外接球的球心
在上下两个三角形中心连线的中点上，连接球心和任意一个顶点的
线段长为球的半径，则R2＝12
空间几何体的表面积与体积的复习课课件
2. 所 有 棱 长 为 1 的 正 三 棱 锥 的 全 面 积 3 为 . 解析 3 2 S＝4× × ＝ 3. 1 4
3. 如 图 所 示 ， 在 棱 长 为 4 的 正 方 体 ABCD—A1B1C1D1 中，P 是 A1B1 1 上一点，且 PB1＝ A1B1，则多 4 面 体 为
解析
16 3
a，则长方体的体对角线长为 (2a)2＋a2＋a2＝ 6a.又长方体外接球的直径 2R 等于长方体的 体对角线，∴2R＝ 6a.∴S 球＝4πR2＝6πa2.
题型剖析
题型一 几何体的展开与折叠 例 1 有一根长为 3π cm， 底面半径为 1 cm 的圆 柱形铁管，用一段铁丝在铁管上缠绕 2 圈， 并使铁丝的两个端点落在圆柱的同一母线 的两端，求铁丝的最短长度为多少？ 思维启迪： 把圆柱沿这条母线展开，将问题转
P—BCC1B1 的 体 积 .
∵四棱锥 P—BB1C1C 的底面积为 16，
高 PB1＝1， 1 16 ∴VP—BB1C1C＝ × 1＝ . 16× 3 3
4. 若正方体的棱长为 2，则以该正方体各个 面的中心为顶点的凸多面体的体积为( B ) 2 2 3 2 A. B. C. D. 6 3 3 3
化为平面上两点间的最短距离.
解
把圆柱侧面及缠绕其上的铁丝展开，在平
面上得到矩形 ABCD(如图所示)， 由题意知 BC ＝3π cm，AB＝4π cm， A 点 与点 C 分别是铁丝的起、 止 位置，故线段 AC 的长度即 为铁丝的最短长度. AC＝ AB2＋BC2＝5π cm， 故铁丝的最短长度为 5π cm.
1 V＝ (S 上＋S 下 3 圆台 ＋ S上S下)h＝ π(r1＋r2)l S 侧＝________ 1 π(r2＋r2＋ 3 1 2 r1r2)h 直棱 柱 正棱 锥
高一数学《第一章空间几何体》复习课件
A
B. 1cm 3 D. 4cm 3
正视图
3cm
侧视图
B
C
俯视图
A'
B'
C'
你能说说如何画空间 几何体的直观图吗？
z y′ A′ B′ y A o B x′
x
D′ A′ D′ z D C′ A B B′
C′
C
A′ D
y B′ Q
o
C x 你能说说如何画空间 几何体的直观图吗？
A
P
B
作业：
P36复习参考题A组：6，7. P37复习参考题B组：2，4.
2 2 2
图（1）
思考：若不通过计算，你能判断哪种设计比较省？
来做个题吧！
在梯形ABCD中，B是直角，CD=BC=1，AB=2， 请 选择其中的一边作为旋转轴，求出该旋转体的表 面积。
D
C
A
B
来做个题吧！
有一个正三棱柱，其三视图如图： 则其体积等于（ ）
2cm
A. 3cm 3 3 3 3 C. cm 2
球，圆柱，圆台的组合体
球，正四棱柱，正四棱台的组合体
算一算
如果奖杯是实心的，则选取哪种设计用料比较省？ （见图（1）（2））
8
8 20
4
14 20
图（1） 台体的体积： V 球的体积：
图（2）
V sh 1 锥体的体积：V sh 3
柱体的体积：
1 ' ( s s ' s s )h 3
1、将一个钢球放入底面半径为4厘米的圆柱容器 中，水面升高9厘米，则钢球的半径是……厘米； 2、如图所示是水平放置的三角形的直观图，D是 线段BC的中点，则三条线段AB、AC、BC中， 最长的是……；最短的是……。
B. 1cm 3 D. 4cm 3
正视图
3cm
侧视图
B
C
俯视图
A'
B'
C'
你能说说如何画空间 几何体的直观图吗？
z y′ A′ B′ y A o B x′
x
D′ A′ D′ z D C′ A B B′
C′
C
A′ D
y B′ Q
o
C x 你能说说如何画空间 几何体的直观图吗？
A
P
B
作业：
P36复习参考题A组：6，7. P37复习参考题B组：2，4.
2 2 2
图（1）
思考：若不通过计算，你能判断哪种设计比较省？
来做个题吧！
在梯形ABCD中，B是直角，CD=BC=1，AB=2， 请 选择其中的一边作为旋转轴，求出该旋转体的表 面积。
D
C
A
B
来做个题吧！
有一个正三棱柱，其三视图如图： 则其体积等于（ ）
2cm
A. 3cm 3 3 3 3 C. cm 2
球，圆柱，圆台的组合体
球，正四棱柱，正四棱台的组合体
算一算
如果奖杯是实心的，则选取哪种设计用料比较省？ （见图（1）（2））
8
8 20
4
14 20
图（1） 台体的体积： V 球的体积：
图（2）
V sh 1 锥体的体积：V sh 3
柱体的体积：
1 ' ( s s ' s s )h 3
1、将一个钢球放入底面半径为4厘米的圆柱容器 中，水面升高9厘米，则钢球的半径是……厘米； 2、如图所示是水平放置的三角形的直观图，D是 线段BC的中点，则三条线段AB、AC、BC中， 最长的是……；最短的是……。
高中数学必修2第一章-空间几何体PPT优秀课件
棱柱的侧面: 其余各面；
棱柱的侧棱: 相邻侧面的公共边；E'
棱柱的顶点: 侧面与底面 A'
的公共顶点.
B'
D' C'
E
A
D
B
C
3. 棱柱——分类 以底面多边形的边数作为分类的标
准分为三棱柱、四棱柱、五棱柱等.
4. 棱锥——定义
有一个面是多边形，其余各面都是
有一个公共顶点的三角形，由这些面所
围成的几何体叫棱锥.
由简单几何体拼接而成的； 简单几何体截去或挖去一部分而成的.
练习
1. 已知圆锥的轴截面等腰三角形的腰长为 5cm, 面积为12cm2,求圆锥的底面半径.
2. 已知圆cm柱2 的底面半径为3cm，轴截面面 积为24cmc2 m2，求圆柱的母线长.
3. 正四棱锥的底面积为48 cm2，侧面等 腰三角形面积为6cm2，求正四棱锥侧棱.
x
GO
H
CF D
第二十一讲 空间几何体的表面积和体积
一、引言 （一）本节的地位：空间几何体的表面积和 体积是从度量的角度认识空间几何体，是空 间几何体学习的重要内容，也是继续研究和 学习立体几何的基础，具体有两个任务：一 是根据空间几何体的结构特征并结合它们的 展开图，推导它们的表面积的计算公式；二 是在初中学习几何体体积的基础上进一步学 习几何体的体积.
上底面
侧面
母线
轴
下底面
讨论：棱台、圆台分别具有一些什么 几何性质？
四．球体的结构特征： ①定义：以半圆的直径所在直线为旋转 轴，半圆面旋转一周形成的几何体，叫 球体.
半径
O
球心
3．简单组合体的结构特征：
第一章空间几何体优秀复习高一数学-资料.ppt
7.球的定义： 以半圆的直径所在直线为旋转轴，半圆面旋转 一周形成的几何体叫做球体，简称球。
圆柱,圆锥,圆台及球体都是旋转体
二、空间几何体的三视图与直观图
1.几何体的三视图
正视图:光线从几何体的前面向后面正投影 得到的投影图. 侧视图:光线从几何体的左面向右面正投 影得到的投影图.
俯视图:光线从几何体的上面向下面正
A.6 3 B.24 3 C.242 3 D.32
• 11．（07年广东 本小题满分12分） 已知某几何体的俯视图是如图所示的矩形，正视图（或称 主视图）是一个底边长为8，高为4的等腰三角形，侧视图 （或称左视图）是一个底边长为6，高为4的等腰三角形.（ 1）求该几何体的体积；（2）求该几何体的侧面积．
14.已知某个几何体的三视图如图（主视图中的弧线是半圆），
根据图中标出的尺寸（单位：cm ），可得这个几何体的体积
A 是(
)cm3 ．
A .8
C .12
B .8 2
3
D .12 2
3
1 2 2 主视图
3 侧视图
2 俯视图
已知一几何体的三视图如下图，试求其表面积与
体积.
1
1
1
主视图
侧视图
4.球的表面积公式 S球 面4 R2
空间几何体的表面积和体积 圆柱的侧面积：S2rl
面积
圆锥的侧面积：S rl
圆台的侧面积：S(rr)l
球的表面积： S4R2
柱体的体积：V Sh
体积
锥体的体积：V 1 S h 3
台体的体积：V1(S SSS)h 3
球的体积：V 4 R 3
3
1.如图，一个空间几何体的正视
投影得到的投影图.
圆柱,圆锥,圆台及球体都是旋转体
二、空间几何体的三视图与直观图
1.几何体的三视图
正视图:光线从几何体的前面向后面正投影 得到的投影图. 侧视图:光线从几何体的左面向右面正投 影得到的投影图.
俯视图:光线从几何体的上面向下面正
A.6 3 B.24 3 C.242 3 D.32
• 11．（07年广东 本小题满分12分） 已知某几何体的俯视图是如图所示的矩形，正视图（或称 主视图）是一个底边长为8，高为4的等腰三角形，侧视图 （或称左视图）是一个底边长为6，高为4的等腰三角形.（ 1）求该几何体的体积；（2）求该几何体的侧面积．
14.已知某个几何体的三视图如图（主视图中的弧线是半圆），
根据图中标出的尺寸（单位：cm ），可得这个几何体的体积
A 是(
)cm3 ．
A .8
C .12
B .8 2
3
D .12 2
3
1 2 2 主视图
3 侧视图
2 俯视图
已知一几何体的三视图如下图，试求其表面积与
体积.
1
1
1
主视图
侧视图
4.球的表面积公式 S球 面4 R2
空间几何体的表面积和体积 圆柱的侧面积：S2rl
面积
圆锥的侧面积：S rl
圆台的侧面积：S(rr)l
球的表面积： S4R2
柱体的体积：V Sh
体积
锥体的体积：V 1 S h 3
台体的体积：V1(S SSS)h 3
球的体积：V 4 R 3
3
1.如图，一个空间几何体的正视
投影得到的投影图.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
优秀课件
23
作业：
P36复习参考题A组：6，7. P37复习参考题B组：2，4.
优秀课件
24
1、将一个钢球放入底面半径为4厘米的圆柱容器 中，水面升高9厘米，则钢球的半径是……厘米；
2、如图所示是水平放置的三角形的直观图，D是 线段BC的中点，则三条线段AB、AC、BC中， 最长的是……；最短的是……。
优秀课件
5
5 4
3
正视图
侧视图
俯视图
优秀课件
6
3
5
4
正视图
侧视图
俯视图
优秀课件
7
4 5
3
正视图
侧视图
俯视图
优秀课件
8
例2 有一个几何体由8个面围成，每
一个面都是正三角形，并且有四个顶点A，
B，C，D在同一个平面内，ABCD是边长为
30cm的正方形.说明这个几何体的结构特
征，画出其直观图和三视图，并求出它
第一章 空间几何体单元复习
优秀课件
1
知识框架
一、空间几何体的结构
柱体
棱柱 圆柱
锥体 台体
棱锥
圆锥 棱台 圆台
球体
优秀课件
简单组合体
2
t
二、空间几何体的三视图和直观图 p
1 2
5730
投影
中心投影
平行投影
三视图 直观图
优秀课件
正视图 侧视图 俯视图
斜二测 画法
3
三、空间几何体的表面积和体积 圆柱的侧面积：
A. 3cm3
B. 1cm3
C.
3 3 cm3 2
D. 4cm3
A
B
C
A' B'
优秀课件
C'
正视图
2cm 3cm
侧视图
俯视图
21
你能说说如何画空间 几何体的直观图吗？
z
y′
A′
B′
x′ y
A
oB x
优秀课件
22
D′
z
C′
A′ D
y B′
Q
C
o
x
A
PB
D′ A′
D
A
C′ B′
C
B
你能说说如何画空间 几何体的直观图吗？
64 1576 1777
优秀课件
18
思考：若不通过计算，你能判断哪种设计比较省？
优秀课件
19
来做个题吧！
在梯形ABCD中，B是直角，CD=BC=1，AB=2， 请 选择其中的一边作为旋转轴，求出该旋转体的表 面积。
D
C
A
优秀课件
B
20
来做个题吧！
有一个正三棱柱，其三视图如图： 则其体积等于（ ）
4 43 42 20 1（ 72 72 102 102） 4
3
3
（256 612） 2190
3
优秀课件
15
图（2）
若奖杯是空心（表面厚度忽略不计），则选用哪种设计 用料比较省？（见图（1）（2））
8
8 20
4
14
20
图（1）
图（2）
S圆柱表 2 r2 2 rl S圆台表 r'2 r2 r'l rl
的表面积和体积.
P
D
两个共底四棱锥 A
C
B
优秀课件
Q
9
P
D A
C B
Q
S 1800 3cm2
正视图
V 9000 2cm3
俯视图
优秀课件
侧视图
10
例3：如图，圆柱内有一个三棱柱，三棱柱
的底面在圆柱的底面内，并且底面是正三角
形，如果圆柱的体积是v，底面直径和母线
相等，求三棱柱的体积是多少？
C1
O`
A1
B1
C
A
O
优秀课件
B
11
想一想
运动会组委会决定由学生设计运动会的奖杯，其中奖杯 的正视图与侧视图要求如图所示。(最下部分为等腰梯形）
8
8 20
4
14
20
A、球，圆柱，圆台的组合体 B、球，圆柱，正四棱台的组合体 C、球，正四棱柱，正四棱台的组合体 D、球，正四棱柱，圆台的组合体
优秀课件
12
画画一一画画
面积 体积
圆锥的侧面积：S rl
圆台的侧面积： S (r r)l
球的表面积： S 4 R2
柱体的体积：V Sh
锥体的体积： V 1 Sh
3
台体的体积：V 1 (S SS S )h
3
球的体积：优秀课件V 4 R3
4
3
综合应用
例1 直角三角形的三边长分别为3cm、 4cm、5cm，绕三边旋转一周分别形成三 个几何体.说明它们的结构特征，画出 其直观图和三视图，并求出它们的表面 积和体积.
S圆锥表 r2 rl
S球 优秀4课件r2
16
O
EO
O'
O'
H
F
优秀课件
17
S总 S球 S圆柱侧 S圆台全 4 42 2 4 20 72 102 1（2 7 2 10）5 2
458 1438
图（2） 图（1）
S总 S球 S棱柱侧 S棱台全 4 42 8420 142 202 1（14 4 20 4）5 2
锥体的体积：V 1 sh 3
图（1）
台体的体积：V
1 (s'
图（2）
s's s)h
球优的秀体课积件：
V
4
3
r3
14
图（1）
V总 V球 V棱柱 V棱台
4 43 82 20 1（142 14 20 202）4
3
3
256 1280 1168 2716
3
V总 V球 V圆柱 V圆台
如如果果选选用用下下面面两两种种设设计计，，同同学学们们能能否否选画择出奖它杯的其俯中视的图一？ 部分画出它的直观图？
球，圆柱，圆台的组合体
优秀课球件，正四棱柱，正四棱台的组合体 13
算一算
如果奖杯是实心的，则选取哪种设计用料比较省？ （见图（1）（2））
8
8 20
4
14
20
柱体的体积： V sh
A
O
B
D
C
X
优秀课件
25
例1：下图是一个空间几何体的三视图。 试试画出该几何体的直观图。
优秀课件
26
例2：请画出下面空间几何体的三视图
优秀课件
27
例4：一个长方体的三条棱长之比是
1：2：3，它的体积是48，求它的 表面积。
优秀课件
28