2020年八年级下册数学培优第一讲二次根式专题

二次根式竞赛培优题（含解析）一．选择题（共5小题）1．计算：=（）A．3994001B．3994002C．3994003D．39940002．计算：=（）A．B．C．D．3．的结果是（）A．B．C．D．4．的值是（）A．B．C．1D．5．在这1000个二次根式中，与是同类二次根式的个数共有（）A．3B．4C．5D．6二．填空题（共24小题）6.已知实数x1，x2，x3，…，x1999满足．则x1+2x2+3x3+…+1999x1999的值为．7．化简=．8．化简．9．观察图形，用S i表示第i个三角形的面积，有；；，…，若S1+S2+S3+…+S n＞10，则n的最小值为．10．方程的解是x=11．设M=+++┉+，N=1﹣2+3﹣4+5﹣6+┉+1993﹣1994，则=．12．计算：=（其中a＞0）13．的值为．14．已知：对于正整数n，有，若某个正整数k满足，则k=．15．若n为整数，且是自然数，则n=．16．如果，并且表示为时的值，即，表示当时的值，即，那么的值为．17．若u、v满足v=，则u2﹣uv+v2=．18．已知a为实数，且与都是整数，则a的值是．19．使得++=1的一组正整数（a，b，c）为：．20．计算﹣20062的结果是．21．设=．22．若，，则x6+y6的值是．23．当时，的值为．24．已知，，则k=．25．当1≤x≤2时，经化简等于．26．计算=．27．已知x=，那么+1的值是．28．化简：，得到．29．=．三．解答题（共1小题）30．计算：（1）；（2）；（3）；（4）．二次根式竞赛培优题（含解析）参考答案与试题解析一．选择题（共5小题）1．计算：=（）A．3994001B．3994002C．3994003D．3994000【分析】设1998=a，把被开方数变形后，利用多项式的乘法法则计算后，加上a2再减去a2，前三项结合提取a2，剩下的三项利用完全平方公式化简，接着三项合并后提取2a，整体再利用完全平方公式化简，从而得到被开方数为一个数的完全平方，利用化简公式=|a|及a大于0即可得到最后结果．【解答】解：设1998=a，则1997×1998×1999×2000+1=（a﹣1）a（a+1）（a+2）+1=a4+2a3+a2﹣a2﹣a2﹣2a+1=a2（a+1）2﹣2a（a+1）+1=[a（a+1）﹣1]2，所以==1998×1999﹣1=3994001．故选：A．【点评】此题考查了二次根式的化简求值，考查了换元的思想，本题的技巧性比较强，要求学生熟练掌握完全平方公式的结构特点，同时注意利用凑项的方法构造满足公式的特征，以及注意二次根式的化简公式=|a|的运用．2．计算：=（）A．B．C．D．【分析】根据每个加数的特点，推出一般规律为，将所得式子化简，分别取n=1，2，3，…，40，寻找抵消规律，得出结论．【解答】解：∵=（）=（）=（）=（﹣）∴分别取n=1，2，3， (40)原式=[（1﹣）+（﹣）+（﹣）+…+（﹣）]=（1﹣）=．故选：B．【点评】本题考查了二次根式的化简求值，观察式子的特点，得出一般规律，将一般规律化简代值，再观察抵消规律是解题的关键．3．的结果是（）A．B．C．D．【分析】把每个加数分母有理化，然后通分计算即可．【解答】解：=（）=．故选：D．【点评】主要考查二次根式的分母有理化．主要利用了平方差公式，所以一般二次根式的有理化因式是符合平方差公式的特点的式子．4．的值是（）A．B．C．1D．【分析】认真观察式子的特点，总结规律，可发现，，，据此作答．【解答】解：由题意可知第k项是∴原式=（++=1﹣=1﹣=．故选：B．【点评】此题考查二次根式的化简求值，关键是审清题意，找准规律答题．5．在这1000个二次根式中，与是同类二次根式的个数共有（）A．3B．4C．5D．6【分析】找到1000＜5×x2＜2000中符合x的整数值即可得出答案．【解答】解：由题意得：与=20，是同类二次根的被开方数一定为5，由此及题意可：1000＜5×x2＜2000，x可取15、16、17、18、19，共5个．故选：C．【点评】本题考查同类二次根式的知识，有一定难度，关键是根据同类二次根式的形式得出的同类二次根式应该满足．二．填空题（共24小题）6．已知实数x1，x2，x3，…，x1999满足．则x1+2x2+3x3+…+1999x1999的值为3998000．【分析】由等式可知=x1，=x2，…解得x1=x2=x3=…=x1999=2，由此代入求得数值即可．【解答】解：∵，∴=x1，=x2，…∴x1=x2=x3=…=x1999=2，∴x1+2x2+3x3+…+1999x1999=2×（1+2+3+ (1999)=2×（1999+1）×1999÷2=3998000．故答案为：3998000．【点评】此题考查二次根式的化简求值，解答此题的关键是找出对应关系，求出x1、x2、x3、…、x1999的值．7．化简=2011．【分析】先根据平方差公式和二次根式的性质得到=，然后根据同样的方法由内到外依次化简即可得到答案．【解答】解：∵=，∴原式=======2011．故答案为2011．【点评】本题考查了二次根式的性质与化简：=|a|．也考查了平方差公式．8．化简后2．【分析】由于===﹣1，其他根式也可以进行同样的化简，然后合并同类二次根式即可求解．【解答】解：=﹣1+﹣++++++=3﹣1=2．故答案为：2．【点评】此题主要考查了二次根式的化简求值，解题的关键是利用完全平方公式化简二次根式从而达到化简题目的目的．9．观察图形，用S i表示第i个三角形的面积，有；；，…，若S1+S2+S3+…+S n＞10，则n的最小值为10．【分析】利用不等式≤，结合S1+S2+S3+…+S n ＞10，解不等式即可．【解答】解：∵S i表示第i个三角形的面积，由不等式≤n，得≤n=n，而S1+S2+S3+…+S n=，S1+S2+S3+…+S n＞10，∴n＞10，即n2（n+1）＞800，n为正整数，n的最小值为9．但n=9时，代入S1+S2+S3+…+S n＜10，不符合题意，故n=10．【点评】本题考查了二次根式的运用．利用均值不等式和不等式的传递性解题．10．方程的解是x=2011【分析】将各分式中的分母有理化，再通分，注意观察抵消规律．【解答】解：原方程化为：+++…+=，通分得=，解得x=2011．故答案为：2011．【点评】本题考查了二次根式的化简在解方程中的运用．关键是将各分式的分母有理化，寻找抵消规律．11．设M=+++┉+，N=1﹣2+3﹣4+5﹣6+┉+1993﹣1994，则=﹣．【分析】首先将M式中各个分式进行分母有理化，再求出N式的值，代入代数式求值即可解答．【解答】解：将M分母有理化可得M=（﹣1）+（﹣）+（﹣）+…+（﹣）=﹣1．N=1﹣2+3﹣4+5﹣6+┉+1993﹣1994=（1﹣2）+（3﹣4）+（5﹣6）+┉+（1993﹣1994）=﹣1×997=﹣997，∴==﹣．故答案为﹣．【点评】本题主要考查分母有理化的方法，正确选择两个二次根式，使它们的积符合平方差公式是解答问题的关键．12．计算：=4（其中a＞0）【分析】仔细观察会发现有以下规律：第1项加上第8项等于1，第2项加上第7项等于1，依此类推最后求得的结果4．【解答】解：第一项与最后一项相加得：+，=+，=，=1，同理可得：第二项与倒数第二项的和也是1；第三项与倒数第三项的和也是1；所以原式=1+1+1+1=4．故应填：4．【点评】本题考查了二次根式的加减运算，同时也考查了学生的逻辑思维能力，是一道不错的规律型问题．13．的值为1998999.5．【分析】本题涉及数字大且数字之间有联系，可用换元法解题，设k=2000，将所求算式转化为关于k的算式，将被开方数配成完全平方式，开平方，再将k的值代入即可．【解答】解：设k=2000，原式=====，当k=2000时，原式=1998999.5．故本题答案为：1998999.5．【点评】本题考查了二次根式的化简求值，当算式数字较大，并且数字之间有联系时，用换元法解题，可使运算简便．14．已知：对于正整数n，有，若某个正整数k满足，则k=8．【分析】读懂规律，按所得规律把左边所有的加数写成的形式，把互为相反数的项结合，可使运算简便．【解答】解：∵，∴+，即1﹣，∴，解得k=8．故答案为：8．【点评】解答此题的关键是读懂题意，总结规律答题．15．若n为整数，且是自然数，则n=﹣14或﹣7或﹣2或5．【分析】设=p，再把等式两边同时乘以4，利用平方差公式把等式左边化为两个因式积的形式，列出关于p、n的方程组，求出n 的值即可．【解答】解：∵设=p（P为非负整数），则n2+9n+30=p2，∴4n2+36n+120=4p2，∴（2n+9）2+39=4p2，∴（2p+2n+9）（2p﹣2n﹣9）=39，∴或或或，解得或或或，∴n=﹣14或﹣7或﹣2或5．故答案为：﹣14或﹣7或﹣2或5．【点评】本题考查的是二次根式的性质与化简，先根据题意把原式化为两个因式积的形式是解答此题的关键．16．如果，并且表示为时的值，即，表示当时的值，即，那么的值为2012.5．【分析】根据新定理得f（）=，f（）=，则f（）+f（）=1；f（）=，f（）=，则f（）+f（）=1，由此得到f（）+f（）=1（n≥2的整数），所以原式=+．【解答】解：f（）=，∵f（）==，f（）=，则f（）+f（）=1，f（）==，f（）==，则f（）+f（）=1，∴f（）+f（）=1，∴=+=2012.5．故答案为2012.5．【点评】本题考查了二次根式的化简求值：二次根式的化简求值，一定要先化简再代入求值．也考查了阅读理解能力．17．若u、v满足v=，则u2﹣uv+v2=．【分析】根号里面的式子大于等于0，从而可得≥0，﹣≥0，从而能得出u和v的值，继而可得出答案．【解答】解：由题意得：≥0，﹣≥0，从而=0，2u﹣v=0，u=v，又v=，∴u=，∴u2﹣uv+v2=．故答案为．【点评】本题考查二次根式有意义的条件，注意掌握根号里面的式子大于等于0这个知识点比较关键．18．已知a为实数，且与都是整数，则a的值是或．【分析】由是正整数可得，a是含﹣2的代数式；再由是整数，可得化简后为﹣2的代数式分母有理化后，是1或﹣1，据此确定a的值．【解答】解：∵是正整数，∴a是含﹣2的代数式；∵是整数，∴化简后为﹣2的代数式分母有理化后，是1或﹣1，∴a=或．故答案为：或．【点评】此题主要考查二次根式的混合运算，要熟练掌握合并同类二次根式和分母有理化．19．使得++=1的一组正整数（a，b，c）为：答案不唯一；如（288，8，8），（48，24，8）．【分析】由于三个复合二次根式的和为1，则它们的被开方数为完全平方数，设任意一个复合二次根式的被开方数为（）2（x，y为正整数，x＞y），然后通过正整数的含义，得到x，y为两个相邻正整数，即每个复合二次根式化简后为两个相邻正整数的算术平方根．若第一个化简后是﹣1，则第二个复合二次根式化简后必为﹣，第三个复合二次根式化简后必为，最后求的a，b，c的值．【解答】解：因为几个复合二次根式的和为1，则每个复合二次根式的被开方数一定为完全平方数．设==x+y﹣2，（x，y为正整数，x＞y），所以有=x+y，﹣=﹣2．∴a+1=（x+y）2，a=4xy，∴（x﹣y）2=1，即x﹣y=1．则每个复合二次根式化简后为两个相邻正整数的算术平方根．若第一个化简后为﹣1，而要消掉，则第二个复合二次根式化简后必为﹣，要消掉，则第三个复合二次根式化简后必为．最后正好为﹣=1．所以=（﹣1）2=3﹣=3﹣，则a=8，同理得b=24，c=48．故得到一组正整数（a，b，c）为：8，24，48．故答案为8，24，48．【点评】本题考查了二次根式的性质和二次根式的化简：．20．计算﹣20062的结果是2005．【分析】先把“2005×2006×2007×2008+1=（20052+3×2005+1）2”化为完全平方的形式，再开平方，然后再来求值．【解答】解：∵2005×2006×2007×2008+1=2005×（2005+3）×（2005+1）（2005+2）+1=（20052+3×2005）×（20052+3×2005+2）+1=（20052+3×2005）2+2（20052+3×2005）+1=（20052+3×2005+1）2∴=20052+3×2005+1；∴﹣20062=20052+3×2005+1﹣20062=（2005+2006）（2005﹣2006）+3×2005+1=2005；故答案为：2005．【点评】本题主要考查了二次根式的化简求值．解答此题的难点是化“2005×2006×2007×2008+1”为完全平方的形式，并开平方，然后再利用平方差公式求出20052﹣20062=（2005+2006）（2005﹣2006）的值．21．设=．【分析】把已知条件的左边相乘得，这样出现了所求代数式，设=z，代入变形所得的等式，逐步变形，消去x、y，即可求得z．【解答】解：据条件式令=z，则（1）式化为：z+xy+=9，即有9﹣z=xy+，平方得，81﹣18z+z2=x2y2+（x2+1）（y2+4）+2xy（2），又由z2==x2（y2+4）+y2（x2+1）+2xy，代入（2）得，81﹣18z=4，所以．即=，故答案为：．【点评】此题考查二次根式的化简求值，难度较大，多次利用已知条件求解．22．若，，则x6+y6的值是40．【分析】根据题意可求出x2+y2，x2﹣y2，利用平方差公式可求得x4﹣y4，（x2﹣y2）（x4﹣y4）=x6+y6﹣x2y4﹣y2x4，由此可得答案．【解答】解：由题意得：x2+y2=2++2﹣=4，x2﹣y2=2+﹣（2﹣）=2，x4﹣y4=（x2+y2）（x2﹣y2）=8，又（x2﹣y2）（x4﹣y4）=x6+y6+x2y4+y2x4，∴可得：x6+y6=32﹣x2y2（x2+y2）=32+2×4=40．故答案为：40．【点评】本题考查二次根式的乘除法运算，有一定难度，关键是熟练运用平方差及完全平方公式．23．当时，的值为．【分析】利用完全平方公式对代数式化简再把代入化简的结果计算即可．【解答】解：原式=﹣，∵，∴=2005，∴x＜，∴原式=﹣+x，=x，当时，原式=．故答案为．【点评】本题考查的是二次根式的化简求值和二次根式的性质=a（a≥0）的应用．24．已知，，则k=﹣1．【分析】先从等式右边进行分母有理化，即原式=﹣2，然后依次循环即可求k的值．【解答】解：由原式可知=+2﹣4=﹣2，∴4+=+2，依此类推得：=+2，∴k=﹣1．故答案为﹣1．【点评】本题考查了分母有理化的知识，解题时可从等式右边进行分母有理化，那样会简便些．25．当1≤x≤2时，经化简等于2．【分析】先配成完全平方式，再根据二次根式的性质化简计算即可．【解答】解：∵1≤x≤2，∴=+=+1+1﹣=2．故答案为：2．【点评】考查了二次根式的性质，解题的关键是将根号内的式子配成完全平方式．26．计算=2010．【分析】因为=，=，=，…，可发现=1+=1+1﹣，=1+=1+﹣…，依此类推再把1+1﹣，1+﹣…相加可得问题答案．【解答】解：原式=++++…+，=1+1﹣+1+﹣+1+﹣+1+﹣…+1+﹣，=2010+（1﹣+﹣+﹣…+﹣），=2010+（1﹣），=2010．【点评】本题考查了二次根式的化简，在化简中注意有关数列的规律．27．已知x=，那么+1的值是2．【分析】先根据分母有理化得到x=﹣1，所以x+1=，然后将代数式化为含有（x+1）2的形式，把x+1的值代入求出代数式的值．【解答】解：∵x==﹣1，∴x+1=．原式=（3x3+10x2+5x+4）=[（3x3+6x2+3x）+3x2+（x2+2x+1）+3]=[3x（x+1）2+3x2+（x+1）2+3]=[3x•2+3x2+2+3]=[（3x2+6x+3）+2]=[3（x+1）2+2]=（3×2+2）=2．故答案是：2．【点评】本题考查的是二次根式的化简求值，先根据分母有理化把x的值化简，得到x+1=，再把代数式化成含有x+1的形式，然后代入代数式可以求出代数式的值．28．化简：，得到1．【分析】将被开方数的分子、分母提公因式，约分，再开平方，约分即可．【解答】解：原式=（）1004=（）1004（）1004=1．【点评】本题考查了二次根式的化简求值，关键是将被开方数的分子、分母提公因式，约分．29．=﹣3．【分析】因为=，代入并通分计算即可．【解答】解：原式===﹣1﹣1﹣1=﹣3．故答案为：﹣3．【点评】此题考查二次根式的混合运算，关键是求=．三．解答题（共1小题）30．计算：（1）；（2）；（3）；（4）．【分析】（1）设n=1999，从而可将根号里面的数化为完全平方的形式，继而可得出答案．（2）分别将各二次根式配方可得出答案．（3）将分子及分母分别化简，然后运用提公因式的知识将分子及分母简化，继而得出答案．（4）设=a，=b，=c，从而可将原式化简，继而可得出答案．【解答】解：（1）设n=1999，则原式===n2+3n+1，故原式=20002+1999；（2）原式=+++++++=﹣1+﹣+﹣+﹣+﹣+﹣+﹣+﹣，=﹣1，=3﹣1，=2；（3）原式=，=，=+，=﹣；（4）设=a，=b，=c，则原式=++，=，=0．【点评】本题考查了二次根式的混合运算，难度较大，注意换元法及完全平方知识的运用．。

二次根式(g ēnsh ì)培优专题 （一）一、基础知识回顾(hu íg ù)1.二次根式(g ēnsh ì)：式子(sh ì zi)（≥0）叫做(ji àozu ò)二次根式。

2.最简二次根式：必须同时满足下列条件：⑴被开方数中不含开方开的尽的因数或因式； ⑵被开方数中不含分母； ⑶分母中不含根式。

3.同类二次根式：二次根式化成最简二次根式后，若被开方数相同，则这几个二次根式就是同类二次根式。

4.二次根式的性质： （1）（a ≥0）； （2）5.二次根式的运算：（1）因式的外移和内移：如果被开方数中有的因式能够开得尽方，那么，就可以用它的算术根代替而移到根号外面；如果被开方数是代数和的形式，那么先解因式，•变形为积的形式，再移因式到根号外面，反之也可以将根号外面的正因式平方后移到根号里面．（2）二次根式的加减法：先把二次根式化成最简二次根式再合并同类二次根式． （3）二次根式的乘除法：二次根式相乘（除），将被开方数相乘（除），所得的积（商）仍作积（商）的被开方数并将运算结果化为最简二次根式．（4）有理数的加法交换律、结合律，乘法交换律及结合律，•乘法对加法的分配律以及多项式的乘法公式，都适用于二次根式的运算．二、精典考题类型一：考查二次根式的概念（求自变量取值范围）a （a ＞（a ＜1、下列(xiàliè)各式中，不是二次根式的是（）A ．B ．C ．D ．2、二次根式(gēnshì)有意义(yìyì)时的的取值范围(fànwéi)是。

3、已知：，则= 。

类型二：考查二次根式(g ēnshì)的性质（非负性、化简）4、代数式的最大值是。

5、实数在数轴上的位置如图1所示，化简。

（图6、把的根号外的因式移到根号内得；的平方根是。

7、化简：；。

类型三：考查同类二次根式与最简二次根式（化简）8、把，，，按由大到小的顺序排列为：类型四：考查二次根式的运算（加减乘除混合运算、分母有理化）9、若，，则a与b的关系是（）A．互为相反数；B．互为倒数；C．互为负倒数；D．以上均不对。

二次根式1、算术平方根的定义：一般地，如果一个正数x的平方等于a，那么这个正数x叫做a的算术平方根。

2、解不等式（组）：尤其注意当不等式两边乘(除以)同一个负数，不等号方向改变。

如：-2x＞4，不等式两边同除以-2得x＜-2。

不等式组的解集是两个不等式解集的公共部分。

如｛3、分式有意义的条件：分母≠04、绝对值：｜a｜=a （a≥0）；｜a｜= - a （a＜0）一、二次根式的概念一般地，我们把形如 a （a≥0）的式子叫做二次根式，“”称为二次根号。

★正确理解二次根式的概念，要把握以下五点：（1）二次根式的概念是从形式上界定的，必须含有二次根号“”，“”的根指数为2，即“2”，我们一般省略根指数2，写作“”。

如25 可以写作 5 。

（2）二次根式中的被开方数既可以是一个数，也可以是一个含有字母的式子。

（3）式子 a 表示非负数a的算术平方根，因此a≥0， a ≥0。

其中a≥0是 a 有意义的前提条件。

（4）在具体问题中，如果已知二次根式 a ，就意味着给出了a≥0这一隐含条件。

（5）形如b a （a≥0）的式子也是二次根式，b与 a 是相乘的关系。

要注意当b是分数时不能写成带分数，例如832 可写成8 23，但不能写成 2232 。

练习：一、判断下列各式，哪些是二次根式？（1） 6 ；（2）-18 ；（3）x2+1 ；（4）3-8 ；（5）x2+2x+1 ；（6）3｜x｜；（7）1+2x （x＜-12）X≥-2X＜5的解集为-2≤x＜5。

二、当x 取什么实数时，下列各式有意义？（1）2-5x ；（2）4x 2+4x+1二、二次根式的性质：二次根式的性质符号语言文字语言应用与拓展注意a （a ≥0）的性质a ≥0 （a ≥0）一个非负数的算术平方根是非负数。

（1）二次根式的非负性（a ≥0，a ≥0）应用较多，如：a+1 +b-3 =0，则a+1=0，b-3=0，即a= -1，b=3；又如x-a +a-x ，则x 的取值范围是x-a ≥0，a-x ≥0，解得x=a 。

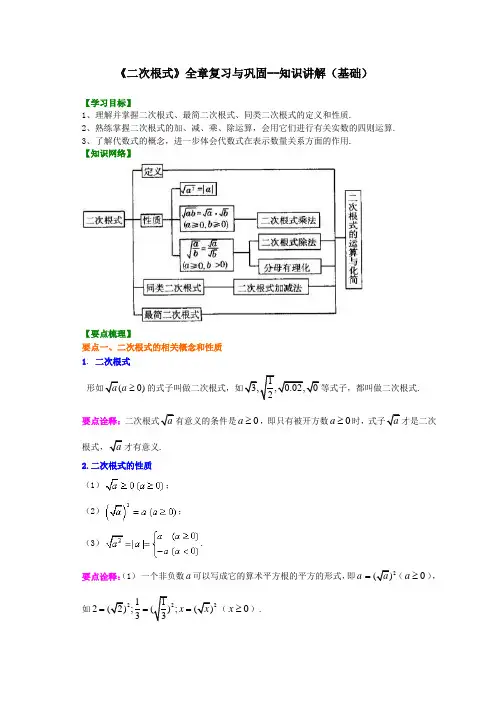
《二次根式》全章复习与巩固--知识讲解（基础）【学习目标】1、理解并掌握二次根式、最简二次根式、同类二次根式的定义和性质.2、熟练掌握二次根式的加、减、乘、除运算，会用它们进行有关实数的四则运算.3、了解代数式的概念，进一步体会代数式在表示数量关系方面的作用. 【知识网络】【要点梳理】要点一、二次根式的相关概念和性质 1. 二次根式形如(0)a a ≥的式子叫做二次根式，如13,,0.02,02等式子，都叫做二次根式. 要点诠释：二次根式a 有意义的条件是0a ≥，即只有被开方数0a ≥时，式子a 才是二次根式，a 才有意义. 2.二次根式的性质 （1）； （2）；（3）.要点诠释：（1） 一个非负数a 可以写成它的算术平方根的平方的形式，即a 2a =（0a ≥），如2221122););)33x x ===（0x ≥）.（2）a 的取值范围可以是任意实数，即不论a .（3a ，再根据绝对值的意义来进行化简.（42的异同a 可以取任何实数，而2中的a 必须取非负数；a ，2=a （0a ≥）.相同点：被开方数都是非负数，当a 2.3. 最简二次根式（1）被开方数是整数或整式；（2)被开方数中不含能开方的因数或因式.满足上述两个条件的二次根式，叫做最简二次根式.次根式.要点诠释：最简二次根式有两个要求：（1）被开方数不含分母；（2）被开方数中每个因式的指数都小于根指数2. 4.同类二次根式几个二次根式化成最简二次根式后，被开方数相同，这几个二次根式就叫同类二次根式. 要点诠释：判断是否是同类二次根式，一定要化简到最简二次根式后，看被开方数是否相同，再判断.显然是同类二次根式. 要点二、二次根式的运算 1. 乘除法（1）乘除法法则： 类型 法则逆用法则二次根式的乘法0,0)a b =≥≥积的算术平方根化简公式：0,0)a b =≥≥二次根式的除法0,0)a b≥>商的算术平方根化简公式：0,0)a b=≥>要点诠释：（1）当二次根式的前面有系数时，可类比单项式与单项式相乘（或相除）的法则，如=（2）被开方数a 、b 一定是非负数（在分母上时只能为正数）.≠. 2.加减法将二次根式化为最简二次根式后，将同类二次根式的系数相加减，被开方数和根指数不变，即合并同类二次根式. 要点诠释：二次根式相加减时，要先将各个二次根式化成最简二次根式，再找出同类二次根式，最后合并同类二次根式.如23252(135)22+-=+-=-. 【典型例题】类型一、二次根式的概念与性质1． 当________时，二次根式3x -在实数范围内有意义. 【答案】x ≥3.【解析】根据二次根式的性质，必须3x -≥0才有意义.【总结升华】本例考查了二次根式成立的条件，要牢记，只有0a ≥时a 才是二次根式. 举一反三【高清课堂：二次根式 高清ID 号：388065 关联的位置名称：填空题5】 【变式】①242x x =-成立的条件是 . ②2233x x x x--=--成立的条件是 . 【答案】① x ≤0；(2422x x x x ==-∴Q≤0.)② 2≤3x <.(20,30,x x -->∴Q ≥2≤3x <)2．当0≤x <1时，化简21x x +-的结果是__________.【答案】 1.【解析】因为x ≥0，所以2x =x ；又因为x <1,即x -1<0,所以1(1)1x x x -=--=-，所以21x x +-=x +1-x =1.【总结升华】利用二次根式的性质化简二次根式，即2a =a ，同时联系绝对值的意义正确解答. 举一反三【变式】（2015春•大冶市期末）已知﹣=2，则+的值为_____________． 【答案】5. 解：∵﹣=2，∴=+2，两边平方得，25﹣x 2=4+15﹣x 2+4，∴2=3，两边平方得4（15﹣x 2）=9， 化简，得x 2=，∴+=+=5．故答案为：5．3.下列二次根式中属于最简二次根式的是（ ）.A. 14B. 48C. abD. 44a + 【答案】A.【解析】选项B ：48=43；选项C ：有分母；选项D ：44a +=21a +，所以选A. 【总结升华】本题考查了最简二次根式的定义.最简二次根式要满足：（1）被开方数是整数或是整式；（2）被开方数中不含能开方的因式或因数. 类型二、二次根式的运算4．（2015•武进区一模）下列运算正确的是（ ）A. B.C.a 6÷a 2=a 3D.【答案】B.【解析】解：A 、与不能合并，所以A 选项错误； B 、原式==，所以B 选项正确；C 、原式=a 4，所以C 选项错误； D 、原式=2，所以D 选项错误． 故选B ．【总结升华】本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．同时也考查了同底数幂的除法． 举一反三 【变式】计算：4854453)833【答案】243610-.5.化简20102011(32)(32)+⋅-. 【答案与解析】201020102010=(32)(32)(32)(32)(32)(32)1(32)3 2.+⋅-⋅-⎡⎤=+⋅-⋅-⎣⎦=⋅-=-原式【总结升华】本题的求解用到了积的乘方的性质，乘法运算律，平方差公式及根式的性质，是一道综合运算题型.6.已知2231,12x x x x=-+求.【答案与解析】2231,1=30,(1)133331=33x x x xx x x =∴->∴=--+==Q 原式当时，原式【总结升华】 化简求值时要注意x 的取值范围，如果未确定要注意分类讨论. 举一反三【高清课堂:二次根式 高清ID 号：388065关联的位置名称：计算技巧6-7】 【变式】已知a b +=-3, ab =1,求ab b a +的值. 【答案】∵a b +=-3,ab =1，∴<0a ,<0b11+==-(+)=-=3--ab ab a bb a b a ab∴+原式.。

二次根式基本定义及其应用一、二次根式的定义一般地，我们把形如)0(≥a a 的式子叫二次根式，其中a 叫被开方数，只有当a 是一个非负数时，a 才有意义。

注意：在二次根式中，被开方数可以是数，也可以是单项式、多项式、分式等代数式，但必须注意：因为负数没有平方根，所以0≥a 是a 为二次根式的前提条件，如5，12+x ，)1(1≥-x x 等是二次根式，而3-，52--x 等都不是二次根式。

二、二次根式的判定三、二次根式有意义的条件1. 单独的二次根式：被开方数大于等于0，如7，5等；2. 含有分母的二次根式：被开方数大于等于0，分母不等于0，二者要综合考虑，如：x 1），001(≠≥x x； 3. 二次根式永远有意义：被开方数为完全平方加正数，如22。

总结：1. 二次根式与分式、函数结合讨论未知数有意义的问题为中考必考内容；2. 所有的二次根式计算至最后都要化成最简二次根式。

例题1 已知，y ＝20-x ＋x -30，且x 、y 均为整数，求x ＋y 的值。

解析：先求出x 的取值范围，再根据x ，y 均为整数，可得x 的值，再分情况得到x ＋y 的值。

答案：由题意知：20≤x≤30，又因为x ，y 均为整数，所以x －20，30－x 均需是一个整数的平方，因而x 只可以取21或29，当x ＝21时，y ＝4，x ＋y 的值为25；当x ＝29时，y ＝4，x ＋y 的值为33。

故x ＋y 的值为25或33。

点拨：考查了二次根式的定义，解题的难点是根据x 、y 均为整数，得到x －20，30－x 均需是一个整数的平方。

例题2 已知点P （x ，y ）在函数y ＝x x -+21的图象上，那么点P 应在平面直角坐标系中的（ ）A. 第一象限B. 第二象限C. 第三象限D. 第四象限解析：因为分式有意义的条件是分母不等于0；二次根式有意义的条件是被开方数大于或等于0。

从而可以得到x ＜0，由x 2＞0，0≥-x 可以得到x x -+21＞0，∴y ＞0，即可求出点P 所在的象限。

浙教版八下第一章二次根式培优练习（教师版）1．小芳在解决问题：已知a＝，求2a2﹣8a+1的值．他是这样分析与解的：a＝＝＝2﹣，∴a＝2﹣，∴（a﹣2）2＝3，a2﹣4a+4＝3，∴a2﹣4a＝﹣1，∴2a2﹣8a+1＝2（a2﹣4a）+1＝2×（﹣1）+1＝﹣1．请你根据小芳的分析过程，解决如下问题：（1）计算：．（2）若a＝．①求4a2﹣8a﹣1的值；②求3a3﹣12a2+9a﹣12的值．【分析】（1）利用分母有理化先化简每一个二次根式，然后再进行计算即可解答；（2）首先化简a的值，①利用配方法把所求的式子变形为4（a﹣1）2﹣5，然后进行计算即可解答；②把所求的式子变形为3a（a2+3）﹣12（a2+1），然后把a的值代入进行计算可解答．【解答】解：（1）＝﹣1+﹣+﹣+...+﹣＝﹣1+；（2）①∵，∴4a2﹣8a﹣1＝4a2﹣8a+4﹣4﹣1＝4（a2﹣2a+1）﹣5＝4（a﹣1）2﹣5＝4×（+1﹣1）2﹣5＝4×2﹣5＝3，∴4a2﹣8a﹣1的值为3；②3a3﹣12a2+9a﹣12＝（3a3+9a）﹣（12a2+12）＝3a（a2+3）﹣12（a2+1）＝3×（+1）（6+2）﹣12×（4+2）＝﹣18，∴3a3﹣12a2+9a﹣12的值为﹣18．【点评】本题考查了二次根式的化简求值，规律型：数字变化类，完全平方式，平方差公式，分母有理化，熟练掌握分母有理化，以及完全平方式是解题的关键．2．小明在解方程﹣＝2时采用了下面的方法：由（﹣）（+）＝（）2﹣（）2＝（24﹣x）﹣（8﹣x）＝16，又有﹣＝2，可得+＝8，将这两式相加可得，将＝5两边平方可解得x＝﹣1，经检验x＝﹣1是原方程的解．请你学习小明的方法，解下面的方程：（1）方程的解是x＝±；（2）解方程+＝4x．【分析】（1）首先把根式有理化，然后分别求出根式和它的有理化因式的值是多少；再根据求出的根式和它的有理化因式的值，求出方程的解是多少即可；（2）首先把根式+有理化，然后分别求出根式+和它的有理化因式的值是多少；再根据求出的根式+和它的有理化因式的值，求出方程+＝4x 的解是多少即可．【解答】解：（1）（）（﹣）＝﹣＝（x2+42）﹣（x2+10）＝32∵，∴﹣＝32÷16＝2，∴∵＝92＝81，∴x＝±，经检验x＝±都是原方程的解，∴方程的解是：x＝±；故答案为：x＝±．（2）（+）（﹣）＝＝（4x2+6x﹣5）﹣（4x2﹣2x﹣5）＝8x∵+＝4x，∴﹣＝8x÷4x＝2，∴，∵，∴4x2+6x﹣5＝4x2+4x+1，∴2x＝6，解得x＝3，经检验x＝3是原方程的解，∴方程+＝4x的解是：x＝3．【点评】此题主要考查了二次根式在解方程中的应用，要熟练掌握，解答此题的关键是在解决实际问题的过程中能熟练应用有关二次根式的概念、性质和运算的方法．3．我们已经学习了整式的乘法，其中完全平方公式为（a±b）2＝a2±2ab+b2．利用这个公式可把3+2配成完全平方的形式：3+2＝（）2+2+12＝（+1）2．（1）根据上述方法，请把下列各式都配成完全平方的形式：①8﹣2；②1﹣；③8+4；④x+y﹣2（x≥0，y≥0）；（2）已知x＝8+4，求﹣的值；（3）计算：+++++++．【分析】（1）利用完全平方公式进行求解即可；（2）利用完全平方公式进行求解即可；（3）利用完全平方公式进行求解即可．【解答】解：（1）①8﹣2＝（）2﹣2+（）2＝（）2；②1﹣＝（）2﹣2×+（）2＝（）2；③8+4＝（）2+4+（）2＝（）2；④x+y﹣2（x≥0，y≥0）＝（）2﹣2+（）2＝（）2；（2）∵x＝8+4，∴x＝8+4＝（）2，x﹣1＝7+4＝（2+）2，∴﹣＝＝＝；（3）+++++++＝++++++ +＝++＝﹣1+3＝2．【点评】本题主要考查二次根式的化简求值，完全平方公式，解答的关键是对完全平方公式的形式的理解与运用．4．阅读下面的解答过程，然后作答：有这样一类题目：将化简，若你能找到两个数m和n，使m2+n2＝a且mn＝，则a+2可变为m2+n2+2mn，即变成（m+n）2，从而使得＝m+n．化简：．∵5+2＝3+2+2＝（）2+（）2+2＝（+）2．∴＝＝+．请你仿照上例将下列各式化简：（1）；（2）．【分析】（1）利用完全平方公式把4+2化为（1+）2，然后利用二次根式的性质化简即可．（2）利用完全平方公式把7﹣2化为（﹣）2然后利用二次根式的性质化简即可．【解答】解：（1）∵4+2＝1+3+2＝12++2＝（1+）2，∴＝＝1+；（2）＝＝＝﹣．【点评】本题主要考查了二次根式的性质与化简，解题的关键是熟记掌握完全平方公式．5．一些含根号的式子可以写成另一个式子的平方，如3+2＝（1+）2．设a+b（其中a、b、m、n均为正整数），则有a+b＝m2+2n2+2mn，∴a ＝m2+2n2，b＝2mn．这样可以把部分a+b的式子化为平方式的方法．请你仿照上述的方法探索并解决下列问题：（1）当a、b、m、n均为正整数时，若a+b＝（m+n）2，用含m、n的式子分别表示a、b，得：a＝m2+3n2，b＝2mn．（2）利用所探索的结论，找一组正整数a、b、m、n填空：21+4＝（1+2）2；（3）化简【分析】（1）将（m+n）2用完全平方公式展开，与原等式左边比较，即可得答案；（2）设a+b＝，则＝m2+2mn+5n2，比较完全平方式右边的值与a+b，可将a和b用m和n表示出来，再给m和n取特殊值，即可得答案；（3）利用题中描述的方法，将要化简的双重根号，先化为一重根号，再利用分母有理化化简，再合并同类二次根式和同类项即可．【解答】解：（1）∵，＝m2+2mn+3n2∴a＝m2+3n2，b＝2mn故答案为：m2+3n2，2mn．（2）设a+b＝则＝m2+2mn+5n2∴a＝m2+5n2，b＝2mn若令m＝1，n＝2，则a＝21，b＝4故答案为：21，4，1，2．（3）＝﹣＝﹣＝﹣＝﹣＝++﹣＝+【点评】本题考查了利用分母有理化和利用完全平方公式对二次根式化简，以及对这种方法的拓展应用，本题具有一定的计算难度．6．阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3+2＝（1+）2．善于思考的小明进行了以下探索：设a+b＝（m+n）2（其中a、b、m、n均为整数），则有a+b＝m2+2n2+2mn．∴a＝m2+2n2，b＝2mn．这样小明就找到了一种把类似a+b的式子化为平方式的方法．请你仿照小明的方法探索并解决下列问题：（1）当a、b、m、n均为正整数时，若a+b＝（m+n）2，用含m、n的式子分别表示a、b，得：a＝m2+3n2，b＝2mn；（2）利用所探索的结论，找一组正整数a、b、m、n填空：7+4＝（2+1）2；（3）若a+6＝（m+n）2，且a、m、n均为正整数，求a的值．【分析】（1）利用完全平方公式展开得到（m+n）2＝m2+3n2+2mn，从而可用m、n表示a、b；（2）先取m＝2，n＝1，则计算对应的a、b的值，然后填空即可；（3）利用a＝m2+3n2，2mn＝6和a、m、n均为正整数可先确定m、n的值，然后计算对应的a 的值．【解答】解：（1）（m+n）2＝m2+3n2+2mn，∴a＝m2+3n2，b＝2mn；（2）m＝2，n＝1，则a＝7，b＝4，∴7+4＝（2+）2，（3）a＝m2+3n2，2mn＝6，∵a、m、n均为正整数，∴m＝3，n＝1或m＝1，n＝3，当m＝3，n＝1时，a＝9+3＝12，当m＝1，n＝3时，a＝1+3×9＝28，∴a的值为12或28．故答案为m2+3n2，2mn；7，4，2，1．【点评】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．7．先阅读下列材料，再解决问题：阅读材料：数学上有一种根号内又带根号的数，它们能通过完全平方公式及二次根式的性质化去里面一层根号．例如：＝＝＝＝1+解决问题：①在括号内填上适当的数：＝＝＝＝3+②根据上述思路，试将予以化简．【分析】①通过完全平方公式，将被开方数化成平方的形式，再根据二次根式的性质，化去里面一层根号．②方法同①，通过完全平方公式及二次根式的性质化去里面一层根号．【解答】解：①＝＝＝＝3+；故答案为：3+；②＝＝＝＝5﹣．【点评】本题主要考查了二次根式的性质以及完全平方公式的运用，解决问题的关键是灵活运用二次根式的性质，选择恰当的解题途径．8．已知：2x＝，求的值．【分析】根据2x＝，可以求得x的值，然后代入，即可求得所求式子的值．【解答】解：∵2x＝＝＝＝，∴x＝，∴1﹣x2＝1﹣[（）]2＝，∴＝＝＝＝+＝．【点评】本题考查二次根式的化简求值，解答本题的关键是明确二次根式化简求值的方法．9．已知＝﹣，求的值．【分析】先将所求式子分母有理化，然后化简，再根据＝﹣，可以用a的代数式表示x，再将关于x的式子代入化简后的式子，整理化简即可．【解答】解：＝＝＝＝＝，∵＝﹣，∴x＝﹣2+a，∴x+2＝+a，x2+4x+2＝a2+，x2+4x＝a2+﹣2，则原式＝＝＝＝＝＝．【点评】本题考查二次根式的混合运算、分母有理化，解答本题的关键是明确二次根式分母有理化的计算方法．10．已知，求的值．【分析】根据算术平方根具有非负性可得a＝+2，b＝﹣2，然后再代入求值即可．【解答】解：由题意得：＝0，＝0，解得：a＝+2，b＝﹣2，＝＝5．【点评】此题主要考查了二次根式的加减，关键是掌握算术平方根具有非负性．。

二次根式（一）基础训练题1.下列各式中：）A.1个B.2个C. 3个D.4个2.下列式子中一定是二次根式的是（）A. B. C. D.3.在实数0，，－1中，最小的数是（）A.－1B.C.0D.4.（2014 x的取值范围是（）A.x＞0B.x≤1C.x＞1D.x≥15.（2014 在实数范围内有意义，则x的取值范围是（）A.x＞0B.x＞3C.x≥3D.x≤36.在下列二次根式中，x的取值范围为x≥2的是（）D.12 x-7.(2014 绵阳)有意义，则x的取值范围是（）A.x＜13B.x≤13C.x＞13D.x≥138.（2013 x的取值范围是.9.a= .10.当x为何值时，下列各式在实数范围内有意义？（1（2；（3（4中档题训练11. (20l4 ·巴中)要使式子11--m m 有意义,则 m 的取值范围是( ） A. m>-1 B. m≥一1 C.m>-1且m≠1 D.m ≧-1且m≠1 12.如果 a 是任意实数,下列式子一定成立的是( ） A.a B.21aC.2aD.2a - 13.一个正方形的面积为 7,估计其边长的范围为( )A.大于1小于2B.大于2小于3C.大于3小于4D.大于4小于5 14.如果 m=7-1,那么 m 的取值范围是( )A.0<:m<1B. 1<m<2C. 2<m<3D. 3<m<4 15.如果代数式xxy 21-+有意义,那么点 A(x ,y )的位置可能在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 16.若x x -+-75有意义,则 .r 的取值范围是 . . 17. (20l3 ·攀枝花)已知实数 x ,y ,m, 满足032=++++m y x x ,且 y 为负数,求 m 的取值范围.18. 已知 a ,b 为一等腰三角形的两边之长,且满足等式423632-=-+-b a a ,求此等腰三角形的周长.综合题训练19.已知 543++=x y ,当 x 取何值时,.y 有最小值?并求出最小值.2.二次根式(二)基础题训练1.4的算术平方根是( ).a .2 B.-2 C.±2 D.16 2.二次根式2)3(-的值是( ).A. -3B.3或一3C.9D.3 3.16的算术平方根是( ).A.士4B.4C.士2D.24.︒)2(的值为( ).A.2B.1C.22D.-1 5.二次根式2)2(±的值是( ).A. -2B.2或一2C.4D.2 6.若2a =a ,则 a 的取值范围是( ).A. ,a >0B. a ≠0C.a <0D.a ≧0 7.下列各式中不正确的是( ). A.2)2(-=2 B. 2)2(-=--2 C.-2)2(-=-2 D.±2)2(-=±28.点 A(-2,2-1)在平面直角坐标系中的( )A.第一象限B.第二象限C.第三象限 C.第四象限 9. (20l4 ·黔南州)实数 a 在数轴上的位置如图,化简a a +-2)1(=10.计算:(1)2)7(; (2)2)7(- (3)2)7((-(4) 2)7((±-; (5)4)2((2-- (6)2)23((-(7)2)3(π- (8))1(122≥+-x x x (9)1224++a a中档题训练11.如果2)12(-a = 1-2a ,则( ).A.a <21 B.a ≤21 C.a >21 D. a ≧2112.当 a ≤21时,化简124412-++-a a a ( )A.2-4aB.2C.4aD. 013. ( 20l4 ·泉州)已知 m,n 为两个连续的整数,且 m<11 <n,则 m 十n= . . 14.若0421=++++-b a b a ,则2015b)-(a = .15.已知n 12是整数,则满足条件的正整数 n 最小为 .16.已知 a ,b ,c 在数轴上的位置如图所示,化简b a c a c b a +--+++222)()(=17.在实数范围内分解因式(1)32-x ; (2)2222++x x .综合题训练18.已知三角形的两边长分别为2和4,第三边长为x ,化简:93414422+--+-x x x x3．二次根式的乘除（一）基础题训练1．使等式b a ab •=成立的条件是（ ）．A ．a ＞0，b ＞0B ．a ＜0，b ＜0C ．a ≥0，b ≥0D ．ab ≥0 2．(2014·上海)计算32•的结果是（ ）．A ．5B ．6C ．32D ．23 3．下列各式成立的是（ ）．A ．585254=⨯B ．5202435=⨯C ．572334=⨯D ． 6202435=⨯ 4．化简二次根式()622⨯-的结果是（ ）． A ．62 B ．62- C ．6 D ．12 5．化简545⨯的结果是（ ）． A ．52B ．2C ．2D ．526．下列各式计算正确的是（ ）．A ．525±=B ．12733=-C ．9218=⨯D ．62324=⨯7．在下列各数中，与3的积为有理数的是（ ） A ．2 B ．13+ C ．3- D ．68．（2014·河北）计算：218+＝ ． 9．化简：1832⨯＝ ；()()2715-⨯-＝ ．10．计算下列各式：（1）82⨯； （2）123⨯； （3）2162⨯； （4）12149⨯； （5）y 4； （6）3216c ab ；（7）10253⨯； （8）15106⨯⨯； （9）54332⨯⨯．中档题训练11．若等式()()3333-•+=-+x x x x 成立，则x 的取值范围是 ．12．计算()()322323-⨯+的结果是（ ）． A ．－1 B ．1 C ．23- D ．23+13．将aa1根号外的部分移到根号内，正确的是（ ）． A ． a B ．a - C ．a - D ．a --14．设矩形的长和宽分别为a ，b ，根据下列条件求面积S ． （1）12=a ，8=b ； （2）243=a ，4821=b ．15．比较下列各组中两个数的大小．（1）72和24； （2）32-和23-．16．计算： （1）3122y x xy •； （2）nm m n m223233•．17．先化简，再求值：121132--÷⎪⎭⎫ ⎝⎛--+x x x x x x，其中23=x ．综合题训练18．已知101=+a a ，求aa 1-的值．4．二次根式的乘除（二）基础题训练1．下列二次根式中：2，21，12，2-x ，12+x ，最简二次根式的个数为（ ）． A ．1个 B ．2个 C ．3个 D ．4个 2．（2014·威海）下列式子中，属于最简二次根式的是（ ）． A ．9 B ．7 C ．20 D ．313．下列根式中属于最简二次根式的是（ ）． A ．a 4 B ．4aC ．4aD ．4a4．（2014·徐州）下列运算中错误的是（ ）．A ．2222=⨯B ．632=⨯C ．228=÷D ．()332=-5．下列计算错误的是（ ）． A ．6319632== B ．xxx x x ==21 C ．a ab aab ab 339332== D ．x x xx x6396322==6．327的相反数是 ； 5的倒数是 ．7．计算：=⨯÷3333 ； =÷xx 1． 8．计算：（1）818÷； （2）8121÷； （3）32241÷； （4）648； （5）2723-； （6）xyy x 322；（7）x y xy ÷； （8）1003； （9）2775；（10）65027÷⨯； （11）531322311⨯÷； （12）43215021122⨯÷．中档题训练9．使等式725725--=--x x x x成立的条件是（ ）．A ．527≤<x B ．527≤≤x C ．27>x D ．5≤x 10．若2381=⨯a ，则a 的值为（ ）． A ．12 B ．32 C ．163D ．4311．化简：（1）x y xy 32÷； （2）227818÷÷； （3）22b a ab a b ⨯÷．12．（2014·苏州）先化简，再求值：⎪⎭⎫⎝⎛--+÷--13112x x x x ，其中23-=x ．13．某建筑施工图纸上有一直角三角形的面积为1410cm 2，一条直角边长为74cm ，求另一直角边的长．综合题训练14．已知a ＋b ＝－3，ab ＝2，求代数式baa b +的值．专题 二次根式的性质一、二次根式有意义的条件1．要使1213-+-x x 有意义，则x 应满足（ ）．A ．321≤≤x B ．3≤x 且21≠x C ．321<<x D ．321≤<x 2．（2013·广西）下列四个式子中，x 的取值范围是2≥x 的是（ ）．A ．22--x x B ．21-x C ．2-x D ．x -2 3．化简：=-+-11x x ．4．当x 为何值时，下列各式在实数范围内有意义？ （1）13-x ； （2）12+x ； （3）21+x ； （4）xx 3+； （5）x x -+1； （6）122-+-x x ．二、利用a 的双重非负性解题5．当a 取何值时，式子112++a 的值最小？并求出这个最小值．6．已知32552--+-=x x y ，求2xy 的值．三、2a 的化简7．若()12212-=-a a ，则a 的取值范围是（ ）． A ． 21<a B ．21≤a C ．21>a D ．21≥a 8．化简下列各式：（1）16 （2）()23-； （3）221⎪⎭⎫⎝⎛-- ； （4）23-；（5）2x ； （6）()23-π； （7）()221--； （8）1224++x x ．专题 二次根式的乘除运算一、二次根式乘除运算1．计算：（1）33× 3 （2）0.5×24（3）45×3223 （4）－12xy ×(－4y )（5）－4318÷28×1354 （6）－2xy ÷(－32x x 2y ×3x )2．先化简：2x •x y •(y x ÷1y )，其中实数x 、y 满足y ＝x －3＋6－2x ＋2．3．先化简，再求值：a 2－2ab ＋b 2a 2－b 2÷(1a －1b )，其中a ＝2＋1，b ＝2－1．二、二次根式乘除公式的逆运用4．已知1－a a 2＝1－a a ，则a 的取值范围是（ ）A ．a ≤0B ．a ＜0C ．0＜a ≤1D ．a ＞0 5．将(a －1)11－a根号外的部分移到根号内，正确的是（ ） A ．－1 B ．1－a C ．－1－a D ．－a －15． 二次根式的加减（一）基础题训练1．（2014·孝感）下列二次根式中，不能与2合并的是（ ）A ．21B ．8C ．12D ．18 2．下列各组根式中，两式可以合并的是（ ）A ．2和12B ．2和0.5C ．4ab 和ab 2D ．a －1和a －1 3．计算12＋3的结果为（ ）A ．2 3B ．3 3C ．15D ．3 2 4．下列四个二次根式：①y x 2；②22xy ；③2xy；④23xy，化为最简二次根式后，被开方数相同的是（ ）A ．①和②B ．②和③C ．①和③D ．②和④ 5．下列各式计算正确的是（ ）A ．2－22＝－2B ．28a ＝4a (a ＞0)C ．6÷3＝3D ．(－4)×(－9)＝－4×－9 6．（2014·聊城）下列各式计算正确的是（ ）A ．23×33＝63B ．2＋3＝5C ．55―22＝33D ．2÷3＝36 7．（2014·云南）计算：8－2的结果是___________．7．矩形的长和宽分别为125和20，则其周长为__________．9．若最简二次根式x ＋1与2x 能合并为一个二次根式，则x ＝___________． 10．计算：（1）12＋27 （2）18＋72－32（3）4x －9x （4）27－12＋43（5）212－613＋348 （6）8－32＋29中档题训练11．计算212－613＋8的结果是（ ）A ．32－23B ．5－2C ．5－ 3D ．2 2 12．一个等腰三角形的两边长分别为23，32，则这个三角形的周长为（ ） A ．32＋4 3 B ．62＋2 3C ．62＋4 3D ．32＋43或62＋2 313．已知a ，b 分别是6－13的整数部分和小数部分，那么2a －b 的值是（ ）A ．3－13B ．4－13C ．13D ．2＋13 14．若最简二次根式5a 2＋1与57a 2－1能进行合并，则结果是__________．15．（2014·凉山州）已知x 1＝3＋2，x 2＝3－2，则x 12＋x 22＝____________． 16．计算下列各式： （1）5－6－20＋23＋95 （2）12－0.5－213－18＋18（3）27a －a 3a ＋3a 3＋12a 75a 3 （4）23x 9x ＋6x yx ＋yx y －x21x17．已知x ＝1＋2，求代数式x 2＋2x ＋1x 2－1－xx －1的值．综合训练18．已知2525x ＋9x 9－2x 2•1x 3＝18，求x 的值．6．二次根式的加减（二）基础题训练1．下列运算错误的是（）A．2＋3＝ 5 B．2 •3＝6C．6÷2＝ 3 D．(－2)2＝22．估计24×12＋3的运算结果应在（）A．2 3 B．3 3 C．15 D．63．12 (75＋313－48)结果是（）A．12 B．4 3 C．23＋6 D．6 4．若x＝m－n,y＝m＋n，则xy的值是（）A．2m B．2n C．m＋n D．m－n 5．下列式子运算正确的是（）A．3－2＝1B．8＝42C．13＝3D．12＋3＋12－3＝46．(2013·哈尔滨)计算：27－32＝_____________．7．若矩形的长为（12＋3）cm，宽为3cm，则此矩形的面积为__________．8．若(548＋12－627)÷a＝4，则a的值是_________．9．计算：（1）3×6－2×6（2）2(2＋3)－3(2－27）（3）(12＋58) 3 （4）(3＋1)(3－2)（5）(23＋32)(23－32) （6）(a＋b)(a－b)（7）(3＋5)2（8）(25－2)2中档题训练10．（2014·安徽）设n为正整数，且n＜65＜n＋1，则n的值为（）A．5 B．6C．7 D．811．若(3＋2)2＝a ＋b 6，且a 、b 为整数，则a ＋b 的值为（ ）A ．3B ．5C ．6D ．712．已知x ＋1x＝a ，则x ＋1x 的值为（ ）A ．a 2－2B ．a 2C ．a 2－4D ．不确定 13．（2014·青岛）计算：5540 ＝_________．14．二次根式5－(16－3m )2有最大值，则m ＝___________． 15．计算：（1）2 3 (12―375＋13108) （2）(2＋1)÷2×(2―1)―(12―1)0（3）(3―22)2014(3＋22)2015 （4）(1＋2＋3)(1＋2―3)16．（2014·襄阳）已知x ＝1－2，y ＝1＋2，求x 2＋y 2－xy －2x ＋2y 的值．17．先化简，再求值：239x ＋6x 4－2x1x ，代入一个合适的x 的值求值．综合题训练17．已知a ＝2－12＋1，b ＝2＋12－1，求b a ＋ab 的值．专题 与根式相关的规律问题1．观察下列各数：2、 …，则第8个数是 ．2 …，请你将发现的规律用含n （n ≥1，且为整数）的等式表示出来： ．3．观察下列各式：，＝…，请你根据以上式子中的规律写出第6个式子为： ．4．…，根据以上式子中的规律计算：＋＋＋…＋＝ ．5． 555555＝5555， (2)333344n n 个…＋…＝ ．6． 10199＝100，9991000，…，9999999999999199999n n n ⨯⨯个个个………＝ ．7．23，27＋＝4，45，…，根据以上 式子中的规律写出第10个式子为： ．8．观察下列式子：①＝1＋112⨯ ，②＝1＋123⨯，③＝1＋134⨯，…，根据上面三个等式提供的信息，请写出第n 个式子： ．9按下面规律排列，若规定（m，n）表示第m排从左至右的第n个数，则表示（10，9）的数是；表示（6，5）和（8，7）的数的积为第一排第二排第三排第四排… …专题根式及其运算一、使二次根式有意义的条件1．下列函数中自变量的取值范围是x≥2的是（）．A．y2B．y＝22x－C．yD．y＝x－22．若x为任意实数，下列函数一定有意义的是（）．A．yB．y＝211x－C．yD．y＝21x3．在函数yx的取值范围是（）．A．x≤13B．x≥13C．x＜13D．y＝x－2二、二次根式的化简、计算4．下列各式计算正确的是（）．ABCD－35．下列各式计算正确的是（）．A±2BC5=10D6．设a＞0，b＞0，则下列运算错误的是（）．Aa b BC．2＝a D=7计算：（1）＋（2）)21－112⎛⎫⎪⎝⎭－＋(01（3； （48．先化简，再求值．（12x ＝4；（2，其中x ＝6．9．一个三角形的三边长分别为，54 （1）求它的周长（要求结果化简）；（2）请你给一个适当的x 值，使它的周长为整数，并求出此时三角形周长的值．。