高二数学练习卷(一)

高二数学试卷练习题及答案第一部分：选择题1. 设直线$l$经过点$P(3，2)$，若$l$的斜率为$-\frac{1}{2}$，则直线$l$的方程是（）A. $y=2- \frac{1}{2}x$B. $y=2+ \frac{1}{2}x$C. $y=2-2x$D. $y=2+x$答案：A解析：直线的斜率$m=-\frac{1}{2}$，过点$P(3，2)$，带入点斜式方程$y-y_1=m(x-x_1)$，可得直线方程为$y=2-\frac{1}{2}x$。

2. 已知函数$f(x)=x^2+ax+b$，经过点$P(1,1)$，则$a+b$的值为（）A. 1B. 2C. 3D. 4答案：A解析：带入点$P(1,1)$，可得方程$1=a+b$，因此$a+b=1$。

3. 已知集合$A=\{x|x^2\leq7\}$，则$A$的解析式为（）A. $A=\{x|x\leq\sqrt{7}\}$B. $A=\{x|x\geq\sqrt{7}\}$C. $A=\{x|x\leq-\sqrt{7}\}$D. $A=\{x|x\geq-\sqrt{7}\}$答案：A解析：由不等式$x^2\leq7$，得$x\leq\sqrt{7}$，因此$A=\{x|x\leq\sqrt{7}\}$。

4. 如果对于所有实数$x$，都有$f(x)=f(-x)$，则函数$f(x)$为（）A. 奇函数B. 偶函数C. 定义在偶数集上的函数D. 定义在奇数集上的函数答案：B解析：当函数$f(x)$满足$f(x)=f(-x)$时，称$f(x)$为偶函数。

第二部分：填空题1. 已知$\tan\theta=\frac{2}{3}$，则$\sin\theta$的值是（）答案：$\frac{2}{\sqrt{13}}$解析：根据正弦定理得$\sin\theta=\frac{\frac{2\sqrt{13}}{3}}{\sqrt{1+(\frac{2}{3})^2}}=\frac{2 }{\sqrt{13}}$。

高二数学同步检测一平面与空间直线说明：本试卷分为第Ⅰ、Ⅱ卷两部分，请将第Ⅰ卷选择题的答案填入题后括号内，第Ⅱ卷可在各题后直接作答 .第Ⅰ卷（选择题）一、选择题（本大题共10 小题 ,在每题给出的四个选项中,选择一个切合题目要求的选项）1.列命题是真命题的是()A.空间不一样三点确立一个平面B.空间两两订交的三条直线确立一个平面C.四边形确立一个平面D.和同向来线都订交的三条平行线在同一平面内答案 :D分析 :依据公义3(经过不在同一条直线上的三点,有且只有一个平面)知不在同向来线上的三点,才能确立一个平面 ,因此 A 错 .如图 (1),a,b,c 三条直线两两订交,但 a,b,c 不共面 ,因此 B 错误 .如图 (2),明显四边形ABCD 不可以确立一个平面.2.已知 AB ∥PQ,BC ∥QR,∠ ABC=30 ° ,则∠ PQR 等于 ()A.30 °B.30 °或 150°° D.以上结论都不对答案 :B分析 :由等角定理可知∠PQR 与∠ ABC 相等或互补 ,即∠ PQR=30°或 150°.3.如右图 ,α∩ β =l,A ∈ β ,B∈ β ,AB ∩ l=D,C ∈α ,则平面 ABC 和平面α的交线是 ()A. 直线C.直线ACABB. 直线D.直线BCCD答案 :D分析 :CD 为平面 ABC 与平面α的交线 .应选 D.4.如图 ,点 P,Q,R,S 分别在正方体的四条棱上,而且是所在棱的中点,则直线PQ 与RS 是异面直的是 () 答案 :C分析 :A,B中的PQ与RS相互平行;D中的PQ与RS订交;由两条直异面的判断定理可知中的 PQ 与 RS 异面 .5.“ a,b 是异面直”的表达，正确的选项是()①a∩ b=且a不平行于b② a平面α ,b平面β 且α ∩β =③ a平面α,b α④不存在平面α,使a平面α 且b平面α 建立A. ①②B.①③C.①④D. ③④C 平面答案 :C分析 :依据“异面直是不一样在任何一个平面内的两条直”的定知,④正确.空不相交的两条直除平行外就是异面 ,故于① ,既然两直不平行 ,必定异面 .分在两个平面内的两条直可能平行 ,故②不正确 .平面内的一条直和平面外的一条直除异面外可能平行或订交 ,故③不正确 .上所述 ,只有①④正确 .6.右是一个无盖的正方体盒子睁开后的平面，体盒子中，∠ ABC 的⋯ ()A 、 B、 C 是睁开上的三点，在正方A.180 °°°°答案 :C分析 :把平面形原立体形，找准 A 、 B 、C 三点相地点,可知∠ABC 在等△ABC 内.7.在空四形ABCD 中,M,N 分是AB,CD 的中点, BC+AD=2a, MN 与 a 的大小关系是( )A.MN>aB.MN=aC.MN<aD.不可以确立答案 :C分析 :如图,取AC中点P,则MP 1 1故 C 正确 . 2BC,NP AD, 且 MP+NP= (BC+AD)=a>MN,28.如图，在棱长为 1 的正方体 ABCD —A 1B1 C1D 1中， O 是底面 ABCD 的中心， E、F 分别是CC1、 AD 的中点，那么异面直线OE 和 FD 1所成的角的余弦值等于 ()10 15 4 2A. B. C. D.5 5 5 3答案 :B分析一 :如图 (1),取面 CC1D1D 的中心为 H，连接 FH 、D 1H.易知 OE∥ FH ，因此∠ D 1FH 为所求异面直线所成的角 .在△ FHD 1中，FD 1= 5， FH=3， D1H=2由余弦定理，得∠D 1FH 的余弦值为15 .2 2 2 5分析二 :如图 (2),取 BC 中点为 G.连接 GC1、 FD1,则 GC1∥ FD1.再取 GC 中点为 H, 连接 HE 、OH，则∠ OEH 为异面直线所成的角 .在△ OEH 中， OE= 3 ,HE= 5，OH= 5 .2 4 4由余弦定理，可得cos∠OEH= 15. 59.空间有四点 A,B,C,D, 每两点的连线长都是2,动点 P 在线段 AB 上 ,动点 Q 在线段 CD 上 ,则P,Q 两点之间的最小距离为( )B.3C. 2D. 3 2答案 :C分析 :PQ的最小值应是AB,CD 的公垂线段长 .易知 P,Q 分别是 AB,CD 中点时 ,PQ⊥ AB,PQ ⊥CD.在 Rt△ BQP 中 ,∵BQ= 3 ,BP=1,∴PQ= 3 1 = 2 .10.右图是正方体的平面睁开图,则在这个正方体中:①BM 与 ED 平行 ;② CN 与 BE 是异面直线 ;③ CN 与 BM 成 60°角 ;④ DM 与 BN 垂直 .以上四个命题中,正确命题的序号是()A. ①②③B. ②④C.③④D.②③④答案 :C分析 :将上边的睁开图复原成以下图正方体.简单知道BM与ED异面,CN与BE平行,故①②不正确 .由于 BE∥ CN, 因此 CN 与 BM 所成的角是∠ EBM=60 ° ,延伸 CD 至 D ′,使 DD ′=DC, 则D ′N ∥ DM, ∠ BND ′就是 DM 与 BN 所成的角 .设正方体的棱长为 1,由于 BN= 3 a,ND ′ = 2 a,BD′= 5 a,因此BN2+D′N2=D′B2,即BN⊥ND′,BN⊥DM.第Ⅱ卷（非选择题）二、填空题（本大题共 4 小题 ,答案需填在题中横线上）11.以下四个命题 :①A ∈ l,A ∈ α,B∈ l,B∈ αl α;②A ∈ α,A∈ β,B∈ α,B∈βα∩β =AB;③l α,A∈ l A a;④A,B,C ∈ α,A,B,C∈ β,且 A,B,C 不共线α与β重合.此中推理正确的序号是__________.答案 :①②④分析 :由公义 1 知①正确 ;由公义 2 知②正确 ;由公义 3 知④正确 ;而③中直线 l 可能与平面 α 订交于 A.故③不正确 .12.空间四条直线 ,两两订交可确立平面的个数最多有 ____________ 个.答案 :6分析 :明显 ,任两条订交直线若都能确立一个平面 (不重复 ),此时平面个数最多 .如图 ,平面 PAB, 平面PAC,平面 PAD,平面 PBC,平面 PCD,平面 PBD, 共 6 个. 13.(2006 全国要点中学一模 ,11)给出三个命题 :①若两条直线和第三条直线所成的角相等 ,则这两条直线相互平行 ; ②若两条直线都与第三条直线垂直 ,则这两条直线相互平行 ; ③若两条直线都与第三条直线平行 ,则这两条直线相互平行 . 此中不正确的序号是 __________. 答案 :①②分析 :在以下图的正方体 ABCD — A 1B 1C 1D 1 中 ,A 1D 1⊥ D 1D,C 1D 1⊥ D 1D,即 A 1D 1 与 D 1D,C 1D 1 与 D 1D 所成的角都是 90°,但 A 1D 1 与 C 1 D 1 不平行 ,可知①②不正确 ,由公义 4 可知③正确 . 14.在正方体ABCD — A 1B 1C 1D 1 中，假如 E 、 F 分别为 AB 、CC 1 的中点，那么异面直线 A 1C与 EF 所成的角等于 _______________. 答案 :arccos23分析 :延伸 AA 1 到 P ，使 A 1P=1 AA 1，2连接 PF ，则 PF ∥ A 1C ，设 A 1A=a.则 PE 2=( 3a)2+( 1a)2=102 2 4 EF 2=( 1 a)2+a 2+( 1 a)2 = 6224a 2，a 2 ，PF 2=A 1C 2=3a 2 .3a 2 6 a 2 10 a 2∴cos ∠ PEF=4 4 2.2 3a6 a 322∴直线 A 1C 与 EF 所成的角等于 arccos.3三、解答题（本大题共 5 小题 ,解答应写出文字说明,证明过程或演算步骤）15.已知正方体ABCD — A 1B1C1D 1中， E、 F 分别是 D1C1、 B1C1的中点， AC∩BD=P ，A 1C1∩ EF=Q，求证：(1)D 、 B、 F、 E 四点共面；(2)若直线 A 1C 交平面 DBFE 于点 R，则 P、 Q、 R 三点共线 .(1)证法一 :∵ EF 是△ D 1B1 C1的中位线 ,∴EF ∥B 1D 1.在正方体 AC 1中， B1 D1∥ BD,∴E F ∥BD.由公义 3 知 EF 、BD 确立一个平面,即 D 、B、 F、 E 四点共面 .证法二 :延伸 BF,CC1交于点 G,延伸 DE,CC 1交于点 G′ .G 与 G′重合 DE,BF 是订交直线D,B,F,E 四点共面 .(2)证明 :正方体 ABCD — A 1B1C1D1中，设 A 1ACC 1确立的平面为α ,设平面 DBFE 为β,Q EF Q∵Q 为α、β的公共点.又Q A1C1Q同理 ,P 亦为α、β的公共点 ,R A1C RR∈ PQ,即 P、 Q、 R 三点共线 .∴又 R由公义 2可知评论 :证明多点共线，可先由两点确立向来线，证其他点在直线上.要证点在一条直线上，只需证明这点是两平面的公共点，而直线是两个平面的交线，这是证点在直线上的常用方法.16.如图，E、F、G、H 分别是空间四边形 ABCD 各边上的点，且有 AE ∶EB=AH ∶ HD=m,CF ∶FB=CG ∶GD=n.(1)证明 E、 F、 G、H 四点共面 .(2)m 、 n 知足什么条件时，EFGH 是平行四边形 ?(3)在（ 2）的条件下，若 AC ⊥ BD ，试证明 EG=FH.(1)证明 :∵AE ∶ EB=AH ∶ HD ，∴ EH ∥ BD.∵C F∶ FB=CG ∶ GD，∴FG∥ BD. ∴ EH ∥ FG.∴ E、 F、 G、H 四点共面 .(2)解 :当且仅当 EH FG 时，四边形 EFGH 为平行四边形 .∵ EH AE m ,∴ EH= m BD.BD AE EB m 1 m 1同理 ,FG= n BD. 由 EH=FG 得 m=n.n 1故当 m=n 时，四边形EFGH 为平行四边形 .(3) 证明 :当 m=n 时， AE ∶ EB=CF ∶ FB,∴ EF∥ AC.又∵ AC ⊥ BD ，∴∠ FEH 是 AC 与 BD 所成的角 .∴∠ FEH=90 ° .进而 EFGH 为矩形，∴ EG=FH.评论 :空间四边形是立体几何的一个基本图形，它各边中点的连线组成平行四边形；当两对角线相等时该平行四边形为菱形；当两对角线相互垂直时，该平行四边形为矩形；当两对角线相等且相互垂直时 ,该平行四边形为正方形 .M,N,P . 分别在直线a,b,c 上 ,点Q 是b 17.如图 ,a,b,c 为不共面的三条直线,且订交于一点O,点上异于 N 的点 ,判断 MN 与 PQ 的地点关系 ,并予以证明证法一 :(反证法 )假定 MN 与 PQ 共面于β ,则点 M,N,P,Q∈ β .又点 N, Q b b OcO b P同理 ,aβ .∴a,b,c 共面 ,与已知 a,b,c 不共面矛盾 .故 MN 与 PQ 为异面直线 .a b0点M , N , Q共面于 MON证法二 : M又 Q b且异于 NN , Q b点Q MN,OP 平面 MON点 P平面MON.P c故平面 MON 内一点 Q 与平面外一点P的连线 PQ 与平面内可是Q 点的直线MN 是异面直线.18.以下图 ,今有一正方体木材ABCD — A 1B 1C1D1,此中M,N分别是AB,CB的中点,要过D 1,M,N 三点将木材锯开 ,请你帮助木匠师傅想方法 ,如何画线才能顺利达成 ?解: 作法以下 :(1) 连接 MN 并延伸交 DC 的延伸线于 F,连接 D 1F 交 CC 1 于 Q,连接 QN; (2) 延伸 NM 交 DA 的延伸线于 E,连接 D 1E 交 A 1A 于 P,连接 MP;(3) 挨次在正方体各个面上画线D 1P,PM,MN,NQ,QD 1,即为木匠师傅所要画的线 .19. 如 图 ,AB,CD是 两 条 异 面 直 线 ,AB=CD=3a,E,F 分 别 是 线 段 AD,BC上 的 点 , 且ED=2AE,FC=2BF,EF=7 a,G ∈ BD,EG ∥ AB.(1) 求 AB 与 CD 所成的角 ; (2) 求△ EFG 的面积 .解 :(1) ∵ ED=2AE,EG ∥AB, ∴ DG=2BG . ∵ F C=2BF, ∴ FG ∥ DC.∴∠ EGF 即为 AB 与 CD 所成的角或其补角 .∵ A B=CD=3a,EG=2a,GF=a, 又 EF= 7 a,EG 2 GF 2 EF 24a 2 a 2 7a 21 ∴cos ∠ EGF=2EG GF2 2a a.2∴∠ EGF=120° .∴ AB 与 CD 所成的角为 60° .1 (2)S △ EFG = EG ·GF · sin120° 2= 1× 2a × a × sin120°23 2=a .2本卷由《 100 测评网》整理上传，专注于中小学生学业检测、练习与提高.。

高二数学导数练习题及答案导数是高中数学中的重要概念之一，它在数学和实际问题中具有广泛的应用。

为了帮助高二学生巩固导数的知识和提高解题能力，本文为大家准备了一些高二数学导数练习题及答案。

希望通过这些练习题的训练，同学们能够更好地理解导数的概念和运用。

练习题一：1. 求函数 f(x) = 2x^3 - 3x^2 + 4x - 1 在点 x = 2 处的导数。

2. 已知函数 f(x) = x^2 + 3x，求函数 f(x) = x^2 + 3x 的导函数。

3. 求函数 f(x) = (x + 1)(x - 2)(x + 3) 在点 x = -1 处的导数。

答案一：1. 函数 f(x) = 2x^3 - 3x^2 + 4x - 1 的导数为：f'(x) = 6x^2 - 6x + 4。

2. 函数 f(x) = x^2 + 3x 的导函数为：f'(x) = 2x + 3。

3. 函数 f(x) = (x + 1)(x - 2)(x + 3) 在点 x = -1 处的导数为：f'(-1) = 0。

练习题二：1. 求函数 f(x) = 3x^4 - 2x^3 + 5x^2 - 4x + 1 的极值点及极值。

2. 已知函数 f(x) = x^3 - 6x^2 + 9x + 2，求函数 f(x) = x^3 - 6x^2 + 9x+ 2 的拐点。

3. 求函数 f(x) = x^3 - 3x 在其定义域内的极值点。

答案二：1. 函数 f(x) = 3x^4 - 2x^3 + 5x^2 - 4x + 1 的极值点为 x = 1/2，极值为 f(1/2) = 47/16。

2. 函数 f(x) = x^3 - 6x^2 + 9x + 2 的拐点为 x = 2。

3. 函数 f(x) = x^3 - 3x 在其定义域内的极值点为 x = 1。

练习题三：1. 求函数 f(x) = e^x 的导数。

2. 已知函数 f(x) = ln(x)，求函数 f(x) = ln(x) 的导函数。

数学练习题及答案高二第一节：选择题1. 若函数 f(x) = ax^2 + bx + c 的图象开口向上，且在点 P(-1, 3) 有极值，那么 a, b, c 的关系是（）(A) a ≠ 0, b = 0, c ≠ 0;(B) a ≠ 0, b ≠ 0, c ≠ 0;(C) a ≠ 0, b ≠ 0, c = 0;(D) a ≠ 0, b = 0, c = 0;答案：(A)解析：由题可知，函数图象开口向上，所以a ≠ 0。

又因为在点 P(-1, 3) 有极值，极值对应的 x 坐标为 -1，代入函数可得 f(-1) = -a + b - c。

由于函数开口向上，所以该极值为极小值，即 f(-1) = -a + b - c > 0。

再结合a ≠ 0，可以得出 b = 0，因为如果b ≠ 0，则在 x = -1 附近 f(-1)不可能为正值。

所以，a ≠ 0，b = 0，c ≠ 0。

2. 已知函数 y = 2x^2 + 3x - 2 的图象与 x 轴交于点 A、B两个地方，那么点 A、B 的纵坐标分别是（）(A) 0，-3;(B) -2，0;(C) 0，-2;(D) -3，0;答案：(C)解析：当函数与 x 轴交于点 A、B 时，函数值 y = 2x^2 + 3x - 2 = 0。

可以通过因式分解或二次方程求根公式来解。

将方程 2x^2 + 3x - 2 = 0 因式分解为 (2x + 1)(x - 2) = 0，得到两个解：x = -1/2，x = 2。

所以，点 A 的纵坐标为 y(A) = 2(-1/2)^2 + 3(-1/2) - 2 = -2，点 B 的纵坐标为 y(B) = 2(2)^2 + 3(2) - 2 = -2。

因此，点 A、B 的纵坐标分别是 0、-2。

第二节：填空题1. 给定矩阵 A = [1 2 3; -1 0 1]，则 A 的转置矩阵为 ______。

答案：[1 -1; 2 0; 3 1]解析：矩阵的转置就是将原矩阵的行变为列，列变为行。

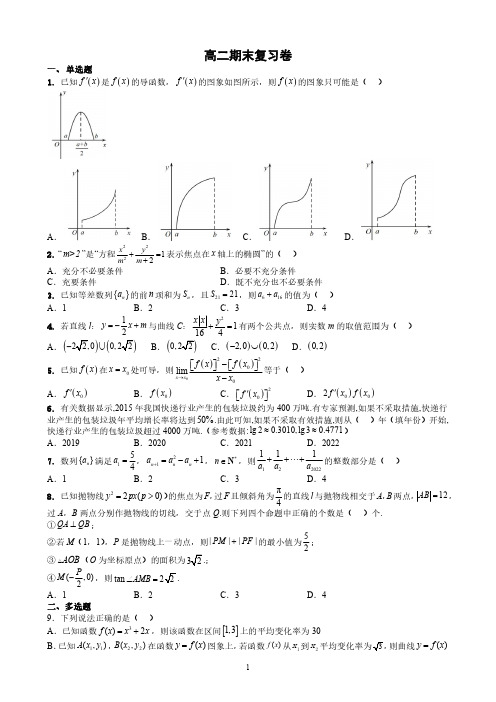
高二期末复习卷一、单选题1.已知()f x '是()f x 的导函数，()f x '的图象如图所示，则()f x 的图象只可能是（）A．B．C．D．2.“m>2”是“方程22212x ym m +=+表示焦点在x 轴上的椭圆”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3.已知等差数列{}n a 的前n 项和为n S ，且2121S =，则616a a +的值为（）A ．1B ．2C ．3D ．44.若直线l ：12y x m =-+与曲线C ：21164x x y +=有两个公共点，则实数m 的取值范围为（）A．()(0,- B．(0,C ．()()2,00,2-⋃D ．()0,25.已知()f x 在0x x =处可导，则()()02200lim x x f x f x x x →-⎡⎤⎡⎤⎣⎦⎣⎦-等于（）A ．()0f x 'B ．()0f x C ．()20f x '⎡⎤⎣⎦D ．()()002f x f x '6.有关数据显示,2015年我国快递行业产生的包装垃圾约为400万吨.有专家预测,如果不采取措施,快递行业产生的包装垃圾年平均增长率将达到50%.由此可知,如果不采取有效措施,则从（）年（填年份）开始,快递行业产生的包装垃圾超过4000万吨.（参考数据:lg 20.3010,lg 30.4771≈≈）A ．2019B ．2020C ．2021D ．20227.数列{}n a 满足154a =，211n n n a a a +=-+，*n ∈N ，则122022111a a a +++ 的整数部分是（）A ．1B ．2C ．3D ．48.已知抛物线22(0)y px p =>）的焦点为F ，过F 且倾斜角为π4的直线l 与抛物线相交于A ，B 两点，12AB =，过A ，B 两点分别作抛物线的切线，交于点Q .则下列四个命题中正确的个数是（）个.①QA QB ⊥；②若M （1，1），P 是抛物线上一动点，则||||PM PF +的最小值为52；③AOB （O为坐标原点）的面积为；④(,0)2PM -，则tan AMB ∠=A ．1B ．2C ．3D ．4二、多选题9．下列说法正确的是（）A ．已知函数3()2f x x x =+，则该函数在区间[]1,3上的平均变化率为30B ．已知11(,)A x y ，22(,)B x y 在函数()y f x =图象上，若函数()f x 从1x 到2x则曲线()y f x =的割线AB 的倾斜角为3πC ．已知直线运动的汽车速度V 与时间t 的关系是221V t =-，则2t =时瞬时加速度为7D ．已知函数()f x x =，则(9.05) 3.008f ≈10．在底面边长为2、高为4的正四棱柱1111ABCD A B C D -中，O 为棱1A A 上一点，且111,4A O A A P Q =､分别为线段1111B D A D ､上的动点，M 为底面ABCD 的中心，N 为线段AQ 的中点，则下列命题正确的是（）A ．CN 与QM 共面B ．三棱锥A DMN -的体积为43C ．PQ QO +的最小值为322D ．当11113D Q D A = 时，过,,A Q M 三点的平面截正四棱柱所得截面的周长为()82103+11．数列{}n a 满足1a a =，2131n n n a a a +=--，则下列说法正确的是（）A ．若1a ≠且2a ≠，数列{}n a 单调递减B ．若存在无数个自然数n ，使得1n n a a +=，则1a =C ．当2a >或1a <时，{}n a 的最小值不存在D ．当3a =时，121111,12222n a a a ⎛⎤++⋅⋅⋅⋅⋅⋅+∈ ⎥---⎝⎦12．设F 是抛物线2:4C y x =的焦点，直线:1l x ty =+与抛物线C 交于,A B 两点，O 为坐标原点，则下列结论正确的是（）A ．||4AB ≥B ．OA OB ⋅可能大于0C ．P 为抛物线上异于A 、B 的点，直线l 与准线交于点T ，当0,t A >为第一象限的点时，若APB α∠=，PF 平分APB ∠，则π2APT +∠=αD ．若在抛物线上存在唯一一点Q (异于,)A B ，使得QA QB ⊥则3t =±三、填空题13．若()f x 为可导函数，且()()0121lim 14x f x f x→--=-，则过曲线()y f x =上点()()1,1f 处的切线斜率为______．14．对于数列{}n a ，若1,n n a a +是关于x 的方程2103n n x c x -+=的两个根，且12a =，则数列{}n c 所有项的和为________．15．法国数学家加斯帕•蒙日被称为“画法几何创始人”、“微分几何之父”.他发现与椭圆相切的两条互相垂直的切线的交点的轨迹是以该椭圆中心为圆心的圆，这个圆称为该椭圆的蒙日圆.若椭圆()2222:10x y a b a bΓ+=>>的蒙日圆为2223:2C x y a +=，过C 上的动点M 作Γ的两条切线，分别与C 交于P ，Q 两点，直线PQ 交Γ于A ，B 两点，则下列说法，正确的有______.①椭圆Γ的离心率为22②MPQ 面积的最大值为232a③M 到Γ的左焦点的距离的最小值为()22a-④若动点D 在Γ上，将直线DA ，DB 的斜率分别记为1k ，2k ，则1212k k =-16．已知数列{}n a 的通项公式为4152nn n a +⎛⎫=-⋅ ⎪⎝⎭，设数列{}n a 的最大项和最小项分别为,M N ，则M N +=______.四、解答题17．已知椭圆()2222:10x y C a b a b+=>>的四个顶点构成的四边形的面积为12．(1)求椭圆C 的标准方程；(2)过椭圆C 右焦点且倾斜角为135︒的直线l 交椭圆C 于M 、N 两点，求MN 的值．18．已知双曲线2222:1(0,0)x y C a b a b -=>>，四点12346,,4,,4,333M M M M ⎛⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭中恰有三点在C 上．(1)求C 的方程；(2)过点(3,0)的直线l 交C 于P ，Q 两点，过点P 作直线1x =的垂线，垂足为A ．证明：直线AQ 过定点．19．如图1，在等腰直角三角形ABC 中，4AC BC ==，D 是AC 的中点，E 是AB 上一点，且DE AB ⊥.将ADE V 沿着DE 折起，形成四棱锥-P BCDE ，其中点A 对应的点为点P ，如图2.(1)在图2中，在线段PB 上是否存在一点F ，使得CF ∥平面PDE ？若存在，请求出PFPB的值，并说明理由；若不存在，请说明理由；(2)在图2中，平面PBE 与平面PCD 所成的锐二面角的大小为3π，求四棱锥-P BCDE 的体积.20．在①11a =，525S =；②35a =，917a =；③416S =，864S =这三个条件中任选一个补充在下面的横线上并解答.已知等差数列{}n a 满足________.(1)求数列{}n a 的通项公式；(2)求数列{3}n n a ⋅的前n 项和.n T (如果选择多个条件分别解答，按第一个解答计分)21．在一个有穷数列的每相邻两项之间插入这两项的和，形成新的数列，我们把这样的操作称为该数列的一次“Z 拓展”．如数列1，2第1次“Z 拓展”后得到数列1，3，2，第2次“Z 拓展”后得到数列1，4，3，5，2．设数列a 、b 、c 经过第n 次“Z 拓展”后所得数列的项数记为n P ，所有项的和记为n S ．(1)求1P 、2P ；(2)若2023n P ≥，求n 的最小值；(3)是否存在实数a 、b 、c ，使得数列{}n S 为等比数列？若存在，求a 、b 、c 满足的条件；若不存在，说明理由．21．记数列{}n a 的前n 项和为111,2,34n n n n S a S S a ++=+=-.(1)求{}n a 的通项公式；(2)设2log n n n b a a =，记{}n b 的前n 项和为n T .若2(1)2n t n T -+≤对于2n ≥且*N n ∈恒成立，求实数t 的取值范围.22．已知抛物线的顶点为原点，焦点F 在x轴的正半轴，F 到直线20x +=的距离为54.点()2,2N ，不过点N 的直线l 与抛物线交于两点,A B ，且2NA NB k k +=-.(1)求抛物线方程及抛物线的准线方程(2)求证：直线AB 过定点，并求该定点坐标.高二期末复习卷(答案)一、单选题1.已知()f x '是()f x 的导函数，()f x '的图象如图所示，则()f x 的图象只可能是（）2.“m>2”是“方程22212x y m m +=+表示焦点在x 轴上的椭圆”的（）A ．充分不必要条件B ．必要不充分条件3.已知等差数列{}n a 的前n 项和为n S ，且2121S =，则616a a +的值为（）A ．1B ．2C ．3D ．4【答案】B【分析】根据等差数列前n 项和公式以及等差数列的性质，可得2121S =与616a a +的关系式，即可求得结果.4.若直线l ：12y x m =-+与曲线C ：21164x x y +=有两个公共点，则实数m 的取值范围为（）A ．()(0,-B ．(0,2,00,2-⋃0,2如图可知，当直线l 介于直线12y x =-和与曲线C 有两个公共点．设1l 的方程为012y x m =-+，()00m >，则有联立220116412x yy x m⎧+=⎪⎪⎨⎪=-+⎪⎩，消去x 并整理得2y 由()2200Δ4840m m =--=，解得022m =故m 的取值范围为()0,22．故选：B ．5.已知()f x 在0x x =处可导，则()()02200lim x x f x f x x x →-⎡⎤⎡⎤⎣⎦⎣⎦-等于（）A ．()0f x 'B ．()0f x C ．()20f x '⎡⎤⎣⎦D ．()()002f x f x '业产生的包装垃圾年平均增长率将达到50%.由此可知,如果不采取有效措施,则从（）年（填年份）开始,快递行业产生的包装垃圾超过4000万吨.（参考数据:lg 20.3010,lg 30.4771≈≈）7.数列{}n a 满足154a =，211n n n a a a +=-+，*n ∈N ，则122022111a a a +++ 的整数部分是（）8.已知抛物线22(0)y px p =>）的焦点为F ，过F 且倾斜角为π4的直线l 与抛物线相交于A ，B 两点，12AB =，过A ，B 两点分别作抛物线的切线，交于点Q .则下列四个命题中正确的个数是（）个.①QA QB ⊥；②若M （1，1），P 是抛物线上一动点，则||||PM PF +的最小值为52；③AOB （O 为坐标原点）的面积为；④(,0)2PM -，则tan AMB ∠=二、多选题9．下列说法正确的是（）A ．已知函数3()2f x x x =+，则该函数在区间[]1,3上的平均变化率为30B ．已知11(,)A x y ，22(,)B x y 在函数()y f x =图象上，若函数()f x 从1x 到2x 则曲线()y f x =的割线AB 的倾斜角为3πC V 与时间t 的关系是221V t =-，则2t =时瞬时加速度为7D ．已知函数()f x =，则(9.05) 3.008f ≈【答案】BD10．在底面边长为2、高为4的正四棱柱1111ABCD A B C D -中，O 为棱1A A 上一点，且11,4A O A A P Q =､分别为线段1111B D A D ､上的动点，M 为底面ABCD 的中心，N 为线段AQ 的中点，则下列命题正确的是（）A ．CN 与QM 共面B ．三棱锥A DMN -的体积为43C ．PQ QO +的最小值为2D ．当11113D Q D A = 时，过,,A Q M 三点的平面截正四棱柱所得截面的周长为83对于C ，如图2，展开平面点P ，交11A D 与点Q ，则此时对于D ，如图3，取11113D H D C =uuuu r uuuu r共面，即过,,A Q M 三点的正四棱柱的截面为梯形，且12233QH AC ==，所以平面截正四棱柱所得截面的周长为故选:ACD.11．数列{}n a 满足1a a =，1n n n +=--，则下列说法正确的是（）A ．若1a ≠且2a ≠，数列{}n a 单调递减B ．若存在无数个自然数n ，使得1n n a a +=，则1a =C ．当2a >或1a <时，{}n a 的最小值不存在D ．当3a =时，121111,12222n a a a ⎛⎤++⋅⋅⋅⋅⋅⋅+∈ ⎥---⎝⎦【答案】ACD【分析】A 选项，根据()2110n n n a a a +=--<-求出1n a ≠，再由21311n n n a a a +=--≠求出2n a ≠，从而得到1a ≠且2a ≠，数列{}n a 单调递减，A 正确；B 选项，可举出反例；与抛物线C 交于两点，O 为坐标原点，则下列结论正确的是（）A ．||4AB ≥B ．OA OB ⋅可能大于0C ．P 为抛物线上异于A 、B 的点，直线l 与准线交于点T ，当0,t A >为第一象限的点时，若APB α∠=，PF 平分APB ∠，则π2APT +∠=α对于D 选项，因QA QB ⊥，则Q 为以因()()1122,,A x y B x y ，，1222y y t +=，212212x xt +=+，2AB 则以AB 为直径的圆的方程为(22x t -将其与2:4C y x =联立，消去x 化简得：注意到()4228166448y t y ty +---4y =()()2244412yty yty =--++，由题可得，联立方程有2440y ty --=，其判别式恒大于0，则24120y ty ++=的判别式216t -故选：ACD【点睛】关键点点睛：本题为直线与抛物线综合题为常用手段；对于C 选项，在抛物线中有很多的等量关系与成比例的关系分解因式处理.三、填空题13．若()f x 为可导函数，且()()121lim14x f x f x→--=-，则过曲线()y f x =上点()()1,1f 处的切线斜率为14．对于数列n a ，若1,n n a a +是关于x 的方程203n n x c x -+=的两个根，且12a =，则数列{}n c 所有项的和为________．【答案】92##4.5种情况进行分类讨论，利用分组和法来求得n T ，进而可利用极限求得“数列所有项的和”.15．法国数学家加斯帕•蒙日被称为“画法几何创始人”、“微分几何之父”.他发现与椭圆相切的两条互相垂直的切线的交点的轨迹是以该椭圆中心为圆心的圆，这个圆称为该椭圆的蒙日圆.若椭圆()2222:10x y a b a bΓ+=>>的蒙日圆为2223:2C x y a +=，过C 上的动点M 作Γ的两条切线，分别与C 交于P ，Q 两点，直线PQ 交Γ于A ，B 两点，则下列说法，正确的有______.①椭圆Γ②MPQ 面积的最大值为232a③M到Γ的左焦点的距离的最小值为(2a④若动点D 在Γ上，将直线DA ，DB 的斜率分别记为1k ，2k ，则1212k k =-16．已知数列{}n a 的通项公式为52n n a +⎛⎫=-⋅ ⎪⎝⎭，设数列{}n a 的最大项和最小项分别为,M N ，则四、解答题17．已知椭圆()2222:10x y C a b a b+=>>的四个顶点构成的四边形的面积为12．18．已知双曲线2222:1(0,0)x yC a ba b-=>>，四点12346,,4,,3M M M M⎛⎛⎛-⎝⎭⎝⎭⎝⎭中恰有三点在C上．(1)求C的方程；将ADEV沿着DE折起，形成四棱锥-P BCDE，其中点A对应的点为点P，如图2.(1)在图2中，在线段PB 上是否存在一点F ，使得CF ∥平面PDE ？若存在，请求出PFPB的值，并说明理由；若不存在，请说明理由；(2)在图2中，平面PBE 与平面PCD 所成的锐二面角的大小为3π，求四棱锥-P BCDE 的体积.3PB 理由如下：过点C 作CH ED ⊥，垂足为H ，在PE 上取一点M ，使得13PM PE =，连接因为13PM PE =，13PF PB =，所以FM 建立空间直角坐标系，设PEB θ∠=，则()2,0,0D -，()22,2,0C -，(P 则()2,2,0DC =- ，(2,2cos DP = 设平面PCD 的法向量为(),,m x y z =，则220,22cos 2sin m DC x y m DP x y θθ⎧⋅=-+=⎪⎨⋅=+⋅+⎪⎩取sin x θ=，则sin y θ=，cos z θ=-所以()sin ,sin ,cos 1m θθθ=--，，948153线上并解答.已知等差数列{}n a满足________.(1)求数列{}n a的通项公式；(2)求数列{3}na⋅的前n项和.n Tn一次“Z拓展”．如数列1，2第1次“Z拓展”后得到数列1，3，2，第2次“Z拓展”后得到数列1，4，3，5，2．设数列a、b、c经过第n次“Z拓展”后所得数列的项数记为n P，所有项的和记为n S．(1)求1P 、2P ；(2)若2023n P ≥，求n 的最小值；(3)是否存在实数a 、b 、c ，使得数列{}n S 为等比数列？若存在，求a 、b 、c 满足的条件；若不存在，说明n 项和为111n n n n ++(1)求{}n a 的通项公式；(2)设2log n n n b a a =，记{}n b 的前n 项和为n T .若2(1)2n t n T -+≤对于2n ≥且*N n ∈恒成立，求实数t 的取值范围.【答案】(1)2nn a =(2)8t ≤【分析】（1）利用n a 与n S 的关系证得数列{}n a 是等比数列，从而求得2n n a =；22．已知抛物线的顶点为原点，焦点F 在x 轴的正半轴，F 到直线20x +=的距离为4.点2,2N ，不过点N 的直线l 与抛物线交于两点,A B ，且2NA NB k k +=-.(1)求抛物线方程及抛物线的准线方程。

高二各知识点数学题高二数学要怎么学好?刚开始要从基础题入手，以课本上的习题为准，反复练习打好基础，再找一些课外的习题，以帮助开拓思路，提高自己的分析、解决能力，掌握一般的解题规律。

今天小编在这给大家整理了高二数学题大全，接下来随着小编一起来看看吧!高二数学题(一)古典概型(习题课)本节是学生们在学习完古典概型的一节习题课，本节的主要任务是通过处理教材上的习题使学生进一步理解古典概型的概念及其计算方法，本着新课程的教学理念，为提高课堂效率，本节课我把讲台让给学生，以学习小组为单位，来进行本节课的教学。

(必修3、P134,第4题)A、B、C、D四名学生按任意次序站成一排，试求下列事件的概率：①A在边上;②A和B都在边上;③A或B在边上;④A和B都不在边上教师：同学们，准备好了吗?现在给大家一分钟的时间看看题，各小组选好自己的代表。

(稍作停留，给学生准备时间)，现在请第一组派代表来讲解第一小问。

学生1：题目中说4名同学站成一排，那么我们就考虑他们站队的情况，也就是基本事件个数有24种，用列举法表示出来就是：ABCD ABDC ACBD ACDB ADBC ADCBBACD BADC BCAD BCDA BDAC BDCACABD CADB CBAD CBDA CDAB CDBADABC DACB DBAC DBCA DCAB DCBA其中A在边上包括有最左边和最右边两种情况：共12种情况所以A在边上的概率学生2：老师，刚才同学1在计算基本事件的时候用列举法表示，考虑了四个人的顺序，而这道题在题目中说按任意的次序站，是没有顺序的，他的做法是不是不对?老师：(心中一惊，看来学生对基本事件中顺序有无的考虑还有所欠缺，还需要加以强调)：那么同学们考虑考虑刚才这位同学的担心对不对?学生3：同学1在刚才考虑的时候，基本事件的24种有顺序，但是所要求的事件A在边上包括12种基本事件也有了顺序，两者都考虑了顺序，所以甲的计算是对的，结果就应该是。

高二数学选修一练习题1. 求解下列方程组：(1) 2x + 3y = 73x + 5y = 11(2) 4x + 5y = 182x - 3y = 6(3) x - y = 2x^2 + y^2 = 25(4) 3x + 4y = 79x^2 + 4y^2 = 1(5) 3x - y = 12x + y = 5解析：(1) 首先，将方程组使用消元法进行求解。

对第二个方程乘以2，得到2(2x - 3y) = 2(6)，化简得4x - 6y = 12。

将第一个方程和第二个方程相加得到(2x + 3y) + (4x - 6y) = 7 + 12，化简得到6x - 3y = 19。

进一步将该方程化简为2(2x - y) = 19，再整理得到2x - y = 19/2。

现在，我们有两个方程，即2x - y = 19/2和2x + 3y = 7。

将这两个方程相加消去x，可以得到2(2x + 3y) + 2(2x - y) = 7 + 19/2。

化简后得到8y = 33/2，解得y = (33/2)/8 = 33/16。

将y的值代入2x + 3y = 7，可以求得x = (7 - 3y)/2 = (7 - 3(33/16))/2= 17/16。

因此，方程组的解为x = 17/16，y = 33/16。

(2) 首先，将方程组使用消元法进行求解。

对第一个方程乘以2，得到2(4x + 5y) = 2(18)，化简得8x + 10y = 36。

将第一个方程和第二个方程相加得到(4x + 5y) + (2x - 3y) = 18 + 6，化简得到6x + 2y = 24。

将该方程化简为3x + y = 12。

现在，我们有两个方程，即3x + y = 12和2x - 3y = 6。

将第一个方程乘以3，得到3(3x + y) = 3(12)，化简得到9x + 3y = 36。

将该方程与第二个方程相加，得到(9x + 3y) + (2x - 3y) = 36 + 6，化简得到11x = 42，解得x = 42/11。

人教A 版数学高二相等向量与共线向量精选试卷练习（含答案)学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列命题中正确的是（ ）A ．若a b v v P ，则a v 在b v 上的投影为a vB ．若(0)a c b c c ⋅=⋅≠r v r r v v ，则a b =v vC ．若,,,A B CD 是不共线的四点，则AB DC =u u u v u u u v 是四边形ABCD 是平行四边形的充要条件D ．若0a b ⋅>v v ，则a v 与b v 的夹角为锐角；若0a b ⋅<v v ，则a v 与b v 的夹角为钝角 2．下列命题中正确的个数为（ ）①两个有共同始点且相等的向量，其终点可能不同；②若非零向量AB u u u v 与CD uuu v 共线，则A 、B 、C 、D 四点共线；③若非零向量a v 与b v 共线，则a b =vv ； ④四边形ABCD 是平行四边形，则必有AB CD =u u u v u u u v ；⑤//a b v v ，则a v 、b v 方向相同或相反.A ．0个B ．1个C ．2个D ．3个 3．在ABC V 中，D 为线段AC 的中点，点E 在边BC 上，且12BE EC =，AE 与BD 交于点O ，则=u u u v AO （ ）A ．1124AB AC +u u u v u u u v B ．1144AB AC +u u u v u u u v C ．1142AB AC +u u u v u u u vD ．1122AB AC +u u u v u u u v 4．O 是平面上一定点，,,A B C 是平面上不共线的三个点，动点P 满足：,[0,)AB AC OP OA AB AC λλ⎛⎫ ⎪=++∈+∞ ⎪⎝⎭u u u v u u u v u u u v u u u v u u u v u u u v ，则P 的轨迹一定通过ABC ∆的( ) A ．内心 B ．垂心 C ．重心D ．外心5．设a v 、b r 都是非零向量，下列四个条件中，一定能使0a b a b+=v v v v v 成立的是（ ） A ．2a b =-r v B ．2a b =r v C ．//a b r v D ．a b ⊥v v6．设0a u u v 为单位向量，①若a v 为平面内的某个向量，则0a a a =u u v v v ；②若a v 与0a u u v 平行，则0a a a =u u v v v ；③若a v 与0a u u v 平行且1a =v ，则0a a =u u v v 上述命题中，假命题的个数是（ ）A ．0B ．1C ．2D ．37．下列说法正确的是（ ）A ．若||=||a b v v ，则a v 、b v 的长度相等且方向相同或相反B ．若向量AB u u u v 、CD uuu v 满足AB CD >u u u v u u u v ，且AB u u u v 与CD uuu v 同向，则AB CD >u u u v u u u vC ．若a b ≠v v ，则a v 与b v 可能是共线向量D ．若非零向量AB u u u v 与CD uuu v平行，则A 、B 、C 、D 四点共线8．下列说法中正确的是（ ）A ．单位向量都相等B ．平行向量不一定是共线向量C ．对于任意向量a v ，b v ，必有a b a b +≤+v v v vD ．若a v ，b v 满足a b >v v 且a v 与b v 同向，则a b >v v9．在四边形ABCD 中，AB AD =u u u v u u u v 且BA CD =u u u v u u u v ，则四边形ABCD 的形状一定是（ ）A ．正方形B ．矩形C ．菱形D ．等腰梯形10．给出下列命题：①零向量的长度为零，方向是任意的；②若,a b v v 都是单位向量，则a b =v v ；③向量AB u u u v 与BA u u u v 相等，则所有正确命题的序号是( )A ．①B ．③C ．①③D ．①② 11．分析下列四个命题并给出判断，其中正确的命题个数是（ ）①若//a b r r ，则a b =r r ； ②若||||a b =r r ，则a b =r r ；③若||||a b =r r ，则//a b r r ④若a b =r r ，则||||a b =r rA ．0B ．1C ．2D ．3 12．下列命题中，正确的是（ ）A ．有相同起点的两个非零向量不共线B ．“a b =v v ”的充要条件是||a b v v |=|且//a b v vC ．若a v 与b v 共线，b v 与c v 共线，则a v 与c v 共线D ．向量a v 与b v 不共线，则a v 与b v 都是非零向量13．下列结论正确的是（ ）A ．||||a b a b =⇒=r r r rB ．a b a c b c ⋅=⋅⇒=r r r r r rC ．//a b r r ，////b c a c ⇒r r r rD ．||||a b a b >⇒>r rr r 14．下列结论正确的是( ) A ．若向量a r ，b r 共线，则向量a r ，b r 的方向相同B ．向量AB u u u r 与向量CD uuu r是共线向量，则A ，B ，C ，D 四点在一条直线上 C ．ABC V 中，D 是BC 中点，则()1AD AB AC 2=+u u u r u u u r u u u r D ．若a //b r r ，则λR ∃∈使a λb =r r 15．下列说法中正确的是( )A ．若AB DC =u u u v u u u v ，则,,,A B CD 四点构成一个平行四边形B ．若//a b v v ，//b c v v ，则//a c v vC ．若a v 和b v 都是单位向量，则a b =v vD ．零向量与任何向量都共线16．如图，在正方形ABCD 中，点E 是DC 的中点，点F 是BC 的一个三等分点， 那么EF u u u v＝( )A ．1123AB AD -u u u v u u u v B ．1142AB AD +u u u v u u u vC ．1132AB AD +u u u v u u u v D ．1223AB AD -u u u v u u u v 17．下列命题正确的是( )． A ．若a b >r r ，则a b r r > B ．若a b =r r ，则a b =r rC ．若a b =r r ，则//a b r rD ．若a b ≠r r ，则a r 与b r 不是共线向量18．下列命题中正确的个数是 ( )（1）若e v 为单位向量，且//a e v v ，则a a e =v v v ； （2）若//a b v v 且//b c v v ，则//a c v v ；（3）3••a a a a =v v v v ； （4）若平面内有四点A 、B 、C 、D ，则必有AC BD BC AD +=+u u u v u u u v u u u v u u u v.A ．0B ．1C ．2D ．3 19．下列命题正确的是A ．若a 、b 都是单位向量，则a =b.B ．若AB DC =u u u v u u u v ，则A ，B ，C ，D 四点构成平行四边形.C ．若两向量a 、b 相等，则它们是始点、终点都相同的向量D ．AB u u u v 与BA u u u v 是两平行向量20．下列说法正确的是A ．向量AB u u u v 与向量CD uuu v 是共线向量，则点,,,A BCD 必在同一条直线上B ．两个有共同终点的向量，一定是共线向量C ．长度相等的向量叫做相等向量D ．两个有共同起点而且相等的向量，其终点必相同21．在ABC V 中，已知AB a =u u u v v ，AC b =u u u v v ，4BC BD =u u u v u u u v ，3CA CE =u u u v u u u v ，则DE =u u u v （ ） A ．43b a -v v B ．53124a b -v v C ．3143a b -v v D ．53124b a -v v 22．下列说法正确的是（ ）A ．若a b >v v ，a b >v vB ．若||a b v v |=|，a b =v vC ．若a b =v v ，则//a b v vD ．若a b ≠v v ，则a v 与b v 不是共线向量23．对于任意向量,,a b c v v v，下列说法正确的是（ ） A ．||a b c a b c ++≥--u u v v v v v vB ．||a b c a b c ++≥+-u u v v v v v vC ．||a b c a b ++≥+u u v v v v vD ．||a b c a b ++≥-u u v v v v v24．已知向量a r 、b r 不共线，若2453AB a b BC a b CD a b =+=--=--u u u r u u u r u u u r r r r r r r ，，，则四边形ABCD 是()n nA ．梯形B ．平行四边形C ．矩形D ．菱形25．已知四个命题：①如果向量a v 与b v 共线，则a b =v v 或a b =-v v ；②3x ≤是3x ≤的必要不充分条件；③命题p ：0(0,2)x ∃∈，200230x x --<的否定p ⌝：(0,2)x ∀∈，2230x x --≥；④“指数函数x y a =是增函数，而1()2x y =是指数函数，所以1()2xy =是增函数” 此三段论大前提错误，但推理形式是正确的.以上命题正确的个数为（ ）A ．0B ．1C ．2D ．3 26．若A 、B 、C 、D 是平面内任意四点，给出下列式子：①AB CD BC DA +=+u u u v u u u v u u u v u u u v ，②AC BD BC AD +=+u u u v u u u v u u u v u u u v ，③AC BD DC AB -=+u u u v u u u v u u u v u u u v ． 其中正确的有（ ）．A ．0个B ．1个C ．2个D ．3个 27．若|r a |=|r b |，那么要使r a =rb ，两向量还需要具备 ( )A ．方向相反B ．方向相同C ．共线D ．方向任意 28．下列说法不正确．．．的是（ ） A ．若12a =v 时，则2a r 为单位向量 B ．若ab →→=，则a b =r r C ．若0a =r ，则0a =r r D ．若非零向量a →与b →不共线，且()//()ka b a kb --r r r r ，则实数1k =±29．已知a ，b ，c 是非零向量，则()++a c b ，()++b a c ，()++b c a ，()++c a b ，()++c b a 中，与向量++a b c 相等的个数为( )A ．5B ．4C ．3D ．230．已知=10AB u u u r ，=7BC u u u r ，则AC u u u r 的取值范围是( )A ．[]3,17B ．[)3,17C ．[]3,10D ．(]3,1031．已知D ，E ，F 分别是△ABC 三边AB ，BC ，CA 的中点，则下列等式不成立的是（ ）A ．FD DA FA +=u u u r u u u r u u u rB ．0FD DE EF ++=u u u r u u u r u u u rC ．DE DA EC +=u u u r u u u r u u u rD ．DA DE DF +=u u u r u u u r u u u r32．下列各式不恒成立的是（ ）A ．a b b a +=+r r r rB ．0a a +=r r rC ．AC CB AB +=u u u r u u u r u u u rD ．a b a b +=+r r r r33．P 为四边形ABCD 所在平面上一点，=PA PB PC PD AB CD ++++u u u r u u u r u u u r u u u r u u u r u u u r ，则P 为（ ）A ．四边形ABCD 对角线交点B ．AC 的中点C ．BD 的中点 D ．CD 边上一点34．AB+BC +CD+DE +EF +FA =u u u r u u u r u u u r u u u r u u u r u u u r ( )A ．0B ．0rC ．2AD u u u r D ．2AD -u u u r二、多选题35．ABC ∆是边长为3的等边三角形，已知向量a r 、b r 满足3AB a =uu u r r ，3AC a b =+u u u r r r ，则下列结论中正确的有（ ）A ．a r 为单位向量B ．//b BC r u u u r C ．a b ⊥r rD ．()6a b BC +⊥r r u u u r三、填空题36．已知O 为平行四边形ABCD 内一点，设OA a =u u u v v ，OB b =u u u v v ，OC c =u u u v v ，则OD =u u u v__________． 37．设向量,a b v v 不平行,向量2a b λ-r r 与2a b +r r 平行,则实数λ=___________.38．已知梯形ABCD ，AB CD ∥，设1AB e =u u u v u v ，向量2e u u v 的起点和终点分别是A 、B 、C 、D 中的两个点，若对平面中任意的非零向量a v ，都可以唯一表示为1e u v 、2e u u v 的线性组合，那么2e u u v 的个数为______.39．如下图，在ABC ∆中，1,2,,2AB AC BC AD DC AE EB ====u u u v u u u v u u u v u u u v ．若12BD AC ⋅=-u u u v u u u v ，则CE AB ⋅=u u u v u u u v __________．40．已知向量=(1,2)a ，写出一个与a 共线的非零向量的坐标__________.41．已知点G 是△ABC 的重心，则GA GB GC ++=u u u r u u u r u u u r ________.42．如图，已知△ABC 是直角三角形且90A ∠=︒，则下列结论中正确的是________．①AB AC BC +=u u u r u u u r u u u r ；②AB BC CA +=u u u r u u u r u u u r ； ③AB CA BC +=u u u r u u u r u u u r ；④222AB AC BC +=u u u r u u u r u u u r .43．若向量a ，b 满足8=a ，2=1b ，则+a b 的最小值是__________．四、解答题44．已知(0,1)A -，(5,1)B -，(7,2)D ，且AB u u u r ∥DC u u u r ，BC AB ⊥u u u r u u u r .（1）求直线CD 的方程（用一般式表示）；（2）求点C 的坐标，并求四边形ABCD 的面积.45．已知定点(1,0)A -，(2,0)B ，圆C ：22230x y x +--+=.（1）过点B 向圆C 引切线l ，求切线l 的方程；（2）过点A 作直线1l 交圆C 于P ，Q ，且AP PQ =u u u v u u u v ，求直线1l 的斜率；（3）定点M ，N 在直线2:1l x =上，对于圆C 上任意一点R 都满足RN =，试求M ，N 两点的坐标.46．已知平面直角坐标系内四点A B '=(1)若四边形OQAP 是平行四边形，求,m k 的值；(2)求cos POQ ∠.47．如图，四边形ABCD 与ABDE 都是平行四边形.(1)用有向线段表示与向量AB u u u r 相等的向量.(2)用有向线段表示与向量AB u u u r共线的向量.48．如图所示菱形ABCD 中，对角线AC ，BD 相交于O 点，∠DAB=60°，分别以A ，B ，C ，D ，O 中的不同两点为始点与终点的向量中，(1)写出与DA u u u r 平行的向量.(2)写出与DA u u u r模相等的向量.49．点D ，E ，F 分别是△ABC 的三边AB ，BC ，CA 的中点，求证： （1）AB BE AC CE +=+u u u r u u u r u u u r u u u r ；（2）0EA FB DC ++=u u u r u u u r u u u r r ．参考答案1．C2．B3．A4．A5．A6．D7．C8．C9．C10．A11．B12．D13．A14．C15．D16．D17．C18．B19．D20．D21．D22．C23．A24．A25．D26．C27．B28．B【答案】A30．A31．B32．D33．B34．B35．ABD36．a c b +-v v v37．4-38．839．43- 40．纵坐标为横坐标2倍即可41．0r42．①②③④43．444．（1）25240x y +-=；（2）(3,6)C -，872.45．（1）x ＝20y +-=（2）315k =（3）(1(1(1(10)33M N M N ，或，，．46．(2)23 47．(1) E D u u u r ，DC uuu r . (2) E D u u u r ，DE u u u r ，DC uuu r ，CD uuu r ，EC u u u r ，CE u u u r ，BA u u u r . 48．(1) A D u u u r ，BC uuu r ，CB u u u r .(2) A D u u u r ，BC uuu r ，CB u u u r ，AB u u u r ，BA u u u r ，DC uuu r ，CD uuu r ，BD u u u r ，DB u u u r.49．详见解析。

高二数学练习题答案题一：解方程1. 解方程：2x - 3 = 7解：将已知方程转化为 x 的形式，2x - 3 = 72x = 7 + 32x = 10x = 10/2x = 5所以，方程的解为 x = 5。

2. 解方程：3(x + 4) = 15解：根据分配律展开括号，3x + 12 = 153x = 15 - 123x = 3x = 3/3x = 1所以，方程的解为 x = 1。

3. 解方程：5x - 1 = 4x + 3解：将已知方程转化为 x 的形式，5x - 4x = 3 + 1x = 4所以，方程的解为 x = 4。

题二：函数1. 已知函数 f(x) = 2x + 3，求 f(4) 的值。

解：将 x = 4 代入函数 f(x)，f(4) = 2(4) + 3f(4) = 8 + 3f(4) = 11所以，f(4) 的值为 11。

2. 已知函数 g(x) = 3x^2 - 2x + 4，求 g(-1) 的值。

解：将 x = -1 代入函数 g(x)，g(-1) = 3(-1)^2 - 2(-1) + 4g(-1) = 3(1) + 2 + 4g(-1) = 3 + 2 + 4g(-1) = 9所以，g(-1) 的值为 9。

3. 已知函数 h(x) = 5/x，求 h(2) 的值。

解：将 x = 2 代入函数 h(x)，h(2) = 5/2所以，h(2) 的值为 5/2。

题三：几何形体1. 已知长方形的长为 6 cm，宽为 3 cm，求其周长和面积。

解：周长 = 2(长 + 宽)周长 = 2(6 + 3)周长 = 2(9)周长 = 18 cm面积 = 长 ×宽面积 = 6 × 3面积 = 18 cm²所以，长方形的周长为 18 cm，面积为 18 cm²。

2. 已知正方形的边长为 5 cm，求其周长和面积。

解：周长 = 4 ×边长周长 = 4 × 5周长 = 20 cm面积 = 边长 ×边长面积 = 5 × 5面积 = 25 cm²所以，正方形的周长为 20 cm，面积为 25 cm²。

高二数学同步检测四两个平面平行的判定和性质说明：本试卷分为第Ⅰ、Ⅱ卷两部分，请将第Ⅰ卷选择题的答案填入题后括号内，第Ⅱ卷可在各题后直接作答.第Ⅰ卷（选择题）一、选择题（本大题共10小题,在每小题给出的四个选项中,选择一个符合题目要求的选项）1设直线l,m,平面α,β,下列条件能得出α∥β的是…( )A.l⊂α,m⊂α,且l∥β,m∥βB.l⊂α,m⊂α,且l∥mC.l⊥α,m⊥β,且l∥mD.l∥α,m∥β,且l∥m答案:C解析:如左上图,A错;如右上图,D错;B显然错.故选C.2下列命题中正确的是( )①平行于同一直线的两个平面平行②平行于同一平面的两个平面平行③垂直于同一直线的两个平面平行④与同一直线成等角的两个平面平行A.①②B.②③C.③④D.②③④答案:B解析:如图(1),①错;如图(2),④错.B.3给出下列四个命题:①夹在两个平行平面间的线段中,较长的线段与平面所成的角较小;②夹在两个平行平面间的线段相等,则它们与两个平面所成的角相等;③夹在两个平行平面间的线段相等,则这两线段必平行;④夹在两个平行平面间的平行线段必相等.其中正确的命题有( )A.①②④B.②③④C.①③D.④解析:由于两个平行平面间的距离是定值，所以①②显然正确;如图,a,b 相等,但ab,故③错;④正确.故选A.4设α,β表示平面,a 表示直线,且直线a 不在平面α或β内,并有①α∥β;②a ⊥α;③a ⊥β.以其中任意两个为条件,另一个为结论,可构造出三个命题.其中正确命题的个数是( ) A.1 B.2 C.3 D.0 答案:C 解析:⇒⎭⎬⎫⊥αβαa //a ⊥β,即①②⇒③.⇒⎭⎬⎫⊥⊥βαa a α∥β,即②③⇒①.⇒⎭⎬⎫⊥ββαa //a ⊥α,即①③⇒②.故选C. 5已知平面α∥平面β,α,β之间的距离等于d,直线a ⊂α,则β( ) A.有且只有一条直线与a 的距离等于d B.有无数条直线与a 的距离等于d C.所有直线与a 的距离都等于d D.仅有两条直线与a 的距离等于d 答案:B解析:过直线a 上任一点作平面β的垂线,垂足为A,过点A 在平面β内作直线b ∥a,此时a 与b 间的距离为d;在平面β内所有与a 异面的直线间的距离也都是d.6如果平面α∥平面β,直线a ⊂平面α,点B ∈β,则平面β内过点B 的所有直线中,下列结论成立的是( )A.不一定存在与a 平行的直线B.不存在与a 平行的直线C.存在唯一一条与a 平行的直线D.存在无数条与a 平行的直线 答案:C解析:如图所示.过直线a 与点B 所确定的平面γ,且γ∩β=b,直线b ∥直线a,且唯一.故选C. 7已知m,n 是不同的直线,α,β是不重合的平面,给出下列命题: ①若m ∥α,则m 平行于平面α内的任意一条直线; ②若α∥β,m ⊂α,n ⊂β,则m ∥n; ③若m ⊥α,n ⊥β,m ∥n,则α∥β; ④若α∥β,m ⊂α,则m ∥β. 其中正确的命题是( )A.①②③B.③④C.②③D.④解析:若m ∥α,则m 平行于过m 所作平面与α相交的交线,并非α内任一条直线,故①错; 若α∥β,m ⊂α,n ⊂β,则可能m ∥n,也可能m,n 异面,故②错;⇒⎭⎬⎫⊥⊥⇒⎭⎬⎫⊥βααn n n m m //α∥β,③正确;⇒⎭⎬⎫⊂αβαm //m ∥β,④正确.8已知平面α∥平面β,C 、A ∈α,B 、D ∈β,AB ⊥CD,且AB=2，直线AB 与平面α所成的角为30°，则线段CD 长的取值范围为( )A.［1，+∞)B.(1,332] C.(332,334) D.［332,+∞)答案:D解析:如图，过D 作DA ′∥AB 交平面α于A ′，由α∥β,故DA ′=AB=2.DA ′与α成30°角，由已知DC ⊥AB,可得DC ⊥DA ′,所以DC 在过DC 且与DA ′垂直的平面γ内.令γ∩α=l,在γDC 0⊥l 时最短，此时DC 0=DA ′·tan30°=332,故CD ≥332. 9已知平面α∥平面β，其间夹一垂线段AB=4，另一斜线段CD=6，且AC=BD=3.E 、F 分别是AB 、CD 的中点，则EF 的长为( )A.1B.2C.2D.5答案:C解析:如图，过F 作AB 的平行线，交α、β于P 、Q 两点，则四边形ABQP 为矩形. ∵E 、F 分别为AB 、CD 的中点，故EF ⊥PQ. 由Rt △EAC ≌Rt △EBD ⇒EC=ED,则△APC 为直角三角形.在Rt △CPF 中，CP 2=CF 2-PF 2=5⇒CP=5. 在Rt △CPA 中，AP 2=AC 2-CP 2=32-(.)2=4. ∴AP=2.而AP=EF ，∴EF=2.10一间民房的屋顶有如下图的三种盖法:①单向倾斜;②双向倾斜;③四向倾斜.记三种盖法的屋顶面积分别为P 1,P 2,P 3.若屋顶斜面与水平面所成的角都是α,则( )A.P 1<P 2<P 3B.P 1=P 2<P 3C.P 1<P 2=P 3D.P 1=P 2=P 3 答案:D解析:由S 底=S 侧cos θ可得P 1=P 2, 而P 3=2θθθcos )(2)cos cos (2121S S S S +=+ 又∵2(S 1+S 2)=S 底,∴P 1=P 2=P 3.第Ⅱ卷（非选择题）二、填空题（本大题共4小题,答案需填在题中横线上）11如下图,点P 是一光源,将一投影片放在平面α内,问投影幕所在平面β与平面α______时,投影图象的形状不发生变化.答案:平行解析:当α∥β时,易证△ABC ∽△A ′B ′C ′,从而形状不会发生变化.12设直线a 在平面M 内,则平面M 平行于平面N 是直线a 平行于平面N 的__________条件.( 答案:充分不必要解析:设p:平面M ∥平面N ，q:直线a ∥平面N.⇒⎭⎬⎫⊂=⋂⇒M a N M N M φ平面平面// a ∩N=∅⇒a ∥N,∴p ⇒q.⇒⎭⎬⎫⊂M a N a 平面//平面N 与平面M 不一定平行,∴qp.13如图，已知平面α∥平面β，线段AB 、CD 夹在α、β之间，AB=13，CD=55，且它们在β内的射影之差为2，则α和β之间的距离是____________.答案:5解析:设A 、C 在平面β上的射影为A ′、C ′，则α、β之间的距离AA ′=CC ′=a,且BA ′、DC ′分别为AB 、CD 在β. 在Rt △ABA ′中，AB=13， 则BA ′=222'213a AA AB -=-.在Rt △CDC ′中，CD=55， 则C ′D=22'2125a C C CD -=-. 又∵C ′D 与A ′B 相差为2，即A ′B-C ′D=2，22212513a a ---=2.∴a=5.∴平面α、β的距离为5.14设P 表示点,m,n,l 表示两两不重合的三条直线,以α,β表示两个不重合的平面,那么下列四个命题:①m ⊥α,若n ⊥α,则m ∥n;②m ⊂α,n ∩α=P,l 是n 在α内的射影.若m ⊥l,则m ⊥n;③m ⊥α,若n ∥a,l ∥α,则m ⊥n,m ⊥l;④m ⊥α,若m ⊥β,则α∥β中逆命题能成立的序号是________. 答案:①②④解析:命题③的逆命题是:m ⊥α,若m ⊥n,m ⊥l,则n ∥α,l ∥α,错误的原因在于满足条件的直线n 和l 可能在平面α内,故①②④能成立.三、解答题（本大题共5小题,解答应写出文字说明,证明过程或演算步骤）15已知平面α∥β,AB 、CD 为夹在α、β间的异面线段，E 、F 分别为AB 、CD 的中点.求证:EF ∥α,EF ∥β.分析:要证EF ∥α，根据线面平行的判定定理，只需在α内找一条直线与EF 平行；或过EF 作一平面，使该平面与α平行，据面面平行的性质定理即可证得.证法一:连结AF 并延长交β于G . ∵AG ∩CD=F,∴AG 、CD 确定平面γ，且γ∩α=AC,γ∩β=DG . ∵α∥β,∴AC ∥DG .∴∠ACF=∠GDF. 又∠AFC=∠DFG ，CF=DF, ∴△ACF ≌△GDF.∴AF=FG . 又AE=BE,∴EF ∥BG . ∵BG ⊂β,∴EF ∥β. 同理,FE ∥α.证法二:∵AB 与CD 为异面直线,∴A ∉CD.在A 、C 、D 确定的平面内过点A 作AG ∥CD 交β于点G ，取AG 的中点H ，连结AC 、HF. ∵α∥β,∴AC ∥DG ∥FH. ∵DG ⊂β,∴HF ∥β. 又∵E 为AB 的中点, ∴EH ∥BG.∴EH ∥β.又EH ∩HF=H,∴平面EHF ∥β.∵EF ⊂平面EHF,∴EF ∥β.同理,EF ∥α.16如果两个平面分别平行于第三个平面,那么这两个平面互相平行.答案:已知:α∥β,γ∥β, 求证:α∥γ.证明:如图,作两个相交平面分别与α,β,γ交于a,c,e 和b,d,f.⇒⎩⎨⎧⎭⎬⎫⇒⇒⇒⎪⎪⎭⎪⎪⎬⎫⎩⎨⎧⇒⎩⎨⎧⇒γγγββα////////////////////b f b a e a f d e c d b c a α∥γ.17如图所示,A,B,C,D 四点在平面M 和N 之外,它们在M 内的射影A 1,B 1,C 1,D 1成一直线,在N内的射影A 2,B 2,C 2,D 2组成一个平行四边形,求证:ABCD 是平行四边形.证明:∵A,B,C,D 四点在平面M 内的射影是一条直线, ∴ABCD 为平面四边形.又AA 2⊥平面N,DD 2⊥平面N, ∴AA 2∥DD 2. ∵A 2B 2∥C 2D 2,∴平面AA 2B 2B ∥平面CC 2D 2D. 又ABCD 为平面四边形, ∴AB ∥CD.同理可证AD ∥BC. ∴ABCD 为平行四边形.18如图,正方体ABCD —A 1B 1C 1D 1的棱长为a,过其对角线BD 1的平面分别与AA 1、CC 1相交于点E,F,求截面四边形BED 1F 面积的最小值.解:由平面与平面平行的性质定理可证BF ∥D 1E,BE ∥D 1F. ∴BED 1F 是平行四边形.作EH ⊥BD 1于H. ∵F BED S 1=2·1BED S =BD 1·EH=EH ·3a,∴要求四边形BED 1F 面积的最小值,转化为求EH 的最小值. ∵AA 1∥平面BDD 1B 1,∴当且仅当EH 为直线AA 1到平面BDD 1B 1的距离时,EH 最小,易得EH min =22. ∴F BED S 1的最小值为26a 2. 19(2006高考天津卷,理19)如图,在五面体ABCDEF 中,点O 是矩形ABCD 的对角线的交点,面CDE 是等边三角形,棱EF21BC.(1)证明FO ∥平面CDE;(2)设BC=3CD,证明EO ⊥平面CDF.证明:(1)取CD 中点M,连结OM,在矩形ABCD 中, OM21BC,又EF 21BC,则EF OM.连结EM, 于是四边形EFOM 为平行四边形. ∴FO ∥EM.又∵FO ⊄平面CDE,且EM ⊂平面CDE, ∴FO ∥平面CDE.(2)连结FM.由(1)和已知条件,在等边△CDE 中,CM=DM,EM ⊥CD 且EM=23CD=21BC=EF. 因此平行四边形EFOM 为菱形,从而EO ⊥FM.∵CD ⊥OM,CD ⊥EM,∴CD ⊥平面EOM.从而CD ⊥EO. 而FM ∩CD=M,所以EO ⊥平面CDF.本卷由《100测评网》整理上传，专注于中小学生学业检测、练习与提升.。

一、选择题1．已知函数()()sin f x A x ωϕ=+(A 、ω、ϕ均为正的常数)的最小正周期为π，当23x π=时，函数()f x 取得最小值，则下列结论正确的是（ ）A ．()()()220f f f -<<B ．()()()220f f f <-<C ．()()()202f f f -<<D ．()()()022f f f <-<2．已知向量a 、b 、c 满足a b c +=，且::1:1:2a b c =a 、b 夹角为（ ） A ．4π B ．34π C ．2π D ．23π 3．将函数sin()cos()22y x x ϕϕ=++的图象沿x 轴向右平移8π个单位后，得到一个偶函数的图象，则ϕ的取值不可能是（ ）A ．54π-B ．4π-C ．4π D ．34π 4．非零向量a b ，满足：a b a -=，()0a a b ⋅-=，则a b -与b 夹角的大小为 A ．135° B ．120° C ．60° D ．45°5．已知P （14，1），Q （54，－1）分别是函数()()cos f x x ωϕ=＋0,2πωϕ⎛⎫>< ⎪⎝⎭的图象上相邻的最高点和最低点，则ωϕ-=（ ） A ．54π-B ．54πC ．－34π D ．34π 6．已知a R ∈，则“cos 02πα⎛⎫+> ⎪⎝⎭”是“α是第三象限角”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件7．函数()sin()A f x x ωϕ=+(0,)2πωϕ><的部分图象如图所示，则()f π=（ ）A ．4B ．23C ．2D ．38．已知函数()(0,0)y sin x ωθθπω=+<为偶函数，其图象与直线1y =的某两个交点横坐标为1x 、2x ，若21x x -的最小值为π，则（ ） A ．2,2πωθ==B ．1,22==πωθ C ．1,24==πωθ D ．2,4==πωθ9．将函数y =2sin （ωx +π6）（ω>0）的图象向右移2π3个单位后，所得图象关于y 轴对称，则ω的最小值为 A ．2 B ．1 C ．12 D ．1410．已知a ，b 是平面内两个互相垂直的单位向量，若向量c 满足()()0a c b c -⋅-=，则c 的最大值是( ) A ．1B ．2C ．D ．11．已知角6πα-的顶点在原点，始边与x 轴正半轴重合，终边过点()5,12P -， 则7cos 12πα⎛⎫+= ⎪⎝⎭( ) A ．17226-B ．7226-C ．226D ．22612．已知4sin 5α，并且α是第二象限的角，那么tan()απ+的值等于 A ．43-B ．34-C ．34D ．4313．已知f (x )=A sin(ωx+θ)(ω>0),若两个不等的实数x 1,x 2∈()2A x f x ⎧⎫=⎨⎬⎩⎭,且|x 1-x 2|min =π,则f (x )的最小正周期是( ) A ．3πB ．2πC ．πD ．π214．已知tan 3a =，则21cos sin 22a a +=（） A ．25-B ．3C ．3-D ．2515．设0002012tan15cos 22,,21tan 15a b c ===+，则有（ ） A ．c a b <<B ．a b c <<C ．b c a <<D ．a c b <<二、填空题16．已知24sin 225θ=，02πθ⎛⎫<< ⎪⎝⎭4πθ⎛⎫- ⎪⎝⎭的值为_______________.17．已知向量a ，b 满足1a =，且()2a a b b -==，则向量a 与b 的夹角是__________．18．已知角θ的终边上的一点P 的坐标为()3,4，则cos 21sin 2θθ=+________________．19．函数()211sinsin (0)222x f x x ωωω=+->，若函数()f x 在区间x ∈(),2ππ内没有零点，则实数ω的取值范围是_____20．三棱锥V-ABC 的底面ABC 与侧面VAB 都是边长为a 的正三角形，则棱VC 的长度的取值范围是_________.21．在矩形ABCD 中， 3AB =， 1AD =，若M ， N 分别在边BC ， CD 上运动（包括端点，且满足BM CN BCCD=，则AM AN ⋅的取值范围是__________．22．设(1,3,2)a =-，(2,+1,1)b m n =-，且a //b ，则实数m n -=_____．23．为得到函数2y sin x =的图象,要将函数24y sin x π⎛⎫=+ ⎪⎝⎭的图象向右平移至少__________个单位. 24．已知已知sin π3()25α+=，α∈π(0,)2，则sin(π＋α)等于__________25．已知向量()()121a b m =-=，，，，若向量a b +与a 垂直，则m =______． 三、解答题26．已知点(2,0)A -,(1,9)B ,(,)C m n ，O 是原点. （1）若点,,A B C 三点共线，求m 与n 满足的关系式； （2）若AOC ∆的面积等于3，且AC BC ⊥,求向量OC . 27．已知4a =，3b =，()()23261a b a b -⋅+=. （1）求向量a 与b 的夹角θ；（2）若()1c ta t b =+-，且0b c ⋅=，求实数t 的值及c . 28．已知函数()2sin 22cos 6f x x x π⎛⎫=-- ⎪⎝⎭. （1）求函数()f x 的单调增区间； （2）求函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的值域. 29．已知圆．（1）求过点(3,0)Q 的圆C 的切线l 的方程；（2）如图，(1,0),A M 定点为圆C 上一动点，点P 在AM 上，点N 在CM 上，且满足2,0,AM AP NP AM =⋅=求N 点的轨迹．30．如图所示,函数()2cos (,0.0)2y x x R πωθωθ=+∈>≤≤的图象与y 轴交于点()0,3,且该函数的最小正周期为π.(1)求θ和ω的值； (2)已知点πA ,02⎛⎫⎪⎝⎭,点P 是该函数图象上一点,点00(,)Q x y 是PA 的中点,当003,,22y x ππ⎡⎤=∈⎢⎥⎣⎦时，求0x 的值.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题1．B2．C3．C4．A5．B6．B7．A8．A9．B10．C11．B12．A13．A14．D15．A二、填空题16．【解析】【分析】由三角函数的基本关系式和正弦的倍角公式求得再由两角差的余弦函数的公式即可求解【详解】由即则又由所以又由【点睛】本题主要考查了三角函数的基本关系式以及正弦的倍角公式和两角差的余弦公式的17．【解析】【分析】先根据条件得再根据向量夹角公式求结果【详解】因为且所以因此【点睛】求平面向量夹角方法：一是夹角公式；二是坐标公式；三是几何方法从图形判断角的大小18．【解析】分析：由角的终边上的一点的坐标为求出的值利用将的值代入即可得结果详解：角的终边上的一点的坐标为那么故答案为点睛：本题主要考查三角函数的定义及二倍角的正弦公式与余弦公式属于中档题给值求值问题求19．【解析】分析：先化简函数f(x)再求得再根据函数在区间内没有零点得到不等式组最后解不等式组即得w的范围详解：由题得f(x)=因为所以当或时f(x)在内无零点由前一式得即由k=0得K取其它整数时无解同20．【解析】分析：设的中点为连接由余弦定理可得利用三角函数的有界性可得结果详解：设的中点为连接则是二面角的平面角可得在三角形中由余弦定理可得即的取值范围是为故答案为点睛：本题主要考查空间两点的距离余弦定21．19【解析】设则也即是化简得到其中故填点睛：向量数量积的计算有3个基本的思路：（1）基底法：如果题设中有一组不共线的向量它们的模长和夹角已知则其余的向量可以用基底向量去表示数量积也就可以通过基底向量22．8【解析】由题意得23．【解析】函数的解析式：则要将函数的图象向右平移至少个单位点睛：由y＝sinx的图象利用图象变换作函数y＝Asin(ωx＋φ)(A＞0ω＞0)(x∈R)的图象要特别注意：当周期变换和相位变换的先后顺序24．【解析】由题意得25．【解析】利用平面向量的加法公式可得：由平面向量垂直的充要条件可得：解方程可得：三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题 1．B 解析：B 【解析】依题意得，函数f （x ）的周期为π， ∵ω＞0，∴ω=2ππ=2．又∵当x=23π 时，函数f （x ）取得最小值， ∴2×23π +φ=2kπ+32π ，k ∈Z ，可解得：φ=2kπ+6π，k ∈Z ， ∴f （x ）=Asin （2x+2kπ+6π）=Asin （2x+6π）． ∴f （﹣2）=Asin （﹣4+6π）=Asin （6π﹣4+2π）＞0． f （2）=Asin （4+6π）＜0， f （0）=Asin 6π=Asin 56π＞0， 又∵32π＞6π﹣4+2π＞56π＞2π，而f （x ）=Asinx 在区间（2π，32π）是单调递减的，∴f （2）＜f （﹣2）＜f （0）． 故选：B ．2．C解析：C 【解析】 【分析】对等式a b c +=两边平方，利用平面向量数量积的运算律和定义得出0a b ⋅=，由此可求出a 、b 的夹角. 【详解】等式a b c +=两边平方得2222a a b b c +⋅+=，即2222cos a b b c a θ+⋅+=，又::1:1:a b c =0a b ⋅=，a b ∴⊥，因此，a 、b 夹角为2π，故选：C. 【点睛】本题考查平面向量夹角的计算，同时也考查平面向量数量积的运算律以及平面向量数量积的定义，考查计算能力，属于中等题.3．C解析：C 【解析】试题分析：()1sin()cos()sin 2222y x x x ϕϕϕ=++=+将其向右平移8π个单位后得到：11sin 2sin 22824y x x ππϕϕ⎛⎫⎛⎫⎛⎫=-+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，若为偶函数必有：()42k k Z ππϕπ-=+∈，解得：()34k k Z πϕπ=+∈，当0k =时，D 正确，1k =-时，B 正确，当2k =-时，A 正确，综上，C 错误. 考点：1.函数的图像变换；2.函数的奇偶性.4．A解析：A 【解析】 【分析】先化简()0a a b ⋅-=得2=a a b ⋅，再化简a b a -=得2b a =，最后求a b -与b 的夹角. 【详解】因为()0a a b ⋅-=，所以220=a a b a a b -⋅=∴⋅，，因为a b a -=，所以2222a a a b b =-⋅+， 整理可得22b a b =⋅， 所以有2b a =，设a b -与b 的夹角为θ，则()2cos a b b a b b a b ba bθ-⋅⋅-===-222222||a a =-， 又0180θ︒≤≤︒，所以135θ=︒， 故选A ． 【点睛】本题主要考查数量积的运算和向量夹角的计算，意在考查学生对这些知识的理解掌握水平和分析推理能力.5．B解析：B 【解析】【分析】由点P,Q 两点可以求出函数的周期，进而求出ω，再将点P 或点Q 的坐标代入，求得ϕ，即求出ωϕ-． 【详解】 因为512244πω⎛⎫-=⎪⎝⎭，所以ωπ=，把1,14P ⎛⎫ ⎪⎝⎭的坐标代入方程()cos y x πϕ=+，得 ()24k k Z ϕππ=-+∈，因为2πϕ<，所以5,44ππϕωϕ=--=，故选B ． 【点睛】本题主要考查利用三角函数的性质求其解析式．6．B解析：B 【解析】 【分析】 先化简“cos 02πα⎛⎫+> ⎪⎝⎭”，再利用充要条件的定义判断. 【详解】 因为cos 02πα⎛⎫+> ⎪⎝⎭，所以-sin 0,sin 0,ααα>∴<∴是第三、四象限和y 轴负半轴上的角.α是第三、四象限和y 轴负半轴上的角不能推出α是第三象限角，α是第三象限角一定能推出α是第三、四象限和y 轴负半轴上的角，所以“cos 02πα⎛⎫+>⎪⎝⎭”是“α是第三象限角”的必要非充分条件. 故答案为：B. 【点睛】(1)本题主要考查充要条件的判断和诱导公式，考查三角函数的值的符号，意在考查学生对这些知识的掌握水平和分析推理能力.(2) 判定充要条件常用的方法有定义法、集合法、转化法.7．A解析：A 【解析】试题分析：根据题意，由于函数()sin()A f x x ωϕ=+(0,)2πωϕ><，那么根据图像可知周期为2π，w=4，然后当x=6π,y=2，代入解析式中得到22sin(4)6πϕ=⨯+，6πϕ=-，则可知()f π=4，故答案为A.考点：三角函数图像点评：主要是考查了根据图像求解析式，然后得到函数值的求解，属于基础题．8．A解析：A 【解析】分析：首先根据12x x -的最小值是函数的最小正周期，求得ω的值，根据函数是偶函数，求得θ的值，从而求得正确的选项.详解：由已知函数sin()(0)y x ωθθπ=+<<为偶函数，可得2πθ=，因为函数sin()(0)y x ωθθπ=+<<的最大值为1，所以21x x -的最小值为函数的一个周期，所以其周期为T π=，即2=ππω，所以=2ω，故选A.点睛：该题考查的是有关三角函数的有关问题，涉及到的知识点有函数的最小正周期的求法，偶函数的定义，诱导公式的应用，正确使用公式是解题的关键，属于简单题目.9．B解析：B 【解析】 将函数y =2sin （ωx +π6）（ω>0）的图象向右移2π3个单位后，可得y =2sin （ωx –2π3ω+π6）的图象，再根据所得图象关于y 轴对称，∴–2π3ω+π6=kπ+π2，k ∈Z ，即ω=–31–22k ，∴当k =–1时，ω取得最小值为1，故选B ． 10．C解析：C 【解析】 【分析】 【详解】 试题分析：由于垂直，不妨设，，，则，，表示到原点的距离，表示圆心，为半径的圆，因此的最大值，故答案为C ．考点：平面向量数量积的运算．11．B解析：B【解析】分析：利用三角函数的定义求得66cos sin ππαα⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭， 结果，进而利用两角和的余弦函数公式即可计算得解．详解：由三角函数的定义可得512,613613cos sin ππαα⎛⎫⎛⎫-=--= ⎪ ⎪⎝⎭⎝⎭， 则773cos cos cos 12661264ππππππααα⎛⎫⎛⎫⎛⎫+=-++=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭33=cos cos sin sin 6464ππππαα⎛⎫⎛⎫⎛⎫⎛⎫--- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭512=1313⎛⎛⎫--= ⎪ ⎝⎭⎝⎭ 点睛：本题考查任意角的三角函数的定义，两角和与差的余弦函数公式，考查了计算能力和转化思想，属于基础题．12．A解析：A 【解析】 【分析】由诱导公式可得()tan tan παα+=，由角的正弦值和角所在的象限，求出角的余弦值，然后，正弦值除以余弦值得正切值．即可得到答案 【详解】 ∵4sin 5α=，并且α是第二象限的角，，35cos α∴-＝ ， ∴tanα＝43-，则么()4tan tan 3παα+==-. 故选A ． 【点睛】本题考查给值求值问题．掌握同角三角函数的基本关系式和诱导公式，并会运用它们进行简单的三角函数式的化简、求值及恒等式证明．13．A解析：A 【解析】 【分析】 由题意可得123ππω⨯=，求得ω的值，可得()f x 的最小正周期是2πω的值 【详解】由题意可得()1sin 2x ωθ+=的解为两个不等的实数1x ，2x且123ππω⨯=，求得23ω= 故()f x 的最小正周期是23ππω=故选A 【点睛】本题主要考查了的是三角函数的周期性及其图象，解题的关键根据正弦函数的图象求出ω的值，属于基础题14．D解析：D 【解析】 【分析】根据正弦的倍角公式和三角函数的基本关系式，化为齐次式，即可求解，得到答案． 【详解】由题意，可得222221cos sin cos cos sin 2cos sin cos 2cos sin a a a a a a a a a a++=+=+221tan 1321tan 135a a ++===++，故选D ．【点睛】 本题主要考查了正弦的倍角公式，以及三角函数的基本关系式的化简、求值，着重考查了推理与运算能力，属于基础题．15．A解析：A 【解析】 【分析】利用两角差的正弦公式化简a ，分子分母同乘以2cos 15结合二倍角的正弦公式化简b ，利用降幂公式化简c ，从而可得结果. 【详解】()sin 302sin28a =︒-︒=︒ ，222sin15cos15sin 30cos 15cos 15b ==+sin28a >=sin25sin28,c a b a c ==︒<︒=∴>>，故选A.【点睛】本题主要考查二倍角的正弦公式、二倍角的余弦公式，两角差的正弦公式，意在考查综合运用所学知识解答问题的能力，属于中档题.二、填空题16．【解析】【分析】由三角函数的基本关系式和正弦的倍角公式求得再由两角差的余弦函数的公式即可求解【详解】由即则又由所以又由【点睛】本题主要考查了三角函数的基本关系式以及正弦的倍角公式和两角差的余弦公式的解析：75【解析】 【分析】由三角函数的基本关系式和正弦的倍角公式，求得249(cos sin )25θθ+=，再由两角差的余弦函数的公式，即可求解． 【详解】 由24sin 225θ=，即242sin cos 25θθ=， 则2222449(cos sin )cos 2sin cos sin 12525θθθθθθ+=++=+=， 又由02πθ<<，所以cos 0,sin 0θθ>>，7cos()cos sin 45πθθθ-=+=．【点睛】本题主要考查了三角函数的基本关系式，以及正弦的倍角公式和两角差的余弦公式的化简、求值，着重考查了推理与运算能力，属于基础题．17．【解析】【分析】先根据条件得再根据向量夹角公式求结果【详解】因为且所以因此【点睛】求平面向量夹角方法：一是夹角公式；二是坐标公式；三是几何方法从图形判断角的大小 解析：120︒【解析】 【分析】先根据条件得a b ⋅，再根据向量夹角公式求结果. 【详解】因为1a =，且()2a a b ⋅-=，所以2-2,121,a a b a b ⋅=∴⋅=-=- 因此112πcos ,,1223a b a b a b a b⋅-===-∴=⨯⋅. 【点睛】求平面向量夹角方法：一是夹角公式cos a b a bθ⋅=⋅；二是坐标公式cos θ=；三是几何方法，从图形判断角的大小.18．【解析】分析：由角的终边上的一点的坐标为求出的值利用将的值代入即可得结果详解：角的终边上的一点的坐标为那么故答案为点睛：本题主要考查三角函数的定义及二倍角的正弦公式与余弦公式属于中档题给值求值问题求解析：17-【解析】分析：由角θ的终边上的一点P 的坐标为()3,4，求出,cos sin θθ的值，利用2cos 212sin 1212cos sin sin θθθθθ-=++，将,cos sin θθ的值代入即可得结果. 详解：角θ的终边上的一点P 的坐标为()3,4，43,cos 55y x sin r r θθ∴====， 那么216712cos 212sin 1252543491212cos 7125525sin sin θθθθθ-⨯--====-+++⨯⨯，故答案为17-. 点睛：本题主要考查三角函数的定义及二倍角的正弦公式与余弦公式，属于中档题.给值求值问题，求值时要注意：(1)观察角，分析角与角之间的差异以及角与角之间的和、差、倍的关系，巧用诱导公式或拆分技巧；(2)观察名，尽可能使三角函数统一名称；(3)观察结构，以便合理利用公式，整体化简求值.19．【解析】分析：先化简函数f(x)再求得再根据函数在区间内没有零点得到不等式组最后解不等式组即得w 的范围详解：由题得f(x)=因为所以当或时f(x)在内无零点由前一式得即由k=0得K 取其它整数时无解同解析：][1150,,848⎛⎤⋃ ⎥⎝⎦【解析】分析：先化简函数f(x) )24wx π=-,再求得(,2),444wx w w πππππ-∈--再根据函数()f x 在区间x ∈ (),2ππ内没有零点得到不等式组，最后解不等式组即得w 的范围. 详解：由题得f(x)=1cos 1111sin sin cos )222224wx wx wx wx wx π-+-=-=-, 因为x ∈ (),2ππ，所以(,2),444wx w w πππππ-∈--当(,2)(2,2),44w w k k k z πππππππ--⊆+∈或(,2)(2,2),44w w k k k z πππππππ--⊆-∈时，f(x)在(),2ππ内无零点，由前一式得24,224k w w k πππππππ⎧≤-⎪⎪⎨⎪-≤+⎪⎩即152,48k w k +≤≤+由k=0得1548w ≤≤， K 取其它整数时无解，同理，由后一式，解得1(0,]8w ∈， 综上，w 的取值范围是][1150,,848⎛⎤⋃ ⎥⎝⎦. 点睛：（1）本题主要考查三角恒等变换，考查三角函数的图像和性质，考查三角函数的零点问题，意在考查学生对这些知识的掌握水平和分析推理能力数形结合的思想方法.(2)解答本题的关键有两点，其一是分析得到当(,2)(2,2),44w w k k k z πππππππ--⊆+∈或(,2)(2,2),44w w k k k z πππππππ--⊆-∈时，f(x)在(),2ππ内无零点，其二是进一步转化得到不等式组解不等式组. 20．【解析】分析：设的中点为连接由余弦定理可得利用三角函数的有界性可得结果详解：设的中点为连接则是二面角的平面角可得在三角形中由余弦定理可得即的取值范围是为故答案为点睛：本题主要考查空间两点的距离余弦定解析：)【解析】分析：设AB 的中点为D ，连接,,VD CD VC ，由余弦定理可得22233cos 22VC a a VDC =-∠，利用三角函数的有界性可得结果. 详解：设AB 的中点为D ， 连接,,VD CD VC，则VD VC ==VDC ∠是二面角V AB C --的平面角， 可得0,1cos 1VDC VDC π<∠<-<∠<，在三角形VDC 中由余弦定理可得，2222cos VC VDC ⎫⎫=+-∠⎪⎪⎪⎪⎝⎭⎝⎭ 2233cos 22a a VDC =-∠22030VC a VC <<⇒<<，即VC的取值范围是()，为故答案为().点睛：本题主要考查空间两点的距离、余弦定理的应用，意在考查空间想象能力、数形结合思想的应用，属于中档题.21．19【解析】设则也即是化简得到其中故填点睛：向量数量积的计算有3个基本的思路：（1）基底法：如果题设中有一组不共线的向量它们的模长和夹角已知则其余的向量可以用基底向量去表示数量积也就可以通过基底向量解析：[1,9] 【解析】设,BM BC CN CD λλ==，则()()··AM AN AB BM AD DN =++，也即是()()··1AM AN AB BC AD DC λλ⎡⎤=++-⎣⎦，化简得到·98AM AN λ=-，其中[]0,1λ∈，故[]·1,9AM AN ∈，填[]1,9．点睛：向量数量积的计算有3个基本的思路：（1）基底法：如果题设中有一组不共线的向量，它们的模长和夹角已知，则其余的向量可以用基底向量去表示，数量积也就可以通过基底向量间的运算去考虑；（2）坐标法：建立合适的坐标系，把数量积的计算归结为坐标的运算；（2）靠边靠角转化：如果已知某些边和角，那么我们在计算数量积时尽量往这些已知的边和角去转化．22．8【解析】由题意得解析：8 【解析】 由题意得2115,3,8132m n m n m n +-==∴==--=- 23．【解析】函数的解析式：则要将函数的图象向右平移至少个单位点睛：由y ＝sinx 的图象利用图象变换作函数y ＝Asin(ωx ＋φ)(A ＞0ω＞0)(x ∈R)的图象要特别注意：当周期变换和相位变换的先后顺序解析：8π 【解析】 函数的解析式：sin 2sin 248y x x ππ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭. 则要将函数24y sin x π⎛⎫=+ ⎪⎝⎭的图象向右平移至少8π个单位. 点睛：由y ＝sin x 的图象，利用图象变换作函数y ＝A sin(ωx ＋φ)(A ＞0，ω＞0)(x ∈R)的图象，要特别注意：当周期变换和相位变换的先后顺序不同时，原图象沿x 轴的伸缩量的区别．先平移变换再周期变换(伸缩变换)，平移的量是|φ|个单位；而先周期变换(伸缩变换)再平移变换，平移的量是ϕω个单位．24．【解析】由题意得解析：4-5【解析】 由题意得3π44cos ,(0,)sin ,sin(π)sin 5255ααααα=∈∴=+=-=- 25．【解析】利用平面向量的加法公式可得：由平面向量垂直的充要条件可得：解方程可得： 解析：7【解析】利用平面向量的加法公式可得：()1,3a b m +=-+，由平面向量垂直的充要条件可得：()()()()1,31,2160a b a m m +⋅=-+⋅-=--++=， 解方程可得：7m =.三、解答题 26．（1）360n m --=（2）()4,3OC =或()5,3OC =- 【解析】 【分析】(1)由题意结合三点共线的充分必要条件确定m ,n 满足的关系式即可； (2)由题意首先求得n 的值，然后求解m 的值即可确定向量的坐标. 【详解】（1）()3,9AB =，()2,AC m n =+， 由点A ，B ，C 三点共线，知AB ∥AC ， 所以()3920n m -+=，即360n m --=； （2）由△AOC 的面积是3，得1232n ⨯⨯=，3n =±， 由AC BC ⊥，得0AC BC ⋅=，所以()()2,1,90m n m n +⋅--=，即22920m n m n ++--=, 当3n =时，2200m m +-=， 解得4m =或5m =-， 当3n =-时，2340m m ++=，方程没有实数根， 所以()4,3OC =或()5,3OC =-． 【点睛】本题主要考查三点共线的充分必要条件，向量垂直的充分必要条件等知识，意在考查学生的转化能力和计算求解能力.27．（1）23πθ=；（2）35t =，c =63. 【解析】 【分析】（1）由向量的数量积，代值计算即可； （2）由数量积为0，代入计算即可. 【详解】（1）因为()()23261a b a b -⋅+= 故2244361a a b cos b θ-⋅-=解得：12cos θ=-因为[]0,θπ∈，所以23πθ=. （2）0b c ⋅= 则()()10b ta t b ⋅+-=()210ta b t b ⋅+-=化简得：159t = 解得：35t = 此时3255c a b =+ 23255a b ⎫+⎪⎭ 224122525a b a b ++⋅【点睛】本题考查向量数量积的运算，属基础题.28．（1）()π5ππ,π1212k k k Z ⎡⎤-+∈⎢⎥⎣⎦；（2）512⎡⎤-⎢⎥⎣⎦.【解析】 【分析】 化简()f x 解析式.（1）根据三角函数单调区间的求法，求得函数()f x 的单调增区间；（2）根据三角函数值域的求法，求得函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的值域.【详解】 依题意()()ππsin 2cos cos 2sin 1cos 266f x x x x =--+33sin 2cos 2122x x =--π3sin 213x ⎛⎫=-- ⎪⎝⎭.（1）由πππ2π22π232k x k -+≤-≤+，解得π5πππ1212k x k -≤≤+，所以()f x 的单调增区间为()π5ππ,π1212k k k Z ⎡⎤-+∈⎢⎥⎣⎦. （2）由于π02x ≤≤，所以ππ2π2333x -≤-≤，所以π53sin 21,3132x ⎛⎫⎡⎤--∈-- ⎪⎢⎥⎝⎭⎣⎦.所以()f x 在0,2π⎡⎤⎢⎥⎣⎦上的值域为5,312⎡⎤--⎢⎥⎣⎦. 【点睛】本小题主要考查三角恒等变换，考查三角函数单调区间的求法，考查三角函数值域的求法，考查运算求解能力，属于基础题.29．（1），（2）【解析】 【分析】 【详解】（1）由题意知所求的切线斜率存在，设其方程为，即； 由得，解得， 从而所求的切线方程为，．（2）∴NP 为AM 的垂直平分线，∴|NA|=|NM|． 又∴动点N 的轨迹是以点C （－1，0），A （1，0）为焦点的椭圆． 且椭圆长轴长为焦距2c=2．∴点N 的轨迹是方程为30．(1)πθ6=.ω2=.(2)023x π=，或034x π=. 【解析】试题分析：(1)由三角函数图象与y 轴交于点(3可得3cos 2θ=，则6πθ=.由最小正周期公式可得2ω=.(2)由题意结合中点坐标公式可得点P 的坐标为0232x π⎛-⎝.代入三角函数式可得053cos 46x π⎛⎫-= ⎪⎝⎭，结合角的范围求解三角方程可得023x π=，或034x π=. 试题解析：(1)将0,3x y ==()2cos y x ωθ=+中，得3cos θ=， 因为02πθ≤≤，所以6πθ=.由已知T π=，且0ω>，得222T ππωπ===. (2)因为点()00,0,,2A Q x y π⎛⎫⎪⎝⎭是PA 的中点， 03y =P 的坐标为0232x π⎛- ⎝.又因为点P 在2cos 26y x π⎛⎫=+ ⎪⎝⎭的图象上，且02x ππ≤≤，所以053cos 462x π⎛⎫-= ⎪⎝⎭，且075194666x πππ≤-≤， 从而得0511466x ππ-=，或0513466x ππ-=，即023x π=，或034x π=.。

高二上期数学练习题及答案题一：解方程。

已知方程3x^2+5x-2=0，请计算方程的解。

解析：根据一元二次方程的求解公式x=(-b±√(b^2-4ac))/(2a)，可以得出：a=3, b=5, c=-2将a、b、c的值带入公式，可以得出：x1=(-5+√(5^2-4*3*(-2)))/(2*3)=(-5+√(25+24))/(6)=(-5+√49)/(6)=(-5+7)/6=2/6=1/3x2=(-5-√(5^2-4*3*(-2)))/(2*3)=(-5-√(25+24))/(6)=(-5-√49)/(6)=(-5-7)/6=-12/6=-2答案：方程的解为x=1/3和x=-2。

题二：概率问题。

某班级学生的身高数据如下：150cm、160cm、165cm、170cm、175cm、180cm、185cm、190cm、195cm、200cm从中随机选择一个学生，求他身高大于等于170cm的概率。

解析：学生身高大于等于170cm的有5位（170cm、175cm、180cm、185cm、190cm），总共有10位学生。

所以，概率为5/10，即1/2。

答案：选择的学生身高大于等于170cm的概率为1/2。

题三：平面几何。

已知正方形ABCD的边长为4cm，点E是AB的中点，连接DE并延长到F点，使得EF=3DE。

连接AF，求AF的长度。

解析：由题意可知，DE=1/3EF。

设EF=x，则DE=1/3x。

根据勾股定理和正方形的性质可知，AF^2=DF^2+AD^2=(DE+EF)^2+AB^2=(1/3x+x)^2+4^2。

展开后化简，得到AF^2=(10/9)x^2+16根据勾股定理可知，AF=sqrt((10/9)x^2+16)。

答案：AF的长度为sqrt((10/9)x^2+16)。

题四：函数问题。

已知函数f(x)=3x^2+2x+1，请计算f(2)的值。

解析：f(2)=3(2)^2+2(2)+1=3*4+4+1=12+6+1=19答案：f(2)的值为19。

高二数学练习题及答案电子版下面是一份高二数学练习题及答案的电子版，供同学们参考和复习使用。

1. 线性方程组1.1 解线性方程组 2x + 3y = 7，3x - 4y = 6。

解答：先用第一个方程解出 x：2x = 7 - 3yx = (7 - 3y)/2将 x 的值代入第二个方程中：3(7 - 3y)/2 - 4y = 6化简得：21 - 9y - 8y = 12-17y = -9y = 9/17将 y 的值代入第一个方程中，求得 x：2x + 3(9/17) = 72x + 27/17 = 72x = 7 - 27/17 = 119/17 - 27/17 = 92/17x = 92/17 * 1/2 = 46/17所以，该线性方程组的解为 x = 46/17，y = 9/17。

2. 数列与数列求和2.1 求等差数列 2，5，8，11，... 的第 n 项公式和前 n 项和公式。

解答：等差数列的通项公式可以表示为 an = a1 + (n - 1)d，其中 a1 是首项，d 是公差。

首项 a1 = 2公差 d = 5 - 2 = 3第 n 项公式 an = 2 + (n - 1)3 = 3n - 1前 n 项和公式 Sn = (n/2)(a1 + an) = (n/2)(2 + 3n - 1) = (n/2)(3n + 1)所以，该等差数列的第 n 项公式为 3n - 1，前 n 项和公式为 (n/2)(3n + 1)。

3. 函数与方程3.1 求函数 f(x) = 2x^2 + 3x - 4 的极值点和拐点。

解答：首先，求函数的导数 f'(x)：f'(x) = 4x + 3令 f'(x) = 0，解得极值点 x = -3/4。

然后，求函数的二阶导数 f''(x)：f''(x) = 4由于二阶导数恒为正数，所以没有拐点。

所以，函数 f(x) = 2x^2 + 3x - 4 的极值点为 (-3/4, f(-3/4))，没有拐点。

高二数学上学期期末模拟试卷一、单选题：本大题共8个小题，每个小题5分，共40分.在每小题给出的选项中，只有一项是符合题目要求的.１.抛物线y =4ax 2a <0 的焦点坐标是()A.14a ,0B.0,116aC.0,-116aD.116a ,0２.已知向量a =m ,2,1 ，b =-1,0,4 ，且a ⊥b，则实数m 的值为()．A.4B.-4C.2D.-2３.若直线l 1:ax +4y +8=0与直线l 2:3x +(a +1)y -6=0平行，则a 的值为()A.-4B.3C.3或-4D.-3或6４.如图所示,在正方体ABCD -A 1B 1C 1D 1中,点F 是侧面CDD 1C 1的中心,设AD =a ,AB =b ,AA 1=c,则AF =()A.a +12b +12cB.12a +b +12cC.-a +12b +12cD.12a +12b +c５.已知直线y -x +1=0与圆x 2+y 2=1相交于点A ，B ，点P 为圆上一动点，则△ABP 面积的最大值是()A.2+12B.22+1 C.2D.12６.已知数列a n 满足a 1=2，a n +1=1-1a n，则a 2022=()A.1B.2C.-1D.1.5７.若方程x2a2+y 2a +6=1表示焦点在y 轴上的椭圆,则实数a 的取值范围是()A.a >3B.a <-2C.a >3或a <-2D.-2<a <0或0<a <3８.已知F 1，F 2是椭圆与双曲线的公共焦点，P 是它们的一个公共点，且PF 1> PF 2 ，线段PF 1的垂直平分线过F 2，若椭圆的离心率为e 1，双曲线的离心率为e 2，则2e 1+e 22的最小值为()A.8B.6C.4D.2二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.９.已知圆C :(x +2)2+y 2=4，直线l :m +1 x +2y -1+m =0m ∈R ，则()A.直线l 恒过定点-1,1B.当m =0时，圆C 上恰有三个点到直线l 的距离等于1C.直线l 与圆C 有一个交点D.若圆C 与圆x 2+y 2-2x +8y +a =0恰有三条公切线，则a =8１０.已知等差数列{a n }的公差为d ，其前n 项之和为T n ，且满足a 1<0，T 4045=0，则()A.d >0B.a 2021+a 2023<0C.T 2023的值是T n 中最小的D.{|a n |}的前5000项的和为T 5000+2T 4045１１.如图，在长方体ABCD -A 1B 1C 1D 1中，AB =3AD =3AA 1=3，点P 为线段A 1C 上的动点，则下列结论正确的是()A.当A 1C =2A 1P时，B 1，P ，D 三点共线B.当AP ⊥A 1C 时，AP ⊥D 1PC.当A 1C =3A 1P时，D 1P ⎳平面BDC 1D.当A 1C =5A 1P时，A 1C ⊥平面D 1AP１２.已知抛物线C :y 2=4x 的焦点为F 、准线为l ，过点F 的直线与抛物线交于两点P x 1,y 1 、Q x 2,y 2 ，点P 在l 上的射影为P 1，则()A.若x 1+x 2=6，则PQ =8B.以PQ 为直径的圆与准线l 相切C.设M 0,1 ，则PM +PP 1 ≥2D.过点M 0,1 与抛物线C 有且仅有一个公共点的直线至多有2条三、填空题：本题共4小题，每小题5分，共20分１３.已知等差数列a n 的前n 项和为S n ,a2=2,S 5=15，则数列1a n a n +1的前2017项和.１４.如图所示，长方体ABCD -A 1B 1C 1D 1的底面ABCD 是边长为1的正方形，长方体的高为2，E ､F 分别在A 1D ､AC 上，且EF ∥BD 1，则直线EF 与直线BD 1的距离为.１５.当点P 在圆x 2+y 2=1上运动时，连接点P 与定点Q (3,0)，则线段PQ 的中点M 的轨迹方程为.１６.椭圆C ：x 218+y 2b2=1的上、下顶点分别为A ，C ，如图，点B 在椭圆上，平面四边形ABCD 满足∠BAD =∠BCD =90°，且S △ABC =2S △ADC ，则该椭圆的短轴长为．四、解答题：本小题共6小题，共70分。

高二第一次月考试题（空间向量、直线与圆）第I 卷（选择题）一、单选题（本大题8个小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．（2022·甘肃定西·高二开学考试（理））在长方体1111ABCD A B C D -中，下列关于1AC uuur 的表达中错误的一个是（）A ．11111AA AB A D ++ B ．111AB DD D C ++ C ．111AD CC D C ++ D ．()111112AB CD A C ++ 111111AB DD D C AB DC DC DC AC ++=+=+≠ AD CC D C AD AA D C AD D C ++=++=+ 2．（2022·全国·高二课时练习）在正三棱柱111-ABC A B C 中，122AA AB ==，E 为棱AB 的中点，F 为线段1BB 上的一点，且1AC EF ⊥，则1B F FB =（）A ．10B ．12C ．15D ．20故选：C3．（2022·全国·高二课时练习）若直线l 的一个方向向量为m ，平面α的一个法向量为n ，则可能使//l α的是（）A ．()1,0,0m = ，()2,0,0n =-B ．()1,3,5m = ，()1,0,1n =C ．()0,2,1m = ，()1,0,1n =--D ．()1,1,3m =- ，()0,3,1n = 【答案】D【分析】根据题意可得0m n ⋅=r r ，再逐个选项代入判断即可.【详解】要使//l α成立，需使0m n ⋅=r r ，将选项一一代入验证，只有D 满足1013310m n ⋅=⨯-⨯+⨯=r r .故选：D.4．（2021·黑龙江黑河·高二阶段练习）直线l 经过点()1,1P -和以()()3,1,3,2M N -为端点的线段相交，直线l 斜率的取值范围是（）A ．3,2⎛⎤-∞ ⎥⎝⎦B ．1,2⎡⎫-+∞⎪⎢⎣⎭C ．13,22⎡⎤-⎢⎥⎣⎦D ．13,,22⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭5．（2021·陕西汉中·高二期末（理））正方体1111ABCD A B C D -中，E ，F 分别为11D C ，1BB 的中点，则异面直线AE 与FC 所成角的余弦值为（）A ．515B ．4515C ．2515-D ．215【答案】D【分析】建立空间直接坐标系，利用空间向量求解.【详解】如图，建立空间直接坐标系，设正方体的棱长为2，因为E ，F 分别为11D C ，1BB 的中点，易知，C (0，2，0)，F (2，2，1)，所以所以cos <,AE CF>==||||AE CF AE CF ⋅⋅ 因为异面直线AE 与FC 所成角为锐角所以异面直线AE 与FC 所成角的余弦值为故选：D.6．（2020·北京十五中高二期中）经过三个点00()(02)()0A B C -,,,,的圆的方程为（）A ．()()22312x y -++=B ．(()2212x y +-=C ．()()22314x y -++=D ．(()2214x y +-=【答案】C【分析】根据三点在坐标系的位置，确定出为BC 的一半，圆心坐标为BC 【详解】由已知得，00()A B ,,∴AB AC ⊥，∴经过三点圆的半径为12r BC =圆心坐标为BC 的中点232⎛+ ⎝∴圆的标准方程为()23x -+故选：C.7．（2022·福建南平·高一期末）如图，正方体1111ABCD A B C D -中，1AN NA = ，11A M MD = ，11B E B C λ= ，当直线1DD 与平面MNE 所成的角最大时，λ=（）A ．12B ．13C ．14D ．15则()(111,0,1,1,0,,0,1,0,1,1,122M N C B ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭所以()111,0,1B E B C λλ==-- ，(1E -设平面MNE 的法向量为(),,m x y z =，则∴11022102x z x y z λλ⎧-=⎪⎪⎨⎛⎫⎪-+-= ⎪⎪⎝⎭⎩，令1x =，可得又()10,0,1DD = ，设直线1DD 与平面MNE 所成的角为α。

高二数学上册练习题及答案1. (a) 求解方程：3x - 2 = 7(b) 求解方程：2(x - 3) + 5 = 17解答：(a) 3x - 2 = 7将-2移到等式右边：3x = 7 + 23x = 9将系数3移到等式右边，同时将9除以3：x = 3(b) 2(x - 3) + 5 = 17将2乘以括号里的表达式：2x - 6 + 5 = 17合并同类项：2x - 1 = 17将-1移到等式右边：2x = 17 + 12x = 18将系数2移到等式右边，同时将18除以2： x = 92. 计算下列代数式的值：(给定变量a = 3, b = 5)(a) a^2 - b^2(b) a^3 + b^3解答：(a) a^2 - b^2替换变量的值：3^2 - 5^2计算指数运算：9 - 25提取结果：-16(b) a^3 + b^3替换变量的值：3^3 + 5^3计算指数运算：27 + 125提取结果：1523. 解下列不等式，并将解表示在数轴上：(a) 2x + 3 ≤ 9(b) 5 - x > 2x + 1解答：(a) 2x + 3 ≤ 9将3移到不等式右边：2x ≤ 9 - 3简化不等式：2x ≤ 6将系数2移到不等式右边，同时将6除以2：x ≤ 3将解表示在数轴上，标记点3及其左侧为解的区间。

(b) 5 - x > 2x + 1将5移到不等式右边：-x > 2x + 1 - 5简化不等式：-x > 2x - 4将系数-1移到不等式右边，将解取反，同时将4加到2x上： 3x < 4将解表示在数轴上，标记点4及其左侧为解的区间。

4. 求解下列线性不等式组，并将解表示在数轴上：(a) { x + 1 > 3{ 2x - 5 ≤ 9(b) { 3x - 2 ≤ 10{ 4 - x > 2x - 1解答：(a) { x + 1 > 3{ 2x - 5 ≤ 9对第一个不等式进行简化：x > 3 - 1x > 2对第二个不等式进行简化：2x ≤ 9 + 52x ≤ 14x ≤ 7综合两个不等式的解：x > 2 且x ≤ 7将解表示在数轴上，标记点2及其右侧和标记点7及其左侧为解的区间。

高二数学题(人教版)高二数学要怎么学好?实践证明：越到关键时候，你所表现的解题习惯与平时练习无异。

如果平时解题时随便、粗心、大意等，往往在大考中充分暴露，故在平时养成良好的解题习惯是非常重要的。

今天小编在这给大家整理了高二数学题大全，接下来随着小编一起来看看吧!高二数学题(一)一、选择题：(共12小题，每小题5分，共60分)在下列各小题的四个选项中，只有一项是符合题目要求的.请将选项前的字母填入下表相应的空格内.1.对抛物线，下列描述正确的是()A.开口向上，焦点为B.开口向上，焦点为C.开口向右，焦点为D.开口向右，焦点为2.已知A和B是两个命题，如果A是B的充分条件，那么是的()A.充分条件B.必要条件C.充要条件D.既不充分也不必要条件3.抛物线的准线方程是()A.B.C.D.4.有下列4个命题：①“菱形的对角线相等”;②“若，则x，y互为倒数”的逆命题;③“面积相等的三角形全等”的否命题;④“若，则”的逆否命题。

其中是真命题的个数是()A.1个B.2个C.3个D.4个5.如果p是q的充分不必要条件，r是q的必要不充分条件;那么()A.B.C.D.6.若方程x2+ky2=2表示焦点在x轴上的椭圆，则实数k的取值范围为()A.(0，+∞)B.(0，2)C.(1，+∞)D.(0，1)7.已知命题p:成等比数列，命题q：，那么p是q的()A.必要不充分条件B.充要条件C.充分不必要条件D.既不充分也不必要条件8.下列说法中正确的是()A.一个命题的逆命题为真，则它的逆否命题一定为真B.“”与“”不等价C.“,则全为”的逆否命题是“若全不为,则”D.一个命题的否命题为真，则它的逆命题一定为真9.已知函数在R上满足，则曲线在点处的切线方程是()A.B.C.D.10.已知圆的方程，若抛物线过定点且以该圆的切线为准线，则抛物线焦点的轨迹方程是()A.B.C.D.11.函数的单调递增区间是()A.B.(0,3)C.(1,4)D.12.已知直线y=x+1与曲线相切，则α的值为()A.1B.2C.-1D.-2第II卷(非选择题共90分)二、填空题：(共4小题，每小题5分，共20分)请将答案直接添在题中的横线上.13.曲线在点处的切线方程为________.14.命题“”的否定是.15.以为中点的抛物线的弦所在直线方程为：.16.若表示双曲线方程，则该双曲线的离心率的值是.三、解答题：(共6小题，共70分)解答应写出文字说明，证明过程或演算步骤。