纳米Al2O3-40%TlO2复相陶瓷颗粒增强镍基合金复合涂层的摩擦学性能

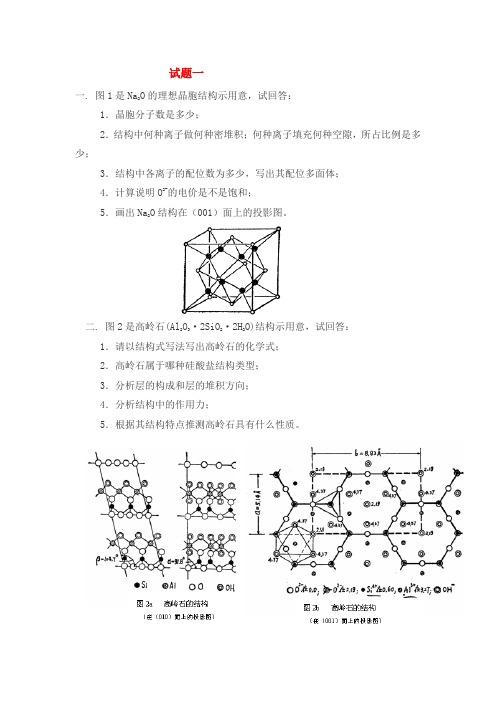
试题一一. 图1是Na2O的理想晶胞结构示用意，试回答：1．晶胞分子数是多少；2．结构中何种离子做何种密堆积；何种离子填充何种空隙，所占比例是多少；3．结构中各离子的配位数为多少，写出其配位多面体；4．计算说明O2-的电价是不是饱和；5．画出Na2O结构在（001）面上的投影图。

二. 图2是高岭石(Al2O3·2SiO2·2H2O)结构示用意，试回答：1．请以结构式写法写出高岭石的化学式；2．高岭石属于哪种硅酸盐结构类型；3．分析层的构成和层的堆积方向；4．分析结构中的作用力；5．根据其结构特点推测高岭石具有什么性质。

三. 简答题：1.晶体中的结构缺陷按几何尺寸可分为哪几类？2.什么是负扩散？3．烧结初期的特征是什么？4.硅酸盐晶体的分类原则是什么？5.烧结推动力是什么？它可凭哪些方式推动物质的迁移？6.相变的含义是什么？从热力学角度来划分，相变可以分为哪几类？四. 出下列缺陷反应式：形成肖特基缺陷；形成弗仑克尔缺陷（Ag+进入间隙）；掺入到Nb2O3中，请写出二个合理的方程，并判定可能成立的方程是哪一种？再写出每一个方程的固溶体的化学式。

溶入CaCl2中形成空位型固溶体五. 表面力的存在使固体表面处于高能量状态，然而，能量愈高系统愈不稳定，那么固体是通过何种方式降低其过剩的表面能以达到热力学稳定状态的。

六.粒径为1μ的球状Al2O3由过量的MgO微粒包围，观看尖晶石的形成，在恒定温度下，第一个小时有20%的Al2O3起了反映，计算完全反映的时刻：⑴用杨德方程计算；⑵用金斯特林格方程计算。

七.请分析熔体结构中负离子团的堆积方式、聚合度及对称性等与玻璃形成之关系。

八.试从结构和能量的观点解释为什么D晶界>D晶内？九.试分析二次再结晶过程对材料性能有何影响？工艺上如何防止或延缓二次再结晶的发生？十.图3是A-B-C三元系统相图，根据相图回答下列问题：1．写出点P，R，S的成分；2．设有2kgP，问需要多少何种成分的合金Z才可混熔成6kg成分为R的合金。

固体,颗粒,粉末散装物料堆积密度表1(信息来源:介可视公司)散装物料堆积密度?(kg/l) A蚕豆0,75?-?0,85活性炭0,21氧化铝0,80?-?1,05碱纤维素0,25铝渣1,90?-?2,20氧化铝0,90硅酸铝0,78硫酸铝0,85氨0,90茴香0,35?-?0,40苹果籽? 0,60苹果粉0,50?-?0,60杏脯，干0,50?-?0,60石棉纤维0,26灰（渣）0,90灰分，干燥0,55?-?0,65B面包粉0,55?-?0,65砖块，磨碎1,40香蕉粉0,40?-?0,50紫淑，切丝0,30?-?0,40棉花片0,42棉籽粕0,30棉油渣0,40膨润土0,72?-?0,94混凝土砾石1,72?-?1,86酒糟0,25?-?0,30浮石砂0,70苦羽扇豆（种子）0,76?-?0,83泡沫玻璃0,20?-?0,40膨松珍珠岩0,05?-?0,15陶粒0,30?-?0,80氧化铅0,95?-?2,40铅尘3,00豆子0,65硼酸0,90啤酒酒糟，干燥0,45啤酒大麦，干燥0,55 散装物料堆积密度?(kg/l) 硅胶0,04明矾1,20铸造砂1,45铝片1,30氢氧化铝0,25铝粉0,90铝屑，精细0,11硝酸铵0,72苯胺1,89苹果，干燥，榨取0,24?-?0,30苹果果胶0,51橘皮，干0,24氧化砷1,60?-?1,90石棉粉0,39灰分，湿0,70?-?0,90破碎的沥青0,72?-?0,95发酵粉0,70香蕉片0,25?-?0,30玄武岩片1,60棉绒0,07?-?0,09棉籽0,60棉花片0,20矾土1,20混凝土拌合物2,10啤酒酵母，干燥0,40?-?0,55浮石粉0,64泻盐0,80?-1,00沥青颗粒0,75云母粉0,06?-?0,17膨松页岩0,40?-?0,85铅矿砂3,20?-?4,32铅盐，?砷酸1,10血粉0,50硼砂0,97啤酒糟粕，潮湿0,90啤酒大麦，潮湿0,90褐煤，精细0,65?-?0,75褐煤，干燥0,70?-?0,90褐煤粉0,40?-?0,60褐煤，湿的0,90?-?1,00 褐煤，焦炭0,67糙米0,75?-?0,78 青铜粉4,10荞麦0,60?-?0,65 C玻璃片0,46干香菇0,35?-?0,45 D枣，干?燥0,45?-?0,60 莳萝，干燥? 0,25?-?0,35 鳕鱼肝粉0,70?-?0,75 糖衣片0,55?-?0,85 E硬橡胶1,04?-?1,12 火山泥0,80碎冰0,90氧化铁0,87?-?1,30 铁屑2,00冰淇淋粉0,35环氧树脂粉0,80豌豆麸皮0,20?-?0,25 泥土，干燥1,60花生，带壳0,25?-?0,35 矿石1,40?-?2,60 F矿泥0,80煤粉0,85?-?1,00 茴香0,35?-?0,45 鱼粉0,60?-?0,75 鱼粉，沙丁鱼0,58亚麻籽0,70?-?0,75 肉粉0,55?-?0,65 氟石1,40?-?1,70 氟石，研磨1,40?-?1,60 果汁，速溶0,45?-?0,60 果糖0,45?-?0,55 饲料石灰1,50?-?1,80 G虾仁，干燥0,40?-?0,45 园艺碎屑1,30?-?1,35 家禽饲料0,64明胶胶囊0,30?-?0,45 大麦（酿造）0,68?-?0,72 大麦麸皮0,20?-?0,25 煤球（普通）0,75?-?0,82 碎玻璃1,40?-?1,90 荞麦粉0,30?-?0,35 棉花籽0,35葡萄糖0,57白云石1,60鳕鱼粉0,60?-?0,65 农用石灰1,26煤球0,70?-?0,82 鸡蛋粉0,25铁矿石1,60?-?3,20 铁粉3,50硫酸亚铁0,90?-?1,20 珐琅粉1,10豌豆0,75?-?0,85 豌豆粉0,35?-?0,45 花生，去壳0,50花生种子0,64彩色颜料0,65长石1,20?-?1,80 鱼饲料0,77鱼粉，鲈鮋0,59亚麻粉0,40瓶盖0,35?-?0,45 粉煤灰0,45?-?0,50 氟石，破碎1,20?-?1,55 型砂0,90?-?1,30 涂巧克力的水果0,50?-?0,70 漂白土0,35?-?0,60 虾粉0,48气焦0,40明胶0,74黄芥末0,72大麦（饲料）0,60?-?0,66 大麦粉0,35?-?0,40 谷物0,60石膏（建筑石膏）0,90玻璃，研磨1,70玻璃纤维0,20玻璃珠1,78玻璃微珠，空心0,40芒硝1,40云母，烧焦0,10云母，原料0,83石墨片0,40大麦粗粉0,55?-?0,60 混合香料0,40?-?0,70 石膏粉尘0,96?-?1,12 碎玻璃1,30?-?1,65 玻璃配合料0,80?-?1,60 玻璃微珠1,50玻璃碎片1,65云母片0,16云母，研磨0,25花岗岩，破碎1,50?-?1,60 石墨颗粒1,12草粉0,25?-?0,30 米粒0,50?-?0,65 青麦0,50?-?0,60 橡胶颗粒0,46橡胶片0,40 石墨粉0,45?-?0,58 草籽0,16粗粒粉0,66绿麦芽0,40橡胶颗粒0,80?-?0,88 铸铁屑2,08?-?3,20散装物料堆积密度?(kg/l) H燕麦0,50燕麦粥0,45?-?0,50玫瑰果，干燥0,45尿素0,65?-?0,75榛子仁，切碎0,50干草颗粒0,40?-?0,70高粱0,70?-?0,80高炉矿渣1,50高炉水泥0,90?-1,20木炭0,20?-?0,40木渣0,16?-?0,50木材刨花0,20?-?0,30木棉0,02酒花颗粒0,50鸡饲料0,55?-?0,65炉渣0,65?-?0,90I姜，干燥，压扁0,45?-?0,55K奶酪，磨碎的0,35咖啡豆，烘焙0,35?-?0,45咖啡粉（速溶）0,18可可粉0,45?-?0,55钾盐1,10?-?1,20碳酸钾0,82硫酸钾1,80石灰，?熟化0,70 散装物料堆积密度?(kg/l) 燕麦片0,35?-?0,40燕麦麸0,32?-?0,35玫瑰果，干燥，切碎0,50榛子仁0,58榛子仁，烘烤0,45山核桃（坚果肉）0,35小米粉0,40?-?0,45高炉矿渣砂0,7木片，干燥0,54?-?0,60木粉0,25?-?0,45木屑0,30木尘，干燥0,35蛇麻草，干燥0,35牛角花0,83狗饲料，干燥0,50?-?0,80熟石灰0,33?-?0,45咖啡，压扁的0,50?-?0,60咖啡豆，绿色0,45?-?0,65可可豆0,45?-?0,65可可粗粉0,51氯化钾2,00硝酸钾0,75石灰0,96熟石灰1,00?-?1,20方解石1,38石灰石，破碎1,30?-?1,60电石1,20甘菊茶，研磨0,25?-?0,30石灰灰泥，干燥1,65石灰石，破碎2,60石灰石粉1,25洋甘菊0,175加那利籽0,55?-?0,65 小豆蔻，研磨0,37马铃薯粉0,70马铃薯淀粉0,70猫粮，干燥0,50?-?0,80 砂岩1,50?-?1,90 硅藻土0,17?-?0,22 麸皮0,25?-?0,30 大蒜粉0,33氯化钠0,67?-?0,80 椰肉干，糊状物0,45煤渣1,00焦炭0,35?-?0,60 焦粉0,82芫荽，整个0,50?-?0,55 软木，细磨0,20?-?0,25 浓缩饲料0,54水晶砂，干燥1,46孜然，压扁的0,40塑料片0,10?-?0,150 铜渣1,70L乳糖0,45?-?0,55 壤土，湿润2,00胶粉0,60?-?0,65 亚麻籽粕0,40?-?0,50 M镁石2,40氧化镁0,62硫酸镁0,66玉米，小粒0,80?-?0,88 玉米蛋白粉0,40?-?0,50 玉米粉0,46麦芽，干燥0,30?-?0,50 麦芽粉0,63杏仁0,48硫酸锰1,10大理石粉1,20麻子，压扁的0,45金属粉3,04奶粉（脂肪）0,35 高岭土0,80马铃薯片0,25?-?0,30 马铃薯0,75酪蛋白0,55锅炉灰渣0,95?-?1,00 二氧化硅1,05硅酸0,06苜蓿草籽0,82骨粉0,75?-?0,85 椰肉干，破碎0,65椰子粕0,65煤粉0,45焦炭灰? 0,70?-?0,90 转炉炉尘2,70芫荽，研磨0,40?-?0,55 软木屑0,18?-?0,25 粉笔1,40香芹籽0,45人工肥料1,0?-?1,10 铜矿石2,00?-?2,40 月桂，压扁的0,35壤土，干燥1,60亚麻籽0,50?-?0,60 扁豆0,80?-?0,85 碳酸镁0,25硬脂酸镁0,34玉米，粗粒0,75?-?0,80 玉米糁0,65玉米皮0,25?-?0,30 玉米淀粉0,48麦芽，干燥0,10?-?0,15 麦芽粒0,40锰矿石1,80木薯粉0,50?-?0,60 大理石碎片1,50机用石膏，干燥0,60?-?1,00 甲基纤维素0,37奶粉0,30?-?0,40 乳糖0,60?-?0,70 混合沙1,54砂浆，石灰1,70砂浆，水泥-石灰2,00罂粟籽0,65肉豆蔻（坚果）0,65表土1,80奶粉（脱脂）0,55混合饲料0,50砂浆，石膏1,20砂浆，水泥2,00罂粟0,40?-?0,50 乳清粉0,65?-?0,70 肉豆蔻，研磨0,46N碳酸氢钠0,98氢氧化钠1,35磷酸钠0,65浮石，精细0,80?-?0,90 丁香，研磨0,45O油籽0,70油质黏结剂0,30?-0,55 橄榄,?干燥0,50?-?0,60 草酸，晶体1,00P面包屑0,40?-?0,55 巴西坚果果仁0,65?-?0,72 蒸谷米，长粒，白米0,76?-?0,80 巴尔马干酪，研磨0,50?-?0,75 苏籽0,55?-?0,60 珍珠岩，膨松0,12PET-颗粒0,85辣椒，白，研磨0,47马饲料0,60?-?0,70 李子，干燥0,50?-?0,60 色素染料0,50?-?0,80 多香果，压扁的0,50?-?0,55 松子0,55开心果0,55?-?0,70 聚乙烯（颗粒）0,50聚乙烯（粉末）0,45聚酰胺（颗粒)? 0,55?-?0,60 瓷土1,40硅酸盐水泥，振动1,60?-?1,90 煤饼1,00聚四氟乙烯（粉末）0,51爆米花0,05聚氯乙烯（颗粒）0,50?-?0,60 PVC板0,60热解焦0,60?-?1,00 氯化钠1,30硝酸钠1,35硫酸钠1,35浮石，粗糙0,45?-?0,55 核级煤0,80?-?0,95 油籽粕0,50油萝卜籽0,75橘皮，干燥0,24胡椒粉0,40?-?0,50 蒸谷米，长粒，糙米0,75蒸谷米，中粒，白米0,83?-?0,84 青霉素0,55珍珠岩（岩石）1,17珍珠岩颗粒0,09?-?0,11 辣椒，黑，研磨0,50花椒0,27鸡油菌，干燥0,35?-?0,45 酚醛树脂0,52磷酸盐2,00聚碳酸酯0,67聚酯纤维0,70聚丙烯（颗粒）0,50聚丙烯（粉末）0,54聚苯乙烯(扩大的) 0,10聚苯乙烯（颗粒）0,60聚苯乙烯（粉末）0,55硅酸盐水泥，松散0,90?-?1,20 钾肥1,12聚四氟乙烯（颗粒）0,53布丁粉0,50聚氯乙烯（聚结块）0,40聚氯乙烯（粉末）0,57PVC，软质（扁平状）0,40散装物料堆积密度 (kg/l)散装物料堆积密度 (kg/l)Q夸克粉0,45?-?0,55 石英粉1,00?-?1,20 石英粉尘1,12?-?1,28 R油菜籽0,56?-?0,60 水稻0,65?-?0,75 大米，糙米0,57稻壳0,105米磨面0,35?-?0,40 树皮碎片，云杉/松木，潮湿0,70?-?0,85 油炸洋葱，干燥的0,45?-?0,60 黑麦?（沙地）0,72?-?0,76 黑麦麸皮，精细0,34?-?0,38 黑麦面粉0,47?-?0,55 磷矿石1,50原盐0,72?-?0,83 葡萄干0,62迷迭香，干燥0,25?-?0,35 甜菜根，块茎0,60甜菜籽0,74烟灰0,35S锯末0,29?-?0,45 锯屑0,35?-?0,55 盐（氯化钠）0,75砂，精细，湿润1,00水洗砂1,32?-?1,62 粘土1,80泡沫片0,02板岩，破碎1,38?-?1,56 高炉炉渣0,85?-?1,00 研磨粉2,30快速煮饭米，长粒0,40?-?0,60 巧克力粉0,65巧克力豆0,60?-?0,80 红茶0,30?-?0,45 皂片0,20?-?0,40 皂粉0,58芥末籽0,45?-?0,55 硅粒1,20硅粉1,20苏打1,00轻质苏打0,74大豆粉0,42 石英砾石1,60石英砂1,50源面粉0,40?-?0,55 草坪肥料0,86?-?0,95 大米，精制0,75米片0,19?-?0,21 米粉0,38?-?0,45 稻壳0,11?-?0,12 蓖麻子0,40黑麦（山区）0,66?-?0,70 黑麦粗粉0,52?-?0,55 黑麦麸皮，粗糙0,29?-?0,32 黑麦面粉（中间产物）0,35?-?0,45 稻米（水稻），预净化0,51?-?0,60 原糖0,95迷迭香，研磨0,36鲈鮋鱼粉0,59甜菜0,65圆砾石，洗过的1,52?-?1,62 烟尘（碳黑颗粒）0,10锯末，干燥0,11?-?0,19 硝铵1,30盐（岩盐）1,40砂，精细，干燥1,30?-?1,40 沙丁鱼鱼粉0,58泡沫玻璃颗粒0,12?-?0,16 洗衣粉1,00板岩粉1,10?-?1,30 炉渣，多孔性，破碎0,45?-?0,50 除蛞蝓药0,82快速煮饭米，中粒0,55?-?0,65 巧克力片0,50?-?0,65 砾石（卵石）1,40重晶石1,20肥皂条0,60块根芹0,60硅胶0,68碳化硅0,80?-?1,00 烧结浮石0,40?-?0,80 重质纯碱0,88?-?1,04 黄豆0,70豆粕0,50?-?0,55 葵花籽0,35干质菠菜粉0,42稳定剂1,10夏季油菜0,68酱汁粉0,40?-?0,55 洗净砾石1,36?-?1,48 淀粉0,40?-?0,65 钢珠4,42煤粉0,70硬煤，干燥0,83岩盐,?磨碎0,45?-?0,75 块煤0,90汤粉0,40?-?0,60 聚苯乙烯泡沫塑料球0,029T烟草切丝0,24?-?0,40 滑石粉0,65?-?0,95 茶叶0,39动物粉0,50?-?0,55 番茄汁（即溶）0,45?-?0,55 粘土颗粒1,25陶土，干燥的0,55?-?0,85 泥炭，干燥的0,35浮石凝灰岩, 磨碎的0,93饲料酵母0,17?-?0,23 V香草，研磨0,35香草糖0,95W杜松果，干燥0,55核桃，带壳0,45?-0,55 洗衣粉0,30白米，长粒0,75?-?0,85 白米，圆粒0,81?-?0,85 小麦，软质0,73?-?0,78 小麦粉，粗糙0,50?-?0,55 麦麸，精细0,28?-?0,35 面粉?(405-630) 0,55?-?0,60 面粉（中间产品）0,35?-?0,45 碎小麦，粗糙0,50?-?0,52 野豌豆0,75?-?0,80 Z醋酸纤维素0,55纤维素粉0,23水泥熟料1,20?-?1,30 菊苣粉0,35废砖1,30锌粒4,00 钢丸3,70钢切屑1,60?-?2,40 硬煤，潮湿1,00岩盐? 1,20岩棉-细颗粒0,08?-?0,11 过磷酸盐0,80聚苯乙烯0,05烟粉0,35?-?0,40 滑石0,80?-?1,00 饲料0,50?-?0,80 二氧化钛0,79粘土，干燥1,90湿润粘土1,20?-?1,60 泥炭，潮湿0,50?-?0,60 蛋糕奶油粉0,55?-?0,65 干燥谷物0,26香草粉0,45维生素0,45?-?1,00 晶片0,30?-?0,55 核桃仁0,50白米，破碎0,81?-?0,84 白米，中粒0,80?-?0,83 小麦，硬质0,80?-?0,85 小麦粉，精细0,55?-?0,60 麦胚，干燥0,20麦麸，粗糙0,18?-?0,25 面粉?(812-1200)? 0,45?-?0,55 碎小麦，精细0,55?-?0,60 小麦淀粉0,45?-?0,55 钨粉4,00纤维素片0,04?-?0,08 水泥1,30?-?1,45 水泥原料0,96粘土1,20碎砖0,75?-?1,40 氧化锌0,60?-?1,00 硬脂酸锌0,22柠檬酸0,80?-?0,90 糖（水晶）1,02锌粉2,30硫酸锌0,80褐糖0,70?-?0,88 糖粉0,62。

上海市晋元高级中学2025届化学高一上期中复习检测试题注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题（每题只有一个选项符合题意）1、在相同温度和压强下，三个容积相同的容器中分别盛有N2、O 2、空气，下列说法正确的是（ ）A ．三种气体质量之比为1∶1∶2B ．三种气体的密度之比为1∶1∶1C ．三种气体的分子数之比为1∶1∶1D ．三种气体原子数之比为1∶1∶22、下列溶液中导电性最强的是A ．1L0.1mol/L 醋酸B ．0.1L 0.1mol/L H 2SO 4溶液C ．0.5L 0.1mol/L 盐酸D ．2L 0.1mol/L H 2SO 3溶液 3、下列选项的括号内是除去杂质所用的试剂，其中错误的是（ ）A ．二氧化氮中混有NO （水）B ．NaNO 3溶液中混有Na 2SO 4［Ba （NO 3）2］C ．氯气中混有水蒸气（浓硫酸）D ．氨气中混有水蒸气（碱石灰固体）4、已知aRO 4x-+bH ++cCl -=dR 2++5Cl 2↑+8H 2O ，则RO 4x-中R 的化合价为A ．+4B ．+5C ．+6D ．+75、在酸性条件下，可发生如下反应： 3ClO -+2M 3++4H 2O=27M O n -+Cl －+8H +， 27M O n -中M 的化合价是 （ ）A ．+4B ．+5C ．+6D ．+76、下列有关用途说法不正确．．．的是 A ．溴化银是重要感光材料可用于人工降雨B ．热的纯碱溶液显碱性可用于除去金属表面的油污C ．汽车车灯使用高压钠灯是因为黄光透雾力强、射程远D ．明矾可用于净水是因为在水中生成氢氧化铝胶体吸附了水中悬浮的杂质7、将9g 由CO 和H 2组成的混合气体在足量的O 2中充分燃烧后，将生成的所有产物通过足量的Na 2O 2固体，Na 2O 2固体增加的质量为( )A ．8gB ．9gC ．12gD ．13.5g8、如图为常见玻璃仪器组成的六种实验装置，根据需要加入液体或者固体试剂。

新高考数学计算题型精练三角恒等变换1．cos70cos20sin70sin160︒︒-︒︒=（）A．0B．12C D．1【答案】A【详解】cos20cos70sin160sin70︒︒-︒︒()cos20cos70sin18020sin70=︒︒-︒-︒︒cos20cos70sin20sin70=︒︒-︒︒()cos2070cos900=︒+︒=︒=．故选：A．2．sin40°cos10°+cos140°sin10°＝（）A B C．﹣12D．12【答案】D【详解】sin40°cos10°+cos140°sin10°，=sin40°cos10°-cos40°sin10°，=sin（40°-10°），=sin30°＝12.故选：D3．sin20cos40cos20sin140︒︒︒︒+=A．B．2C．12-D．12【答案】B【详解】sin20cos40cos20sin140sin20cos40cos20sin40sin(2040)sin60︒︒+︒︒=︒︒+︒︒=︒+︒=︒故选B4．已知π1cos63α⎛⎫-=⎪⎝⎭，则πsin26α⎛⎫+=⎪⎝⎭（）A．79-B．79C．3-D．3【答案】A【详解】因为π1 cos63α⎛⎫-=⎪⎝⎭，故2πππππ27sin 2sin 2()cos 2()2cos ()116626699αααα⎛⎫⎡⎤+=-+=-=--=-=- ⎪⎢⎥⎝⎭⎣⎦，故选：A 5．若cos tan 3sin ααα=-，则sin 22πα⎛⎫+= ⎪⎝⎭（）A ．23B ．13C ．89D ．79【答案】D【详解】因为cos tan 3sin ααα=-，所以sin cos cos 3sin αααα=-，即223sin sin cos ααα-=，所以223sin sin cos 1ααα=+=，即1sin 3α=，所以27sin 2cos212sin 2π9ααα⎛⎫+==-= ⎪⎝⎭，故选：D ．6．sin 20cos 40sin 70sin 40︒︒+︒︒=（）AB ．12C．2D ．1【答案】A【详解】已知可化为：()sin 20cos 40cos 20sin 40sin 20402︒︒︒+︒=︒+︒=.故选：A7．若πtan 28α⎛⎫-= ⎪⎝⎭，则πtan 24α⎛⎫-= ⎪⎝⎭（）A ．34B ．34-C ．43D ．43-【答案】D【详解】由2π2tan()π448tan 2π41431tan ()8ααα-⎛⎫-===- ⎪-⎝⎭--.故选：D8．已知π0,2α⎛⎫∈ ⎪⎝⎭π2sin 4αα⎛⎫=+ ⎪⎝⎭，则sin 2α=（）A ．34-B ．34C ．1-D ．1【答案】B【详解】π2sin(4αα=+Q，)22(sin cos )2cos sin αααα=+-Q,1(cos sin )(cos sin )02αααα∴+--=，又π0,2α⎛⎫∈ ⎪⎝⎭，则sin 0,cos 0αα>>，即cos sin 0αα+>所以1cos sin 2αα-=，因为π0,2α⎛⎫∈ ⎪⎝⎭，所以2(0,π)α∈，sin 20α>.由1cos sin 2αα-=平方可得11sin 24α-=，即3sin 24α=，符合题意.综上，3sin 24α=.故选：B.9．已知5π4sin 125θ⎛⎫+= ⎪⎝⎭，则πsin 23θ⎛⎫+= ⎪⎝⎭（）A ．2425-B ．725-C ．725D ．2425【答案】C【详解】5ππππ4sin sin cos 12212125θθθ⎡⎤⎛⎫⎛⎫⎛⎫+=--=-= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，所以22πππ47cos 2cos 22cos 1216612525θθθ⎛⎫⎛⎫⎛⎫⎛⎫-=-=--=⨯-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，得ππππ7sin 2sin 2cos 2326625θθθ⎡⎤⎛⎫⎛⎫⎛⎫+=+-=-= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.故选：C.10．已知tan 2α=，则213cos sin2αα-=（）A ．12B ．14C ．2D ．4【答案】A【详解】因为tan 2α=，所以222213cos sin 2cos tan 221sin22sin cos 2tan 42αααααααα---====，故选：A.11．化简：()22sin πsin 22cos 2ααα-+=（）A ．sin αB ．sin 2αC ．2sin αD ．sin2α【答案】C【详解】根据题意可知，利用诱导公式可得()222sin πsin 22sin sin 22cos 2cos 22αααααα-++=再由二倍角的正弦和余弦公式可得()()222sin 1cos 2sin 1cos 2sin sin 22sin 1cos 2cos2cos22αααααααααα+++===+，即()22sin πsin 22sin 2cos2αααα-+=.故选：C12．cos78cos18sin 78sin18︒︒+︒︒的值为（）A ．12B ．13CD【答案】A【详解】依题意由两角差的余弦公式可知，()1cos78cos18sin 78sin18cos 7818cos602︒︒+︒︒=︒-︒==.故选：A13．若tan 2θ=-，则()()()πsin 1sin22sin πcos πθθθθ⎛⎫+- ⎪⎝⎭=-++____________【答案】35-/-0.6【详解】()()()()22πsin 1sin2cos sin cos 2cos sin cos sin πcos πsin cos θθθθθθθθθθθθ⎛⎫+- ⎪-⎝⎭==--++-22222tan 1213cos sin 1tan 1(2)5cossin cos θθθθθθ-=---===-+++-，故答案为：35-14．已知ππ2θ<<，且4cos 5θ=-，则tan 2θ=______．【答案】247-【详解】4cos 5θ=-，3sin 5θ==±，ππ2θ<< ，3sin 5θ∴=.sin 3tan cos 4θθθ∴==-,232tan 242tan 291tan 7116θθθ-===---.故答案为：247-.15．已知cos 24π7sin 4αα=⎛⎫+ ⎪⎝⎭，则sin 2α的值是______．【答案】4149【详解】22cos 2442cos sin π777sin 422αααα=⇒⇒-=⎛⎫+ ⎪⎝⎭228841cos 2sin cos sin 1sin 2sin 2494949αααααα⇒-+=⇒-=⇒=，故答案为：414916．已知()0,απ∈，若sin 6πα⎛⎫-= ⎪⎝⎭cos 26πα⎛⎫+= ⎪⎝⎭_________.【答案】3±【详解】因为sin 63πα⎛⎫-= ⎪⎝⎭，()0,απ∈，所以cos 6πα⎛⎫-== ⎪⎝⎭所以sin 2=2sin cos =6663πππααα⎛⎫⎛⎫⎛⎫---±⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以cos 2cos 2cos 2sin 2=6326263ππππππαααα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=-+=-+=--± ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦.故答案为：17．若3,0,sin 25⎛⎫∈-=- ⎪⎝⎭x x π，则tan 2x =________.【答案】247-【详解】343,0,sin cos ,tan 2554x x x x π⎛⎫∈-=-∴==-⎪⎝⎭Q 232tan 242tan 291tan 7116x x x -∴===---故答案为：247-18．已知(),2αππ∈，cos 3sin 1αα-=，则cos 2α=_______________________．【答案】【详解】因为(),2αππ∈，所以,22αππ⎛⎫∈ ⎪⎝⎭，由cos 3sin 1αα-=可得212sin 6sin cos 1222ααα--=，整理可得sin 3cos 22αα=-，22sin 3cos 22sin cos 12222ααααπαπ⎧=-⎪⎪⎪+=⇒⎨⎪⎪<<⎪⎩cos 2α=故答案为：19．若πcos 0,,tan 22sin αααα⎛⎫∈= ⎪⎝⎭，则α=__________.【答案】6π/16π【详解】依题意，πcos 0,,tan 22sin αααα⎛⎫∈= ⎪⎝⎭，所以2222tan 1,2tan 1tan 1tan tan ααααα==--，21tan 3α=，而α为锐角，所以πtan 6αα=.故答案为：π620．已知tan 3α=，则sin 2α=______．【答案】35【详解】22222sin cos 2tan 233sin 2sin cos tan 1315ααααααα⨯====+++.故答案为：3521．已知α是第二象限的角，1cos24α=，则tan α=________．【答案】5/【详解】因为21cos 212sin 4αα=-=，又α是第二象限的角，所以6sin 4α=，cos 4α=，所以5tan α=-.故答案为：5-22．已知22cos 5sin 10αα-+=，则cos 2=α______．【答案】12/0.5【详解】解：已知()2222cos 5sin 121sin 5sin 12sin 5sin 30αααααα-+=--+=--+=，即()()22sin 5sin 32sin 1sin 30αααα+-=-+=，解得1sin 2α=或sin 3α=-（舍），211cos 212sin 1242αα∴=-=-⨯=，故答案为：12.23．若tan 2θ=，则sin cos 2cos sin θθθθ=-_________.【答案】65/1.2/115【详解】()()22sin cos sin sin cos 2sin cos sin cos sin cos sin θθθθθθθθθθθθ-==+--222222sin cos sin tan tan 246sin cos sin sin cos tan 155θθθθθθθθθθθ+++=+====++.故答案为：65.24．函数()sin 2sin 1cos x xf x x=+的值域__________．【答案】14,2⎛⎤- ⎥⎝⎦【详解】因为()()222221cos cos sin 2sin 2sin cos 11=2cos 2cos 2cos 1cos 1cos 1cos 22x x x x x x f x x x x x x x -⎛⎫===-+=--+ ⎪+++⎝⎭，因为1cos 1x -≤≤，当1cos 2x =时，()f x 取得最大值12，当cos 1x =-时，()f x 取得最小值4-，又因为1cos 0x +≠，所以()f x 的值域为14,2⎛⎤- ⎝⎦．故答案为：14,2⎛⎤- ⎥⎝⎦.25．已知sin 2cos αα=，π0,2α⎛⎫∈ ⎪⎝⎭，tan α=________．【详解】sin 2cos 2sin cos αααα==，π0,2α⎛⎫∈ ⎪⎝⎭，则cos 0α≠，1sin 2α=，π6α=，故tan α=26．（1）计算：cos157sin 97sin 60cos 97︒+︒︒︒；（2）已知tan 1α=-，求2cos 2sin cos 1ααα--的值．【答案】（1）12；（2）12【详解】（1）cos157sin 97sin 60cos97︒+︒︒︒()cos 9760sin 97sin 60cos 97︒+︒+︒︒=︒cos 97cos 60sin 97sin 60sin 97sin 60cos 97︒︒-︒︒+︒︒=︒cos 60=︒12=．（2）2cos 2sin cos 1ααα--222cos 2sin cos 1cos sin ααααα-=-+212tan 11tan αα-=-+()()2121111-⨯-=-+-12=．。

第二章平面解析几何2.3圆及其方程2.3.1圆的标准方程课后篇巩固提升必备知识基础练1.圆心为(-3,4),半径是2的圆的标准方程为()A.(x+3)2+(y-4)2=4B.(x-3)2+(y+4)2=4C.(x+3)2+(y-4)2=2D.(x-3)2+(y+4)2=22.方程y=√9-x 2表示的曲线是()A.一条射线B.一个圆C.两条射线D.半个圆3.如图,圆C 的部分圆弧在如图所示的网格纸上(小正方形的边长为1),图中直线与圆弧相切于一个小正方形的顶点,若圆C 经过点A (2,15),则圆C 的半径为()A.7√2B.8C.8√2D.10圆C 经过点(2,1)和点(2,15),故圆心在直线y=8上.又过点(2,1)的圆的切线为y-1=-(x-2),故圆心在直线y-1=x-2上,即圆心在直线x-y-1=0上.由{y =8,x -y -1=0可得圆心为(9,8), 故圆的半径为√(9-2)2+(8-1)2=7√2.4.已知一圆的圆心为点A (2,-3),一条直径的端点分别在x 轴和y 轴上,则圆的标准方程为()A.(x+2)2+(y-3)2=13B.(x-2)2+(y+3)2=13C.(x-2)2+(y+3)2=52D.(x+2)2+(y-3)2=52,结合圆的性质可知,原点在圆上,圆的半径为r=√(2-0)2+(-3-0)2=√13.故所求圆的标准方程为(x-2)2+(y+3)2=13.5.已知直线l 过圆x 2+(y-3)2=4的圆心,且与直线x+y+1=0垂直,则l 的方程为()A.x+y-2=0B.x-y+2=0C.x+y-3=0D.x-y+3=0x 2+(y-3)2=4的圆心坐标为(0,3).因为直线l 与直线x+y+1=0垂直,所以直线l 的斜率k=1.由点斜式得直线l 的方程是y-3=x-0, 化简得x-y+3=0.6.将圆x 2+y 2=2沿x 轴正方向平移2个单位后得到圆C ,则圆C 的标准方程为.x-2)2+y 2=27.当a 为任意实数时,直线(a-1)x-y+a+1=0恒过定点C ,则以点C 为圆心,√5为半径的圆的标准方程是.x+1)2+(y-2)2=5(x+1)a-(x+y-1)=0,可知直线恒过点(-1,2),从而所求圆的标准方程为(x+1)2+(y-2)2=5.8.若圆的方程为(x +k 2)2+(y+1)2=1-34k 2,则当圆的面积最大时,圆心坐标和半径分别为、.-1)1圆的方程为(x +k 2)2+(y+1)2=1-34k 2, ∴r 2=1-34k 2>0,r max =1,此时k=0.∴圆心为(0,-1).9.求以A (2,2),B (5,3),C (3,-1)为顶点的三角形的外接圆的标准方程.(x-a )2+(y-b )2=r 2,则有{(2-a )2+(2-b )2=r 2,(5-a )2+(3-b )2=r 2,(3-a )2+(-1-b )2=r 2,解得{a =4,b =1,r 2=5,10.已知点A (-1,2)和B (3,4).求:(1)线段AB 的垂直平分线l 的方程;(2)以线段AB 为直径的圆的标准方程.AB 的中点C 的坐标为(1,3).(1)∵A (-1,2),B (3,4), ∴直线AB 的斜率k AB =4-23-(-1)=12.∵直线l 垂直于直线AB ,∴直线l 的斜率k l =-1k AB =-2, ∴直线l 的方程为y-3=-2(x-1),即2x+y-5=0.(2)∵A (-1,2),B (3,4), ∴|AB|=√(3+1)2+(4-2)2=√20=2√5,∴以线段AB 为直径的圆的半径R=12|AB|=√5.又圆心为C (1,3),∴所求圆的标准方程为(x-1)2+(y-3)2=5.关键能力提升练11.方程(x-1)√x 2+y 2-3=0所表示的曲线是()A.一个圆B.两个点C.一个点和一个圆D.一条直线和一个圆x-1)√x 2+y 2-3=0可化为x-1=0或x 2+y 2=3,∴方程(x-1)√x 2+y 2-3=0表示一条直线和一个圆.12.已知直线(3+2λ)x+(3λ-2)y+5-λ=0恒过定点P ,则与圆C :(x-2)2+(y+3)2=16有公共的圆心且过点P 的圆的标准方程为()A.(x-2)2+(y+3)2=36B.(x-2)2+(y+3)2=25C.(x-2)2+(y+3)2=18D.(x-2)2+(y+3)2=9(3+2λ)x+(3λ-2)y+5-λ=0,得(2x+3y-1)λ+(3x-2y+5)=0,则{2x +3y -1=0,3x -2y +5=0,解得{x =-1,y =1,即P (-1,1). ∵圆C :(x-2)2+(y+3)2=16的圆心坐标是(2,-3),∴|PC|=√(-1-2)2+(1+3)2=5,13.数学家欧拉于1765年在他的著作《三角形的几何学》中首次提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后人称为三角形的欧拉线.在平面直角坐标系中作△ABC ,在△ABC 中,AB=AC=4,点B (-1,3),点C (4,-2),且其“欧拉线”与圆(x-3)2+y 2=r 2相切,则该圆的半径r 为()A.1B.√2C.2D.2√2△ABC 中,AB=AC=4,点B (-1,3),点C (4,-2),可得BC 边上的高线、垂直平分线和中线三线合一,则其“欧拉线”为△ABC 边BC 的垂直平分线,可得BC 的中点为(32,12),直线BC 的斜率为3+2-1-4=-1,则BC 的垂直平分线的斜率为1,所以BC 的垂直平分线方程为y-12=x-32,即为x-y-1=0,其“欧拉线”与圆(x-3)2+y 2=r 2相切,所以圆心(3,0)到“欧拉线”的距离为d=√2=√2,即半径r=√2.14.已知点A (-a ,0),B (a ,0)(a>0),点C 在圆(x-2)2+(y-2)2=2上,且满足∠ACB=90°,则a 的最小值是. √2C (2+√2cos α,2+√2sin α),∴AC ⃗⃗⃗⃗⃗ =(2+√2cos α+a ,2+√2sin α),BC ⃗⃗⃗⃗⃗ =(2+√2cos α-a ,2+√2sin α),∵∠ACB=90°,∴AC ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =(2+√2cos α)2-a 2+(2+√2sin α)2=0,∴a 2=10+4√2(sin α+cos α)=10+8sin α+π4∈[2,18].∵a>0,∴a ∈[√2,3√2],∴a 的最小值是√2.15.已知圆C 与圆(x-1)2+y 2=1关于直线y=-x 对称,则圆C 的标准方程为.2+(y+1)2=1(x-1)2+y 2=1,设其圆心为C 1,则圆C 1的圆心坐标为(1,0),半径长r 1=1.设圆心C 1(1,0)关于直线y=-x 对称的点的坐标为(a ,b ),即圆心C 的坐标为(a ,b ),则{ba -1·(-1)=-1,-a+12=b 2,解得{a =0,b =-1.所以圆C 的标准方程为x 2+(y+1)2=1.16.已知三点A (3,2),B (5,-3),C (-1,3),以点P (2,-1)为圆心作一个圆,使A ,B ,C 三点中一点在圆外,一点在圆上,一点在圆内,求这个圆的标准方程.A ,B ,C 三点中一点在圆外,一点在圆上,一点在圆内,则圆的半径是|PA|,|PB|,|PC|的中间值.因为|PA|=√10,|PB|=√13,|PC|=5,所以|PA|<|PB|<|PC|,所以圆的半径r=|PB|=√13.故所求圆的标准方程为(x-2)2+(y+1)2=13.17.已知圆C 与y 轴相切,圆心在直线x-2y=0上,且圆C 被直线y=x 截得的弦长为2√14,求圆C 的方程.C (2y 0,y 0),半径r=|2y 0|,圆心到直线x-y=0的距离为00√2=0√2,由半径、弦心距、半弦长的关系得4y 02=14+y 022,∴y 0=±2.当y 0=2时,圆心C (4,2),半径r=4,此时圆C 为(x-4)2+(y-2)2=16,当y 0=-2时,圆心C (-4,-2),半径r=4,此时圆C 为(x+4)2+(y+2)2=16.学科素养拔高练18.阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一,指的是:已知动点M 与两定点A ,B 的距离之比为λ(λ>0,λ≠1),那么点M 的轨迹就是阿波罗尼斯圆.下面,我们来研究与此相关的一个问题.已知圆:x 2+y 2=1和点A (-12,0),点B (1,1),M 为圆O 上动点,则2|MA|+|MB|的最小值为. √10,取点K (-2,0),连接OM ,MK.∵|OM|=1,|OA|=12,|OK|=2,∴|OK ||OM |=|OM ||OA |=2.又∵∠MOK=∠AOM ,∴△MOK ∽△AOM ,∴|MK ||MA |=|OM ||OA |=2,∴|MK|=2|MA|,∴|MB|+2|MA|=|MB|+|MK|,|MB|+|MK|≥|BK|,∴|MB|+2|MA|=|MB|+|MK|的最小值为|BK|,∵B (1,1),K (-2,0),∴|BK|=√(-2-1)2+(0-1)2=√10.19.已知圆C 的圆心在直线x-3y=0上,且与y 轴相切于点(0,1).(1)求圆C的方程;(2)若圆C与直线l:x-y+m=0交于A,B两点,分别连接圆心C与A,B两点,若CA⊥CB,求m的值.设圆心坐标为C(a,b),则a=3b,∵圆与y轴相切于点(0,1),则b=1,r=|a-0|,∴圆C的圆心坐标为(3,1),半径r=3.故圆的方程为(x-3)2+(y-1)2=9.(2)∵CA⊥CB,|CA|=|CB|=r,∴△ABC为等腰直角三角形,∵|CA|=|CB|=r=3,∴圆心C到直线l的距离d=3√22.则d=√2=32√2,解得m=1或-5.。

2023-2024学年安徽省合肥一中高一（上）期中数学试卷一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．1．已知全集U ＝{1，2，3，4，5}，集合A ＝{1，5}，B ＝{2，4}，则（∁U A ）∩B ＝（ ） A ．{4}B ．{2，4}C ．{2，3，4}D ．{1，2，3，4}2．命题“∃x ∈R ，x 2﹣3x +3≥0”的否定是（ ） A ．∀x ∈R ，x 2﹣3x +3＜0 B ．∀x ∈R ，x 2﹣3x +3≥0 C ．∃x ∈R ，x 2﹣3x +3≤0 D ．∃x ∈R ，x 2﹣3x +3＜03．函数y =√x 2+2x−3x−1的定义域是（ ）A ．[﹣3，1]B ．[﹣1，1）∪（1，3]C ．（﹣∞，﹣3]∪[1，+∞）D ．（﹣∞，﹣3]∪（1，+∞）4．对于实数a ，b ，c ，下列说法正确的是（ ） A ．若a ＜b ，则1a＞1bB ．若a ＜b ，则ac 2＜bc 2C ．若a ＜0＜b ，则ab ＜b 2D ．若c ＞a ＞b ，则1c−a＜1c−b5．函数f(x)=9−3xx−2(x ＞3)的值域为（ ） A ．（﹣3，0）B ．（0，+∞）C ．（﹣1，0）D ．（﹣2，0）6．已知函数f(x)={x 2−(a +2)x +3，x ≤1a x，x ＞1是R 上的减函数，则实数a 的取值范围是（ ）A ．（0，2]B ．（0，1]C ．[1，2]D ．（0，+∞）7．对实数a 和b ，定义运算“◎”：a ◎b ={a ，a −b ≤2b ，a −b ＞2，设函数f （x ）＝（x 2﹣1）◎（5x ﹣x 2）（x ∈R ），若函数y ＝f （x ）﹣m 的图象与x 轴恰有1个公共点，则实数m 的取值范围是（ ） A ．（﹣1，6]￥D ．[−114，−1)∪[6，8]8．已知函数f （x ）是定义在R 上的奇函数，f （1）＝3，若∀x 1，x 2∈（0，+∞），且x 1≠x 2，都有（x 1﹣x 2）[x 1f （x 1）﹣x 2f （x 2）]＞0，则不等式（x +3）f （x +3）＞3的解集为（ ） A ．（﹣∞，﹣4）∪（﹣2，+∞） B ．（﹣∞，2）∪（4，+∞） C ．（﹣∞，3）D ．（3，+∞）二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分． 9．下列函数中，与函数y ＝x +1是同一函数的是（ ） A ．y =(√x +1)2 B ．y =√x 33+1C ．y =√(x +1)33D ．y =x 2+1x−110．设x ∈R ，不等式ax 2﹣2ax ﹣2＜0恒成立的充分不必要条件可以是（ ） A ．﹣1＜a ＜0B ．﹣2＜a ＜0C ．﹣3＜a ≤0D ．0≤a ＜111．十六世纪中叶，英国数学家雷科德在《砺智石》一书中先把“＝”作为等号使用，后来英国数学家哈利奥特首次使用“＜”和“＞”符号，并逐步被数学界接受，不等号的引入对不等式的发展影响深远，下列说法正确的是（ ） A ．糖水加糖更甜可用式于a+m b+m＞ab表示，其中a ＞b ＞0，m ＞0B ．当x ＞32时，y =2x −1+12x−3的最小值为4 C ．若x ＞0，y ＞0，2x +y ＝1，则√2x +√y ≤√2D ．若a 2（b 2﹣2）＝4，则a 2+b 2的最小值为6 12．已知函数f(x)=x1+|x|（x ∈R ），则（ ） A ．函数f （x ）为奇函数B ．函数f （x ）的值域是（﹣1，1）C ．函数f （x ）在R 上单调递减D ．若对任意的x ∈[﹣1，1]，f （x ）≤t 2﹣2at +12恒成立，则当a ∈[﹣1，1]时，t ≥2或t ＝0或t ≤﹣2 三、填空题：本题共4小题，每小题5分，共20分．13．已知函数f(x)={x 2−1，x ≤0x −3，x ＞0，则f （f （﹣2））＝ ．14．下列命题中，真命题的编号是 ． ①∀x ∈R ，x 2﹣2x +3＞0；②∃x ∈N *，x 为方程2x 2﹣3＝0的根； ③∀x ∈{﹣1，0，1}，2x +1＞0； ④∃x ，y ∈Z ，使3x ﹣2y ＝10．15．已知a ，b 为正实数，满足（a +b ）（2a +b ）＝3，则10a +7b 的最小值为 ．16．已知函数y ＝f （x ）的定义域为R ，满足f （x ）＝2f （x ﹣1），且当x ∈（0，1]时，f （x ）＝x （1﹣x ），若对任意x ∈（﹣∞，m ]，都有f(x)≤32，则m 的最大值是 ．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．（10分）已知集合A ＝{x |﹣2＜x ＜8}，B ＝{x |m ﹣3＜x ＜3m ﹣1}． （1）当m ＝2时，求A ∩B ；（2）若A ∪B ＝A ，求实数m 的取值范围．18．（12分）已知集合A ＝{x |x 2﹣x ﹣6＜0}，B ＝{x |x 2+2mx ﹣3m 2＜0}． （1）若集合B ＝{x |﹣6＜x ＜2}，求实数m 的值；（2）若m ≥0，“x ∈A ”是“x ∈B ”的充分不必要条件，求实数m 的取值范围． 19．（12分）已知幂函数f （x ）＝（m 2﹣5m +7）x m 为奇函数． （1）求f （x ）的解析式；（2）若函数g （x ）是定义在R 上的偶函数，当x ≥0时，g （x ）＝f （x ）﹣x 2，求函数g （x ）的解析式． 20．（12分）已知函数f （x ）＝x 2﹣4x +a ．（1）在①∃x ∈[1，5]，②∀x ∈[1，5]这两个条件中任选一个，补充到下面问题中的横线上，并求解该问题．若命题：“_____，f （x ）＞0”为真命题，求实数a 的取值范围； （2）求函数F(x)=12[f(x)+f(|x|)]的单调递增区间．21．（12分）如图，某学校欲建矩形运动场，运动场左侧为围墙，三面通道各宽2m ，运动场与通道之间由栅栏隔开．（1）若运动场面积为3200m 2，求栅栏总长的最小值；（2）若运动场与通道占地总面积为3200m 2，求运动场面积的最大值．22．（12分）已知函数f(x)=x 2+a x+b 是奇函数，且f(−2)=−52．（1）判断并根据定义证明函数f （x ）在（0，1），（1，+∞）上的单调性；（2）设函数h （x ）＝f 2（x ）﹣2tf （x ）﹣2（t ＜0），若对∀x 1，x 2∈[13，3]，都有|h （x 1）﹣h （x 2）|≤8，求实数t 的取值范围．2023-2024学年安徽省合肥一中高一（上）期中数学试卷参考答案与试题解析一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．1．已知全集U＝{1，2，3，4，5}，集合A＝{1，5}，B＝{2，4}，则（∁U A）∩B＝（）A．{4}B．{2，4}C．{2，3，4}D．{1，2，3，4}解：由已知得∁U A＝{2，3，4}，所以（∁U A）∩B＝{2，4}．故选：B．2．命题“∃x∈R，x2﹣3x+3≥0”的否定是（）A．∀x∈R，x2﹣3x+3＜0B．∀x∈R，x2﹣3x+3≥0C．∃x∈R，x2﹣3x+3≤0D．∃x∈R，x2﹣3x+3＜0解：∃x∈R，x2﹣3x+3≥0的否定是：∀x∈R，x2﹣3x+3＜0．故选：A．3．函数y=√x2+2x−3x−1的定义域是（）A．[﹣3，1]B．[﹣1，1）∪（1，3] C．（﹣∞，﹣3]∪[1，+∞）D．（﹣∞，﹣3]∪（1，+∞）解：要使得函数y=√x2+2x−3x−1有意义，则x2+2x﹣3≥0，且x﹣1≠0，解得x＞1或x≤﹣3，故定义域为（﹣∞，﹣3]∪（1，+∞）．故选：D．4．对于实数a，b，c，下列说法正确的是（）A．若a＜b，则1a ＞1bB．若a＜b，则ac2＜bc2C．若a＜0＜b，则ab＜b2D．若c＞a＞b，则1c−a ＜1c−b解：若a＜0，b＞0，则1a ＜1b，故A错误；若c＝0，则ac2＝bc2，故B错误；因为a＜0＜b，所以ab﹣b2＝b（a﹣b）＜0，即ab＜b2，故C正确；因为c＞a＞b，所以0＜c﹣a＜c﹣b，所以1c−a ＞1c−b＞0，故D错误．故选：C．5．函数f(x)=9−3xx−2(x ＞3)的值域为（ ） A ．（﹣3，0） B ．（0，+∞） C ．（﹣1，0） D ．（﹣2，0）解：由题意，函数f(x)=9−3x x−2=−3+3x−2（x ＞3）， 令t ＝x ﹣2，则t ＞1，可得3t∈(0，3)，故f(x)=−3+3x−2（x ＞3）的值域为（﹣3，0）． 故选：A ．6．已知函数f(x)={x 2−(a +2)x +3，x ≤1a x ，x ＞1是R 上的减函数，则实数a 的取值范围是（ ）A ．（0，2]B ．（0，1]C ．[1，2]D ．（0，+∞）解：二次函数y ＝x 2﹣（a +2）x +3的对称轴为x =a+22， 因为函数f(x)={x 2−(a +2)x +3，x ≤1ax，x ＞1是R 上的减函数，所以有{a+22≥1，a ＞01−a −2+3≥a，解得0＜a ≤1．故选：B ．7．对实数a 和b ，定义运算“◎”：a ◎b ={a ，a −b ≤2b ，a −b ＞2，设函数f （x ）＝（x 2﹣1）◎（5x ﹣x 2）（x ∈R ），若函数y ＝f （x ）﹣m 的图象与x 轴恰有1个公共点，则实数m 的取值范围是（ ） A ．（﹣1，6] B ．(−∞，−1]∪(−114，6) C ．(−114，+∞)D ．[−114，−1)∪[6，8]解：当x 2﹣1﹣（5x ﹣x 2）≤2⇒2x 2﹣5x ﹣3≤0⇒−12≤x ≤3时，f （x ）＝x 2﹣1； 当x 2﹣1﹣（5x ﹣x 2）＞2⇒2x 2﹣5x ﹣3＞0⇒x ＜−12或x ＞3时，f （x ）＝5x ﹣x 2， 作出f （x ）的图象，如图所示：函数y＝f（x）﹣m的图象与x轴恰有1个公共点，转化为函数f（x）的图象与直线y＝m恰有1个交点，由图象并结合各分段区间上的f（x）的值，可得：6≤m≤8或−114≤m＜﹣1，则实数m的取值范围是[−114，﹣1）∪[6，8]，故D项正确．故选：D．8．已知函数f（x）是定义在R上的奇函数，f（1）＝3，若∀x1，x2∈（0，+∞），且x1≠x2，都有（x1﹣x2）[x 1f （x 1）﹣x 2f （x 2）]＞0，则不等式（x +3）f （x +3）＞3的解集为（ ） A ．（﹣∞，﹣4）∪（﹣2，+∞） B ．（﹣∞，2）∪（4，+∞） C ．（﹣∞，3）D ．（3，+∞）解：由∀x 1，x 2∈（0，+∞），且x 1≠x 2，都有（x 1﹣x 2）[x 1f （x 1）﹣x 2f （x 2）]＞0， 不妨令x 1＜x 2⇒x 1f （x 1）＜x 2f （x 2）可知函数xf （x ）在（0，+∞）上单调递增， 记g （x ）＝xf （x ），则g （﹣x ）＝（﹣x ）f （﹣x ）＝﹣x [﹣f （x ）]＝xf （x ）＝g （x ），所以g （x ）为偶函数，因此g （x ）在（﹣∞，0）上单调递减，且g （﹣1）＝g （1）＝1×f （1）＝3， 不等式（x +3）f （x +3）＞3等价于g （x +3）＞g （1），故|x +3|＞1，解得x ＞﹣2或x ＜﹣4，故不等式的解集为：（﹣∞，﹣4）∪（﹣2，+∞）． 故选：A ．二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分． 9．下列函数中，与函数y ＝x +1是同一函数的是（ ） A ．y =(√x +1)2 B ．y =√x 33+1C ．y =√(x +1)33D ．y =x 2+1x−1解：由题意知函数y ＝x +1的定义域为R ，值域为R ，y =(√x +1)2的定义域为[﹣1，+∞），与函数y ＝x +1的定义域不同，不是同一函数，故A 错误； y =√x 33+1=x +1定义域为R ，定义域与对应关系和y ＝x +1相同，为同一函数，故B 正确； y =√(x +1)33=x +1定义域R ，定义域与对应关系和y ＝x +1相同，为同一函数，故C 正确；y =x 2+1x−1的定义域为{x ∈R |x ≠1}，与函数y ＝x +1的定义域不同，不是同一函数，故D 错误．故选：BC ．10．设x ∈R ，不等式ax 2﹣2ax ﹣2＜0恒成立的充分不必要条件可以是（ ） A ．﹣1＜a ＜0B ．﹣2＜a ＜0C ．﹣3＜a ≤0D ．0≤a ＜1解：当a ＝0时，不等式ax 2﹣2ax ﹣2＜0为﹣2＜0，满足题意；a ≠0时，不等式ax 2﹣2ax ﹣2＜0恒成立，则必有a ＜0且Δ＝（﹣2a ）2+4a ×2＜0， 解得﹣2＜a ＜0，故a 的取值范围为﹣2＜a ≤0，由题意知所选不等式ax 2﹣2ax ﹣2＜0恒成立的充分不必要条件中不等式相应集合应为（﹣2，0]的真子集，结合选项可知﹣1＜a ＜0，﹣2＜a ＜0所对应集合为（﹣2，0]的真子集， 故选项A ，B 满足条件．故选：AB ．11．十六世纪中叶，英国数学家雷科德在《砺智石》一书中先把“＝”作为等号使用，后来英国数学家哈利奥特首次使用“＜”和“＞”符号，并逐步被数学界接受，不等号的引入对不等式的发展影响深远，下列说法正确的是（ ） A ．糖水加糖更甜可用式于a+m b+m＞ab表示，其中a ＞b ＞0，m ＞0B ．当x ＞32时，y =2x −1+12x−3的最小值为4 C ．若x ＞0，y ＞0，2x +y ＝1，则√2x +√y ≤√2D ．若a 2（b 2﹣2）＝4，则a 2+b 2的最小值为6解：对于选项A ，当a ＝2，b ＝1，m ＝1时，a b=2，a+m b+m=32＜2，当a ＞b 时，糖水不等式不成立，故A 不正确； 对于选项B ，因为x ＞32，y =2x −1+12x−3=2x −3+12x−3+2≥2√(2x −3)×(12x−3)+2=4， 当且仅当2x ﹣3=12x−3，即x ＝2时取等号，故B 正确； 对于选项C ，因为2x +y =1≥2√2xy ，所以xy ≤18，当且仅当2x ＝y ，即x =14，y =12时等号成立， 所以(√2x +√y)2=2x +y +2√2⋅√xy ≤1+2√2⋅√18=2， 即√2x +√y ≤√2，当且仅当x =14，y =12时等号成立，故C 正确； 对于选项D ，因为a 2（b 2﹣2）＝4， 所以a 2=4b 2−2＞0，所以a 2+b 2=4b 2−2+b 2=4b 2−2+（b 2﹣2）+2≥2√4b 2−2⋅(b 2−2)+2＝6，当且仅当b 2−2=4b 2−2，即a 2＝2，b 2＝4时，等号成立，故D 正确．故选：BCD ．12．已知函数f(x)=x1+|x|（x ∈R ），则（ ） A ．函数f （x ）为奇函数B ．函数f （x ）的值域是（﹣1，1）C ．函数f （x ）在R 上单调递减D ．若对任意的x ∈[﹣1，1]，f （x ）≤t 2﹣2at +12恒成立，则当a ∈[﹣1，1]时，t ≥2或t ＝0或t ≤﹣2 解：选项A ，由题意得x ∈R ，f （﹣x ）=−x 1+|−x|=−x 1+|x|=−f （x ），所以函数f （x ）是奇函数，故A 正确；选项B ，C ，由函数解析式可得f （x ）={x 1+x ，x ≥0x 1−x ，x ＜0={1−1x+1，x ≥011−x−1，x ＜0，函数图象如图所示：所以f （x ）的值域是（﹣1，1），在R 上单调递增，故B 正确，C 错误； 选项D ，由函数f （x ）在R 上单调递增， 则当x ∈[﹣1，1]时，f （x ）max ＝f （1）=12，f （x ）≤t 2﹣2at +12恒成立，则t 2﹣2at +12≥12恒成立， 即t 2﹣2at ≥0恒成立，令h （a ）＝﹣2at +t 2，即a ∈[﹣1，1]时，h （a ）≥0恒成立， 则{ℎ(1)=t 2−2t ≥0ℎ(−1)=t 2+2t ≥0，解得：t ≤﹣2或t ≥2或t ＝0，故D 正确． 故选：ABD ．三、填空题：本题共4小题，每小题5分，共20分．13．已知函数f(x)={x 2−1，x ≤0x −3，x ＞0，则f （f （﹣2））＝ 0 ．解：f(x)={x 2−1，x ≤0x −3，x ＞0，则f （﹣2）＝3，所以f （f （﹣2））＝f （3）＝0．故答案为：0．14．下列命题中，真命题的编号是 ①④ ． ①∀x ∈R ，x 2﹣2x +3＞0；②∃x ∈N *，x 为方程2x 2﹣3＝0的根； ③∀x ∈{﹣1，0，1}，2x +1＞0； ④∃x ，y ∈Z ，使3x ﹣2y ＝10．解：x 2﹣2x +3＝（x ﹣1）2+2＞0恒成立，故①正确； 由2x 2﹣3＝0，解得x =±√62∉N ∗，故②错误；﹣1×2+1＝﹣1＜0，故③错误， x ＝4，y ＝1满足题意，故④正确． 故答案为：①④．15．已知a ，b 为正实数，满足（a +b ）（2a +b ）＝3，则10a +7b 的最小值为 12 ． 解：因为a ，b 为正实数，满足（a +b ）（2a +b ）＝3，所以（4a +4b ）（6a +3b ）＝36，所以（4a +4b ）（6a +3b ）=36≤(4a+4b+6a+3b)24=(10a+7b)24， 则10a +7b ≥12，当且仅当{4a +4b =6a +3b (a +b)(2a +b)=3，即a =12，b ＝1时，等号成立，故10a +7b 的最小值为12． 故答案为：12．16．已知函数y ＝f （x ）的定义域为R ，满足f （x ）＝2f （x ﹣1），且当x ∈（0，1]时，f （x ）＝x （1﹣x ），若对任意x ∈（﹣∞，m ]，都有f(x)≤32，则m 的最大值是134．解：因为函数y ＝f （x ）的定义域为R ，满足f （x ）＝2f （x ﹣1）， 当x ∈（0，1]时，f （x ）＝x （1﹣x ）， 当x ∈（1，2]时，x ﹣1∈（0，1]，则f （x ）＝2f （x ﹣1）＝2（x ﹣1）[1﹣（x ﹣1）]＝﹣2（x ﹣1）（x ﹣2）=−2(x −32)2+12∈[0，12]， 当x ∈（2，3]时，x ﹣2∈（0，1]，则f （x ）＝4f （x ﹣2）＝4（x ﹣2）[1﹣（x ﹣2）]＝﹣4（x ﹣2）（x ﹣3）=−4(x 2−5x +6)=−4(x −52)2+1∈[0，1]，当x ∈（3，4]时，x ﹣3∈（0，1]，则f （x ）＝8f （x ﹣3）＝8（x ﹣3）[1﹣（x ﹣3）]＝﹣8（x ﹣3）（x ﹣4）=−8(x 2−7x +12)=−8(x −72)2+2∈[0，2]，因为对任意x ∈（﹣∞，m ]，都有f(x)≤32， 当x ∈（3，4]时，令f(x)=−8(x 2−7x +12)=32， 解得x =134或x =154，如下图所示：由图可知，m ≤134，故实数m 的最大值为134． 故答案为：134．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（10分）已知集合A ＝{x |﹣2＜x ＜8}，B ＝{x |m ﹣3＜x ＜3m ﹣1}．（1）当m ＝2时，求A ∩B ；（2）若A ∪B ＝A ，求实数m 的取值范围．解：（1）当m ＝2时，B ＝{x |﹣1＜x ＜5}，所以A ∩B ＝{x |﹣1＜x ＜5}；（2）因为A ∪B ＝A ，所以B 是A 的子集，①B ＝∅，即3m ﹣1≤m ﹣3，解得m ≤﹣1；②B ≠∅，则{m −3≥−23m −1≤83m −1＞m −3，所以1≤m ≤3，综上所述，实数m 的取值范围为{m |m ≤﹣1或1≤m ≤3}．18．（12分）已知集合A ＝{x |x 2﹣x ﹣6＜0}，B ＝{x |x 2+2mx ﹣3m 2＜0}．（1）若集合B ＝{x |﹣6＜x ＜2}，求实数m 的值；（2）若m ≥0，“x ∈A ”是“x ∈B ”的充分不必要条件，求实数m 的取值范围．解：（1）因为B ＝{x |x 2+2mx ﹣3m 2＜0}＝{x |﹣6＜x ＜2}，所以方程x 2+2mx ﹣3m 2＝0的两根分别为﹣6和2，由韦达定理得{−6+2=−2m −6×2=−3m 2，解得m ＝2． 所以实数m 的值为2．（2）由x 2﹣x ﹣6＜0，得﹣2＜x ＜3，A ＝{x |﹣2＜x ＜3}，由于“x ∈A ”是“x ∈B ”的充分不必要条件，则A ⫋B ，当m ＝0时，B ＝{x |x 2＜0}＝∅，此时A ⫋B ，不成立；当m ＞0时，B ＝{x |x 2+2mx ﹣3m 2＜0}＝{x |﹣3m ＜x ＜m }，因为A ⫋B ，则有{−3m ≤−2m ≥3，解得m ≥3； 综上所述，实数m 的取值范围是[3，+∞）．19．（12分）已知幂函数f （x ）＝（m 2﹣5m +7）x m 为奇函数．（1）求f （x ）的解析式；（2）若函数g （x ）是定义在R 上的偶函数，当x ≥0时，g （x ）＝f （x ）﹣x 2，求函数g （x ）的解析式． 解：（1）因为f （x ）为幂函数，所以m 2﹣5m +7＝1，解得m ＝2或m ＝3；当m ＝2时，f （x ）＝x 2是偶函数，不是奇函数；当m ＝3时，f （x ）＝x 3是奇函数，所以m ＝3．故f （x ）的解析式f （x ）＝x 3．（2）由（1）得，当x ≥0时，g （x ）＝f （x ）﹣x 2＝x 3﹣x 2，对于x ＜0，则﹣x ＞0，g （﹣x ）＝（﹣x ）3﹣（﹣x ）2＝﹣x 3﹣x 2，又因为函数g （x ）是定义在R 上的偶函数，所以g （﹣x ）＝g （x ），所以g （x ）＝﹣x 3﹣x 2（x ＜0），所以函数g （x ）的解析式g(x)={x 3−x 2，x ≥0−x 3−x 2，x ＜0． 20．（12分）已知函数f （x ）＝x 2﹣4x +a ．（1）在①∃x ∈[1，5]，②∀x ∈[1，5]这两个条件中任选一个，补充到下面问题中的横线上，并求解该问题．若命题：“_____，f （x ）＞0”为真命题，求实数a 的取值范围；（2）求函数F(x)=12[f(x)+f(|x|)]的单调递增区间．解：（1）由f （x ）＞0，得x 2﹣4x +a ＞0，即a ＞﹣x 2+4x ，令g （x ）＝﹣x 2+4x ，g （x ）＝﹣（x ﹣2）2+4，所以g （x ）在[1，2]上单调递增，在[2，5]上单调递减，则在[1，5]上g （x ）的最小值为g （5）＝﹣5，最大值为g （2）＝4．选择条件①，∃x ∈[1，5]使得a ＞﹣x 2+4x 成立，则a ＞g （x ）min ，所以a ＞﹣5，故实数a 的取值范围是（﹣5，+∞）．选择条件②，∀x ∈[1，5]使得a ＞﹣x 2+4x 恒成立，则a ＞g （x ）max ，所以a ＞4，故实数a 的取值范围是（4，+∞）．（2）当x ≥0时，F(x)=12[f(x)+f(|x|)]=12[f(x)+f(x)]=f(x)，＝x 2﹣4x +a ＝（x ﹣2）2+a ﹣4，所以F （x ）在[0，2）上单调递减，在[2，+∞）上单调递增；当x ＜0时，F(x)=12[f(x)+f(|x|)]=12[f(x)+f(−x)]=12[x 2−4x +a +(−x)2+4x +a]=x 2+a ， 所以F （x ）在（﹣∞，0）上单调递减，综上函数F （x ）的单调递增区间为[2，+∞）．21．（12分）如图，某学校欲建矩形运动场，运动场左侧为围墙，三面通道各宽2m ，运动场与通道之间由栅栏隔开．（1）若运动场面积为3200m 2，求栅栏总长的最小值；（2）若运动场与通道占地总面积为3200m 2，求运动场面积的最大值．解：（1）设矩形运动场的长、宽分别为a ，b （如图，单位：m ），由题意，ab ＝3200，所以2a +b ≥2√2ab =160，当且仅当{a =40b =80时，取“＝”， 故栅栏总长的最小值为160m ．（2）由题意（a +2）（b +4）＝3200，整理得ab +4a +2b ﹣3192＝0，而4a +2b =3192−ab ≥2√8ab =4√2ab ，故ab +4√2ab −3192≤0，令√ab =t （t ＞0），则t 2+4√2t −3192≤0，解得0＜t ≤38√2，所以√ab ≤38√2，即ab ≤2888，当且仅当{b =2a √ab =38√2，即{a =38b =76时，取“＝”， 故运动场面积的最大值为2888m 2．22．（12分）已知函数f(x)=x 2+a x+b 是奇函数，且f(−2)=−52．（1）判断并根据定义证明函数f （x ）在（0，1），（1，+∞）上的单调性；（2）设函数h （x ）＝f 2（x ）﹣2tf （x ）﹣2（t ＜0），若对∀x 1，x 2∈[13，3]，都有|h （x 1）﹣h （x 2）|≤8，求实数t 的取值范围．（1）解：因为f(−2)=−52，且f （x ）是奇函数，所以f(2)=52，所以{4+a 2+b =524+a −2+b =−52，解得{a =1b =0，所以f(x)=x +1x ． 此时，f(x)+f(−x)=x +1x +(−x)+1−x=0， 所以f （x ）是奇函数，满足要求； 函数f （x ）在（0，1）上单调递减，在（1，+∞）上单调递增， 证明如下：任取x 1，x 2∈（0，1），且x 1＜x 2，则f(x 1)−f(x 2)=(x 1+1x 1)−(x 2+1x 2)=(x 1−x 2)(x 1x 2−1x 1x 2)， 因为x 1，x 2∈（0，1），且x 1＜x 2，所以x 1﹣x 2＜0，0＜x 1x 2＜1，所以x 1x 2﹣1＜0， 所以f （x 1）﹣f （x 2）＞0，即f （x 1）＞f （x 2），所以函数f （x ）在（0，1）上单调递减；同理可证明函数f （x ）在（1，+∞）上单调递增．（2）由题意知ℎ(x)=x 2+1x 2−2t(x +1x )， 令z =x +1x ，y ＝z 2﹣2tz ﹣2，由（1）可知函数z =x +1x 在[13，1]上单调递减，在[1，3]上单调递增， 所以z ∈[2，103]，因为函数y ＝z 2﹣2tz ﹣2的对称轴方程为z ＝t ＜0，所以函数y ＝z 2﹣2tz ﹣2在[2，103]上单调递增， 当z ＝2时，y ＝z 2﹣2tz ﹣2取得最小值，y min ＝﹣4t +2；当z =103时，y ＝z 2﹣2tz ﹣2取得最大值，y max =−203t +829．所以h （x ）min ＝﹣4t +2，ℎ(x)max =−203t +829，又因为对∀x1，x2∈[13，3]都有|h（x1）﹣h（x2）|≤8恒成立，所以h（x）max﹣h（x）min≤8，即−203t+829−(−4t+2)≤8，解得t≥−13，又因为t＜0，所以t的取值范围是[−13，0)．。

2023届福建省百校联考高三上学期第一次联考数学试题一、单选题1．已知集合{}|237A x x =+<，(){}|ln 3B x y x ==+，则A B =（ ） A ．{}32x x -≤< B ．{}|32x x -<< C ．{}|32x x -<<- D ．{}32x x x -或【答案】B【分析】解不等式得到集合A ，求对数型函数的定义域得到集合B ，最后根据交集的定义求交集即可.【详解】因为{}2A x x =<，{}3B x x =>-，所以{}|32A B x x ⋂=-<<. 故选：B.2．命题“Q x ∃∈Q ”的否定是（ ）A ．Q x ∀∈QB ．Q x ∀∉QC ．∃∈x Q QD ．Q x ∀∈Q 【答案】A【分析】根据特称命题的否定即可得答案.【详解】解：因为命题“Q x ∃∈Q ”为特称命题，所以命题“Q x ∃∈Q ”的否定是：Q x ∀∈Q . 故选：A.3．青花瓷，又称白地青花瓷，常简称青花，是中国瓷器的主流品种之一.如图，这是景德镇青花瓷，现往该青花瓷中匀速注水，则水的高度y 与时间x 的函数图像大致是（ ）A ．B ．C ．D ．【答案】C【分析】根据瓷器的形状：中间粗，上下细来分析水的增高速度.【详解】由图可知该青花瓷上､下细，中间粗，则在匀速注水的过程中，水的高度先一直增高，且开始时水的高度增高的速度越来越慢，到达瓷瓶最粗处之后，水的高度增高的速度越来越快，直到注满水，结合选项所给图像，只有先慢后快的趋势的C 选项符合. 故选：C4．在四边形ABCD 中，//AB CD ，则“90BAD ︒∠=”是“四边形ABCD 为直角梯形”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】D【分析】分别判断命题的充分性和必要性，即可得到答案.【详解】若90BAD ︒∠=，则四边形ABCD 为矩形或直角梯形，若四边形ABCD 为直角梯形，则BAD ∠不一定为90︒，所以“90BAD ︒∠=”是“四边形ABCD 为直角梯形”的既不充分也不必要条件. 故选：D5．已知0a >，0b >，直线2e y x b -=+与曲线ln y x a =-相切，则11a b+的最小值是（ ） A ．16 B ．12 C ．8D ．4【答案】D【分析】设直线2e y x b -=+与曲线ln y x a =-的切点为()00,ln x x a -，求导，根据导数的几何意义求出切点处的切线方程，再结合已知方程求出,a b 的关系，再根据不等式中“1”的整体代换即可得出答案.【详解】解：设直线2e y x b -=+与曲线ln y x a =-的切点为()00,ln x x a -， 因为ln y x a =-，所以1y x'=， 切线方程为()0000011ln ln 1y x x x a x x a x x =-+-=+--， 所以21e x -=，0ln 1x a b --=，所以1a b +=，又0a >，0b >， 所以()111124b a a b a b a b a b ⎛⎫+=++=++≥ ⎪⎝⎭，当且仅当12a b ==时，等号成立， 故11a b+的最小值是4. 故选：D. 6．()sin π2cos 15ππsin 2cos 22θθθθ-+=⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭已知，则cos 2θ=（ ） A ．45-B ．35-C ．45 D ．35【答案】C【分析】应用诱导公式化简条件得cos 3sin θθ=，再由平方关系及倍角余弦公式即可求值.【详解】由sin(π)2cos 2cos sin 15ππcos 2sin sin()2cos()22θθθθθθθθ-+-==+++-，则2c o s s i n c o s 2s i n θθθθ-=+，所以cos 3sin θθ=，又222cos sin 10sin 1θθθ+==，即21sin 10θ=， 则24cos 212sin 5θθ=-=. 故选：C7．定义在R 上的偶函数()f x 满足()()40f x f x +-=，且当[]0,2x ∈时，()24f x x =-+，则()2021f =（ ） A ．4- B ．3-C ．3D ．0【答案】B【分析】依题意可得()f x 的周期为8，再由周期性计算可得. 【详解】解：由()+(4)=0f x f x -①，则(+4)+()=0f x f x -， 因为()f x 为偶函数，所以()=()f x f x -， 所以(4)()0f x f x ++=②，由①②知，(4)=(+4)=(4)f x f x f x --，所以()(8)f x f x =+，故()f x 的周期为8，所以()()()()2021=253?83=3=3f f f f --， 而()()3+43=0f f -，即()()3=1f f -，当[]0,2x ∈时，()2=+4f x x -，所以()()()()22021=3=1=1+4=3f f f ----．故选：B ．8．已知2log 3a =，35b =，则6log 15=（ ） A ．1a aba ++ B ．+1a a C ．1a abab ++ D ．1aab + 【答案】A【分析】利用换底公式用a ，b 表示lg2，lg3，然后将6log 15换底可求得答案. 【详解】解：由题意得： 因为2lg3log 3lg 2a ==，3lg51lg 2log 5lg3lg3b -=== 所以1lg2=+1ab ，lg31a ab =+，则611lg15lg3lg5lg3lg 2111log 151lg 6lg3lg 2lg3lg 2111a a abab ab a a ab ab -++-++++=====++++++.故选：A二、多选题9．已知函数()32f x x kx x a =+++有两个极值点()1212,x x x x <,则( )A ．1x 是()f x 的极大值点, 2x 是()f x 的极小值点B ．1213x x +=C ．1213x x =D．k <【答案】AC【分析】求导，根据导函数有两个变号零点分析即可【详解】()2321f x x kx '=++,因为()f x 存在两个极值点()1212,x x x x <,所以24120k ->解得k >k <当()1,x x ∈-∞和()2,x +∞时,()0f x '>,()f x 单调递增 当()12,x x x ∈时,()0f x '<,()f x 单调递减 故1x 是()f x 的极大值点, 2x 是()f x 的极小值点 且1223+=-kx x ,1213x x = 故选：AC10．已知函数()()πsin 0,0,02f x A x A ωϕωϕ⎛⎫=+>><< ⎪⎝⎭）的部分图像如图所示，则（ ）A ．3A =，3ω=，6π=ϕ B ．π62f ⎛⎫= ⎪⎝⎭C ．直线3π4x =是()f x 图像的一条对称轴 D ．函数π4f x ⎛⎫+ ⎪⎝⎭在π0,3⎛⎫ ⎪⎝⎭上单调递减【答案】BC【分析】由函数的图像的顶点坐标求出A ，由周期求出ω，代点求出φ的值，可得f （x ）的解析式，再利用正弦函数的图像和性质，得出结论． 【详解】由题可知，3A =，()f x 的最小正周期2π45π5π2π512123T ω⎛⎫==⨯+= ⎪⎝⎭，解得3ω=，5π5π3sin 3124f ϕ⎛⎫⎛⎫=+=- ⎪ ⎪⎝⎭⎝⎭，则5π3π2π,Z 42k k ϕ+=+∈，又π02ϕ<<，所以π4ϕ=，A 不正确；()π3sin 34f x x ⎛⎫=+ ⎪⎝⎭π3π3sin 64f ⎛⎫== ⎪⎝⎭B 正确；当3π4x =时，π5π342x +=，所以直线3π4x =是()f x 图像的一条对称轴，C 正确；πsin 34f x x ⎛⎫+=- ⎪⎝⎭，当π03x <<时，03πx <<，函数π4f x ⎛⎫+ ⎪⎝⎭不单调，D 不正确．故选：BC11．若0c b a <<<，则（ ） A ．a c b c -<-B ．c b b a < C ． c b c a a c +>+D ．1a b ca b b c a c++>+++ 【答案】BCD【分析】利用不等式性质可判断AB ，作差比较可判断C ，利用放缩法可判断D. 【详解】b a <，由不等式的性质可得，b c a c -<-，故A 错误；0c b a <<<，||||b a ∴>，0c b ->->，||||c b b a ∴->-，即c b b a <，故B 正确； ()()()()()()b a c a b c c b a b b c a a c a a c a a c a a c ++-+-=-=++++，由0c b a <<<，得0b a -<，0a c +<，所以()()0c b a a a c ->+，即b b ca a c+>+，C 正确；因为a a ab a bc >+++，b b b c a b c >+++，c ca c ab c>+++，所以1a b c a b c a b b c a c a b c a b c a b c++>++=+++++++++，D 正确． 故选：BCD12．已知58ln 2a =-，44ln3b =-，54e 4c =-，则（ ） A ．b a > B ．c a >C ．b c >D ．a c >【答案】ABC【分析】构造函数()e 41xf x x =-+，利用导数得()f x 单调性，构造()ln 1g x x x =-+确定比较5ln3<<ln44，进而可得,,a b c 的大小关系.【详解】设函数()e 41x f x x =-+，则()e 4xf x '=-．由()0f x '>．得ln 4x >；由()0f x '<，得ln 4x ≤．则()f x 在(),ln 4-∞上单调递减，在()ln 4,+∞上单调递增． 设()ln 1g x x x =-+，则()111xg x x x-'=-=．()0g x '>，得01x <<；由()0g x '<，得1x >.所以()g x 在()0,1上单调递增，在()1,+∞上单调递减，所以()()10g x g ≤=，即ln 1x x ≤-，则33ln 1e e≤-，故35ln 3e 4≤<.因为ln 1x x ≤-，所以11ln1x x ≤-，所以1ln 1x x ≥-（当且仅当=1x 时，等号成立），所以4e ln 1e 4>-，即e 5ln4244>->.因为()ln 4a f =，()ln 3b f =，54c f ⎛⎫= ⎪⎝⎭，且5ln3<<ln44，()f x 在(),ln 4-∞，上单调递减，所以b c a >>. 故选：ABC.三、填空题13．所数y =______.【答案】(]3,3-【分析】根据分母不为零，偶次方根的被开方数大于等于零得到不等式组，解得即可.【详解】解：因为y =290+30x x -≥≠⎧⎨⎩，解得33x -<≤，即函数的定义域为(]3,3-； 故答案为：(]3,3-14．函数()22x f x a +=+（0a >，且1a ≠）的图象过定点P .则点P 的坐标是_________.【答案】()2,3-【分析】令20x +=，可计算得()0223f a -=+=，从而可得定点坐标.【详解】当20x +=，即2x =-时，()0223f a -=+=，所以函数()f x 的图象过定点()2,3-. 故答案为：()2,3-15．已知正数a ，b 满足①27ab a b ++=，②2a b ab +=两个条件中的一个，则+a b 的最小值为______.【答案】选①：3；选②：【分析】根据所选条件利用基本不等式计算可得. 【详解】解：因为0a >，0b >，若选①，由27ab a b ++=，可得()()219a b ++=，因为()()221212a b a b +++⎛⎫++≤ ⎪⎝⎭，所以()2336a b ++≥，所以3a b +≥，当且仅当213a b +=+=，即=1a 、=2b 时取等号；若选②，2a b ab +=，可得211b a+=，所以()212333a b a b a b b a b a ⎛⎫+=++=++≥++ ⎪⎝⎭当且2a bb a=，即1a =，2b = 故答案为：选①：3；选②：16．已知函数241,0,()22,0,x x x x f x x ⎧--≥=⎨-<⎩若方程2[()]2()40f x af x -+=有5个不同的实数解，则实数a 的取值范围为___________． 【答案】522a -<<- 【分析】令()t f x =，则2240t at -+=在(5,2)--，(2,1)--上各有一个实数解或2240t at -+=的一个解为1-，另一个解在(2,1)--内，或2240t at -+=的一个解为2-，另一个解在(2,1)--内.【详解】函数()f x 的大致图象如图所示，对于方程2[()]2()40f x af x -+=有5个不同的实数解，令()t f x =，则2240t at -+=在(5,2)--，(2,1)--上各有一个实数解或2240t at -+=的一个解为1-，另一个解在(2,1)--内，或2240t at -+=的一个解为2-，另一个解在(2,1)--内， 当2240t at -+=在(5,2)--，(2,1)--上各有一个实数解时，设2()24g t t at -=+，则()()()24160,2840,1520,529100,a g a g a g a ⎧=->⎪-=+<⎪⎨-=+>⎪⎪-=+>⎩解得522a -<<-，当2240t at -+=的一个解为1-时，52a =-，此时方程的另一个解为4-，不在(2,1)--内，不满足题意， 当2240t at -+=的一个解为2-时，2a =-，此时方程的另一个解为2-，不在(2,1)--内，不满足题意， 综上可知，实数a 的取值范围为522a -<<-，故答案为：522a -<<-．四、解答题17．设集合{}2340A x x x =--≤， {}221B x a x a =-<<+.(1)当0a =时，求A B ； (2)若A B A ⋃=，求a 的取值范围. 【答案】(1){}11A B x x ⋂=-≤< (2)(]3,31,2⎡⎤-∞-⋃⎢⎥⎣⎦.【分析】（1）先求解集合A ，当0a =时，得集合B ，直接求解交集即可；（2）利用集合之间的关系确定B A ⊆，分类讨论当B =∅时，当B ≠∅时，分别满足B A ⊆，得a 的取值范围.【详解】(1)解：由题意得{}{}234014A x x x x x =--≤=-≤≤.当0a =时，集合{}21B x x =-<<， 则{}11A B x x ⋂=-≤<.(2)解：因为A B A ⋃=，所以B A ⊆.①当B =∅时，则221a a -≥+，解得3a ≤-；②当B ≠∅时，则22121421a a a a -<+⎧⎪+≤⎨⎪-≥-⎩，解得312a ≤≤.综上，a 的取值范围为(]3,31,2⎡⎤-∞-⋃⎢⎥⎣⎦.18．已知幂函数()()211m m m f x x +=+-在()0,+∞上是减函数.(1)求()f x 的解析式；(2)若()()11521mma a ->-，求a 的取值范围. 【答案】(1)()1f x x= (2)（2，5）.【分析】（1）根据幂函数的性质可求得m 的值.（2）根据幂函数的单调性解不等式求参数. 【详解】(1)解：由题意得：根据幂函数的性质可知211m m +-=，即220m m +-=，解得2m =-或=1m . 因为()f x 在()0,∞+上是减函数，所以10+<m ，即1m <-，则2m =-.故()11x xf x -==. (2)由（1）可得2m =-，设()12g x x -=，则()g x 的定义域为()0,+∞，且()g x 在定义域上为减函数.因为()()1122521a a --->-，所以50,210,521,a a a a ->⎧⎪->⎨⎪-<-⎩解得25a <<.故a 的取值范围为（2，5）.19．已知函数()cos (0)f x x x ωωω=->．(1)若()f x 在(0,π)上有且仅有2个极值点，求ω的取值范围； (2)将()f x 的图象向右平移π12个单位长度后，再将所得图象各点的横坐标缩短为原来的12，纵坐标不变，得到函数()g x 的图象，若()g x 的最小正周期为π，求()g x 的单调递减区间．【答案】(1)58,33⎛⎤⎥⎝⎦；(2)3π7ππ,π()88k k k ⎡⎤++∈⎢⎥⎣⎦Z .【分析】（1）根据辅助角公式，结合函数极值的性质进行求解即可；（2）根据正弦型函数图象变换性质，结合正弦型函数的周期公式、单调性进行求解即可.【详解】(1)π()2sin 6f x x ω⎛⎫=- ⎪⎝⎭，因为0>ω，所以当π()0,x ∈时，πππ,π666t x ωω⎛⎫=-∈-- ⎪⎝⎭，依题意可得，函数2sin y t =在ππ,π66ω⎛⎫-- ⎪⎝⎭上有且只有2个极值点，则3ππ5ππ262ω<-≤，解得5833ω<≤，故ω的取值范围是58,33⎛⎤⎥⎝⎦；(2)依题意可得，ππ()2sin 2612g x x ωω⎛⎫=-- ⎪⎝⎭， 因为()g x 的最小正周期为π，所以2ππ2ω=，即1ω=， 所以π()2sin 24g x x ⎛⎫=- ⎪⎝⎭，令ππ3π2π22π242k x k +≤-≤+，k ∈Z ， 则3π7πππ88k x k +≤≤+，k ∈Z ， 故()g x 的单调递减区间为3π7ππ,π()88k k k ⎡⎤++∈⎢⎥⎣⎦Z ． 20．据国家气象局消息，今年各地均出现了极端高温天气.漫漫暑期，空调成了很好的降温工具，而物体的降温遵循牛顿冷却定律.如果某物体的初始温度为0T ，那么经过t 分钟后，温度T 满足()012t ha a T T T T ⎛⎫-=- ⎪⎝⎭，其中a T 为室温，h 为半衰期.为模拟观察空调的降温效果，小明把一杯75C 的茶水放在25C o 的房间，10分钟后茶水降温至50C .（参考数据：lg 20.30,lg30.48≈≈）(1)若欲将这杯茶水继续降温至35C ，大约还需要多少分钟？（保留整数）(2)为适应市场需求，2022年某企业扩大了某型号的变频空调的生产，全年需投入固定成本200万元，每生产x 千台空调，需另投入成本()f x 万元，且()2460,040,36003013700,40.x x x f x x x x ⎧+<<⎪=⎨+-⎪⎩…已知每台空调售价3000元，且生产的空调能全部销售完.问2022年该企业该型号的变频空调的总产量为多少千台时，获利最大？并求出最大利润.【答案】(1)13分钟(2)当该企业该型号的变频空调总产量为30千台时，获利最大，最大利润为3400万元.【分析】（1）由题意列方程求解（2）由题意得出利润与x 的函数关系，结合基本不等式求解最值【详解】(1)由题意可得()101502575252h⎛⎫-=⨯- ⎪⎝⎭，解得10h =.设经过t 分钟，这杯茶水降温至35C ，则()101352550252t ⎛⎫-=⨯- ⎪⎝⎭， 解得2110log 51010213lg2t ⎛⎫=-=⨯-≈ ⎪⎝⎭（分钟）.故欲将这杯茶水降温至35C ，大约还需要13分钟.(2)设2022年该企业该型号的变频空调的利润为()W x ，当040x <<时，()223002004604(30)3400W x x x x x =---=--+，当30x =时，()W x 取得最大值3400万元；当40x …时，()3600360030020030137003500W x x x x x x ⎛⎫=---+=-+ ⎪⎝⎭，因为3600120x x+…，当且仅当60x =时，等号成立， 则当60x =时，()W x 取得最大值3380万元.因为34003380>，所以当该企业该型号的变频空调总产量为30千台时，获利最大，最大利润为3400万元.21．已知函数()431f x x ax =+-．(1)若()f x 在[]1,2上有零点，求a 的取值范围．(2)试问直线52y x =-+能否为曲线()=y f x 的一条切线？说明你的理由．【答案】(1)15,08⎡⎤-⎢⎥⎣⎦(2)答案见解析【分析】（1）由()=0f x 得31a x x =-，构造函数31()(12)g x x x x =-剟，求出()g x 的值域即可得解；（2）设切点为(,52)m m -+，由题意列出关于m 的方程组，得出41090m m -+=，由=1m 是该方程的一个解，即可得出结论．【详解】(1)由()=0f x ，得31a x x =-， 设函数31()(12)g x x x x =-剟，则()g x 为减函数， 因为15(1)0,(2)8g g ==-， 所以()g x 的值域为15,08⎡⎤-⎢⎥⎣⎦， 因为()f x 在[1,2]上有零点，所以a 的取值范围是15,08⎡⎤-⎢⎥⎣⎦． (2)直线52y x =-+可能为曲线=()y f x 的一条切线．证明如下：32()43f x x ax '=+，设切点为(,52)m m -+，则32434+3=5,+1=5+2,m am m am m ---⎧⎨⎩消去a ，得41090m m -+=，因为=1m 是方程41090m m -+=的一个解，所以该方程至少有一个解，当=1m 时，3a =-，直线52y x =-+为曲线=()y f x 的一条切线．故直线52y x =-+可能为曲线=()y f x 的一条切线．22．已知函数()()22e 21x f x x a x =-+--(1)若0a =，证明：当0x >时，()0f x >.(2)若()0,x ∀∈+∞，()()ln 1f x a x >+，求a 的取值范围.【答案】(1)证明见解析(2)[)2,-+∞【分析】（1）求导得到()()222e 222e 1x x f x x x =--=--'，构造()2e 1x g x x =--，求导，得到函数的单调性，从而得到()()00g x g >=，进而得到()0f x '>，()f x 在()0,+∞上单调递增，证明出结论；（2）利用同构构造()2ln h x x a x =+，得到()()e 1x h h x >+，证明出e 11x x >+>，结合()22x a h x x+'=，分2a ≥-与2a <-讨论得到答案. 【详解】(1)证明：因为()22e 21x f x x x =---，所以()()222e 222e 1x x f x x x =--=--'今函数()2e 1x g x x =--，则()22e 1x g x '=-当0x >时，()0g x '>，所以()g x 在()0,+∞上单调递增，故()()00g x g >=，即()0f x '>，则()f x 在()0,+∞上单调递增.故当0x >时，()()00f x f >=(2)()()ln 1f x a x >+等价于()()22e 21ln 1x x a x a x -+-->+等价于()()22e ln 1n e l 1x x a a x x +>+++令函数()2ln h x x a x =+，则()()22e lne ln 11x x a a x x +>+++等价于()()e 1x h h x >+ 令函数()e 1x x x ϕ'=--，则()e 1x x ϕ'=-．当(),0x ∈-∞时，()0x ϕ'<，()x ϕ单调递减，当()0,x ∈+∞时，()0x ϕ'>，()x ϕ单调递增，故()()00x ϕϕ≥=，即e 11x x >+>恒成立．若2a ≥-，则()2220a x a h x x x x+'=+=≥在()1,+∞上恒成立，()h x 单调递增， ()()e 1x h h x >+恒成立．符合题意.若2a <-，则()222a x a h x x x x x =+=='+，当x ⎛∈ ⎝时，()0h x '<，()h x 单调递减；当x ∞⎫∈+⎪⎪⎭时，()0h x '>，()h x 单调递增．此时e 1h h h ⎛⎛⎫=≤ ⎪ ⎪ ⎝⎭⎝⎭，这与()()e 1x h h x >+恒成立矛盾，不符合题意． 综上所述，a 的取值范为[)2,-+∞．【点睛】同构是一种重要方法，常常用在处理复杂的函数，且同时存在e x 与ln x 的函数，要注意总结常用的同构函数.。

2024-2025学年湖南省益阳市箴言中学高二上学期9月月考数学试卷一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知A={x|x≤1}，B={x|x−2x−a≤0}，若A∪B={x|x≤2}，则实数a的取值范围是( )A. a≥2B. a≤2C. a≥1D. a≤12.已知空间向量a=(1,0,3),b=(2,1,0),c=(5,2,z)，若a,b,c共面，则实数z的值为( )A. 4B. 3C. 2D. 13.在▵ABC中，若AB⋅BC−AB2=0，则▵ABC的形状一定是( )A. 等边三角形B. 直角三角形C. 锐角三角形D. 钝角三角形4.命题p:f(x)={x2+2ax−7,−1≤x≤2(a+4)ln(x+2)−a−1,−2<x<−1在x∈(−2,2]上为减函数，命题q:g(x)=ax+4x−1在(1,+∞)为增函数，则命题p是命题q的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件5.某学校10位同学组成的志愿者组织分别由李老师和张老师负责，每次献爱心活动均需该组织4位同学参加．假设李老师和张老师分别将各自活动通知的信息独立、随机地发给4位同学，且所发信息都能收到，则甲同学收到李老师或张老师所发活动通知信息的概率为( )A. 25B. 1225C. 1625D. 456.定义运算：|a1&a2a3&a4|=a1a4−a2a3，将函数f(x)=|3&sinωx1&&cosωx|(ω>0)的图像向左平移2π3个单位所得图像对应的函数为偶函数，则ω的最小值是( )A. 54B. 14C. 74D. 347.已知f(x)是定义在实数集R上的函数，在(0,+∞)内单调递增，f(2)=0，且函数f(x+1)关于点(−1,0)对称，则不等式x⋅f(1−x)<0的解集是( )A. (−∞,−2)∪(−1,0)∪(2,+∞)B. (−∞,−2)∪(2,+∞)C. (−1,0)∪(1,3)D. (−∞,−1)∪(0,1)∪(3,+∞)8.已知椭圆C1与双曲线C2有共同的焦点F1，F2，P是椭圆C1与双曲线C2的一个公共点，且∠F1PF2=π3，其离心率分别为e1，e2，则3e21+e22的最小值为( )A. 3B. 4C. 6D. 12二、多选题：本题共3小题，共18分。

2023~2024学年第二学期高三3月月考试卷数学考生注意：1．本试卷分选择题和非选择题两部分。

满分150分，考试时间120分钟。

2．答题前，考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚。

3．考生作答时，请将答案答在答题卡上。

选择题每小题选出答案后，用2B 铅笔把答题卡上应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效。

4．本卷命题范围：高考范围。

一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是合题目要求的。

1．已知集合(){6,},{lg 20}A xx x B x x =<∈=-<N ∣∣，则()R A B = ð（ ）A ．{}1,2,3,4,5B ．{}0,1,2,3,4,5C ．{}0,1,4,5D ．{02x x ≤≤∣，或36}x ≤<2．已知复数512i z =+，则2i z --=（ ）A B ．C 1D 3．已知D 是ABC △的AB 边上一点，若()1,,2AD DB CD CA CB λμλμ==+∈R ，则λμ-=（ ）A ．23B ．13C ．0D ．13-4．已知函数()2log ,02,23,2,x x f x x x <≤⎧=⎨->⎩若()()1210f a f a +--≥，则实数a 的取值范围是（ ）A ．(],2-∞B ．[)2,+∞C ．[]2,6D ．1,22⎛⎤ ⎥⎝⎦5．已知12,F F 是椭圆()2222:10x y C a b a h+=>>的两个焦点，若C 上存点P ，使12PF PF =则C 的离心率的取值范围是（）A ．10,3⎛⎤ ⎥⎝⎦B ．10,2⎛⎤ ⎥⎝⎦C ．1,13⎡⎫⎪⎢⎣⎭D ．1,12⎡⎫⎪⎢⎣⎭6．已知各项都是正数的等比数列{}n a 的前3项和为21，且312a =，数列{}n b 中，131,0b b ==，若{}n n a b +是等差数列，则12345b b b b b ++++=（ ）A ．153B ．91C ．33D ．－337．已知e 是自然对数的底数，212e sin ,e ln2a b c ===，则（ ）A ．a b c >>B ．c a b>>C ．a c b >>D ．b c a >>8．在棱长为4的正方体1111ABCD A B C D -中，E 是CD 的中点，F 是1CC 上的动点，则三棱锥A DEF -外接球半径的最小值为（）A ．3B ．CD 二、选择题：本题共3小题，每小题6分，共18分。

影响密封性能的其它因素1）O形圈的硬度O形圈材料硬度是评定密封性能最重要的指标。

硬度决定了O形圈的压缩量和沟槽最大允许挤出间隙。

由于邵氏A70的丁晴密封都能满足大部分的使用条件，故对密封材料不作特殊说明，一般提供邵氏A70的丁晴橡胶。

2）挤出间隙最大允许挤出间隙gmax和系统压力、O形圈截面直径以及和材料的硬度有关。

通常，工作压力越高，最大允许挤出间隙gmax取值越小。

如果间隙g超过允许范围，就会导致O 形圈被挤出损坏。

最大允许挤出间隙gmax压力MPa O形圈截面直径W1.782.623.53 5.33 7.00邵氏硬度A70≤3.50 0.08 0.09 0.10 0.13 0.15≤7.00 0.05 0.07 0.08 0.09 0.10≤10.50 0.03 0.04 0.05 0.07 0.08邵氏硬度A80≤3.50 0.10 0.13 0.15 0.18 0.20≤7.00 0.08 0.09 0.10 0.13 0.15≤10.50 0.05 0.07 0.08 0.09 0.10≤14.00 0.03 0.04 0.05 0.07 0.08≤17.50 0.02 0.02 0.03 0.03 0.04邵氏硬度A90≤3.50 0.13 0.15 0.20 0.23 0.25≤7.00 0.10 0.13 0.15 0.18 0.20≤10.50 0.07 0.09 0.10 0.13 0.15≤14.00 0.05 0.07 0.08 0.09 0.10≤17.50 0.04 0.05 0.07 0.08 0.09≤21.00 0.03 0.04 0.05 0.07 0.08≤35.00 0.02 0.03 0.03 0.04 0.04注：1、当压力超过5MPa时，建议使用挡圈；2、对静密封应用场合，推荐配合为H7/g6。

3）压缩永久变形评定O形圈密封性能的另一指标，即该材料的压缩永久变形。

in2o3的晶格常数晶格常数是物理和化学科学中特定晶体结构的重要参数，它们描述了原子或分子单元之间的平均距离，并影响晶体的热力学性质，结构性质，电学性质，化学性质等。

铟锡酸铋（In2O3）是一种广泛应用于传感器，电子元器件，新能源和太阳能电池中的重要电子器件材料。

本文介绍In2O3的晶格常数，其价值在于它可以提供In2O3的晶体结构的定性和定量的信息。

In2O3是一种重要的稀土氧化物，它以双玻璃状结晶形式存在，在室温下具有五角晶体结构，空间群为Pa3，属于一种非等的晶体结构，晶胞方向的参数为a=5.362，b=5.580，c=7.741，=90.00°，β=112.70°，γ=90.00°。

其中，a、b、c代表晶胞四维空间坐标系中原子位置的投影轴线，α、β、γ表示晶体四维空间中原子位置的夹角大小。

因此，In2O3的晶格常数由以下六个参数组成：a=5.362，b=5.580，c=7.741，=90.00°，β=112.70°，γ=90.00°。

除了晶格参数，In2O3的其它物理和化学特性也很重要，包括熔点、比表面积、热和光学性质、光电子能谱、碳酸盐反应和携带电荷反应等。

In2O3的熔点约为1450℃，比表面积约为14.5 m2 /g，光谱上In2O3具有宽带离子跃迁现象，而电子能谱表明In2O3是p型半导体，具有良好的非晶状态结构，在低温下具有良好的电学性能。

此外，In2O3还可以反应吸收碳酸盐的反应，并且可以用于携带电荷反应，从而使其具有传感、存储等功能。

In2O3晶体结构的晶格常数可以用来研究In2O3材料的物理和化学性质，包括热力学性质，结构性质，电学性质，化学性质等。

因此，掌握In2O3的晶格参数，对于研究其物理和化学性质和应用价值具有重要意义。

In2O3的晶格参数往往是在实验测定的材料结构时发现的，因此，准确描述In2O3的晶体结构需要对其进行实验测定。

PSA 标致－雪铁龙集团C21 4360重复使用汽车零件镶嵌式圆头螺母带凸缘的类型页码 1/1无使用限制目录1 主题内容 (1)2 螺母的选择 (1)3 螺母的定义 (2)3.1 标准螺母 (2)3.2 专用螺母（非攻丝） (2)4 预冲孔的定义 (3)5 规范 (3)6 螺纹的供应 (4)7 优先螺母的编号 (4)8 标准演变和引用文件 (5)8.1 标准演变 (5)8.1.1 创建 (5)8.1.2 修改内容 (5)8.2 引用文件 (5)8.2.1 PSA文件 (5)8.2.2 外部文件 (5)8.3 等效于 (5)8.4 符合于 (5)8.5 关键词 (5)1 主题内容本标准规定了镶嵌式带凸缘类型的圆头螺母的特性，规定的镶嵌式带凸缘类型的圆头螺母为ISO公制螺纹，非攻丝，包括螺母7/16-20-UNF。

螺母必须同时符合标准C21 4350中规定的特性要求。

2 螺母的选择只要编号出现在优先选择编号章节的表上的编号螺母都是合适的，除非技术上不可行。

如果必须要与其他质量级别、其他保护层或者其他尺寸的相配套，可咨询当地的“代表零件的标准代表”（每个研究基地都有），获得零件的编号。

3 螺母的定义3.1 标准螺母DD±0,1d2±0,15d3±0,2d4-0,5L1±0,2L2±0,2L3±0,2M6 9,7 7,5 9,7 16,0 10,5 7,5 3,5M8 12,8 9,6 12,8 21,1 12,7 9,1 4,6M10 15,0 11,5 15,0 26,0 15,0 11,0 5,5 M12 16,2 13,5 16,2 28,0 17,0 13,0 7,03.2 专用螺母（非攻丝）出于重量的考虑，不能使用这种螺母。

Pour vis * dxpas D ±0,05D±0,1d2± 0,1d3± 0,1d4±0,1L1±0,1L2±0,1L3±0,16x1,00 5,5 9,7 7,5 9,7 16,0 10,5 7,5 3,5 8x1,25 7,5 12,8 9,5 12,8 21,0 12,5 9,0 4,5 注意：材料与攻丝螺母的材料相同（参见标准螺母章节）。

1.下列哪个表达式是二次根式的标准形式？A.√(2x+1)B.√(x2+2x+1)C.√(x2) （答案）D.√(x3)2.若一个三角形的两边长分别为3和4，则第三边的长度可能是？A.8B. 2C. 6 （答案）D. 13.下列哪个方程是一元二次方程？A.x2 + 2x = yB.x2 - 4 = 0 （答案）C.x + y = 2D.x3 - 2x = 14.已知直角三角形的两直角边长为a和b，斜边长为c，则下列关系正确的是？A. a + b = cB.a2 + b2 = c2 （答案）C.a2 - b2 = c2D.a2 * b2 = c25.下列哪个点位于函数y = 2x + 1的图像上？A.(0, -1)B.(1, 3) （答案）C.(2, 0)D.(-1, 2)6.若一个正方形的面积为16，则其边长为？A. 2B. 4 （答案）C.8D.167.下列哪个不等式组有解？A.{ x > 3, x < 2 }B.{ x ≥ 3, x ≤ 2 }C.{ x > 3, x ≥ 4 } （答案）D.{ x < 3, x > 4 }8.已知一次函数的图像与y轴的交点为(0, -2)，且斜率为3，则该函数的解析式为？A.y = 3x + 2B.y = 3x - 2 （答案）C.y = -3x + 2D.y = -3x - 29.下列哪个数是无理数？A.√4B. 3.14C.π（答案）D.010.若一个圆的半径为r，则其面积为？A.2πrB.πr2 （答案）C.πr3D.2πr2。

辽宁省丹东市2024年数学（高考）统编版真题(培优卷)模拟试卷一、单项选择题（本题包含8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题几何体的三视图如图所示,则这个几何体的直观图可以是（）A．B．C．D．第(2)题设，且，记，则的最小值为A．1B．C．2D．第(3)题若集合，则（）A．B．C．D．第(4)题已知集合，，则（）A．B．C．D．第(5)题已知有公共焦点的椭圆与双曲线的中心为原点，焦点在x轴上，左右焦点分别为，，且它们在第一象限的交点为P，是以为底边的等腰三角形.若，双曲线的离心率的取值范围为，则该椭圆的焦距的取值范围是（）A．B．C．D．第(6)题我国元代瓷器元青花团菊花纹小盏如图所示，撇口，深弧壁，圈足微微外撇，底心有一小乳突．器身施白釉，以青花为装饰，釉质润泽，底足露胎，胎质致密，碗内口沿饰有一周回纹，内底心书有一文字，碗外壁绘有一周缠枝团菊纹，下笔流畅，纹饰洒脱．该元青花团菊花纹小盏口径8.3厘米，底径2.8厘米，高4厘米，它的形状可近似看作圆台，则其侧面积约为（）（单位：平方厘米）A．B．C．D．第(7)题已知函数，其中，对于任意且，均存在唯一实数，使得，且，若有4个不相等的实数根，则的取值范围是A．B．C．D．第(8)题若，，则的元素个数为A．0B．1C．2D．3二、多项选择题（本题包含3小题，每小题6分，共18分。

在每小题给出的四个选项中，至少有两个选项正确。

全部选对的得6分，选对但不全的得3分，有选错或不答的得0分） (共3题)第(1)题如图，为圆的一条直径，点是圆周上的动点，是直径上关于圆心对称的两点，且，则（）A．B．C．D．第(2)题已知样本数据：1，2，3，4，5，6，7，8，9，则（）A．极差为8B．方差为6C．平均数为5D．80百分位数为7第(3)题下列双曲线的渐近线方程为的是（）A．B．C．D．三、填空（本题包含3个小题，每小题5分，共15分。

1大同中学2024学年第一学期高三年级数学周测2024.09一、填空题（本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分） 1．不等式221x −>的解集为________． 2．i 为虚数单位，若复数41iz i=−，则Im z =________． 3．在6的二项展开式中，常数项为________． 4．若双曲线221y x b+=的离心率为2，则b =________． 5．设a R ∈，若抛物线214y x a =+的焦点为坐标原点，则a =________．6．下表中是某公司一年中每月的广告投入费用与销售额的情况，设广告投入费用为x （单位：万元），销售额为y （单位：万元），则y 关于x 的回归方程为_________．（回归系数精确到0.01）7．设x R ∈，若52345012345(3)(1)(1)(1)(1)(1)x a a x a x a x a x a x +=++++++++++，则12345a a a a a −+−+=________．8．在△ABC 中，E ，F 分别是线段AB ，AC 的中点，点P 在直线EF 上，若△ABC 的面积为2，则2PB PC BC ⋅+的最小值是________．29．将由曲线1x x y y +=、1y =−、0x =所围成的封闭区域绕y 轴旋转一周后得到的旋转体记为Ω，则该旋转体Ω的体积为________．10．某医药研究所将在7天时间内检测3种不同抗生素类药品、3种不同抗过敏类药品、1种降压类药品.若每天只能检测1种药品，且降压类药不在第1天或第7天检测，3种不同抗生素类药品中恰有2种在相邻两天被检测，则不同的检验时间安排方案的个数为________．11．如图，半椭圆22221(0)x y x a b +=≥与半椭圆22221(0)y x x b c+=<组成的曲线称为“果圆”，其中222a b c =+，0a >，0b c >>．“果圆”与x 轴的交点分别为1A 、2A ，若在“果圆”y 轴右侧部分上存在点P 使得122πA PA ∠=，则c a 的取值范围为________．12．已知三角形ABC 的面积为2024，110AC =，341123tan tan A B+=，则AB =________． 二、选择题（本题共4题，满分18分，其中第13-14题每题4分，第15-16题每题5分）．13．事件A 与B 独立，A 、B 分别是A 、B 的对立事件，则下列命题中成立的是（ ） A ．()()()P AB P A P B = B ．()()()P AB P A P B =+C ．()()()P AB P A P B =D ．()()1()P A B P A P B =+−14．已知等差数列{}n a 中，615a a=，且公差0d <，则其前n 项和取得最大值时n 的值为（ ）3A ．8B ．9C ．10D ．1115．经过点()1,2P −可以作与曲线3230x x y −−=相切的不同直线共有（ ） A ．0条 B ．1条 C ．2条 D ．3条16．如图所示，四面体ABCD 的体积为V ，点M 为棱BC 的中点，点E 、F 分别为线段DM 的三等分点，点N 为线段AF 的中点，过点N 的平面α与棱AB 、AC 、AD 分别交于O 、P 、Q ，设四面体AOPQ 的体积为V '，则V V'的最小值为（ ） A ．14 B ．18 C ．116 D ．127三、解答题（本大题共有5题，满分78分）．17．（本题满分14分）（本题共有2个小题，第1小题满分6分，第2小题满分8分） 已知函数()sin()f x x =ω+ϕ，其中0ω>，2πϕ<（1）若3cos cos sin sin 044ππϕ−ϕ=，求ϕ的值；（2）在（1）的条件下，若函数()f x 的图像的相邻两条对称轴之间的距离等于3π，求函数()f x 的解析式；并求最小正实数m ，使得函数()f x 的图像象左平移m 个单位所对应的函数是偶函数．418．（本题满分14分）（本题共有2个小题，第1小题满分6分，第2小题满分8分） 如图，在直角梯形ABCD 中，∥AB DC ，90ABC ∠=︒，22AB DC BC ==，E 为AB 的中点，沿DE 将△ADE 折起，使得点A 到点P 位置，且PE EB ⊥，M 为PB 的中点，N 是线段BC 上的动点．（1）求证：平面EMN ⊥平面PBC ；（2）当三棱锥M EBN −与四棱锥P EBCD −的体积之比为16M EBN P EBCD V V −−=时，求直线EN 与平面PBC 所成角的正弦值．19．（本题满分14分）（本题共有3个小题，第1小题满分6分，第2小题满分8分）某网站的电子邮箱如果在一天内出现3次密码尝试错误，该邮箱将被锁定24小时．某同学忘记了该邮箱密码，但可以确定该邮箱的正确密码是他常用的6个密码之一，他决定从中不重复地随机选择，逐个进行尝试．若密码正确，则结束尝试；否则继续尝试，直至该邮箱被锁定．（1）求当天该同学的邮箱被锁定的概率；（2）设当天该同学尝试邮箱密码的次数为X，求X的分布及[]D X的值．E X，[]20．（本题满分18分）（本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分）已知双曲线22Q．Γ−=的左、右顶点分别为点A、B，M为双曲线Γ上的动点，点(0,2) x y:1（1）求点M到Γ的两条渐近线的距离之积；（2）求经过点Q的双曲线Γ的切线方程；（3）设点P在第一象限，且在渐近线的上方，直线PA，PB分别与y轴交于点C，D．过点P作Γ的两条切线，分别与y轴交于点E，F（E在F的上方），证明：CE DF=．5621．（本题满分18分）（本题共有3个小题，第1、2小题满分各6分，第3小题满分8分）． 设2ea <，已知函数()y f x =的解析为()2()(2)22x f x x e a x x =−−−+． （1）当0a =时，求函数()y f x =的最小值； （2）证明当(],0a ∈−∞时函数()f x 至多有两个零点；（3）如果函数()y f x =有3个不同的零点，分别设为1x 、2x 、3x ，求实数a 的取值范围；如果130x x ⋅<，进一步证明存在唯一的实数a ，使得1x 、2x 、3x 成等差数列．7参考答案一、填空题1.(()),1,1−∞⋃−⋃+∞; 2.2; 3.160; 4.3−; 5.1−;6.17.68284.88y x =+; 7.31;8. 9.2π; 10.2016；11.12⎛ ⎝⎭12.46或二、选择题13. C 14.C 15.D 16.C 三．解答题 17.（1）4πϕ=（2）512m π=18.（1）证明略（219.（1）12P = （2）()()57,212E X D X ==20．【答案】（1）12（2101022y y x x +−=+−=或（3）证明略21．（本题满分18分）（本题共有3个小题，第1、2小题满分各6分，第3小题满分8分）． 设2ea <，已知函数()y f x =的解析为()2()(2)22x f x x e a x x =−−−+． （1）当0a =时，求函数()y f x =的最小值； （2）证明当(],0a ∈−∞时函数()f x 至多有两个零点；8（3）如果函数()y f x =有3个不同的零点，分别设为1x 、2x 、3x ，求实数a 的取值范围；如果130x x ⋅<，进一步证明存在唯一的实数a ，使得1x 、2x 、3x 成等差数列． 【答案】（1）()()12min f x f e==−（2）证明略（3）110222a ,,e ⎛⎫⎛⎫∈⋃− ⎪ ⎪⎝⎭⎝⎭，证明见解析【解析】(1) 当0a =时,()()22x f x x e =−+, 则()()'1x f x x e =−, 令()'0f x <, 可得1x <, 此时函数()f x 单调递减,令()'0f x >, 可得1x >, 此时函数()f x 单调递增,则()()12min f x f e ==−. (2) 证明略（3）因为()()()2222x f x x e a x x =−−−+, 则()()()()()'12112x x f a x x e a x x e =−−=−−− ①当02ea <<时, 由()'0f x =可得1x =或21x ln a =<, 列表如下:由题意可知，()f x 有 3 个不同的零点，则()()12020f a e f ln a ⎪=+−>⎧⎪⎨⎩<又因为()()22222f ln a a ln a =−−+()()ln 2222222222a e ln a ln a −+=−−+令()21t ln a ,=∈−∞, 记()()2f ln a g t =,则()()2222t e t g t −=−+, 其中1t <,9则()()2'2tt t e g t −=−，当()01t ,∈时,()'0g t >, 此时函数()g t 单调递增；当()0t ,∈−∞时,()'0g t <, 此时函数()g t 单调递减,所以()()00g t g =…, 即()20f ln a …, 当且仅当12a =时, 等号成立,故不等式组()()12020f a e f ln a ⎪=+−>⎧⎪⎨⎩<的解集为110222,,e ⎛⎫⎛⎫⋃− ⎪ ⎪⎝⎭⎝⎭.因为()1220,0f f a ⎛⎫=>−< ⎪⎝⎭,故当110222a ,,e ⎛⎫⎛⎫∈⋃− ⎪⎪⎝⎭⎝⎭时, 函数()f x 有 3个不同的零点; ②当0a …时,20x e a −>恒成立,当1x <时,()'0f x <, 此时函数()f x 单调递减, 当1x >时,()'0f x >, 此时函数()f x 单调递增, 此时函数()f x 至多两个零点, 不合乎题意; 综上所述, 实数a 的取值范围是110222,,e ⎛⎫⎛⎫⋃− ⎪ ⎪⎝⎭⎝⎭.证明:因为()()00,22f f ==, 结合 (2)中的结论可知()312x ,∈,①当102a ,⎛⎫∈ ⎪⎝⎭时, 若存在符合题意的实数a , 则由于130x x <,因此,1320,0x x x <<=,因此,123,,x x x 成等差数列可得出31x x =−,考虑()()()()220220x xx e ax x e ax −⎧−−+=⎪⎨−−++=⎪⎩,即22022x x e e x x −+−−=+−, 这等价于()()2480x xe e x−+−+=,令()()()248x xg x e e x−=+−+,()()()()2'24,x x x x g x x e e e e x −−=++−−令()()()()224,x x x xp x x e e e e x−−=++−−则()()()()2'62,x x x x p x x e e e e x −−=++−+当12x <<时,()'0p x >, 则函数()'f x 单调递增, 所以()()5130p x p e e>=−>, 故函数()'g x 单调递增,10因为()()54'120,'240g e g e e e=−<=+>,所以()'g x 在()12,上存在唯一零点, 记为0x , 当01x x <<时,()'0g x <, 即函数()g x 在(1,0x )上单调递减, 当02x x <<时,()'0g x >, 即函数()g x 在()0,2x 上单调递增, 由于()()031380,0,g e g x e=−−+<<()280,g => 因此()g x 在()01,x 上无零点, 在()02x ,上存在唯一的零点3x , 所以存在唯一的实数102a ,⎛⎫∈ ⎪⎝⎭, 使得12,x x 、3x 成等差数列;②当122a ,e ⎛⎫∈− ⎪⎝⎭时,1230x x x =<<, 不合乎题意。