五年级上册数学竞赛试题-第七节 数字与数位页码(二)(A班)-全国通用(无答案)
- 格式:docx
- 大小:83.07 KB
- 文档页数:8

2021年秋季五年级数学素质评估试卷满分:100分+20分一、填空题。
(34分,第1小题和15小题每空1分,其余每空1.5分) 1.找规律填数。
3.125,( ),12.5,( ),( ),1002.甲、乙两数的和是495,甲数的小数点向左移动一位就等于乙数。
甲数是( ),乙数是( )。
3.一个三位小数四舍五入到百分位约是1.65,这个三位小数最大是( ),最小是( )。
4.在一次登山比赛中,李刚上山时每分钟走40米,18分钟到达山顶。
然后按原路下山,每分钟走60米。
李刚全程平均每分钟走( )米。
5.学校购进36套桌椅,共用去3672元,已知1张桌子的价钱相当于3把椅子的价钱。
每把椅子( )元。
6.计算4÷7,并将结果用“四舍五入”法精确到小数点后第100位。
第100位上的数字是( )。
7.一条船在静水中每小时航行18千米,水流速度是每小时2千米,此船从甲地逆水航行到乙地需要15小时。
甲、乙两地间的距离是( )千米。
这条船从乙地回到甲地需要( )小时。
8.做一个奶油蛋糕要用5.5克奶油。
65克奶油最多可以做( )个这样的蛋糕。
9.袋子里有10个黑球和2个白球,至少要摸出( )个球,才能保证有不同颜色的球。
10.等腰三角形顶角是a 度,它的底角是( )度。
11.若A ▲B=(A+3B )×(A+B ),则5▲7=( )。
12.护士每隔5小时为病人量一次体温,在第12次量体温时,时钟时针指向9。
第一次量体温时,时针指向( )。
13.如果将一个数的小数部分乘以3,这个数变成了3.4;如果将这个数的小数部分乘以6,这个数就变成了5.8,这个数原来是( )。
14.用一根27分米的铁丝围成一个长方形,长比宽的2倍少1.5分米,围成的长方形面积是( )平方分米。
15.如图,10在第1行第2个。
19在第2行第4个。
12在第( )行第( )个。
按照这样的排列规律,47在第( )行第( )个。
第七节数字与数位页码(二)【知识要点】页码中的数学问题,是研究“页码”与“组成它的数字个数”之间的关系问题。
一位数共有9个,组成所有的一位数需要9个数码;两位数共有90个,组成所有的两位数需要2×90=180个数码;三位数共有900个,组成所有的三位数需要3×900=2700个数码。
为了清楚起见,我们将N位数的个数、组成所有N位数需要的数码个数、组成所有不大于N的位数需要的数码个数之间的关系列表如下:【典型例题】例1 一本书共有340页,在这本书的页码中共用了多少个数字?例2 一本书的页码中共用了3429个数字,这本书有多少页?例3 已知小数A=0.123456789101112…979899,它的小数后面的数字是由自然数1到99依次排列而成的。
问:小数点后边第68位上的数字是多少?例4 一本英汉辞典有1034页,在这本辞典的页码中,数字0和5出现了多少次?例5 一本书的页码一共含有100个数码5,则这本书至少有页,至多有页。
例6 甲、乙两册书的页码共用了777个数码,且甲册比乙册多7页。
甲册书有多少页?随堂小测1.一本漫画书有176页,在编排书的页码时,共需要多少个数字?2.一本中篇小说的页码,在排版时必须用2211个数码,问这本书共有多少页?3.有一列数:1234567891011……887888889,各个数字是顺次从1至889,问第555个数字是几?4.有一本书共1000页,编上页码1,2,3…。
问:数字2在页码中出现多少次?5.一本书的页码里共含有88个数字“8”,这本书至少有多少页?至多有多少页?6.上、下两册书的页码共有687个数字,且上册比下册多5页,则上册书有多少页?课后作业1.给一本书编页码,一共用了723个数字,这本书一共有多少页?2.一本小说的页码,在印刷时必须用1989个铅字,这本书共有多少页?3.小冬将连续自然数1,2,3…逐个相加,直到某个自然数为止。

五年 级数学第一学期能力检测试题一.填空(每题 2 分,共36分)1. ÷ 的商用循环小数表示是( ),保留两位小数是( )。
2. 甲、乙两数的和是 ,甲数的小数点向右移动一位等于乙数,甲数是( ) 。
3.一个两位数,个位数字与十位数字的和是 7,如果把这个数的个位数字 与十位数字对调,得到的新两位数比原来的两位数大 9,那么原来的两 位数是( ) 。
4、 一个三角形的面积是 5.6 平方米,高是 2 米,底是( )米。
5、 有一个直角三角形的两条直角边分别为 30 厘米和 40 厘米,它的斜边 是 50 厘米,斜边上的高是( )厘米。
6、 一个三位小数四舍五入保留两位小数的近似值是 ,这个三位小数 最大是( ) ,最小是( ) 。
7、右面平行四边形的面积是40平方厘米,涂色部分三角形的面积是( )平方厘米。
8、753的分数单位是( ),有( )个这样的单位,再去掉( )个分数单位就是3。
9、把5米长的绳子平均分成8段,每段长( ),每段占全长的( ),每段是5米的( )。
10、下面一组图形的阴影变化是有规律的,请根据这个规律把第四幅图的阴影部分画出来.11、填质数:21=( )+( );12、在1、2、3、…… 99、100中,数字2在一共出现了()次。
13、五年级开展数学竞赛,一共20题,答对一题得7分,答错一题扣4分,王磊得74分,他答对了()题。
14、甲、乙两数是互质数,且最小公倍数是156,那么甲、乙两数可能是()和()。
15、一只皮箱的密码是一个三位数。
小光说:“它是954。
”小明说:“它是358。
”小亮说:“它是214。
”小强说:“你们每人都只猜对了位置不同的一个数字。
”这只皮箱的密码是( )。
16、一个三位数,它是2和5的倍数,百位上的数是最小的质数,十位上的数是百位上的数的倍数,这个三位数最大是()。
17、36的因数有()个,这些因数的和是()。
18、正方形有()条对称轴。

沪教版【word直接打印】小学五年级上学期数学竞赛试题(含答案)图文百度文库一、拓展提优试题1.幼儿园给小朋友派礼物,如果有2人各派4个,其余各派3个,则还剩余11个,如果4人各派3个,其余各派6个,则剩余10个,问一共有多少件礼物?2.先将从1开始的自然数排成一列:123456789101112131415…然后按一定规律分组:1,23,456,7891,01112,131415,…在分组后的数中,有一个十位数,这个十位数是.3.鸡与兔共100只,鸡的脚比兔的脚多26只.那么,鸡有只.4.小松鼠储藏了一些松果过冬.小松鼠原计划每天吃6个松果,实际每天比原计划多吃2个,结果提前5天吃完了松果.小松鼠一共储藏了个松果.5.商店对某饮料推出“第二杯半价”的促销办法.那么,若购买两杯这种饮料,相当于在原价的基础上打折.6.某次入学考试有1000人参加,平均分是55分,录取了200人,录取者的平均分与未录取的平均分相差60分,录取分数线比录取者的平均分少4分.录取分数线是分.7.一艘船从甲港到乙港,逆水每小时行24千米,到乙港后又顺水返回甲港,已知顺水航行比逆水航行少用5小时,水流速度为每小时3千米,甲、乙两港相距千米.8.某商店的同种点心有大小两种包装礼盒,大盒85.6元一盒,内有点心32块,小盒46.8元一盒,内有点心15块,若王雷用654元买了9盒点心,则他可得点心块.9.如图,若长方形S长方形ABCD=60平方米,S长方形XYZR=4平方米,则四边形S四边=平方米.形EFGH10.四位数的所有因数中,有3个是质数,其它39个不是质数.那么,四位数有个因数.11.如图,魔术师在一个转盘上的16个位置写下来了1﹣16共16个数,四名观众甲、乙、丙、丁参与魔术表演.魔术师闭上眼,然后甲从转盘中选一个数,乙、丙、丁按照顺时针方向依次选取下一个数,图示是一种可能的选取方式,魔术师睁开眼,说:“选到偶数的观众请举手.”,这时候,只有甲和丁举手,这时候魔术师就大喝一声:“我知道你们选的数了!”.你认为甲和丁选的数的乘积是.12.一次数学竞赛中,某小组10个人的平均分是84分,其中小明得93分,则其他9个人的平均分是分.13.大于0的自然数n是3的倍数,3n是5的倍数,则n的最小值是.14.(8分)一个大于1的正整数加1能被2整除,加2能被3整除,加3能被4整除,加4能被5整除,这个正整数最小是.15.观察下面数表中的规律,可知x=.【参考答案】一、拓展提优试题1.【分析】假设第一次每人都派3个,则还剩余2×(4﹣3)+11=13个,第二次如每人都派6个,同时少了4×(6﹣3)﹣10=2个,就是每人多派6﹣3=3个,则需要13+2=15个礼物,据此可求出人数,进而可求出礼物数.解:[2×(4﹣3)+11+4×(6﹣3)﹣10]÷(6﹣3)=[2×1+11+4×3﹣10]÷3=[2+11+12﹣10]÷3=15÷3=5(人)2×4+(5﹣2)×3+11=8+3×3+11=8+9+11=28(件)答:一共有28件礼物.2.解:方法一:据分组律可得:从131415向后为1617181,92021222,324252627,2829303132(十位数),…;方法二:位数之前应该有1+2+3+…+9=45位.1位数有9位,10﹣19有20位,20﹣27有16位,所以十位数的开头应为28,为2829303132.故填:2829303132.3.解:设鸡有x只,则兔就有100﹣x只,根据题意可得方程:2x﹣4×(100﹣x)=26,2x﹣400+4x=26,6x=426,x=71,答:鸡有71只.故答案为:71.4.解:(6+2)×[(5×6)÷2]=8×15,=120(个).答:小松鼠一共储藏了120个松果.故答案为:120.5.解:设这种饮料每杯10,两杯售价是20元,实际用了:10+10×,=10+5,=15(元),15÷20=0.75=75%,所以是打七五折;故答案为:七五.6.解:设录取者的平均成绩为X分,我们可以得到方程,200X+(1000﹣200)×(X﹣60)=55×1000,200X+800(X﹣60)=55000,1000X﹣48000=55000,1000X=103000,X=103;所以录取分数线是103﹣4=99(分).答:录取分数线是99分.故答案为:99.7.解:顺水速度为:24+3+3=30(千米/小时);甲、乙两港相距:5÷(+), =5÷, =(千米); 答:甲、乙两港相距千米. 故答案为:.8.设大合x 盒,小盒y 盒,依题意有方程:85.6x +46.8(9﹣x )=654解方程得x =6,9﹣6=3.所以大合6盒,小盒3盒,共有32×6+15×3=237块.答:可得点心237块.9.解:根据分析,如下图所示:长方形S 长方形ABCD =S 长方形XYZR +△AEF +△EFR +△FBG +△FGX +△HCG +△HGY +△DHE +△HEZ=S 长方形XYZR +2×(a +b +c +d )⇒60=4+2×(a +b +c +d )⇒a +b +c +d =28四边形S 四边形EFGH =△EFR +△FGX +△HGY +△HEZ +S 长方形XYZR=a +b +c +d +S 长方形XYZR=28+4=32(平方米).故答案是:32.10.解:首先根据奇偶位数和相等一定是11的倍数.因数一共的个数是3+39=42(个),将42分解成3个数字相乘42=2×3×7.=a×b2×c6.如果是11×52×26=17600(不是四位数不满足条件).再看一下如果这个数字最小是=11×32×26=6336.=3663=11×37×32.因数的个数共2×2×3=12(个).故答案为:12个.11.解:依题意可知:2个偶数中间间隔是2个奇数.发现只有数字10,11,9,12是符合条件的数字.乘积为10×12=120.故答案为:12012.解:(84×10﹣93)÷(10﹣1)=747÷9=83(分)答:其他9个人的平均分是83分.故答案为:83.13.解:3n是5的倍数,3n的个数一定是0或5又因为大于0的自然数n是3的倍数,所以3n最小是453n=45n=15所以n最小取15时,n是3的倍数,3n是5的倍数.答:n的最小值是15.故答案为:15.14.解:根据分析:这个数除以2,3,4,5均余1,那么这个数减去1后就能同时被2,3,4,5整除;2,3,4,5的最小公倍数是60,则这个数为60的倍数加1.又因为这个数大于1,所以这个数最小是61.故答案为:61.15.解:根据分析可得,81=92,所以,x=9×5=45;故答案为:45.。

漳县金钟镇大石门小学五年级上册数学竞赛试卷一、填空 (共28分,每空2分)1. 两个数的和是61.6,其中一个数的小数点向右移动一位,就与另一个数相同。
两个数分别是( )、( )。
2. 有三根木料,打算把每根锯成3段,每锯开一处需要3分钟,全部锯完需要( )分钟。
3. 笑笑同学的家住在5楼,每层楼梯有16级,她从1楼走到5楼,共要走( )级楼梯。
4. 把一张边长24厘米的正方形纸对折4次后得到一个小正方形,这个小正方形的面积是( )平方厘米。
5. 李师傅3小时生产96个零件,照这样计算生产288个零件要( )小时。
6. 一个长方形的长为9厘米,把它的长的一边减少3厘米,另一边不变,面积就减少9平方厘米,这时变成的梯形面积是( )平方厘米。
7. 小明和小英两人同时从甲、乙两地相向而行,小明每分钟行a米,小英每分钟行b米,行了4分钟两人相遇。
甲、乙两地的路程是( )米。
8.哥哥7年前的年龄和妹妹5年后的年龄相等,当哥哥( )岁时,正好是妹妹年龄的3倍。
9.按规律在括号里填数。
(1)1、3、7、15、31、( )、( )。
(2)2、8、5、20、7、28、11、44、( )、12。
(3)1,1,2,3,5,8,( ),21。
10. 五(1)班的同学去划船。
他们算了一下,如果增加一条船,正好每条船坐6人;如果减少一条船,正好每条船坐9人。
这个班共有( )名同学。
二、判断 (正确的在括号里画“√”,错误的画“×”。
共15分,每小题3分)11.用10张同样长的纸条接成一条长31厘米的纸带,如果每个接头都重叠1厘米,那么每张纸条长4.1厘米。
( )12.用三个长3厘米、宽2厘米,高1厘米的长方体,拼成一个大长方体,有3种拼法。
( )13.把一批圆木自上而下按1、2、3……14、15根放在一起,这批圆木共有240根。
( )14.在a÷b=5……3中,把a、b同时扩大3倍,商是5,余数是3。

【经典】小学五年级上学期数学竞赛试题(含答案)图文百度文库一、拓展提优试题1.(7分)后羿朝三个箭靶分别射了三支箭,如图:他在第一个箭靶上得了29分,第二个箭靶上得了43分.请问他在第三个箭靶上得了分.2.有一行数:1,1,2,3,5,8,13,21,…,从第三个数开始,每个数都是前两个数的和,问在前2007个数中,有是偶数.3.用1,2,3,4,5,6,7,8这八个数字组成两个不同的四位数(每个数字只用一次)使他们的差最小,那么这个差是.4.数一数,图中有多少个正方形?5.数学家维纳是控制论的创始人.在他获得哈佛大学博士学位的授予仪式上,有人看他一脸稚气的样子,好奇地询问他的年龄.维纳的回答很有趣,他说:“我的年龄的立方是一个四位数,年龄的四次方是一个六位数,这两个数刚好把0﹣9这10个数字全都用上了,不重也不漏,”那么,维纳这一年岁,(注:数a的立方等于a×a×a,数a的四次方等于a×a×a×a)6.(8分)小张有200支铅笔,小李有20支钢笔.每次小张给小李6支铅笔,小李还给小张1支钢笔.经过次这样的交换后,小张手中铅笔的数量是小李手中钢笔数量的11倍.7.小胖和小亚两人在生日都是在五月份,而且都是星期三.小胖的生日晚,又知两人的生日日期之和是38,小胖的生日是5月日.8.定义新运算:a&b=(a+1)÷b,求:2&(3&4)的值为.9.李双骑车以320米分钟的速度从A地驶向B地,途中因自行车故障推车继续向前步行5分钟到距B地1800米的某地修车,15分钟后以原来骑车速度的1.5倍继续向前驶向B地,到达B地时,比预计时间多用17分钟,则李双推车步行的速度是米/分钟.10.如图,将一个等腰三角形ABC沿EF对折,顶点A与底边的中点D重合,若△ABC的周长是16厘米,四边形BCEF的周长是10厘米,则BC=厘米.11.如图,魔术师在一个转盘上的16个位置写下来了1﹣16共16个数,四名观众甲、乙、丙、丁参与魔术表演.魔术师闭上眼,然后甲从转盘中选一个数,乙、丙、丁按照顺时针方向依次选取下一个数,图示是一种可能的选取方式,魔术师睁开眼,说:“选到偶数的观众请举手.”,这时候,只有甲和丁举手,这时候魔术师就大喝一声:“我知道你们选的数了!”.你认为甲和丁选的数的乘积是.12.(8分)如果两个质数的差恰好是2,称这两个质数为一对孪生质数.例如3和5是一对孪生质数,29和31也是一对孪生质数.在数论研究中,孪生质数是最热门的研究课题之一.华裔数学家张益唐在该课题的研究中取得了令人瞩目的成就,他的事迹激励着更多的青年学子投身数学研究.在不超过100的整数中,一共可以找到对孪生质数.13.某长方体的长、宽、高(长、宽、高均大于1)是三个彼此互质的自然数,若这个长方体的体积是665,则它的表面积是.14.用一根34米长的绳子围成一个矩形,且矩形边长都是整数米,共有种不同的围法(边长相同的矩形算同一种围法).15.某场考试共有7道题,每道题问的问题都只与这7道题的答案有关,且答案只能是1、2、3、4中的一个.已知题目如下:①有几道题的答案是4?②有几道题的答案不是2也不是3?③第⑤题和第⑥题的答案的平均数是多少?④第①题和第②题的答案的差是多少?⑤第①题和第⑦题的答案的和是多少?⑥第几题是第一个答案为2的?⑦有几种答案只是一道题的答案?那么,7道题的答案的总和是.【参考答案】一、拓展提优试题1.【分析】这个箭靶共三个环,设最小的环为a分,中间环为b分,最外环为c分,得:第一个靶得分为:2b+c=29①第二个靶得分为:2a+c=43②第三个靶得分为:a+b+c③通过等量代换,解决问题.解:设最小的环为a分,中间环为b分,最外环为c分,得:第一个靶得分为:2b+c=29①第二个靶得分为:2a+c=43②第三个靶得分为:a+b+c③由①+②得:2a+2b+2c=29+43=72即a+b+c=36即第三个靶的得分为36分.答:他在第三个箭靶上得了36分故答案为:36.2.【分析】因为前两个数相加得偶数,即奇数+奇数=偶数;同理,第四个数是:奇数+偶数=奇数,以此类推,总是奇数、奇数、偶数、奇数、奇数、偶数…;每三个数一个循环周期,然后确定2007个数里面有几个循环周期,再结合余数,即可得出偶数的个数.解:2007÷3=669,又因为,每一个循环周期中有2个奇数,1个偶数,所以前2007个数中偶数的个数是:1×669=669;答:前2007个数中,有699是偶数.故答案为:699.3.【分析】设这两个数为a,b.,且a<b.千位最小差只能是1.为了让差尽量小,只能使a其它位数最大,b的其它位数最小.所以要尽量使a的百位大于b的百位,a的十位大于b的十位,a的个位大于b的个位.因此分别是8和1,7和2,6和3,剩下的4,5分给千位.据此解答.解:设这两个数为a,b.,且a<b.千位最小差只能是1.根据以上分析,应为:5123﹣4876=247故答案为:247.4.解:通过有规律的数,得出:(1)边长为1的正方形有4×3=12(个);(2)边长为2的正方形有6个;(3)边长为3的正方形有2个.(4)以小正方形的对角线为边的正方形有8个;(5)以对角线的一半为边长的正方形是17个;(6)以3个对角线的一半为边长的正方形有1个.所以图中共有正方形:12+6+2+8+17+1=46(个).答:图中有46个正方形.5.解:先用估值的方法大概确定一下维纳的年龄范围.根据174=83521,184=104976,194=130321,根据题意可得:他的年龄大于或等于18岁;再看,183=5832,193=6859,213=9261,223=10648,说明维纳的年龄小于22岁.根据这两个范围可知可能是18、19、20、21的一个数.又因为20、21无论是三次方还是四次方,它们的尾数分别都是:0、1,与“10个数字全都用上了,不重也不漏”不符,所以不用考虑了.只剩下18、19这两个数了.一个一个试,18×18×18=5832,18×18×18×18=104976;19×19×19=6859,19×19×19×19=130321;符合要求是18.故答案为:18.6.解:依题意可知:当第一次过后,小张剩余194只铅笔,小李剩余19只钢笔.当第二次过后,小张剩余188只铅笔,小李剩余18只钢笔.当第三次过后,小张剩余182只铅笔,小李剩余17只钢笔.当第四次过后,小张剩余176只铅笔,小李剩余16只钢笔.正好是11倍.故答案为:四7.解:38=7+31=8+30=9+29=10+28=11+27=12+26=13+25=14+24=15+23=16+22,因为二人的生日都是星期三,所以他们的生日相差的天数是7的倍数;经检验,只有26﹣12=14,14是7的倍数,即小亚的生日是5月12日,小胖的生日是5月26日时它们相差14天,符合题意,答:小胖的生日是5月26日.故答案为:26.8.解:2&(3&4),=(2+1)÷[(3+1)÷4],=3÷1,=3;故答案为:3.9.解:1800÷320﹣1800÷(320×1.5)=5.625﹣3.75=1.875(分钟)320×[5﹣(17﹣15+1.875)]÷5=320×[5﹣3.875]÷5=320×1.125÷5=360÷5=72(米/分钟)答:李双推车步行的速度是72米/分钟.故答案为:72.10.解:△ABC的周长是16厘米,可得△AEF的周长为:16÷2=8 (厘米),△AEF和四边形BCEF周长和为:8+10=18(厘米),所以BC=18﹣16=2(厘米),答:BC=2厘米.故答案为:2.11.解:依题意可知:2个偶数中间间隔是2个奇数.发现只有数字10,11,9,12是符合条件的数字.乘积为10×12=120.故答案为:12012.解:在不超过100的整数中,以下8组:3,5;5,7;11,13;17,19;29,31;41,43;59,61;71,73是孪生质数.故答案为8.13.解:665=19×7×5,因为长、宽、高(长、宽、高均大于1)是三个彼此互质的自然数,所以长、宽、高分别是19、7、5,(19×7+19×5+7×5)×2=(133+95+35)×2=263×2=526,答:它的表面积是526.故答案为:526.14.解:设矩形的长为am,宽为bm,且a≥b,根据题意,a+b=17,由于a,b均为整数,因此(a,b)的取值有以下8种:(16,1),(15,2),(14,3),(13,4),(12,5),(11,6),(10,7),(9,8),故答案为8.15.解:因为每道题的答案都是1、2、3、4的一个,所以①的答案不宜太大,不妨取1,此时②的答案其实就是7个答案中1和4的个数,显然只能取2、3、4中的一个,若取2,则意味着剩余的题目只能有一道题答案为1,这是④填1,⑦填2,⑤填3,⑥填2,而③无法填整数,与题意矛盾;所以②的答案取3,则剩余的题目答案为1和4各有1道,此时④填2,显然⑦只能填1,那么⑤填2,则4应该是⑥的答案,从而③填3,此时7道题的答案如表;它们的和是1+3+3+2+2+4+1=16.。

小学五年级上学期数学竞赛试题(含答案)一图文百度文库一、拓展提优试题1.(7分)后羿朝三个箭靶分别射了三支箭,如图:他在第一个箭靶上得了29分,第二个箭靶上得了43分.请问他在第三个箭靶上得了分.2.(7分)棱长都是1厘米的63个白色小正方体和1个黑色小正方体,可以拼成一个大正方体,问:一共可以拼成种不同的含有64个小正方体的大正方体.3.先将从1开始的自然数排成一列:123456789101112131415…然后按一定规律分组:1,23,456,7891,01112,131415,…在分组后的数中,有一个十位数,这个十位数是.4.星期天早晨,哥哥和弟弟去练习跑步,哥哥每分钟跑110米,弟弟每分钟跑80米,弟弟比哥哥多跑了半小时,结果比哥哥多跑了900米,那么,哥哥跑了米.5.小明带了30元钱去买文具,买了3个笔记本和5支笔,剩余的钱,如果再买2支笔还差0.4元,如果再买2个笔记本则还差2元,那么,笔记本每个元,笔每支元.6.已知一个五位回文数等于45与一个四位回文数的乘积(即=45×),那么这个五位回文数最大的可能值是59895.7.如图,正方形的边长是6厘米,AE=8厘米,求OB=厘米.8.定义新运算:a&b=(a+1)÷b,求:2&(3&4)的值为.9.如图中,A、B、C、D为正六边形四边的中点,六边形的面积是16,阴影部分的面积是.10.(8分)图中所示的图形是迎春小学数学兴趣小组的标志,其中,ABCDEF 是正六边形,面积为360,那么四边形AGDH的面积是.11.如果2头牛可以换42只羊,3只羊可以换26只兔,2只兔可以换3只鸡,则3头牛可以换多少只鸡?12.(8分)小胖把这个月的工资都用来买了一支股票.第一天该股票价格上涨,第二天下跌,第三天上涨,第四天下跌,此时他的股票价值刚好5000元,那么小胖这个月的工资是元.13.观察下面数表中的规律,可知x=.14.如图是一个正方体的平面展开图,若该正方体相对的两个面上的数值相等,则a﹣b×c的值是.15.(7分)对于a、b,定义运算“@”为:a@b=(a+5)×b,若x@1.3=11.05,则x=.【参考答案】一、拓展提优试题1.【分析】这个箭靶共三个环,设最小的环为a分,中间环为b分,最外环为c分,得:第一个靶得分为:2b+c=29①第二个靶得分为:2a+c=43②第三个靶得分为:a+b+c③通过等量代换,解决问题.解:设最小的环为a分,中间环为b分,最外环为c分,得:第一个靶得分为:2b+c=29①第二个靶得分为:2a+c=43②第三个靶得分为:a+b+c③由①+②得:2a+2b+2c=29+43=72即a+b+c=36即第三个靶的得分为36分.答:他在第三个箭靶上得了36分故答案为:36.2.【分析】一共64个,4×4×4,①把黑色正方体放在顶点处,1种;②把黑色正方体放在棱中间,任选一个,2种;③把正方体放在每个面的中间4个,任选一个,4种;④把黑色正方体放在里面,从外边看不到,8种;然后把几种情况的种数相加即可.解:①把黑色正方体放在顶点处,1种;②把黑色正方体放在棱中间,任选一个,2种;③把正方体放在每个面的中间4个,任选一个,4种;④把黑色正方体放在里面,从外边看不到,8种;共:1+2+4+8=15(种);答:一共可以拼成15种不同的含有64个小正方体的大正方体.故答案为:15.3.解:方法一:据分组律可得:从131415向后为1617181,92021222,324252627,2829303132(十位数),…;方法二:位数之前应该有1+2+3+…+9=45位.1位数有9位,10﹣19有20位,20﹣27有16位,所以十位数的开头应为28,为2829303132.故填:2829303132.4.解:设哥哥跑了X分钟,则有:(X+30)×80﹣110X=900,80x+2400﹣110x=900,2400﹣30x=900,X=50;110×50=5500(米);答:哥哥跑了5500米.故答案为:5500.5.解:根据题干分析可得:5个笔记本+5支笔=32元;则1个笔记本+1支笔=6.4(元),3个笔记本+3支笔+4支笔=30.4(元),所以4支笔=30.4﹣3×6.4=11.2(元),所以1支笔的价格是:11.2÷4=2.8(元),则每个笔记本的价钱是:6.4﹣2.8=3.6(元).答:每个笔记本3.6元,每支笔2.8元.故答案为:3.6;2.8.6.解:根据分析,得知,=45=5×9既能被5整除,又能被9整除,故a的最大值为5,b=9,45被59□95整除,则□=8,五位数最大为59895故答案为:598957.解:6×6÷2=18(平方厘米),18×2÷8=4.5(厘米);答:OB长4.5厘米.故答案为:4.5.8.解:2&(3&4),=(2+1)÷[(3+1)÷4],=3÷1,=3;故答案为:3.9.解:如图:连接正方形的一条对角线,延长DA,与最上边正六边形边的延长线交与一点,这样可得两个三角形①、②三角形①和三角形②是全等三角形,它们的面积相等,进而可得出阴影部分两侧的三角形可补到六边形的角上,这样就成了一个长方形,阴影部分的面积等于空白部分的面积,所以阴影部分的面积是正六边形面积的一半16÷2=8答:阴影部分的面积是8.故答案为:8.10.解:根据分析,(1)△ABC面积等于六边形面积的,连接AD,四边形ABCD是正六边形面积的,故△ACD面积为正六边形面积的(2)S△ABC :S△ACD=1:2,根据风筝模型,BG:GD=1:2;(3)S△BGC:S CGD=BG:GD=1:2,故;故AGDH面积=六边形总面积﹣(S△ABC +S△CGD)×2=360﹣(+40)×2=160.故答案是:16011.解:42÷2=21(只)21÷3×26=7×26=182(只)182÷2×3=91×3=273(只)273×3=819(只)答:3头牛可以换819只鸡.12.解:5000÷(1﹣)÷(1+)÷(1﹣)÷(1+)=5000××××=5000(元)答:小胖这个月的工资是5000元.故答案为:5000.13.解:根据分析可得,81=92,所以,x=9×5=45;故答案为:45.14.解:依题意可知:3a+2与17是对立面,3a+2=17,所以a=5;7b﹣4与10是对立面,7b﹣4=10,所以b=2;a+3b﹣2c与11的对立面,5+3×2﹣2c=11,所以c=0;所以a﹣b×c=5故答案为:515.解:由定义可知:x@1.3=11.05,(x+5)1.3=11.05,x+5=8.5,x=8.5﹣5=3.5故答案为:3.5。

人教版小学五年级上册数学竞赛试题二班级———姓名————座号——评分————一、我会填。
(23分;其中11至14题每空2分)1、一个三位小数四舍五入到百分位是3.32;这个数最大是();最小是()。
2、两个数相除的商是0.8;被除数扩大100倍;除数缩小10倍;商是()。
3、11÷7的商小数点后第50位是()。
4、在0.978、0.978、0.978、0.978四个数中最大的是();最小是()。
5、一条彩带长6.4米;每1.6米剪一段;需要剪()次才能完成。
6、60升的油装入容量为6.5升的油桶中;需要()只这样的油桶才够装。
7、用一杯子向空瓶倒水;如果倒进3杯水;连瓶共重440克;如果倒进5杯水;连瓶共重600克;一杯水重()克;空瓶重()克。
8、把一个小数的小数点向右移动二位后;所得的数比原数增加了267.3;原数是()。
9、a去除一个数商7余5;这个数可表示为()。
10、在括号里填上﹥、﹤或= 。
0.95×2.34()2.34 0.98×0.87()0.87÷0.984.85×99+4.85()4.85×10011、甲对乙说:“我的年龄是你的3倍;”;乙队甲说;“我5年后的年龄和你去年的年龄一样”;乙今年()岁。
12、一个停车场停一次车至少要交0.5元的停车费;如果停车超时1小时;每多停0.5小时就要多交0.5元;这辆车一共交了5.5元;这辆车一共停了()小时。
13、小东奶奶今年的年龄减去15后;缩小4倍;再减去6之后;扩大10倍;恰好是100岁;小东的奶奶今年()岁。
14、右图中有()个三角形。
二、判断题。
(5分)1、小数点的后面添上0或去掉0;小数的大小不变。
()2、一个因数比1小时;积一定小于另一个因数。
()3、观察一个物体时;一次最多能看到3个面。
()4、无限小数一定大于有限小数。
()5、含有未知数的式子一定是方程。
()三、我会选(把正确答案的序号天灾括号里)。

【精选】小学五年级数学竞赛试卷及答案word百度文库一、拓展提优试题1.(7分)爱尔兰作家刘易斯曾写过一篇反讽寓言,文中描述了一个名为尼亚特泊的野蛮国家.在这个国家里使用西巴巴数字.西巴巴数字的形状与通用的阿拉伯数字相同,但含义相反.如“0”表示“9”,“1”表示“8”,以次类推.他们写数字是从左到右,使用的运算符号也与我们使用的一样.例如,他们用62代表我们所写的37.按照尼亚特泊人的习惯,应怎样写837+742的和是419.【分析】“0”表示“9”,0+9=9,“1”表示“8”,1+8=9,由此可知西巴巴数字,表示的数字与正常数字的和都是9;由此找出837、742表示的数字,然后相加即可.2.用长是5厘米、宽是4厘米、高是3厘米的长方体木块叠成一个正方体,至少需要这种长方体木块块.3.小胖和小亚两人在生日都是在五月份,而且都是星期三.小胖的生日晚,又知两人的生日日期之和是38,小胖的生日是5月日.4.小明从家到学校去上课,如果每分钟走60米,可提前10分钟到校;如果每分钟走50米,要迟到4分钟到校.小明家到学校相距米.5.如图:平行四边形ABCD中,OE=EF=FD.平行四边形面积是240平方厘米,阴影部分的面积是平方厘米.6.用0、1、2、3、4这五个数字可以组成个不同的三位数.7.(1)数一数图1中有个三角形.(2)数一数图2中有个正方形.8.(8分)有一种细胞,每隔1小时死亡2个细胞,余下的每个细胞分裂成2个.若经过5小时后细胞的个数记为164.最开始的时候有个细胞.9.同时掷4个相同的小正方体(小正方体的六个面上分别写有数字1、2、3、4、5、6,则朝上一面的4个数字的和有种.10.某长方体的长、宽、高(长、宽、高均大于1)是三个彼此互质的自然数,若这个长方体的体积是665,则它的表面积是.11.大于0的自然数n是3的倍数,3n是5的倍数,则n的最小值是.12.从1、2、3、4、5中任取3个组成一个三位数,其中不能被3整除的三位数有个.13.观察下表中的数的规律,可知第8行中,从左向右第5个数是.14.定义新运算:θa=,则(θ3)+(θ5)+(θ7)(+θ9)+(θ11)的计算结果化成最简真分数后,分子与分母的和是.15.(7分)如图,按此规律,图4中的小方块应为个.【参考答案】一、拓展提优试题1.解:西巴巴数字8表示阿拉伯数字9﹣8=1,西巴巴数字3表示阿拉伯数字9﹣3=6,西巴巴数字7表示阿拉伯数字9﹣7=2,西巴巴数字4表示阿拉伯数字9﹣4=5,西巴巴数字2表示阿拉伯数字9﹣2=7,所以837+742表示的正常算式为:162+257=419.故答案为:419.2.解:正方体的棱长应是5,4,3的最小公倍数,5,4,3的最小公倍数是60;所以,至少需要这种长方体木块:(60×60×60)÷(5×4×3),=216000÷60,=3600(块);答:至少需要这种长方体木3600块.故答案为:3600.3.解:38=7+31=8+30=9+29=10+28=11+27=12+26=13+25=14+24=15+23=16+22,因为二人的生日都是星期三,所以他们的生日相差的天数是7的倍数;经检验,只有26﹣12=14,14是7的倍数,即小亚的生日是5月12日,小胖的生日是5月26日时它们相差14天,符合题意,答:小胖的生日是5月26日.故答案为:26.4.解:(60×10+50×4)÷(60﹣50),=(600+200)÷10,=800÷10,=80(分钟),60×(80﹣10),=60×70,=4200(米).答:小明家到学校相距4200米.故答案为:4200.5.解:因为平行四边形ABCD中,AC和BD是对角线,把平行四边形ABCD 的面积平分4份,平行四边形面积是240平方厘米,所以S△DOC=240÷4=60(平方厘米),又因为△OCE、△ECF、△FCD和△DOC等高,OE=EF=FD,所以S△ECF=S△DOC=×60=20(平方厘米),所以阴影部分的面积是 20平方厘米.故答案为:20.6.解:4×4×3,=16×3,=48(种);答:这五个数字可以组成 48个不同的三位数.故答案为:48.7.解:(1)三角形有:8+4+4=16(个);(2)正方形有:20+10+4+1=35(个),故答案为:16,35.8.解:第5小时开始时有:164÷2+2=84(个)第4小时开始时有:84÷2+2=44(个)第3小时开始时有:44÷2+2=24(个)第2小时开始时有:24÷2+2=14(个)第1小时开始时有:14÷2+2=9(个)答:最开始的时候有 9个细胞.故答案为:9.9.解:根据分析可得,朝上一面的4个数字的和最小是:1×4=4,最大是6×4=24,24﹣4+1=21(种)答:朝上一面的4个数字的和有 21种.故答案为:21.10.解:665=19×7×5,因为长、宽、高(长、宽、高均大于1)是三个彼此互质的自然数,所以长、宽、高分别是19、7、5,(19×7+19×5+7×5)×2=(133+95+35)×2=263×2=526,答:它的表面积是526.故答案为:526.11.解:3n是5的倍数,3n的个数一定是0或5又因为大于0的自然数n是3的倍数,所以3n最小是453n=45n=15所以n最小取15时,n是3的倍数,3n是5的倍数.答:n的最小值是15.故答案为:15.12.解:1+2+3=6,1+2+4=7,1+2+5=8,2+3+4=9,2+3+5=10,3+4+5=12,其中不能被3整除的数的和是7、8、10,即有三组(1、2、4),(1、2、5)(2、3、5),每一组可以组成3×2×1=6个,三组共可以组成6×3=18个,即不能被3整除的数共有18个.故答案为:18.13.解:由图可知,第1行的数为1,第2行的最后一个数为2×2=4,第3行的最后一个数为3×3=9,…所以第7行最后一个数为7×7=49,则第8行第1个数为49+1=50,第5个数为50+4=54,故答案为:54.14.解:原式=++++=++++=×(﹣+﹣+…+﹣)=×()=5+24=29故答案为:2915.解:因为图1中小方块的个数为1+2×3=7个,图2中小方块的个数为1+(1+2)+3×4=16个,图3中小方块的个数为1+(1+2)+(1+2+3)+4×5=30个,所以图4中小方块的个数为1+(1+2)+(1+2+3)+(1+2+3+4)+5×6=50个,故答案为:50.。

城关小学五年级上册数学竞赛试题评分标准及答案(试题115分,卷面5分,总分120分)一、算一算。
(共40分)1、 直接写得数。
(4分)2.5×4=10 5×0.05= 0.253.2÷4=0.8 0.39÷0.03=130.45×0.1= 0.045 0.2×11= 0.22 3.6÷2= 1.8 1.2÷0.02= 602、列竖式计算。
(6分)(第②小题得数保留两位小数)① 1.05×2.4 =2.52② 5.63÷6.1 ≈0.923、用简便方法计算,写出必要的计算过程。
(12分)8.56×2.7+1.44×2.7 =271.25×2.5×4×0.8 =10 5.74×99+5.74 =574 72×0.03+0.3×2.8=34、计算下列各题。
(12分)(1)9÷[(38.02+1.98)×0.5] =0.45(2)1.2×(3.2-2.99÷2.3)=2.28(3)(1.79+1.2×0.1)÷0.25=7.64(4) 5.8÷[8×(1.8-1.3)]=1.45 5.解方程。
(6分)(1)5.6 X -8.6=19.4 X=5(2) 3.2 X -1.5 X=0.51 X=0.3 二、填一填。
(28分)1、3吨50千克=(3.05 )吨 5.06平方米=( 5 )平方米( 6 )平方分米2、一个平行四边形的底是4.2厘米,高是3厘米,与它等底等高的三角形的面积是( 6.3 )平方厘米。
3、在○里填上“>”、“<”或“=”(1)1.96÷1.01○1.96 “<” (2)2.85×2.6○2.85 “>” (3)1.25÷0.36○1.25 “>” (4)2.83×0.9○2.83÷0.9 “<”4、3.0506506506……把它保留两位小数是(3.05 ),精确到千分位是( 3.051 )。

小学五年级上册数学竞赛试题下载五年级上册数学竞赛试题一、脱式计算(50分,能用简便运算的就用简便方式。
)1.08×0.8÷0.27 44.28÷0.9÷4.12.05÷0.82+33.66×0.36+0.6×26.40.5×12.5×64×0.251.25×3.28+12.5×0.241+125×0.04310.125×8.8 999×27-333×51+666×353.35+4.5-0.35+0.65 0.25×4÷0.25×4二、解决问题(50分)1.一列火车长180米,以每秒15米的速度通过一座大桥用了60秒。
大桥长多少米?2.甲、乙两个书店存书册数相等,甲书店售出3000册,乙书店购入XX册,这时乙书店存书的册数是甲的2倍,甲、乙两书店原先共有存书多少册?3.甲、乙、丙三人参加数学竞赛,甲、乙的总分是153分,乙、丙的总分是173分,甲、丙的总分是160分,甲、乙、丙三人各得多少分?4.明明和婷婷用自己的压岁钱购买学习用品,明明买2支铅笔,5个笔记本,用去7元;婷婷买4支铅笔,7个笔记本,用去10.4元。
铅笔和笔记本的单价各是多少元?5.甲乙两辆汽车同时从东站开往西站。
甲车每小时比乙车多行12千米,甲车行驶四个半小时抵达西站后,没有停留,当即从原路返回,在距离西站31.5千米的地址和乙车相遇,甲车每小时行多少千米?五年级上册数学竞赛试题一、脱式计算(50分,能用简便运算的就用简便方式。
)1.08×0.8÷0.27 44.28÷0.9÷4.12.05÷0.82+33.66×0.36+0.6×26.40.5×12.5×64×0.251.25×3.28+12.5×0.241+125×0.04310.125×8.8 999×27-333×51+666×353.35+4.5-0.35+0.65 0.25×4÷0.25×4二、解决问题(50分)1.一列火车长180米,以每秒15米的速度通过一座大桥用了60秒。
人教版小学五年级上册数学竞赛试卷五年级数学竞赛试卷一、 填空(20分)1. 一个两位小数的小数点向右移动一位后;与原数的和是8.58;这个数是 。
2. 一个三位小数保留两位小数后的近似值是4.85;这个数最大是 ;最小是 。
3. 根据题意;将算式中的符号填入题中的空格内;△ ÷(□+○)= ◇某班有 人;规定每个小组有男生 人;有女生 人;正好组成若干个小组;该班有 个小组。
4. 在下面的方框里填上合适的数:1.5÷〔(150.4+14.6)×□-23〕=0.15 5. 水果店有苹果X 千克;每天卖出6千克;Y 天后还剩 千克。
6. 已知:1÷A =0.0909……;2÷A=0.1818……;3÷A=0.2727……;4÷A=0.3636……;那么9÷A 的商是 。
7.有一列数;共7个;已知这七个数的平均数是28;前四个数的平均数是30;后四个数的平均数是25;那么第四个数是 。
8. 一个长方形的周长为60米;长比宽多4米;这个长方形的面积是 。
9. △+△=a ;△-△=b ;△×△=c ;△÷△ =d ;且 a + b + c + d = 100;那么△= 。
10.李师傅加工一批零件;4分钟加工了20个;那么李师傅平均加工1个零件需要 分钟;1分钟能加工这种零件 个。
二、 判断(10分) 1.a 2和2 a 表示的意义相同。
( ).从上面、正面、右面看到的图形都相同。
( ) 2. 3.方程的两边同时加上或减去一个相同的数;等式成立。
( ) 4.面积相等的两个三角形一定可以拼成一个平行四边形。
( ) 5.用四根木条钉成的长方形;把它拉成平行四边形;它的面积变大了;周长没变。
( ) 三、计算(35分)学校 姓名1.直接写得数:3.5×0.1= 43÷0.1= 200×0.04= 12-1.2= 1.3×0.5=0.42÷0.6= 6.3÷0.7= 0.21×0.3= 5.69÷0.5= 5.5÷11=2.能简算的要简算:3.85×42+385×0.63-38.5×0.5 0.8×2.7×12.54.7×2.34-34×0.047 1.9+19.9+199.9+0.33.解方程:5X – 2 + 1.8 = 3.6 7(X – 1.2)= 2.12X-4.2÷0.14 = 2.4 1.6×8 -7X = 2.34.列式计算:①一个数的3.9倍与它的2.5倍的和是16;这个数是多少?②用3.6与0.5的积去除8.28;商是多少?三、解决问题(35分)1.有一篮鸡蛋;第一次取出全部的一半还多1个;第二次取出余下的一半少1个;篮里还剩20个;篮里原有鸡蛋多少个?2.小强前几次数学考试平均成绩是84分;这次要考100分;才能使平均成绩达到86分;这是第几次考试?3.如图;已知正方形ABCD的边长是15㎝;长方形EFGH的四个顶点三等分正方形的每条边;问长方形EFGH的面积是多少?4.一列火车长240米;这列火车每秒行15米;从车头进山洞到车尾出山洞共用20秒;山洞长多少米?5.王兰有64张画片;雷江送给她12张;这时王兰和雷江的画片数相等。
五年级数学竞赛试题一、填空。
(16分)1、14.1÷11的商是()循环小数,商可以简写作(),得数保留三位小数约是()。
2、把2.54、2.54·、2.545和2.55……用“>”按顺序排列起()。
(3分)3、在○填上“<”、“>”或“=”号。
(1)0.18÷0.09〇0.18×0.09 (2)0.7×0.7〇0.7+0.7(3)3.07×0.605〇0.307×6.05 (4)4.35×10〇0.8×43.54、一桶豆油重100千克,每天用去千克,6天后还剩下79千克,用方程表示是()=79;=()。
5、小明今年a岁,爸爸的年龄比他的3倍大b岁,爸爸今年()岁。
6、100千克花生可榨油39千克,照这样计算,每千克花生可榨油()千克。
7、两个因数的积是3.6,如果一个因数扩大2倍,另一个因数扩大10倍,积是()。
8、686.8÷0.68的商的最高位在()位上。
二、选一选。
(把正确答案的字母填在括号里)(10分)1、下列算式中与99÷0.03结果相等的式子是()。
A、9.9÷0.003B、990÷0.003C、9900÷302、把一个平行四边形拉成一个长方形(边长不变),它的面积()。
A、比原大B、比原小C、与原一样大3、因为38×235=8930,所以0.38×2.35+100=()。
A.189.3B. 108.93C.100.8934、47.88÷24=1.995,按四舍五人法精确到百分位应写作()。
A. 2.0B. 2.00C. 1.995、一个三角形中,其中两个角的平均度数是45度,这个三角形是()三角形。
A. 锐角B. 直角C. 钝角三、小小神算手。
(40分)1、直接写出得数。
(5分)0.001+10.099=3-0.98=6×0.25=0.63÷0.9=11.8×0.4=8.95÷0.895= 1.2×4= 3.9×0.01=2.33×1.2= 1.25×0.8=2、竖式计算。
五年级上册数学比赛试题定边第二小学2014— 2015 学年度第一学期五年级数学能力检测试题一. 填空(每题2分,共36分)1.40.8 ÷ 1.32 的商用循环小数表示是 ( ) ,保存两位小数是 ( )。
2.甲、乙两数的和是 145.2 ,甲数的小数点向右挪动一位等于乙数,甲数是()。
3. 一个两位数,个位数字与十位数字的和是7 ,假如把这个数的个位数字与十位数字对换,获得的新两位数比原的两位数大9 ,那么原的两位数是()。
4、一个三角形的面积是 5.6平方米,高是2米,底是()米。
5、有一个直角三角形的两条直角边分别为30厘米和40 厘米,它的斜边是50厘米,斜边上的高是()厘米。
6、一个三位小数四舍五入保存两位小数的近似值是3.90 ,这个三位小数最大是(),最小是()。
7、右边平行四边形的面积是40 平方厘米,涂色部分三角形的面积是()平方厘米。
8、的分数单位是(),有()个这样的单位,再去掉()个分数单位就是3。
2016 崭新精选资料 - 崭新公函范文 -全程指导写作–独家原创1 / 59、把 5 米的子均匀分红8 段,每段(),每段占全的(),每段是 5 米的()。
10、下边一形的暗影化是有律的, 依据个律把第四幅的暗影部分画出.11 、填数: 21=()+();12 、在 1、 2、 3、⋯⋯ 99 、 100 中,数字 2 在一共出了()次。
13、五年展开数学,一共20 ,答一得7 分,答一扣4 分,王磊得74 分,他答了()。
14、甲、乙两数是互数,且最小公倍数是156,那么甲、乙两数可能是()和()。
15、一只皮箱的密是一个三位数。
小光:“它是954。
”小明:“它是 358。
”小亮:“它是 214。
”小:“你每人都只猜了地点不一样的一个数字。
” 只皮箱的密是( ) 。
16、一个三位数,它是 2 和 5 的倍数,百位上的数是最小的数,十位上的数是百位上的数的倍数,个三位数最大是()。
第六节 数字与数位页码(一)日期:____________ 姓名:____________【知识要点】1.数码:用来记数的符号叫做数字,是指0、1、2、3、4、5、6、7、8、9这10个阿拉伯数字。
这10个阿拉伯数字我们叫做数码。
2.数位:记数时,常常把数字(或数码)并排成横列,一个数字占有一个位置,这些位置都叫做数位。
3.整数的表示方法之一:ABCD 表示一个十进制的四位数,ABCD =1000A+100B+10C+D=D C B A +⨯+⨯+⨯10101023【典型例题】例1 一个自然数各位上的数字和是35,这个数最小是多少?例2 求从1到999(包括1和999在内),各自然数的数字总和是多少?例3 有一个六位数,它的个位数字是9,如果把9移到这个数的首位,得到的新数是原数的4倍。
原数是多少?例4 一个两位数在它的前面写上5,所成的三位数比原两位数的8倍少18,原来的两位数是多少?例5 一个两位数,在它的前面写上8,得到一个三位数叫做甲数,在它的后面写上8,又得到一个三位数叫做乙数。
如果甲数比乙数多414,那么,原来的两位数是多少?例6 一个两位数的两个数字之和是9,将这个两位数的十位与个位上的数字加以交换,得到一个新的两位数(称为原两位数的倒转数)。
如果原来的两位数比新的两位数多45,原来的两位数是多少?随堂小测姓名:__________成绩:__________ 1.一个自然数各位上的数字之和为28,且各数字都不相等,求符合条件的最大与最小的数各是多少?2.求1、2、3、4、5、……,1997,1998,1999这些自然数中所有数字之和。
3.已知F A B CD E⨯5,求十进制数A B CD E F=ABCDEF是多少?4.一个两位数,在它的后面写上2,所成的三位数比原两位数多758,问原来的两位数是多少?5.一个两位数,十位上的数字是个位上数字的2倍,如果把个位上的数字与十位上的数字对调,那么,所得的两位数比原两位数小36,原来这两位数是多少?6.A 、B 、C 是不同的数,如果132=++CA BC AB ,那么A ×B ×C 最大的是( )。
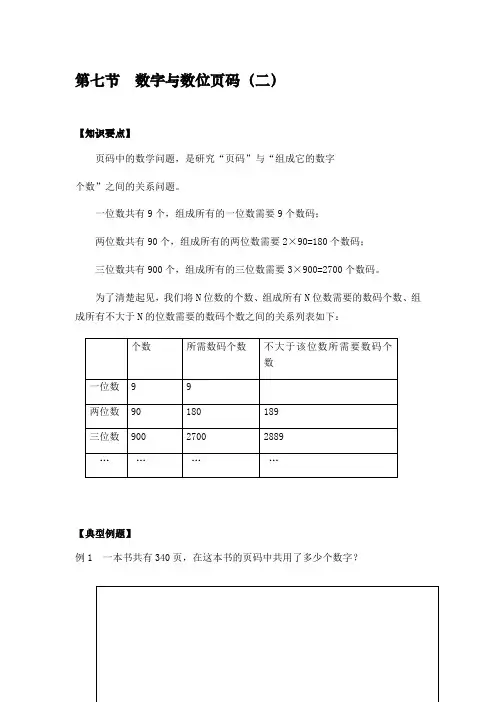
第七节 数字与数位页码(二)
【知识要点】
页码中的数学问题,是研究“页码”与“组成它的数字
个数”之间的关系问题。
一位数共有9个,组成所有的一位数需要9个数码;
两位数共有90个,组成所有的两位数需要2×90=180个数码; 三位数共有900个,组成所有的三位数需要3×900=2700个数码。
为了清楚起见,我们将N 位数的个数、组成所有N 位数需要的数码个数、组成所有不大于N 的位数需要的数码个数之间的关系列表如下:
【典型例题】
例1 一本书共有340页,在这本书的页码中共用了多少个数字?
例2 一本书的页码中共用了3429个数字,这本书有多少页?
例3 已知小数A=0.123456789101112…979899,它的小数后面的数字是由自然数1到99依次排列而成的。
问:小数点后边第68位上的数字是多少?
例4 一本英汉辞典有1034页,在这本辞典的页码中,数字0和5出现了多少次?
例5 一本书的页码一共含有100个数码5,则这本书至少有页,至多有页。
例6 甲、乙两册书的页码共用了777个数码,且甲册比乙册多7页。
甲册书有多少页?
随堂小测
1.一本漫画书有176页,在编排书的页码时,共需要多少个数字?
2.一本中篇小说的页码,在排版时必须用2211个数码,问这本
书共有多少页?
3.有一列数:1234567891011……887888889,各个数字是顺次从1至889,问第555个数字是几?
4.有一本书共1000页,编上页码1,2,3…。
问:数字2在页
码中出现多少次?
5.一本书的页码里共含有88个数字“8”,这本书至少有多少页?至多有多少页?
6.上、下两册书的页码共有687个数字,且上册比下册多5页,则上册书有多少页?
课后作业
1.给一本书编页码,一共用了723个数字,这本书一共有多少页?
2.一本小说的页码,在印刷时必须用1989个铅字,这本书共有
多少页?
3.小冬将连续自然数1,2,3…逐个相加,直到某个自然数为止。
由于计算时漏加了一个自然数而得出了错误的和为1999,这个漏
加的自然数是多少?
4.有一本600页的字典,在它的页码中,含有数字6的数有多少个?含有数字0的有多少个?
5.一本书的页码中,一共用了60个0,问这本书至少有多少页?
☆ 6.自然数的平方按从大小排成1,4,9,16,25,36,49…
问:第612个位置的数字是几?。