四年级奥数第53讲勾股定理与弦图

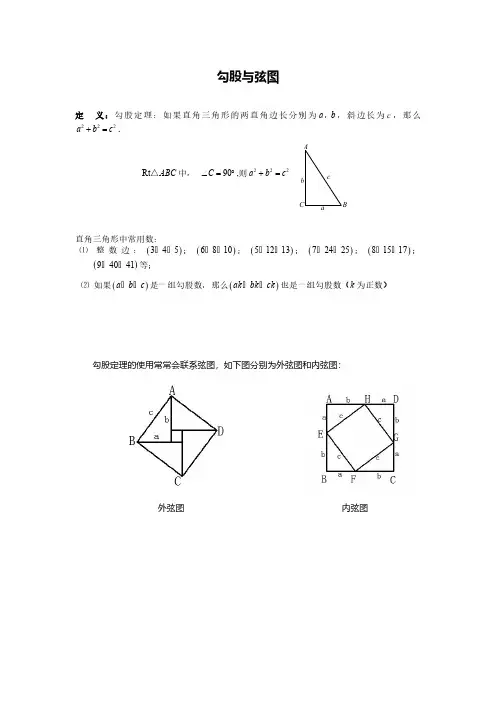
勾股与弦图定 义：勾股定理：如果直角三角形的两直角边长分别为，斜边长为，那么a b ，c ．222a b c +=中， ,则Rt ABC △90C ∠=︒222a b c +=直角三角形中常用数：⑴ 整数边：；；；；；()345，，()6810，，()51213，，()72425，，()81517，，等；()94041，，⑵ 如果是一组勾股数，那么也是一组勾股数（k 为正数） ()a b c ，，()ak bk ck ，，勾股定理的使用常常会联系弦图，如下图分别为外弦图和内弦图：外弦图内弦图cba C B A【例1】如图，要将楼梯铺上地毯，则需要 米的地毯．【例2】如图，以三角形ABC的三边为边长向外作三个正方形，正方形内的数代表正方形的面积，求未知正方形的面积.【例3】如图，是由一个直角边都是1的直角三角形向外作直角三角形得到，形成一个美丽的螺旋图案，第8个直角三角形的斜边是多少？【例4】如图所示，三角形都是直角三角形，四边形都是正方形，最大正方形的边长是7，问：除最大正方形外的所有正方形的面积之和是多少？【例5】如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为 ．【例6】下图是学校一个正方形花圃的设计图，图中阴影部分是花圃，空白部分是草坪。

求花圃的面积是多少平方米？【例7】 如图，是由四个完全相同的长方形拼成，大正方形的面积是100平方分米，小正方形的面积是16平方分米，则每个长方形的面积是多少平方分米，长方形的短边是多少分米？【例8】如图，CDEF 是正方形，ABCD 是等腰梯形，它的上底AD=23厘米，下底BC=35厘米，求三角形ADE 的面积.【例9】如下图所示，两个正方形ABCD 和DEFG 的边长都是整数厘米，点E 在线段CD 上，且CE<DE,线段CF=5厘米，则五边形ABCFG 的面积等于多少平方厘米？FGDECB A【例10】如下图所示，一个边长为10厘米的正方形木板斜靠在墙角上（木板厚度不计），AO距离为8厘米，那么点C距离地面的高度是多少厘米？。

(一)勾股定理1：勾股定理 如果直角三角形的两条直角边长分别为a 、b ，斜边长为c,那么a 2+b 2＝c 2我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.要点诠释：2、勾股定理反映了直角三角形三边之间的关系，是直角三角形的重要性质之一，其主要应用：（1）已知直角三角形的两边求第三边（在ABC ∆中，90C ∠=︒，则c，b，a ）（2）已知直角三角形的一边与另两边的关系，求直角三角形的另两边 （3）利用勾股定理可以证明线段平方关系的问题 3：勾股定理的证明勾股定理的证明方法很多，常见的是拼图的方法，用拼图的方法验证勾股定理的思路是 ①图形经过割补拼接后，只要没有重叠，没有空隙，面积不会改变②根据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理常见方法如下：方法一：4EFGHS S S ∆+=正方形正方形ABCD，2214()2ab b a c ⨯+-=，化简可证．方法二：四个直角三角形的面积与小正方形面积的和等于大正方形的面积．四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=方法三：1()()2S a b a b =+⋅+梯形，2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形，化简得证cbaHG F EDCBAa bcc baED CBA bacbac cabcab 弦股勾4：勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数，即222a b c +=中，a ，b ，c 为正整数时，称a ，b ，c 为一组勾股数②记住常见勾股数可以提高解题速度，如3,4,5；6,8,10；5,12,13；7,24,25；8,15,17；9,40,41等③用含字母的代数式表示n 组勾股数：221,2,1n n n -+（2,n ≥n 为正整数）；2221,22,221n n n n n ++++（n 为正整数）2222,2,m n mn m n -+（,m n >m ，n 为正整数）5、注意：（1）勾股定理的证明实际采用的是图形面积与代数恒等式的关系相互转化证明的。

【导语】数学应⽤之⼴泛，⼩⾄⽇常⽣活中柴⽶油盐酱醋茶的买卖、利率、保险、医疗费⽤的计算，⼤⾄天⽂地理、环境⽣态、信息络、质量控制、管理与预测、⼤型⼯程、农业经济、国防科学、航天事业均⼤量存在着运⽤数学的踪影。

以下是整理的相关资料，希望对您有所帮助。

【篇⼀】 关于勾股定理，我们已经谈过很多了。

中国、希腊、埃及这些⽂明古国，处于不同的地区，然⽽却都很早地，独⽴地发现了勾股定理。

那么，勾股定理到底是谁最先发现的呢?我们可以⾃豪地说：是我们中国⼈最先发现的。

证据就是《周髀算经》中的记载。

《周髀算经》⼀开始，就记载了我国周朝初年的⼤政治家周公旦与当时的数学家商⾼的⼀段话。

在这段话中，周公和商⾼讨论了关于直⾓三⾓形的⼀些问题。

其中就说到了“勾三股四弦五”的问题。

周公问商⾼：“我听说您很精通于数，请问数是从哪⾥来的呢?” ⼩学⽣经典数学故事《谁最先发现了勾股定理》：商⾼回答说：“数的艺术是从研究圆形和⽅形中开始的，圆形是由⽅形产⽣的，⽽⽅形是由折成直⾓的矩尺产⽣的。

在研究矩形前需要知道九九⼝诀，设想把⼀个矩形沿对⾓线切开，使得短直⾓边(勾)的长度为3，长直⾓边(股)的长度为4，斜边(弦)长则为5，并⽤四个上述直⾓三⾓形⼀样的半矩形把它围起来拼成⼀个⽅形盘，从它的总⾯积49中减去由勾股弦均分别为3、4、5的四个直⾓三⾓形构成的两个矩形的⾯积24，便得到最初所作正⽅形的⾯积25，这种⽅法称为‘积矩’。

” 商⾼对“勾三股四弦五”的描述，已经具备了勾股定理的所有条件。

⽽我们已经讲过的毕达哥拉斯发现勾股定理的年代是⽐周朝的商⾼要晚的，所以证明，我国的数学家商⾼是最早发现勾股定理的⼈。

⽽“勾股定理”⼀开始也叫“勾股弦定理”，这也形象地点明了这⼀定理的具体内容。

【篇⼆】 1.如果直⾓三⾓形的三条边长分别为2、4、a，那么a的取值可以有()A.0个B.1个C.2个D.3个 答案：C 说明：①若a为斜边长，则由勾股定理有22+42=a2，可得a=2;②若a为直⾓边长，则由勾股定理有22+a2=42，可得a=2，所以a的取值可以有2个，答案为C. 2.⼩明搬来⼀架2.5⽶长的⽊梯，准备把拉花挂在2.4⽶⾼的墙上，则梯脚与墙脚的距离为()⽶A.0.7B.0.8C.0.9D.1.0 答案：A 说明：因为墙与地⾯的夹⾓可看作是直⾓，所以利⽤勾股定理，可得出梯脚与墙脚的距离为===0.7，答案为A. 3.⼀个直⾓三⾓形的斜边长⽐直⾓边长⼤2，另⼀直⾓边长为6，则斜边长为()A.6B.8C.10D.12 答案：C 说明：设直⾓边长为x，则斜边为x+2，由勾股定理得x2+62=(x+2)2，解之得x=8，所以斜边长为8+2=10，答案为C.【篇三】 ⼀、等量代换法 已知三⾓形ABC的⾯积为56平⽅厘⽶，是平⾏四边形DEFC的2倍。

勾股定理基本知识哎，你知道吗？数学里头有个超级牛的定理，叫做勾股定理。

这不仅仅是个公式，简直就是数学界的“武林秘籍”，让人一看就忍不住想大喊一声“哇塞”！想象一下，你手里有个直角三角形，就是三条边，其中一个角是90度的那种。

这时候，勾股定理就闪亮登场了，它告诉你：直角三角形的两条直角边的平方和，等于斜边的平方。

换句话说，如果你知道其中两边的长度，就能算出第三边的长度，是不是很神奇？咱们先聊聊“勾”和“股”这两个词。

听起来是不是有点像武侠小说里的招式？其实啊，“勾”就是直角三角形的短的那条直角边，“股”就是长的那条直角边。

而斜边呢，就像是武侠小说里的大侠，高高在上，俯视着其他两条边。

记得小时候，数学老师拿着粉笔在黑板上画了一个直角三角形，然后一脸神秘地说：“同学们，这就是传说中的勾股定理！”那时候，我们一个个都瞪大了眼睛，生怕错过任何一个细节。

老师接着写道：“a²+ b²= c²”，那时候，我觉得这简直就是天书啊！不过，随着学习的深入，我渐渐发现，勾股定理其实挺接地气的。

比如说，你家里要装修，需要量一下墙角到墙角的距离，但是中间有个障碍物挡着，怎么办？这时候，你就可以用勾股定理来算一下，保证准确无误。

还有啊，如果你在户外探险，需要知道两座山峰之间的距离，但是你又不想爬上去，怎么办？这时候，你可以找个平坦的地方，用勾股定理算一下，就能知道个大概了。

是不是觉得数学也挺有用的？勾股定理不仅实用，还蕴含着深刻的哲理。

它告诉我们，事物之间都是有联系的，就像这三条边一样，虽然它们看起来是独立的，但实际上却紧密相连。

这就像我们的人生，有时候你觉得一件事情和另一件事情毫无关系，但仔细一想，却发现它们之间有着千丝万缕的联系。

而且啊，勾股定理还教会了我们一个道理，那就是“知难而进”。

你看，这个定理虽然看起来简单，但是要想真正掌握它，却需要付出很多努力。

就像我们在学习、工作和生活中遇到的困难一样，只有勇敢地面对它们，才能不断进步，不断成长。

勾股定理勾股定理在我国，把直角三角形的两直角边的平方和等于斜边的平方这一特性叫做勾股定理或勾股弦定理，又称毕达哥拉斯定理或毕氏定理（Pythagoras Theorem）。

数学公式中常写作a^2+b^2=c^2目录概述定义简介勾股定理指出勾股数组推广勾股定理定理勾股定理的来源毕达哥拉斯树常见的勾股数勾、股、弦的比例最早的勾股定理应用《周髀算经》中勾股定理的公式与证明加菲尔德证明勾股定理的故事多种证明方法证法1证法2证法3证法4证法5(欧几里得的证法)证法6（欧几里德(Euclid)射影定理证法）证法七（赵爽弦图）证法8（达芬奇的证法）证法9习题及答案定义介绍勾股定理逆定理概述定义简介勾股定理指出勾股数组推广勾股定理定理勾股定理的来源毕达哥拉斯树常见的勾股数勾、股、弦的比例最早的勾股定理应用《周髀算经》中勾股定理的公式与证明加菲尔德证明勾股定理的故事多种证明方法证法1证法2证法3证法4证法5(欧几里得的证法)证法6（欧几里德(Euclid)射影定理证法）证法七（赵爽弦图）证法8（达芬奇的证法）证法9习题及答案定义介绍勾股定理逆定理展开编辑本段概述定义在任何一个直角三角形中，两条直角边的长的平方和等于斜边长的平方。

勾股定理(6张)简介勾股定理是余弦定理的一个特例。

这个定理在中国又称为“商高定理”，在外国称为“毕达哥拉斯定理”或者“百牛定理“。

（毕达哥拉斯发现了这个定理后，即斩了百头牛作庆祝，因此又称“百牛定理”），法国、比利时人又称这个定理为“驴桥定理”。

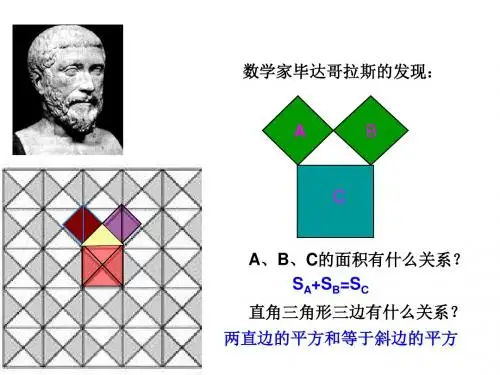
他们发现勾股定理的时间都比我国晚，我国是最早发现这一几何宝藏的国家。

目前初二学生学，教材的证明方法采用赵爽弦图，证明使用青朱出入图。

勾股定理是一个基本的几何定理，它是用代数思想解决几何问题的最重要的工具之一，是数形结合的纽带之一。

直角三角形两直角边的平方和等于斜边的平方。

如果用a、b和c分别表示直角三角形的两直角边和斜边，那么a^2+b^2=c^2。

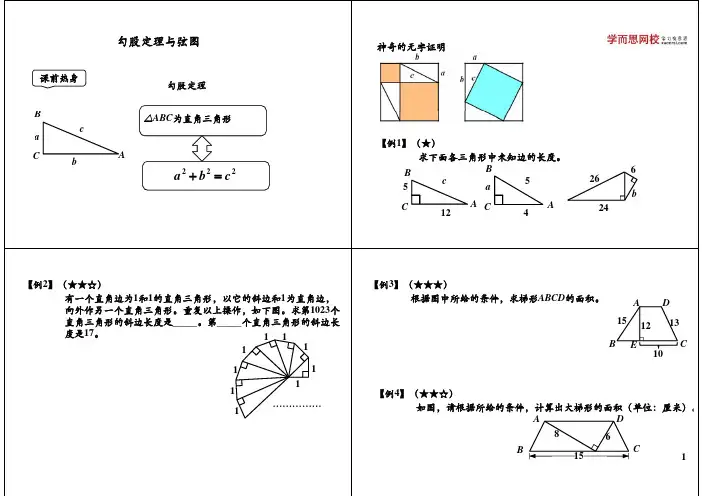
勾股定理与弦图【例1】(★★)
求下面各三角形中未知边的长度。

课前热身
神奇的无字证明
【例2】(★★★) 【例3】(★★★)
有一个直角边为1 和1 的直角三角形，以它的斜边和1 为直角边，向外作另根据图中所给的条件，求梯形ABCD的面积。

一个直角三角形。

重复以上操作，如下图。

求第1023 个直角三角形的斜边
长度是_____。

第_____个直角三角形的斜边长度是17。

【例4】(★★★)
如图，请根据所给的条件，计算出大梯形的面积（单位：厘米）。

1
弦图
【例5】(★★★★)
如图，在四边形ABCD 中，AB＝30 ，AD＝48，BC＝14 ，CD＝40，∠ADB
＋∠DBC＝90°。

请问：四边形ABCD 的面积是多少？
⑴大正方形边长为：a＋b
⑵小正方形边长为：a－b
⑶中正方形边长为：c
本讲总结
【例6】(★★★)
一个直角三角形的斜边长8 厘米，两个直角边的长度差为2 厘
米，求这个三角形的面积？
【例7】(★★★★★)
从一块正方形玻璃上裁下宽为16 分米的一长方形条后，剩下的那块长方形
的面积为336 平方分米，原来正方形的面积是多少平方分重点例题：例1，例2，例6，例7
米？
2。

这篇关于《⼩学奥数⼏何专题：勾股定理与弦图练习》，是特地为⼤家整理的，希望对⼤家有所帮助！
1．如果直⾓三⾓形的三条边长分别为2、4、a，那么a的取值可以有( )
A．0个 B．1个 C．2个 D．3个
答案：C
说明：①若a为斜边长，则由勾股定理有22+42=a2，可得a=2 ；②若a为直⾓边长，则由勾股定理有22+a2=42，可得a=2 ，所以a的取值可以有2个，答案为C．
2．⼩明搬来⼀架2.5⽶长的⽊梯，准备把拉花挂在2.4⽶⾼的墙上，则梯脚与墙脚的距离为( )⽶
A．0.7 B． 0.8 C．0.9 D．1.0
答案：A
说明：因为墙与地⾯的夹⾓可看作是直⾓，所以利⽤勾股定理，可得出梯脚与墙脚的距离为 = = =0.7，答案为A．
3．⼀个直⾓三⾓形的斜边长⽐直⾓边长⼤2，另⼀直⾓边长为6，则斜边长为( )
A．6 B． 8 C．10 D．12
答案：C
说明：设直⾓边长为x，则斜边为x+2，由勾股定理得x2+62=(x+2)2，解之得x=8，所以斜边长为8+2=10，答案为C．。