点的合成运动 习题解答
- 格式:doc
- 大小:1.98 MB
- 文档页数:11

第八章 点的合成运动8-1 M 点沿y 轴作谐运动,运动方程为:0=x ,()β+=kt a y cos 。
如将M 点放映到银幕上,此银幕以匀速v 向左运动。
试分析M 点的牵连、相对和绝对运动,并求M 点映在银幕上的轨迹。
答案:相对运动方程 ()⎩⎨⎧+='='βkt a y vt x cos ;相对运动轨迹 ⎪⎭⎫ ⎝⎛+'='βx v k a y cos8-2 M 点沿圆盘直径AB 以v 匀速运动,当开始时,M 点在圆盘中心,且直径AB 与Ox 轴重合。
如圆盘以匀角速度w 绕O 轴转动,求M 点的绝对轨迹。
答案:轨迹方程:ϕωv r =8-3 半径为r 的齿轮Ⅱ由曲柄OA 带动沿同样半径的固定齿轮Ⅰ而滚动,曲柄以角速度w 0绕O 轴转动。
设在曲柄OA 上固连一动系,试求动齿轮上B 、C 、D 三点的牵连速度。
答案:0003,5,ωωωr v r v r v eD eB eC ===8-4 河的两岸相互平行,设各处河水流速均匀且不随时间改变。
一船由点A 朝与岸垂直的方向等速驶出,经10min 到达对岸,这时船到达点B 下游120m 的点C 。
为使船从点A 能垂直到达对岸的点B ,船应逆流并保持与直线AB 成某一角度的方向航行。
再此情况下,船经12.5min 到达对岸。
求河宽L 、船对水的相对流速v r 和水的流速v 的大小。
答案:200m L =;m /s 333.0=r v ;m/s 2.0=v8-5 水流在水轮机工作轮入口处的绝对速度m/s 15=a v ,并与铅垂直径成︒=60ϕ角。
工作轮的半径m 2R =,转速r/min 30n =。
为避免水流对工作轮叶片想冲击,叶片应恰当的安装,以使水流对工作轮的相对速度与叶片相切。
求在工作轮外缘处水流对工作轮的相对速度的大小和方向。
答案:m /s 06.10=r v ; v r 与半径的夹角为︒8.418-6 矿砂从传送带A 落到另一传送带B ,其绝对速度m /s 4v 1=,方向与铅直线成︒30角。


第五章 点的合成运动本章要点一、绝对运动、相对运动和牵连运动一个动点,两个参照系: 定系,动系;三种运动:绝对运动、相对运动和牵连运动, 包括三种速度:绝对速度、相对速度和牵连速度; 三种加速度:绝对加速度、相对加速度和牵连加速度;牵连点:动参考系上瞬时与动点相重合的那一点称为动参考系上的牵连点。
二、速度合成定理动点的绝对速度,等于它在该瞬时的牵连速度与相对速度的矢量和,即r e a v v v +=解题要领1 定系一般总是取地面,相对定系运动的物体为动系,动点不能在动系上.2 牵连速度是牵连点的速度.3 速度合成定理中的三个速度向量,涉及大小方向共六个因素,能且只能存在两个未知数方能求解,因此,至少有一个速度向量的大小方向皆为已知的.4 作速度平行四边形时,注意作图次序:一定要先画大小方向皆为已知的速度向量,然后再根据已知条件画上其余两个速度向量,特别注意,绝对速度处于平行四边形的对角线位置.5 用解三角形的方法解速度合成图. 三、加速度合成定理1 牵连运动为平移时的加速度合成定理当牵连运动为平移时,动点的绝对加速度等于牵连加速度与相对加速度的矢量和,即r e a a a a +=,当点作曲线运动时,其加速度等于切向加速度和法向加速度的矢量和,因此上式还可进一步写成n r t r ne t e n a t a a a a a a a +++=+其中 t v a d d a t a=,a 2a n a ρv a =,t v a d d e t e =,e2e n e ρv a =,t v a d d r t r =,r 2r nr ρv a =,r e a ,,ρρρ依次为绝对轨迹、牵连轨迹和相对轨迹的曲率半径。
解题要领1牵连运动为平移时的加速度合成定理只对“牵连运动为平移时”成立,因此,判定牵连运动是否为平移至关重要.2 牵连运动为平移时的加速度合成定理涉及的三个加速度,每一加速度都可能有切向和法向加速度。

习 题7-1 如图7-26所示,光点M 沿y 轴作谐振动,其运动方程为:x = 0,)cos(θω+=t A y ,式中,A 、ω、θ均为常数。
如将点M 投影到感光记录纸上,此纸以等速v e 向左运动,试求点在记录纸上的轨迹。
图7-26t v x e =')cos()cos(eθωθω+'=+=='x v A t A y y7-2 用车刀切削工件的端面,车刀刀尖M 的运动方程为 t b x ωsin =,其中b 、ω为常数,工件以等角速度ω逆时针方向转动,如图7-27所示。
试求车刀在工件端面上切出的痕迹。
图7-27t b t y t x x ωωωsin sin cos ='-'= 0cos sin ='+'=t y t x y ωω 解得)2sin(2cos sin sin tan cos sin t b t t b t t t t b x ωωωωωωω==+=' ]1)2[cos(2sin tan 2-=-='-='t bt b t x y ωωω4)2()(222b b y x =+'+'7-3 河的两岸相互平行,如图7-28所示。
设各处河水流速均匀且不随时间改变。
一船由点A 朝与岸垂直的方向等速驶出,经过10 min 到达对岸,这时船到达点B 的下游120 m 处的点C 。
为使船A 能垂直到达对岸的点B ,船应逆流并保持与直线AB 成某一角度的方向航行。
在此情况下,船经12.5 min 到达对岸。
试求河宽L 、船相对于水的相对速度v r 和水的流速v 的大小。
图7-28m/s 2.0600120==v 600r L v =船A 能垂直到达对岸的点B750a L v = 2a22r v v v += 2222.0)750()600(+=L L m 200)7501()6001(2.022=-=L m/s 31r =v7-4 半径R = 60mm 的半圆管BC 绕定轴OO 1按规律)5(t t -=ϕ转动,点在管内运动,相对于管子的运动方程为2π10t BM =(弧长的单位为mm),如图7-29所示。

第 5 章点的合成运动习题解答0 8 08 1 4第五章点的合成运动本章要点一、绝对运动、相对运动和牵连运动一个动点,两个参照系:定系,动系;三种运动:绝对运动、相对运动和牵连运动,包括三种速度:绝对速度、相对速度和牵连速度;三种加速度:绝对加速度、相对加速度和牵连加速度;牵连点:动参考系上瞬时与动点相重合的那一点称为动参考系上的牵连点。
二、速度合成定理动点的绝对速度,等于它在该瞬时的牵连速度与相对速度的矢量和,即V a V e V r解题要领1定系一般总是取地面,相对定系运动的物体为动系,动点不能在动系上.2牵连速度是牵连点的速度•3速度合成定理中的三个速度向量,涉及大小方向共六个因素,能且只能存在两个未知数方能求解,因此,至少有一个速度向量的大小方向皆为已知的.4作速度平行四边形时,注意作图次序:一定要先画大小方向皆为已知的速度向量,然后再根据已知条件画上其余两个速度向量,特别注意,绝对速度处于平行四边形的对角线位置.5用解三角形的方法解速度合成图.三、加速度合成定理1牵连运动为平移时的加速度合成定理当牵连运动为平移时,动点的绝对加速度等于牵连加速度与相对加速度的矢量和,即a a a e a r ,当点作曲线运动时,其加速度等于切向加速度和法向加速度的矢量和,因此上式还可进一步写成a;a a a e n t na e a r a r其中a;dv;,n aa2V a tdV e n,a e ,a e2Ve a t,a r dV r,a n2v■ ?a, e, r依次dt a dt e dt r为绝对轨迹、牵连轨迹和相对轨迹的曲率半径。
解题要领1牵连运动为平移时的加速度合成定理只对“牵连运动为平移时”成立,因此,判定牵连运动是否为平移至关重要.2牵连运动为平移时的加速度合成定理涉及的三个加速度,每一加速度都可能有切向和法向加速度。
但是,法向加速度只与速度有关,因此,可以通过速度分析予以求解,从而在此处是作为已知的。
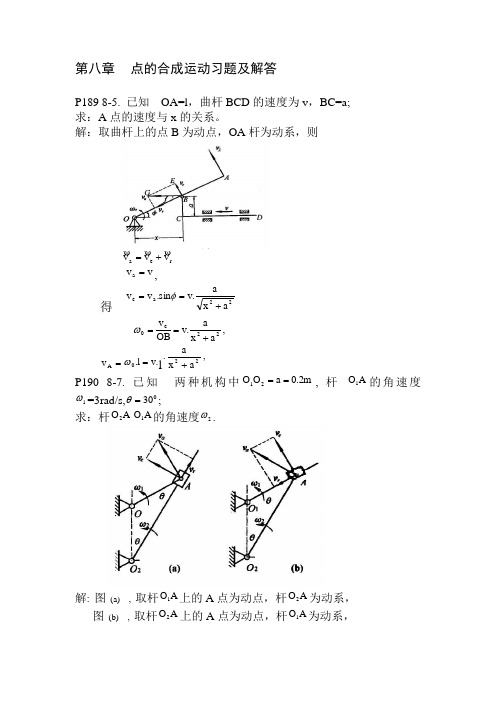
第八章 点的合成运动习题及解答P189 8-5. 已知 OA=l ,曲杆BCD 的速度为v ,BC=a; 求:A 点的速度与x 的关系。
解:取曲杆上的点B 为动点,OA 杆为动系,则r e a v v v +=v v a =,得22a e a x a .v s i n .v v +==φ ,a x a.v OB v 22e 0+==ω=A v .v l .0=ωl ,a x a .22+P190 8-7. 已知 两种机构中2m .0a O O 21==, 杆 A O 1的角速度1ω=3rad/s,030=θ;求:杆A O 2A O 1的角速度2ω.解: 图 (a) , 取杆A O 1上的A 点为动点,杆A O 2为动系,图 (b) , 取杆A O 2上的A 点为动点,杆A O 1为动系,由: r e av v v += 分别作速度矢量图。
由图 (a) 解出23a.cos30.v v 10a e ω==,,s /rad 5.12A O v 12e 2===ωω由图 (b) 解出32.a .cos30v v 10e a ω==, ,s /5r a d .12A O v 12e 2===ωω.s /rad 232A O v 12a 2===ωωP190 8-9. 已知 ==V v AB 常数,当t=0时,0=ϕ;求:045=ϕ时,点C 的速度的大小。
解: 取杆AB 上的A 点为动点,杆OC 为动系,由: r e av v v += 作速度矢量图。
ϕϕcos .v cos .v v a e ==,lcos .a OA OC .v v e c ϕ==解出 l a .c o svv 2c ϕ=,当045=ϕ时, 2l av v c =P190 8-10. 已知,轮C 半径为R ,偏心距OC=e, 角速度 ω=常数;求:00=ϕ时,平底杆AB 的速度。
解: 取轮心C 为动点,平底杆AB 为动系,由: r e av v v += 作速度矢量图。
第7章 点的合成运动一、是非题(正确的在括号内打“√”、错误的打“×”)1.点的速度和加速度合成定理建立了两个不同物体上两点之间的速度和加速度之间的 关系。
( √ ) 2.根据速度合成定理,动点的绝对速度一定大于其相对速度。
( × )3.应用速度合成定理,在选取动点和动系时,若动点是某刚体上的一点,则动系不可以固结在这个刚体上。
( √ )4.从地球上观察到的太阳轨迹与同时在月球上观察到的轨迹相同。
( × ) 5.在合成运动中,当牵连运动为转动时,科氏加速度一定不为零。
( × ) 6.科氏加速度是由于牵连运动改变了相对速度的方向而产生的加速度。
( √ ) 7.在图中,动点M 以常速度r v 相对圆盘在圆盘直径上运动,圆盘以匀角速度ω绕定轴O 转动,则无论动点运动到圆盘上的什么位置,其科氏加速度都相等。
( √ )二、填空题1.已知r 234=++v i j k ,e 63=-ωi k ,则k =a 18 i + -60 j + 36 k 。
2.在图中,两个机构的斜杆绕O 2的角速度均为2ω,O 1O 2的距离为l ,斜杆与竖直方向的夹角为θ,则图(a)中直杆的角速度=1ωθθωcos sin 2,图(b)中直杆的角速度=1ω2ω。
图 图3.科氏加速度为零的条件有:动参考系作平动、0=r v 和r e v ω//。
4.绝对运动和相对运动是指动点分别相对于定系和动系的运动,而牵连运动是指牵连点相对于定系的运动。
牵连点是指某瞬时动系上和动点相重合的点,相应的牵连速度和加速度是指牵连点相对于定系的速度和加速度。
5.如图所示的系统,以''Ax y 为动参考系,Ax'总在水平轴上运动,AB l =。
则点B 的相对轨迹是圆周,若kt ϕ= (k 为常量),点B 的相对速度为lk ,相对加速度为2lk 。
图6.当点的绝对运动轨迹和相对运动轨迹都是曲线时,牵连运动是直线平动时的加速度合成定理表达式是a e r =+a a a ;牵连运动是曲线平动时的加速度合成定理表达式是 a e r =+a a a ;牵连运动是转动时的加速度合成定理表达式是a e r k =++a a a a 。
点的合成运动作业参考答案(求加速度和角加速度)1、图示倾角ϕ =30º的尖劈以匀速v =200mm/s 沿水平面向右运动,使杆OB 绕定轴O 转动;r =2003mm 。
求当θ =ϕ 时,杆OB 的角速度和角加速度。
思路: 以杆OB 上的点B 为动点,动系与尖劈固结,则绝对轨迹为圆弧,相对轨迹是尖劈上的倾斜直线,牵连运动是水平直线平移。
答案: , rad/s 31=ω逆时针;2rad/s 273 =α ;顺时针。
2、图示小环M 套在半径OC = R =120mm 的固定半圆环和作平动的直杆AB 上。
当OB =BC =60mm 瞬时,AB 杆以速度为30mm/s 及加速度为30mm/s 2向右加速运动;试求小环M 的相对速度和相对加速度。
思路: 以小环M 为动点,动系与杆AB 固结,则绝对轨迹为圆弧,相对轨迹是铅垂直线,牵连运动是水平直线平移。
答案: 2r r mm/s 3310 mm/s, 310==a v3、已知直角弯杆OAB 绕轴O 以匀角速度ω 转动,小环M 同时套在半径为R 的固定圆环和直角弯杆OAB 上(圆环与直角弯杆在同一平面内),几何尺寸如图9 。
在图示瞬时,AB 水平且通过圆环中心C 。
求该瞬时小环M 的绝对速度和绝对加速度。
思路: 以小环M 为动点,动系与直角弯杆OAB 固结,则绝对轨迹为圆弧,相对轨迹是水平直线,牵连运动是绕轴O 的定轴转动。
答案: ↑==→==↑== , , 2ta t2na na ωωωR a a R a a R v v M M M22ωR a M =与水平线夹角450 。
4、机构如图所示,已知圆盘半径为r ,可绕水平轴O 定轴转动;杆AB 可在水平滑道中移动。
其端点A 始终与圆盘边缘接触且在圆盘边缘上运动,若图示瞬时杆AB 以匀速v 向左运动,求该瞬时圆盘的角速度和角加速度。
思路1: 以杆端A 为动点,动系与圆盘C 固结,则绝对轨迹为水平直线,相对轨迹是以点C 为圆心的圆弧,牵连运动是绕轴O 的定轴转动。
2-1 凸轮以匀角速度ω绕O 轴转动,杆AB 的A 端搁在凸轮上。
图示瞬时AB 杆处于水平位置,OA 为铅直。
试求该瞬时AB 杆的角速度的大小及转向。
解: r e a v v v += 其中,22e r v e -=ωe v v e a ωφ==tg所以 le l v a AB ωω==(逆时针)2-2. 平底顶杆凸轮机构如图所示,顶杆AB 可沿导轨上下移动,偏心圆盘绕轴O 转动,轴O 位于顶杆轴线上。
工作时顶杆的平底始终接触凸轮表面。
该凸轮半径为R ,偏心距e OC =,凸轮绕轴O 转动的角速度为ω,OC 与水平线成夹角ϕ。
求当︒=0ϕ时,顶杆的速度。
(1)运动分析 |轮心C 为动点,动系固结于AB ;牵连运动为上下直线平移,相对运动为与平底平行直线,绝对运动为绕O 圆周运动。
(2)速度分析,如图b 所示2-3. 曲柄CE 在图示瞬时以ω0绕轴E 转动,并带动直角曲杆ABD 在图示平面内运动。
若d 为已知,试求曲杆ABD 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e av v v +=0a 2ωl v =;0e a 2ωl v v ==01e1ωω==AO v BC O (顺时针) 2-4. 在图示平面机构中,已知:AB OO =1,cm 31===r B O OA ,摇杆D O 2在D 点与套在AE 杆上的套筒铰接。
OA 以匀角速度rad/s 20=ω转动,cm 332==l D O 。
试求:当︒=30ϕ时,D O 2的角速度和角加速度。
.解:取套筒D 为动点,动系固连于AE 上,牵连运动为平动 (1)由r e a v v v += ①*得D 点速度合成如图(a )得 ϕtg e a v v =, 而r v e 0ω= 因为 r v a 0331ω⨯=,所以 rad/s 67.02==lv aD O ω 方向如图(a)所示(2)由r e na a a a a a +=+τ ②得D 点加速度分析如图(b ) 将②式向DY 轴投影得θϕϕτsin sin cos e n a a a a a -=-而r a la e D O na 2022ωω==θϕsin sin r l =/所以ϕθϕτcos sin sin e na a a a a -=2rad/s 05.2cos sin sin 2-=-==ϕθϕετl a a l a e n a a DO ,方向与图(b)所示相反。
.2-5.图示铰接平行四边形机构中,m m 10021==B O A O ,又AB O O =21,杆A O 1以等角速度s rad 2=ω绕1O 轴转动。
杆AB 上有一套筒C ,此筒与杆CD 相铰接。
机构的各部件都在同一铅直面内。
求当︒=60ϕ时,杆CD 的速度和加速度。
2-6图示圆盘绕AB 轴转动,其角速度rad/s 2t =ω。
点M 沿圆盘半径ON 离开中心向外缘运动,其运动规律为mm 402t OM =。
半径ON 与AB 轴间成︒60倾角。
求当s 1=t 时点M 的绝对加速度的大小。
解 点M 为动点,动系Oxyz 固结于圆盘;牵连运动为定轴转动,相对运动为沿径向直线运动,绝对运动为空间曲线。
其中轴x 垂直圆盘指向外,加速度分析如图所示,当t =1 s 时,代入数据得2-7. 图示直角曲杆OBC 绕O 轴转动,使套在其上的小环P 沿固定直杆OA 滑动。
已知:m 1.0=OB ,曲杆的角速度s rad 5.0=ω,角加速度为零。
求当︒=60ϕ时,小环P 的速度和加速度。
解:1、运动分析(图5-4):动点:小环M ;动系:固连于OBC ; ~绝对运动:沿OA 杆的直线运动; 相对运动:沿BC 杆的直线运动;牵连运动:绕O 点的定轴转动。
2、速度分析:r e a v v v += (a ) 其中 v a 、v e 、v r 方向如图所示。
v e =OP ω⋅=×=0.1m/s ;于是(a)式中只有v a 、v r 二者大小未知。
从而由速度平行四边形解得小环M 的速度v a =3e v =0.173m/s此外,还可求得…v r =2 v e =0.2m/s 。
2.加速度分析(图5-10)。
绝对加速度a a牵连加速度en a相对加速度r a<科氏加速度C a 大小 未知 22.0ω未知2v r 方向沿OA指向O 点¥沿BC垂直BCa a =en a +r a +C a应用投影方法,将上式加速度合成定理的矢量方程沿垂直BC 方向投影,有a en cos cos C a a a =-+ϕϕ a en 2C a a a =-+ 由此解得35.0a ==a a M m/s 2方向如图所示。
"2-8 半径为R 的圆轮,以匀角速度ω0绕O 轴沿逆时针转动,并带动AB 杆绕A 轴转动。
在图示瞬时,OC 与铅直线的夹角为60,AB 杆水平,圆轮与AB 杆的接触点D 距A 为3R 。
求此时AB 杆的角加速度。
解:1.运动分析:动点:C ,动系:杆AB ,绝对运动:圆周运动,相对运动:直线,牵连运动:定轴转动。
2.速度分析(图a ) r e a v v v += e 0a v R v ==ω $220e ωω==R v AB 0r =v3.加速度分析(图b )t e ne r a a a a a ++=沿铅垂方向投影:︒-︒=︒30sin 30cos 60cos n e t e a a a a R R R a a a 202020n ea te23)2(31)(30tan ωωω=+=+︒=;20t e 43ωα==CA a AB 习题5-15图@ ω0 R C D A R 3 O v a :v r 60 ω0 R C D > R 3Oa a a r te a ne a2-10 曲柄 O 1M 1以匀角速度ω1=3 rad /s 绕 O 1轴沿逆时针转动。
T 形构件作水平往复运动,M 2为该构件上固连的销钉。
槽杆O 2E 绕O 2轴摆动。
已知O 1M 1=r =20cm ,l =30 cm 。
当机构运动到如图所示位置时,θ=φ=30,求此时O解:1.运动分析:动点:M 1,动系:杆AB ,绝对运动:圆周运动,相对运动:直线,牵连运动:平移。
速度分析(图a ):r1e1a1v v v +=6011a ==ωr v cm/s ;30sin 1a 1e ==θv v cm/s加速度分析(图b ): e1r1a1a a a +=沿铅垂方向投影:39023cos 211a 1e ===r a a ωθ cm/s 22.运动分析:动点:M 2,动系:杆O 2E ,绝对运动:直线,相对运动:直线,牵连运动:定轴转动。
—速度分析(图a ):r2e2a2v v v +=301e 2a ==v v cm/s ;315cos 2a 2e ==ϕv v cm/s ;15sin 2a 2r ==ϕv v cm/s ;75.0cos 2e 2==ϕωlv E O rad/s O 1 θ φAB!DCM 2EO 2lω1 O 1θφABM 1>CM 2EO 2lω1 习题5-16图(a )(b )\v a2v e1v e2v r1 v r2a a1a a2a r1a r2@t 2e an 2e aa e1加速度分析(图b ): 2C te2n e2r2a2a a a a a +++=沿a C 方向投影:C t 2e 2a cos a a a +-=-ϕ;5.15775.015213530cos 2C 1e t 2e =⨯⨯+=+︒=a a a cm/s 2 55.46035.157cos t 2e 2===ϕαl a EO rad/s 22-12.绕轴O 转动的圆盘及直杆OA 上均有一导槽,两导槽间有一活动销子M 如图所示,m 1.0=b 。
设在图示位置时,圆盘及直杆的角速度分别为s rad 91=ω和s rad 32=ω。
角加速度均为零。
求此瞬时销子M 的速度和加速度。
解(1)运动分析①活动销子M 为动点,动系固结于轮O;牵连运动为绕O 定轴转动,相对运动为沿轮上导槽直线,绝对运动为平面曲线。
②活动销子M 为动点,动系固结于杆OA;牵连运动为绕O 定轴转动,相对运动为沿OA 直线,绝对运动为平面曲线。
速度分析如图b 所示,由式(1)、(2)得21220111012122112221118736865030363093654542041414359..)a a (a .sin a a a .a cos a a .a ,.a .a .a .a .a a a a a a a a /y x n e r c n e x r r c n e c n e c r n e c r n e a ==+==-==+=======++=++=α22y 2222222cm/s 6 cm/s m/sm/s m/s m/s m/s m/s m/s --。