三角形的重心 PPT
- 格式:ppt
- 大小:178.00 KB
- 文档页数:11

三角形的重心课件关键信息项:1、课件的使用目的:____________________________2、课件的版权归属:____________________________3、课件的更新与维护责任:____________________________4、课件的适用范围:____________________________5、课件的使用期限:____________________________6、对课件内容的保密要求:____________________________7、违反协议的责任与处罚:____________________________11 协议的背景和目的本协议旨在规范关于三角形的重心课件的使用、传播、更新和维护等相关事宜,以确保该课件能够有效地服务于其预期的教育目的,并保障相关各方的合法权益。
111 三角形的重心课件的定义本协议中所提及的三角形的重心课件,是指一套专门用于讲解三角形重心相关知识的多媒体教学材料,包括但不限于演示文稿、动画、视频、练习题等。
12 协议的适用范围本协议适用于所有获得、使用或传播三角形的重心课件的个人和机构。
21 课件的使用目的该课件仅用于教育和学习目的,不得用于任何商业盈利活动。
使用者可以将其用于课堂教学、自主学习、辅导教学等与教育相关的活动。
211 禁止的使用方式使用者不得对课件进行修改、篡改、反编译或以其他方式破坏其完整性和功能性,不得将其用于非法、有害、淫秽或违背社会公德的目的。
22 课件的版权归属三角形的重心课件的版权归创作者所有,未经版权所有者的明确书面授权,任何人不得擅自复制、分发、传播或对其进行二次创作。
221 授权使用范围版权所有者授予使用者在一定范围内非独家的使用权利,但使用者必须遵守本协议的各项规定。
31 课件的更新与维护责任版权所有者有责任对课件进行必要的更新和维护,以确保其内容的准确性和时效性。
但在合理的范围内,使用者也有义务向版权所有者反馈发现的错误或需要改进的地方。



第八讲三角形的重心-CAL-FENGHAI.-(YICAI)-Company One1第八讲 三角形的重心、垂心、外心和内心初中阶段我们已经学习了关于三角形的边和角的许多性质,也涉及三角形边上中线、高线、垂直平分线以及内角平分线的一些性质。
例如,线段(如三角形的一边)的垂直平分线上的点和这条线段两站点的距离相等。
反之,和一条线段两个端点距离相等的点在这线段的垂直平分线上;角(如三角形的一个内角)的平分线上的点到这个角的两边的距离相等。
反之,到一个角的两边距离相等的点在这个角的平分线上,诸如此类。
涉及一个三角形的三条中线、三条高线、三条边的垂直平分线以及三个内角平分线的性质及相互关系是中学平面几何的重要内容。
在高中学习中,会涉及三角形三条中线交点、三条高线交点、三条边的垂直平分线交点以及三个内角平分线交点,即三角形的几个“巧合点”。
本节将对这些知识作较系统的阐述。
一、三角形的重心如图8-1,在△ABC 中,AD 、BD 是两条中线,记它们的交点为G ,连接DE 、DE 是三角形的中位线。
∴DE ∥AB ,且.21AB DE ∴∠GAB=∠GDE ,∠GBA=∠GED.∴△AGB ∽△DGE ,且相似比为2:1.∴AG=2GD ,BG=2GE. 于是得到关于三角形中线的一个重要性质:三角形的两条中线的交点把这两条中线都分成2:1的两段。
现在再研究第三条中线与其他两条中线交点有什么特殊性质。
图8-1图8-2如图8-2,设△ABC 的两条中线AD 、BE 交于G ,中线CF 、BE 交于G ′.由已知的三角形中线的性质,则有BG=2GE ,且BG ′=2G ′E ,CG ′=2G ′F.∴G ′与G 重合,则三角形的三条中线相交于一点,且该点把三角形的各中线分成长度比为2:1的两段,这个交点称为三角形的重心。
三角形的重心必在三角形的内部。
今后我们也常说:三角形的重心把中线分成2:1的两段。
例1 如图8-3,已知E 、F 分别是平行四边形ABCD 边AD 、CD 的中点,BE 和BF 分别交对角线AC 于M 、N ,求证:AM=MN=NC 。

三角形的重心性质目录1. 三角形的重心性质1.1 重心的定义1.2 重心的位置1.2.1 等边三角形的重心1.2.2 直角三角形的重心1.3 重心和质心的区别1.3.1 定义区别1.3.2 几何性质区别2. 重心与三角形内部区域的关系2.1 重心到顶点的距离比2.2 重心将三角形分割的性质2.2.1 重心将三角形分割成三等面积的三角形2.2.2 重心将三角形分割成六等面积的三角形2.2.3 重心将三角形分割成三个面积比为1:2的三角形三角形的重心性质1.1 重心的定义三角形的重心是指三条中线的交点,即由三条中线交汇形成的点称为三角形的重心。
1.2 重心的位置1.2.1 等边三角形的重心在等边三角形中,三角形的重心和质心重合,且重心距离任何一个顶点和中心的距离都相等。
1.2.2 直角三角形的重心对于直角三角形,重心位于斜边上离直角边的邻边的1/3处。
1.3 重心和质心的区别1.3.1 定义区别重心是在三角形内部的点,是由三条中线交汇形成的点;而质心是三角形的三条边上的距离各角相等的点。
1.3.2 几何性质区别重心是三角形的一个几何中心,质心是三角形的一个几何参数。
重心与三角形内部区域的关系2.1 重心到顶点的距离比三角形的重心到各个顶点的距离比为2:1,即重心到顶点的距离是中位线长度的两倍。
2.2 重心将三角形分割的性质2.2.1 重心将三角形分割成三等面积的三角形三角形的重心将三角形分割成三个面积相等的三角形。
2.2.2 重心将三角形分割成六等面积的三角形三角形的重心将三角形分割成六个面积相等的三角形。
2.2.3 重心将三角形分割成三个面积比为1:2的三角形三角形的重心将三角形分割成三个面积比为1:2的三角形,其中比重心到顶点的距离2/3的那一个三角形面积为整个三角形面积的1/4,另外两个的面积之和为3/4。

第八讲 三角形的重心、垂心、外心和内心初中阶段我们已经学习了关于三角形的边和角的许多性质,也涉及三角形边上中线、高线、垂直平分线以及内角平分线的一些性质。
例如,线段(如三角形的一边)的垂直平分线上的点和这条线段两站点的距离相等。
反之,和一条线段两个端点距离相等的点在这线段的垂直平分线上;角(如三角形的一个内角)的平分线上的点到这个角的两边的距离相等。
反之,到一个角的两边距离相等的点在这个角的平分线上,诸如此类。
涉及一个三角形的三条中线、三条高线、三条边的垂直平分线以及三个内角平分线的性质及相互关系是中学平面几何的重要内容。
在高中学习中,会涉及三角形三条中线交点、三条高线交点、三条边的垂直平分线交点以及三个内角平分线交点,即三角形的几个“巧合点”。
本节将对这些知识作较系统的阐述。
一、三角形的重心如图8-1,在△ABC 中,AD 、BD 是两条中线,记它们的交点为G ,连接DE 、DE 是三角形的中位线。
∴DE ∥AB ,且.21AB DE ∴∠GAB=∠GDE ,∠GBA=∠GED.∴△AGB ∽△DGE ,且相似比为2:1.∴AG=2GD ,BG=2GE. 于是得到关于三角形中线的一个重要性质:三角形的两条中线的交点把这两条中线都分成2:1的两段。
现在再研究第三条中线与其他两条中线交点有什么特殊性质。
图8-1 图8-2如图8-2,设△ABC 的两条中线AD 、BE 交于G ,中线CF 、BE 交于G ′.由已知的三角形中线的性质,则有BG=2GE ,且BG ′=2G ′E ,CG ′=2G ′F.∴G ′与G 重合,则三角形的三条中线相交于一点,且该点把三角形的各中线分成长度比为2:1的两段,这个交点称为三角形的重心。
三角形的重心必在三角形的内部。
今后我们也常说:三角形的重心把中线分成2:1的两段。
例1 如图8-3,已知E 、F 分别是平行四边形ABCD 边AD 、CD 的中点,BE 和BF 分别交对角线AC 于M 、N ,求证:AM=MN=NC 。
![53231_三角形的重心[4页]](https://uimg.taocdn.com/5d65e327af1ffc4ffe47acaf.webp)

§3 三角形的重心基础知识性质1 三角形的重心是三角形三条中线的交点.性质2 设G 为ABC ∆的重心,连AG 并延长交BC 于D , 则D 为BC 的中点,AG :GD 2=:1, 且()22224121BC AC AB AD -+=. 性质3 设G 为ABC ∆的重心,过G 作DE ∥BC 交AB 于D , 交AC 于E ,过G 作PF ∥AC 交AB 于P ,交BC 于F , 过G 作KH ∥AB 交AC 于K ,交BC 于H ,则 (1)32===AB KH CA FP BC DE ; (2)2=++ABKH CA FP BC DE . 性质4 设G 为ABC ∆的重心,P 为ABC ∆内任一点,则 (1)22222223PG CG BG AG CP BP AP +++=++; (2)()22222231CA BC AB GC GB GA ++=++. 注 三角形中的莱布尼兹公式:()2222222313CA BC AB PG CP BP AP +++=++ 性质5 设G 为ABC ∆内一点,G 为ABC ∆的重心的充要条件是下列条件之一:(了解必要性即可) (1)ABC GAB GCA GBC S S S S ∆∆∆∆===31; (2)当点G 在三边BC 、CA 、AB 上的射影分别为D 、E 、F 时,GF GE GD ⋅⋅值最大; (3)当AG 、BG 、CG 的延长线交三边于D 、E 、F 时,CEG BDG AFG S S S ∆∆∆==; (4)过G 的直线交AB 于P ,交AC 于Q 时,3=+AQACAP AB ; (5)222222333GC AB GB CA GA BC +=+=+.性质6 设P 是锐角ABC ∆内一点,射线AP 、BP 、CP 分别交边BC 、CA 、AB 于点D 、E 、F ,则P 为ABC ∆重心的 充分必要条件是DEF ∆∽ABC ∆.例题讲解例1 过ABC ∆的重心G 任作一条直线把这个三角形分成两部分.试证:这两部分面积之差不大于整个三角形面积的91.例2 在ABC ∆中,G 为重心,P 为形内一点,直线PG. 求证:3=''+''+''GC PC G B P B G A P A .例3 如图,M 、N 、P 分别为正ABC ∆、正DCE ∆、正BEF ∆的重心.求证:MNP ∆为正三角形.例4 设O 为ABC ∆的外心,AC AB=,D 是AB 的中点,G 是ACD ∆的重心.求证:CD OG ⊥.ABCBCBCEBF例1 过ABC 的重心G 任作一条直线把这个三角形分成两部分.试证:这两部分面积之差不大于整个三角形面积的91. 证明:如图,作三角形三边的两个三等分点,过三等分点作边的平行线,分该三角形为9个等面积的小三角形。

第三讲三角形的重心与垂心一、基础知识1.重心的定义:三角形的三中线(或二中线)的交点叫做三角形的重心.2.重心的性质1)三角形的重心必在三角形的內部;2)三角形的重心到顶点的距离等于过这顶点的中线长的三分之二;3)三角形三中线分原三角形为六个等面积的三角形;4)三角形重心到三顶点的连线分原三角形为三个等面积的三角形;5)到三角形的三个顶点距离的平方和最小的点是这个三角形的重心;3.垂心的定义:三角形的三条高线的交点叫做三角形的垂心.4.垂心的性质1)锐角三角形垂心在三角形内部,直角三角形垂心在三角形直角顶点,钝角三角形垂心在三角形外部;2)垂心会在三角形内部产生很多相似直角三角形;同时会出现四点共圆问题;二、例题部分第一部分重心例1. 如图,已知△ABC与△CDA全等,点G、H分别是△ABC、△CDA的重心,则△AGH 的面积与△ABC的面积的比为 ( )A.4:9 B.2:3 C.1:3 D.1:6例2. 在△ABC中,BC=3,AC=4,BC和AC的中线AE、BD互相垂直,则AB等于 ( )A.36 B.5 C.22 D.7例3. 在直角三角形ABC 中. ∠A=90,G 为重心,且GA=2,则22GB GC += .例4. 设M 是△ABC 的重心,过M 的线段交AB ,AC 于P 、Q ,且AP PB =m ,AQ QC =n ,则11m n + =( )A .2B .1C .12D .13第二部分 垂心例5. (2000年,四川省中考题)如图,已知△ABC 的内切圆0与各边相切于D 、E 、F ,那么点0是△DEF的 ( )A .三条中线的交点B .三条高的交点C .三条角平分线的交点D .三条边的垂直平分线的交点例6. 如图,△ABC 中,高BD 、CE 相交于点F , ∠A=45,△ DEF 的面积为S ,则△BFC 的面积为 .例7. 如图,已知H 是△ABC 的垂心,△ABC 外接圆的半径为R ,那么sin BH BCH∠= .例8. 如图,已知⊙0中,直径AB 与弦CD 垂直,垂足为E ,CH 切⊙0于点C ,且与AB 的延长线交于H ,P 是CD 延长线上一点,PA 交⊙0于F ,AD 平分∠HAP 并交HP 于M .求证:(1)点D 是△AHP 的垂心;(2)AH :AB=AE :AF .第三部分 综合题目例9. (1998年,全国竞赛试题)如图,已知P 为ABCD 内一点,O 为AC 与BD 的交点,M 、N 分别为PB 、PC 的中点,Q 为AN 与DM 的交点,求证:(1)P 、Q 、O 三点在一条直线上;(2)PQ=20Q .例10. 如图,设G 为△ABC 的重心,P 为△ABC 内部的任意一点,直线PG 交BC 、CA 、AB 或其延长线于A '、B '、C '.求证:3A P B P C P A G B G C G'''++='''.三、课后练习1. ABC的中线AD、BE相交于O,F、G分别是OB、OA的中点,则四边形DEGF是( )A.梯形 B.正方形 C.平分四边形 D.菱形2. 在△ABC中,BC=a,AC=b,AB=c,∠C=90,CD和BE是△ABC的两条中线,且CD⊥BE,那么a:b:c=( )A.1:2:3 B.3:2:1 C..3:2:1 D.1:2:33.如图,AD是△ABC的高,G是三角形垂心,∠C=60,则∠BGD= .4. 如图,已知点P是△ABC的垂心,PD⊥AC,垂足D.延长PC交AB于E,连结DE,若BC=2DE,则tanA= .5.在△ABC中,∠A是锐角,0是垂心,AO=BC,则∠0BC+∠0CB=.。

三角形的重心在我们的数学世界中,三角形是一个基础而重要的图形。
而三角形的重心,作为三角形的一个重要特性,具有着独特的地位和意义。
首先,咱们来聊聊什么是三角形的重心。
简单来说,三角形的重心就是三角形三条中线的交点。
那什么又是中线呢?就是连接三角形一个顶点和它对边中点的线段。
比如说,在三角形 ABC 中,连接顶点 A 和对边 BC 中点的线段就是中线。
那为什么要研究三角形的重心呢?这是因为它有着很多有趣且实用的性质。
重心有一个非常重要的特点,就是它把每条中线都分成了 1 : 2 的两段。
比如说,假设三角形 ABC 的中线 AD 与重心 G 相交,那么 AG :GD = 2 : 1 。
这意味着,如果中线 AD 的长度是 6 ,那么 AG 的长度就是 4 ,GD 的长度就是 2 。
这个比例关系在解决很多与三角形相关的问题时非常有用。
三角形的重心还有一个有趣的性质,就是它到三角形三个顶点的距离的平方和最小。
这可能有点抽象,咱们来举个例子。
想象一下,有一个质量均匀的三角形薄板,如果你用一个手指去支撑它,让它能够保持平衡,那么你手指支撑的那个点大概率就是三角形的重心。
这是因为重心是这个薄板的“平衡点”,从物理的角度也能反映出它的特殊性质。
在实际生活中,三角形重心的概念也有着广泛的应用。
比如在工程设计中,当设计一个三角形的结构时,如果需要找到一个平衡点来保证结构的稳定性,那么重心就是一个关键的参考点。
在物理学中,研究物体的重心对于理解物体的运动和平衡状态也非常重要。
再来说说如何找到三角形的重心。
对于一个给定的三角形,我们只需要画出它的三条中线,它们的交点就是重心。
这个过程并不复杂,但需要我们仔细和准确地作图。
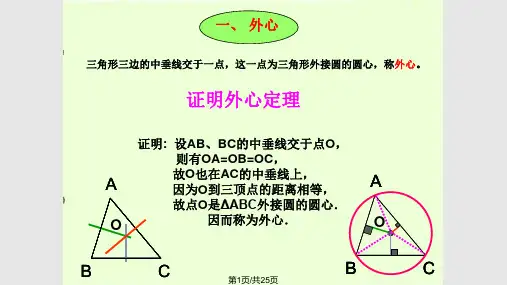
那么,三角形的重心和其他重要的点,比如外心、内心和垂心,又有什么区别和联系呢?外心是三角形外接圆的圆心,也就是三角形三条边的垂直平分线的交点;内心是三角形内切圆的圆心,是三角形三条角平分线的交点;垂心则是三角形三条高的交点。