新人教版高中物理必修二5.2运动的合成与分解

运动的合成与分解科学态度与责任：通过学生间的对蜡块的运动讨论，培养他们的团结协作精神以及谦虚好学的思想和实事求是的态度。

【教学重点】对一个运动能正确地进行合成和分解【教学难点】具体问题中的合运动和分运动的判定。

【教学过程】教学环节教师活动学生活动设计意图导入新课对于直线运动中，建立一维坐标，据运动规律，就可以确定任意时刻的位置，进而知道它的运动轨迹。

出示图片：小车在一维坐标上的运动出示图片：小球的抛体运动如果研究复杂的运动，我们怎么办呢？本节所学的运动的合成与分解是解决这一问题的基本方法。

学生观察图片思考：如果研究复杂的运动，我们怎么办？激发学生的学习兴趣，引出本节课题讲授新课一、红蜡块在平面内的运动演示：观察蜡块的运动1．实验器材红蜡做的小圆柱体、一端封闭长约1m 的玻璃管、清水2．实验步骤（1）在一端封闭、长约1m的玻璃管内注满清水，水中放一个红蜡做的小圆柱体A，将玻璃管的开口端用橡胶塞塞紧。

（图甲）（2）把玻璃管倒置（图乙），蜡块A沿玻璃管上升，观察玻璃管上升的速度。

学生了解实验器材和实验步骤，观察老师的演示实验学生观看视频总结实验结论学生阅读课文回答：如何建立坐标系？蜡块的位置P的坐标是通过对实验的仔细观察，了解蜡块的运动情况锻炼学生观察总结能力锻炼学生的自主学习能力锻炼学生的计算能力，理解蜡块的运动轨迹是直线的原因。

帮助学生（3）在蜡块匀速上升的同时，将玻璃管紧贴着黑板沿水平方向向右匀速移动（图丙），观察蜡块的运动情况。

说明：蜡的密度略小于水的密度。

在蜡块上升的初期，它做加速运动，随后由于受力平衡而做匀速运动。

出示蜡块运动的视频教师归纳实验结论3．实验结论（1）水平方向：蜡块随管向右做匀速直线运动。

（2）竖直方向：蜡块相对管向上做匀速直线运动。

（3）在黑板的背景前我们看到蜡块相对黑板是向右上方运动的。

那么，蜡块向右上方的这个运动是什么样的运动呢？要想定量地研究蜡块的运动，就要建立坐标系，具体分析。

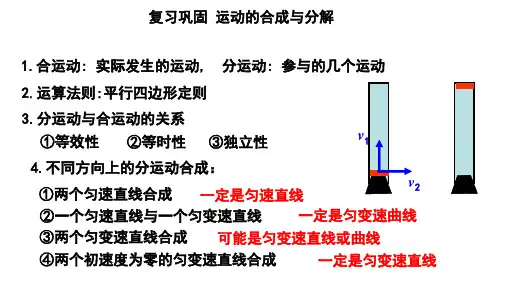
5.2 运动的合成与分解【学习目标】1.知道什么是运动的合成与分解，理解合运动与分运动等有关物理量之间的关系.2.会确定互成角度的两分运动的合运动的运动性质.3.会分析小船渡河问题．【知识要点】一、位移和速度的合成与分解1．合运动和分运动：一个物体同时参与两种运动时，这两种运动是分运动，而物体的实际运动叫做合运动．2．位移的合成与分解：一个物体同时发生两个方向的分位移与这个物体的合位移的效果可以相互替代．由分位移求合位移叫做位移的合成；由合位移求分位移叫做位移的分解．位移的合成与分解遵循矢量合成的平行四边形定则．3．速度的合成与分解：物体同时发生的两个方向上的分速度与这个物体的合速度的效果也可以相互替代，速度的合成与分解也遵循平行四边形定则．注：合运动与分运动的关系(1)等时性：合运动与分运动经历的时间相等，即同时开始，同时进行，同时停止．(2)独立性：一个物体同时参与了几个分运动，各分运动独立进行、互不影响，因此在研究某个分运动时，就可以不考虑其他分运动，就像其他分运动不存在一样．(3)等效性：各分运动的相应参量叠加起来与合运动的参量相同．3．合运动性质的判断分析两个直线分运动的合运动的性质时，应先根据平行四边形定则，求出合运动的合初速度V0和合加速度a，然后进行判断．(1)判断是否做匀变速运动①若a＝0时，物体沿合初速度v0的方向做匀速直线运动．②若a≠0且a恒定时，做匀变速运动．③若a≠0且a变化时，做非匀变速运动．(2)判断轨迹的曲直①若a与速度共线，则做直线运动．②若a与速度不共线，则做曲线运动．二、小船渡河问题小船渡河问题一般有渡河时间最短和航程最短两类问题：图31．关于最短时间，可根据运动等时性原理由船对静水的分运动时间来求解，由于河宽一定，当船对静水速度v1垂直河岸时，如图3所示，垂直河岸方向的分速度最大，所以必有t min＝d v1.图42．关于最短航程，一般考察水流速度v 2小于船对静水速度v 1的情况较多，此种情况船的最短航程就等于河宽d ，此时船头指向应与上游河岸成θ角，如图4所示，且cos θ＝v 2v 1；若v 2＞v 1，则最短航程s ＝v 2v 1d ，此时船头指向应与上游河岸成θ′角，且cos θ′＝v 1v 2. 三、关联物体速度的分解绳、杆等连接的两个物体在运动过程中，其速度通常是不一样的，但两者的速度是有联系的(一般两个物体沿绳或杆方向的速度大小相等)，我们称之为“关联”速度．解决此类问题的一般步骤如下： 第一步：先确定合运动，物体的实际运动就是合运动．第二步：确定合运动的两个实际作用效果，一是沿牵引方向的平动效果，改变速度的大小；二是沿垂直于牵引方向的转动效果，改变速度的方向．第三步：按平行四边形定则进行分解，作好运动矢量图． 第四步：根据沿绳或杆牵引方向的速度相等列方程．例如，小车通过跨过滑轮的绳牵引小船B ，某一时刻绳与水平方向的夹角为θ，如图所示．小船速度v B 有两个效果(两个分运动)：一是沿绳方向的平动，二是垂直绳方向的转动．将v B 沿着这两个方向分解，其中v 1＝v B cos θ＝v A ，v 2＝v B sin θ. 【题型分类】题型一、运动的合成与分解【例1】质量m ＝2 kg 的物体在光滑水平面上运动，其分速度v x 和v y 0随时间变化的图线如图(a)、(b)所示，求：(1) 物体所受的合外力； (2)物体的初速度； (3)t ＝8 s 时物体的速度； (4)t ＝4 s 内物体的位移． 【同类练习】1．在长约80cm-100cm 一段封闭的玻璃管中注满清水，水中放一个用红蜡做成的小圆柱体（小圆柱体恰能在管中匀速上浮），将玻璃管的开口端用胶塞塞紧，然后将玻璃管竖直倒置，在红蜡烛匀速上浮的同时使玻璃管紧贴黑板面在水平方向上匀加速移动，你正对黑板面将看到红蜡块相对于黑板面的移动轨迹可能是下列选项中的（ ）2．关于运动的合成，下列说法中正确的是()A．两个直线运动的合运动，一定是直线运动B．两个直线运动的合运动，可能是曲线运动C．两个互成角度的匀速直线运动的合运动，一定是匀速直线运动D．两个互成角度的匀加速直线运动的合运动，一定是匀加速直线运动题型二、小船渡河问题例2已知某船在静水中的速率为v1＝4 m/s，现让船渡过某条河，假设这条河的两岸是理想的平行线，河宽为d＝100 m，河水的流动速度为v2＝3 m/s，方向与河岸平行．试分析：(1)欲使船以最短时间渡过河去，船的航向怎样？最短时间是多少？到达对岸的位置怎样？船发生的位移是多大？(2)欲使船渡河过程中的航行距离最短，船的航向又应怎样？渡河所用时间是多少？【同类练习】1.河宽为d，水流速度为v1，小汽艇在静水中航行的速度为v2，且v v12<，如果小汽艇航向与河岸成θ角，斜向上游航行，求：（1）它过河需要多少时间？（2）到达对岸的位置？（3）若以最短的时间渡河，航向应如何？（4）若要直达正对岸，航向又应怎样？题型三、关联物体的速度分解问题例3如图所示，做匀速直线运动的汽车A通过一根绕过定滑轮的长绳吊起一重物B，设重物和汽车的速度的大小分别为v B、v A，则()A．v A＝v B B．v A＜v BC．v A＞v B D．重物B的速度逐渐增大【同类练习】1.如图所示，中间有孔的物块A套在光滑的竖直杆上，通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动．则关于拉力F及拉力作用点的移动速度v的下列说法正确的是()A．F不变、v不变B．F增大、v不变C．F增大、v增大D．F增大、v减小【成果巩固训练】1.关于运动的合成和分解，下列说法正确的是A．合运动的速度一定大于两个分运动的速度B．合运动的时间一定大于分运动的时间C．两个直线运动的合运动一定是直线运动D．两个匀速直线运动合运动一定是直线运动2．两个互相垂直的匀变速直线运动，初速度分别为V1和V2，加速度分别为a1和a2，它们的合运动轨迹()．A．轨迹一定是直线B．如果V1=0，V2=0，那么轨迹一定是曲线C．轨迹一定是曲线D．如果，那么轨迹一定是直线3．如图所示，跳伞员在降落伞打开一段时间以后，在空中做匀速运动．若跳伞员在无风时竖直匀速下落，着地速度大小是4.0 m/s.当有正东方向吹来的风，风速大小是3.0m/s，则跳伞员着地时的速度()A．大小为5.0 m/s，方向偏西B．大小为5.0 m/s，方向偏东C．大小为7.0 m/s，方向偏西D．大小为7.0 m/s，方向偏东4．如图所示，在水平地面上做匀速直线运动的汽车，通过定滑轮用绳子吊起一个物体，若汽车和被吊物体在同一时刻的速度分别为v1和v2，则下面说法正确的是()A ．物体做匀速运动，且v 2＝v 1B ．物体做加速运动，且v 2>v 1C ．物体做加速运动，且v 2<v 1D ．物体做减速运动，且v 2<v 15．在宽度为d 的河中，水流速度为v 2，船在静水中速度为v 1（且v 1<v 2），船头方向可以选择，现让该船开始渡河，则该船A ．不管船头与河岸夹角是多少，渡河时间和水速均无关B ．过河的最短渡河时间为1dv ，此时需船头垂直河岸，但不是垂直过河C ．过河的最短位移是21v d vD ．当最短位移过河时，船头与河岸夹角为α，12sin v v α=，船身斜向下游过河 6．一小船欲渡过宽为d 的河流，船头方向始终与河岸垂直，河水的流速1v 与时间t 的关系如图甲所示，小船在静水中的速度2v 与时间t 的关系如图乙所示．设小船从t=0时开始出发，t=t 0时恰好到达河对岸，则下列说法正确的是( )A 02vB 02vC 2dD ．小船到达河对岸的过程中做匀变速运动7．质量为2kg 的物体在x-y 平面上作曲线运动，在x 方向的速度图象和y 方向的位移图象如图所示，下列说法正确的是（ ）A ．质点初速度的方向与合外力方向垂直B ．2s 末质点速度大小为6m/sC ．质点的初速度为5m/sD ．质点所受的合外力为3N8．如图所示，人在岸上拉船，已知船的质量为m ，水的阻力恒为f ，当轻绳与水平面的夹角为θ时，人的速度为v ，人的拉力为F (不计滑轮与绳之间的摩擦)，则以下说法正确的是( )A ．船的速度为cos vθ B ．船的速度为v sin θ C ．船的加速度为cos F fmθ- D ．船的加速度为F fm- 9．如图甲所示，在杂技表演中，猴子沿竖直杆向上运动，其v t -图像如图乙所示，同时人顶着杆沿水平地面运动的x t -图像如图丙所示。

课题 5.2运动的合成和分解课型新授课课时 1教学目标（一）知识教学点1．知道合运动、分运动、知道合运动和分运动是同时发生的，并且互不影响，能在具体的问题中分析和判断．2．理解运动的合成、运动的分解的具体意义．理解运动的合成和分解遵循平行四边形定则．3．会用图示方法和教学方法求解位移，速度合成、分解的问题．（二）能力训练点培养观察和推理的能力、分析和综合的能力．（三）教育渗透点辩证地看待问题（四）美育渗透点学生在学习过程运用概念进行推理、判断，能体会到物理学科中所渗透出的逻辑美．教学重点难点1．重点明确一个复杂的运动可以等效为两个简单的运动的合成或等效分解为两个简单的运动，理解运动合成、分解的意义和方法．2．难点认识分运动和分运动相互独立、互不相干；分运动和合运动的同时性．理解两个直线运动的合运动可以是直线运动，也可以是曲线运动．教学准备教材实验装置课件：运动的合成和分解多媒体设备教学过程（一）明确目标（略）（二）整体感知本节的地位比较特殊．为知识的学习，涉及到许多基本概念和基本规律；作为方法的介绍，体会把较复杂的运动看作是几个简单运动的合成；作为能力的培养，提高观察和推理能力，分析和综合的能力．（三）重点、难点的学习与目标完成过程1．什么是分运动、合运动?演示实验（具体操作见课本）学生观察蜡块的运动：由A到B沿玻璃管竖直向上匀速直线运动；由A到D随玻璃管向右匀速直线运动；蜡块实际的运动是上述两个运动的合成．即由A到C的匀速直线运动，如图5－2所示．②定量分析，在x 方向有x ＝21a 2t ，在y 方向有y ＝y v t ，约去时间t 得 k y a v x y y222= 故2y ＝kx ．此为抛物线型方程，表明合运动是曲线运动．（定量分析可结合学生情况留给学生课后思考）（2）一个曲线运动可以分解为两个方向上的直线运动既然两个直线运动的合运动可以是曲线运动，反过来，一个曲线运动可以用两个方向上的直线运动来等效替代．也就是说，分别研究这两个方向上的受力情况和运动情况，弄清楚分运动是直线运动的规律，就可以知道作为合运动的曲线运动的规律．作 业布 置练习二 （1）（2）（3）（4） 课堂总结 1．在进行运动的合成和分解时，一定要明确合运动是物体实际的运动．分运动是假想的，这与力的合成和分解是有区别的，如图5－3所示．通过一定滑轮拉一物体，使物体在水平面上运动，如果是讨论运动的合成和分解，物体实际运动即合运动的速度方向是水平的，沿绳方向的速度是分运动的速度；如果是讨论力的合成和分解，沿绳方向的拉力是物体实际受到的力，沿水平方向的力是拉力的分力．图5－32．合成和分解的精髓是“等效”的思想．学习时要深刻体会，可以结合课本“思考和讨论”进一步说明．。

高中物理必修第二册全册知识点汇总第五章抛体运动 (1)5.1曲线运动 (1)5.2运动的合成与分解 (6)5.3实验：探究平抛运动的特点 (17)5.4抛体运动的规律 (24)专题抛体运动规律的应用 (33)第六章圆周运动 (38)6.1圆周运动 (38)6.2向心力 (46)6.3向心加速度 (53)6.4生活中的圆周运动 (58)专题课向心力的应用和计算 (70)专题课生活中的圆周运动 (74)第七章万有引力与宇宙航行 (78)7.1行星的运动 (78)7.2万有引力定律 (83)7.3万有引力理论的成就 (91)7.4宇宙航行 (98)7.5相对论时空观与牛顿力学的局限性 (107)第八章机械能守恒定律 (111)8.1功与功率 (111)8.2重力势能 (122)8.3动能和动能定理 (128)8.4机械能守恒定律 (135)8.5实验：验证机械能守恒定律 (141)专题动能定理和机械能守恒定律的应用 (148)第五章抛体运动5.1曲线运动一、曲线运动的速度方向1．曲线运动运动轨迹是曲线的运动称为曲线运动。

[特别提示]数学中的切线不考虑方向，但物理学中的切线具有方向。

如图所示，若质点沿曲线从A运动到B，则质点在a点的速度方向(切线方向)为v1的方向，若从B运动到A，则质点在a点的速度方向(切线方向)为v2的方向。

2．速度的方向质点在某一点的速度方向，沿曲线在这一点的切线方向。

3．运动性质由于曲线运动中速度方向是变化的，所以曲线运动是变速运动。

二、物体做曲线运动的条件1．当物体所受合力的方向与它的速度方向不在同一直线上时，物体做曲线运动。

2．当物体加速度的方向与速度的方向不在同一直线上时，物体做曲线运动。

曲线运动的速度方向丢出的沙包在空中做什么运动？沙包运动的速度在不同时刻有什么特点？曲线运动一定是变速运动吗？速度方向时刻发生变化，都沿该时刻曲线的切线方向；曲线运动一定是变曲线运动的速度方向：曲线运动中某时刻的速度方向就是该相应位置点的切线方向。

运动的合成与分解的概念
运动的合成与分解的概念如下：
1. 运动的合成：从已知的分运动来求合运动，叫做运动的合成。

包括位移、速度和加速度的合成，由于它们都是矢量，所以遵循平行四边形定则。

重点在于判断合运动和分运动，一般地，物体的实际运动就是合运动。

2. 运动的分解：求一个已知运动的分运动，叫运动的分解。

解题时应按实际效果分解，或正交分解。

合运动与分运动之间具有以下关系：
1. 等效性：合运动与分运动在效果上等同，也就是说，一个物体在实际运动中受到的合外力与其分力相同。

2. 等时性：合运动与分运动所用的时间相同。

这意味着，无论我们将物体的运动分解为多少个分运动，它们所花费的时间总和与物体实际运动所花费的时间相同。

3.独立性：合运动与分运动之间相互独立，互不干扰。

这意味着，物体在合运动过程中，各个分运动可以分别进行，而不会受到其他分运动的影响。

4.矢量性：合运动与分运动都是矢量，因此在合成和分解过程中需要遵循平行四边形定则。

物体的运动性质由加速度决定，而运动轨迹（直线还是曲线）则由物体的速度和加速度的方向关系决定。

例如，当物体的速度和加速度方向相同时，物体将沿直线运动；而当它们的方向不同时，物体将沿曲线运动。

掌握运动的合成与分解对于理解物体的运动规律至关重要。

通过学习这些概念，我们可以更好地分析物体的运动状态，并运用数学方法求解相关问题。

然而，要全面了解运动的合成与分解，还需查阅相关资料或咨询专业人士以获取更准确、更详细的信息。

希望本文能为大家提供一定的帮助。