龙城初中_期末复习测试题1(1)

一、选择题：本题共10小题，每小题3分，共30分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.一个由长方体截去一部分后得到的几何体如图水平放置，其俯视图是2023-2024学年广东省深圳市龙岗区龙城初级中学九年级（上）期末数学试卷( )A. B. C. D.2.如图，点D 、E 分别是上AB 、AC 边上的中点，为阴影部分．现有一小孩向其投一小石子且已投中，则石子落在阴影部分的概率是( )A. B. C. D.3.已知关于x 的方程没有实数根，则m 的取值范围是( )A.B. C.D.4.关于反比例函数，点在它的图象上，下列说法中错误的是( )A. 当时，y 随x 的增大而增大B. 图象位于第二、四象限C. 点和都在该图象上D. 当时，5.下列命题是真命题的是( )A. 四边相等的四边形是正方形B. 物体在任何光线照射下影子的方向都是相同的C. 如果，则D. 有一个角为的两个等腰三角形相似6.如图，把一根长为的竹竿AB斜靠在石坝旁，量出竿长1m处离地面的高度为，则石坝的高度为( )A. B. C. D.7.在中，，用直尺和圆规在AC上确定点D，使∽，根据作图痕迹判断，正确的是( )A. B.C. D.8.由12个有公共顶点O的直角三角形拼成如图所示的图形，…若，则图中与位似的三角形的面积为( )A. B. C. D.9.定义新运算：a※，例如：4※，4※那么函数※的图象大致是( )A. B. C. D.10.如图，反比例函数图象经过正方形OABC的顶点A，BC边与y轴交于点D，若正方形OABC的面积为12，，则k的值为( )A. 3B.C.D.二、填空题：本题共5小题，每小题3分，共15分。

11.已知正方形ABCD的对角线长为6cm，则正方形ABCD的面积为______12.规定：在实数范围内定义一种运算“◎”，其规则为a◎，方程◎的根为______.13.我国古代著作《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，请人去买几株椽．每株脚钱三文足，无钱准与一株椽．”其大意：现请人代买一批椽，这批椽的价钱为6210文．如果每株椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？若设这批椽的数量为x株，则可列分式方程为______.14.如图，在中，，，点D是AB的中点，连接CD，将沿射线CA方向平移，在此过程中，的边CD与的边AB、AC分别交于点E、F，当的面积是面积的时，则平移的距离是______ .15.如图，在矩形ABCD中，点E在AD上，若且，，则AB的长为______.三、解答题：本题共7小题，共55分。

深圳龙岗区龙城初级中学九年级上册期末精选试卷检测题一、初三数学一元二次方程易错题压轴题（难）1．阅读下面材料：一般地，如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫等差数列，这个常数叫做等差数列的公差，它通常用字母d表示，我们可以用公式(1)2n nS na d-=+⨯来计算等差数列的和．（公式中的n表示数的个数，a表示第一个数的值，）例如：3＋5＋7＋9＋11＋13＋15＋17＋19＋21＝10×3＋10(101)2-×2＝120．用上面的知识解决下列问题．（1）计算：2+8+14+20+26+32+38+44+50+56+62+68+74+80+86+92+98+104+110+116（2）某县决定对坡荒地进行退耕还林．从2009年起在坡荒地上植树造林，以后每年植树后坡荒地的实际面积按一定规律减少，下表为2009、2010、2011、2012四年的坡荒地面积的统计数据．问到哪一年，可以将全县所有坡荒地全部种上树木．【答案】（1）1180；（2）到2017年，可以将全县所有的坡荒地全部种上树木．【解析】【分析】（1）根据题意，由公式(1)2n nS na d-=+⨯来计算等差数列的和，即可得到答案；（2）根据题意，设再过x年可以将全县所有的坡荒地全部种上树木．列出方程，解方程即可得到答案．【详解】解：（1）由题意，得6d=，20n=，2a=，∵(1)2n nS na d-=+⨯，∴20(201)22062S-=⨯+⨯401140=1180=+；（2）解：设再过x年可以将全县所有的坡荒地全部种上树木．根据题意，得1200x+(1)2x x-×400＝25200，整理得：（x﹣9）（x+14）＝0，∴x＝9或x＝﹣14（负值舍去）．∴2009+9-1=2017；答：到2017年，可以将全县所有的坡荒地全部种上树木．【点睛】本题考查了一元二次方程的应用，解一元二次方程，以及计算等差数列的和公式，解题的关键是熟练掌握题意，正确找出等量关系，列出方程进行解题．2．已知二次函数y＝9x2﹣6ax+a2﹣b，当b＝﹣3时，二次函数的图象经过点（﹣1，4）①求a的值；②求当a≤x≤b时，一次函数y＝ax+b的最大值及最小值；【答案】①a的值是﹣2或﹣4；②最大值＝13，最小值＝9【解析】【分析】①根据题意解一元二次方程即可得到a的值；②根据a≤x≤b，b＝﹣3求得a=-4，由此得到一次函数为y＝﹣4x﹣3，根据函数的性质当x＝﹣4时，函数取得最大值，x＝﹣3时，函数取得最小值，分别计算即可.【详解】解：①∵y＝9x2﹣6ax+a2﹣b，当b＝﹣3时，二次函数的图象经过点（﹣1，4）∴4＝9×（﹣1）2﹣6a×（﹣1）+a2+3，解得，a1＝﹣2，a2＝﹣4，∴a的值是﹣2或﹣4；②∵a≤x≤b，b＝﹣3∴a＝﹣2舍去，∴a＝﹣4，∴﹣4≤x≤﹣3，∴一次函数y＝﹣4x﹣3，∵一次函数y＝﹣4x﹣3为单调递减函数，∴当x＝﹣4时，函数取得最大值，y＝﹣4×（﹣4）﹣3＝13x＝﹣3时，函数取得最小值，y＝﹣4×（﹣3）﹣3＝9.【点睛】此题考查解一元二次方程，一次函数的性质，（2）是难点，正确理解a、b的关系得到函数解析式是解题的关键.3．随着经济收入的不断提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，汽车消费成为新亮点．抽样调查显示，截止2008年底全市汽车拥有量为14.4万辆．已知2006年底全市汽车拥有量为10万辆．（1）求2006年底至2008年底我市汽车拥有量的年平均增长率；（2）为保护城市环境，要求我市到2010年底汽车拥有量不超过15.464万辆，据估计从2008年底起，此后每年报废的汽车数量是上年底汽车拥有量的10%，那么每年新增汽车数量最多不超过多少辆？（假定每年新增汽车数量相同）【答案】详见解析【解析】试题分析：（1）主要考查增长率问题，一般用增长后的量=增长前的量×（1+增长率）解决问题；（2）参照增长率问题的一般规律，表示出2010年的汽车拥有量，然后根据关键语列出不等式来判断正确的解．试题解析：（1）设年平均增长率为x，根据题意得：10（1+x）2=14.4，解得x=﹣2.2（不合题意舍去）x=0.2，答：年平均增长率为20%；（2）设每年新增汽车数量最多不超过y万辆，根据题意得：2009年底汽车数量为14.4×90%+y，2010年底汽车数量为（14.4×90%+y）×90%+y，∴（14.4×90%+y）×90%+y≤15.464，∴y≤2．答：每年新增汽车数量最多不超过2万辆．考点：一元二次方程—增长率的问题4．如图，在平面直角坐标系中，正方形ABCD的顶点A在y轴正半轴上，顶点B在x轴正半轴上，OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根（OA＞OB）．（1）求点D的坐标．（2）求直线BC的解析式．（3）在直线BC上是否存在点P，使△PCD为等腰三角形？若存在，请直接写出点P的坐标；若不存在，说明理由．【答案】（1）D（4，7）（2）y=3944x （3）详见解析【解析】试题分析：（1）解一元二次方程求出OA、OB的长度，过点D作DE⊥y于点E，根据正方形的性质可得AD=AB，∠DAB=90°，然后求出∠ABO=∠DAE，然后利用“角角边”证明△DAE和△ABO全等，根据全等三角形对应边相等可得DE=OA，AE=OB，再求出OE，然后写出点D的坐标即可；（2）过点C作CM⊥x轴于点M，同理求出点C的坐标，设直线BC的解析式为y=kx+b （k≠0，k、b为常数），然后利用待定系数法求一次函数解析式解答；（3）根据正方形的性质，点P与点B重合时，△PCD为等腰三角形；点P为点B关于点C 的对称点时，△PCD为等腰三角形，然后求解即可．试题解析：（1）x2﹣7x+12=0，解得x1=3，x2=4，∵OA＞OB，∴OA=4，OB=3，过D作DE⊥y于点E，∵正方形ABCD，∴AD=AB，∠DAB=90°，∠DAE+∠OAB=90°，∠ABO+∠OAB=90°，∴∠ABO=∠DAE，∵DE⊥AE，∴∠AED=90°=∠AOB，∵DE⊥AE∴∠AED=90°=∠AOB，∴△DAE≌△ABO（AAS），∴DE=OA=4，AE=OB=3，∴OE=7，∴D（4，7）；（2）过点C作CM⊥x轴于点M，同上可证得△BCM≌△ABO，∴CM=OB=3，BM=OA=4，∴OM=7，∴C（7，3），设直线BC的解析式为y=kx+b（k≠0，k、b为常数），代入B（3，0），C（7，3）得，，解得，∴y=x﹣；（3）存在．点P 与点B 重合时，P 1（3，0）， 点P 与点B 关于点C 对称时，P 2（11，6）．考点：1、解一元二次方程；2、正方形的性质；3、全等三角形的判定与性质；4、一次函数5．在等腰三角形△ABC 中，三边分别为a 、b 、c ，其中ɑ＝4，若b 、c 是关于x 的方程x 2﹣（2k +1）x +4（k ﹣12）＝0的两个实数根，求△ABC 的周长． 【答案】△ABC 的周长为10． 【解析】 【分析】分a 为腰长及底边长两种情况考虑：当a=4为腰长时，将x=4代入原方程可求出k 值，将k 值代入原方程可求出底边长，再利用三角形的周长公式可求出△ABC 的周长；当a=4为底边长时，由根的判别式△=0可求出k 值，将其代入原方程利用根与系数的关系可求出b+c 的值，由b+c=a 可得出此种情况不存在．综上即可得出结论． 【详解】当a ＝4为腰长时，将x ＝4代入原方程，得：()214421402k k ⎛⎫-++-= ⎪⎝⎭解得：52k = 当52k =时，原方程为x 2﹣6x +8＝0， 解得：x 1＝2，x 2＝4，∴此时△ABC 的周长为4+4+2＝10；当a ＝4为底长时，△＝[﹣（2k +1）]2﹣4×1×4（k ﹣12）＝（2k ﹣3）2＝0， 解得：k ＝32， ∴b +c ＝2k +1＝4． ∵b +c ＝4＝a ，∴此时，边长为a，b，c的三条线段不能围成三角形．∴△ABC的周长为10．【点睛】本题考查了根的判别式、根与系数的关系、一元二次方程的解、等腰三角形的性质以及三角形的三边关系，分a为腰长及底边长两种情况考虑是解题的关键．二、初三数学二次函数易错题压轴题（难）6．如图，抛物线y=﹣x2+mx+n与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．（1）求抛物线的表达式；（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；（3）点E时线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．【答案】(1)抛物线的解析式为：y=﹣x2+x+2(2)存在，P1（，4），P2（，），P3（，﹣）(3)当点E运动到（2，1）时，四边形CDBF的面积最大，S四边形CDBF的面积最大=．【解析】试题分析：（1）将点A、C的坐标分别代入可得二元一次方程组，解方程组即可得出m、n的值；（2）根据二次函数的解析式可得对称轴方程，由勾股定理求出CD的值，以点C为圆心，CD为半径作弧交对称轴于P1；以点D为圆心CD为半径作圆交对称轴于点P2，P3；作CH 垂直于对称轴与点H，由等腰三角形的性质及勾股定理就可以求出结论；（3）由二次函数的解析式可求出B点的坐标，从而可求出BC的解析式，从而可设设E点的坐标，进而可表示出F的坐标，由四边形CDBF的面积=S△BCD+S△CEF+S△BEF可求出S与a的关系式，由二次函数的性质就可以求出结论．试题解析：（1）∵抛物线y=﹣x2+mx+n经过A（﹣1，0），C（0，2）．解得：，∴抛物线的解析式为：y=﹣x2+x+2；（2）∵y=﹣x2+x+2，∴y=﹣（x﹣）2+，∴抛物线的对称轴是x=．∴OD=．∵C（0，2），∴OC=2．在Rt△OCD中，由勾股定理，得CD=．∵△CDP是以CD为腰的等腰三角形，∴CP1=CP2=CP3=CD．作CH⊥x轴于H，∴HP1=HD=2，∴DP1=4．∴P1（，4），P2（，），P3（，﹣）；（3）当y=0时，0=﹣x2+x+2∴x1=﹣1，x2=4，∴B（4，0）．设直线BC的解析式为y=kx+b，由图象，得，解得：，∴直线BC的解析式为：y=﹣x+2．如图2，过点C作CM⊥EF于M，设E（a，﹣a+2），F（a，﹣a2+a+2），∴EF=﹣a2+a+2﹣（﹣a+2）=﹣a2+2a（0≤x≤4）．∵S四边形CDBF=S△BCD+S△CEF+S△BEF=BD•OC+EF•CM+EF•BN，=+a（﹣a2+2a）+（4﹣a）（﹣a2+2a），=﹣a2+4a+（0≤x≤4）．=﹣（a﹣2）2+∴a=2时，S四边形CDBF的面积最大=，∴E（2，1）．考点：1、勾股定理；2、等腰三角形的性质；3、四边形的面积；4、二次函数的最值7．如图，直线l：y＝﹣3x+3与x轴，y轴分别相交于A、B两点，抛物线y＝﹣x2+2x+b经过点B．（1）该抛物线的函数解析式；（2）已知点M 是抛物线上的一个动点，并且点M 在第一象限内，连接AM 、BM ，设点M 的横坐标为m ，△ABM 的面积为S ，求S 与m 的函数表达式，并求出S 的最大值； （3）在（2）的条件下，当S 取得最大值时，动点M 相应的位置记为点M '． ①写出点M '的坐标；②将直线l 绕点A 按顺时针方向旋转得到直线l '，当直线l ′与直线AM '重合时停止旋转，在旋转过程中，直线l '与线段BM '交于点C ，设点B ，M '到直线l '的距离分别为d 1，d 2，当d 1+d 2最大时，求直线l '旋转的角度（即∠BAC 的度数）．【答案】（1）2y x 2x 3=-++；（2）21525228S m ⎛⎫=--+ ⎪⎝⎭ ，258；（3）①57,24M ⎛⎫' ⎪⎝⎭；②45°【解析】 【分析】（1）利用直线l 的解析式求出B 点坐标，再把B 点坐标代入二次函数解析式即可求出b 的值．（2）设M 的坐标为（m ，﹣m 2+2m +3），然后根据面积关系将△ABM 的面积进行转化．（3）①由（2）可知m ＝52，代入二次函数解析式即可求出纵坐标的值． ②可将求d 1+d 2最大值转化为求AC 的最小值． 【详解】（1）令x ＝0代入y ＝﹣3x+3， ∴y ＝3， ∴B （0，3），把B （0，3）代入y ＝﹣x 2+2x+b 并解得：b ＝3， ∴二次函数解析式为：y ＝﹣x 2+2x+3． （2）令y ＝0代入y ＝﹣x 2+2x+3，∴0＝﹣x2+2x+3，∴x＝﹣1或3，∴抛物线与x轴的交点横坐标为-1和3，∵M在抛物线上，且在第一象限内，∴0＜m＜3，令y＝0代入y＝﹣3x+3，∴x＝1，∴A的坐标为（1，0），由题意知：M的坐标为（m，﹣m2+2m+3），∴S＝S四边形OAMB﹣S△AOB＝S△OBM+S△OAM﹣S△AOB＝12×m×3+12×1×（-m2+2m+3）-12×1×3＝﹣12（m﹣52）2+258，∴当m＝52时，S取得最大值258．（3）①由（2）可知：M′的坐标为（52，74）．②设直线l′为直线l旋转任意角度的一条线段，过点M′作直线l1∥l′，过点B作BF⊥l1于点F，根据题意知：d1+d2＝BF，此时只要求出BF 的最大值即可， ∵∠BFM′＝90︒， ∴点F 在以BM′为直径的圆上，设直线AM′与该圆相交于点H ，∵点C 在线段BM′上，∴F 在优弧'BM H 上，∴当F 与M′重合时，BF 可取得最大值，此时BM′⊥l 1，∵A （1，0），B （0，3），M′（52，74）， ∴由勾股定理可求得：AB ＝10，M′B ＝55，M′A ＝85， 过点M′作M′G ⊥AB 于点G ，设BG ＝x ，∴由勾股定理可得：M′B 2﹣BG 2＝M′A 2﹣AG 2，∴8516﹣（10﹣x ）2＝12516﹣x 2， ∴x ＝510， cos ∠M′BG ＝'BG BM ＝22，∠M′BG= 45︒ 此时图像如下所示，∵l 1∥l′，F 与M′重合，BF ⊥l 1∴∠B M′P=∠BCA ＝90︒，又∵∠M′BG=∠CBA= 45︒∴∠BAC ＝45︒．【点睛】本题主要考查了一次函数与二次函数的综合以及一次函数旋转求角度问题，正确掌握一次函数与二次函数性质及综合问题的解法是解题的关键．8．已知点P(2，﹣3)在抛物线L ：y ＝ax 2﹣2ax+a+k （a ，k 均为常数，且a≠0）上，L 交y 轴于点C ，连接CP ．（1）用a 表示k ，并求L 的对称轴及L 与y 轴的交点坐标；（2）当L 经过(3，3)时，求此时L 的表达式及其顶点坐标；（3）横、纵坐标都是整数的点叫做整点．如图，当a ＜0时，若L 在点C ，P 之间的部分与线段CP 所围成的区域内（不含边界）恰有4个整点，求a 的取值范围；（4）点M(x 1，y 1)，N(x 2，y 2)是L 上的两点，若t≤x 1≤t+1，当x 2≥3时，均有y 1≥y 2，直接写出t 的取值范围．【答案】（1）k=-3-a ；对称轴x ＝1；y 轴交点(0，-3)；（2）2y=2x -4x-3，顶点坐标(1，-5)；（3）-5≤a ＜-4；（4）-1≤t ≤2．【解析】【分析】（1）将点P(2，-3)代入抛物线上，求得k 用a 表示的关系式；抛物线L 的对称轴为直线2a x==12a--，并求得抛物线与y 轴交点； （2）将点(3，3)代入抛物线的解析式，且k=-3-a ，解得a=2，k=-5，即可求得抛物线解析式与顶点坐标；（3）抛物线L 顶点坐标(1，-a-3)，点C ，P 之间的部分与线段CP 所围成的区域内（不含边界）恰有4个整点，这四个整点都在x=1这条直线上，且y 的取值分别为-2、-1、0、1，可得1＜-a-3≤2，即可求得a 的取值范围；（4）分类讨论取a ＞0与a ＜0的情况进行讨论，找出1x 的取值范围，即可求出t 的取值范围．【详解】解：（1）∵将点P(2，-3)代入抛物线L ：2y=ax -2ax+a+k ，∴-3=4a 4a a+k=a+k -+∴k=-3-a ；抛物线L 的对称轴为直线-2a x=-=12a，即x ＝1； 将x=0代入抛物线可得：y=a+k=a+(-3-a)=-3，故与y 轴交点坐标为(0，-3)； （2）∵L 经过点(3，3)，将该点代入解析式中，∴9a-6a+a+k=3，且由（1）可得k=-3-a ，∴4a+k=3a-3=3，解得a=2，k=-5，∴L 的表达式为2y=2x -4x-3；将其表示为顶点式：2y=2(x-1)-5，∴顶点坐标为(1，-5)；（3）解析式L 的顶点坐标(1，-a-3)，∵在点C ，P 之间的部分与线段CP 所围成的区域内（不含边界）恰有4个整点，这四个整点都在x=1这条直线上，且y 的取值分别为-2、-1、0、1，∴1＜-a-3≤2，∴-5≤a ＜-4；（4）①当a ＜0时，∵2x 3≥，为保证12y y ≥，且抛物线L 的对称轴为x=1，∴就要保证1x 的取值范围要在[-1,3]上，即t ≥-1且t+1≤3，解得-1≤t ≤2；②当a ＞0时，抛物线开口向上，t ≥3或t+1≤-1，解得：t ≥3或t ≤-2，但会有不符合题意的点存在，故舍去，综上所述：-1≤t ≤2．【点睛】本题考查二次函数的图象及性质；熟练掌握二次函数的图象及性质，数形结合解题是关键．9．如图所示，在平面直角坐标系中，抛物线2(0)y ax bx c a =++≠的顶点坐标为()3, 6C ，并与y 轴交于点()0, 3B ，点A 是对称轴与x 轴的交点．(1)求抛物线的解析式;(2)如图①所示, P 是抛物线上的一个动点,且位于第一象限，连结BP 、AP ,求ABP ∆的面积的最大值;(3)如图②所示，在对称轴AC 的右侧作30ACD ∠=交抛物线于点D ,求出D 点的坐标;并探究:在y 轴上是否存在点Q ,使60CQD ∠=?若存在，求点Q 的坐标;若不存在，请说明理由．【答案】（1）21233y x x =-++；（2）当92n =时，PBA S ∆最大值为818；（3）存在，Q 点坐标为((0,-或，理由见解析【解析】【分析】(1)利用待定系数法可求出二次函数的解析式；(2)求三角形面积的最值，先求出三角形面积的函数式.从图形上看S △PAB=S △BPO+S △APO-S △AOB,设P 21,233n n n ⎛⎫-++ ⎪⎝⎭求出关于n 的函数式，从而求S △PAB 的最大值.(3) 求点D 的坐标，设D 21,233t t t ⎛⎫-++ ⎪⎝⎭,过D 做DG 垂直于AC 于G,构造直角三角形，利用勾股定理或三角函数值来求t 的值即得D 的坐标;探究在y 轴上是否存在点Q ,使60CQD ∠=?根据以上条件和结论可知∠CAD=120°,是∠CQD 的2倍，联想到同弧所对的圆周角和圆心角，所以以A 为圆心，AO 长为半径做圆交y 轴与点Q,若能求出这样的点，就存在Q 点.【详解】解：()1抛物线顶点为()3,6∴可设抛物线解析式为()236y a x =-+将()0,3B 代入()236y a x =-+得 396a =+13a ∴=- ∴抛物线()21363y x =--+，即21233y x x =-++ ()2连接,3, 3OP BO OA ==，PBA BPO PAO ABO S S S S ∆∆∆∆=+-设P 点坐标为21,233n n n ⎛⎫-++ ⎪⎝⎭1133222BPO x S BO P n n ∆=== 2211119323322322PAO y S OA P n n n n ∆⎛⎫==-++=-++ ⎪⎝⎭11933222ABO S OA BO ∆==⨯⨯= 22231991919813222222228PBA S n n n n n n ∆⎛⎫⎛⎫=+-++-=-+=--+ ⎪ ⎪⎝⎭⎝⎭ ∴当92n =时，PBA S ∆最大值为818()3存在，设点D 的坐标为21,233t t t ⎛⎫-++ ⎪⎝⎭ 过D 作对称轴的垂线，垂足为G ,则213,6233DG t CG t t ⎛⎫=-=--++ ⎪⎝⎭30ACD ∠=2DG DC ∴=在Rt CGD ∆中有222243CG CD DG DG DG DG =+=-=)21336233t t t ⎛⎫-=--++ ⎪⎝⎭化简得(1133303t t ⎛⎫---= ⎪⎝⎭13t ∴=（舍去），2333t =+∴点D(333+3,33AG GD ∴==连接AD ，在Rt ADG ∆中229276AD AG GD =+=+=6,120AD AC CAD ∴==∠=Q ∴在以A 为圆心，AC 为半径的圆与y 轴的交点上此时1602CQD CAD ∠=∠= 设Q 点为(0,m), AQ 为A 的半径 则AQ ²=OQ ²+OA ², 6²=m ²+3²即2936m += ∴1233,33m m ==-综上所述，Q 点坐标为()()0,330,33-或故存在点Q ，且这样的点有两个点.【点睛】(1)本题考查了利用待定系数法求二次函数解析式，根据已知条件选用顶点式较方便；(2)本题是三角形面积的最值问题，解决这个问题应该在分析图形的基础上，引出自变量，再根据图形的特征列出面积的计算公式，用含自变量的代数式表示面积的函数式,然后求出最值.(3)先求抛物线上点的坐标问题及符合条件的点是否存在.一般先假设这个点存在，再根据已知条件求出这个点.10．如图，抛物线y =ax 2+bx +2经过点A(−1，0)，B(4，0)，交y 轴于点C ；（1）求抛物线的解析式(用一般式表示)；（2）点D 为y 轴右侧抛物线上一点，是否存在点D 使S △ABC =23S △ABD ?若存在，请求出点D 坐标；若不存在，请说明理由；（3）将直线BC 绕点B 顺时针旋转45°，与抛物线交于另一点E ，求BE 的长.【答案】（1）213222y x x =-++（2）存在，D （1，3）或（2，3）或（5，3-）（3）10【解析】【分析】 （1）由A 、B 的坐标，利用待定系数法可求得抛物线解析式；（2）由条件可求得点D 到x 轴的距离，即可求得D 点的纵坐标，代入抛物线解析式可求得D 点坐标；（3）由条件可证得BC ⊥AC ，设直线AC 和BE 交于点F ，过F 作FM ⊥x 轴于点M ，则可得BF=BC ，利用平行线分线段成比例可求得F 点的坐标，利用待定系数法可求得直线BE 解析式，联立直线BE 和抛物线解析式可求得E 点坐标，则可求得BE 的长．【详解】解：（1）∵抛物线y=ax 2+bx+2经过点A （-1，0），B （4，0），∴2016420a b a b -+=⎧⎨++=⎩，解得：1232a b ⎧=-⎪⎪⎨⎪=⎪⎩， ∴抛物线解析式为：213222y x x =-++； （2）由题意可知C （0，2），A （-1，0），B （4，0），∴AB=5，OC=2，∴S △ABC =12AB•OC=12×5×2=5， ∵S △ABC =23S △ABD ， ∴S △ABD =315522⨯=， 设D （x ，y ）， ∴11155222AB y y •=⨯•=， 解得：3y =；当3y =时，2132322y x x =-++=， 解得：1x =或2x =，∴点D 的坐标为：（1，3）或（2，3）；当3y =-时，2132322y x x =-++=-， 解得：5x =或2x =-（舍去），∴点D 的坐标为：（5，-3）；综合上述，点D 的坐标为：（1，3）或（2，3）或（5，-3）；（3）∵AO=1，OC=2，OB=4，AB=5，∴22125AC =+=,222425BC =+=，∴222AC BC AB +=，∴△ABC 为直角三角形，即BC ⊥AC ，如图，设直线AC 与直线BE 交于点F ，过F 作FM ⊥x 轴于点M ，由题意可知∠FBC=45°，∴∠CFB=45°，∴25CF BC ==∴AO AC OM CF =，即1525OM = 解得：2OM =， ∴OC AC FM AF =，即2535FM = 解得：6FM =，∴点F 为（2，6），且B 为（4，0），设直线BE 解析式为y=kx+m ，则2640k m k m +=⎧⎨+=⎩，解得312k m =-⎧⎨=⎩，∴直线BE解析式为：312y x=-+；联立直线BE和抛物线解析式可得：231213222y xy x x=-+⎧⎪⎨=-++⎪⎩，解得：4xy=⎧⎨=⎩或53xy=⎧⎨=-⎩，∴点E坐标为：(5,3)-，∴22(54)(3)10BE=-+-=.【点睛】本题为二次函数的综合应用，涉及待定系数法、三角形面积、勾股定理及其逆定理、平行线分线段成比例、函数图象的交点、等腰直角三角形的性质、方程思想及分类讨论思想等知识．在（1）中注意待定系数法的应用，在（2）中求得D点的纵坐标是解题的关键，在（3）中由条件求得直线BE的解析式是解题的关键．本题考查知识点较多，综合性较强，特别是最后一问，有一定的难度．三、初三数学旋转易错题压轴题（难）11．如图1，在正方形ABCD中，点E、F分别在边BC，CD上，且BE=DF，点P是AF的中点，点Q是直线AC与EF的交点，连接PQ，PD．（1）求证：AC垂直平分EF；（2）试判断△PDQ的形状，并加以证明；（3）如图2，若将△CEF绕着点C旋转180°，其余条件不变，则（2）中的结论还成立吗？若成立，请加以证明；若不成立，请说明理由．【答案】（1）证明见解析；（2）△PDQ是等腰直角三角形；理由见解析（3）成立；理由见解析.【解析】试题分析：（1）由正方形的性质得出AB=BC=CD=AD，∠B=∠ADF=90°，∠BCA=∠DCA=45°，由BE=DF，得出CE=CF，△CEF是等腰直角三角形，即可得出结论；（2）由直角三角形斜边上的中线的性质得出PD=AF，PQ=AF，得出PD=PQ，再证明∠DPQ=90°，即可得出结论；（3）由直角三角形斜边上的中线的性质得出PD=AF，PQ=AF，得出PD=PQ，再证明点A、F、Q、P四点共圆，由圆周角定理得出∠DPQ=2∠DAQ=90°，即可得出结论．试题解析：（1）证明：∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠B=∠ADF=90°，∠BCA=∠DCA=45°，∵BE=DF，∴CE=CF，∴AC垂直平分EF；（2）解：△PDQ是等腰直角三角形；理由如下：∵点P是AF的中点，∠ADF=90°，∴PD=AF=PA，∴∠DAP=∠ADP，∵AC垂直平分EF，∴∠AQF=90°，∴PQ=AF=PA，∴∠PAQ=∠AQP，PD=PQ，∵∠DPF=∠PAD+∠ADP，∠QPF=∠PAQ+∠AQP，∴∠DPQ=2∠PAD+2∠PAQ=2（∠PAD+∠PAQ）=2×45°=90°，∴△PDQ是等腰直角三角形；（3）成立；理由如下：∵点P是AF的中点，∠ADF=90°，∴PD=AF=PA，∵BE=DF，BC=CD，∠FCQ=∠ACD=45°，∠ECQ=∠ACB=45°，∴CE=CF，∠FCQ=∠ECQ，∴CQ⊥EF，∠AQF=90°，∴PQ=AF=AP=PF，∴PD=PQ=AP=PF，∴点A、F、Q、P四点共圆，∴∠DPQ=2∠DAQ=90°，∴△PDQ是等腰直角三角形．考点：四边形综合题．12．请阅读下列材料：问题：如图1，在等边三角形ABC内有一点P，且PA=2，PB=3，PC=1、求∠BPC度数的大小和等边三角形ABC的边长．李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形（如图2），连接PP′，可得△P′PB是等边三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可证），从而得到∠BPC=∠AP′B=__________；，进而求出等边△ABC的边长为__________；问题得到解决．请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD内有一点P，且PA=5，BP=2，PC=1．求∠BPC度数的大小和正方形ABCD的边长．【答案】（17；（25【解析】试题分析：（1）利用旋转的性质，得到全等三角形.(2)利用（1）中的解题思路，把△BPC,旋转，到△BP’A,连接PP’,BP’，容易证明△APP’是直角三角形，∠BP’E=45°，已知边BP’=BP2，BE=BP’=1，勾股定理可求得正方形边长.（17（2）将△BPC绕点B逆时针旋转90°，得△BP′A，则△BPC≌△BP′A．∴AP′=PC=1，BP=BP′2；连接PP′，在Rt△BP′P中，∵BP=BP′2，∠PBP′=90°，∴PP′=2，∠BP′P=45°；在△AP′P中，AP′=1，PP′=2，AP5∵222125+，即AP′2+PP′2=AP2；∴△AP′P是直角三角形，即∠AP′P=90°，∴∠AP′B=135°，∴∠B PC=∠AP′B=135°．过点B作BE⊥AP′，交AP′的延长线于点E；则△BEP′是等腰直角三角形，∴∠EP′B=45°，∴EP′=BE=1，∴AE=2；∴在Rt△ABE中，由勾股定理，得AB5∴∠BPC=135°5点睛：本题利用题目中的原理迁移解决问题，解题利用了旋转的性质，一般利用正方形，等腰，等边三角形的隐含条件，构造全等三角形，把没办法利用的已知条件转移到方便利用的图形位置,从而求解.13．综合与实践 问题情境在综合与实践课上，老师让同学们以“三角形的旋转”为主题开展教学活动老师给每个小组发了两个等模直角三角形ABC 和DEC ，其中90,2,2ACB DCE AC CD ︒∠=∠===.观案发现（1）将两个等腰直角三角形如图①摆放，设DE 的中点是,F AE 的中点是,H BD 的中点是G ，则HFG ∠=______度；操作证明（2）将图①中的DEC 绕点C 顺时针（逆时针）旋转，使点A C E 、、三点在一条直线上，如图②，其余条件不变，小明通过测量发现，此时FH FG =，请你帮助小明证明这个结论.探究发现（3）将图①中的DEC 绕点C 顺时针（逆时针）旋转，旋转角为()0180αα︒︒<<，DEC 在旋转的过程中，当直线FH 经过点C 时，如图③，请求出线段FG 的长.（4）在旋转过程中，在Rt ABC 和Rt CDE △中，始终有由,AC BC CE CD ⊥⊥，你在图③中还能发现哪两条线段在旋转过程中始终互相垂直？请找出并直接写出这两条线段.【答案】（1）90；（2）证明见解析；（3）31BD =；（4）AD BE ⊥【解析】【分析】（1）根据题意，运用中点的性质找到线段之间的位置关系即可求解；（2）根据旋转的性质及等腰三角形ABC 可知()ACD BCE SAS ∆≅∆，进而通过中位线定理即可得到FH FG =；（3）根据旋转的性质及勾股定理，先求出BF 的长，再由BD BF DF =-即可求出BD 的长；（4）根据旋转的性质及垂直的判定可知AD BE ⊥.【详解】（1）,,90CE CD AC BC ECA DCB ==∠=∠=︒，BE AD ∴=，F 是DE 的中点，H 是AE 的中点，G 是BD 的中点，//,//HF AD FG BE ∴，AD BE ⊥，HF GF ∴⊥， 90HFG ∴∠=︒；（2）证明：如下图，连接AD BE ，，由旋转可知CE CD =，90ECD ACD ∠=∠=︒，又∵AC=BC ，()ACD BCE SAS ∴∆≅∆，AD BE ∴=，F 是DE 的中点，H 是AE 的中点，G 是BD 的中点，11,22FH AD FG BE ∴==， FH FG ∴=；（3）解：由题意可得CF DE CFD CFE ⊥∆∆，，都是等腰直角三角形，2CD =1CF DF ∴==，2BC AC ==，223BF BC CF ∴=-=31BD BF DF ∴=-=，G 是BD 的中点，31DG -∴=31BD BF DF ∴=-=；（4）AD BE ⊥. 连接AD ，由（3）知，CF DE ⊥，∵ECD ∆是等腰直角三角形，∴F 是ED 中点，又∵H是AE中点，∴AD∥HF，∵HF⊥ED，∴AD BE.【点睛】本题主要考查了中的的性质，中位线定理，三角形全等，勾股定理等三角形综合证明，熟练掌握三角形的相关知识点是解决本题的关键.错因分析：（1）不能熟练运用重点的性质找到线段之间的关系；（2）未掌握旋转的性质；（3）不能将题目探究中的发现进行推广.14．已知△ABC是边长为4的等边三角形，边AB在射线OM上，且OA＝6，点D是射线OM上的动点，当点D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE．（1）如图1，求证：△CDE是等边三角形．（2）设OD＝t，①当6＜t＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE周长的最小值；若不存在，请说明理由．②求t为何值时，△DEB是直角三角形（直接写出结果即可）．【答案】(1)见解析;(2)①见解析;②t＝2或14.【解析】【分析】（1）由旋转的性质得到∠DCE=60°，DC=EC，即可得到结论；（2）①当6＜t＜10时，由旋转的性质得到BE=AD，于是得到C△DBE=BE+DB+DE=AB+DE=4+DE，根据等边三角形的性质得到DE=CD，由垂线段最短得到当CD⊥AB时，△BDE的周长最小，于是得到结论；②存在，当点D与点B重合时，D，B，E不能构成三角形；当0≤t＜6时，由旋转的性质得到∠ABE=60°，∠BDE＜60°，求得∠BED=90°，根据等边三角形的性质得到∠DEB=60°，求得∠CEB=30°，求得OD=OA-DA=6-4=2=t；当6＜t＜10时，此时不存在；当t＞10时，由旋转的性质得到∠DBE=60°，求得∠BDE＞60°，于是得到t=14．【详解】（1）∵将△ACD绕点C逆时针方向旋转60°得到△BCE，∴∠DCE＝60°，DC＝EC，∴△CDE是等边三角形；（2）①存在，当6＜t＜10时，由旋转的性质得，BE＝AD，∴C△DBE＝BE+DB+DE＝AB+DE＝4+DE，由（1）知，△CDE是等边三角形，∴DE＝CD，∴C△DBE＝CD+4，由垂线段最短可知，当CD⊥AB时，△BDE的周长最小，此时，CD＝，∴△BDE的最小周长＝CD+4＝；②存在，∵当点D与点B重合时，D，B，E不能构成三角形，∴当点D与点B重合时，不符合题意；当0≤t＜6时，由旋转可知，∠ABE＝60°，∠BDE＜60°，∴∠BED＝90°，由（1）可知，△CDE是等边三角形，∴∠DEB＝60°，∴∠CEB＝30°，∵∠CEB＝∠CDA，∴∠CDA＝30°，∵∠CAB＝60°，∴∠ACD＝∠ADC＝30°，∴DA＝CA＝4，∴OD＝OA﹣DA＝6﹣4＝2，∴t＝2；当6＜t＜10时，由∠DBE＝120°＞90°，∴此时不存在；当t＞10时，由旋转的性质可知，∠DBE＝60°，又由（1）知∠CDE＝60°，∴∠BDE＝∠CDE+∠BDC＝60°+∠BDC，而∠BDC＞0°，∴∠BDE＞60°，∴只能∠BDE＝90°，从而∠BCD＝30°，∴BD＝BC＝4，∴OD＝14，∴t＝14，综上所述：当t＝2或14时，以D、E、B为顶点的三角形是直角三角形．【点睛】本题考查了旋转的性质，等边三角形的判定和性质，三角形周长的计算，直角三角形的判定，熟练掌握旋转的性质是解题的关键．15．两块等腰直角三角板△ABC和△DEC如图摆放，其中∠ACB=∠DCE=90°，F是DE的中点，H是AE的中点，G是BD的中点．（1）如图1，若点D、E分别在AC、BC的延长线上，通过观察和测量，猜想FH和FG的数量关系为______和位置关系为______；（2）如图2，若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时，其余条件均不变，则（1）中的猜想是否还成立，若成立，请证明，不成立请说明理由；（3）如图3，将图1中的△DEC绕点C顺时针旋转一个锐角，得到图3，（1）中的猜想还成立吗？直接写出结论，不用证明．【答案】（1）相等，垂直．（2）成立，证明见解析；（3）成立，结论是FH=FG，FH⊥FG．【解析】试题分析：（1）证AD=BE，根据三角形的中位线推出FH=12AD，FH∥AD，FG=12BE，FG∥BE，即可推出答案；（2）证△ACD≌△BCE，推出AD=BE，根据三角形的中位线定理即可推出答案；（3）连接BE、AD，根据全等推出AD=BE，根据三角形的中位线定理即可推出答案．试题解析：（1）解：∵CE=CD，AC=BC，∠ECA=∠DCB=90°，∴BE=AD，∵F是DE的中点，H是AE的中点，G是BD的中点，∴FH=12AD，FH∥AD，FG=12BE，FG∥BE，∴FH=FG，∵AD⊥BE，∴FH⊥FG，故答案为相等，垂直．（2）答：成立，证明：∵CE=CD，∠ECD=∠ACD=90°，AC=BC，∴△ACD≌△BCE∴AD=BE，由（1）知：FH=12AD，FH∥AD，FG=12BE，FG∥BE，∴FH=FG，FH⊥FG，∴（1）中的猜想还成立．（3）答：成立，结论是FH=FG ，FH ⊥FG ．连接AD ，BE ，两线交于Z ，AD 交BC 于X ，同（1）可证∴FH=12AD ，FH ∥AD ，FG=12BE ，FG ∥BE ， ∵三角形ECD 、ACB 是等腰直角三角形，∴CE=CD ，AC=BC ，∠ECD=∠ACB=90°，∴∠ACD=∠BCE ， 在△ACD 和△BCE 中AC BC ACD BCE CE CD ⎧⎪∠∠⎨⎪⎩＝＝＝ ， ∴△ACD ≌△BCE ，∴AD=BE ，∠EBC=∠DAC ，∵∠DAC+∠CXA=90°，∠CXA=∠DXB ，∴∠DXB+∠EBC=90°，∴∠EZA=180°﹣90°=90°，即AD ⊥BE ，∵FH ∥AD ，FG ∥BE ，∴FH ⊥FG ，即FH=FG ，FH ⊥FG ，结论是FH=FG ，FH ⊥FG.【点睛】运用了等腰直角三角形的性质、全等三角形的性质和判定、三角形的中位线定理，旋转的性质等知识点的理解和掌握，能熟练地运用这些性质进行推理是解此题的关键．四、初三数学 圆易错题压轴题（难）16．已知：图1 图2 图3（1）初步思考：如图1， 在PCB ∆中，已知2PB =，BC=4，N 为BC 上一点且1BN =，试说明：12PN PC = （2）问题提出：如图2，已知正方形ABCD 的边长为4，圆B 的半径为2，点P 是圆B 上的一个动点，求12PD PC +的最小值． （3）推广运用：如图3，已知菱形ABCD 的边长为4，∠B ﹦60°，圆B 的半径为2，点P 是圆B 上的一个动点，求12PD PC -的最大值． 【答案】（1）详见解析；（2）5；（3）最大值37DG =【解析】【分析】（1）利用两边成比例，夹角相等，证明BPN ∆∽BCP ∆，得到PN BN PC BP =，即可得到结论成立；（2）在BC 上取一点G ，使得BG=1，由△PBG ∽△CBP ，得到12PG PC =，当D 、P 、G 共线时，12PD PC +的值最小，即可得到答案； （3）在BC 上取一点G ，使得BG=1，作DF ⊥BC 于F ，与（2）同理得到12PG PC =，当点P 在DG 的延长线上时，12PD PC -的值最大，即可得到答案. 【详解】（1）证明：∵2,1,4PB BN BC ===，∴24,4PB BN BC =⋅=，∴2PB BN BC =⋅， ∴BN BP BP BC=，。

广西柳州市城中学区龙城中学2024届数学七年级第一学期期末质量检测试题 请考生注意：1．请用2B 铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。

写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题(每小题3分,共30分)1．2016年某市用于资助贫困学生的助学金总额是9680000元，将9680000用科学记数法表示为（ ）A ．96.8×105B ．9.68×106C ．9.68×107D ．0.968×1082．已知一个等腰三角形的底角为50︒，则这个三角形的顶角为（ ）A ．40︒B ．50︒C ．80︒D ．100︒3．下列计算错误的是( ).A ．7.2-(-4.8)=2.4B ．(-4.7)+3.9=-0.8C ．(-6)×(-2)=12D ．4．下列方程变形正确的是（ ）A ．由35x +=得53x =+B ．由74x =-得74x =-C ．由3y 08=得3-8y =D ．由32x =-得23x =+5．若ABC 的三边分别为,,a b c ,且()()2a b a b c +-=,则（ ）A ．ABC 不是直角三角形B ．a 的对角为直角C ．b 的对角为直角D ．c 的对角为直角6．某商品的价格标签已丢失，售货员只知道”它的进价为80元，打七折出售后，仍可获利5％”你认为售货员应标在标签上的价格为（ ）A ．110元B ．120元C ．130元D ．140元7．现实生活中，如果收入1000元记作+1000元，那么﹣800表示（ ）A ．支出800元B ．收入800元C ．支出200元D ．收入200元8．下列图案中，是中心对称图形，但不是轴对称图形的是（ ）A ．B ．C ．D ．9．如图，从A 地到B 地有三条路可走，为了尽快到达，人们通常选择其中的直路．能正确解释这一现象的数学知识是（ ）A ．两点之间线段最短B ．两点确定一条直线C ．垂线段最短D ．在同一平面内，过一点有一条且只有一条直线垂直于已知直线10．我国作家莫言获得诺贝尔文学奖后，某出版社统计他的代表作品《蛙》的销售量达到2100000，把2100000用科学记数法表示为（ ）．A ．70.2110⨯B ．62110⨯C ．62.110⨯D ．72.110⨯二、填空题(本大题共有6小题，每小题3分，共18分)11．写出一个大于3且小于4的无理数：___________．12．33°52′＋21°54′＝_____；33°52′－21°54′＝_____．13．超市把a 元/千克的软糖m 千克，b 元/千克的水果糖n 千克，混合在一起，则混合后糖果的平均价格为______元/千克．14．甲、乙两队开展足球对抗赛，规定胜一场得3分，平一场得1分，负一场得0分，甲、乙两队共比赛6场，甲队保持不败，共得14分，甲队胜______场.15．在同一平面内利用一副三角板，可以直接画出的除三角板本身角的度数以外且小于平角的角度有___（例举四个即可）．1616-125的立方根的和为______．三、解下列各题(本大题共8小题，共72分)17．（8分）在下面对应的网格中画出左边立体图形的三视图.18．（8分）把()()()325,2,0,2,25,1--------表示在数轴上，并经它们按从小到大的顺序排列．19．（8分）如图，射线OC 、OD 在AOB ∠的内部．（1）169AOB ∠=︒，90AOC BOD ∠=∠=︒，求COD ∠的度数．（2）当90AOC BOD ∠=∠=︒，试判断AOD ∠与BOC ∠的关系，说明理由．（3）当AOC BOD α∠=∠=，（2）中的结论还存在吗？为什么？20．（8分）如图，已知点A ，B ，C ，D ，请按要求画出图形.（1）画直线AB 和射线CB ；（2）连结AC ，并在直线AB 上用尺规作线段AE ，使2AE AC =.（要求保留作图痕迹）（3）在直线AB 上确定一点P ，使PC PD +的和最短，并写出画图的依据.21．（8分）如图，点C 是线段AB 上一点，点M 、N 分别是线段AC 、BC 的中点；⑴若16AB =,6AM =,求线段MN 的长．⑵若8NM =,求线段AB 的长． 22．（10分）请先阅读下列内容，然后解答问题：因为：111122=-⨯，1112323=-⨯，1113434=-⨯，…，111910910=-⨯ 所以：112+⨯123⨯+134⨯+…+1910⨯ ＝112-+1231-+1341-+ (11910)＝1 110 -＝9 10（1）猜想并写出：11)n n⋅+（＝；（n为正整数）（2）直接写出下面式子计算结果：112+⨯123⨯+134⨯+…+120192020⨯＝；（3）探究并计算：131+⨯153⨯+117597+⨯⨯+…+112017201520192017+⨯⨯23．（10分）（1）试验探索：如果过每两点可以画一条直线，那么请下面三组图中分别画线，并回答问题：第（1）组最多可以画______条直线；第（2）组最多可以画______条直线；第（3）组最多可以画______条直线．（2）归纳结论：如果平面上有n（n≥3）个点，且每3个点均不在一条直线上，那么最多可以画出直线______条．（作用含n的代数式表示）（3）解决问题：某班50名同学在毕业后的一次聚会中，若每两人握一次手问好，则共握次手；最后，每两个人要互赠礼物留念，则共需件礼物．24．（12分）红星服装厂要生产一批某种型号的学生服装，已知3米长的布料可做上衣2件或裤子3条，一件上衣和一条裤子为一套，计划用600米长的这种布料生产，应分别用多少布料生产上衣和裤子才能恰好配套？共能生产多少套？参考答案一、选择题(每小题3分,共30分)1、B【解题分析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n 是负数．所以将9680000用科学记数法表示为：9.68×106， 故选B.2、C【分析】根据等腰三角形的性质和三角形内角和定理求解即可.【题目详解】∵等腰三角形的底角为50︒∴这个三角形的顶角为180505080︒-︒-︒=︒故选C【题目点拨】本题主要考查等腰三角形的性质和三角形内角和定理，掌握等腰三角形的性质和三角形内角和定理是解题的关键. 3、A【解题分析】利用有理数的混合运算即可解答.【题目详解】A. 7.2-(-4.8)=12≠2.4，故符合题意，B,C,D 的计算都正确，不符合题意.故选A.【题目点拨】此题考查有理数的混合运算，解题关键在于掌握运算法则.4、D【分析】根据等式的性质即可得出答案.【题目详解】A ：由35x +=可得53x =-，故A 错误；B ：由74x =-可得47x =-，故B 错误； C ：由3y 08=可得y=0，故C 错误； D ：由32x =-可得x=2+3，故D 正确；故答案选择D.【题目点拨】本题考查的是等式的性质，比较简单，需要熟练掌握等式的基本性质.5、B【分析】把式子写成a2−b2＝c2的形式，确定a为最长边，则可判断边a的对角是直角．【题目详解】∵（a＋b）（a−b）＝c2，∴a2−b2＝c2，∴a为最长边，∴边a的对角是直角．故选：B．【题目点拨】此题考查勾股定理逆定理的应用，判断最长边是关键．6、B【分析】根据题意得等量关系为：售价×折扣-进价=利润，列出方程，解之即可得出答案.【题目详解】设售货员应标在标签上的价格为x元，依题可得：70%x-80=80×5%，解得：x=120.故答案为B.【题目点拨】本题考查一元一次方程的实际应用-销售问题，解题的关键是根据题意找出等量关系.7、A【分析】此题主要用正负数来表示具有意义相反的两种量：收入记为正，则支出就记为负，直接得出结论即可．【题目详解】根据题意得，如果收入1000元记作+1000元，那么-800表示支出800元．故选A．【题目点拨】本题考查的知识点是负数的意义及其应用，解题关键是熟记负数的意义.8、B【分析】根据轴对称图形与中心对称图形的概念求解．【题目详解】解：A、不是中心对称图形，是轴对称图形，不符合题意；B、是中心对称图形，不是轴对称图形，符合题意；C、不是中心对称图形，也不是轴对称图形，不符合题意；D、是轴对称图形，也是中心对称图形，不符合题意．故选：B．【题目点拨】此题主要考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合，中心对称图形是要寻找对称中心，图形旋转180度后与原图形重合．9、A【分析】根据线段的性质，可得答案．【题目详解】从A地到B地有三条路可走，为了尽快到达，人们通常选择其中的直路，理由是两点之间线段最短．故选A．【题目点拨】本题考查了线段的性质，熟记线段的性质并应用是解题的关键．10、C【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．【题目详解】解：2100000＝2.1×106，故选：C．【题目点拨】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．二、填空题(本大题共有6小题，每小题3分，共18分)11π等，答案不唯一．【题目详解】本题考查无理数的概念.无限不循环小数叫做无理数.介于3和4之间的无理数有无穷多个，因为22==，故而9和16,15都是无理数.39,41612、55°46′11°58′【分析】（1）两个度数相加，度与度，分与分对应相加，分的结果若满60，则转化为度，从而得出答案；（2）两个度数相减，度与度，分与分对应相减，被减数分不够减的则向度借1变为60分，从而得出答案．【题目详解】33°52′＋21°54′＝55°46′；33°52′－21°54′＝11°58′.故答案为：55°46′；11°58′.【题目点拨】本题考查了度、分、秒之间的换算的应用，能正确进行度、分、秒之间的加减、乘除运算是解此题的关键，注意：1°=60′，1′=60″．13、am bn m n++ 【分析】先求出两种糖果的总价值，再根据“平均价格=总价值÷总重量”即可得．【题目详解】两种糖果的总价值为()am bn +元 混合后糖果的平均价格为am bn m n ++（元/千克） 故答案为：am bn m n++． 【题目点拨】本题考查了列代数式，理解题意，掌握等量关系是解题关键．14、4【分析】根据题意，甲队获胜场的分数+甲队平的场数的分数=14，解方程即可．【题目详解】∵甲队保持不败∴设甲胜x 场，平（6-x ）场由题可知，3x+(6-x)=14解得，x=4∴甲队胜4场．【题目点拨】本题考查一元一次方程的实际应用，属于简单题．找到两个未知量之间的关系是解题关键．15、15º；75º；105º；120º；135º；150º【分析】一副三角板可以直接得到30°、45°、60°、90°四种角，进行加减运算可得．【题目详解】一副三角板可以直接得到30°、45°、60°、90°四种角，小于平角的角度有：15º；75º；105º；120º；135º；150º．故答案为：15º；75º；105º；120º；135º；150º. 【题目点拨】此题考查角的计算，解题关键在于先找角与角之间的关系．16、-3或-7的平方根与-125的立方根，再相加即可．4=，的平方根为2或-2，-125的立方根为-5，则16的平方根与-125的立方根的和为：()253+-=-或()257-+-=-．故答案为：3-或7-．【题目点拨】本题主要考查了算术平方根、立方根的定义，解题的关键是熟练掌握基本概念．三、解下列各题(本大题共8小题，共72分)17、见解析【分析】从正面看到的是主视图，从左面看到的是左视图，从上面看到的是俯视图，据此进一步画出相应的图形即可.【题目详解】如图所示：【题目点拨】本题主要考查了几何体的三视图，熟练掌握相关概念是解题关键.18、数轴表示见解析，从小到大的顺序为：32(2)|5|20(1)(25)-<--<-<<--<--【分析】先在数轴上表示各个数,再根据数轴上点的特征比较即可．【题目详解】解:因为()3255,28,00,24--=--=-=-=-， (25)3,(1)1--=--=所以在数轴上表示为:从小到大的顺序为:32(2)|5|20(1)(25)-<--<-<<--<--.【题目点拨】本题主要考查了数轴和有理数的大小比较法则,能熟记有理数的大小比较法则是解此题的关键,注意:在数轴上表示的数,右边的数总比左边的数大．19、（1）11°；（2）∠AOD =∠BO C ，详见解析；（3）存在，仍然有∠AOD =∠BOC ，理由见解析【分析】（1）先根据角的和差求出∠BOC 的度数，再利用∠COD =∠BOD －∠BOC 计算即可；（2）根据余角的性质解答即可；（3）根据角的和差和等量代换即可推出结论．【题目详解】解：（1）因为∠AOB =169，∠AOC =∠BOD =90︒，所以∠BOC =∠AOB －∠AOC =169°－90︒=79°，所以∠COD =∠BOD －∠BOC =90︒－79°=11︒； （2）∠AOD =∠BOC ，理由：因为∠AOC =∠BOD =90︒，所以∠AOD +∠DOC =90︒，∠BOC +∠DOC =90︒所以∠AOD =∠BOC ．（3）存在，仍然有∠AOD =∠BOC ．理由：因为∠AOD=∠AOC －∠DOC ，∠BOC=∠BOD －∠DOC ．又因为AOC BOD α∠=∠=，所以∠AOD =∠BOC ．【题目点拨】本题考查了角的和差计算以及余角的性质等知识，属于基本题型，熟练掌握基本知识是解题的关键．20、解：（1）作图见解析；（2）作图见解析；（3）作图见解析；画图的依据：两点之间，线段最短.【分析】（1）根据直线是向两方无限延伸的画直线AB 即可，根据射线是向一方无限延伸的画射线CB ； （2）首先画出线段AC ，在AB 的延长线上依次截取两次AC ，使得2AE AC =；（3）连接AB,CD ，AB 与CD 的交点就是P 点．【题目详解】解：（1）如图所示，直线AB, 射线CB 即为所求；（2）如图所示，线段AC 、AE 即为所求；（3）如图所示，点P 即为所求，画图的依据：两点之间，线段最短.【题目点拨】本题考查了线段，射线，直线的概念和画法，掌握线段，射线，直线的概念以及两点之间，线段最短是解题的关键.21、（1）8MN =（2）16AB =．【分析】（1）先根据中点的定义求出AC ，再利用线段的和差求出BC ，然后再根据中点的定义求出CN ，即可求出MN ；（2）根据中点的定义可求得AC 和BC 分别等于2MC 和2CN ，再根据8NM MC CN =+=，即可求出AB 的长．【题目详解】解：（1）因为M 、N 分别是线段AC 、BC 的中点， 所以12,2AC AM CN BC ==， 又因为16AB =,6AM =，所以212,4AC AM BC AB AC ===-=， 所以122CN BC ==， 所以628MN MC CN =+=+=；（2）因为M 、N 分别是线段AC 、BC 的中点，所以2,2AC MC BC CN ==，所以222()216AB AC BC MC CN MC CN NM ．【题目点拨】本题考查线段中点的有关计算，线段的和差．掌握线段的中点的性质、线段的和差运算是解题的关键．22、（1）111n n -+；（2）20192020；（3）10042019【分析】（1）根据给出的具体例子，归纳式子特征为：分子为1，分母是两个连续自然数的乘积，等于这两个连续自然数的倒数差，因此猜想第n 项可转化为111•(1)1n n n n =-++； （2）按照（1）得出的规律，进行计算即可；（3）观察式子的每一项，归纳出：分子为1，分母是两个连续奇数的乘积，第n 项可转化为1111()(21)(21)22121n n n n =--+-+，依次抵消即可求解 【题目详解】解：（1）111•(1)1n n n n =-++， 故答案为：111n n -+ （2）112+⨯123⨯+134⨯+…+120192020⨯ =111111112233420192020-+-+-++- =112020-=2019 2020，故答案为：2019 2020（3）原式＝113153+⨯⨯+175⨯+…+120192017⨯＝1111111233557⎛⨯-+-+-+⎝…+1120172019⎫-⎪⎭＝111 22019⎛⎫⨯-⎪⎝⎭＝2019 128201⨯＝1004 2019【题目点拨】考查了与分式混合运算有关的规律性问题，解决这类题目要找出变化规律，消去中间项，只剩首末两项，使运算变得简单23、（1）见解析（2）()12n n-（3）1225；2450【分析】（1）根据两点确定一条直线画出直线，观察后即可解答问题；（2）根据上面得到的规律用代数式表示即可；（3）将n=50代入可求得握手次数，送礼物时是双向的，因此是握手次数的2倍，由此即可求解．【题目详解】（1）图形如下：根据图形得：第（1）组最多可以画3条直线；第（2（组最多可以画6条直线；第（3）组最多可以画10条直线；（2）由（1）可知：平面上有3个点时，最多可画直线1+2=3条，平面上有4个点时，最多可画直线1+2+3=6条，平面上有5个点时，最多可画直线1+2+3+4=10条，……所以平面上有n （n≥3）个点，且每3个点均不在1条直线上，那么最多可以画1+2+3+…+n -1=()12n n -条直线， 故答案为()12n n -； （3）某班50名同学在毕业后的一次聚会中，若每两人握1次手问好，那么共握()505012⨯-=1225次手， 互赠礼物为：1225×2=2450件， 故答案为1225，2450.【题目点拨】本题考查了图形的变化类问题，解题的关键是仔细的观察图形并找到其中的规律．24、用360米生产上衣，240米生产裤子才能配套，共能生产240套【解题分析】设用x 米布料生产上衣，y 米布料生产裤子才能配套，则600{23x y x y +==解得360{240x y == 答：用360米生产上衣，240米生产裤子才能配套，共能生产240套设用x 米布料生产上衣，y 米布料生产裤子才能配套．等量关系：①共用布600米；②上衣的件数和裤子的条数相等．。

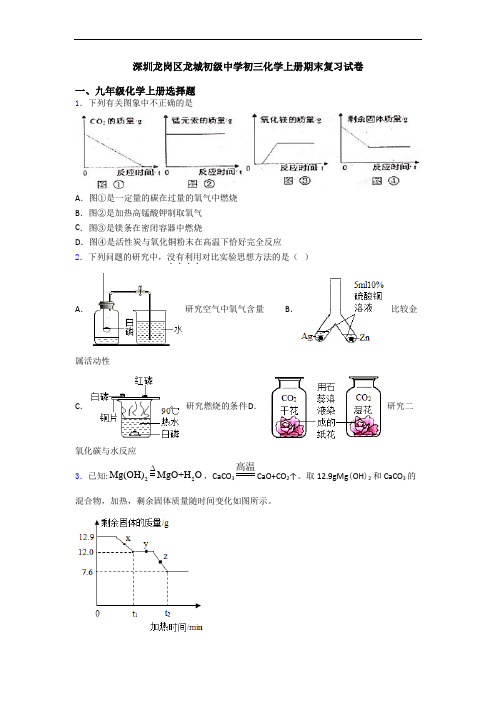
深圳龙岗区龙城初级中学初三化学上册期末复习试卷一、九年级化学上册选择题 1．下列有关图象中不正确的是A ．图①是一定量的碳在过量的氧气中燃烧B ．图②是加热高锰酸钾制取氧气C ．图③是镁条在密闭容器中燃烧D ．图④是活性炭与氧化铜粉末在高温下恰好完全反应 2．下列问题的研究中，没有利用．．．．对比实验思想方法的是（ ） A ．研究空气中氧气含量 B ．比较金属活动性C ．研究燃烧的条件D ．研究二氧化碳与水反应 3．已知:22Mg OH M O (gO+H )，CaCO 3高温CaO+CO 2↑。

取12.9gMg (OH )2和CaCO 3的混合物，加热，剩余固体质量随时间变化如图所示。

下列说法错误的是A．x点剩余固体成分为CaCO3、MgO和Mg（OH）2 B．y点剩余固体中镁元素质量为1.2gC．z点发生的反应为CaCO3高温CaO+CO2↑D．若剩余固体中钙元素的质量分数为36.0％，则剩余固体的成分为CaCO3和MgO4．运用推理、归纳、类比、对比的方法得出下列结论，其中合理的是( )A．不同元素组成的物质是化合物，同种元素组成的物质是单质B．水和过氧化氢的组成元素相同，则两者的化学性质相同C．Na+、Mg2+、Cl-的最外层电子数均为8，由此得出离子的最外层电子数均为8D．同温下分解氯酸钾,加催化剂的反应速率快，说明催化剂可以改变反应速率5．实验是进行科学探究的重要手段，实验方案的设计是实验成功的基本保证。

下列实验方法设计不合理的是（）选项实验目的实验方法A检验一瓶气体是否为氧气将带火星的木条伸入瓶中B鉴别空气和氧气将燃着的木炭放入集气瓶中C鉴别食盐和白糖观察颜色进行区别D验证浓度对反应的影响将燃着的木条分别伸入氧气和空气中A．A B．B C．C D．D6．由X、Y两种元素组成的化合物，其相对分子质量为76，已知Y元素核内有8个质子和8个中子，X元素核内质子数和中子数分别比Y元素少1个，则该化合物化学式为A．X2Y5B．X2Y3C．XY2D．X2Y7．小希设计如图的实验，并完成下列的操作步骤：①未点燃酒精灯，观察白磷未燃烧②点燃酒精灯片刻，观察到白磷燃烧③熄灭酒精灯，冷却到室温，观察到水位上升到刻度 1 处④点燃酒精灯，剩余的白磷不燃烧下列说法正确的是（）A．酒精灯加热铜丝，白磷燃烧，铜丝变黑，可见白磷的金属活动性比铜强B．操作②中除了观察到白磷燃烧，铜丝也变黑，会使“空气中氧气含量”的测定的结果大于 1/5C．对比①②中的现象，说明可燃物燃烧需要氧气D．对比②④中的现象，说明可燃物燃烧需要氧气8．如图所示为硫化氢(H2S)与氧气反应的微观示意图。

深圳龙城初级中学人教版七年级上册数学期末试卷及答案-百度文库一、选择题1．如图，将线段AB延长至点C，使12BC AB=,D为线段AC的中点，若BD=2，则线段AB的长为（）A．4 B．6 C．8 D．122．有理数a，b在数轴上的对应点的位置如图所示，则下列各式成立的是（）A．a＞b B．﹣ab＜0 C．|a|＜|b| D．a＜﹣b 3．-2的倒数是（）A．-2 B．12-C．12D．24．一张普通A4纸的厚度约为0.000104m，用科学计数法可表示为() mA．21.0410-⨯B．31.0410-⨯C．41.0410-⨯D．51.0410-⨯5．已知2a﹣b＝3，则代数式3b﹣6a+5的值为( )A．﹣4 B．﹣5 C．﹣6 D．﹣76．一根绳子弯曲成如图①所示的形状．当用剪刀像图②那样沿虚线a把绳子剪断时，绳子被剪为5段；当用剪刀像图③那样沿虚线b（b∥a）把绳子再剪一次时，绳子就被剪为9段．若用剪刀在虚线a、b之间把绳子再剪（n﹣2）次（剪刀的方向与a平行），这样一共剪n次时绳子的段数是（）A．4n+1 B．4n+2 C．4n+3 D．4n+57．﹣3的相反数是（）A．13-B．13C．3-D．38．若OC是∠AOB内部的一条射线，则下列式子中，不能表示“OC是∠AOB的平分线”的是( )A．∠AOC＝∠BOC B．∠AOB＝2∠BOCC．∠AOC＝12∠AOB D．∠AOC＋∠BOC＝∠AOB9．有理数a、b在数轴上的位置如图所示，则下列结论中正确的是（）A ．a+b ＞0B ．ab ＞0C ．a ﹣b ＜oD ．a÷b ＞010．“植树时只要定出两棵树的位置，就能确定这一行树所在的直线”，用数学知识解释其道理应是（ ） A ．两点确定一条直线B ．两点之间，线段最短C ．直线可以向两边延长D ．两点之间线段的长度，叫做这两点之间的距离11．已知105A ∠=︒，则A ∠的补角等于（ ） A ．105︒B ．75︒C ．115︒D ．95︒12．某同学晚上6点多钟开始做作业，他家墙上时钟的时针和分针的夹角是120°，他做完作业后还是6点多钟，且时针和分针的夹角还是120°，此同学做作业大约用了（ ） A ．40分钟B ．42分钟C ．44分钟D ．46分钟二、填空题13．甲乙两个足够大的油桶各装有一定量的油，先把甲桶中的油的一半给乙桶，然后把乙桶中的油倒出18给甲桶，若最终两个油桶装有的油体积相等，则原来甲桶中的油是乙桶中油的______倍。

广西柳州市城中学区龙城中学2023-2024学年物理八年级第一学期期末达标检测试题学校_______ 年级_______ 姓名_______注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题（每题1分，共30题，30分）1．下列数值最接近生活实际情况的是（）A．普通中学生步行的速度约为8m/sB．一名普通初中学生的质量约为1.5tC．初中物理课本的宽度约为18dmD．一个鸡蛋的质量约为45g2．和谐号动车组列车与和谐型大功率机车的上线，宣告我国动车组开始了第六次大提速。

从科学的角度看，当列车进站时，乘客需站在安全线外的原因是（）A．车与人之间的空气流速减小，压强增大B．车与人之间的空气流速减小，压强减小C．车与人之间的空气流速加大，压强增大D．车与人之间的空气流速加大，压强减小3．下列物理量最接近实际的是A．你所在考场室温约2℃B．你所用的新2B 铅笔长度约18cmC．你的质量约为5kg D．你的心跳大约1 分钟7 次4．如图是穿行在餐厅的机器人端着托盘送餐的情景．若认为机器人是静止的，则选择的参照物是（）A．地面B．托盘C．餐桌D．墙壁5．下列数据中最接近实际的是（）A．成都三环路限速950km/hB．PM2.5是指空气中直径为2.5cm的固体颗粒C．一个鸡蛋的质量约为500gD．人体感觉适宜的温度约为23℃6．“北风乱/夜未央/你的影子剪不断/徒留我孤单/在湖面/成双/”是《菊花台》中的一段歌词。

深圳龙城初级中学人教版八年级上册生物期末试卷及答案-百度文库一、选择题1．通过观察，可以发现水螅的身体只能分出（）A．前后B．左右C．背腹D．上下2．下列各项中，不是线形动物主要特征的是A．身体背腹扁平，体表有刺细胞B．身体细长，成圆柱形C．体表有角质层D．有口有肛门3．关于节肢动物的说法正确的是（）A．昆虫是唯一能飞行的节肢动物类群B．一般没有灵敏的感觉器官、发达的脑和独特的呼吸器官C．大多数昆虫对人类是有害的D．身体的外骨骼可保护内部器官，但不能防止体内水分蒸发4．“生物体的结构与其功能相适应”是重要的生物学观点，下列叙述与此观点不相符的是（）A．鲫鱼身体呈流线型，鳞片表面有黏液，有利于减少水的阻力B．肺泡壁和毛细血管壁都是由一层扁平上皮细胞构成，这有利于血液与肺泡间的气体交换C．小肠绒毛和绒毛内毛细血管的壁都很薄，有利于食物的消化D．昆虫的外骨骼能够保护内部柔软结构，防止体内水分散失5．下列关于蛇的特征描述，不正确的是（）A．用肺呼吸兼用皮肤呼吸B．体表覆盖角质的鳞片C．卵表面有坚韧的卵壳保护D．能真正适应陆地生活6．图是某哺乳动物的牙齿示意图，下列说法错误的是（）A．牙齿的分化有助于摄食和消化B．是食肉动物的牙齿C．①适于切断食物D．②适于咀嚼食物7．下列有关动物形态结构的叙述，正确的是A．节肢动物的身体分为头、胸、腹三部分，有外骨骼B．猪肉涤虫身体背腹扁平，两侧对称，有口无肛门C．家鸽的心脏和肺位于胸腔内，胃、肠等位于腹腔内D．软体动物体表有坚硬的外壳，有蜕皮现象8．下列关于胎生、哺乳的叙述正确的是（）A．所有哺乳动物都是以胎生的方式繁殖后代 B．哺乳为幼仔成长提供优越的营养条件C．胎生提高了哺乳动物的产仔率D．胎生、哺乳提高了幼仔的死亡率9．如图能正确表示骨、骨连接和骨骼肌关系的是（）A．B．C．D．10．骨、关节、肌肉关系图正确的是（）A．B．C．D．11．关节是能活动的骨连结，在运动中起支点的作用．如图是关节结构模式图，下列说法正确的是（）A．1使关节灵活B．4使关节牢固C．3和5共同围成2 D．2内的滑液由1分泌12．教育部、国家体育总局和共青团中央提出“阳光体育”——“每天锻炼一小时，健康生活一辈子”，关于体育锻炼作用的叙述，下面哪一项最全面A．能使关节囊和韧带增厚B．能加强骨的营养C．能使肌肉发达D．以上三项都是13．下列不属于．．．动物运动的意义的是A．可以主动出击去获取食物B．使体形不断增大C．可以逃避敌害和迁移到适宜的场所D．可以完成求偶和交配14．下列几种动物中，具有社会行为特征的是A．狒狒B．鸭子C．蝗虫D．沙丁鱼15．如图是白蚁家族成员示意图，下列关于白蚁群体的行为特点的叙述，不正确．．．的是①社会行为，成员之间有明确分工②社会行为，该群体成员中形成了等级③共生行为，群体内部形成了一定的组织④社会行为，各成员之间都是用声音进行信息交流的A．①②B．②③C．③④D．②③④16．下列关于动物运动和行为的叙述，错误的是A．动物的运动有利于动物寻觅食物、躲避敌害、争夺栖息地和繁殖后代B．躯体运动产生的过程是：神经传来的兴奋→骨骼肌收缩→牵引骨绕关节活动C．学习行为是在先天性行为的基础上，由生活经验和学习获得的行为D．“探究菜青虫的取食行为”可用野外采集的幼虫和新鲜白菜叶作为实验材料17．关于“小鼠走迷宫”的探究实验，下列说法正确的是A．这是探究小鼠的先天性行为B．小鼠“尝试与错误”的次数远少于蚯蚓C．不同小鼠熟悉迷宫的能力都一样D．小鼠一旦学会走迷宫，就不会忘记18．从行为获得的途径来看，下列动物行为属于学习行为的是A．马随着音乐的节奏踏起优美的舞B．乌贼遇到敌害时能迅速喷出大量墨汁C．失去蛋的企鹅把鹅卵石当企鹅蛋孵化D．刚出生的小羊碰到母羊乳头吮吸乳汁19．下列动物行为中，属于攻击行为的是（）A．一条蛇追捕一只青蛙B．两只狗因争夺食物而打架C．蜜蜂叮咬人D．螃蟹反击天敌的进攻20．宠物作为伴侣动物，是我们人类获得幸福和健康生活的一个来源。

龙城初中2022—2023学年第一学期期末试题九年级英语第一部分选择题（50分）I. 完形填空(10分)阅读下面短文，从短文后所给的A、B、C、D四个选项中选出能填入相应空白处的最佳选项，并在答题卡上将相应的字母编号涂黑。

（共10小题，每小题1分）Last month some parents visited a pizza restaurant in Florida with their children. On the door, they saw a sign “NO 1 .” “Why can't we bring our children?” “What on earth does the owner want to do?” The parents were surprised and 2 angrily.So why did the restaurant 3 the sign on its door?Troy Taylor, the 4 of the pizza restaurant, found that many parents couldn't control their children and many children couldn't have meals 5 , so they disturbed other customers. Some people said that this was unfair. Mr. Taylor 6 his decision. He said that the restaurant was near a 7 road, so there might be some danger if the parents didn’t take good care of their children. So he made up his mind to ban(禁止) children from his restaurant.Others supported his decision, they said they were 8 noisy children in restaurants and now they could finally have a place for adults only.9 ，many other restaurants have also met the same problem. Some have done nothing and others have tried to ban children during certain times of the day. There’s one restaurant in Italy. It has been creative in dealing with the problem. They rewarded well-behaved children to 10 parents to control their children.These methods may be useful for a while, but it is difficult to solve this problem completely.1. A. ENTRANCE B. CHILDREN C. ADULTS D. SMOKING2. A. compared B. celebrated C. complained D. calculated3. A. put up B. put out C. put on D. put off4. A. waiter B. cook C. customer D. owner5. A. happily B. quietly C. quickly D. regularly6. A. accepted B. explained C. announced D. discovered7. A. busy B. narrow C. lonely D. free8. A. fond of B. tired of C. proud of D. ashamed of9. A. For example B. In addition C. In fact D. As usual10. A. allow B. force C. remind D. encourage Ⅱ．阅读理解。

七年级第一学期语文期末测练题第一部分基础训练（32分）1.加点字注音完全正确的一项是（）（2分）A.煞．费苦心（shá）言简意赅．（gāi）戏谑．（xuè）趾．高气扬（zhǐ）B.乳臭．未干（xiù）怨天尤．人（yóu）寂寥．（liáo）随声附和．（hé）C.博闻强识．（zhì）杳．无音信（yǎo）伶．仃（líng）无边无垠． (yín)D.苦心孤诣．（yì）恍．然大悟（huǎng）冗．长（chén）泯．然众人（mǐn）2.下列各句书写完全正确的一项是（）（2分）A.对于现代的文艺作品，那些写得朦朦胧胧的，堆砌了许多华丽的词句的、无病而呻、自作多情的风华雪月的文字，我一看就从脑中抹去。

B.杨柳已经发芽，早的山桃也多吐雷，和孩子们的天上的点缀相照映，打成一片春日的温和。

C.几年里，邓稼先和老科学家们坚苦创业，新中国第一所近代物理的研究机构渐渐强大起来。

D.周围是无银的空间，一切都是那么莫声。

3.下列句子中加点的成语使用不恰当的一项是（）（2分）A.一旦打开心灵之窗，写出来的东西往往就能扣人心弦．．．．。

B.每到夜幕降临，柳州的小吃街便人声鼎沸．．．．，那场面十分壮观。

C.读书是游历世界最经济、最省事的途径，我们足不出户，便可以大饱眼福．．．．。

D.柳州电视台的“摆古”栏目办得惟妙惟肖．．．．，赢得了观众的一致好评。

4.下列句子，没有语病的一项是（）（2分）A.我们并不否认这部小说没有某些不尽如人意之处，但总体上是成功的。

B.学校实施愉快教育后，学生的学习热情有了明显的进步。

C.在会议上，校长虚心接受和听取了老师同学们的批评，并表示要及时整改。

D.学习语文，除了要扩大阅读量，课内外多练习写作外，培养良好的学习习惯也十分重要。

5.下列描写手法判断有误的一项是（）（2分）A.我也不停步，只在心里思量：“又出了什么事啦？”（心理描写）B.“妈妈！”我奔过去，为自己的虚荣，为自己的无知流着泪。

深圳龙城初级中学人教版七年级上册数学期末试卷及答案-百度文库一、选择题1．如图，直线AB ⊥直线CD ，垂足为O ，直线EF 经过点O ,若35BOE ∠=，则FOD ∠=( )A ．35°B ．45°C ．55°D ．125°2．球从空中落到地面所用的时间t （秒）和球的起始高度h （米）之间有关系式5h t =，若球的起始高度为102米，则球落地所用时间与下列最接近的是（ ） A ．3秒 B ．4秒 C ．5秒 D ．6秒 3．一个角是这个角的余角的2倍，则这个角的度数是（ ）A ．30B ．45︒C ．60︒D ．75︒4．一项工程，甲独做需10天完成，乙单独做需15天完成，两人合作4天后，剩下的部分由乙独做全部完成，设乙独做x 天，由题意得方程（ ） A ．410 +415x -=1 B ．410 +415x +=1 C ．410x + +415=1 D ．410x + +15x=1 5．王老师有一个实际容量为()201.8GB 1GB 2KB =的U 盘，内有三个文件夹.已知课件文件夹占用了0.8GB 的内存，照片文件夹内有32张大小都是112KB 的旅行照片，音乐文件夹内有若干首大小都是152KB 的音乐.若该U 盘内存恰好用完，则此时文件夹内有音乐()首. A ．28B ．30C ．32D ．346．一根绳子弯曲成如图①所示的形状．当用剪刀像图②那样沿虚线a 把绳子剪断时，绳子被剪为5段；当用剪刀像图③那样沿虚线b （b ∥a ）把绳子再剪一次时，绳子就被剪为9段．若用剪刀在虚线a 、b 之间把绳子再剪（n ﹣2）次（剪刀的方向与a 平行），这样一共剪n 次时绳子的段数是（ ）A ．4n+1B ．4n+2C ．4n+3D ．4n+57．计算：31﹣1=2，32﹣1=8，33﹣1=26，34﹣1=80，35﹣1=242，…，归纳各计算结果中的个位数字的规律，猜测32018﹣1的个位数字是（ ）A．2 B．8 C．6 D．0 8．如图是由下列哪个立体图形展开得到的？（）A．圆柱B．三棱锥C．三棱柱D．四棱柱9．下列各数中，绝对值最大的是（）A．2 B．﹣1 C．0 D．﹣3 10．下列式子中，是一元一次方程的是（）A．3x+1=4x B．x+2＞1 C．x2－9=0 D．2x－3y=011．按如图所示图形中的虚线折叠可以围成一个棱柱的是（）A．B．C．D．12．有理数a、b在数轴上的位置如图所示，则下列结论中正确的是（）A．a+b＞0 B．ab＞0 C．a﹣b＜o D．a÷b＞0 13．单项式﹣6ab的系数与次数分别为（）A．6，1 B．﹣6，1 C．6，2 D．﹣6，2 14．下列变形中，不正确的是( )A．若x=y，则x+3=y+3 B．若-2x=-2y，则x=yC．若x ym m=，则x y=D．若x y=，则x ym m=15．如图的几何体，从上向下看，看到的是（）A．B．C．D．二、填空题16．若代数式mx2+5y2﹣2x2+3的值与字母x的取值无关，则m的值是__．17．若x＝2是关于x的方程5x+a＝3（x+3）的解，则a的值是_____．18．如图，是一个正方体的表面展开图，则原正方体中“国”字所在的面相对的面上标的字是_____．19．=38A∠︒，则A∠的补角的度数为______.20．把53°24′用度表示为_____．21．一个商店把某件商品按进价提高20%作为定价，可是总卖不出去；后来按定价减价20%出售，很快卖掉，结果这次生意亏了4元．那么这件商品的进价是________元．22．已知a，m，n均为有理数，且满足5,3a m n a-=-=，那么m n-的值为______________.23．单项式22ab-的系数是________.24．因原材料涨价,某厂决定对产品进行提价,现有三种方案:方案一,第一次提价10%，第二次提价30%;方案二，第一次提价30%，第二次提价10%；方案三，第一、二次提价均为20%.三种方案提价最多的是方案_____________．25．﹣30×（1223-+45）＝_____．26．如图，在长方形ABCD中，10,13.,,,AB BC E F G H==分别是线段,,,AB BC CD AD上的定点，现分别以,BE BF为边作长方形BEQF,以DG为边作正方形DGIH.若长方形BEQF与正方形DGIH的重合部分恰好是一个正方形，且,BE DG=,Q I均在长方形ABCD内部.记图中的阴影部分面积分别为123,,s s s.若2137SS=,则3S=___27．计算221b aa b a b⎛⎫÷-⎪-+⎝⎭的结果是______28．若2a +1与212a +互为相反数，则a ＝_____． 29．已知一个角的补角是它余角的3倍，则这个角的度数为_____．30．观察一列有规律的单项式：x ，23x ，35x ，47x ，59x ⋅⋅⋅，它的第n 个单项式是______.三、压轴题31．小刚运用本学期的知识，设计了一个数学探究活动.如图1，数轴上的点M ，N 所表示的数分别为0，12.将一枚棋子放置在点M 处，让这枚棋子沿数轴在线段MN 上往复运动（即棋子从点M 出发沿数轴向右运动，当运动到点N 处，随即沿数轴向左运动，当运动到点M 处，随即沿数轴向右运动，如此反复⋯）.并且规定棋子按照如下的步骤运动：第1步，从点M 开始运动t 个单位长度至点1Q 处；第2步，从点1Q 继续运动2t 单位长度至点2Q 处；第3步，从点2Q 继续运动3t 个单位长度至点3Q 处…例如：当3t =时，点1Q 、2Q 、3Q 的位置如图2所示.解决如下问题：（1）如果4t =，那么线段13Q Q =______；（2）如果4t <，且点3Q 表示的数为3，那么t =______； （3）如果2t ≤，且线段242Q Q =，那么请你求出t 的值.32．如图，从左到右依次在每个小方格中填入一个数，使得其中任意三个相邻方格中所填数之和都相等． 6abx-1-2 ...（1）可求得 x =______，第 2021 个格子中的数为______； （2）若前 k 个格子中所填数之和为 2019，求 k 的值；（3）如果m ，n 为前三个格子中的任意两个数，那么所有的|m -n | 的和可以通过计算|6-a |+|6-b|+|a -b|+|a -6| +|b -6|+|b -a| 得到．若m ，n 为前8个格子中的任意两个数，求所有的|m-n|的和.33．已知有理数a ，b ，c 在数轴上对应的点分别为A ，B ，C ，且满足（a-1）2+|ab+3|=0，c=-2a+b ．（1）分别求a，b，c的值；（2）若点A和点B分别以每秒2个单位长度和每秒1个单位长度的速度在数轴上同时相向运动，设运动时间为t秒．i）是否存在一个常数k，使得3BC-k•AB的值在一定时间范围内不随运动时间t的改变而改变？若存在，求出k的值；若不存在，请说明理由．ii）若点C以每秒3个单位长度的速度向右与点A，B同时运动，何时点C为线段AB的三等分点？请说明理由．34．对于数轴上的点P，Q，给出如下定义：若点P到点Q的距离为d(d≥0)，则称d为点P 到点Q的d追随值，记作d[PQ]．例如，在数轴上点P表示的数是2，点Q表示的数是5，则点P到点Q的d追随值为d[PQ]=3．问题解决：(1)点M，N都在数轴上，点M表示的数是1，且点N到点M的d追随值d[MN]=a(a≥0)，则点N表示的数是_____(用含a的代数式表示)；(2)如图，点C表示的数是1，在数轴上有两个动点A，B都沿着正方向同时移动，其中A点的速度为每秒3个单位，B点的速度为每秒1个单位，点A从点C出发，点B表示的数是b，设运动时间为t(t>0)．①当b=4时，问t为何值时，点A到点B的d追随值d[AB]=2；②若0<t≤3时，点A到点B的d追随值d[AB]≤6，求b的取值范围．35．如图，在平面直角坐标系中，点M的坐标为（2，8），点N的坐标为（2，6），将线段MN向右平移4个单位长度得到线段PQ（点P和点Q分别是点M和点N的对应点），连接MP、NQ，点K是线段MP的中点．（1）求点K的坐标；（2）若长方形PMNQ以每秒1个单位长度的速度向正下方运动，（点A、B、C、D、E分别是点M、N、Q、P、K的对应点），当BC与x轴重合时停止运动，连接OA、OE，设运动时间为t秒，请用含t的式子表示三角形OAE的面积S（不要求写出t的取值范围）；（3）在（2）的条件下，连接OB、OD，问是否存在某一时刻t，使三角形OBD的面积等于三角形OAE的面积？若存在，请求出t值；若不存在，请说明理由．36．如图，P是定长线段AB上一点，C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动（C在线段AP上，D在线段BP上）（1）若C、D运动到任一时刻时，总有PD＝2AC，请说明P点在线段AB上的位置：（2）在（1）的条件下，Q是直线AB上一点，且AQ﹣BQ＝PQ，求PQAB的值．（3）在（1）的条件下，若C、D运动5秒后，恰好有1CD AB2，此时C点停止运动，D点继续运动（D点在线段PB上），M、N分别是CD、PD的中点，下列结论：①PM﹣PN的值不变；②MNAB的值不变，可以说明，只有一个结论是正确的，请你找出正确的结论并求值．37．如图1，O为直线AB上一点，过点O作射线OC，∠AOC=30°，将一直角三角尺（∠M=30°）的直角顶点放在点O处，一边ON在射线OA上，另一边OM与OC都在直线AB的上方．(1)若将图1中的三角尺绕点O以每秒5°的速度，沿顺时针方向旋转t秒，当OM恰好平分∠BOC时，如图2．①求t值；②试说明此时ON平分∠AOC；(2)将图1中的三角尺绕点O顺时针旋转，设∠AON=α，∠COM=β，当ON在∠AOC内部时，试求α与β的数量关系；(3)若将图1中的三角尺绕点O以每秒5°的速度沿顺时针方向旋转的同时，射线OC也绕点O以每秒8°的速度沿顺时针方向旋转，如图3，那么经过多长时间，射线OC第一次平分∠MON?请说明理由．38．从特殊到一般，类比等数学思想方法，在数学探究性学习中经常用到，如下是一个具体案例，请完善整个探究过程。