针对练习-历届高考数学真题汇编专题7_平面向量_理-含答案

专题07 平面向量【2020年】1.（2020·新课标Ⅲ）已知向量a ，b 满足||5a =，||6b =，6a b ⋅=-，则cos ,=+a a b （ ） A. 3135-B. 1935-C.1735D.1935【答案】D 【解析】5a =，6b =，6a b ⋅=-，()225619a a b a a b ∴⋅+=+⋅=-=.()22222526367a b a ba ab b +=+=+⋅+=-⨯+=，因此，()1919cos ,5735a a ba ab a a b⋅+<+>===⨯⋅+. 2.（2020·山东卷）已知P 是边长为2的正六边形ABCDEF 内的一点，则AP AB ⋅ 的取值范用是（ ） A. ()2,6- B. (6,2)- C. (2,4)- D. (4,6)-【答案】A 【解析】AB 的模为2，根据正六边形的特征，可以得到AP 在AB 方向上的投影的取值范围是(1,3)-， 结合向量数量积的定义式，可知AP AB ⋅等于AB 的模与AP 在AB 方向上的投影的乘积， 所以AP AB ⋅的取值范围是()2,6-，3.（2020·北京卷）已知正方形ABCD 的边长为2，点P 满足1()2AP AB AC =+，则||PD =_________；PB PD ⋅=_________．【答案】 (1).5 (2). 1-【解析】以点A 为坐标原点，AB 、AD 所在直线分别为x 、y 轴建立如下图所示的平面直角坐标系，则点()0,0A 、()2,0B 、()2,2C 、()0,2D ，()()()()1112,02,22,1222AP AB AC =+=+=， 则点()2,1P ，()2,1PD ∴=-，()0,1PB =-， 因此，()22215PD =-+=，()021(1)1PB PD ⋅=⨯-+⨯-=-.4.（2020·天津卷）如图，在四边形ABCD 中，60,3B AB ︒∠==，6BC =，且3,2AD BC AD AB λ=⋅=-，则实数λ的值为_________，若,M N 是线段BC 上的动点，且||1MN =，则DM DN ⋅的最小值为_________．【答案】 (1). 16 (2). 132【解析】AD BC λ=，//AD BC ∴，180120BAD B ∴∠=-∠=，cos120AB AD BC AB BC AB λλ⋅=⋅=⋅1363922λλ⎛⎫=⨯⨯⨯-=-=- ⎪⎝⎭，解得16λ=， 以点B 为坐标原点，BC 所在直线为x 轴建立如下图所示的平面直角坐标系xBy ，()66,0BC C =∴，,∵3,60AB ABC =∠=︒，∴A 的坐标为3332A ⎛ ⎝⎭,∵又∵16AD BC =,则533,22D ⎛⎫ ⎪ ⎪⎝⎭，设(),0M x ，则()1,0N x +（其中05x ≤≤）， 533,2DM x ⎛=- ⎝⎭，333,2DN x ⎛=- ⎝⎭，()222533321134222222DM DN x x x x x ⎛⎛⎫⎛⎫⋅=--+=-+=-+ ⎪⎪ ⎝⎭⎝⎭⎝⎭， 所以，当2x =时，DM DN ⋅取得最小值132. 5.（2020·浙江卷）设1e ，2e 为单位向量，满足21|22|-≤e e ，12a e e =+，123b e e =+，设a ，b 的夹角为θ，则2cos θ的最小值为_______． 【答案】2829【解析】12|2|2e e -≤，124412e e ∴-⋅+≤，1234e e ∴⋅≥， 222121222121212(44)4(1)()cos (22)(106)53e e e e a b e e e e e e a bθ+⋅+⋅⋅∴===+⋅+⋅+⋅⋅12424228(1)(1)3332953534e e =-≥-=+⋅+⨯. 6.（2020·江苏卷）在△ABC 中，43=90AB AC BAC ==︒，，∠，D 在边BC 上，延长AD 到P ，使得AP =9，若3()2PA mPB m PC =+-（m 为常数），则CD 的长度是________．【答案】185【解析】∵,,A D P 三点共线， ∴可设()0PA PD λλ=>， ∵32PA mPB m PC ⎛⎫=+- ⎪⎝⎭，∴32PD mPB m PC λ⎛⎫=+- ⎪⎝⎭，即32m m PD PB PC λλ⎛⎫- ⎪⎝⎭=+， 若0m ≠且32m ≠，则,,B D C 三点共线， ∴321m m λλ⎛⎫- ⎪⎝⎭+=，即32λ=， ∵9AP =，∴3AD =，∵4AB =,3AC =,90BAC ∠=︒， ∴5BC =，设CD x =，CDA θ∠=，则5BD x =-，BDA πθ∠=-.∴根据余弦定理可得222cos 26AD CD AC xAD CD θ+-==⋅，()()()222257cos 265x AD BD AB AD BD x πθ--+--==⋅-，∵()cos cos 0θπθ+-=，∴()()2570665x x x --+=-，解得185x =，∴CD 的长度为185.当0m =时， 32PA PC =，,C D 重合，此时CD 的长度为0， 当32m =时，32PA PB =，,B D 重合，此时12PA =，不合题意，舍去.7.（2020·新课标Ⅱ）已知单位向量a ，b 的夹角为45°，ka –b 与a 垂直，则k =__________.【答案】2【解析】由题意可得：211cos 452a b →→⋅=⨯⨯=， 由向量垂直的充分必要条件可得：0k a b a →→→⎛⎫-⋅= ⎪⎝⎭，即：202k a a b k →→→⨯-⋅=-=，解得：2k =.8.（2020·新课标Ⅰ）设,a b 为单位向量，且||1+=a b ，则||a b -=______________.【解析】因为,a b 为单位向量，所以1a b == 所以()2222221a b a b a a b b a b +=+=+⋅+=+⋅=解得：21a b ⋅=- 所以()22223a b a b a a b b -=-=-⋅+=【2019年】1．【2019年高考全国I 卷理数】已知非零向量a ，b 满足||2||=a b ，且()-a b ⊥b ，则a 与b 的夹角为A ．π6 B ．π3C ．2π3D ．5π6【答案】B【解析】因为()-a b ⊥b ，所以2()-⋅=⋅-a b b a b b =0，所以2⋅=a b b ，所以cos θ=22||12||2⋅==⋅a b b a b b ，所以a 与b 的夹角为π3，故选B ．2．【2019年高考全国II 卷理数】已知AB →=(2,3)，AC →=(3，t )，BC →=1，则AB →·BC →= A ．−3 B ．−2 C ．2D ．3【答案】C【解析】由BC →=AC →—AB →=（1，t-3），211BC ==，得3t =，则(1,0)BC =，(2,3)(1,0)21302AB BC ==⨯+⨯=．故选C ．3．【2019年高考北京卷理数】设点A ，B ，C 不共线，则“AB →与AC →的夹角为锐角”是“||||AB AC BC +>”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】C【解析】AB 与AC 的夹角为锐角，所以2222||||2||||2AB AC AB AC AB AC AB AC ++⋅>+-⋅，即22||||AB AC AC AB +>-，因为AC AB BC -=，所以|AB +AC |>|BC |；当|AB +AC |>|BC |成立时，|AB +AC |2>|AB -AC |2AB ⇒•AC >0，又因为点A ，B ，C 不共线，所以AB 与AC 的夹角为锐角.故“AB 与AC 的夹角为锐角”是“|AB +AC |>|BC |”的充分必要条件,故选C ．4．【2019年高考全国III 卷理数】已知a ，b 为单位向量，且a ·b =0，若2=c a ，则cos ,=a c ___________. 【答案】23【解析】因为2=c a ，0⋅=a b ，所以22⋅=⋅a c a b 2=，222||4||5||9=-⋅+=c a b b ，所以||3=c ，所以cos ,=a c 22133⋅==⨯⋅a c a c ．5．【2019年高考天津卷理数】在四边形ABCD 中，,5,30AD BC AB AD A ==∠=︒∥，点E在线段CB 的延长线上，且AE BE =，则BD AE ⋅=_____________．【答案】1-【解析】建立如图所示的直角坐标系，∠DAB =30°，23,5,AB AD ==则(23,0)B ，535(,)22D . 因为AD ∥BC ，30BAD ∠=︒，所以30ABE ∠=︒， 因为AE BE =，所以30BAE ∠=︒， 所以直线BE 的斜率为33，其方程为3(23)3y x =-， 直线AE 的斜率为33-，其方程为33y x =-. 由3(23),333y x y x ⎧=-⎪⎪⎨⎪=-⎪⎩得3x =，1y =-， 所以(3,1)E -.所以35(,)(3,1)122BD AE =-=-.6．【2019年高考江苏卷】如图，在ABC △中，D 是BC 的中点，E 在边AB 上，BE =2EA ，AD 与CE 交于点O .若6AB AC AO EC ⋅=⋅，则ABAC的值是_____.【答案】3.【解析】如图，过点D 作DF //CE ，交AB 于点F ，由BE =2EA ，D 为BC 的中点，知BF =FE =EA ,AO =OD ．()()()3632AO EC AD AC AE AB AC AC AE =-=+-，()223131123233AB AC AC AB AB AC AB AC AB AC ⎛⎫⎛⎫=+-=-+- ⎪ ⎪⎝⎭⎝⎭22223211323322AB AC AB AC AB AC AB AC AB AC ⎛⎫=-+=-+= ⎪⎝⎭， 得2213,22AB AC =即3,AB AC =故3ABAC=【2018年】1．【2018·全国I 卷 】在ABC △中，AD 为BC 边上的中线，E 为AD 的中点，则EB =A ．3144AB AC -B ．1344AB AC - C ．3144AB AC +D ．1344AB AC +【答案】A【解析】根据向量的运算法则，可得()111111222424BE BA BD BA BC BA BA AC =+=+=++ 1113124444BA BA AC BA AC =++=+，所以3144EB AB AC =-. 故选A.2．【2018·全国II 卷 】已知向量a ，b 满足||1=a ，1⋅=-a b ，则(2)⋅-=a a b A ．4 B ．3 C ．2 D ．0【答案】B【解析】因为()()22222||1213⋅-=-⋅=--=+=a a b a a b a 所以选B.3．（2018·浙江卷）已知a ，b ，e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为π3，向量b 满足b 2−4e ·b +3=0，则|a −b |的最小值是 A ．3−1 B ．3+1 C ．2 D ．2−3【答案】A【解析】设，则由得，由b 2−4e ·b +3=0得因此|a −b |的最小值为圆心到直线的距离23=32减去半径1，为选A.4．【2018·天津卷 】如图，在平面四边形ABCD 中，,,120,AB BC AD CD BAD ⊥⊥∠=1,AB AD ==若点E 为边CD 上的动点，则AE BE ⋅的最小值为A ．2116 B ．32C ．2516D ．3【答案】A【解析】连接AD ,取AD 中点为O ,可知ABD △为等腰三角形，而,AB BC AD CD ⊥⊥，所以BCD △为等边三角形，3BD =. 设()01DE tDC t =≤≤AE BE ⋅ ()()()2232AD DE BD DE AD BD DE AD BD DE BD DE DE =+⋅+=⋅+⋅++=+⋅+ =233322t t -+ ()01t ≤≤ 所以当14t =时，上式取最大值2116，故选A.5．【2018·北京卷 】设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的 A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件D ．既不充分也不必要条件【答案】C 【解析】222222699+63333-=+-=⇔⇔-++⋅=⋅+a a b a b a b a b a b b a a b b ，因为a ，b 均为单位向量，所以2222699+6=0-⋅+=⋅+⇔⋅⇔a a b b a a b b a b a ⊥b ，即“33-=+a b a b ”是“a ⊥b ”的充分必要条件.故选C.6．【2018·全国III 卷 】已知向量()=1,2a ，()=2,2-b ，()=1,λc ．若()2∥c a +b ，则λ=___________． 【答案】12【解析】由题可得()24,2+=a b ，()2∥c a +b ，()=1,λc ，420λ∴-=，即12λ=，故答案为12.7．【2018·上海卷】在平面直角坐标系中，已知点()10A -，、()20B ，，E 、F 是y 轴上的两个动点，且||2EF =，则AE BF ⋅的最小值为___________． 【答案】-3【解析】根据题意，设E （0，a ），F （0，b ）； ∴2EF a b =-=； ∴a =b +2，或b =a +2； 且()()1,2,AE a BF b ==-，； ∴2AE BF ab ⋅=-+；当a =b +2时，()22222AE BF b b b b ⋅=-++⋅=+-； ∵b 2+2b ﹣2的最小值为8434--=-； ∴AE BF ⋅的最小值为﹣3，同理求出b =a +2时，AE BF ⋅的最小值为﹣3． 故答案为：﹣3．8．【2018·江苏卷】在平面直角坐标系xOy 中，A 为直线:2l y x =上在第一象限内的点，()5,0B ，以AB 为直径的圆C 与直线l 交于另一点D ．若0AB CD ⋅=，则点A 的横坐标为___________． 【答案】3【解析】设(),2(0)A a a a >，则由圆心C 为AB 中点得5,,2a C a +⎛⎫⎪⎝⎭易得()()():520C x x a y y a --+-=，与2y x =联立解得点D 的横坐标1,D x =所以()1,2D .所以()55,2,1,22a AB a a CD a +⎛⎫=--=-- ⎪⎝⎭，由0AB CD ⋅=得()()()2551220,230,32a a a a a a a +⎛⎫--+--=--== ⎪⎝⎭或1a =-， 因为0a >，所以 3.a =【2017年】1．【2017·全国III 卷 】在矩形ABCD 中，AB =1，AD =2，动点P 在以点C 为圆心且与BD 相切的圆上.若AP AB AD λμ=+，则λμ+的最大值为 A ．3B ．22C ．5D ．2【答案】A【解析】如图所示，建立平面直角坐标系.设()()()()()0,1,0,0,2,0,2,1,,A B C D P x y ， 易得圆的半径5r =C 的方程是()22425x y -+=，()()(),1,0,1,2,0AP x y AB AD =-=-=，若满足AP AB AD λμ=+，则21x y μλ=⎧⎨-=-⎩ ，,12x y μλ==-，所以12xy λμ+=-+，设12x z y =-+，即102x y z -+-=，点(),P x y 在圆()22425x y -+=上， 所以圆心(20),到直线102xy z -+-=的距离d r ≤21514z -≤+，解得13z ≤≤， 所以z 的最大值是3，即λμ+的最大值是3，故选A ．2．【2017·全国II 卷 】已知ABC △是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+的最小值是 A ．2-B ．32-C ．43-D ．1-【答案】B【解析】如图，以BC 为x 轴，BC 的垂直平分线DA 为y 轴，D 为坐标原点建立平面直角坐标系，则3)A ，(1,0)B -，(1,0)C ，设(,)P x y ，所以(3)PA x y =-，(1,)PB x y =---，(1,)PC x y =--，所以(2,2)PB PC x y +=--，22()22(3)22(PA PB PC x y y x y ⋅+=-=+-2333)22-≥-，当3P 时，所求的最小值为32-，故选B ．3．【2017·北京卷 】设m ,n 为非零向量，则“存在负数λ，使得λ=m n ”是“0<⋅m n ”的 A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】A【解析】若0λ∃<，使λ=m n ，则两向量,m n 反向，夹角是180︒，那么cos180⋅=︒=m n m n0-<m n ；若0⋅<m n ，那么两向量的夹角为(]90,180︒︒，并不一定反向，即不一定存在负数λ，使得λ=m n ，所以是充分而不必要条件，故选A.4．【2017·全国I 卷 】已知向量a ，b 的夹角为60°，|a |=2，|b |=1，则| a +2b |=___________． 【答案】23【解析】方法一：222|2|||44||4421cos60412+=+⋅+=+⨯⨯⨯+=a b a a b b ， 所以|2|1223+==a b 方法二：利用如下图形，可以判断出2+a b 的模长是以2为边长，一夹角为60°的菱形的对角线的长度，则为235．【2017·江苏卷】如图，在同一个平面内，向量OA ，OB ，OC 的模分别为1，1，2，OA 与OC 的夹角为α，且tan α=7，OB 与OC 的夹角为45°．若OC mOA nOB =+(,)m n ∈R ，则m n +=___________．【答案】3【解析】由tan 7α=可得72sin α=2cos α= 易得cos 45cos 2sin 45sin 0n m n m αα⎧︒+=⎪⎨︒-=⎪⎩2222720210n m ⎧=⎪⎪-=⎪⎩，即510570n m n m +=⎧⎨-=⎩，即得57,44m n ==，所以3m n +=．6．【2017·天津卷】在ABC △中，60A =︒∠，3AB =，2AC =．若2BD DC =，AE AC λ=-()AB λ∈R ，且4AD AE ⋅=-，则λ的值为___________．【答案】311【解析】由题可得1232cos 603,33AB AC AD AB AC ⋅=⨯⨯︒==+， 则12()33AD AE AB AC ⋅=+2123()34934333311AC AB λλλλ-=⨯+⨯-⨯-⨯=-⇒=． 7．【2017·山东卷 】已知12,e e 123-e e 与12λ+e e 的夹角为60︒，则实数λ的值是___________．【解析】∵221212112122)()λλλλ-⋅+=⋅-⋅-e e e e e e e ，12|2-==e ，12||λ+===e e ，cos60λ=︒=λ=． 8．【2017·浙江卷】已知向量a ，b 满足1,2,==a b 则++-a b a b 的最小值是________，最大值是___________．【答案】4，【解析】设向量,a b 的夹角为θ，则-==a b+==a b则++-=a b a b令y =[]21016,20y =+，据此可得：()()maxmin 4++-==++-==a b a ba b a b ，即++-a b a b 的最小值是4，最大值是 【2016年】1.【2016高考山东理数】已知非零向量m ，n 满足4│m │=3│n │，cos<m ，n >=13.若n ⊥（t m +n ），则实数t 的值为（ ） （A ）4 （B ）–4 （C ）94（D ）–94【答案】B【解析】由43=m n ，可设3,4(0)k k k ==>m n ，又()t ⊥+n m n ， 所以22221()cos ,34(4)41603t t n n t t k k k tk k ⋅+=⋅+⋅=⋅+=⨯⨯⨯+=+=n m n n m m n m n n , 所以4t =-，故选B.2.【2016高考新课标2理数】已知向量(1,)(3,2)a m a =-，=，且()a b b ⊥+，则m =（ ） （A ）－8 （B ）－6 （C ）6 （D ）8 【答案】D【解析】向量a b (4,m 2)+=-，由(a b)b +⊥得43(m 2)(2)0⨯+-⨯-=，解得m 8=，故选D.3.【2016高考新课标3理数】已知向量1(2BA = ，31()2BC = ，则ABC ∠=（ ） (A)30︒ (B)45︒ (C)60︒ (D)120︒【答案】A【解析】由题意，得112222cos 11||||BA BC ABC BA BC ⋅∠===⨯，所以30ABC ∠=︒，故选A ． 4.【2016年高考北京理数】设a ，b 是向量，则“||||a b =”是“||||a b a b +=-”的（ ） A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 【答案】D【解析】由22||||()()0a b a b a b a b a b a b +=-⇔+=-⇔⋅=⇔⊥，故是既不充分也不必要条件，故选D.5.【2016高考天津理数】已知△ABC 是边长为1的等边三角形，点E D ,分别是边BC AB ,的中点，连接DE 并延长到点F ，使得EF DE 2=，则BC AF ⋅的值为（ ） （A ）85-（B ）81 （C ）41 （D ）811【答案】B【解析】设BA a =，BC b =，∴11()22DE AC b a ==-，33()24DF DE b a ==-， 1353()2444AF AD DF a b a a b =+=-+-=-+，∴25353144848AF BC a b b ⋅=-⋅+=-+=，故选 B.6.【2016年高考四川理数】在平面内，定点A ，B ，C ，D 满足DA=DB =DC ,DA ⋅DB =DB ⋅DC =DC ⋅DA =-2，动点P ，M 满足AP =1，PM =MC ，则2BM 的最大值是( ) （A ）434 （B ）494 （C ）37634+ （D ）372334+ 【答案】B【解析】甴已知易得1220,DA ADC ADB D D BDC B C ∠=∠====∠=︒.以D 为原点，直线DA 为x 轴建立平面直角坐标系，如图所示，则()()()2,0,1,3,1,3.A B C ---设(),,P x y 由已知1AP =，得()2221x y -+=，又13133,,,,,2222x y x y PM MC M BM ⎛⎫⎛⎫-+++=∴∴= ⎪ ⎪⎝⎭⎝⎭()()222+1334x y BM ++∴=，它表示圆()2221x y -+=上的点()x y ，与点()1,33--的距离的平方的14，()()2222max149333144BM⎛⎫∴=++= ⎪⎝⎭，故选B.7.【2016高考新课标1卷】设向量a =(m ,1),b =(1,2),且|a +b |2=|a |2+|b |2,则m = . 【答案】－2【解析】由222||||||+=+a b a b ,得⊥a b ,所以1120m ⨯+⨯=,解得2m =-.8.【2016高考江苏卷】如图，在ABC ∆中，D 是BC 的中点，,E F 是,A D 上的两个三等分点，4BC CA ⋅=，1BF CF ⋅=- ，则BE CE ⋅ 的值是 ▲ .【答案】78【解析】因为222211436=42244AD BC FD BC BA CA BC AD BC AD --⋅=-⋅--==（）（）， 2211114123234FD BCBF CF BC AD BC AD -⋅=-⋅--==-（）（），因此22513,82FD BC ==，2222114167.22448ED BC FD BC BE CE BC ED BC ED --⋅=-⋅--===（）（） 9.【2016高考浙江理数】已知向量a 、b , ｜a ｜ =1，｜b ｜ =2，若对任意单位向量e ，均有 ｜a ·e ｜+｜b ·e ｜≤,则a ·b 的最大值是 ． 【答案】12【解析】221|(a b)||a ||b |6|a b |6|a ||b |2a b 6a b 2e e e +⋅≤⋅+⋅≤⇒+≤⇒++⋅≤⇒⋅≤，即最大值为12。

高考数学真题汇编---平面向量学校：___________姓名：___________班级：___________考号：___________一．选择题（共10小题）1．（2017•新课标Ⅱ）设非零向量，满足|+|=|﹣|则（）A．⊥B．||=||C．∥D．||＞||2．（2017•新课标Ⅲ）在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若=λ+μ，则λ+μ的最大值为（）A．3 B．2C．D．23．（2017•新课标Ⅱ）已知△ABC是边长为2的等边三角形，P为平面ABC内一点，则•（+）的最小值是（）A．﹣2 B．﹣C．﹣D．﹣14．（2017•浙江）如图，已知平面四边形ABCD，AB⊥BC，AB=BC=AD=2，CD=3，AC与BD交于点O，记I1=•，I2=•，I3=•，则（）A．I1＜I2＜I3B．I1＜I3＜I2C．I3＜I1＜I2D．I2＜I1＜I35．（2016•新课标Ⅲ）已知向量=（，），=（，），则∠ABC=（）A．30°B．45°C．60°D．120°6．（2016•新课标Ⅱ）已知向量=（1，m），=（3，﹣2），且（+）⊥，则m=（）A．﹣8 B．﹣6 C ．6 D．87．（2016•天津）已知△ABC是边长为1的等边三角形，点D、E分别是边AB、BC的中点，连接DE并延长到点F，使得DE=2EF，则•的值为（）A．﹣B．C．D．8．（2016•山东）已知非零向量，满足4||=3||，cos＜，＞=．若⊥（t+），则实数t的值为（）A．4 B．﹣4 C．D．﹣9．（2016•四川）在平面内，定点A，B，C，D满足==，•=•=•=﹣2，动点P，M满足=1，=，则||2的最大值是（）A．B．C．D．10．（2016•四川）已知正三角形ABC的边长为2，平面ABC内的动点P，M 满足||=1，=，则||2的最大值是（）A．B．C．D．二．填空题（共20小题）11．（2017•山东）已知向量=（2，6），=（﹣1，λ），若，则λ=．12．（2017•新课标Ⅲ）已知向量=（﹣2，3），=（3，m），且，则m=．13．（2017•新课标Ⅰ）已知向量=（﹣1，2），=（m，1），若向量+与垂直，则m=．14．（2017•新课标Ⅰ）已知向量，的夹角为60°，||=2，||=1，则|+2|=．15．（2017•山东）已知，是互相垂直的单位向量，若﹣与+λ的夹角为60°，则实数λ的值是．16．（2017•江苏）在平面直角坐标系xOy中，A（﹣12，0），B（0，6），点P在圆O：x2+y2=50上．若≤20，则点P的横坐标的取值范围是．17．（2017•北京）已知点P在圆x2+y2=1上，点A的坐标为（﹣2，0），O为原点，则•的最大值为．18．（2017•江苏）如图，在同一个平面内，向量，，的模分别为1，1，，与的夹角为α，且tanα=7，与的夹角为45°．若=m+n（m，n∈R），则m+n=．19．（2017•天津）在△ABC中，∠A=60°，AB=3，AC=2．若=2，=λ﹣（λ∈R），且=﹣4，则λ的值为．20．（2016•新课标Ⅱ）已知向量=（m，4），=（3，﹣2），且∥，则m=．21．（2016•上海）在平面直角坐标系中，已知A（1，0），B（0，﹣1），P是曲线y=上一个动点，则•的取值范围是．22．（2016•新课标Ⅰ）设向量=（m，1），=（1，2），且|+|2=||2+||2，则m=．23．（2016•山东）已知向量=（1，﹣1），=（6，﹣4），若⊥（t+），则实数t的值为．24．（2016•新课标Ⅰ）设向量=（x，x+1），=（1，2），且⊥，则x=．25．（2016•浙江）已知平面向量，，||=1，||=2，=1，若为平面单位向量，则||+||的最大值是．26．（2016•上海）如图，已知点O（0，0），A（1，0），B（0，﹣1），P是曲线y=上一个动点，则•的取值范围是．27．（2016•江苏）如图，在△ABC中，D是BC的中点，E，F是AD上的两个三等分点，•=4，•=﹣1，则•的值是．28．（2016•北京）已知向量=（1，），=（，1），则与夹角的大小为．29．（2016•上海）如图，在平面直角坐标系xOy中，O为正八边形A1A2…A8的中心，A1（1，0）任取不同的两点A i，A j，点P满足++=，则点P落在第一象限的概率是．30．（2016•浙江）已知向量，，||=1，||=2，若对任意单位向量，均有|•|+|•|≤，则•的最大值是．三．解答题（共1小题）31．（2017•山东）在△ABC中，角A，B，C的对边分别为a，b，c，已知b=3，= =3，求A和a．﹣6，S△ABC高考数学真题汇编---平面向量参考答案与试题解析一．选择题（共10小题）1．【分析】由已知得，从而=0，由此得到．【解答】解：∵非零向量，满足|+|=|﹣|，∴，解得=0，∴．故选：A．2．【分析】如图：以A为原点，以AB，AD所在的直线为x，y轴建立如图所示的坐标系，先求出圆的标准方程，再设点P的坐标为（cosθ+1，sinθ+2），根据=λ+μ，求出λ，μ，根据三角函数的性质即可求出最值．【解答】解：如图：以A为原点，以AB，AD所在的直线为x，y轴建立如图所示的坐标系，则A（0，0），B（1，0），D（0，2），C（1，2），∵动点P在以点C为圆心且与BD相切的圆上，设圆的半径为r，∵BC=2，CD=1，∴BD==∴BC•CD=BD•r，∴r=，∴圆的方程为（x﹣1）2+（y﹣2）2=，设点P的坐标为（cosθ+1，sinθ+2），∵=λ+μ，∴（cosθ+1，sinθ+2）=λ（1，0）+μ（0，2）=（λ，2μ），∴cosθ+1=λ，sinθ+2=2μ，∴λ+μ=cosθ+sinθ+2=sin（θ+φ）+2，其中tanφ=2，∵﹣1≤sin（θ+φ）≤1，∴1≤λ+μ≤3，故λ+μ的最大值为3，故选：A．3．【分析】根据条件建立坐标系，求出点的坐标，利用坐标法结合向量数量积的公式进行计算即可．【解答】解：建立如图所示的坐标系，以BC中点为坐标原点，则A（0，），B（﹣1，0），C（1，0），设P（x，y），则=（﹣x，﹣y），=（﹣1﹣x，﹣y），=（1﹣x，﹣y），则•（+）=2x2﹣2y+2y2=2[x2+（y﹣）2﹣]∴当x=0，y=时，取得最小值2×（﹣）=﹣，故选：B．4．【分析】根据向量数量积的定义结合图象边角关系进行判断即可．【解答】解：∵AB⊥BC，AB=BC=AD=2，CD=3，∴AC=2，∴∠AOB=∠COD＞90°，由图象知OA＜OC，OB＜OD，∴0＞•＞•，•＞0，即I3＜I1＜I2，故选：C．5．【分析】根据向量的坐标便可求出，及的值，从而根据向量夹角余弦公式即可求出cos∠ABC的值，根据∠ABC的范围便可得出∠ABC 的值．【解答】解：，；∴；又0°≤∠ABC≤180°；∴∠ABC=30°．故选：A．【分析】求出向量+的坐标，根据向量垂直的充要条件，构造关于m的方程，解得答案．【解答】解：∵向量=（1，m），=（3，﹣2），∴+=（4，m﹣2），又∵（+）⊥，∴12﹣2（m﹣2）=0，解得：m=8，故选：D．7．【分析】由题意画出图形，把、都用表示，然后代入数量积公式得答案．【解答】解：如图，∵D、E分别是边AB、BC的中点，且DE=2EF，∴•========．故选：C．【分析】若⊥（t+），则•（t+）=0，进而可得实数t的值．【解答】解：∵4||=3||，cos＜，＞=，⊥（t+），∴•（t+）=t•+2=t||•||•+||2=（）||2=0，解得：t=﹣4，故选：B．9．【分析】由==，可得D为△ABC的外心，又•=•=•，可得可得D为△ABC的垂心，则D为△ABC的中心，即△ABC为正三角形．运用向量的数量积定义可得△ABC的边长，以A为坐标原点，AD所在直线为x轴建立直角坐标系xOy，求得B，C的坐标，再设P（cosθ，sinθ），（0≤θ＜2π），由中点坐标公式可得M的坐标，运用两点的距离公式可得BM的长，运用三角函数的恒等变换公式，结合正弦函数的值域，即可得到最大值．【解答】解：由==，可得D为△ABC的外心，又•=•=•，可得•（﹣）=0，•（﹣）=0，即•=•=0，即有⊥，⊥，可得D为△ABC的垂心，则D为△ABC的中心，即△ABC为正三角形．由•=﹣2，即有||•||cos120°=﹣2，解得||=2，△ABC的边长为4cos30°=2，以A为坐标原点，AD所在直线为x轴建立直角坐标系xOy，可得B（3，﹣），C（3，），D（2，0），由=1，可设P（cosθ，sinθ），（0≤θ＜2π），由=，可得M为PC的中点，即有M（，），则||2=（3﹣）2+（+）2=+==，当sin（θ﹣）=1，即θ=时，取得最大值，且为．故选：B．10．【分析】如图所示，建立直角坐标系．B（0，0），C．A．点P的轨迹方程为：=1，令x=+cosθ，y=3+sinθ，θ∈[0，2π）．又=，可得M，代入||2=+3sin，即可得出．【解答】解：如图所示，建立直角坐标系．B（0，0），C．A．∵M满足||=1，∴点P的轨迹方程为：=1，令x=+cosθ，y=3+sinθ，θ∈[0，2π）．又=，则M，∴||2=+=+3sin≤．∴||2的最大值是．也可以以点A为坐标原点建立坐标系．解法二：取AC中点N，MN=，从而M轨迹为以N为圆心，为半径的圆，B，N，M三点共线时，BM为最大值．所以BM最大值为3+=．故选：B．二．填空题（共20小题）11．【分析】利用向量共线定理即可得出．【解答】解：∵，∴﹣6﹣2λ=0，解得λ=﹣3．故答案为：﹣3．12．【分析】利用平面向量数量积坐标运算法则和向量垂直的性质求解．【解答】解：∵向量=（﹣2，3），=（3，m），且，∴=﹣6+3m=0，解得m=2．故答案为：2．13．【分析】利用平面向量坐标运算法则先求出，再由向量+与垂直，利用向量垂直的条件能求出m的值．【解答】解：∵向量=（﹣1，2），=（m，1），∴=（﹣1+m，3），∵向量+与垂直，∴（）•=（﹣1+m）×（﹣1）+3×2=0，解得m=7．故答案为：7．14．【分析】根据平面向量的数量积求出模长即可．【解答】解：【解法一】向量，的夹角为60°，且||=2，||=1，∴=+4•+4=22+4×2×1×cos60°+4×12=12，∴|+2|=2．【解法二】根据题意画出图形，如图所示；结合图形=+=+2；在△OAC中，由余弦定理得||==2，即|+2|=2．故答案为：2．15．【分析】根据平面向量的数量积运算与单位向量的定义，列出方程解方程即可求出λ的值．【解答】解：【方法一】由题意，设=（1，0），=（0，1），则﹣=（，﹣1），+λ=（1，λ）；又夹角为60°，∴（﹣）•（+λ）=﹣λ=2××cos60°，即﹣λ=，解得λ=．【方法二】，是互相垂直的单位向量，∴||=||=1，且•=0；又﹣与+λ的夹角为60°，∴（﹣）•（+λ）=|﹣|×|+λ|×cos60°，即+（﹣1）•﹣λ=××，化简得﹣λ=××，即﹣λ=，解得λ=．故答案为：．16．【分析】根据题意，设P（x0，y0），由数量积的坐标计算公式化简变形可得2x0+y0+5≤0，分析可得其表示表示直线2x+y+5≤0以及直线下方的区域，联立直线与圆的方程可得交点的横坐标，结合图形分析可得答案．【解答】解：根据题意，设P（x0，y0），则有x02+y02=50，=（﹣12﹣x0，﹣y0）•（﹣x0，6﹣y0）=（12+x0）x0﹣y0（6﹣y0）=12x0+6y+x02+y02≤20，化为：12x0﹣6y0+30≤0，即2x0﹣y0+5≤0，表示直线2x﹣y+5=0以及直线上方的区域，联立，解可得x0=﹣5或x0=1，结合图形分析可得：点P的横坐标x0的取值范围是[﹣5，1]，故答案为：[﹣5，1]．17．【分析】设P（cosα，sinα）．可得=（2，0），=（cosα+2，sinα）．利用数量积运算性质、三角函数的单调性与值域即可得出．【解答】解：设P（cosα，sinα）.=（2，0），=（cosα+2，sinα）．则•=2（cosα+2）≤6，当且仅当cosα=1时取等号．故答案为：6．18．【分析】如图所示，建立直角坐标系．A（1，0）．由与的夹角为α，且tanα=7．可得cosα=，sinα=．C．可得cos（α+45°）=．sin（α+45°）=．B．利用=m+n（m，n∈R），即可得出．【解答】解：如图所示，建立直角坐标系．A（1，0）．由与的夹角为α，且tanα=7．∴cosα=，sinα=．∴C．cos（α+45°）=（cosα﹣sinα）=．sin（α+45°）=（sinα+cosα）=．∴B．∵=m+n（m，n∈R），∴=m﹣n，=0+n，解得n=，m=．则m+n=3．故答案为：3．19．【分析】根据题意画出图形，结合图形，利用、表示出，再根据平面向量的数量积列出方程求出λ的值．【解答】解：如图所示，△ABC中，∠A=60°，AB=3，AC=2，=2，∴=+=+=+（﹣）=+，又=λ﹣（λ∈R），∴=（+）•（λ﹣）=（λ﹣）•﹣+λ=（λ﹣）×3×2×cos60°﹣×32+λ×22=﹣4，∴λ=1，解得λ=．故答案为：．20．【分析】直接利用向量共线的充要条件列出方程求解即可．【解答】解：向量=（m，4），=（3，﹣2），且∥，可得12=﹣2m，解得m=﹣6．故答案为：﹣6．21．【分析】设P（cosα，sinα），α∈[0，π]，则=（1，1），=（cosα，sinα+1），由此能求出•的取值范围．【解答】解：∵在平面直角坐标系中，A（1，0），B（0，﹣1），P是曲线y=上一个动点，∴设P（cosα，sinα），α∈[0，π]，∴=（1，1），=（cosα，sinα+1），=cosα+sinα+1=，∴•的取值范围是[0，1+]．故答案为：[0，1+]．22．【分析】利用已知条件，通过数量积判断两个向量垂直，然后列出方程求解即可．【解答】解：|+|2=||2+||2，可得•=0．向量=（m，1），=（1，2），可得m+2=0，解得m=﹣2．故答案为：﹣2．23．【分析】根据向量的坐标运算和向量的数量积计算即可．【解答】解：∵向量=（1，﹣1），=（6，﹣4），∴t+=（t+6，﹣t﹣4），∵⊥（t+），∴•（t+）=t+6+t+4=0，解得t=﹣5，故答案为：﹣5．24．【分析】根据向量垂直的充要条件便可得出，进行向量数量积的坐标运算即可得出关于x的方程，解方程便可得出x的值．【解答】解：∵；∴；即x+2（x+1）=0；∴．故答案为：．25．【分析】由题意可知，||+||为在上的投影的绝对值与在上投影的绝对值的和，由此可知，当与共线时，||+||取得最大值，即．【解答】解：||+||=，其几何意义为在上的投影的绝对值与在上投影的绝对值的和，当与共线时，取得最大值．∴=．故答案为：．26．【分析】设出=（x，y），得到•=x+，令x=cosθ，根据三角函数的性质得到•=sinθ+cosθ=sin（θ+），从而求出•的范围即可．【解答】解：设=（x，y），则=（x，），由A（1，0），B（0，﹣1），得：=（1，1），∴•=x+，令x=cosθ，θ∈[0，π]，则•=sinθ+cosθ=sin（θ+），θ∈[0，π]，故•的范围是[﹣，1，]，故答案为：[﹣1，]．27．【分析】由已知可得=+，=﹣+，=+3，=﹣+3，=+2，=﹣+2，结合已知求出2=，2=，可得答案．【解答】解：∵D是BC的中点，E，F是AD上的两个三等分点，∴=+，=﹣+，=+3，=﹣+3，∴•=2﹣2=﹣1，•=92﹣2=4，∴2=，2=，又∵=+2，=﹣+2，∴•=42﹣2=，故答案为：28．【分析】根据已知中向量的坐标，代入向量夹角公式，可得答案．【解答】解：∵向量=（1，），=（，1），∴与夹角θ满足：cosθ===，又∵θ∈[0，π]，∴θ=，故答案为：．29．【分析】利用组合数公式求出从正八边形A1A2…A8的八个顶点中任取两个的事件总数，满足++=，且点P落在第一象限，则需向量+的终点落在第三象限，列出事件数，再利用古典概型概率计算公式求得答案．【解答】解：从正八边形A1A2…A8的八个顶点中任取两个，基本事件总数为．满足++=，且点P落在第一象限，对应的A i，A j，为：（A4，A7），（A5，A8），（A5，A6），（A6，A7），（A5，A7）共5种取法．∴点P落在第一象限的概率是，故答案为：．30．【分析】根据向量三角形不等式的关系以及向量数量积的应用进行计算即可得到结论．【解答】解：由绝对值不等式得≥|•|+|•|≥|•+•|=|（+）•|，于是对任意的单位向量，均有|（+）•|≤，∵|（+）|2=||2+||2+2•=5+2•，∴|（+）|=，因此|（+）•|的最大值≤，则•≤，下面证明：•可以取得，（1）若|•|+|•|=|•+•|，则显然满足条件．（2）若|•|+|•|=|•﹣•|，此时|﹣|2=||2+||2﹣2•=5﹣1=4，此时|﹣|=2于是|•|+|•|=|•﹣•|≤2，符合题意，综上•的最大值是，法2：由于任意单位向量，可设=，则|•|+|•|=||+||≥||+|=||=|+|，∵|•|+|•|≤，∴|+|≤，即（+）2≤6，即||2+||2+2•≤6，∵||=1，||=2，∴•≤，即•的最大值是．法三：设=，=，=，则=+，=﹣，|•|+|•|=||+||=||≤||，由题设当且仅当与同向时，等号成立，此时（+）2取得最大值6，第21页（共22页）由于|+|2+|﹣|）2=2（||2+||2）=10，于是（﹣）2取得最小值4，则•=，•的最大值是．故答案为：．三．解答题（共1小题）31．【分析】根据向量的数量积和三角形的面积公式可得tanA=﹣1，求出A和c的值，再根据余弦定理即可求出a．【解答】解：由=﹣6可得bccosA=﹣6，①，由三角形的面积公式可得S△ABC=bcsinA=3，②∴tanA=﹣1，∵0＜A＜180°，∴A=135°，∴c==2，由余弦定理可得a2=b2+c2﹣2bccosA=9+8+12=29∴a=第22页（共22页）。

一、多选题1．在ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，ABC 的面积为S .下列ABC 有关的结论，正确的是（ ） A ．cos cos 0A B +>B ．若a b >，则cos2cos2A B <C ．24sin sin sin S R A B C =，其中R 为ABC 外接圆的半径D ．若ABC 为非直角三角形，则tan tan tan tan tan tan A B C A B C ++=2．已知ABC 的面积为3，在ABC 所在的平面内有两点P ，Q ，满足20PA PC +=，2QA QB =，记APQ 的面积为S ，则下列说法正确的是（ ）A ．//PB CQ B ．2133BP BA BC =+ C ．0PA PC ⋅<D ．2S =3．ABC 是边长为2的等边三角形，已知向量a ，b 满足2AB a =，2AC a b =+，则下列结论正确的是（ ） A ．a 是单位向量 B ．//BC b C ．1a b ⋅=D ．()4BC a b ⊥+4．设a ，b ，c 是任意的非零向量，且它们相互不共线，给出下列选项，其中正确的有（ ）A ．()a cbc a b c ⋅-⋅=-⋅ B ．()()b c a c a b ⋅⋅-⋅⋅与c 不垂直 C ．a b a b -<-D ．()()22323294a b a b a b +⋅-=-5．已知ABC ∆是边长为2的等边三角形，D ，E 分别是AC 、AB 上的两点，且AE EB =，2AD DC =，BD 与CE 交于点O ，则下列说法正确的是（ ）A ．1AB CE ⋅=- B ．0OE OC +=C ．32OA OB OC ++=D ．ED 在BC 方向上的投影为766．在ABC 中，内角,,A B C 所对的边分别为,,a b c .根据下列条件解三角形，其中有两解的是（ ）A ．10,45,70b A C ==︒=︒B ．45,48,60b c B ===︒C ．14,16,45a b A ===︒D ．7,5,80a b A ===︒7．下列各式中，结果为零向量的是（ ）A ．AB MB BO OM +++ B ．AB BC CA ++ C ．OA OC BO CO +++D ．AB AC BD CD -+-8．八卦是中国文化的基本哲学概念，如图1是八卦模型图，其平面图形记为图2中的正八边形ABCDEFGH ，其中1OA =，则下列结论正确的有（ ）A ．2OA OD ⋅=-B ．2OB OH OE +=-C ．AH HO BC BO ⋅=⋅D ．AH 在AB 向量上的投影为2-9．在△ABC 中,若cos cos a A b B =,则△ABC 的形状可能为( ) A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．等边三角形10．设向量a ，b 满足1a b ==，且25b a -=，则以下结论正确的是（ ） A ．a b ⊥B ．2a b +=C ．2a b -=D ．,60a b =︒11．在△ABC 中，AB ＝AC ，BC ＝4，D 为BC 的中点，则以下结论正确的是（ ） A ．BD AD AB -= B ．1()2AD AB AC =+ C ．8BA BC ⋅=D ．AB AC AB AC +=-12．下列命题中，结论正确的有（ ） A ．00a ⨯=B ．若a b ⊥，则||||a b a b +=-C ．若//AB CD ，则A ､B ､C ､D 四点共线；D ．在四边形ABCD 中，若0AB CD +=，0AC BD ⋅=，则四边形ABCD 为菱形. 13．给出下面四个命题，其中是真命题的是（ ） A ．0ABBA B ．AB BC AC C ．AB AC BC += D ．00AB +=14．设,a b 是两个非零向量，则下列描述正确的有（ ） A ．若||||||a b a b +=-，则存在实数λ使得a b λ= B ．若a b ⊥，则||||a b a b +=-C ．若||||||a b a b +=+，则a 在b 方向上的投影为||bD ．若存在实数λ使得a b λ=，则||||||a b a b +=- 15．已知ABC ∆的面积为32,且2,3b c ==,则A =( ) A ．30°B ．60°C ．150°D ．120°二、平面向量及其应用选择题16．如图，四边形ABCD 是平行四边形，E 是BC 的中点，点F 在线段CD 上，且2CF DF =，AE 与BF 交于点P ，若AP AE λ=，则λ=（ ）A ．34B ．58C ．38D ．2317．在ABC ∆中，E ，F 分别为AB ，AC 的中点，P 为EF 上的任一点，实数x ，y 满足0PA xPB yPC ++=，设ABC ∆、PBC ∆、PCA ∆、PAB ∆的面积分别为S 、1S 、2S 、3S ，记ii S Sλ=（1,2,3i =），则23λλ⋅取到最大值时，2x y +的值为（ ） A ．－1B ．1C ．32-D ．3218．已知两不共线的向量()cos ,sin a αα=，()cos ,sin b ββ=，则下列说法一定正确的是（ ）A ．a 与b 的夹角为αβ-B ．a b ⋅的最大值为1C ．2a b +≤D ．()()a b a b +⊥-19．三角形ABC 所在平面内一点P 满足PA PB PB PC PC PA ⋅=⋅=⋅，那么点P 是三角形ABC 的（ ） A ．重心B ．垂心C ．外心D ．内心20．已知,a b 是两个单位向量，则下列等式一定成立的是( ) A ．0a b -=B ．1a b ⋅=C ．a b =D ．0a b ⋅=21．在三角形ABC 中，若三个内角,,A B C 的对边分别是,,a b c ，1a =，42c =45B =︒，则sin C 的值等于（ ）A ．441B ．45C ．425D 44122．在ABC 中，AD 、BE 、CF 分别是BC 、CA 、AB 上的中线，它们交于点G ，则下列各等式中不正确．．．的是（ ）A ．23BG BE =B ．2CG GF =C ．12DG AG =D ．0GA GB GC ++=23．在ABC 中，若()()0CA CB CA CB +⋅-=，则ABC 为（ ） A ．正三角形B ．直角三角形C ．等腰三角形D ．无法确定24．在ABC ∆中，已知2AB =，4AC =，若点G 、W 分别为ABC ∆的重心和外心，则()AG AW BC +⋅=（ ）A ．4B ．6C ．10D ．1425．已知1a =，3b =，且向量a 与b 的夹角为60︒，则2a b -=（ ） A ．7 B ．3C ．11D ．1926．题目文件丢失！27．已知圆C 的方程为22(1)(1)2x y -+-=，点P 在直线3y x上，线段AB 为圆C的直径，则PA PB ⋅的最小值为（） A ．2B ．52C ．3D ．7228．如图，为测得河对岸塔AB 的高，先在河岸上选一点C ，使C 在塔底B 的正东方向上，测得点A 的仰角为60°，再由点C 沿北偏东15°方向走10m 到位置D ，测得45BDC ∠=︒，则塔AB 的高是（单位：m ）（ ）A ．102B ．106C ．103D ．1029．如图所示，矩形ABCD 的对角线相交于点O ，E 为AO 的中点，若(),DE AB AD R λμλμ=+∈，则λμ⋅等于（ ）A ．316- B ．316 C ．12D ．12-30．已知菱形ABCD 边长为2，∠B ＝3π，点P 满足AP ＝λAB ，λ∈R ，若BD ·CP ＝－3，则λ的值为( ) A ．12B ．－12C ．13D ．－1331．已知ABC ∆的内角A 、B 、C 满足()()1sin 2sin sin 2A ABC C A B +-+=--+，面积S 满足12S ≤≤，记a 、b 、c 分别为A 、B 、C 所对的边，则下列不等式一定成立的是（ ） A ．()8bc b c +> B ．()162ab a b +> C ．612abc ≤≤D ．1224abc ≤≤32．如图，在直角梯形ABCD 中，22AB AD DC ==，E 为BC 边上一点，BC 3EC =，F 为AE 的中点，则BF ＝（ ）A ．2133AB AD - B ．1233AB AD - C ．2133AB AD -+ D ．1233AB AD -+ 33．如图所示，在坡度一定的山坡A 处测得山顶上一建筑物CD 的顶端C 对于山坡的斜度为15°，向山顶前进50 m 到达B 处，又测得C 对于山坡的斜度为45°，若CD ＝50 m ，山坡对于地平面的坡度为θ，则cos θ等于（ ）A 3B 2C 31- D 21 34．设ABC ∆中BC 边上的中线为AD ，点O 满足2AO OD =，则OC =（ ）A ．1233AB AC -+ B ．2133AB AC - C ．1233AB AC -D ．2133AB AC -+35．在ABC 中，角A 、B 、C 所对的边分别是a 、b 、c ，若1c =，45B =︒，3cos 5A =，则b 等于（ ）A ．35 B ．107C ．57D【参考答案】***试卷处理标记，请不要删除一、多选题 1．ABD 【分析】对于A ，利用及余弦函数单调性，即可判断；对于B ，由，可得，根据二倍角的余弦公式，即可判断；对于C ，利用和正弦定理化简，即可判断；对于D ，利用两角和的正切公式进行运算，即可判断. 【 解析：ABD 【分析】对于A ，利用A B π+<及余弦函数单调性，即可判断；对于B ，由a b >，可得sin sin A B >，根据二倍角的余弦公式，即可判断；对于C ，利用in 12s S ab C =和正弦定理化简，即可判断；对于D ，利用两角和的正切公式进行运算，即可判断. 【详解】对于A ，∵A B π+<，∴0A B ππ<<-<，根据余弦函数单调性，可得()cos cos cos A B B π>-=-，∴cos cos 0A B +>，故A 正确；对于B ，若sin sin a b A B >⇔>，则22sin sin A B >，则2212sin 12sin A B -<-，即cos2cos2A B <，故B 正确；对于C ，211sin 2sin 2sin sin 2sin sin sin 22S ab C R A R B C R A B C ==⋅⋅⋅=，故C 错误；对于D ，在ABC 为非直角三角形，()tan tan tan tan 1tan tan B CA B C B C+=-+=--⋅，则tan tan tan tan tan tan A B C A B C ++=，故D 正确. 故选：ABD. 【点睛】本题主要考查了正弦定理在解三角形中的应用，三角函数基本性质．考查了推理和归纳的能力．2．BCD 【分析】本题先确定B 是的中点，P 是的一个三等分点，判断选项A 错误，选项C 正确；再通过向量的线性运算判断选项B 正确；最后求出，故选项D 正确. 【详解】 解：因为，，所以B 是的中点，P 是的解析：BCD 【分析】本题先确定B 是AQ 的中点，P 是AC 的一个三等分点，判断选项A 错误，选项C 正确； 再通过向量的线性运算判断选项B 正确；最后求出2APQ S =△，故选项D 正确. 【详解】解：因为20PA PC +=，2QA QB =，所以B 是AQ 的中点，P 是AC 的一个三等分点，如图：故选项A 错误，选项C 正确；因为()121333BP BA AP BA BC BA BA BC =+=+-=+，故选项B 正确； 因为112223132APQ ABCAB hS S AB h ⨯⨯==⋅△△，所以，2APQ S =△，故选项D 正确. 故选：BCD 【点睛】本题考查平面向量的线性运算、向量的数量积、三角形的面积公式，是基础题.3．ABD 【分析】A. 根据是边长为2的等边三角形和判断；B.根据，，利用平面向量的减法运算得到判断；C. 根据，利用数量积运算判断；D. 根据， ，利用数量积运算判断. 【详解】A. 因为是边长解析：ABD 【分析】A. 根据ABC 是边长为2的等边三角形和2AB a =判断；B.根据2AB a =，2AC a b =+，利用平面向量的减法运算得到BC 判断；C. 根据1,2a ABb BC ==，利用数量积运算判断；D. 根据b BC =， 1a b ⋅=-，利用数量积运算判断. 【详解】A. 因为ABC 是边长为2的等边三角形，所以2AB =，又2AB a =，所以 a 是单位向量，故正确；B. 因为2AB a =，2AC a b =+，所以BC AC AB b =-=，所以//BC b ，故正确；C. 因为1,2a AB b BC ==，所以1122cos120122a b BC AB ⋅=⋅=⨯⨯⨯︒=-，故错误； D. 因为b BC =， 1a b ⋅=-，所以()()2444440BC a b b a b a b b ⋅+=⋅+=⋅+=-+=，所以()4BC a b ⊥+，故正确. 故选：ABD 【点睛】本题主要考查平面向量的概念，线性运算以及数量积运算，还考查了运算求解的能力，属于中档题.4．ACD 【分析】A ，由平面向量数量积的运算律可判断；B ，由平面向量垂直的条件、数量积的运算律可判断；C ，由与不共线，可分两类考虑：①若，则显然成立；②若，由、、构成三角形的三边可进行判断；D ，由平解析：ACD 【分析】A ，由平面向量数量积的运算律可判断；B ，由平面向量垂直的条件、数量积的运算律可判断；C ，由a 与b 不共线，可分两类考虑：①若a b ≤，则a b a b -<-显然成立；②若a b >，由a 、b 、a b -构成三角形的三边可进行判断；D ，由平面向量的混合运算将式子进行展开即可得解. 【详解】选项A ，由平面向量数量积的运算律，可知A 正确； 选项B ，()()()()()()()()0b c a c a b c b c a c c a b c b c a c b c c a ⎡⎤⋅⋅-⋅⋅⋅=⋅⋅⋅-⋅⋅⋅=⋅⋅⋅-⋅⋅⋅=⎣⎦，∴()()b c a c a b ⋅⋅-⋅⋅与c 垂直，即B 错误； 选项C ，∵a 与b 不共线，∴若a b ≤，则a b a b -<-显然成立； 若a b >，由平面向量的减法法则可作出如下图形：由三角形两边之差小于第三边，可得a b a b -<-.故C 正确；选项D ，()()22223232966494a b a b a a b a b b a b +⋅-=-⋅+⋅-=-，即D 正确. 故选：ACD 【点睛】本小题主要考查向量运算，属于中档题.5．BCD 【分析】以E 为原点建立平面直角坐标系，写出所有点的坐标求解即可. 【详解】由题E 为AB 中点，则，以E 为原点，EA ，EC 分别为x 轴，y 轴正方向建立平面直角坐标系，如图所示： 所以，，解析：BCD 【分析】以E 为原点建立平面直角坐标系，写出所有点的坐标求解即可. 【详解】由题E 为AB 中点，则CE AB ⊥，以E 为原点，EA ，EC 分别为x 轴，y 轴正方向建立平面直角坐标系，如图所示：所以，123(0,0),(1,0),(1,0),3),()3E A B C D -， 设123(0,),3),(1,),(,33O y y BO y DO y ∈==--，BO ∥DO ， 所以2313y y =-，解得：3y =， 即O 是CE 中点，0OE OC +=，所以选项B 正确；322OA OB OC OE OC OE ++=+==，所以选项C 正确； 因为CE AB ⊥，0AB CE ⋅=，所以选项A 错误；123(3ED =，(1,3)BC =，ED 在BC 方向上的投影为127326BC BCED +⋅==，所以选项D 正确.故选：BCD 【点睛】此题考查平面向量基本运算，可以选取一组基底表示出所求向量的关系，对于特殊图形可以考虑在适当位置建立直角坐标系，利于计算.6．BC 【分析】根据题设条件和三角形解的个数的判定方法，逐项判定，即可求解，得到答案. 【详解】对于选项A 中：由，所以，即三角形的三个角是确定的值，故只有一解； 对于选项B 中：因为，且，所以角有两解析：BC 【分析】根据题设条件和三角形解的个数的判定方法，逐项判定，即可求解，得到答案. 【详解】对于选项A 中：由45,70A C =︒=︒，所以18065B A C =--=︒，即三角形的三个角是确定的值，故只有一解；对于选项B 中：因为csin sin 115B C b ==<，且c b >，所以角C 有两解；对于选项C 中：因为sin sin 17b A B a ==<，且b a >，所以角B 有两解； 对于选项D 中：因为sin sin 1b A B a =<，且b a <，所以角B 仅有一解. 故选：BC .【点睛】本题主要考查了三角形解得个数的判定，其中解答中熟记三角形解得个数的判定方法是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.7．BD【分析】根据向量的加法和减法运算，对四个选项逐一计算，即可得正确答案.【详解】对于选项：，选项不正确；对于选项： ，选项正确；对于选项：，选项不正确；对于选项：选项正确.故选：解析：BD【分析】根据向量的加法和减法运算，对四个选项逐一计算，即可得正确答案.【详解】对于选项A ：AB MB BO OM AB +++=，选项A 不正确；对于选项B ： 0AB BC CA AC CA ++=+=，选项B 正确；对于选项C ：OA OC BO CO BA +++=，选项C 不正确；对于选项D ：()()0AB AC BD CD AB BD AC CD AD AD -+-=+-+=-= 选项D 正确.故选：BD【点睛】本题主要考查了向量的线性运算，属于基础题. 8．AB【分析】直接利用向量的数量积的应用，向量的夹角的应用求出结果．【详解】图2中的正八边形，其中，对于；故正确．对于，故正确．对于，，但对应向量的夹角不相等，所以不成立．故错误．对于解析：AB【分析】直接利用向量的数量积的应用，向量的夹角的应用求出结果．【详解】图2中的正八边形ABCDEFGH ，其中||1OA =，对于3:11cos 42A OA OD π=⨯⨯=；故正确． 对于:22B OB OH OA OE +==-，故正确．对于:||||C AH BC =，||||HO BO =，但对应向量的夹角不相等，所以不成立．故错误． 对于:D AH 在AB 向量上的投影32||cos||42AH AH π=-，||1AH ≠，故错误． 故选：AB ．【点睛】本题考查的知识要点：向量的数量积的应用，向量的夹角的应用，主要考查学生的运算能力和转换能力及思维能力，属于中档题． 9．ABCD【分析】应用正弦定理将边化角，由二倍角公式有即或，进而有△ABC 可能为:直角三角形,等腰三角形,等腰直角三角形,等边三角形【详解】根据正弦定理,即.,或.即或解析：ABCD【分析】应用正弦定理将边化角，由二倍角公式有sin 2sin 2A B =即A B =或2A B π+=，进而有△ABC 可能为:直角三角形,等腰三角形,等腰直角三角形,等边三角形【详解】 根据正弦定理sin sin a b A B= cos cos a A b B =sin cos sin cos A A B B =,即sin 2sin 2A B =.2,2(0,2)A B π∈, 22A B =或22A B π+=.即A B =或2A B π+=,△ABC 可能为:直角三角形,等腰三角形,等腰直角三角形,等边三角形.故选：ABCD【点睛】本题考查了正弦定理的边化角，二倍角公式解三角形判断三角形的形状，注意三角形内角和为180°10．AC【分析】 由已知条件结合向量数量积的性质对各个选项进行检验即可.【详解】，且,平方得，即，可得，故A 正确；，可得，故B 错误；，可得，故C 正确；由可得，故D 错误;故选：AC【点睛】解析：AC 【分析】 由已知条件结合向量数量积的性质对各个选项进行检验即可.【详解】1a b ==，且25b a -=,平方得22445b a a b +-⋅=，即0a b ⋅=，可得a b ⊥，故A 正确；()22222a b a b a b +=++⋅=，可得2a b +=，故B 错误； ()22222a b a b a b -=+-⋅=，可得2a b -=，故C 正确； 由0a b ⋅=可得,90a b =︒，故D 错误;故选：AC【点睛】本题考查向量数量积的性质以及向量的模的求法，属于基础题.11．BC【分析】根据向量的加法和减法运算，以及向量的数量积运算可选项.【详解】对于A 选项：，故A 错；对于 B 选项：因为D 为BC 的中点，，故B 正确；对于C 选项：，故正确；对于D 选项：，而，故解析：BC【分析】根据向量的加法和减法运算，以及向量的数量积运算可选项.【详解】对于A 选项：BD AD BD DA BA -=+=，故A 错；对于 B 选项：因为D 为BC 的中点，()111++++()222AD AB BD AB BC AB BA AC AB AC ====+，故B 正确； 对于C 选项：cos 248BD BA BC BA BC B BA BC BA ⋅=⋅⋅∠=⋅⋅=⨯=，故正确；对于D 选项：2,AB AC AD AB AC CB +=-=，而2AD CB ≠，故D 不正确. 故选：BC.【点睛】本题考查向量的线性运算和向量的数量积运算，属于基础题.12．BD【分析】根据平面向量的数量积及平行向量共线定理判断可得；【详解】解：对于A ，，故A 错误；对于B ，若，则，所以，，故，即B 正确；对于C ，，则或与共线，故C 错误；对于D ，在四边形中，若解析：BD【分析】根据平面向量的数量积及平行向量共线定理判断可得；【详解】解：对于A ，00a ⨯=，故A 错误；对于B ，若a b ⊥，则0a b ⋅=，所以2222||2a b a b a b a b +=++⋅=+，2222||2a b a b a b a b -=+-⋅=+，故||||a b a b +=-，即B 正确；对于C ，//AB CD ，则//AB CD 或AB 与CD 共线，故C 错误；对于D ，在四边形ABCD 中，若0AB CD +=，即AB DC =，所以四边形ABCD 是平行四边形，又0AC BD ⋅=，所以AC BD ⊥，所以四边形ABCD 是菱形，故D 正确； 故选：BD【点睛】本题考查平行向量的数量积及共线定理的应用，属于基础题.13．AB【解析】【分析】 根据向量加法化简即可判断真假.【详解】因为，正确；，由向量加法知正确；，不满足加法运算法则，错误；，所以错误.故选：A B.【点睛】本题主要考查了向量加法的解析：AB【解析】【分析】根据向量加法化简即可判断真假.【详解】因为0AB BA AB AB ，正确；AB BC AC ，由向量加法知正确；AB AC BC +=，不满足加法运算法则，错误；0,AB AB +=，所以00AB +=错误.故选：A B .【点睛】本题主要考查了向量加法的运算，属于容易题.14．AB【分析】若，则反向，从而；若，则，从而可得；若，则同向，在方向上的投影为若存在实数使得，则共线，但是不一定成立.【详解】对于选项A ，若，则反向，由共线定理可得存在实数使得；对于选解析：AB【分析】若||||||a b a b +=-，则,a b 反向，从而a b λ=；若a b ⊥，则0a b ⋅=，从而可得||||a b a b +=-；若||||||a b a b +=+，则,a b 同向，a 在b 方向上的投影为||a若存在实数λ使得a b λ=，则,a b 共线，但是||||||a b a b +=-不一定成立.【详解】对于选项A ，若||||||a b a b +=-，则,a b 反向，由共线定理可得存在实数λ使得a b λ=；对于选项B ，若a b ⊥，则0a b ⋅=，222222||2,||2a b a a b b a b a a b b +=+⋅+-=-⋅+,可得||||a b a b +=-； 对于选项C ，若||||||a b a b +=+，则,a b 同向，a 在b 方向上的投影为||a ; 对于选项D ，若存在实数λ使得a b λ=，则,a b 共线，但是||||||a b a b +=-不一定成立. 故选：AB.【点睛】本题主要考查平面向量的性质及运算，明确向量的性质及运算规则是求解的关键，侧重考查逻辑推理的核心素养.15．BD【分析】由三角形的面积公式求出即得解.【详解】因为,所以,所以,因为,所以或120°.故选：BD【点睛】本题主要考查三角形面积的应用，意在考查学生对这些知识的理解掌握水平. 解析：BD【分析】由三角形的面积公式求出sin A =即得解. 【详解】 因为13sin 22S bc A ==,所以13222A ⨯=,所以sin A =,因为0180A ︒︒<<, 所以60A =或120°.故选：BD【点睛】本题主要考查三角形面积的应用，意在考查学生对这些知识的理解掌握水平.二、平面向量及其应用选择题16．A【分析】设出()()()11AP mAB m AF mAB m AD DF =+-=+-+，求得()2113m AP AB m AD +=+-，再利用向量相等求解即可. 【详解】 连接AF ，因为B ，P ，F 三点共线，所以()()()11AP mAB m AF mAB m AD DF =+-=+-+，因为2CF DF =，所以1133DF DC AB ==， 所以()2113m AP AB m AD +=+-. 因为E 是BC 的中点， 所以1122AE AB BC AB AD =+=+. 因为AP AE λ=， 所以()211132m AB m AD AB AD λ+⎛⎫+-=+ ⎪⎝⎭，则2131 12 mmλλ+⎧=⎪⎪⎨⎪-=⎪⎩，解得34λ=.故选：A【点睛】本题主要考查平面向量的线性运算，考查了平面向量基本定理的应用，属于基础题. 17．D【分析】根据三角形中位线的性质，可得P到BC的距离等于△ABC的BC边上高的一半，从而得到12312S S S S==+，由此结合基本不等式求最值，得到当23λλ⋅取到最大值时，P为EF的中点，再由平行四边形法则得出1122PA PB PC++=，根据平面向量基本定理可求得12x y==，从而可求得结果.【详解】如图所示：因为EF是△ABC的中位线，所以P到BC的距离等于△ABC的BC边上高的一半，所以12312S S S S==+，由此可得22232322322()1216S SS S SSS S S Sλλ+=⨯=≤=，当且仅当23S S=时，即P为EF的中点时，等号成立，所以0PE PF+=，由平行四边形法则可得2PA PB PE+=，2PA PC PF+=，将以上两式相加可得22()0PA PB PC PE PF++=+=，所以1122PA PB PC++=，又已知0PA xPB yPC ++=， 根据平面向量基本定理可得12x y ==， 从而132122x y +=+=. 故选：D【点睛】本题考查了向量加法的平行四边形法则，考查了平面向量基本定理的应用，考查了基本不等式求最值，属于中档题.18．D【分析】由向量夹角的范围可判断A 选项的正误；计算出a b ⋅，利用余弦函数的值域以及已知条件可判断B 选项的正误；利用平面向量模的三角不等式可判断C 选项的正误；计算()()a b a b +⋅-的值可判断D 选项的正误.综合可得出结论.【详解】()cos ,sin a αα=，()cos ,sin b ββ=，则2cos 1a α==，同理可得1b =，a 与b 不共线，则()sin cos cos sin sin 0αβαβαβ-=-≠，则()k k Z αβπ-≠∈. 对于A 选项，由题意知，a 与b 的夹角的范围为()0,π，而()R αβ-∈且()k k Z αβπ-≠∈，A 选项错误；对于B 选项，设向量a 与b 的夹角为θ，则0θπ<<，所以，()cos cos 1,1a b a b θθ⋅=⋅=∈-，B 选项错误；对于C 选项，由于a 与b 不共线，由向量模的三角不等式可得2a b a b +<+=，C 选项错误；对于D 选项，()()22220a b a b a b a b +⋅-=-=-=，所以，()()a b a b +⊥-，D 选项正确.故选：D.【点睛】本题考查平面向量有关命题真假的判断，涉及平面向量的夹角、数量积与模的计算、向量垂直关系的处理，考查运算求解能力与推理能力，属于中等题.19．B【分析】先化简得0,0,0PA CB PB CA PC AB ⋅=⋅=⋅=，即得点P 为三角形ABC 的垂心.【详解】由于三角形ABC 所在平面内一点P 满足PA PB PB PC PC PA ⋅=⋅=⋅，则()()()0,0,0PA PB PC PB PA PC PC PB PA ⋅-=⋅-=⋅-=即有0,0,0PA CB PB CA PC AB ⋅=⋅=⋅=，即有,,PA CB PB CA PC AB ⊥⊥⊥，则点P 为三角形ABC 的垂心.故选：B.【点睛】本题主要考查向量的运算和向量垂直的数量积，意在考查学生对这些知识的理解掌握水平. 20．C【分析】取,a b 夹角为3π，计算排除ABD ，得到答案. 【详解】取,a b 夹角为3π，则0a b -≠，12a b ⋅=，排除ABD ，易知1a b ==. 故选：C .【点睛】本题考查了单位向量，意在考查学生的推断能力.21．B【分析】在三角形ABC 中，根据1a=，c =45B =︒，利用余弦定理求得边b ,再利用正弦定理sin sin b c B C=求解. 【详解】 在三角形ABC 中， 1a=，c =45B =︒，由余弦定理得：2222cos b a c ac B =+-，13221252=+-⨯⨯=， 所以5b =，由正弦定理得：sin sin b c B C=，所以2sin 42sin 55c B C b ===，故选：B【点睛】本题主要考查余弦定理和正弦定理的应用，所以考查了运算求解的能力，属于中档题. 22．C【分析】由三角形的重心定理和平面向量的共线定理可得答案． 【详解】ABC 中，AD 、BE 、CF 分别是BC 、CA 、AB 上的中线，它们交于点G ，可得G为重心，则23BG BE =，2CG GF =，12DG GA =且0GA GB GC ++=故选：C 【点睛】本题考查了三角形的重心定理和向量共线定理，属于中档题． 23．C 【分析】利用平面向量的数量积的运算性质可得(CA CB + 2222)()0CA CB CA CB b a -=-=-=，从而可得答案． 【详解】 解：在ABC 中，(CA CB + 2222)()0CA CB CA CB b a -=-=-=，a b ∴=，ABC ∴为等腰三角形， 故选：C ． 【点睛】本题考查三角形形状的判断，考查向量的数量积的运算性质，属于中档题． 24．C 【解析】 【分析】取BC 的中点D ，因为G 、W 分别为ABC ∆的重心和外心，则0DW BC ⋅=， 再用AB 、AC 表示AW ，AG ，BC 再根据向量的数量积的运算律计算可得. 【详解】解：如图，取BC 的中点D ，因为G 、W 分别为ABC ∆的重心和外心 0DW BC ∴⋅=()()22113323AG AD AB AC AB AC ∴==⨯+=+ ()12AW AD DW AB AC DW =+=++ ()()()115326AW AG AB AC AB AC DW AB AC DW +=++++=++ ()()()5566AB AC DW AB AG AW BC BC B W C BC AC D ⎡⎤∴+⋅=⋅=⋅⋅⎢++++⎥⎣⎦()56AB A BC C =⋅+()()56C AC AB AB A =⋅+- ()()222242105566AC AB =-=-= 故选：C【点睛】本题考查平面向量的数量积的定义和性质，考查三角形的重心和外心的性质及向量中点的向量表示，考查运算能力，属于中档题． 25．A 【分析】根据向量的数量积的运算公式，以及向量的模的计算公式，准确运算，即可求解. 【详解】因为1a =，3b =，a 与b 的夹角为60︒，所以2224424697a a b b a b =-⋅+=-+=-，则27a b -=. 故选：A. 【点睛】本题主要考查了向量的数量积的运算，以及向量的模的求解，其中解答中熟记向量的数量积的运算公式是解答的关键，着重考查推理与运算能力.26．无27．B 【分析】将PA PB ⋅转化为2||2PC -，利用圆心到直线的距离求得||PC 的取值范围求得PA PB ⋅的最小值. 【详解】()()()()PA PB PC CA PC CB PC CA PC CA ⋅=+⋅+=+⋅-2222||||||222PC CA PC =-=-≥-52=.故选B. 【点睛】本小题主要考查向量的线性运算，考查点到直线距离公式，考查化归与转化的数学思想方法，属于中档题. 28．B 【分析】设塔高为x 米，根据题意可知在△ABC 中，∠ABC=90°，∠ACB=60°，AB=x ，从而有x ，在△BCD 中，CD=10，∠BCD=105°，∠BDC=45°，∠CBD=30°，由正弦定理可求 BC ，从而可求x 即塔高． 【详解】设塔高为x 米，根据题意可知在△ABC 中，∠ABC=90°，∠ACB=60°，AB=x ，从而有BC=3x ，AC=3x ， 在△BCD 中，CD=10，∠BCD=60°+30°+15°=105°，∠BDC=45°，∠CBD=30° 由正弦定理可得，sin sin BC CDBDC CBD=可得，BC=10sin 45sin 30x ==.则；所以塔AB 的高是米； 故选B ． 【点睛】本题主要考查了正弦定理在实际问题中的应用，解决本题的关键是要把实际问题转化为数学问题，即正确建立数学模型，结合已知把题目中的数据转化为三角形中的数据，进而选择合适的公式进行求解． 29．A 【分析】利用平面向量的线性运算，将DE 用AB 和AD 表示，可得出λ和μ的值，由此可计算出λμ⋅的值.【详解】E 为AO 的中点，且O 为AC 的中点，所以，()111244AE AO AC AB AD ===+， ()113444DE AE AD AB AD AD AB AD ∴=-=+-=-，14λ∴=，34μ=-.因此，1334416λμ⎛⎫⋅=⨯-=- ⎪⎝⎭，故选：A.【点睛】本题考查利用基底表示向量，要充分利用平面向量的加减法法则，考查运算求解能力，属于中等题.【分析】根据向量的基本定理，结合数量积的运算公式，建立方程即可得到结论． 【详解】法一：由题意可得BA ·BC ＝2×2cos3π＝2， BD ·CP ＝(BA ＋BC )·(BP －BC ) ＝(BA ＋BC )·[(AP －AB )－BC ] ＝(BA ＋BC )·[(λ－1)·AB －BC ] ＝(1－λ) BA 2－BA ·BC ＋(1－λ)·BA ·BC －BC 2 ＝(1－λ)·4－2＋2(1－λ)－4 ＝－6λ＝－3， ∴λ＝12，故选A. 法二：建立如图所示的平面直角坐标系，则B (2,0)，C (1，)，D (－13．令P (x,0)，由BD ·CP ＝(－33)·(x －13＝－3x ＋3－3＝－3x ＝－3得x ＝1. ∵AP ＝λAB ，∴λ＝12.故选A. 【点睛】1.已知向量a ，b 的坐标，利用数量积的坐标形式求解． 设a ＝(a 1，a 2)，b ＝(b 1，b 2)，则a ·b ＝a 1b 1＋a 2b 2. 2.通过建立平面直角坐标系，利用数量积的坐标形式计算. 31．A 【分析】由条件()()1sin 2sin sin 2A A B C C A B +-+=--+化简得出1sin sin sin 8A B C =，设ABC ∆的外接圆半径为R ，根据12S ≤≤求得R 的范围，然后利用不等式的性质判断即【详解】ABC ∆的内角A 、B 、C 满足()()1sin 2sin sin 2A ABC C A B +-+=--+，即()()1sin 2sin sin 2A A B C A B C +-+++-=，即()()1sin 2sin sin 2A ABC A B C +--++-=⎡⎤⎣⎦， 即()12sin cos 2sin cos 2A A ABC +-=，即()()12sin cos 2sin cos 2A B C A B C -++-=，即()()12sin cos cos 4sin sin sin 2A B C B C A B C --+==⎡⎤⎣⎦，1sin sin sin 8A B C ∴=，设ABC ∆的外接圆半径为R ，则2sin sin sin a b cR A B C===， []2111sin 2sin 2sin sin 1,2224S ab C R A R B C R ==⨯⨯⨯=∈，2R ∴≤≤338sin sin sin abc R A B C R ⎡∴=⨯=∈⎣，C 、D 选项不一定正确；对于A 选项，由于b c a +>，()8bc b c abc ∴+>≥，A 选项正确；对于B 选项，()8ab a b abc +>≥，即()8ab a b +>成立，但()ab a b +>成立. 故选：A. 【点睛】本题考查了利用三角恒等变换思想化简、正弦定理、三角形的面积计算公式、不等式的基本性质等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题． 32．C 【分析】根据平面向量的三角形法则和共线定理即可得答案. 【详解】解：111222BF BA AF BA AE AB AD AB CE ⎛⎫=+=+=-+++ ⎪⎝⎭111223AB AD AB CB ⎛⎫=-+++ ⎪⎝⎭111246AB AD AB CB =-+++()111246AB AD AB CD DA AB =-+++++ 11112462AB AD AB AB AD AB ⎛⎫=-+++--+ ⎪⎝⎭111124126AB AD AB AB AD =-+++- 2133AB AD =-+ 故选：C . 【点睛】本题考查用基底表示向量，向量的线性运算，是中档题. 33．C 【分析】易求30ACB ∠=︒，在ABC 中，由正弦定理可求BC ，在BCD 中，由正弦定理可求sin BDC ∠，再由90BDC θ∠=+︒可得答案． 【详解】45CBD ∠=︒，30ACB ∴∠=︒，在ABC 中，由正弦定理，得sin sin BC AB CAB ACB =∠∠，即50sin15sin30BC =︒︒，解得BC =-，在BCD 中，由正弦定理，得sin sin BC CD BDC CBD=∠∠50sin 45=︒，sin BDC ∴∠=sin(90)θ+︒=cos θ∴=故选：C ． 【点睛】该题考查正弦定理在实际问题中的应用，由实际问题恰当构建数学模型是解题关键． 34．A 【分析】作出图形，利用AB 、AC 表示AO ，然后利用平面向量减法的三角形法则可得出OC AC AO =-可得出结果.【详解】 如下图所示：D 为BC 的中点，则()1122AD AB BD AB BC AB AC AB =+=+=+-1122AB AC =+，2AO OD =，211333AO AD AB AC ∴==+， 11123333OC AC AO AC AB AC AB AC ⎛⎫∴=-=-+=-+ ⎪⎝⎭，故选：A. 【点睛】本题考查利用基底表示向量，考查了平面向量减法和加法三角形法则的应用，考查计算能力，属于中等题. 35．C 【分析】利用同角三角函数基本关系式可得sin A ，进而可得cos (cos cos sin sin )C A B A B =--，再利用正弦定理即可得出． 【详解】 解：3cos 5A =，(0,180)A ∈︒︒．∴24sin 15A cos A =-，32422cos cos()(cos cos sin sin )(55C A B A B A B =-+=--=--=． 272sin 110C cos C ∴=-=． 由正弦定理可得：sin sin b cB C=， ∴21sin 52sin 772c B b C ===． 故选：C ． 【点睛】本题考查了同角三角函数基本关系式、正弦定理、两角和差的余弦公式，考查了推理能力与计算能力，属于中档题．。

高考数学（理）真题专题汇编：平面向量一、选择题1.【来源】2019年高考真题——理科数学（北京卷）设点A ，B ，C 不共线，则“AB 与AC 的夹角为锐角”是“||||AB AC BC +>”的 A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件D. 既不充分也不必要条件2.【来源】2019年高考真题——理科数学（全国卷Ⅱ） 已知AB =(2,3)，AC =(3，t )，BC =1，则AB BC ⋅= A ．－3 B ．－2C ．2D ．33.【来源】2019年高考真题——理科数学（全国卷Ⅰ） 已知非零向量a ，b 满足||2||=a b ，且()-a b ⊥b ，则a 与b 的夹角为A ．π6B ．π3C ．2π3D ．5π64.【来源】2018年高考真题——理科数学（天津卷）如图，在平面四边形ABCD 中，AB BC ⊥，AD CD ⊥，120BAD ∠=︒，1AB AD ==. 若点E 为边CD 上的动点，则⋅AE BE 的最小值为(A) 2116(B) 32(C) 2516(D) 35.【来源】2018年高考真题——理科数学（全国卷II ） 已知向量a ，b 满足|a |=1，a ·b =－1，则a ·(2a －b )= A ．4B ．3C ．2D ．06.【来源】2018年高考真题——理科数学（全国卷Ⅰ） 在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则=A.43AB －41ACB. 41AB －43AC C. 43AB ＋41AC D. 41AB ＋43AC7.【来源】2016年高考真题——理科数学（天津卷）已知△ABC 是边长为1的等边三角形，点E D ,分别是边BC AB ,的中点，连接DE 并延长到点F ，使得EF DE 2=，则BC AF ⋅的值为（ ）（A ）85-（B ）81（C ）41（D ）8118.【来源】2017年高考真题——数学（浙江卷）如图，已知平面四边形ABCD ，AB ⊥BC ，AB ＝BC ＝AD ＝2，CD ＝3，AC 与BD 交于点O ，记I 1=OB OA ⋅，I 2=OC OB ⋅，I 3=OD OC ⋅，则A ．I 1＜I 2＜I 3B ．I 1＜I 3 ＜I 2C ．I 3＜I 1＜I 2D ． I 2＜I 1＜I 39.【来源】2017年高考真题——理科数学（全国Ⅲ卷）在矩形ABCD 中，AB =1，AD =2，动点P 在以点C 为圆心且与BD 相切的圆上．若AP AB AD λμ=+，则λμ+的最大值为（）A ．3B ．22C 5D ．210.【来源】2017年高考真题——理科数学（全国Ⅱ卷）已知△ABC 是边长为2的等边三角形，P 为平面ABC 内一点，则)(PC PB PA +⋅的最小值是（ ）A.-2B.23-C. 43-D.-111.【来源】2016年高考真题——理科数学（新课标Ⅱ卷）12.【来源】2014高考真题理科数学（福建卷）在下列向量组中，可以把向量()2,3=a 表示出来的是（ ） A.)2,1(),0,0(21==e e B .)2,5(),2,1(21-=-=e e C.)10,6(),5,3(21==e e D.)3,2(),3,2(21-=-=e e二、填空题13.【来源】2019年高考真题——数学（浙江卷）已知正方形ABCD 的边长为1，当每个(1,2,3,4,5,6)i i λ=取遍±1时，123456||AB BC CD DA AC BD λλλλλλ+++++的最小值是________；最大值是_______.14.【来源】2019年高考真题——理科数学（天津卷）在四边形ABCD 中，,23,5,30ADBC AB AD A ==∠=︒∥，点E 在线段CB 的延长线上，且AE BE =，则BD AE ⋅= . 15.【来源】2019年高考真题——理科数学（全国卷Ⅲ）已知a ，b 为单位向量，且a ·b =0，若25=-c a b ，则cos ,<>=a c ___________. 16.【来源】2019年高考真题——理科数学（全国卷Ⅰ）已知双曲线C ：22221(0,0)x y a b a b -=>>的左、右焦点分别为F 1，F 2，过F 1的直线与C 的两条渐近线分别交于A ，B 两点．若1F A AB =，120F B F B ⋅=，则C 的离心率为____________．17.【来源】2019年高考真题——数学（江苏卷）如图，在△ABC 中，D 是BC 的中点，E 在边AB 上，BE =2EA ，AD 与CE 交于点O .若6AB AC AO EC ⋅=⋅，则ABAC的值是_____.18.【来源】2018年高考真题——数学理（全国卷Ⅲ）已知向量()=1,2a ，()=2,2-b ，()=1,λc ．若()2∥c a +b ，则λ=________． 19.【来源】2018年高考真题——数学（江苏卷）在平面直角坐标系xOy 中，A 为直线:2l y x =上在第一象限内的点，(5,0)B ，以AB 为直径的圆C 与直线l 交于另一点D ．若0AB CD ⋅=，则点A 的横坐标为 ▲ ． 20.【来源】2017年高考真题——数学（浙江卷）已知向量a ，b 满足|a |=1，|b |=2，则|a +b |+|a －b |的最小值是________，最大值是_______．21.【来源】2017年高考真题——数学（江苏卷）在平面直角坐标系xOy 中，A （－12，0），B （0，6），点P 在圆O ：x 2+y 2=50上，若20≤⋅PB PA ，则点P 的横坐标的取值范围是 .22.【来源】2017年高考真题——数学（江苏卷）如图，在同一个平面内，向量OA ，OB ，OC 的模分别为1，1，2，OA 与OC 的夹角为α，且tan α=7，OB 与OC 的夹角为45°。

【高考真题与模拟题汇编】一、选择题（共28题）1＠（安徽卷）如果111A B C ∆的三个内角的余弦值分别等于222A B C ∆的三个内角的正弦值，则A ＠111A B C ∆和222A B C ∆都是锐角三角形B ＠111A B C ∆和222A B C ∆都是钝角三角形C ＠111A B C ∆是钝角三角形，222A B C ∆是锐角三角形D ＠111A B C ∆是锐角三角形，222A B C ∆是钝角三角形2＠（北京卷）若a 与b c - 都是非零向量，则“a b a c ⋅=⋅ ”是“()a b c ⊥-”的（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件3＠（福建卷）已知︱︱=1，︱︱=3,∙=0,点C 在∠AOB 内，且∠AOC =30°，设OC =m OA +n OB (m 、n ∈R)，则nm等于 A ＠31 B ＠3 C ＠33 D ＠34＠（福建卷）已知向量a 与b 的夹角为120o，3,a a b =+= 则b 等于（A ）5 （B ）4 （C ）3 （D ）1 解析：向量a 与b的夹角为120o，3,a a b =+=3||||cos120||2a b a b b ⋅=⋅⋅︒=-，222||||2||a b a a b b +=+⋅+ ，∴ 21393||||b b =-+ ，则b =－1(舍去)或b=4，选B ＠5＠（广东卷）如图1所示，D 是ABC ∆的边AB 上的中点，则向量CD =A ＠12BC BA -+ B ＠12BC BA -- C ＠12BC BA - D ＠12BC BA +解析：BA BC BD CB CD 21+-=+=，故选A ＠6＠（湖北卷）已知向量a =，b 是不平行于x 轴的单位向量，且a b = 则b =A ＠12） B ＠（12 C ＠（14） D ＠（1,0）7＠（湖北卷）已知非零向量a 、b ，若a ＋2b 与a －2b 互相垂直，则=baA＠41 B ＠4 C ＠21 D ＠2 解：由a ＋2b 与a －2b 互相垂直⇒（a ＋2b ）∙（a －2b ）＝0⇒a 2－4b 2＝0 即|a |2＝4|b |2⇒|a |＝2|b |，故选D8＠（湖南卷）已知||2||0a b =≠ ,且关于x 的方程2||0x a x a b ++⋅= 有实根,则a 与b 的夹角的取值范围是( )ACB图A ＠[0,6π] B ＠[,]3ππ C ＠2[,]33ππ D ＠[,]6ππ9＠（湖南卷）已知向量),2,1(),,2(==b t a若1t t =时，a ∥b ；2t t =时，b a ⊥，则A ＠1,421-=-=t t B ＠1,421=-=t t C ＠1,421-==t t D ＠1,421==t t10＠（湖南卷）如图1：OM ∥AB ，点P 由射线OM 、线段OB 及AB 的延长线围成的阴影区域内（不含边界）＠且OB y OA x OP +=，则实数对（x ,y ）可以是A ＠)43,41( B ＠)32,32(-C ＠)43,41(- D ＠)57,51(-解析：如图，OM ∥AB ，点P 由射线OM 、线段OB 及AB 的延长线围成的阴影区域内（不含边界）＠且y x +=，由图知，x<0，当x=－41时，即OC =－41OA，P 点在线段DE 上，CD =41OB ，CE =45OB ，而41<43<45，∴ 选C ＠11＠（辽宁卷）ABC 的三内角,,A B C 所对边的长分别为,,a b c 设向量(,)p a c b =+ ,(,)q b a c a =-- ,若//p q,则角C 的大小为(A)6π (B)3π (C) 2π (D) 23πA12＠（辽宁卷）设(0,0)O ,(1,0)A ,(0,1)B ,点P 是线段AB 上的一个动点,AP AB λ=,若OP AB PA PB ⋅≥⋅,则实数λ的取值范围是(A)112λ≤≤(B) 11λ-≤≤(C) 112λ≤≤+(D) 11λ≤≤+【点评】本题考查向量的表示方法,向量的基本运算,定比分点中定比的范围等等＠13＠（辽宁卷）已知等腰ABC △的腰为底的2倍，则顶角A 的正切值是（ ）Ａ＠2Ｂ＠Ｃ＠8Ｄ＠7解：依题意，结合图形可得tan 215A =，故222tan2tan 1tan 2AA A ===- D 14＠（全国卷I ）ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ，若a 、b 、c 成等比数列，且2c a =，则cos B =A ＠14 B ＠34 C ＠4 D ＠315＠（全国卷I ）设平面向量1a 、2a 、3a 的和1230a a a ++=。

亲爱的同学：经过一番刻苦学习，大家一定跃跃欲试地展示了一下自己的身手吧！那今天就来小试牛刀吧! 注意哦：在答卷的过程中一要认真仔细哦！不交头接耳，不东张西望！不紧张！养成良好的答题习惯也要取得好成绩的关键！祝取得好成绩！一次比一次有进步!UMrl 7. = = y =-Z,即I和牡皿®B-2.[2012高考真题浙江理5】设a, b是两个非零向量。

A.若 | a+b | = | a | -1 b |,则a丄b的中点,则刊2+岡2A. 2B. 4C. 5D. 10B.若 a 丄b,则 I a+b | = | a | -1 b |C ・若|a+b| = |a|-|b|,则存在实数入,使得b=X a D.若存在实数入，使得b= Xa,贝ij | a+b = | a | -1 b |imc[解折】柯期觀河IK 却EcCJElAtt.・・T 卄,|=|・|一|测■■ 昨＞ 叭相9k 儿！«»尸丄从ttjfflUi I 卄■ 河九耶1AB 共駅佝■＞觀蚯 若・丄Jb 由正方J 明»|卄创=阍一|刑不换 J &E D ：若存在3爱人 师尸小•呵为 冃向的期fii], IU 嘶I 卄时=治_国不虑立.-- b3. [2012高考真题四川理7】设d 、b 都是非零向量，下列四个条件屮，使＜- = ＜-成立的⑷\b\充分条件是()A ＞ a = -bB 、cillbC 、a = 2b D^ allb 且|Q |=|引【答案】Cf f ii 【解析】A.可以推得纟为既不充分也不必要条件；B.可以推得上-=2Rz| \b\⑷ \b\或上=-2 为必要不充分条件；C.为充分不必要条件；D 同B.⑷ \b\4. [2012高考真题辽宁理3】己知两个非零向量臼，方满足|丹方|二|臼一力|,则下面结论正确的是(A) a//b (B)乳L 方 (C) {0, 1,3}(D)时戻日一力【答案】£【解析】根据向量加法、减法的几何意义可知|M 衬与冷-创分别为以向量爲&为邻辺的平 行四边形的两条对角线的长，因为所以该平行四辺形为矩形，所以 心 故选B5. [2012高考真题江西理7】在直角三角形ABC^，点D 是斜边AB 的屮点，点P 为线段CD（解析】将亶用三角樁敢入・角坐标系中.U9心0艸期心5 ■咱4 眄环喷以似才=（歹十（爭备煌网二®+（卜吩P务-两疇询和》、鲁唸网加、旁警導十討唸寻ilM加气詳必皿6.[2012 高考真题湖南理7】在Z\ABC 屮，AB二2, AC=3, ABLBC= 1 则BC =—A. V3B. y/lC. 2A/2D. >/23【答案】A【解析】由下图知丑五=|78||5C|cos(^-5) = 2x|Jc|x(-cos5) = 1.r r r二cos B = —^—•又由余弦定理知cos B =,解得BC仝.-2BC2[2012高考真题广东理3】若向量瓯二ABBC(2,3), CA= (4,7),则就二A. (-2,-4)B. (3,4)C. (6, 10)D. (-6, -10)【答案】八【解析】BC = BA-CA = (2,3) - (4,7) = (-2,-4).8. 【2012高考真题广东理8】对任意两个非零的平面向量a 和B,定义二字纟.若平面向量a, b 满足|a|^|b|>0,a 与b 的夹角(0上)，且“b 和b 。

装--------------------订--------------------线-------------------------------------------------------------试题共页第页试题共页第页试题共页第页试题共页第页式作差整理后得到(1＋λ)c＝(1＋μ)a，∵向量a，c不共线，∴1＋λ＝0,1＋μ＝0，即λ＝－1，μ＝－1，∴a＋b＝－c，即a＋b＋c＝0.故选D.10．解析：由题意，不妨设a＝(1,0)，b＝⎝⎛⎭⎪⎫－12，32，p＝(x，y)，∵p·a＝p·b＝12，∴⎩⎪⎨⎪⎧x＝12，－12x＋32y＝12，解得⎩⎪⎨⎪⎧x＝12，y＝32，∴|p|＝x2＋y2＝1，故选B. 11．解析：由|AB→＋AC→|＝|AB→－AC→|，化简得AB→·AC→＝0，又因为AB和AC为三角形的两条边，它们的长不可能为0，所以AB→与AC→垂直，所以△ABC为直角三角形．以AC所在直线为x轴，以AB所在直线为y轴建立平面直角坐标系，如图所示，则A(0,0)，B(0,2)，C(1,0)．不妨令E为BC的靠近C的三等分点，则E⎝⎛⎭⎪⎫23，23，F⎝⎛⎭⎪⎫13，43，所以AE→＝⎝⎛⎭⎪⎫23，23，AF→＝⎝⎛⎭⎪⎫13，43，所以AE→·AF→＝23×13＋23×43＝109.答案：B12．解析：由⎩⎨⎧a⊥c，b∥c⇒⎩⎨⎧2x－4＝0，2y＋4＝0⇒⎩⎨⎧x＝2，y＝－2，∴a＝(2，1)，b＝(1，－2)，a＋b＝(3，－1)，∴|a＋b|＝10，故选B.二、填空题13．解析：∵λa＋b＝0，即λa＝－b，∴|λ||a|＝|b|.∵|a|＝1，|b|＝5，∴|λ|＝ 5.---------------------------------------------------------------装--------------------订--------------------线------------------------------------------------------------- 答案： 514．解析：∵OA→⊥AB→，∴OA→·AB→＝0，即OA→·(OB→－OA→)＝0，∴OA→·OB→＝OA2→＝9.答案：915．解析：∵a⊥b，∴a·b＝2m－6＝0，m＝3，∴a－b＝(1,7)，∴|a－b|＝1＋49＝5 2.答案：5 216．解析：如图所示，BD→·AE→＝(AD→－AB→)·(AB→＋BE→)＝⎝⎛⎭⎪⎫12AC→－AB→·⎝⎛⎭⎪⎫AB→＋13AC→－13AB→＝⎝⎛⎭⎪⎫12AC→－AB→·⎝⎛⎭⎪⎫13AC→＋23AB→＝16AC2→－23AB2→＝16×4－23×4＝－2. 答案：－2试题共页第页B卷答案解析一、选择题1．解析：∵A(1,3)，B(4，－1)，∴AB→＝(3，－4)，又∵|AB→|＝5，∴与AB→同向的单位向量为AB→|AB→|＝⎝⎛⎭⎪⎫35，－45.故选A.答案：A2．解析：由|a＋b|＝|a－b|可知a⊥b，设AB→＝b，AD→＝a，作矩形ABCD，可知AC→＝a＋b，BD→＝a－b，设AC与BD的交点为O，结合题意可知OA＝OD＝AD，∴∠AOD＝π3，∴∠DOC＝2π3，又向量a＋b与a－b的夹角为AC→与BD→的夹角，故所求夹角为2π3，选D.答案：D3．解析：由题意可得OD→＝kOC→＝kλOA→＋kμOB→(0＜k＜1)，又A，D，B三点共线，所以kλ＋kμ＝1，则λ＋μ＝1k＞1，即λ＋μ的取值范围是(1，＋∞)，选项B 正确．答案：B4．解析：∵a＝(1，3)，b＝(3，m)，∴|a|＝2，|b|＝9＋m2，a·b＝3＋3m，又a，b的夹角为π6，试题共页第页可化为x2＋y2－2x≤0，即(x－1)2＋y2≤1，故选C.答案：C10．解析：由题知AD→＝12(AB→＋AC→)，∵AB→·AC→＝－16，∴|AB→|·|AC→|cos∠BAC＝－16.在△ABC中，|BC→|2＝|AB→|2＋|AC→|2－2|AB→||AC→|·cos∠BAC，∴102＝|A B→|2＋|AC→|2＋32，|AB→|2＋|AC→|2＝68，∴|AD→|2＝14(AB→2＋AC→2＋2AB→·AC→)＝14(68－32)＝9，∴|AD→|＝3.答案：D11．解析：如图，设A(m,0)，B(0，n)，∴mn＝2，则a＝(1,0)，b＝(0,1)，OP→＝a＋2b＝(1,2)，P A→＝(m－1，－2)，PB→＝(－1，n－2)，P A→·PB→＝5－(m＋2n)≤5－22nm＝1，当且仅当m＝2n，即m＝2，n＝1时，等号成立．答案：A12．解析：由a，b为单位向量且a·b＝0，可设a＝(1,0)，b＝(0,1)，又设c＝(x，y)，代入|c－a－b|＝1得(x－1)2＋(y－1)2＝1，又|c|＝x2＋y2，故由几何性质得12＋12－1≤|c|≤12＋12＋1，即2－1≤|c|≤2＋1.答案：A二、填空题13．解析：AB→＝OB→－OA→＝(3,2－t)，由题意知OB→·AB→＝0，所以2×3＋2(2－t)＝0，解得t＝5.答案：514．解析：由|2a－b|≤3可知，4a2＋b2－4a·b≤9，所以4a2＋b2≤9＋4a·b，而---------------------------------------------------------------装--------------------订--------------------线------------------------------------------------------------- 4a2＋b2＝|2a|2＋|b|2≥2|2a|·|b|≥－4a·b，所以a·b≥－98，当且仅当2a＝－b时取等号．答案：－9815．解析：作CO⊥AB于O，建立如图所示的平面直角坐标系，则A⎝⎛⎭⎪⎫－32，0，B⎝⎛⎭⎪⎫12，0，C⎝⎛⎭⎪⎫0，32，D⎝⎛⎭⎪⎫－1，32，所以E⎝⎛⎭⎪⎫16，33，F⎝⎛⎭⎪⎫－56，32，所以AE→·AF→＝⎝⎛⎭⎪⎫53，33·⎝⎛⎭⎪⎫23，32＝109＋12＝2918.答案：291816．解析：如图，AE→＝AB→＋BE→＝AB→＋13BC→，AF→＝AD→＋DF→＝AD→＋1λDC→＝BC→＋1λAB→，所以AE→·AF→＝⎝⎛⎭⎪⎫AB→＋13BC→·⎝⎛⎭⎪⎫BC→＋1λAB→＝⎝⎛⎭⎪⎫1＋13λAB→·BC→＋1λAB→2＋13BC→2＝⎝⎛⎭⎪⎫1＋13λ×2×2×cos 120°＋4λ＋43＝1，解得λ＝2.答案：2。

一、多选题1．已知ABC 的三个角A ，B ，C 的对边分别为a ，b ，c ，若cos cos A bB a=，则该三角形的形状是（ ） A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰或直角三角形2．给出下列结论，其中真命题为（ ） A ．若0a ≠，0a b ⋅=，则0b =B ．向量a 、b 为不共线的非零向量，则22()a b a b ⋅=⋅ C ．若非零向量a 、b 满足222a ba b +=+，则a 与b 垂直D ．若向量a 、b 是两个互相垂直的单位向量，则向量a b +与a b -的夹角是2π 3．已知在平面直角坐标系中，点()10,1P ，()24,4P .当P 是线段12PP 的一个三等分点时，点P 的坐标为（ ） A ．4,23⎛⎫⎪⎝⎭B ．4,33⎛⎫⎪⎝⎭C ．()2,3D ．8,33⎛⎫ ⎪⎝⎭4．在ABC ∆中,内角,,A B C 的对边分别为,,,a b c 若,2,6A a c π===则角C 的大小是( ) A ．6π B ．3π C ．56π D ．23π 5．在△ABC 中，点E ，F 分别是边BC 和AC 上的中点，P 是AE 与BF 的交点，则有（ ）A ．1122AE AB AC →→→=+B ．2AB EF →→=C ．1133CP CA CB →→→=+D ．2233CP CA CB →→→=+6．下列结论正确的是（ ）A ．在ABC 中，若AB >，则sin sin A B >B ．在锐角三角形ABC 中，不等式2220b c a +->恒成立 C ．若sin 2sin 2A B =，则ABC 为等腰三角形D ．在ABC 中，若3b =，60A =︒，三角形面积S = 7．设P 是ABC 所在平面内的一点，3AB AC AP +=则（ ） A ．0PA PB += B ．0PB PC += C ．PA AB PB +=D ．0PA PB PC ++=8．在ABC 中，若30B =︒，AB =2AC =，则C 的值可以是（ ）A ．30°B ．60°C ．120°D ．150°9．已知M 为ABC 的重心，D 为BC 的中点，则下列等式成立的是（ ） A ．1122AD AB AC =+ B ．0MA MB MC ++= C ．2133BM BA BD =+ D ．1233CM CA CD =+10．在△ABC 中，AB ＝AC ，BC ＝4，D 为BC 的中点，则以下结论正确的是（ ） A ．BD AD AB -= B ．1()2AD AB AC =+ C ．8BA BC ⋅=D ．AB AC AB AC +=-11．在ABC 中，15a =，20b =，30A =，则cos B =（ ）A ．B ．23C ．23-D 12．有下列说法，其中错误的说法为（ ）． A ．若a ∥b ，b ∥c ，则a ∥cB ．若PA PB PB PC PC PA ⋅=⋅=⋅，则P 是三角形ABC 的垂心 C ．两个非零向量a ，b ，若a b a b -=+，则a 与b 共线且反向D ．若a ∥b ，则存在唯一实数λ使得a b λ= 13．给出下面四个命题，其中是真命题的是（ ） A ．0ABBA B ．AB BC AC C ．AB AC BC += D ．00AB +=14．对于ABC ∆，有如下判断，其中正确的判断是（ ） A ．若sin 2sin 2A B =，则ABC ∆为等腰三角形 B ．若A B >，则sin sin A B >C ．若8a =，10c =，60B ︒=，则符合条件的ABC ∆有两个D ．若222sin sin sin A B C +<，则ABC ∆是钝角三角形15．点P 是ABC ∆所在平面内一点,满足20PB PC PB PC PA --+-=,则ABC ∆的形状不可能是( ) A ．钝角三角形B ．直角三角形C ．等腰三角形D ．等边三角形二、平面向量及其应用选择题16．设(),1A a ，()2,1B -，()4,5C 为坐标平面上三点，O 为坐标原点，若OA 与OB 在OC 方向上的投影相同，则a =（ ）A ．12-B ．12C ．-2D ．217．在ABC ∆中，角A ，B ，C 所对的边分别是a ，b ，c ，设S 为ABC ∆的面积，满足cos cos b A a B =，且角B 是角A 和角C 的等差中项，则ABC ∆的形状为（ ）A ．不确定B ．直角三角形C ．钝角三角形D ．等边三角形18．若△ABC 中，2sin()sin()sin A B A B C +-=，则此三角形的形状是（ ） A ．直角三角形B ．等腰三角形C ．等边三角形D ．等腰直角三角形19．设θ为两个非零向量,a b →→的夹角，已知对任意实数t ，||b t a →→-的最小值为1，则（ ）A ．若θ确定，则||a →唯一确定 B ．若θ确定，则||b →唯一确定 C ．若||a →确定，则θ唯一确定D ．若||b →确定，则θ唯一确定20．如图，在ABC 中，60,23,3C BC AC ︒===，点D 在边BC 上，且27sin 7BAD ∠=，则CD 等于（ ）A 23B 3C 33D 4321．在ABC 中，若()()0CA CB CA CB +⋅-=，则ABC 为（ ） A ．正三角形B ．直角三角形C ．等腰三角形D ．无法确定22．著名数学家欧拉提出了如下定理：三角形的外心、重心、垂心依次位于同一直线上，且重心到外心的距离是重心到垂心距离的一半．此直线被称为三角形的欧拉线，该定理则被称为欧拉线定理．设点O ，H 分别是△ABC 的外心、垂心，且M 为BC 中点，则 （ ）A ．33AB AC HM MO +=+ B ．33AB AC HM MO +=- C ．24AB AC HM MO +=+D ．24AB AC HM MO +=-23．已知20a b =≠，且关于x 的方程20x a x a b ++⋅=有实根，则a 与b 的夹角的取值范围是( ) A ．06,π⎡⎤⎢⎥⎣⎦B ．,3ππ⎡⎤⎢⎥⎣⎦C ．2,33ππ⎡⎤⎢⎥⎣⎦D ．,6ππ⎡⎤⎢⎥⎣⎦24．O 为ABC ∆内一点内角A 、B 、C 所对的边分别为a 、b 、c ，已知0a OA b OB c OC ⋅+⋅+⋅=，且tan tan tan 0A OA B OB C OC ⋅+⋅+⋅=，若3a =边BC 所对的ABC ∆外接圆的劣弧长为（ ）A ．23π B ．43π C ．6π D ．3π 25．在ABC 中，三内角A ，B ，C 的对边分别为a ，b ，c ，面积为S ，若()22S a b c +=+，则cos A 等于（ ）A ．45B ．45-C ．1517D ．1517-26．如图所示，在坡度一定的山坡A 处测得山顶上一建筑物CD 的顶端C 对于山坡的斜度为15°，向山顶前进50 m 到达B 处，又测得C 对于山坡的斜度为45°，若CD ＝50 m ，山坡对于地平面的坡度为θ，则cos θ等于（ ）A ．32B ．22C ．312- D ．212- 27．如图所示，在正方形ABCD 中，E 为BC 的中点，F 为AE 的中点，则DF =（ ）A ．1324AB AD -+ B ．1223AB AD + C ．1132AB AD - D ．1324AB AD - 28．如图所示，在ABC 中，点D 是边BC 上任意一点，M 是线段AD 的中点，若存在实数λ和μ，使得BM AB AC λμ=+，则λμ+=（ ）A ．1-B ．12-C ．2-D ．32-29．在梯形ABCD 中，//AD BC ，90ABC ∠=︒，2AB BC ==，1AD =，则BD AC ⋅=（ ）A ．2-B ．3-C ．2D ．530．在ABC ∆中，下列命题正确的个数是（ ）①AB AC BC -=；②0AB BC CA ++=；③点O 为ABC ∆的内心，且()()20OB OC OB OC OA -⋅+-=，则ABC ∆为等腰三角形；④0AC AB ⋅>，则ABC ∆为锐角三角形．A ．1B ．2C ．3D ．431．在ABC ∆中，8AB =，6AC =，60A ∠=，M 为ABC ∆的外心，若AM AB AC λμ=+，λ、R μ∈，则43λμ+=（ ）A ．34B ．53C ．73D ．8332．如图，在ABC 中，14AD AB →→=，12AE AC →→=，BE 和CD 相交于点F ，则向量AF →等于（ ）A ．1277AB AC →→+B ．1377AB AC →→+C ．121414AB AC →→+ D ．131414AB AC →→+ 33．已知1a b ==，12a b ⋅=，(),1c m m =-，(),1d n n =-(m ，n R ∈).存在a ，b ，对于任意实数m ，n ，不等式a c b d T -+-≥恒成立，则实数T 的取值范围为（ ） A ．(32-∞B ．)32,⎡+∞⎣C ．(32-∞D ．)32,⎡+∞⎣34．已知ABC 中，1,3,30a b A ︒===，则B 等于（ ）A ．60°B ．120°C ．30°或150°D ．60°或120°35．在△ABC 中，M 为BC 上一点，60,2,||4ACB BM MC AM ∠=︒==，则△ABC 的面积的最大值为（ ） A ．123B ．3C ．12D ．183【参考答案】***试卷处理标记，请不要删除1．D 【分析】在中，根据，利用正弦定理得，然后变形为求解. 【详解】 在中，因为， 由正弦定理得， 所以，即， 所以或， 解得或.故是直角三角形或等腰三角形. 故选： D. 【点睛】 本题主要考查 解析：D 【分析】 在ABC 中，根据cos cos A b B a =，利用正弦定理得cos sin cos sin A BB A=，然后变形为sin 2sin 2A B =求解.【详解】在ABC 中，因为cos cos A bB a =， 由正弦定理得cos sin cos sin A BB A=， 所以sin cos sin cos A A B B =，即sin 2sin 2A B =， 所以22A B =或22A B π=-，解得A B =或2A B π+=.故ABC 是直角三角形或等腰三角形. 故选： D. 【点睛】本题主要考查利用正弦定理判断三角形的形状，还考查了运算求解的能力，属于基础题.2．CD 【分析】对于A 由条件推出或，判断该命题是假命题；对于B 由条件推出，判断该命题是假命题；对于C 由条件判断与垂直，判断该命题是真命题；对于D 由条件推出向量与的夹角是，所以该命题是真命题. 【详解解析：CD对于A 由条件推出0b =或a b ⊥，判断该命题是假命题；对于B 由条件推出()()()222a b a b ⋅≠⋅，判断该命题是假命题；对于C 由条件判断a 与b 垂直，判断该命题是真命题；对于D 由条件推出向量a b +与a b -的夹角是2π，所以该命题是真命题. 【详解】对于A ，若0a ≠，0a b ⋅=，则0b =或a b ⊥，所以该命题是假命题； 对于B ，()()22222cos cos a ba b a b αα⋅==，而()()2222a ba b ⋅=，由于a 、b 为不共线的非零向量，所以2cos 1α≠，所以()()()222a b a b ⋅≠⋅，所以该命题是假命题；对于C ，若非零向量a 、b 满足222a ba b +=+，22222a b a b a b ++⋅=+，所以0a b ⋅=，则a 与b 垂直，所以该命题是真命题；对于D ，以a 与b 为邻边作平行四边形是正方形，则a b +和a b -所在的对角线互相垂直，所以向量a b +与a b -的夹角是2π，所以该命题是真命题. 故选：CD. 【点睛】本题考查平面向量的线性运算与数量积运算、向量垂直的判断，是基础题.3．AD 【分析】设，则，然后分点P 靠近点，靠近点两种情况，利用平面向量的线性运算求解. 【详解】 设，则，当点P 靠近点时，， 则， 解得， 所以，当点P 靠近点时，， 则， 解得， 所以， 故选：解析：AD设(),P x y ，则()()12,1,4,4=-=--PP x y PP x y ，然后分点P 靠近点1P ，靠近点2P 两种情况，利用平面向量的线性运算求解. 【详解】设(),P x y ，则()()12,1,4,4=-=--PP x y PP x y ， 当点P 靠近点1P 时，1212PPPP =， 则()()1421142x x y y ⎧=-⎪⎪⎨⎪-=-⎪⎩，解得432x y ⎧=⎪⎨⎪=⎩，所以4,23P ⎛⎫ ⎪⎝⎭， 当点P 靠近点2P 时，122PP PP =， 则()()24124x x y y ⎧=-⎪⎨-=-⎪⎩，解得833x y ⎧=⎪⎨⎪=⎩，所以8,33P ⎛⎫ ⎪⎝⎭， 故选：AD 【点睛】本题主要考查平面向量的线性运算，还考查了运算求解的能力，属于基础题.4．BD 【分析】由正弦定理可得,所以,而,可得,即可求得答案. 【详解】 由正弦定理可得, ,而, , , 故或.【点睛】本题考查了根据正弦定理求解三角形内角,解题关键是掌握解析：BD 【分析】由正弦定理可得sin sin a c A C =,所以sin sin c C A a ==,而a c <,可得A C <,即可求得答案. 【详解】 由正弦定理可得sin sin a cA C=,∴ sin sin 2c C A a ==,而a c <,∴ A C <, ∴566C ππ<<, 故3C π=或23π. 故选:BD. 【点睛】本题考查了根据正弦定理求解三角形内角,解题关键是掌握正弦定理和使用正弦定理多解的判断,考查了分析能力和计算能力,属于中等题.5．AC 【分析】由已知结合平面知识及向量共线定理分别检验各选项即可. 【详解】 如图：根据三角形中线性质和平行四边形法则知， , A 是正确的；因为EF 是中位线，所以B 是正确的； 根据三角形重心解析：AC 【分析】由已知结合平面知识及向量共线定理分别检验各选项即可. 【详解】 如图：根据三角形中线性质和平行四边形法则知，111()()222AE AB BE AB BC AB AC AB AC AB →→→→→→→→→→=+=+=+-=+, A 是正确的；因为EF 是中位线，所以B 是正确的；根据三角形重心性质知，CP =2PG ，所以22113323CP CG CA CB CA CB →→→→→→⎛⎫⎛⎫==⨯+=+ ⎪ ⎪⎝⎭⎝⎭，所以C 是正确的，D 错误. 故选：AC 【点睛】本题主要考查了平面向量基本定理的简单应用，熟记一些基本结论是求解问题的关键，属于中档题.6．AB 【分析】由正弦定理及三角形性质判断A ，由余弦定理判断B ，由正弦函数性质判断C ，由三角形面积公式，余弦定理及正弦定理判断D ． 【详解】中，，由得，A 正确； 锐角三角形中，，∴，B 正确； 中，解析：AB 【分析】由正弦定理及三角形性质判断A ，由余弦定理判断B ，由正弦函数性质判断C ，由三角形面积公式，余弦定理及正弦定理判断D ． 【详解】ABC 中，A B a b >⇔>，由sin sin a b A B=得sin sin A B >，A 正确； 锐角三角形ABC 中，222cos 02b c a A bc+-=>，∴2220b c a +->，B 正确；ABC 中，若sin 2sin 2A B =，则22A B =或22180A B +=︒，即A B =或90A B +=︒，ABC 为等腰三角形或直角三角形，C 错； ABC 中，若3b =，60A =︒，三角形面积33S =11sin 3sin 6022S bc A c ==⨯︒=4c =，∴2222cos 13a b c bc A =+-=，a =，∴2sin a R A ===，R =D 错． 故选：AB ． 【点睛】本题考查正弦定理，余弦定理，正弦函数的性质，三角形面积公式等，考查学生的逻辑推理能力，分析问题解决问题的能力．7．CD 【分析】转化为，移项运算即得解 【详解】 由题意： 故 即 , 故选：CD 【点睛】本题考查了向量的线性运算，考查了学生概念理解，转化划归，数学运算能力，属于基础题.解析：CD 【分析】转化3AB AC AP +=为())(AB AP AC AP AP +=--，移项运算即得解 【详解】由题意：3AB AC AP += 故())(AB AP AC AP AP +=-- 即PB PC AP +=0C PA PB P ++=∴,PA AB PB +=故选：CD 【点睛】本题考查了向量的线性运算，考查了学生概念理解，转化划归，数学运算能力，属于基础题.8．BC 【分析】由题意结合正弦定理可得，再由即可得解.【详解】由正弦定理可得，所以， 又，所以， 所以或. 故选：BC. 【点睛】本题考查了正弦定理的应用，考查了运算求解能力，属于基础题.解析：BC 【分析】由题意结合正弦定理可得sin 2C =，再由()0,150C ∈︒︒即可得解. 【详解】由正弦定理可得sin sin AB AC C B =，所以1sin 2sin 2AB B C AC ⋅===， 又30B =︒，所以()0,150C ∈︒︒， 所以60C =︒或120C =︒. 故选：BC. 【点睛】本题考查了正弦定理的应用，考查了运算求解能力，属于基础题.9．ABD 【分析】根据向量的加减法运算法则依次讨论即可的答案. 【详解】解：如图，根据题意得为三等分点靠近点的点.对于A 选项，根据向量加法的平行四边形法则易得，故A 正确； 对于B 选项，，由于为三解析：ABD 【分析】根据向量的加减法运算法则依次讨论即可的答案. 【详解】解：如图，根据题意得M 为AD 三等分点靠近D 点的点. 对于A 选项，根据向量加法的平行四边形法则易得1122AD AB AC =+，故A 正确； 对于B 选项，2MB MC MD +=，由于M 为AD 三等分点靠近D 点的点，2MA MD =-，所以0MA MB MC ++=，故正确；对于C 选项，()2212=3333BM BA AD BA BD BA BA BD =+=+-+，故C 错误；对于D 选项，()22123333CM CA AD CA CD CA CA CD =+=+-=+，故D 正确. 故选：ABD【点睛】本题考查向量加法与减法的运算法则，是基础题.10．BC 【分析】根据向量的加法和减法运算，以及向量的数量积运算可选项. 【详解】对于A 选项：，故A 错；对于 B 选项：因为D 为BC 的中点，，故B 正确； 对于C 选项：，故正确； 对于D 选项：，而，故解析：BC 【分析】根据向量的加法和减法运算，以及向量的数量积运算可选项. 【详解】对于A 选项：BD AD BD DA BA -=+=，故A 错； 对于 B 选项：因为D 为BC 的中点，()111++++()222AD AB BD AB BC AB BA AC AB AC ====+，故B 正确；对于C 选项：cos 248BD BA BC BA BC B BA BC BA⋅=⋅⋅∠=⋅⋅=⨯=，故正确；对于D 选项：2,AB AC AD AB AC CB +=-=，而2AD CB ≠，故D 不正确. 故选：BC. 【点睛】本题考查向量的线性运算和向量的数量积运算，属于基础题.11．AD 【分析】利用正弦定理可求得的值，再利用同角三角函数的平方关系可求得的值. 【详解】由正弦定理，可得， ，则，所以，为锐角或钝角. 因此，. 故选：AD. 【点睛】本题考查利用正弦定理与同解析：AD 【分析】利用正弦定理可求得sin B 的值，再利用同角三角函数的平方关系可求得cos B 的值. 【详解】由正弦定理sin sin b a B A=，可得120sin 22sin 153b A B a ⨯===， b a >，则30B A >=，所以，B 为锐角或钝角.因此，cos 3B ==±. 故选：AD. 【点睛】本题考查利用正弦定理与同角三角函数的基本关系求值，考查计算能力，属于基础题.12．AD 【分析】分别对所给选项进行逐一判断即可. 【详解】对于选项A ，当时，与不一定共线，故A 错误； 对于选项B ，由，得，所以，，同理，，故是三角形的垂心，所以B 正确； 对于选项C ，两个非零向量解析：AD 【分析】分别对所给选项进行逐一判断即可. 【详解】对于选项A ，当0b =时，a 与c 不一定共线，故A 错误；对于选项B ，由PA PB PB PC ⋅=⋅，得0PB CA ⋅=，所以PB CA ⊥，PB CA ⊥， 同理PA CB ⊥，PC BA ⊥，故P 是三角形ABC 的垂心，所以B 正确；对于选项C ，两个非零向量a ，b ，若a b a b -=+，则a 与b 共线且反向，故C 正确；对于选项D，当0b=，0a≠时，显然有a∥b，但此时λ不存在，故D错误.故选：AD【点睛】本题考查与向量有关的命题的真假的判断，考查学生对基本概念、定理的掌握，是一道容易题.13．AB【解析】【分析】根据向量加法化简即可判断真假.【详解】因为，正确；，由向量加法知正确；，不满足加法运算法则，错误；，所以错误.故选：A B.【点睛】本题主要考查了向量加法的解析：AB【解析】【分析】根据向量加法化简即可判断真假.【详解】因为0AB BA AB AB，正确；AB BC AC，由向量加法知正确；+=，不满足加法运算法则，错误；AB AC BCAB AB+=，所以000,+=错误.AB故选：A B.【点睛】本题主要考查了向量加法的运算，属于容易题.14．BD【分析】对于A，根据三角函数的倍角公式进行判断；对于B，根据正弦定理即可判断证明；对于C，利用余弦定理即可得解；对于D，根据正弦定理去判断即可．【详解】在中，对于A ，若，则或， 当A ＝解析：BD 【分析】对于A ，根据三角函数的倍角公式进行判断；对于B ，根据正弦定理即可判断证明；对于C ，利用余弦定理即可得解；对于D ，根据正弦定理去判断即可． 【详解】 在ABC ∆中，对于A ，若sin 2sin 2A B =，则22A B =或22A B π+=， 当A ＝B 时，△ABC 为等腰三角形； 当2A B π+=时，△ABC 为直角三角形，故A 不正确，对于B ，若A B >，则a b >，由正弦定理得sin sin a b A B=，即sin sin A B >成立．故B 正确；对于C ，由余弦定理可得：b C 错误； 对于D ，若222sin sin sin A B C +<，由正弦定理得222a b c +<，∴222cos 02a b c C ab+-=<，∴C 为钝角，∴ABC ∆是钝角三角形，故D 正确；综上，正确的判断为选项B 和D ． 故选：BD ． 【点睛】本题只有考查了正弦定理，余弦定理，三角函数的二倍角公式在解三角形中的综合应用，考查了转化思想，属于中档题．15．AD 【解析】 【分析】由条件可得，再两边平方即可得答案. 【详解】∵P 是所在平面内一点，且， ∴， 即， ∴，两边平方并化简得， ∴，∴，则一定是直角三角形，也有可能是等腰直角三角形，故解析：AD 【解析】 【分析】由条件可得||||AB AC AC AB -=+，再两边平方即可得答案. 【详解】∵P 是ABC ∆所在平面内一点，且|||2|0PB PC PB PC PA --+-=， ∴|||()()|0CB PB PA PC PA --+-=， 即||||CB AC AB =+， ∴||||AB AC AC AB -=+， 两边平方并化简得0AC AB ⋅=， ∴AC AB ⊥，∴90A ︒∠=，则ABC ∆一定是直角三角形，也有可能是等腰直角三角形， 故不可能是钝角三角形，等边三角形， 故选：AD. 【点睛】本题考查向量在几何中的应用，考查计算能力，是基础题.二、平面向量及其应用选择题16．A 【分析】根据平面向量的投影的概念，结合向量的数量积的运算公式，列出方程，即可求解. 【详解】由题意，点(),1A a ，()2,1B -，()4,5C ， O 为坐标原点， 根据OA 与OB 在OC 方向上的投影相同，则OA OC OB OC OCOC⋅⋅=,即OA OC OB OC ⋅=⋅，可得4152415a +⨯=⨯-⨯，解得12a =-. 故选：A. 【点睛】本题主要考查了平面向量的数量积的坐标运算，以及向量的投影的定义，其中解答中熟记向量投影的定义，以及向量的数量积的运算公式，列出方程是解答的关键，着重考查运算与求解能力. 17．D 【分析】先根据cos cos b A a B =得到,A B 之间的关系，再根据B 是,A C 的等差中项计算出B 的大小，由此再判断ABC 的形状. 【详解】因为cos cos b A a B =，所以sin cos sin cos =B A A B ， 所以()sin 0B A -=，所以A B =， 又因为2B A C B π=+=-，所以3B π=，所以3A B π==，所以ABC 是等边三角形.故选：D. 【点睛】本题考查等差中项以及利用正弦定理判断三角形形状，难度一般.（1）已知b 是,a c 的等差中项，则有2b a c =+；（2）利用正弦定理进行边角互化时，注意对于“齐次”的要求. 18．A 【分析】已知等式左边第一项利用诱导公式化简，根据sin C 不为0得到sin()sin A B C -=，再利用两角和与差的正弦函数公式化简. 【详解】ABC ∆中，sin()sin A B C +=，∴已知等式变形得：2sin sin()sin C A B C -=，即sin()sin sin()A B C A B -==+，整理得：sin cos cos sin sin cos cos sin A B A B A B A B -=+，即2cos sin 0A B =，cos 0A ∴=或sin 0B =（不合题意，舍去），0A π<< 90A ∴=︒，则此三角形形状为直角三角形． 故选：A 【点睛】此题考查了正弦定理，以及三角函数中的恒等变换应用，熟练掌握公式是解本题的关键，属于中档题． 19．B 【分析】2222||2b ta b a bt a t -=-⋅+，令222()2f t b a bt a t =-⋅+，易得2cos b a b t a aθ⋅==时，222min 244()()14a b a b f t a-⋅==，即222||cos 1b b θ-=，结合选项即可得到答案. 【详解】2222||2b ta b a bt a t -=-⋅+，令222()2f t b a bt a t =-⋅+，因为t R ∈，所以当2cos b a b t a aθ⋅==时，222min 244()()4a b a b f t a -⋅=，又||b t a →→-的最小值为1，所以2||b ta -的最小值也为1，即222min244()()14a b a b f t a-⋅==，222||cos 1b b θ-=，所以22||sin 1(0)b b θ=≠，所以1sin b θ=，故若θ确定，则||b →唯一确定. 故选：B 【点睛】本题考查向量的数量积、向量的模的计算，涉及到二次函数的最值，考查学生的数学运算求解能力，是一道容易题. 20．A 【分析】首先根据余弦定理求AB ，再判断ABC 的内角，并在ABD △和ADC 中，分别用正弦定理表示AD ，建立方程求DC 的值. 【详解】AB =3==， 222cos 22AB BC AC B AB BC +-∴===⋅，又因为角B 是三角形的内角，所以6B π=，90BAC ∴∠=，sin 7BAD ∠=，cos 7BAD ∴∠==， sin cos 7DAC BAD ∴∠=∠=， 在ABD △中，由正弦定理可得sin sin BD BAD BAD ⋅=∠，在ADC 中，由正弦定理可得sin sin DCCAD DAC⋅=∠，()1DC DC ⨯=，解得：DC =. 故选：A【点睛】本题考查正余弦定理解三角形，重点考查数形结合，转化与化归，推理能力，属于中档题型.21．C【分析】利用平面向量的数量积的运算性质可得(CA CB+2222-=-=-=，从CA CB CA CB b a)()0而可得答案．【详解】解：在ABC中，(CA CB+2222-=-=-=，)()0CA CB CA CB b a∴=，a b∴为等腰三角形，ABC故选：C．【点睛】本题考查三角形形状的判断，考查向量的数量积的运算性质，属于中档题．22．D【分析】构造符合题意的特殊三角形（例如直角三角形），然后利用平面向量的线性运算法则进行计算即可得解．【详解】∆，其中角B为直角，则垂心H与B重合，解：如图所示的Rt ABC∆的外心，OA OCO为ABC∴=，即O为斜边AC的中点，又M为BC中点，∴2=，AH OMM为BC中点，∴22()2(2)+==+=+．AB AC AM AH HM OM HMOM HM HM MO=+=-4224故选：D．【点睛】本题考查平面向量的线性运算，以及三角形的三心问题，同时考查学生分析问题的能力和推理论证能力．23．B【分析】根据方程有实根得到24cos 0a a b θ∆=-≥，利用向量模长关系可求得1cos 2θ≤，根据向量夹角所处的范围可求得结果. 【详解】关于x 的方程20x a x a b ++⋅=有实根 240a a b ∴∆=-⋅≥设a 与b 的夹角为θ，则24cos 0a a b θ-≥ 又20a b =≠ 24cos 0b b θ∴-≥ 1cos 2θ∴≤又[]0,θπ∈ ,3πθπ⎡⎤∴∈⎢⎥⎣⎦本题正确选项：B 【点睛】本题考查向量夹角的求解问题，关键是能够利用方程有实根得到关于夹角余弦值的取值范围，从而根据向量夹角范围得到结果. 24．A 【分析】 根据题意得出tan tan tan A B Ca b c==，利用正弦定理边化角思想和切化弦思想得出A B C ==，从而可得知ABC ∆为等边三角形，进而可求得BC 所对的ABC ∆外接圆的劣弧长. 【详解】0a OA b OB c OC ⋅+⋅+⋅=，a bOC OA OB c c∴=--，同理可得tan tan tan tan A B OC OA OB C C =--，tan tan tan tan a A c Cb Bc C ⎧-=-⎪⎪∴⎨⎪-=-⎪⎩，tan tan tan A B Ca b c∴==， 由正弦定理得tan tan tan sin sin sin A B C A B C ==，所以，111cos cos cos A B C==， cos cos cos A B C ∴==，由于余弦函数cos y x =在区间()0,π上单调递减，所以，3A B C π===， 设ABC∆的外接圆半径为R ，则22sin aR A===，1R ∴=，所以，边BC 所对的ABC ∆外接圆的劣弧长为222133R A ππ⨯=⨯=. 故选：A. 【点睛】本题考查弧长的计算，涉及正弦定理边角互化思想、切化弦思想以及正弦定理的应用，考查计算能力，属于中等题. 25．D 【分析】由22()S a b c +=+，利用余弦定理、三角形的面积计算公式可得：1sin 2cos 22bc A bc A bc =+，化为sin 4cos 4A A -=，与22sin cos 1A A +=．解出即可． 【详解】解：22()S a b c +=+，2222S b c a bc ∴=+-+， ∴1sin 2cos 22bc A bc A bc =+， 所以sin 4cos 4A A -=， 因为22sin cos 1A A +=． 解得15cos 17A =-或cos 1A =-． 因为1cos 1A -<<，所以cos 1A =-舍去．15cos 17A ∴=-． 故选：D ． 【点睛】本题考查了余弦定理、三角形的面积计算公式、同角三角函数基本关系式，考查了推理能力与计算能力，属于中档题． 26．C 【分析】易求30ACB ∠=︒，在ABC 中，由正弦定理可求BC ，在BCD 中，由正弦定理可求sin BDC ∠，再由90BDC θ∠=+︒可得答案． 【详解】45CBD ∠=︒，30ACB ∴∠=︒，在ABC 中，由正弦定理，得sin sin BC AB CAB ACB =∠∠，即50sin15sin30BC =︒︒，解得BC =-，在BCD 中，由正弦定理，得sin sin BC CD BDC CBD=∠∠50sin 45=︒，sin BDC ∴∠=sin(90)θ+︒=cos θ∴=故选：C ． 【点睛】该题考查正弦定理在实际问题中的应用，由实际问题恰当构建数学模型是解题关键． 27．D 【分析】利用向量的三角形法则和向量共线定理可得：DF AF AD =-，1=2AF AE ，=AE AB BE +，1=2BE BC ，=BC AD ，即可得出答案. 【详解】利用向量的三角形法则，可得DF AF AD =-，=AE AB BE +，E 为BC 的中点，F 为AE 的中点，则1=2AF AE ，1=2BE BC 1111==()=+2224DF AF AD AE AD AB BE AD AB BC AD ∴=--+-- 又=BC AD1324DF AB AD ∴=-. 故选D.【点睛】本题考查了向量三角形法则、向量共线定理，考查了推理能力与计算能力. 向量的运算有两种方法：一是几何运算，往往结合平面几何知识和三角函数知识解答，运算法则是： （１）平行四边形法则（平行四边形的对角线分别是两向量的和与差）； （２）三角形法则（两箭头间向量是差，箭头与箭尾间向量是和）；二是坐标运算，建立坐标系转化为解析几何问题解答（求最值与范围问题，往往利用坐标运算比较简单）． 28．B 【分析】由题意结合中点的性质和平面向量基本定理首先表示出向量BD ，BM ，然后结合平面向量的运算法则即可求得最终结果. 【详解】如图所示，因为点D 在线段BC 上，所以存在t R ∈，使得()BD tBC t AC AB ==-， 因为M 是线段AD 的中点，所以：()()()111112222BM BA BD AB t AC t AB t AB t AC =+=-+-=-++， 又BM AB AC λμ=+，所以()112t λ=-+，12t μ=， 所以12λμ+=-. 故选：B.【点睛】(1)应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算．(2)用向量基本定理解决问题的一般思路是：先选择一组基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决． 29．A 【解析】分析：根据向量加法、减法法则将BD AC ⋅转化为()()AD AB AB BC -+即可求解. 详解：由题可得：BD AC ⋅=()()AD AB AB BC -+=2211()()24222BC AB AB BC BC AB -+=-=-=-,故选A. 点睛：考查向量的线性运算，将问题转化为已知的信息()()AD AB AB BC -+是解题关键. 30．B 【解析】 【分析】利用向量的定义和运算法则逐一考查所给的命题是否正确即可得到正确命题的个数. 【详解】逐一考查所给的命题：①由向量的减法法则可知：AB AC CB -=，题中的说法错误； ②由向量加法的三角形法则可得：0AB BC CA ++=，题中的说法正确； ③因为()(2)0OB OC OB OC OA -⋅+-=，即()0CB AB AC ⋅+=； 又因为AB AC CB -=， 所以()()0AB AC AB AC -⋅+=， 即||||AB AC =，所以△ABC 是等腰三角形.题中的说法正确；④若0AC AB ⋅>，则cos 0AC AB A ⨯⨯>，据此可知A ∠为锐角，无法确定ABC ∆为锐角三角形，题中的说法错误． 综上可得，正确的命题个数为2. 故选：B . 【点睛】本题主要考查平面向量的加法法则、减法法则、平面向量数量积的应用，由平面向量确定三角形形状的方法等知识，意在考查学生的转化能力和计算求解能力. 31．C 【分析】作出图形，先推导出212AM AB AB ⋅=，同理得出212AM AC AC ⋅=，由此得出关于实数λ、μ的方程组，解出这两个未知数的值，即可求出43λμ+的值.【详解】如下图所示，取线段AB 的中点E ，连接ME ，则AM AE EM =+且EM AB ⊥，()212AM AB AE EM AB AE AB EM AB AB ∴⋅=+⋅=⋅+⋅=， 同理可得212AM AC AC ⋅=，86cos6024AB AC ⋅=⨯⨯=，由221212AM AB AB AM AC AC ⎧⋅=⎪⎪⎨⎪⋅=⎪⎩，可得()()3218AB AC AB AB AC AC λμλμ⎧+⋅=⎪⎨+⋅=⎪⎩，即642432243618λμλμ+=⎧⎨+=⎩，解得512λ=，29，因此，52743431293λμ+=⨯+⨯=. 故选：C. 【点睛】本题考查利用三角形外心的向量数量积的性质求参数的值，解题的关键就是利用三角形外心的向量数量积的性质列方程组求解，考查分析问题和解决问题的能力，属于中等题. 32．B 【分析】过点F 分别作//FM AB 交AC 于点M ，作//FN AC 交AB 于点N ，由平行线得出三角形相似，得出线段成比例，结合14AD AB →→=，12AE AC →→=，证出37AM AC →→=和17AN AB →→=，最后由平面向量基本定理和向量的加法法则，即可得AB →和AC →表示AF →.【详解】解：过点F 分别作//FM AB 交AC 于点M ，作//FN AC 交AB 于点N ，已知14AD AB →→=，12AE AC →→=，//FN AC ，则MFE ABE △△和MCF ACD △△， 则：MF ME AB AE =且MF MCAD AC=， 即：2MF ME AB AC=且14MF MC AC AB =，所以124MCMF ME AB AC AC ==，则：8MC ME =，所以37AM AC =，解得：37AM AC →→=，同理//FM AB ，NBF ABE △△和NFD ACD △△，则：NF NB AE AB =且NF NDAC AD =， 即：12NF NB AB AC =且14NF ND AC AB=，所以142NBNF ND AC AB AB ==， 则：8NB ND =，即()8AB AN AD AN -=-， 所以184AB AN AB AN ⎛⎫-=- ⎪⎝⎭，即28AB AN AB AN -=-， 得：17AN AB =，解得：17AN AB →→=，四边形AMFN 是平行四边形，∴由向量加法法则，得AF AN AM →→→=+，所以1377AF AB AC →→→=+.故选：B.【点睛】本题考查平面向量的线性运算、向量的加法法则和平面向量的基本定理，考查运算能力. 33．A 【分析】不等式a c b d T -+-≥恒成立，即求a c b d -+-最小值，利用三角不等式放缩+=+()a c b d a c b d a b c d -+-≥---+，转化即求+()a b c d -+最小值，再转化为等边三角形OAB 的边AB 的中点M 和一条直线上动点N 的距离最小值. 当M N ，运动到MN CD ⊥时且,OM ON 反向时，MN 取得最小值得解. 【详解】1a b ==，12a b ⋅=,易得,3a b π<>= 设,,,OA a OB b OC c OD d ====，AB 中点为M ，CD 中点为N 则,A B 在单位圆上运动，且三角形OAB 是等边三角形,(.1),(,1)1CD C m m D n n k ，CD 所在直线方程为10x y +-=因为a c b d T -+-≥恒成立，+=+()a c b d a c b d a b c d -+-≥---+,(当且仅当a c -与b d -共线同向，即a b +与c d +共线反向时等号成立)即求+()a b c d -+最小值.+()=()()a b c d OA OB OC OD -++-+=22=2OM ON NM -三角形OAB 是等边三角形，,A B 在单位圆上运动，M 是AB 中点，∴ M 的轨迹是以原点为圆心，半径为32的一个圆.又N 在直线方程为10x y +-=上运动，∴ 当M N ，运动到MN CD ⊥时且,OM ON 反向时，MN 取得最小值此时M 到直线10x y +-=的距离322MN232T NM故选：A 【点睛】本题考查平面向量与几何综合问题解决向量三角不等式恒成立.平面向量与几何综合问题的求解坐标法：把问题转化为几何图形的研究，再把几何图形放在适当的坐标系中，则有关点与向量就可以用坐标表示，这样就能进行相应的代数运算和向量运算，从而使问题得到解决． 34．D 【分析】由正弦定理可得，3sin B =，根据b a >，可得B 角的大小. 【详解】由正弦定理可得，sin 3sin 2b A B a ==， 又0,,π<<>∴>B b a B A ，60︒∴=B 或120B =. 故选：D 【点睛】本题考查了正弦定理的应用，考查了运算求解能力和逻辑推理能力，属于基础题目. 35．A 【分析】由已知条件，令||AC a =，||BC b =，则在△ACM 中结合余弦定理可知48ab ≤，根据三角形面积公式即可求最大值。

高考数学《平面向量的线性运算》一轮复习练习题（含答案）一、单选题1．已知向量(2,1),(5,2)a m b ==，若//a b ，则m 的值为（ ）A ．15-B ．15C ．52-D ．542．在平行四边形ABCD 中，,M N 分别是,AD CD 的中点，BM a =，BN b =，则BD =（ ）A ．3243a b +B ．2233ab C ．2334a b +D ．3344a b +3．已知四边形ABCD 的对角线交于点O ，E 为AO 的中点，若AE AB AD λμ=+，则λμ+=（ ） A ．12B ．13C ．14D ．14．如图，在平行四边形ABCD 中，下列结论正确的是（ ）A ．AB CD = B ．AB DA BD +=C ．AB AD DB -=D ．0AD BC +=5．如图，已知ABC 中，D 为边BC 上靠近B 点的三等分点，连接AD ，E 为线段AD 的中点，若CE mAB nAC =+，则2m n +=( )A ．16-B ．12-C ．14-D ．126．如图，ABC 中，AD 为BC 边上的中线，M 为AD 的中点，若BM BA BC λμ=+，则实数对(),λμ=（ ）A ．11,24⎛⎫ ⎪⎝⎭B ．1,12⎛⎫ ⎪⎝⎭C ．11,42⎛⎫ ⎪⎝⎭D ．11,2⎛⎫ ⎪⎝⎭7．在ABC 中，AD 是BC 边上的中线，点M 满足2AM MD =，则CM =（ ）A ．1233AB AC -+B ．2133AB AC -+ C ．1233AB AC -D ．2133AB AC -8．已知a b ，是平面内两个不共线向量，2AB ma b =+，3BC a b =-，A ，B ，C 三点共线，则m ＝（ ） A ．－23B ．23C ．－6D ．69．已知a ，b 是不共线的向量，且2AB a b =+，2AC a b =+，33CD a b =-，则（ ） A ．A ，B ，C 三点共线 B ．A ，C ，D 三点共线 C ．B ，C ，D 三点共线D ．A ，B ，D 三点共线10．在ABC 中，角,,A B C 所对的边分别为,,a b c ，且点D 满足2,2CD DA BD ==，若1cos 4ABC ∠=，则2c a +的最大值为（ ） A 125B 65C 5D ．3511．设D 是ABC 所在平面内一点，3BC CD =，则AD =（ ）A ．4133+AB ACB ．4133AB AC -C ．1433AB AC -D ．1433AB AC -+12．已知△ABC 中，22AB AC ==()min 2AB BC R λλ+=∈，2AM MB =，22sin cos AP AB AC αα=⋅+⋅，,63ππα⎡⎤∈⎢⎥⎣⎦，则MP 的最小值为（ ） A 3B ．23C 5D 6二、填空题13．在△ABC 中，点D 是线段BC 的中点，点E 在线段AD 上，且满足AE ＝2ED ，若CE AB AC λμ=+，则λ＋μ＝_________．14．已知ABC 是腰长为1的等腰直角三角形，其中90A ∠=，点O 是ABC 所在平面上的任意一点，则向量()()OA OC OB OC -+-的模为________15．已知向量AB ，CD 在正方形网格中的位置如图所示.若网格上小正方形的边长为1，则AB CD ⋅=________.16．正ABC 的边长为1，中心为O ，过O 的动直线l 与边AB ，AC 分别相交于点M 、N ，AM AB λ=，AN AC μ=，BD DC =．给出下列四个结论：①1133AO AB AC =+； ②若2AN NC =，则14AD NC ⋅=； ③11λμ+不是定值，与直线l 的位置有关；④AMN 与ABC 的面积之比的最小值为49． 其中所有正确结论的序号是______． 三、解答题17．设a 、b 是不共线的两个非零向量．(1)若2OA a b =-，3OB a b =+，3OC a b =-，求证：A 、B 、C 三点共线； (2)若8a kb +与2ka b +共线，求实数k 的值．18．如图，在ABC 中，AB AC =，M ，N 分别是AB ，AC 的中点.（1）设AB a =，AC b =，试用a ，b 表示BN ，CM ； （2）若BN CM ⊥，求cos BAC ∠.19．如图，在矩形ABCD 中，点E 是BC 边上的中点，点F 在边CD 上.（1）若点F 是CD 上靠近C 的三等分点，设EF AB AD λμ=+，求λμ+的值； （2）若3,2AB BC ==，求AF EF ⋅的取值范围.20．已知13,22a ⎛⎫= ⎪ ⎪⎝⎭，1b =，且a ，b 的夹角为3π. （1）求2a b +；（2）若()()//a kb ka b ++，求实数k 的值.21．如图所示，在ABC 中，点D 是边BC 的中点，点E 是线段AD 的中点.过点E 的直线与边AB ，AC 分别交于点P ，Q .设PB AP λ=，QC AQ μ=，其中0λμ≥，(1)试用AD 与BC 表示AB 、AC ； (2)求证：λμ+为定值，并求此定值；(3)设APQ △的面积为1S ，ABC 的面积为2S ，求12S S 的取值范围.22．如图所示，在ABC 中，1,,3AQ QC AR AB BQ ==与CR 相交于点I .(1)用AB 和AC 分别表示BQ 和CR ； (2)若AI mAB nAC =+，求实数m 和n 的值.23．如图，在ABC 中，设AC a =，AB b =，||2a =，||3b =，已知2DB AD =，2CE EB =，60BAC ∠=︒，CD 与AE 交于点O ．(1)求AE DC ⋅的值； (2)若0OC OD μλ+=，求λμ的值．24．如图所示，ABC 中，AB a =，AC b =，D 为AB 的中点，E 为CD 上的一点，且4DC EC =，AE 的延长线与BC 的交点为F .(1)用向量a ，b 表示AE ；(2)用向量a ，b 表示AF ，并求出:AE EF 和:BF FC 的值。

专题07 平面向量1．【2022年全国乙卷】已知向量a ⃑=(2,1)，b ⃑⃑=(−2,4)，则|a ⃑−b ⃑⃑|（ ） A ．2 B ．3 C ．4 D ．5【答案】D 【解析】 【分析】先求得a ⃑−b ⃑⃑，然后求得|a ⃑−b ⃑⃑|. 【详解】因为a ⃑−b ⃑⃑=(2,1)−(−2,4)=(4,−3)，所以|a ⃑−b ⃑⃑|=√42+(−3)2=5. 故选：D2．【2022年全国乙卷】已知向量a ⃑,b ⃑⃑满足|a ⃑|=1,|b ⃑⃑|=√3,|a ⃑−2b ⃑⃑|=3，则a ⃑⋅b ⃑⃑=（ ） A ．−2 B ．−1 C ．1 D ．2【答案】C 【解析】 【分析】根据给定模长，利用向量的数量积运算求解即可. 【详解】解：∵|a ⃗−2b ⃑⃗|2=|a ⃗|2−4a ⃗⋅b ⃑⃗+4|b ⃑⃗|2， 又∵|a ⃗|=1,|b ⃑⃗|=√3,|a ⃗−2b ⃑⃗|=3, ∴9=1−4a ⃗⋅b ⃑⃗+4×3=13−4a ⃗⋅b ⃑⃗， ∴a ⃗⋅b ⃑⃗=1 故选：C.3．【2022年新高考1卷】在△ABC 中，点D 在边AB 上，BD =2DA ．记CA ⃑⃑⃑⃑⃑⃑=m ⃑⃑⃗，CD ⃑⃑⃑⃑⃑⃑=n ⃑⃗，则CB ⃑⃑⃑⃑⃑⃑=（ ） A ．3m ⃑⃑⃗−2n ⃑⃗ B ．−2m ⃑⃑⃗+3n ⃑⃗C ．3m ⃑⃑⃗+2n ⃑⃗D ．2m ⃑⃑⃗+3n ⃑⃗【答案】B 【解析】【分析】根据几何条件以及平面向量的线性运算即可解出． 【详解】因为点D 在边AB 上，BD =2DA ，所以BD ⃑⃑⃑⃑⃑⃑⃑=2DA ⃑⃑⃑⃑⃑⃑，即CD ⃑⃑⃑⃑⃑⃑−CB ⃑⃑⃑⃑⃑⃑=2(CA ⃑⃑⃑⃑⃑⃑−CD ⃑⃑⃑⃑⃑⃑)， 所以CB ⃑⃑⃑⃑⃑⃑= 3CD ⃑⃑⃑⃑⃑⃑−2CA ⃑⃑⃑⃑⃑⃑=3n ⃑⃑−2m ⃑⃑⃑ =−2m ⃑⃑⃗+3n ⃑⃗． 故选：B ．4．【2022年新高考2卷】已知向量a ⃑=(3,4),b ⃑⃑=(1,0),c ⃑=a ⃑+tb ⃑⃑，若<a ⃑,c ⃑>=<b ⃑⃑,c ⃑>，则t =（ ） A ．−6 B ．−5 C ．5 D ．6【答案】C 【解析】 【分析】利用向量的运算和向量的夹角的余弦公式的坐标形式化简即可求得 【详解】解：c ⃗=(3+t,4),cos 〈a ⃗,c ⃗〉=cos 〈b,c ⃗〉,即9+3t+165|c⃗|=3+t|c ⃗|,解得t =5,故选：C5．【2022年北京】在△ABC 中，AC =3,BC =4,∠C =90°．P 为△ABC 所在平面内的动点，且PC =1，则PA ⃑⃑⃑⃑⃑⃑⋅PB ⃑⃑⃑⃑⃑⃑的取值范围是（ ） A ．[−5,3] B ．[−3,5]C ．[−6,4]D ．[−4,6]【答案】D 【解析】 【分析】依题意建立平面直角坐标系，设P (cosθ,sinθ)，表示出PA ⃑⃑⃑⃑⃑⃑，PB ⃑⃑⃑⃑⃑⃑，根据数量积的坐标表示、辅助角公式及正弦函数的性质计算可得； 【详解】解：依题意如图建立平面直角坐标系，则C (0,0)，A (3,0)，B (0,4)，因为PC =1，所以P 在以C 为圆心，1为半径的圆上运动， 设P (cosθ,sinθ)，θ∈[0,2π]，所以PA⃑⃑⃑⃑⃑⃑=(3−cosθ,−sinθ)，PB ⃑⃑⃑⃑⃑⃑=(−cosθ,4−sinθ)， 所以PA⃑⃑⃑⃑⃑⃑⋅PB ⃑⃑⃑⃑⃑⃑=(−cosθ)×(3−cosθ)+(4−sinθ)×(−sinθ) =cos 2θ−3cosθ−4sinθ+sin 2θ=1−3cosθ−4sinθ=1−5sin (θ+φ)，其中sinφ=35，cosφ=45，因为−1≤sin (θ+φ)≤1，所以−4≤1−5sin (θ+φ)≤6，即PA ⃑⃑⃑⃑⃑⃑⋅PB ⃑⃑⃑⃑⃑⃑∈[−4,6]； 故选：D6．【2022年全国甲卷】已知向量a ⃑=(m,3),b ⃑⃑=(1,m +1)．若a ⃑⊥b ⃑⃑，则m =______________．【答案】−34##−0.75 【解析】 【分析】直接由向量垂直的坐标表示求解即可. 【详解】由题意知：a ⃑⋅b ⃑⃑=m +3(m +1)=0，解得m =−34.故答案为：−34.7．【2022年全国甲卷】设向量a ⃑，b ⃑⃑的夹角的余弦值为13，且|a ⃑|=1，|b ⃑⃑|=3，则(2a ⃑+b ⃑⃑)⋅b ⃑⃑=_________． 【答案】11 【解析】 【分析】设a ⃑与b ⃑⃑的夹角为θ，依题意可得cosθ=13，再根据数量积的定义求出a ⃑⋅b ⃑⃑，最后根据数量积的运算律计算可得． 【详解】解：设a ⃑与b ⃑⃑的夹角为θ，因为a ⃑与b ⃑⃑的夹角的余弦值为13，即cosθ=13， 又|a ⃑|=1，|b ⃑⃑|=3，所以a ⃑⋅b ⃑⃑=|a ⃑|⋅|b ⃑⃑|cosθ=1×3×13=1， 所以(2a ⃑+b ⃑⃑)⋅b ⃑⃑=2a ⃑⋅b ⃑⃑+b ⃑⃑2=2a ⃑⋅b ⃑⃑+|b ⃑⃑|2=2×1+32=11． 故答案为：11．8．【2022年浙江】设点P 在单位圆的内接正八边形A 1A 2⋯A 8的边A 1A 2上，则PA ⃑⃑⃑⃑⃑⃑12+PA 2⃑⃑⃑⃑⃑⃑⃑⃑2+⋯+PA ⃑⃑⃑⃑⃑⃑82的取值范围是_______． 【答案】[12+2√2,16] 【解析】 【分析】根据正八边形的结构特征，分别以圆心为原点，A 7A 3所在直线为x 轴，A 5A 1所在直线为y 轴建立平面直角坐标系，即可求出各顶点的坐标，设P(x,y)，再根据平面向量模的坐标计算公式即可得到PA ⃑⃑⃑⃑⃑⃗12+PA ⃑⃑⃑⃑⃑⃗22+⋯+PA ⃑⃑⃑⃑⃑⃗82=8(x 2+y 2)+8，然后利用cos22.5∘≤|OP|≤1即可解出． 【详解】以圆心为原点，A 7A 3所在直线为x 轴，A 5A 1所在直线为y 轴建立平面直角坐标系，如图所示：则A 1(0,1),A 2(√22,√22),A 3(1,0),A 4(√22,−√22),A 5(0,−1),A 6(−√22,−√22),A 7(−1,0),A 8(−√22,√22)，设P(x,y),于是PA ⃑⃑⃑⃑⃑⃗12+PA ⃑⃑⃑⃑⃑⃗22+⋯+PA ⃑⃑⃑⃑⃑⃗82=8(x 2+y 2)+8，因为cos22.5∘≤|OP|≤1，所以1+cos45∘2≤x 2+y 2≤1，故PA ⃑⃑⃑⃑⃑⃗12+PA ⃑⃑⃑⃑⃑⃗22+⋯+PA ⃑⃑⃑⃑⃑⃗82的取值范围是[12+2√2,16].故答案为：[12+2√2,16]．1．（2022·陕西·西北工业大学附属中学模拟预测（理））在直角坐标系xOy 中的三点(),3M m ，()4,N n ，()2,2E -，若向量OM 与ON 在向量OE 方向上的投影相等，则m 与n 的关系为（ ）A ．7m n +=B ．3m n -=C ．m n =D ．m n =-【答案】A 【解析】 【分析】根据向量在向量上的投影的定义列式可求出结果. 【详解】(),3OM m =,(4,)ON n =,(2,2)OE =-,向量OM 在向量OE 方向上的投影为||OM OE OE ⋅==向量ON 在向量OE 方向上的投影为8||ON OE OE ⋅=，=7m n +=. 故选：A.2．（2022·山东潍坊·三模）已知a ，b 是平面内两个不共线的向量，AB a b λ=+，AC a b μ=+，λ，μ∈R ，则A ，B ，C 三点共线的充要条件是（ ）A ．1λμ-=B ．2λμ+=C ．1λμ=D ．1λμ= 【答案】C 【解析】 【分析】利用向量共线的充要条件有AB mAC =且R m ∈，即可得答案. 【详解】由A ，B ，C 三点共线的充要条件是AB mAC =且R m ∈，所以1m mμλ=⎧⎨=⎩，故1λμ=.故选：C3．（2022·江苏苏州·模拟预测）在ABC 中，π3A =，点D 在线段AB 上，点E 在线段AC 上，且满足22,2AD DB AE EC ====，CD 交BE 于F ，设AB a =，AC b =，则AF BC ⋅=（ ）A ．65B ．175C ．295D ．325【答案】B 【解析】 【分析】根据平面共线向量的性质，结合平面向量数量积的运算性质、平面向量数量积的定义、平面向量的加法的几何意义进行求解即可. 【详解】设DF DC λ=，EF EB μ=，因为11111()(),33333AF AD DF AB DC AB DA AC AB AB AC AB AC λλλλλ-=+=+=++=+-+=+11111()(),22222AF AE EF AC EB AC EA AB AC AC AB AC AB μμμμμ-=+=+=++=+-+=+所以有21531152λλμμμλ-⎧⎧==⎪⎪⎪⎪⇒⎨⎨-⎪⎪==⎪⎪⎩⎩，因此AF BC ⋅=2212121()()55555+-+=-+-⋅AB AC AB AC AB AC AC AB ，因为π3A =，3AB =，4AC =，所以AF BC ⋅=1211179163455525⋅=-⨯+⨯-⨯⨯⨯=AF BC ，故选：B4．（2022·内蒙古·满洲里市教研培训中心三模（文））若(2,3a =-，(2sin ,2cos)66b ππ=，下列正确的是（ ） A ．//()b a b -B ．()b a b ⊥-C ．a 在b 方向上的投影是12-D ．()a b a b +⊥-（）【答案】C 【解析】 【分析】根据向量平行的坐标表示判断A ，根据向量垂直的坐标表示判断BC ，根据向量的投影的定义判断C. 【详解】由已知(2,3a =-，(1,3)b =，所以(((2,3=1,a b -=---，((()2,3=3,0a b+=-+， 因为1(10⨯-≠，所以b ab -，不平行，A 错， 因为(10⨯-≠，所以b a b -，不垂直，B 错，因为a 在b 方向上的投影为2211cos ,=21a b a a b b ⋅⨯-==-+，C 对，因为(13+00⨯-⨯≠，所以a b a b +-，不垂直，D 错， 故选：C.5．（2022·内蒙古赤峰·模拟预测（理））若向量a ，b 满足1a =，2b =，()235a a b ⋅+=，则a 与b 的夹角为（ ）A ．6πB ．3π C ．23π D ．56π 【答案】B 【解析】 【分析】根据数量积的运算律得到a b ⋅，再根据cos a b a bθ⋅=⋅计算可得；【详解】解：因为1a =，2b =，()235a a b ⋅+=，所以2235a a b +⋅=，即2235a a b +⋅=，所以1a b ⋅=，设a 与b 的夹角为θ， 则1cos 2a b a bθ⋅==⋅，因为[]0,θπ∈，所以3πθ=； 故选：B6．（2022·北京·潞河中学三模）已知菱形ABCD 的边长为,60a ABC ∠=，则DB CD ⋅=（ ） A ．232a -B ．234a -C ．234aD ．232a【答案】A 【解析】 【分析】将,DB CD 分别用,BA BC 表示，再根据数量积的运算律即可得出答案. 【详解】解：,DB DA AB BC BA CD BA =+=--=，则()22221322DB CD BC BA BA BC BA BA a a a ⋅=--⋅=-⋅-=--=-.故选：A.7．（2022·湖北·华中师大一附中模拟预测）已知向量(,3)a m =，(1,)b m =，若a 与b 反向共线，则3a b -的值为（ ）A ．0B ．48C ．D ．【答案】C 【解析】 【分析】由向量反向共线求得m =3a b -. 【详解】由题意23m =，得m =又a 与b 反向共线，故m =3(23,6)a b -=-， 故3=43a b -. 故选：C.8．（2022·山东淄博·三模）如图在ABC 中，90ABC ∠=︒，F 为AB 中点，3CE =，8CB =，12AB =，则EA EB ⋅=（ ）A ．15-B ．13-C ．13D ．15【答案】C 【解析】 【分析】建立平面直角坐标系，利用坐标法求出平面向量的数量积； 【详解】解：建立如图所示的平面直角坐标系， 则(12,0)A ，(0,0)B ，(0,8)C ，(6,0)F ， 又3CE =，8CB =，12AB =，则10CF ， 即310CE FC =，即710FE FC =， 则()()9286,67710100,8,55BE BF FC ⎛⎫=+=+-= ⎪⎝⎭， 则,552851EA ⎛⎫=-⎪⎝⎭，928,55EB ⎛⎫=-- ⎪⎝⎭， 则25281355951EA EB ⎛⎫⎛⎫⋅=⨯-+-= ⎪ ⎪⎝⎭⎝⎭；故选：C ．9．（2022·河北·石家庄二中模拟预测）数学家欧拉于1765年在他的著作《三角形的几何学》中首次提出定理：三角形的外心､重心､垂心依次位于同一条直线上，且重心到外心的距离是重心到垂心距离的一半，该直线被称为三角形的欧拉线，设点,,O G H 分别为任意ABC 的外心､重心､垂心，则下列各式一定正确的是（ ）A ．12OG OH =B ．23OH GH =C ．23AO AHAG +=D ．23BO BHBG +=【答案】D 【解析】 【分析】根据三点共线和长度关系可知AB 正误；利用向量的线性运算可表示出,AG BG ，知CD 正误. 【详解】,,O G H 依次位于同一条直线上，且重心到外心的距离是重心到垂心距离的一半，12OG GH ∴=，13OG OH ∴=，32OH GH =，A 错误，B 错误；()112333AO AHAG AO OG AO OH AO AH AO +=+=+=+-=，C 错误； ()112333BO BHBG BO OG BO OH BO BH BO +=+=+=+-=，D 正确. 故选：D.10．（2022·江苏·南京外国语学校模拟预测）已知,,OA OB OC 均为单位向量，且满足102OA OB OC ++=，则AB AC ⋅的值为（ ） A ．38B ．58C ．78D ．198【答案】B 【解析】 【分析】通过向量的线性运算进行化简求值即可. 【详解】()2,32AO OB OC AB OB OC =+=+，同理23AC OB OC =+()()2274(),,32238AO OB OC OB OC AB AC OB OC OB OC =+∴⋅=-⋅=++2291566136688OB OC OB OC =++⋅=+-=． 故选：B.11．（2022·辽宁沈阳·三模）已知椭圆()22:40C x y m m +=>的两个焦点分别为12,F F ，点P是椭圆上一点，若12PF PF ⋅的最小值为1-，则12PF PF ⋅的最大值为（ ） A ．4 B ．2C ．14D ．12【答案】D 【解析】 【分析】设00(,)P x y ，求出焦点坐标，利用向量的坐标运算得出12PF PF ⋅，再根据椭圆的范围利用二次函数求最值即可得解. 【详解】设00(,)P x y ，由()22:40C x y m m +=>可知1(F ，2F ，100(,)PF x y ∴=---，0023(,)2PF x y =--， 22222012000033311(4)44442x m m PF PF x y x m x m ∴⋅=-++=-++-=-，0m x -≤≤00x ∴=时，12PF PF ⋅的最小值为112m -=-，解得2m =.当0x =12PF PF ⋅的最大值为312142⨯-=.故选：D12．（2022·安徽师范大学附属中学模拟预测（理））非零向量,a b 满足2a b a b a +=-=，则a b -与a 的夹角为（ ） A ．6π B ．3π C ．23π D ．56π 【答案】B 【解析】 【分析】根据给定条件，求出a b ⋅，再利用向量夹角公式计算作答. 【详解】由a b a b +=-得：22()()a b a b +=-，即222222a a b b a a b b +⋅+=-⋅+，解得0a b ⋅=，因此，22()1cos ,2||||2||a b a a a b a b a a b a a -⋅-⋅〈-〉===-，而,[0,π]a b a 〈-〉∈，解得π,3a b a 〈-〉=，所以a b -与a 的夹角为3π. 故选：B13．（2022·浙江省江山中学模拟预测）在ABC 中，E ，F 分别为,AC BC 的中点，点D 是线段AF （不含端点）内的任意一点，AD mAB nAE =+，则（ ） A ．(0,1)m ∈ B ．(0,2)n ∈ C ．2n m = D ．1m n +=【答案】C 【解析】 【分析】根据向量的线性运算的定义和平面向量基本定理确定,m n 的关系和范围. 【详解】因为点D 是线段AF （不含端点）内的任意一点， 所以可设(01)AD AF λλ=<<， 因为E ，F 分别为,AC BC 的中点，所以11112222AF AB BF AB BC AB AC AB AE =+=+=+=+，所以2AD AB AE λλ=+，又AD mAB nAE =+，所以10,22m λ⎛⎫=∈ ⎪⎝⎭，()0,1n λ=∈，2n m =，32m n λ+=， 所以A ，B ，D 错误，C 正确， 故选：C.14．（2022·安徽·合肥一中模拟预测（文））已知向量(1,0)a =，(1,1)b =，向量a b 与a 垂直，则实数λ的值为（ ） A ．2- B ．2 C ．1- D ．1【答案】C 【解析】 【分析】由题得()0λ+⋅=a b a 化简即得解. 【详解】 因为ab 与a 垂直，所以()20,0λλ+⋅=∴+⋅=a b a a a b ， 所以1+(10)0,1λλ⨯+=∴=-. 故选：C.15．（2022·海南华侨中学模拟预测）已知不共线的平面向量,,a b c 两两所成的角相等，且1,4,7a b a b c ==++=，则c =（ ）A B ．2 C ．3 D ．2或3【答案】D 【解析】 【分析】 先求出23πθ=，转化2()7a b c a b c ++=++=，列方程即可求出. 【详解】由不共线的平面向量a ，b ，c 两两所成的角相等，可设为θ，则23πθ=.设|c |=m. 因为147a b a b c ==++=，，，所以27a b c ++=， 即2222227a a b b b c a c c +⋅++⋅+⋅+=，所以2222221214cos424cos 21cos 7333m m m πππ+⨯⨯++⨯⨯+⨯⨯+= 即2560m m -+=，解得：2m =或3. 所以|c |=2或3 故选：D16．（2022·贵州贵阳·模拟预测（理））已知()1,2a =，()2,1b =-，()1,c λ=，且()c a b ⊥+，则λ=______． 【答案】3- 【解析】 【分析】由向量垂直的坐标表示计算可得． 【详解】由题意()()3,1a b +=，又()c a b ⊥+，则()()()1,3,130c a b λλ⋅+=⋅=+=，故3λ=-． 故答案为：3-．17．（2022·河北·沧县中学模拟预测）已知向量,a b 的夹角为23π，4a =，3b =，则a b +=___________．【解析】 【分析】根据2222a b a a b b +=+⋅+求解即可. 【详解】 21cos43632a b a b π⎛⎫⋅==⨯⨯-=- ⎪⎝⎭， 则()222222426313a b a a b b +=+⋅+=+⨯-+=， 则13a b +=．18．（2022·安徽·合肥一六八中学模拟预测（文））已知向量||1b =，向量(1,3)a =，且|2|6a b -=，则向量,a b 的夹角为___________.【答案】2π##90 【解析】 【分析】由|2|6a b -=两边平方，结合数量积的定义和性质化简可求向量,a b 的夹角 【详解】因为(1,3)a =，所以(21+a =因为|2|6a b -=，所以2222+26a ab b -=，又||1b =，所以426b -⋅+=，所以0a b ⋅=， 向量,a b 的夹角为θ,则cos 0a b θ⋅= 所以cos 0θ=，则2πθ=.故答案为：2π. 19．（2022·陕西·交大附中模拟预测（理））已知在平行四边形ABCD 中，11,,2,622DE EC BF FC AE AF ====AC DB ⋅值为__________． 【答案】94##2.25【解析】 【分析】由向量加法的几何意义及数量积运算律有22D AC DB C CB ⋅=-，再由1313AE BC DC AF DC BC⎧=+⎪⎪⎨⎪=+⎪⎩结合数量积运算律，即可得结果. 【详解】由题设可得如下图：,AC AD DC DB DC CB =+=+，而AD CB =-，所以22D AC DB C CB ⋅=-， 又11,,2,622DE EC BF FC AE AF ==== 所以1313AE AD DE BC DC AF AB BF DC BC ⎧=+=+⎪⎪⎨⎪=+=+⎪⎩，则22222143921639BC BC DC DC DC BC DC BC ⎧+⋅+=⎪⎪⎨⎪+⋅+=⎪⎩，故228()29DC BC -=，可得2294DC BC -=，即94AC DB =⋅. 故答案为：9420．（2022·浙江·镇海中学模拟预测）设,a b 为不共线的向量，满足,342(,R)c a b λμλμλμ=++=∈，且c a c b c --==，若3a b -=，则()22()⋅⋅-a ba b 的最大值为________． 【答案】324【解析】 【分析】采用建系法，令,,a OA b OB c OC ===，将各个点用坐标表示，然后表达出OAB 面积的最大值，进而求得()22()⋅⋅-a b a b 的最大值；【详解】令,,a OA b OB c OC ===，又因为c a c b c --==， 即==OC CA CB ，则点C 为OAB 的外心，因为3-==a b AB ， 设33,0,,0,(0,)22⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭B AC m ，不妨取0m >则点()00,O x y 在圆2229:()4+-=+C x y m m 上， 由OC OA OB λμ=+，代入坐标，()00000033,,,22λμ⎛⎫⎛⎫---=--+--- ⎪ ⎪⎝⎭⎝⎭x m y x y x y ，解得003(),211-+=⋅-=----mx y m μλμλλμλμ，联立342+=u λ和2229:()4+-=+C x y m m ，解得12λ⎫<⎪⎭m，故0()1μλλμ+=+--m y m622λ=≤-+ ⎪⎝⎭，1λ=-时取“=”. 故01||92=⋅≤OABSAB y ，于是 ()22222max max(||||)()||||1cos a b a b OA OB AOB ⎡⎤⎡⎤⋅-⋅=⋅⋅-∠⎣⎦⎣⎦ ()2222maxmax||||sin 4324OAB OA OB AOB S ⎡⎤=⋅⋅∠==⎣⎦△.故答案为：324 【点睛】求两个向量的数量积有三种方法：利用定义；利用向量的坐标运算；利用数量积的几何意义．具体应用时可根据已知条件的特征来选择，同时要注意数量积运算律的应用．。

新数学《平面向量》高考知识点(1)一、选择题1．已知ABC V 中，2,3,60,2,AB BC ABC BD DC AE EC ==∠=︒==，则AD BE ⋅=u u u r u u u r（ ）A ．1B ．2-C ．12D ．12-【答案】C 【解析】 【分析】以,BA BC u u u r u u u r为基底，将,AD BE u u u r u u u r 用基底表示，根据向量数量积的运算律，即可求解.【详解】222,,33BD DC BD BC AD BD BA BC BA ===-=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r,11,22AE EC BE BC BA =∴=+u u u r u u u r u u u r,211()()322AD BE BC BA BC BA ⋅=-⋅+u u u r u u u r u u ur u u u r u u u r u u u r22111362BC BC BA BA =-⋅-u u ur u u u r u u u r u u u r 111123622=-⨯⨯⨯=.故选:C. 【点睛】本题考查向量的线性运算以及向量的基本定理，考查向量数量积运算，属于中档题.2．在ABC ∆中，0OA OB OC ++=u u u r u u u r u u u r r ，2AE EB =u u u r u u u r，AB AC λ=u u u r u u u r ，若9AB AC AO EC ⋅=⋅u u u r u u u r u u u r u u u r，则实数λ=( )A 3B 3C 6D 6【答案】D 【解析】 【分析】将AO u u u r 、EC uuu r 用AB u u u r 、AC u u ur 表示，再代入9AB AC AO EC ⋅=⋅u u u r u u u r u u u r u u u r 中计算即可.【详解】由0OA OB OC ++=u u u r u u u r u u u r r，知O 为ABC ∆的重心，所以211()323AO AB AC =⨯+=u u u r u u u r u u u r ()AB AC +u u u r u u u r ，又2AE EB =u u u r u u u r ，所以23EC AC AE AC AB =-=-u u u r u u u r u u u r u u u r u u u r ，93()AO EC AB AC ⋅=+⋅u u u r u u u r u u u r u u u r 2()3AC AB -u u ur u u u r2223AB AC AB AC AB AC =⋅-+=⋅u u u r u u u r u u u r u u u r u u u r u u u r ，所以2223AB AC=u u u r u u u r ，||||AB AC λ===u u u ru u u r . 故选：D 【点睛】本题考查平面向量基本定理的应用，涉及到向量的线性运算，是一道中档题.3．已知在平面直角坐标系xOy 中，O 为坐标原点，()0,2A ，2220OB OA +=，若平面内点P 满足3PB PA =u u u r u u u r，则PO 的最大值为（ ）A ．7B ．6C ．5D ．4【答案】C 【解析】 【分析】设(),P x y ，(),B m n ，根据3PB PA =u u u r u u u r可得262m x n y=-⎧⎨=-⎩，再根据2220OB OA +=可得点P 的轨迹，它一个圆，从而可求PO 的最大值. 【详解】设(),P x y ，(),B m n ，故(),PB m x n y =--u u u r ，(),2PA x y =--u u u r. 由3PB PA =u u u r u u u r可得363m x x n y y-=-⎧⎨-=-⎩，故262m x n y=-⎧⎨=-⎩，因为2220OB OA +=，故()22443420x y +-+=，整理得到()2234x y +-=，故点P 的轨迹为圆，其圆心为()0,3，半径为2，故PO 的最大值为325+=， 故选：C. 【点睛】本题考查坐标平面中动点的轨迹以及圆中与距离有关的最值问题，一般地，求轨迹方程，可以动点转移法，也可以用几何法，而圆外定点与圆上动点的连线段长的最值问题，常转化为定点到圆心的距离与半径的和或差，本题属于中档题.4．已知向量a r 与向量b r满足||2a =r ，||b =r ||||a b a b +⋅-=r r r r，则向量a r与向量b r的夹角为( )A ．4π或34π B ．6π或56πC ．3π或23πD ．2π 【答案】A 【解析】 【分析】设向量a r ，b r的夹角为θ，则2||1282cos a b θ+=+r r ，2||1282cos a b θ-=-r r ，即可求出2cos θ，从而得到向量的夹角； 【详解】解：设向量a r ，b r的夹角为θ，222||||||2||||cos 4882cos a b a b a b θθ+=++=++r r r r r r1282cos θ=+，222||||||2||||cos 4882cos 1282cos a b a b a b θθθ-=+-=+-=-r r r r r r，所以2222||||144128cos (45)80a b a b θ+⋅-=-==r r r r ，21cos 2θ∴=，因为[0,)θπ∈，故4πθ=或34π，故选：A. 【点睛】本题考查平面向量的数量积的运算律，及夹角的计算，属于中档题.5．如图，圆O 是等边三角形ABC 的外接圆，点D 为劣弧AC 的中点，则OD =u u u r（ ）A ．2133BA AC +u uu r u u u rB ．2133BA AC -u uu r u u u rC ．1233BA AC +u uu r u u u rD ．4233BA AC +u uu r u u u r【答案】A 【解析】 【分析】连接BO ，易知B ，O ，D 三点共线，设OD 与AC 的交点为E ，列出相应式子得出结论. 【详解】解：连接BO ，易知B ，O ，D 三点共线，设OD 与AC 的交点为E ，则()()221121332333OD BO BE BA BC BA BA AC BA AC ===⨯+=++=+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u uu r u u u r . 故选：A.【点睛】本题考查向量的表示方法，结合几何特点，考查分析能力，属于中档题.6．在ABC V 中，4AC AD =u u u r u u u r，P 为BD 上一点，若14AP AB AC λ=+u u u r u u u r u u u r ，则实数λ的值（ ）A ．34B ．320C ．316D ．38【答案】C 【解析】 【分析】根据题意，可得出144λ=+u u u r u u u r u u u rAP AB AD ，由于B ，P ，D 三点共线，根据向量共线定理，即可求出λ. 【详解】解：由题知：4AC AD =u u u r u u u r ，14AP AB AC λ=+u u ur u u u r u u u r ，所以144λ=+u u u r u u u r u u u r AP AB AD ，由于B ，P ，D 三点共线，所以1414λ+=， ∴316λ=． 故选：C.【点睛】本题考查平面向量的共线定理以及平面向量基本定理的应用.7．已知向量(sin ,cos )a αα=r，(1,2)b =r， 则以下说法不正确的是（ ） A ．若//a b rr，则1tan 2α=B ．若a b ⊥rr，则1tan 2α=C ．若()f a b α=⋅rr 取得最大值，则1tan 2α= D ．||a b -rr 1 【答案】B 【解析】 【分析】根据向量平行、垂直、模以及向量的数量积的坐标运算即可判断. 【详解】A 选项，若//a b r r ，则2sin cos αα=，即1tan 2α=，A 正确.B 选项，若a b ⊥r r，则sin 2cos 0αα+=，则tan 2α=-，B 不正确.C 选项，若()f a b α=⋅r r取得最大值时，则())f ααϕ=+，取得最大值时，()sin 1αϕ+=，2,2k k Z παϕπ+=+∈，又tan 2ϕ=，则1tan 2α=，则C 正确.D 选项，||a b -==r r的最大值为1=，选项D 正确.故选：B . 【点睛】本题主要考查向量的坐标运算，以及模的求法，掌握向量平行、垂直、数量积的坐标运算是解题的关键，是基础题.8．已知点M 在以1(,2)C a a -为圆心，以1为半径的圆上，距离为,P Q 在圆222:8120C x y y +-+=上，则MP MQ ⋅u u u r u u u u r的最小值为（ ）A ．18-B ．19-C ．18+D ．19+【答案】B 【解析】 【分析】设PQ 中点D ，得到,MP MD DP MQ MD DQ =+=+u u u r u u u u r u u u r u u u u r u u u u r u u u r，求得23MP MQ MD ⋅=-u u u r u u u u r u u u u r ，再利用圆与圆的位置关系，即可求解故()223MP MQ ⋅≥-u u u r u u u u r ，得到答案.【详解】依题意，设PQ 中点D ，则,MP MD DP MQ MD DQ =+=+u u u r u u u u r u u u r u u u u r u u u u r u u u r，所以23MP MQ MD ⋅=-u u u r u u u u r u u u u r ，22222()12PQ C D QC =-=Q ，D ∴在以1为半径，以2C 为圆心的圆上， 22221[(2)4]2(3)1832C C a a a =+--=-+≥Q ，1221min min MD C C C D MC ∴=--故()2322319122MP MQ ⋅≥--=-u u u r u u u u r .【点睛】本题主要考查了圆的方程，圆与圆的位置关系的应用，以及平面向量的数量积的应用，着重考查了推理论证能力以及数形结合思想，转化与化归思想.9．已知点1F ，2F 分别是椭圆2222:1(0)x y C a b a b+=>>的左，右焦点，过原点O 且倾斜角为60°的直线l 与椭圆C 的一个交点为M ，且1212||||MF MF MF MF +=-u u u u r u u u u r u u u u r u u u u r，则椭圆C的离心率为（ ） A 31 B ．23C ．12D ．22【答案】A 【解析】 【分析】由1212||||MF MF MF MF +=-u u u u r u u u u r u u u u r u u u u r两边平方，得120MF MF ⋅=u u u u r u u u u r ，在12Rt MF F V 中，求出2MF ，1MF ，,a c 的关系，求出离心率可得选项. 【详解】将1212||||MF MF MF MF +=-u u u u r u u u u r u u u u r u u u u r两边平方，得120MF MF ⋅=u u u u r u u u u r ，即12121||2MF MF OM F F c ⊥==，. 又60MOF ∠=︒，∴2MF c =，13MF c =，∴23a c c =+，∴31ce a==. 故选:A. 【点睛】考查了向量的数量积,椭圆的定义，离心率的求法,关键在于得出关于,a c 的关系，属于中档题.10．已知P 为边长为2的正方形ABCD 所在平面内一点，则PC uuu r ()PB PD +⋅u u ur u u u r 的最小值为（ ） A ．1- B ．3-C ．12-D ．32-【答案】A 【解析】 【分析】建立坐标系，写出各点坐标，表示出对应的向量坐标，代入数量积整理后即可求解． 【详解】建立如图所示坐标系，设(,)P x y ，则(0,0),(2,0),(2,2),(0,2)A B C D ，所以(2,2),(2,)(,2)(22,22)PC x y PB PD x y x y x y =--+=--+--=--u u u r u u u r u u u r，故223131()(2)(22)(2)(22)222222PC PB PD x x y y x y ⎛⎫⎛⎫⋅+=--+--=--+-- ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r223322122x y ⎛⎫⎛⎫=-+-- ⎪ ⎪⎝⎭⎝⎭所以当32x y ==时，PC uuu r ()PB PD +⋅u u u r u u u r 的最小值为1-.故选：A ． 【点睛】本题考查利用坐标法求向量数量积的最值问题，涉及到向量的坐标运算，考查学生的运算求解能力，是一道中档题.11．已知点()2,1A ，O 是坐标原点，点(), P x y 的坐标满足：202300x y x y y -≤⎧⎪-+≥⎨⎪≥⎩，设z OP OA =⋅u u u r u u u r，则z 的最大值是（ ）A ．2B ．3C ．4D ．5【答案】C 【解析】 【分析】画出约束条件的可行域，转化目标函数的解析式，利用目标函数的最大值，判断最优解，代入约束条件求解即可. 【详解】解：由不等式组202300x y x y y -≤⎧⎪-+≥⎨⎪≥⎩可知它的可行域如下图：Q ()2,1A ，(), P x y∴2z OP OA x y =⋅=+u u u r u u u r，可图知当目标函数图象经过点()1,2B 时，z 取最大值，即24z x y =+=.故选：C. 【点睛】本题考查线性规划的应用，考查转化思想以及数形结合思想的应用，属于中档题.12．已知椭圆2222:1(0)x y T a b a b +=>>3F 且斜率为()0k k >的直线与T 相交于A ，B 两点，若3AF FB =uu u r uu r，则k =（ ）A ．2B 3C 2D ．1【答案】C 【解析】 【分析】由3e =3a =，3b =，可设椭圆的方程为222334x y c +=，()()1122,,,A x y B x y ，并不妨设B 在x 轴上方，由3AF FB =uu u r uu r得到12123430x x c y y +=⎧⎨+=⎩，再由22211334x y c +=，22222334x y c +=得到A 、B 两点的坐标，利用两点的斜率公式计算即可. 【详解】因为c e a ===，所以2a b =，所以a =，b =，则椭圆方程22221x y a b+=变为222334x y c +=. 设()()1122,,,A x y B x y ，不妨设B 在x 轴上方，则210,0y y ><， 又3AF FB =uu u r uu r，所以()()1122,3,c x y x c y --=-，所以()121233c x x c y y ⎧-=-⎨-=⎩，12123430x x cy y +=⎧⎨+=⎩因为A ，B 在椭圆上，所以22211334x y c +=，① 22222334x y c +=②. 由①—9×②，得2121212123(3)(3)3(3)(3)84x x x x y y y y c +-++-=-，所以21234(3)84c x x c ⨯-=-，所以12833x x c -=-， 所以123x c =，2109x c =，从而13y =-，29y c =所以2(,)33A c -，10(,)99B c c，故9102393c k c c +==- 故选：C. 【点睛】本题考查直线与椭圆的位置关系，当然本题也可以利用根与系数的关系来解决，考查学生的数学运算求解能力，是一道中档题.13．如图，在ABC V 中，已知D 是BC 边延长线上一点，若2B C C D =u u u v u u u v，点E 为线段AD 的中点，34AE AB AC λ=+u u u v u u u v u u u v，则λ=（ ）A ．14B ．14-C ．13D ．13-【答案】B 【解析】 【分析】由12AE AD =u u u r u u u r ，AD BD BA =-u u u r u u u r u u u r ，AC BC BA =-u u ur u u u r u u u r ，32BD BC =u u u r u u u r ，代入化简即可得出．【详解】 13,,,22AE AD AD BD BA BD BC BC AC AB ==-==-u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v，带人可得()13132244AE AC AB AB AB AC ⎡⎤=-+=-+⎢⎥⎣⎦u u u v u u u v u u u v u u u v u u u v u u u v ，可得14λ=-，故选B. 【点睛】本题考查了向量共线定理、向量的三角形法则，考查了推理能力与计算能力，属于中档题．14．已知椭圆C ：2212x y +=的右焦点为F ，直线l ：2x =，点∈A l ，线段AF 交椭圆C于点B ，若3FA FB =u u u v u u u v，则AF u u u v ＝( )A 2B ．2C 3D ．3【答案】A 【解析】 【分析】设点()2,A n ，()00,B x y ，易知F (1,0)，根据3FA FB =u u u v u u u v，得043x =，013y n =，根据点B 在椭圆上，求得n=1，进而可求得2AF =u u u v【详解】 根据题意作图：设点()2,A n ，()00,B x y ．由椭圆C ：2212x y += ，知22a =，21b =，21c =， 即1c =，所以右焦点F (1,0)．由3FA FB =u u u v u u u v ，得()()001,31,n x y =-．所以()0131x =-，且03n y =. 所以043x =，013y n =. 将x 0，y 0代入2212x y +=， 得221411233n ⎛⎫⎛⎫⨯+= ⎪ ⎪⎝⎭⎝⎭.解得21n =， 所以()2212112AF n u u u v =-+=+=故选A【点睛】本题考查了椭圆的简单性质，考查了向量的模的求法，考查了向量在解析几何中的应用；正确表达出各点的坐标是解答本题的关键. 15．设()1,a m =r ，()2,2b =r ，若()2a mb b +⊥r r r ，则实数m 的值为（ ） A ．12 B ．2 C ．13- D ．-3【答案】C【解析】【分析】 计算()222,4a mb m m +=+r r ，根据向量垂直公式计算得到答案.【详解】 ()222,4a mb m m +=+r r ，∵()2a mb b +⊥r r r ，∴()20a mb b +⋅=r r r ，即()22280m m ⋅++=，解得13m =-.故选：C . 【点睛】本题考查了根据向量垂直求参数，意在考查学生的计算能力.16．如图，AB ，CD 是半径为1的圆O 的两条直径，3AE EO =u u u v u u u v ，则•EC ED u u u v u u u v的值是（ ）A ．45-B ．1516-C ．14-D ．58- 【答案】B【解析】【分析】根据向量表示化简数量积，即得结果.【详解】 ()()()()•••EC ED EO OC EO OD EO OC EO OC =++=+-u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v 2221151416EO OC ⎛⎫=-=-=- ⎪⎝⎭u u u v u u u v ,选B. 【点睛】本题考查向量数量积，考查基本分析求解能力，属基础题.17．已知菱形ABCD 的边长为4，60ABC ∠=︒，E 是BC 的中点2DF AF =-u u u r u u u r，则AE BF ⋅=u u u r u u u r （ ）A ．24B ．7-C ．10-D ．12- 【答案】D【解析】【分析】 根据平面向量的基本定理,将AE BF ⋅u u u r u u u r 用基底,AB AD u u u r u u u r 表达,再根据平面向量的数量积公式求【详解】 由已知得13AF AD =u u u r u u u r ,12BE BC =u u u r u u u r ,AD BC =u u u r u u u r ,所以1122AE AB BC AB AD =+=+u u u r u u u r u u u r u u u r u u u r ,13BF AF AB AD AB =-=-u u u r u u u r u u u r u u u r u u u r . 因为在菱形ABCD 中,60ABC ∠=︒,所以120BAD ∠=︒.又因为菱形ABCD 的边长为4,所以1||||cos1204482AB AD AB AD ⎛⎫⋅=⋅︒=⨯⨯-=- ⎪⎝⎭u u u r u u u r u u u r u u u r ,所以1123AE BF AB AD AB AD ⎛⎫⎛⎫⋅=+⋅-+= ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r u u u r u u u r 221111||||16(8)16126666AB AB AD AD --⋅+=--⨯-+⨯=-u u u r u u u r u u u r u u u r . 故选：D【点睛】本题考查平面向量的线性运算及向量的数量积,考查推理论证能力以及数形结合思想. 18．若O 为ABC ∆所在平面内任一点，且满足()()0OB OC OC OA CA AB -⋅-++=u u u r u u u r u u u r u u u r u u r u u u r ，则ABC ∆的形状为（ ）A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．等边三角形 【答案】A【解析】【分析】利用平面向量加法和减法的三角形法则以及向量数量积的性质即可进行判断.【详解】 由()()0OB OC OC OA CA AB -⋅-++=u u u r u u u r u u u r u u u r u u u r u u u r ，即()0CB AC CB CB AB ⋅+=⋅=u u u r u u u r u u u r u u u r u u u r ， 所以，CB AB ⊥，即2B π∠=，故ABC ∆为直角三角形.故选：A.【点睛】 本题主要考查了平面向量加法和减法的三角形法则以及向量数量积的性质的简单应用，属于基础题.19．向量1,tan 3a α⎛⎫= ⎪⎝⎭r ，()cos ,1b α=r ，且//a b r r ，则cos 2πα⎛⎫+= ⎪⎝⎭（ ） A ．13 B．3- C．3- D ．13- 【答案】D【分析】根据向量平行的坐标运算以及诱导公式，即可得出答案.【详解】//a b ∴r r1cos tan sin 3ααα∴=⋅= 1cos sin 23παα⎛⎫∴+=-=- ⎪⎝⎭故选：D【点睛】本题主要考查了由向量平行求参数以及诱导公式的应用，属于中档题.20．在OAB ∆中，已知OB =u u u v 1AB u u u v =，45AOB ∠=︒，点P 满足(),OP OA OB λμλμ=+∈R u u u v u u u v u u u v ，其中λ，μ满足23λμ+=，则OP u u u v 的最小值为（ ） A．5 BC．3 D．2【答案】A【解析】【分析】根据OB =u u u r ,1AB =uu u r ,45AOB ∠=︒,由正弦定理可得OAB ∆为等腰直角三角形,进而求得点A 坐标.结合平面向量的数乘运算与坐标加法运算,用λ,μ表示出OP u u u r .再由23λμ+=,将OP u u u r 化为关于λ的二次表达式,由二次函数性质即可求得OP u u u r的最小值.【详解】 在OAB ∆中,已知OB =u u u r ,1AB =uu u r ,45AOB ∠=︒ 由正弦定理可得sin sin AB OB AOB OAB=∠∠u u u r u u u rsin OAB =∠,解得sin 1OAB ∠= 即2OAB π∠=所以OAB ∆为等腰直角三角形以O 为原点,OB 所在直线为x 轴,以OB 的垂线为y 轴建立平面直角坐标系如下图所示:则点A 坐标为22,22⎛ ⎝⎭所以2222OA ⎛= ⎝⎭u u u r ,)2,0OB =u u u r 因为(),OP OA OB λμλμ=+∈R u u u r u u u r u u u r 则)222,022OP λμ⎛ =+ ⎝⎭u u u r 222,22λμλ⎛⎫ ⎪ ⎪⎝⎭= 则2222222OP λμλ⎛⎫=++⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭u u u r 2222λλμμ=++因为23λμ+=,则32μλ=-代入上式可得 ()()22322232λλλλ+-+-218518λλ-=+299555λ⎛⎫=-+ ⎪⎝⎭所以当95λ=时, min 9355OP ==u u u r 故选:A【点睛】本题考查了平面向量基本定理的应用,正弦定理判断三角形形状,平面向量的坐标运算,属于中档题.。

2022届全国高考数学真题分类（平面向量）汇编一、选择题 1.（2022∙全国乙（文）T3） 已知向量(2,1)(2,4)a b ==- ，，则a b -r r （ ）A. 2B. 3C. 4D. 52.（2022∙全国乙（理）T3） 已知向量,a b 满足||1,||2|3a b a b ==-= ，则a b ⋅= （ ） A. 2- B. 1- C. 1 D. 2 3.（2022∙新高考Ⅰ卷T3） 在ABC 中，点D 在边AB 上，2BD DA =．记CA m CD n == ，，则CB =（ ）A. 32m n -B. 23m n -+C. 32m n +D. 23m n +4.（2022∙新高考Ⅱ卷T4） 已知(3,4),(1,0),t ===+ a b c a b ，若,,<>=<> a c b c ，则t =（ ）A. 6-B. 5-C. 5D. 6二、填空题 1.（2022∙全国甲（文）T13） 已知向量(,3),(1,1)a m b m ==+ ．若a b ⊥ ，则m =______________．2.（2022∙全国甲（理）T13） 设向量a ，b 的夹角的余弦值为13，且1a = ，3b =r ，则()2a b b +⋅= _________．参考答案一、选择题1.【答案】D【答案解析】【名师分析】先求得a b - ，然后求得a b -r r .【答案详解】因为()()()2,12,44,3a b -=--=- ，所以5-== a b .故选：D2.【答案】C【答案解析】【名师分析】根据给定模长，利用向量的数量积运算求解即可. 【答案详解】解：∵222|2|||44-=-⋅+ a b a a b b ，又∵||1,||2|3,==-= a b a b ∴91443134=-⋅+⨯=-⋅ a b a b ， ∴1a b ⋅= 故选：C.3. 【答案】B【答案解析】【名师分析】根据几何条件以及平面向量的线性运算即可解出．【答案详解】因为点D 在边AB 上，2BD DA =，所以2BD DA = ，即()2CD CB CA CD -=- ， 所以CB =3232CD CA n m -=- 23m n =-+．故选：B ．4.【答案】C【答案解析】【名师分析】利用向量的运算和向量的夹角的余弦公式的坐标形式化简即可求得 【答案详解】解：()3,4c t =+ ,cos ,cos ,a c b c = ,即931635t t c c+++= ,解得5t =, 故选：C二、填空题1. 【答案】34-或0.75- 【答案解析】 【名师分析】直接由向量垂直的坐标表示求解即可.【答案详解】由题意知：3(1)0a b m m ⋅=++= ，解得34m =-. 故答案为：34-. 2. 【答案】11【答案解析】【名师分析】设a 与b 的夹角为θ，依题意可得1cos 3θ=，再根据数量积的定义求出a b ⋅ ，最后根据数量积的运算律计算可得．【答案详解】解：设a 与b 的夹角为θ，因为a 与b 的夹角的余弦值为13，即1cos 3θ=， 又1a = ，3b =r ，所以1cos 1313a b a b θ⋅=⋅=⨯⨯= ， 所以()22222221311a b b a b b a b b +⋅=⋅+=⋅+=⨯+= ． 故答案为：11．。

专题7平面向量1．【2019年全国新课标2理科03】已知（2，3），（3，t），||＝1，则•（）A．﹣3 B．﹣2 C．2 D．3【解答】解：∵（2，3），（3，t），∴（1，t﹣3），∵||＝1，∴t﹣3＝0即（1，0），则• 2故选：C．2．【2019年新课标1理科07】已知非零向量，满足||＝2||，且（）⊥，则与的夹角为（）A．B．C．D．【解答】解：∵（）⊥，∴，∴，∵，∴．故选：B．3．【2019年北京理科07】设点A，B，C不共线，则“与的夹角为锐角”是“||＞||”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：点A，B，C不共线，“与的夹角为锐角”⇒“||＞||”，“||＞||”⇒“与的夹角为锐角”，∴设点A，B，C不共线，则“与的夹角为锐角”是“||＞||”的充分必要条件．故选：C．4．【2018年新课标1理科06】在△ABC中，AD为BC边上的中线，E为AD的中点，则（）A．B．C．D．【解答】解：在△ABC中，AD为BC边上的中线，E为AD的中点，（），故选：A．5．【2018年新课标2理科04】已知向量，满足||＝1，1，则•（2）＝（）A．4 B．3 C．2 D．0【解答】解：向量，满足||＝1，1，则•（2）＝22+1＝3，故选：B．6．【2018年浙江09】已知，，是平面向量，是单位向量．若非零向量与的夹角为，向量满足4•3＝0，则||的最小值是（）A． 1 B． 1 C．2 D．2【解答】解：由4•3＝0，得，∴（）⊥（），如图，不妨设，则的终点在以（2，0）为圆心，以1为半径的圆周上，又非零向量与的夹角为，则的终点在不含端点O的两条射线y（x＞0）上．不妨以y为例，则||的最小值是（2，0）到直线的距离减1．即．故选：A．7．【2018年北京理科06】设，均为单位向量，则“|3|＝|3|”是“⊥”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：∵“|3|＝|3|”∴平方得||2+9||2﹣6•9||2+||2+6•，即1+9﹣6•9+1+6•，即12•0，则•0，即⊥，则“|3|＝|3|”是“⊥”的充要条件，故选：C．8．【2018年天津理科08】如图，在平面四边形ABCD中，AB⊥BC，AD⊥CD，∠BAD＝120°，AB＝AD＝1．若点E为边CD上的动点，则的最小值为（）A．B．C．D．3【解答】解：如图所示，以D为原点，以DA所在的直线为x轴，以DC所在的直线为y轴，过点B做BN⊥x轴，过点B做BM⊥y轴，∵AB⊥BC，AD⊥CD，∠BAD＝120°，AB＝AD＝1，∴AN＝AB cos60°，BN＝AB sin60°，∴DN＝1，∴BM，∴CM＝MB tan30°，∴DC＝DM+MC，∴A（1，0），B（，），C（0，），设E（0，m），∴（﹣1，m），（，m），0≤m，∴m2m＝（m）2（m）2，当m时，取得最小值为．故选：A．9．【2017年新课标2理科12】已知△ABC是边长为2的等边三角形，P为平面ABC内一点，则•（）的最小值是（）A．﹣2 B．C．D．﹣1【解答】解：建立如图所示的坐标系，以BC中点为坐标原点，则A（0，），B（﹣1，0），C（1，0），设P（x，y），则（﹣x，y），（﹣1﹣x，﹣y），（1﹣x，﹣y），则•（）＝2x2﹣2y+2y2＝2[x2+（y）2]∴当x＝0，y时，取得最小值2×（），故选：B．10．【2017年新课标3理科12】在矩形ABCD中，AB＝1，AD＝2，动点P在以点C为圆心且与BD相切的圆上．若λμ，则λ+μ的最大值为（）A．3 B．2C．D．2【解答】解：如图：以A为原点，以AB，AD所在的直线为x，y轴建立如图所示的坐标系，则A（0，0），B（1，0），D（0，2），C（1，2），∵动点P在以点C为圆心且与BD相切的圆上，设圆的半径为r，∵BC＝2，CD＝1，∴BD∴BC•CD BD•r，∴r，∴圆的方程为（x﹣1）2+（y﹣2）2，设点P的坐标为（cosθ+1，sinθ+2），∵λμ，∴（cosθ+1，sinθ+2）＝λ（1，0）+μ（0，2）＝（λ，2μ），∴cosθ+1＝λ，sinθ+2＝2μ，∴λ+μcosθsinθ+2＝sin（θ+φ）+2，其中tanφ＝2，∵﹣1≤sin（θ+φ）≤1，∴1≤λ+μ≤3，故λ+μ的最大值为3，故选：A．11．【2017年浙江10】如图，已知平面四边形ABCD，AB⊥BC，AB＝BC＝AD＝2，CD＝3，AC与BD交于点O，记I1•，I2•，I3•，则（）A．I1＜I2＜I3B．I1＜I3＜I2C．I3＜I1＜I2D．I2＜I1＜I3【解答】解：∵AB⊥BC，AB＝BC＝AD＝2，CD＝3，∴AC＝2，∴∠AOB＝∠COD＞90°，由图象知OA＜OC，OB＜OD，∴0••，•0，即I3＜I1＜I2，故选：C．12．【2017年北京理科06】设，为非零向量，则“存在负数λ，使得λ”是“•0”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：，为非零向量，存在负数λ，使得λ，则向量，共线且方向相反，可得•0．反之不成立，非零向量，的夹角为钝角，满足•0，而λ不成立．∴，为非零向量，则“存在负数λ，使得λ”是•0”的充分不必要条件．故选：A．13．【2019年天津理科14】在四边形ABCD中，AD∥BC，AB＝2，AD＝5，∠A＝30°，点E在线段CB 的延长线上，且AE＝BE，则•．【解答】解：∵AE＝BE，AD∥BC，∠A＝30°，∴在等腰三角形ABE中，∠BEA＝120°，又AB＝2，∴AE＝2，∴，∵，∴又，∴•＝﹣125×2＝﹣1故答案为：﹣1．14．【2019年新课标3理科13】已知，为单位向量，且•0，若2，则cos，．【解答】解：22，∵（2）2＝4459，∴||＝3，∴cos，．故答案为：15．【2019年江苏12】如图，在△ABC中，D是BC的中点，E在边AB上，BE＝2EA，AD与CE交于点O．若•6•，则的值是．【解答】解：设λ（），μμ（）＝（1﹣μ）μμ∴，∴，∴（），，6•6（）×（）（），∵•，∴，∴3，∴．故答案为：16．【2019年浙江17】已知正方形ABCD的边长为1．当每个λi（i＝1，2，3，4，5，6）取遍±1时，|λ1λ2λ3λ4λ5λ6|的最小值是，最大值是．【解答】解：正方形ABCD的边长为1，可得，，•0，|λ1λ2λ3λ4λ5λ6|＝|λ1λ2λ3λ4λ5λ5λ6λ6|＝|（λ1﹣λ3+λ5﹣λ6）（λ2﹣λ4+λ5+λ6）|，由于λi（i＝1，2，3，4，5，6）取遍±1，可得λ1﹣λ3+λ5﹣λ6＝0，λ2﹣λ4+λ5+λ6＝0，可取λ5＝λ6＝1，λ1＝λ3＝1，λ2＝﹣1，λ4＝1，可得所求最小值为0；由λ1﹣λ3+λ5﹣λ6，λ2﹣λ4+λ5+λ6的最大值为4，可取λ2＝1，λ4＝﹣1，λ5＝λ6＝1，λ1＝1，λ3＝﹣1，可得所求最大值为2．故答案为：0，2．17．【2018年江苏12】在平面直角坐标系xOy中，A为直线l：y＝2x上在第一象限内的点，B（5，0），以AB为直径的圆C与直线l交于另一点D．若0，则点A的横坐标为．【解答】解：设A（a，2a），a＞0，∵B（5，0），∴C（，a），则圆C的方程为（x﹣5）（x﹣a）+y（y﹣2a）＝0．联立，解得D（1，2）．∴．解得：a＝3或a＝﹣1．又a＞0，∴a＝3．即A的横坐标为3．故答案为：3．18．【2018年新课标3理科13】已知向量（1，2），（2，﹣2），（1，λ）．若∥（2），则λ＝．【解答】解：∵向量（1，2），（2，﹣2），∴（4，2），∵（1，λ），∥（2），∴，解得λ．故答案为：．19．【2018年上海08】在平面直角坐标系中，已知点A（﹣1，0）、B（2，0），E、F是y轴上的两个动点，且||＝2，则的最小值为．【解答】解：根据题意，设E（0，a），F（0，b）；∴；∴a＝b+2，或b＝a+2；且；∴；当a＝b+2时，；∵b2+2b﹣2的最小值为；∴的最小值为﹣3，同理求出b＝a+2时，的最小值为﹣3．故答案为：﹣3．20．【2017年江苏12】如图，在同一个平面内，向量，，的模分别为1，1，，与的夹角为α，且tanα＝7，与的夹角为45°．若m n（m，n∈R），则m+n＝．【解答】解：如图所示，建立直角坐标系．A（1，0）．由与的夹角为α，且tanα＝7．∴cosα，sinα．∴C．cos（α+45°）（cosα﹣sinα）．sin（α+45°）（sinα+cosα）．∴B．∵m n（m，n∈R），∴m n，0n，解得n，m．则m+n＝3．故答案为：3．21．【2017年新课标1理科13】已知向量，的夹角为60°，||＝2，||＝1，则|2|＝．【解答】解：【解法一】向量，的夹角为60°，且||＝2，||＝1，∴4•4＝22+4×2×1×cos60°+4×12＝12，∴|2|＝2．【解法二】根据题意画出图形，如图所示；结合图形2；在△OAC中，由余弦定理得||2，即|2|＝2．故答案为：2．22．【2017年浙江15】已知向量、满足||＝1，||＝2，则||+||的最小值是，最大值是．【解答】解：记∠AOB＝α，则0≤α≤π，如图，由余弦定理可得：||，||，令x，y，则x2+y2＝10（x、y≥1），其图象为一段圆弧MN，如图，令z＝x+y，则y＝﹣x+z，则直线y＝﹣x+z过M、N时z最小为z min＝1+3＝3+1＝4，当直线y＝﹣x+z与圆弧MN相切时z最大，由平面几何知识易知z max即为原点到切线的距离的倍，也就是圆弧MN所在圆的半径的倍，所以z max．综上所述，||+||的最小值是4，最大值是．故答案为：4、．23．【2017年天津理科13】在△ABC中，∠A＝60°，AB＝3，AC＝2．若2，λ（λ∈R），且4，则λ的值为．【解答】解：如图所示，△ABC中，∠A＝60°，AB＝3，AC＝2，2，∴（），又λ（λ∈R），∴（）•（λ）＝（λ）•λ＝（λ）×3×2×cos60°32λ×22＝﹣4，∴λ＝1，解得λ．故答案为：．。

平面向量（一）选择题1、（07山东11）在直角ABC ∆中，CD 是斜边AB 上的高，则下列等式不成立的是（ ） （A ）2AC AC AB =⋅ （B ） 2BC BA BC =⋅ （C ）2AB AC CD =⋅ （D ） 22()()AC AB BA BC CD AB⋅⨯⋅=答案：C2、（07山东文5）已知向量(1)(1)n n ==-，，，a b ，若2-a b 与b 垂直，则=a （ ） A ．1BC ．2D ．4答案：C3.(2009山东卷理)设P 是△ABC 所在平面内的一点，2BC BA BP +=，则（ ） A.0PA PB += B.0PC PA += C.0PB PC += D.0PA PB PC ++= 【解析】:因为2BC BA BP +=，所以点P 为线段AC 的中点，所以应该选B 。

【命题立意】:本题考查了向量的加法运算和平行四边形法则， 4、（2010山东数） (12)定义平面向量之间的一种运算“”如下，对任意的a=(m,n)，b p,q)=（，令a b=mq-np ，下面说法错误的是（ ）A.若a 与b 共线，则a b=0B.ab=b aC.对任意的R λ∈，有a)b=(λλ（ab) D. 2222(ab)+(ab)=|a||b|【解析】若a 与b 共线，则有a b=mq-np=0，故A 正确；因为ba pn-qm =，而a b=mq-np ，所以有ab b a ≠，故选项B 错误，故选B 。

【命题意图】本题在平面向量的基础上，加以创新，属创新题型，考查平面向量的基础知识以及分析问题、解决问题的能力。

5、（2011山东理数12）12．设1A ，2A ，3A ，4A 是平面直角坐标系中两两不同的四点，若1312A A A A λ= （λ∈R ），1412A A A A μ=（μ∈R ），且112λμ+=,则称3A ，4A 调和分割1A ，2A ,已知平面上的点C ，D 调和分割点A ，B 则下面说法正确的是A ．C 可能是线段AB 的中点 B ．D 可能是线段AB 的中点C ．C ，D 可能同时在线段AB 上D ．C ，D 不可能同时在线段AB 的延长线上答案：D6、（2011山东文数12）12．设1A ，2A ，3A ，4A 是平面直角坐标系中两两不同的四点，若1312A A A A λ= （λ∈R ），1412A A A A μ=（μ∈R ），且112λμ+=,则称3A ，4A 调和分割1A ，2A ,已知平面上的点C ，D 调和分割点A ，B 则下面说法正确的是 A ．C 可能是线段AB 的中点 B ．D 可能是线段AB 的中点C ．C ，D 可能同时在线段AB 上D ．C ，D 不可能同时在线段AB 的延长线上答案：D7 (2012山东卷文(16))如图，在平面直角坐标系xOy 中，一单位圆的圆心的初始位置在(0，1)，此时圆上一点P 的位置在(0，0)，圆在x 轴上沿正向滚动.当圆滚动到圆心位于(2，1)时，OP 的坐标为＿＿＿＿. 答案：(2sin 2,1cos2)--8、（2013山东理）15．已知向量AB 与AC 的夹角为120°，且3AB =，2AC =，若AP AB AC λ=+，且AP BC ⊥，则实数λ的值为__________. 答案：15．7129（2013山东数学文）(15)、在平面直角坐标系xOy 中，已知(1,)OA t =-，(2,2)OB =，若90oABO ∠=，则实数t 的值为______ 答案：510（2014山东数学文）(7)、已知向量()1,3a =，()3,b m =.若向量,a b 的夹角为π6，则实数m =（ ）（A）（B（C ）0 （D ）答案：（B ）（二）解答题1．（07山东）20（本小题满分12分）如图,甲船以每小时海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于1A 处时,乙船位于甲船的 北偏西105︒的方向1B 处,此时两船相距20海里.当甲船航 行20分钟到达2A 处时,乙船航行到甲船的北偏西120︒方 向的2B 处,此时两船相距海里,问乙船每小时航行多少海里? 解：如图，连结12AB ，22A B =122060A A =⨯=， 122A A B ∆是等边三角形，1121056045B A B ∠=︒-︒=︒，在121A B B ∆中，由余弦定理得2221211121112222cos 45202202002B B A B A B A B A B =+-⋅︒=+-⨯⨯=，12B B =因此乙船的速度的大小为6020=答：乙船每小时航行海里.2．（07山东文）17．（本小题满分12分）在ABC △中，角A B C ，，的对边分别为tan a b c C =，，，（1）求cos C ； （2）若52CB CA =，且9a b +=，求c ．解：（1）sin tan cos CC C=∴=又22sin cos 1C C += 解得1cos 8C =±．tan 0C >，C ∴是锐角． 1cos 8C ∴=．（2）52CB CA =， 5cos 2ab C ∴=， 20ab ∴=．又9a b +=22281a ab b ∴++=． 2241a b ∴+=．2222cos 36c a b ab C ∴=+-=． 6c ∴=．。

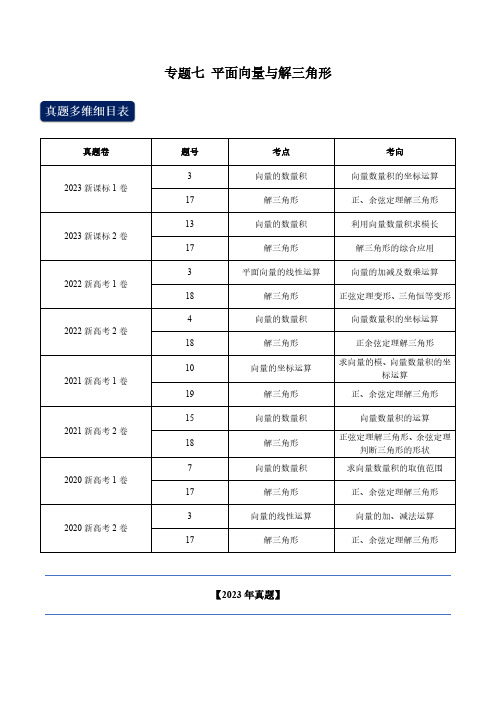
专题七平面向量与解三角形真题卷题号考点考向2023新课标1卷3 向量的数量积向量数量积的坐标运算17 解三角形正、余弦定理解三角形2023新课标2卷13 向量的数量积利用向量数量积求模长17 解三角形解三角形的综合应用2022新高考1卷3 平面向量的线性运算向量的加减及数乘运算18 解三角形正弦定理变形、三角恒等变形2022新高考2卷4 向量的数量积向量数量积的坐标运算18 解三角形正余弦定理解三角形2021新高考1卷10 向量的坐标运算求向量的模、向量数量积的坐标运算19 解三角形正、余弦定理解三角形2021新高考2卷15 向量的数量积向量数量积的运算18 解三角形正弦定理解三角形、余弦定理判断三角形的形状2020新高考1卷7 向量的数量积求向量数量积的取值范围17 解三角形正、余弦定理解三角形2020新高考2卷3 向量的线性运算向量的加、减法运算17 解三角形正、余弦定理解三角形【2023年真题】1.（2023·新课标I 卷 第3题）已知向量(1,1)a = ，(1,1).b=− 若()()a b a b λµ+⊥+，则( ) A. 1λµ+=B.1λµ+=− C. 1λµ= D. 1λµ=−【答案】D 【解析】 【分析】本题考查向量的数量积运算，结合向量垂直，向量的数量积为0，为较易题. 【解答】解：22()()()()2(1)0a b a b a a b b λµλµλµλµ+⋅+=++⋅+=+=，所以1;λµ=−故选.D2. （2023·新课标II 卷 第13题）已知向量a ，b 满足||a b − |||2|a b a b +=− ，则||b = __________【答案】【解析】 【分析】本题考查向量模及向量数量积的运算，属于基础题． 将两等式分别平方，然后化简计算即可． 【解答】 解：将原式平方：化简可得：即23b =，故||b =3. （2023·新课标I 卷 第17题）已知在ABC 中，3A B C +=，2sin()sin .A C B −=(1)求sin A ；(2)设5AB =，求AB 边上的高.【答案】解：(1)3A B C +=，3C C π∴−=，解得.4C π=2sin()sin A C B ∴−=可化为2sin()sin()44A A πππ−=−−，即32sin()sin()44A A ππ−=−，A A A A=，整理得sin3cosA A=，将1cos sin3A A=代入22sin cos1A A+=，得210sin19A=，29sin10A∴=，sin A=(2)由(1)知sin A=，1cos sin3A A==4Cπ=，又sin sinAC ABB C=，sinsinAB BACC∴==AB∴边上的高sin 6.h AC A===【解析】本题考查了三角恒等变换与解三角形的相关知识，属于中等题.(1)根据题意，结合A B Cπ++=可直接求出C，再将C代入2sin()sinA C B−=进行恒等变换得sin3cosA A=，最后再结合同角三角函数的基本关系即可求解；(2)结合三角恒等变换、正弦定理，分别求出sin B和AC，即可得AB边上的高sinAC A的值.4.（2023·新课标II卷第17题）记ABC的内角A，B，C的对边分别为a，b，c，已知ABC，D为BC的中点，且 1.AD=(1)若3ADCπ∠=，求tan B；(2)若228b c+=，求b，.c【答案】解：(1)ABCS=，D为BC的中点，ADCS∴11sin122AD CD ADC CD⋅⋅∠=××=，解得2CD=，则 2.BD=过点A作AE CD⊥于点E，则在ADE中，AE=12DE=，∴在Rt AEB中，52BE BD DE=+=，tanAEBBE==(2) 在ABC 中，1()2AD AB AC =+，222222111||()(||||2)(2cos )444AD AB AC AB AC AB AC c b bc A ∴=+=++⋅=++ ，11(82cos )4bc A ∴=+，即cos 2bc A =−，又1sin 2ABC S bc A == ，sin bc A ∴，sintancos bc A Abc A ∴==23A π∴=，sin A =， 4.bc =再将4b c=代入228b c +=，即可解得 2.b c == 【解析】本题考查了解三角形的综合应用，属于中等题.(1)结合三角形面积和中点关系进行求解；(2)观察题目所给条件，结合中线的向量表示和三角形面积进行求解.【2022年真题】5.（2022·新高考I 卷 第3题）在ABC 中，点D 在边AB 上，2.BD DA =记CA m = ，CD n = ，则CB =( ) A. 32m n −B. 23m n −+C. 32m n +D. 23m n +【答案】B 【解析】 【分析】本题主要考查向量的加减及数乘运算，属于基础题. 【解答】解：2133CD CA CB =+ ，3223.CB CD CA m n =−=−+6.（2022·新高考II 卷 第4题）已知向量(3,4)a = ，(1,0)b = ，c a tb =+ ，若,,a c b c <>=<> ，则实数t =( ) A. 6− B. 5−C. 5D. 6【答案】C 【解析】 【分析】本题考查了向量的坐标运算和夹角运算，属于基础题。

专题07 平面向量【2021年】一、【2021·浙江高考】已知平面向量,,,(0)a b c c ≠满足()1,2,0,0a b a b a b c ==⋅=-⋅=.记向量d 在,a b 方向上的投影分别为x ，y ，d a -在c 方向上的投影为z ，则222x y z ++的最小值为___________.【答案】25 【解析】【分析】设(1,0),(02),(,)a b c m n ===，，由平面向量的知识可得22x y +-=，再结合柯西不等式即可得解.【详解】由题意，设(1,0),(02),(,)a b c m n ===，，则()20a b c m n -⋅=-=，即2m n =，又向量d 在,a b 方向上的投影分别为x ，y ，所以(),d x y=，所以d a-在c 方向上的投影1()||m x ny da c z c -+-⋅===， 即252x yz +=, 所以(()()2222222222112212510105x y z x y z x y z ⎡⎤++=++++≥+=⎢⎥⎣⎦， 当且仅当215252x y x y z ⎧==⎪⎨⎪+=⎩即25155x y z ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩时，等号成立， 所以222x y z ++的最小值为25. 故答案为：25. 【点睛】关键点点睛：解决本题的关键是由平面向量的知识转化出,,x y z 之间的等量关系，再结合柯西不等式变形即可求得最小值.二、【2021·江苏高考】已知O 为坐标原点，点P 1(cosα,sinα)，P 2(cosβ,−sinβ)，P 3(cos(α+β),sin(α+β))，A(1,0)，则( )A. |OP 1⃗⃗⃗⃗⃗⃗⃗ |=|OP 2⃗⃗⃗⃗⃗⃗⃗ |B. |AP 1⃗⃗⃗⃗⃗⃗⃗ |=|AP 2⃗⃗⃗⃗⃗⃗⃗ |C. OA ⃗⃗⃗⃗⃗ ⋅OP 3⃗⃗⃗⃗⃗⃗⃗ =OP 1⃗⃗⃗⃗⃗⃗⃗ ⋅OP 2⃗⃗⃗⃗⃗⃗⃗D. OA ⃗⃗⃗⃗⃗ ⋅OP 1⃗⃗⃗⃗⃗⃗⃗ =OP 2⃗⃗⃗⃗⃗⃗⃗ ⋅OP 3⃗⃗⃗⃗⃗⃗⃗【答案】AC【知识点】向量的数量积【解析】解：∵P 1(cosα,sinα)，P 2(cosβ,−sinβ)，P 3(cos(α+β),sin(α+β))，A(1,0)，∴OP 1⃗⃗⃗⃗⃗⃗⃗ =(cosα,sinα)，OP 2⃗⃗⃗⃗⃗⃗⃗ =(cosβ,−sinβ)，OP 3⃗⃗⃗⃗⃗⃗⃗ =(cos(α+β),sin(α+β))，OA ⃗⃗⃗⃗⃗ =(1,0)，AP 1⃗⃗⃗⃗⃗⃗⃗ =(cosα−1,sinα)，AP 2⃗⃗⃗⃗⃗⃗⃗ =(cosβ−1,−sinβ)，则|OP 1⃗⃗⃗⃗⃗⃗⃗ |=√cos 2α+sin 2α=1，|OP 2⃗⃗⃗⃗⃗⃗⃗ |=√cos 2β+(−sinβ)2=1，则|OP 1⃗⃗⃗⃗⃗⃗⃗ |=|OP 2⃗⃗⃗⃗⃗⃗⃗ |，故A 正确；|AP 1⃗⃗⃗⃗⃗⃗⃗ |=√(cosα−1)2+sin 2α=√cos 2α+sin 2α−2cosα+1=√2−2cosα，|AP 2⃗⃗⃗⃗⃗⃗⃗ |=√(cosβ−1)2+(−sinβ)2=√cos 2β+sin 2β−2cosβ+1=√2−2cosβ， |AP 1⃗⃗⃗⃗⃗⃗⃗ |≠|AP 2⃗⃗⃗⃗⃗⃗⃗ |，故B 错误；OA ⃗⃗⃗⃗⃗ ⋅OP 3⃗⃗⃗⃗⃗⃗⃗ =1×cos(α+β)+0×sin(α+β)=cos(α+β)，OP 1−⋅OP 2⃗⃗⃗⃗⃗⃗⃗ =cosαcosβ−sinαsinβ=cos(α+β)，∴OA ⃗⃗⃗⃗⃗ ⋅OP 3⃗⃗⃗⃗⃗⃗⃗ =OP 1⃗⃗⃗⃗⃗⃗⃗ ⋅OP 2⃗⃗⃗⃗⃗⃗⃗ ，故C 正确；OA ⃗⃗⃗⃗⃗ ⋅OP 1⃗⃗⃗⃗⃗⃗⃗ =1×cosα+0×sinα=cosα，OP 2⃗⃗⃗⃗⃗⃗⃗ ⋅OP 3⃗⃗⃗⃗⃗⃗⃗ =cosβcos(α+β)−sinβsin(α+β)=cos[β+(α+β)]=cos(α+2β)，∴OA ⃗⃗⃗⃗⃗ ⋅OP 1⃗⃗⃗⃗⃗⃗⃗ ≠OP 2⃗⃗⃗⃗⃗⃗⃗ ⋅OP 3⃗⃗⃗⃗⃗⃗⃗ ，故D 错误．故选：AC ．由已知点的坐标分别求得对应向量的坐标，然后逐一验证四个选项得答案．本题考查平面向量数量积的性质及运算，考查同角三角函数基本关系式及两角和的三角函数，考查运算求解能力，是中档题．【2020年】一、【2020·北京高考】已知正方形ABCD 的边长为2，点P 满足AP ⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )，则|PD ⃗⃗⃗⃗⃗ |= ；PB ⃗⃗⃗⃗⃗ ⋅PD⃗⃗⃗⃗⃗ = ． 【答案】√5 −1【知识点】向量的加法、减法、数乘运算、向量的数量积【解析】【分析】本题考查了向量的几何意义和向量的数量积的运算，属于基础题．根据向量的几何意义可得P 为BC 的中点，再根据向量的数量积的运算和正方形的性质即可求出．【解答】解：由AP ⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )，可得P 为BC 的中点， 则|CP|=1，∴|PD|=√22+12=√5，∴PB ⃗⃗⃗⃗⃗ ⋅PD ⃗⃗⃗⃗⃗ =PB ⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ )=−PC ⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ )=−PC ⃗⃗⃗⃗⃗ 2−PC ⃗⃗⃗⃗⃗ ⋅CD ⃗⃗⃗⃗⃗ =−1，故答案为√5；−1．二、【2020·浙江高考】已知单位向量e 1⃗⃗⃗ ，e 2⃗⃗⃗ 满足|2e 1⃗⃗⃗ −e 2⃗⃗⃗ |≤√2，设a ⃗ =e 1⃗⃗⃗ +e 2⃗⃗⃗ ，b ⃗ =3e 1⃗⃗⃗ +e 2⃗⃗⃗ ，向量a⃗ ，b ⃗ 的夹角为θ，则cos 2θ的最小值为 ．【答案】2829【知识点】利用向量的数量积求向量的模、利用向量的数量积求向量的夹角【解析】【分析】本题考查了平面向量的数量积与夹角的运算问题，属于中档题．设e 1⃗⃗⃗ 、e 2⃗⃗⃗ 的夹角为α，由题意求出cosα≥34；再求a⃗ ，b ⃗ 的夹角θ的余弦值cos 2θ的最小值即可． 【解答】解：设e 1⃗⃗⃗ 、e 2⃗⃗⃗ 的夹角为α，由e 1⃗⃗⃗ ，e 2⃗⃗⃗ 为单位向量，满足|2e 1⃗⃗⃗ −e 2⃗⃗⃗ |≤√2，所以4e 1⃗⃗⃗ 2−4e 1⃗⃗⃗ ⋅e 2⃗⃗⃗ +e 2⃗⃗⃗ 2=4−4cosα+1≤2， 解得cosα≥34；又a ⃗ =e 1⃗⃗⃗ +e 2⃗⃗⃗ ，b ⃗ =3e 1⃗⃗⃗ +e 2⃗⃗⃗ ，且a ⃗ ，b ⃗ 的夹角为θ，所以a ⃗ ⋅b ⃗ =3e 1⃗⃗⃗ 2+4e 1⃗⃗⃗ ⋅e 2⃗⃗⃗ +e 2⃗⃗⃗ 2=4+4cosα，a ⃗ 2=e 1⃗⃗⃗ 2+2e 1⃗⃗⃗ ⋅e 2⃗⃗⃗ +e 2⃗⃗⃗ 2=2+2cosα，b ⃗ 2=9e 1⃗⃗⃗ 2+6e 1⃗⃗⃗ ⋅e 2⃗⃗⃗ +e 2⃗⃗⃗ 2=10+6cosα； 则cos 2θ=(a ⃗ ⋅b ⃗ )2a ⃗ 2×b ⃗ 2=(4+4cosα)2(2+2cosα)(10+6cosα)=4+4cosα5+3cosα=43−835+3cosα，所以cosα=34时，cos 2θ取得最小值为43−835+3×34=2829． 故答案为2829．三、【2020·天津高考】如图，在四边形ABCD 中，∠B =60°，AB =3，BC =6，且AD ⃗⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗ ，AD ⃗⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =−32，则实数λ的值为 ，若M ，N 是线段BC 上的动点，且|MN ⃗⃗⃗⃗⃗⃗⃗ |=1，则DM ⃗⃗⃗⃗⃗⃗⃗ ⋅DN⃗⃗⃗⃗⃗⃗ 的最小值为 ． 【答案】16 132【知识点】平面向量的坐标运算、向量的几何运用、向量的加法、减法、数乘运算、二次函数、向量的数量积【解析】【分析】本题考查了向量在几何中的应用，考查了向量的共线和向量的数量积，以及二次函数的性质，属于中档题． 以B 为原点，以BC 为x 轴建立如图所示的直角坐标系，根据向量的平行和向量的数量积即可求出点D 的坐标，即可求出λ的值，再设出点M ，N 的坐标，根据向量的数量积可得关于x 的二次函数，根据二次函数的性质即可求出最小值．【解答】解：以B 为原点，以BC 为x 轴建立如图所示的直角坐标系，∵∠B =60°，AB =3，∴A(32,3√32)， ∵BC =6，∴C(6,0)，∵AD ⃗⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗ ，∴AD//BC ，设D(x 0,3√32)， ∴AD ⃗⃗⃗⃗⃗⃗ =(x 0−32,0)，AB ⃗⃗⃗⃗⃗ =(−32,−3√32)， ∴AD ⃗⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =−32(x 0−32)+0=−32，解得x 0=52， ∴D(52,3√32)， ∴AD ⃗⃗⃗⃗⃗⃗ =(1,0)，BC ⃗⃗⃗⃗⃗ =(6,0)，∴AD ⃗⃗⃗⃗⃗⃗ =16BC ⃗⃗⃗⃗⃗ ， ∴λ=16，∵|MN⃗⃗⃗⃗⃗⃗⃗ |=1， 设M(x,0)，则N(x +1,0)，其中0≤x ≤5，∴DM ⃗⃗⃗⃗⃗⃗⃗ =(x −52,−3√32)，DN ⃗⃗⃗⃗⃗⃗ =(x −32,−3√32)， ∴DM ⃗⃗⃗⃗⃗⃗⃗ ⋅DN ⃗⃗⃗⃗⃗⃗ =(x −52)(x −32)+274=x 2−4x +212=(x −2)2+132， 当x =2时取得最小值，最小值为132，故答案为：16；132．四、【2020·上海高考】已知a 1⃗⃗⃗⃗ ，a 2⃗⃗⃗⃗ ，b 1⃗⃗⃗ ，b 2⃗⃗⃗⃗ ，…，b k ⃗⃗⃗⃗ (k ∈N ∗)是平面内两两互不相等的向量，满足|a 1⃗⃗⃗⃗ −a 2⃗⃗⃗⃗ |=1，且|a i ⃗⃗⃗ −b j ⃗⃗⃗ |∈{1,2}(其中i =1，2，j =1，2，…，k)，则k 的最大值是 ．【答案】6【知识点】向量的几何运用、向量的模【解析】【分析】本题考查两向量的线性运算，考查向量模的求法，正确理解题意是关键，是中档题．设OA 1⃗⃗⃗⃗⃗⃗⃗⃗ =a 1⃗⃗⃗⃗ ，OA 2⃗⃗⃗⃗⃗⃗⃗⃗ =a 2⃗⃗⃗⃗ ，结合向量的模等于1和2画出图形，由圆的交点个数即可求得k 的最大值．【解答】解：如图，设OA 1⃗⃗⃗⃗⃗⃗⃗⃗ =a 1⃗⃗⃗⃗ ，OA 2⃗⃗⃗⃗⃗⃗⃗⃗ =a 2⃗⃗⃗⃗ ，由|a 1⃗⃗⃗⃗ −a 2⃗⃗⃗⃗ |=1，且|a i ⃗⃗⃗ −b j ⃗⃗⃗ |∈{1,2}，分别以A 1，A 2为圆心，以1和2为半径画圆，其中圆的公共点共有6个．故满足条件的k 的最大值为6．故答案为：6．【2019年】一、【2019·北京高考（文）】已知向量a ⃗ =(−4,3)，b ⃗ =(6,m)，且a ⃗ ⊥b ⃗ ，则m =______．【答案】8【知识点】向量垂直的判断与证明、向量的数量积【解析】【分析】本题考查了平面向量的数量积与垂直的关系，属基础题．a ⃗ ⊥b ⃗ 则a ⃗ ⋅b⃗ =0，代入a ⃗ ，b ⃗ ，解方程即可． 【解答】解：由向量a ⃗ =(−4,3)，b ⃗ =(6,m)，且a ⃗ ⊥b ⃗ ，得a ⃗ ⋅b ⃗ =−24+3m =0，∴m =8．故答案为8．二、 【2019·浙江高考】已知正方形ABCD 的边长为1.当每个λi (i =1,2，3，4，5，6)取遍±1时，|λ1AB ⃗⃗⃗⃗⃗ +λ2BC ⃗⃗⃗⃗⃗ +λ3CD ⃗⃗⃗⃗⃗ +λ4DA ⃗⃗⃗⃗⃗ +λ5AC ⃗⃗⃗⃗⃗ +λ6BD⃗⃗⃗⃗⃗⃗ |的最小值是 ，最大值是 ． 【答案】0 2√5【知识点】利用向量的数量积求向量的模、向量在平面几何中的应用【解析】【分析】本题考查向量的加减运算和向量的模的最值求法，注意变形和分类讨论，考查化简运算能力，难度较大．由题意可得AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ ，BD ⃗⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ ，AB ⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗⃗ =0，化简|λ1AB ⃗⃗⃗⃗⃗ +λ2BC ⃗⃗⃗⃗⃗ +λ3CD ⃗⃗⃗⃗⃗ +λ4DA ⃗⃗⃗⃗⃗ +λ5AC⃗⃗⃗⃗⃗ +λ6BD⃗⃗⃗⃗⃗⃗ | =√(λ1−λ3+λ5−λ6)2+(λ2−λ4+λ5+λ6)2，由于λi (i =1,2，3，4，5，6)取遍±1，由完全平方数的最值，可得所求最值．【解答】解：如图，正方形ABCD 的边长为1，可得AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ ，BD ⃗⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ ，AB ⃗⃗⃗⃗⃗ ⋅AD⃗⃗⃗⃗⃗⃗ =0， |λ1AB ⃗⃗⃗⃗⃗ +λ2BC ⃗⃗⃗⃗⃗ +λ3CD ⃗⃗⃗⃗⃗ +λ4DA ⃗⃗⃗⃗⃗ +λ5AC ⃗⃗⃗⃗⃗ +λ6BD⃗⃗⃗⃗⃗⃗ | =|λ1AB ⃗⃗⃗⃗⃗ +λ2BC ⃗⃗⃗⃗⃗ +λ3CD ⃗⃗⃗⃗⃗ +λ4DA ⃗⃗⃗⃗⃗ +λ5 (AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗⃗ )+λ6 (AD ⃗⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )|=|(λ1−λ3+λ5−λ6)AB ⃗⃗⃗⃗⃗ +(λ2−λ4+λ5+λ6)AD⃗⃗⃗⃗⃗⃗ | =√(λ1−λ3+λ5−λ6)2+(λ2−λ4+λ5+λ6)2，由于λi (i =1,2，3，4，5，6)取遍±1，当λ1−λ3+λ5−λ6=0，λ2−λ4+λ5+λ6=0时，可取λ1=λ3=λ5=λ6，λ5=−1，λ6=−1，λ2=1，λ4=−1，可得所求最小值为0；接下来求最大值：∵|λ1−λ3+λ5−λ6|，|λ2−λ4+λ5+λ6|的最大值都为4，但是①当λ5+λ6=2或−2时，λ5−λ6=0，|λ2−λ4+λ5+λ6|可取最大值4，|λ1−λ3+λ5−λ6|最大值只能取2；②当λ5+λ6=0时，λ5−λ6=2或−2，|λ1−λ3+λ5−λ6|可取最大值4，|λ2−λ4+λ5+λ6|最大值只能取2．可得所求最大值为√42+22=2√5．故答案为：0；2√5．三、 【2019·天津高考】在四边形ABCD 中，AD//BC ，AB =2√3，AD =5，∠A =30°，点E 在线段CB的延长线上，且AE =BE ，则BD ⃗⃗⃗⃗⃗⃗ ⋅AE ⃗⃗⃗⃗⃗ = ．【答案】−1【知识点】向量的数乘运算、向量的数量积的概念及其运算【解析】【分析】本题考查了向量的数量积及向量的线性运算，属于中档题．利用向量数量积的运算律，并结合向量的线性运算进行计算即可．【解答】解：∵AE =BE ，AD//BC ，∠A =30°，∴在等腰三角形ABE 中，∠BEA =120°，又AB =2√3，∴AE =BE =2，∴BE ⃗⃗⃗⃗⃗ =−25AD⃗⃗⃗⃗⃗⃗ ， ∵AE ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BE ⃗⃗⃗⃗⃗ ，∴AE ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ −25AD ⃗⃗⃗⃗⃗⃗ ， 又BD ⃗⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗⃗ =−AB ⃗⃗⃗⃗⃗ +AD⃗⃗⃗⃗⃗⃗ ， ∴BD ⃗⃗⃗⃗⃗⃗ ⋅AE ⃗⃗⃗⃗⃗ =(−AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗⃗ )⋅(AB ⃗⃗⃗⃗⃗ −25AD ⃗⃗⃗⃗⃗⃗ )=−AB ⃗⃗⃗⃗⃗ 2+75AB ⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗⃗ −25AD ⃗⃗⃗⃗⃗⃗ 2 =−AB ⃗⃗⃗⃗⃗ 2+75|AB|⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅|AD|⃗⃗⃗⃗⃗⃗⃗⃗⃗ cos∠BAD −25AD ⃗⃗⃗⃗⃗⃗ 2 =−12+75×5×2√3×√32−25×25 =−1．故答案为−1．四、【2019·上海高考】在椭圆x 24+y 22=1上任意一点P ，Q 与P 关于x 轴对称，若有F 1P ⃗⃗⃗⃗⃗⃗⃗ ⋅F 2P ⃗⃗⃗⃗⃗⃗⃗ ≤1，则F 1P ⃗⃗⃗⃗⃗⃗⃗ 与F 2Q ⃗⃗⃗⃗⃗⃗⃗ 的夹角范围为______．【答案】[π−arccos 13,π]或[arccos (−13),π]【知识点】平面向量的坐标运算、向量的夹角、椭圆的概念及标准方程、向量的数量积【解析】【分析】本题考查椭圆的标准方程，平面向量的夹角与数量积，属于中档题．设P(x,y)，则Q(x,−y)，结合F 1P ⃗⃗⃗⃗⃗⃗⃗ ⋅F 2P ⃗⃗⃗⃗⃗⃗⃗ ≤1，x 24+y 22=1可得：y 2∈[1,2]，进而可得F 1P ⃗⃗⃗⃗⃗⃗⃗ 与F 2Q ⃗⃗⃗⃗⃗⃗⃗ 的夹角θ满足：cosθ=F 1P ⃗⃗⃗⃗⃗⃗⃗ ⋅F 2Q⃗⃗⃗⃗⃗⃗⃗ |F 1P ⃗⃗⃗⃗⃗⃗⃗ |⋅|F 2Q ⃗⃗⃗⃗⃗⃗⃗ |的范围，最后得到答案． 【解答】解：设P(x,y)，则Q(x,−y)，椭圆x 24+y 22=1的焦点坐标为F 1(−√2,0)，F 2(√2,0)，∵F 1P ⃗⃗⃗⃗⃗⃗⃗ ⋅F 2P⃗⃗⃗⃗⃗⃗⃗ ≤1， ∴x 2−2+y 2≤1，结合x 24+y 22=1可得：y 2∈[1,2]故F 1P ⃗⃗⃗⃗⃗⃗⃗ 与F 2Q ⃗⃗⃗⃗⃗⃗⃗ 的夹角θ满足：cosθ=F 1P ⃗⃗⃗⃗⃗⃗⃗ ⋅F 2Q ⃗⃗⃗⃗⃗⃗⃗ |F 1P ⃗⃗⃗⃗⃗⃗⃗ |⋅|F 2Q ⃗⃗⃗⃗⃗⃗⃗ |=222+2+y 2)2−8x 2=2−3y 2y 2+2=−3+8y 2+2∈[−1,−13] 故θ∈[π−arccos 13,π]或[arccos (−13),π]故答案为：[π−arccos13,π]或[arccos(−13),π]【2018年】一、【2018·北京高考（文）】设向量a⃗=(1,0)，b⃗ =(−1,m).若a⃗⊥(m a⃗−b⃗ )，则m=．【答案】−1【知识点】向量数量积的坐标表示与向量的垂直关系、向量线性运算的坐标表示【解析】【分析】本题考查向量的数量积的应用，向量的垂直条件的应用，考查计算能力．利用向量的坐标运算，以及向量的垂直，列出方程求解即可．【解答】解：向量a⃗=(1,0)，b⃗ =(−1,m)．m a⃗−b⃗ =(m+1,−m)．∵a⃗⊥(m a⃗−b⃗ )，∴m+1=0，解得m=−1．故答案为−1．二、【2018·浙江高考】已知a⃗，b⃗ ，e⃗是平面向量，e⃗是单位向量．若非零向量a⃗与e⃗的夹角为π3，向量b⃗ 满足b⃗ 2−4e⃗⋅b⃗ +3=0，则|a⃗−b⃗ |的最小值是()A. √3−1B. √3+1C. 2D. 2−√3【答案】A【知识点】向量垂直的判断与证明、数形结合思想、向量的模、圆有关的最值问题、点到直线的距离公式【解析】【分析】本题考查平面向量的数量积运算以及模的应用，考查数学转化思想方法与数形结合的解题思想方法，属较难题．把等式b⃗ 2−4e⃗⋅b⃗ +3=0变形，可得得(b⃗ −e⃗ )⋅(b⃗ −3e⃗ )=0，即(b⃗ −e⃗ )⊥(b⃗ −3e⃗ )，设e⃗=(1,0)，则b⃗ 的终点在以(2,0)为圆心，以1为半径的圆周上，再由已知得到a ⃗ 的终点在不含端点O 的两条射线y =±√3x(x >0)上，画出图形，数形结合得答案． 【解答】解：由b ⃗ 2−4e ⃗ ⋅b ⃗ +3=0，得(b⃗ −e ⃗ )⋅(b ⃗ −3e ⃗ )=0， ∴(b ⃗ −e ⃗ )⊥(b ⃗ −3e ⃗ )， 如图，不妨设e⃗ =(1,0)， 则b ⃗ 的终点在以(2,0)为圆心，以1为半径的圆周上，又非零向量a⃗ 与e ⃗ 的夹角为π3，则a ⃗ 的终点在不含端点O 的两条射线y =±√3x(x >0)上． 不妨以y =√3x 为例，则|a ⃗ −b ⃗ |的最小值是(2,0)到直线√3x −y =0的距离减1． 即|2√3|√3+1−1=√3−1．故选：A ．三、【2018·天津高考（理）】如图，在平面四边形ABCD 中，AB ⊥BC ，AD ⊥CD ，∠BAD =120°，AB =AD =1.若点E 为边CD 上的动点，则AE ⃗⃗⃗⃗⃗ ⋅BE ⃗⃗⃗⃗⃗ 的最小值为( )A. 2116B. 32C. 2516D. 3【答案】A【知识点】向量数量积的坐标运算 【解析】 【分析】本题考查了向量数量积，坐标法解决向量问题，属于中档题．以D 为原点，以DA 所在的直线为x 轴，以DC 所在的直线为y 轴，求出A ，B ，C 的坐标，根据向量的数量积和二次函数的性质即可求出． 【解答】解：如图所示，以D 为原点，以DA 所在的直线为x 轴，以DC 所在的直线为y 轴，过点B 作BN ⊥x 轴，过点B 作BM ⊥y 轴，∵AB ⊥BC ，AD ⊥CD ，∠BAD =120°，AB =AD =1， ∴AN =ABcos60°=12，BN =ABsin60°=√32，∴DN =1+12=32，∴BM =32， ∴CM =MBtan30°=√32， ∴DC =DM +MC =√3， ∴A(1,0)，B(32,√32)，C(0,√3)，设E(0,m)，∴AE ⃗⃗⃗⃗⃗ =(−1,m)，BE ⃗⃗⃗⃗⃗=(−32,m −√32)，0≤m ≤√3， ∴AE ⃗⃗⃗⃗⃗ ⋅BE ⃗⃗⃗⃗⃗ =32+m 2−√32m =(m −√34)2+32−316=(m −√34)2+2116，当m =√34时，取得最小值为2116．故选A ．【2018·天津高考（文）】在如图所示的平面图形中，已知OM =1，ON =2，∠MON =120°，BM ⃗⃗⃗⃗⃗⃗ =2MA ⃗⃗⃗⃗⃗⃗ ，CN⃗⃗⃗⃗⃗⃗ =2NA ⃗⃗⃗⃗⃗⃗ ，则BC ⃗⃗⃗⃗⃗ ⋅OM ⃗⃗⃗⃗⃗⃗⃗ 的值为( )A. −15B. −9C. −6D. 0【答案】C【知识点】向量的数量积的概念及其运算、利用余弦定理解三角形 【解析】 【分析】本题考查了平面向量数量积，余弦定理的应用，是中档题．由题意判断BC//MN ，且BC =3MN ，再利用余弦定理求出MN 和∠OMN 的余弦值，再计算BC ⃗⃗⃗⃗⃗ ⋅OM ⃗⃗⃗⃗⃗⃗⃗ 即可． 【解答】解：连接MN ，由题意，BM ⃗⃗⃗⃗⃗⃗ =2MA ⃗⃗⃗⃗⃗⃗ ，CN ⃗⃗⃗⃗⃗⃗ =2NA ⃗⃗⃗⃗⃗⃗ ， ∴BMMA =CNNA =2，∴BC//MN ，且BC =3MN ，又MN 2=OM 2+ON 2−2OM ⋅ON ⋅cos120°=1+4−2×1×2×(−12)=7， ∴MN =√7；∴BC =3√7， ∴cos∠OMN =OM 2+MN 2−ON 22OM⋅MN=2×1×7=7，∴BC ⃗⃗⃗⃗⃗ ⋅OM ⃗⃗⃗⃗⃗⃗⃗ =|BC ⃗⃗⃗⃗⃗ |×|OM ⃗⃗⃗⃗⃗⃗⃗ |cos(π−∠OMN)=3√7×1×√7)=−6．故选：C ．四、 【2018·上海高考】在平面直角坐标系中，已知点A(−1,0)、B(2,0)，E 、F 是y 轴上的两个动点，且|EF ⃗⃗⃗⃗⃗ |=2，则AE ⃗⃗⃗⃗⃗ ⋅BF ⃗⃗⃗⃗⃗ 的最小值为______． 【答案】−3【知识点】平面向量的坐标运算、二次函数、向量的数量积 【解析】 【分析】本题考查向量的数量积，向量的坐标运算，二次函数，属于中档题．据题意可设E(0,a)，F(0,b)，从而得出|a −b|=2，即a =b +2，或a =b −2，并可求得AE ⃗⃗⃗⃗⃗ ⋅BF ⃗⃗⃗⃗⃗ =−2+ab ，将a =b +2代入上式即可求出AE ⃗⃗⃗⃗⃗ ⋅BF ⃗⃗⃗⃗⃗ 的最小值，同理将a =b −2带入，也可求出AE ⃗⃗⃗⃗⃗ ⋅BF ⃗⃗⃗⃗⃗ 的最小值． 【解答】解：根据题意，设E(0,a)，F(0,b)； ∴|EF ⃗⃗⃗⃗⃗ |=|a −b|=2； ∴a =b +2，或a =b −2； 且AE ⃗⃗⃗⃗⃗ =(1,a),BF ⃗⃗⃗⃗⃗ =(−2,b)； ∴AE ⃗⃗⃗⃗⃗ ⋅BF ⃗⃗⃗⃗⃗ =−2+ab ；当a =b +2时，AE ⃗⃗⃗⃗⃗ ⋅BF ⃗⃗⃗⃗⃗ =−2+(b +2)⋅b =b 2+2b −2； ∵b 2+2b −2的最小值为−8−44=−3；当a =b −2，AE ⃗⃗⃗⃗⃗ ⋅BF ⃗⃗⃗⃗⃗ =−2+(b −2)⋅b =b 2−2b −2； b 2−2b −2最小值也为−8−44=−3，∴AE ⃗⃗⃗⃗⃗ ⋅BF ⃗⃗⃗⃗⃗ 的最小值为−3． 故答案为：−3．【2018·上海高考】已知实数x 1、x 2、y 1、y 2满足：x 12+y 12=1，x 22+y 22=1，x 1x 2+y 1y 2=12，则11√222√2的最大值为 ．【答案】√2+√3【知识点】向量数量积的坐标运算、由标准方程确定圆心和半径、点到直线的距离 【解析】 【分析】本题考查向量数量积的坐标表示和定义，以及圆的方程和运用，考查直线与圆的位置关系，属于较难题． 设A(x 1,y 1)，B(x 2,y 2)，O 为坐标原点，OA ⃗⃗⃗⃗⃗ =(x 1,y 1)，OB ⃗⃗⃗⃗⃗⃗ =(x 2,y 2)，由圆的方程和向量数量积的定义、坐标表示，可得三角形OAB 为等边三角形，AB =1，11√2+22√2的几何意义为点A ，B 两点到直线x +y −1=0的距离d 1与d 2之和，设AB 中点为M ，则距离d 1与d 2之和等于M 到直线l 的距离的两倍，接着求出点M 到直线l 的距离的最大值，由此可求11√222√2的最大值．【解答】解：设A(x 1,y 1)，B(x 2,y 2)，O 为坐标原点， OA ⃗⃗⃗⃗⃗ =(x 1,y 1)，OB⃗⃗⃗⃗⃗⃗ =(x 2,y 2)，由x 12+y 12=1，x 22+y 22=1，x 1x 2+y 1y 2=12，可得A ，B 两点在圆x 2+y 2=1上，且OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =1×1×cos∠AOB =x 1x 2+y 1y 2=12， 即有∠AOB =60°，即三角形OAB 为等边三角形，AB =1，11√222√2的几何意义为点A ，B 两点到直线l:x +y −1=0的距离d 1与d 2之和，设AB 中点为M ，则距离d 1与d 2之和等于M 到直线l 的距离的两倍， 圆心(0,0)到线段AB 中点M 的距离d =√32，圆心到直线l 的距离d′=√2=√22， ∴M 到直线l 的距离的最大值为d +d′=√32+√22，即11√2+22√2的最大值为√2+√3，故答案为：√2+√3．【2017年】一、【2017·北京高考（文）】设m⃗⃗⃗ ，n ⃗ 为非零向量，则“存在负数λ，使得m ⃗⃗⃗ =λn ⃗ ”是“m ⃗⃗⃗ ·n ⃗ <0”的( ) A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件D. 既不充分也不必要条件【答案】A【知识点】向量的数量积的概念及其运算 【解析】 【分析】本题考查了向量的数量积、必要条件、充分条件与充要条件的判断，属于基础题． 从充分性和必要性两方面分别分析即可 【解答】解：m⃗⃗⃗ ，n ⃗ 为非零向量，存在负数λ，使得m ⃗⃗⃗ =λn ⃗ ， 则向量m⃗⃗⃗ ，n ⃗ 共线且方向相反，可得m ⃗⃗⃗ ·n ⃗ <0． 反之不成立，非零向量m⃗⃗⃗ ，n ⃗ 的夹角为钝角，满足m ⃗⃗⃗ ·n ⃗ <0，而m ⃗⃗⃗ =λn ⃗ 不成立． ∴m ⃗⃗⃗ ，n ⃗ 为非零向量，则“存在负数λ，使得m ⃗⃗⃗ =λn ⃗ ”是m ⃗⃗⃗ ·n ⃗ <0”的充分不必要条件．故选A ．二、 【2017·浙江高考】如图，已知平面四边形ABCD ，AB ⊥BC ，AB =BC =AD =2，CD =3，AC 与BD 交于点O ，记I 1=OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ ，I 2=OB ⃗⃗⃗⃗⃗⃗ ⋅OC ⃗⃗⃗⃗⃗ ，I 3=OC ⃗⃗⃗⃗⃗ ⋅OD⃗⃗⃗⃗⃗⃗ ，则( ) A. I 1<I 2<I 3 B. I 1<I 3<I 2 C. I 3<I 1<I 2 D. I 2<I 1<I 3【答案】C【知识点】向量的数量积的概念及其运算 【解析】 【分析】本题主要考查平面向量数量积的应用，根据图象结合平面向量数量积的定义是解决本题的关键． 根据向量数量积的定义结合图象边角关系进行判断即可． 【解答】解：∵AB ⊥BC ，AB =BC =AD =2，CD =3， ∴AC =2√2，∴∠AOB =∠COD >90°， 由图象知OA <OC ，OB <OD ，∴0>OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ >OC ⃗⃗⃗⃗⃗ ⋅OD ⃗⃗⃗⃗⃗⃗ ，OB ⃗⃗⃗⃗⃗⃗ ⋅OC ⃗⃗⃗⃗⃗ >0， 即I 3<I 1<I 2， 故选：C ．【2017·浙江高考】已知向量a ⃗ 、b ⃗ 满足|a ⃗ |=1，|b ⃗ |=2，则|a ⃗ +b ⃗ |+|a ⃗ −b ⃗ |的最小值是 (1) ，最大值是 (2) ． 【答案】42√5【知识点】范围与最值问题、函数的最值、向量的概念及几何表示 【解析】 【分析】本题考查函数的最值及其几何意义，考查数形结合能力，考查运算求解能力，涉及余弦定理、线性规划等基础知识，注意解题方法的积累，属于中档题．通过记∠AOB=α(0≤α≤π)，利用余弦定理可可知|a⃗+b⃗ |=√5+4cosα、|a⃗−b⃗ |=√5−4cosα，进而换元，转化为线性规划问题，计算即得结论．【解答】解：记∠AOB=α，则0≤α≤π，如图，|a⃗+b⃗ |2=|a⃗|2+|b⃗ |2+2|a⃗||b⃗ |cosα=5+4cosα，|a⃗−b⃗ |2=|a⃗|2+|b⃗ |2−2|a⃗||b⃗ |cosα=5−4cosα，∴|a⃗+b⃗ |=√5+4cosα，|a⃗−b⃗ |=√5−4cosα，令x=√5−4cosα，y=√5+4cosα，则x2+y2=10(x、y≥1)，其图象为一段圆弧MN，如图，令z=x+y，则y=−x+z，则直线y=−x+z过M、N时z最小为z min=1+3=3+1=4，当直线y=−x+z与圆弧MN相切时z最大，由平面几何知识易知z max即为原点到切线的距离的√2倍，也就是圆弧MN所在圆的半径的√2倍，所以z max=√2×√10=2√5．综上所述，|a ⃗ +b ⃗ |+|a ⃗ −b ⃗ |的最小值是4，最大值是2√5． 故答案为：4、2√5．三、 【2017·天津高考（理）】在△ABC 中，∠BAC =60°，AB =3，AC =2.若BD ⃗⃗⃗⃗⃗⃗ =2DC ⃗⃗⃗⃗⃗ ，AE ⃗⃗⃗⃗⃗ =λAC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ (λ∈R)，且AD ⃗⃗⃗⃗⃗⃗ ⋅AE ⃗⃗⃗⃗⃗ =−4，则λ的值为 ． 【答案】311【知识点】向量的加减与数乘混合运算、向量的数量积的概念及其运算 【解析】 【分析】本题考查了平面向量的线性运算与数量积运算问题，是中档题．根据题意画出图形，结合图形，利用AB ⃗⃗⃗⃗⃗ 、AC ⃗⃗⃗⃗⃗ 表示出AD ⃗⃗⃗⃗⃗⃗ ，再根据平面向量的数量积结合AD ⃗⃗⃗⃗⃗⃗ ⋅AE ⃗⃗⃗⃗⃗ =−4列出方程求出λ的值． 【解答】 解：如图所示，△ABC 中，∠BAC =60°，AB =3，AC =2， BD ⃗⃗⃗⃗⃗⃗ =2DC ⃗⃗⃗⃗⃗ ，∴AD ⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BD ⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +23BC ⃗⃗⃗⃗⃗=AB ⃗⃗⃗⃗⃗ +23(AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ ) =13AB ⃗⃗⃗⃗⃗ +23AC⃗⃗⃗⃗⃗ ， 又AE ⃗⃗⃗⃗⃗ =λAC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ (λ∈R)，∴AD⃗⃗⃗⃗⃗⃗ ⋅AE ⃗⃗⃗⃗⃗ =(13AB ⃗⃗⃗⃗⃗ +23AC ⃗⃗⃗⃗⃗ )⋅(λAC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )=(13λ−23)AB⃗⃗⃗⃗⃗ ⋅AC⃗⃗⃗⃗⃗ −13AB⃗⃗⃗⃗⃗ 2+23λAC⃗⃗⃗⃗⃗ 2=(13λ−23)×3×2×cos60°−13×32+23λ×22=−4，∴113λ=1，解得λ=311．故答案为311．。

专题07平面向量1.（2021年河南对口高考）已知向量(2,3)a =- ，向量(,6)b x =- ，若a b ⊥，则x 的值为（）A.4B.4- C.9D.9-【答案】D【解析】若a b ⊥ ，则0a b ⋅=，23(6)0x -+⨯-=，9x =-，故选D.2.（2021年河南对口高考）已知a ，b 是单位向量，夹角为60︒，则a b +=.【答案】【解析】因为a ，b是单位向量，夹角为60︒，所以a b +== 3.（2021年河南对口）已知向量()1,3m = ，(1,1)n =-，则||m n -= （）AB ．C ．4D ．8【答案】B【解析】因为()1,3m = ，()1,1n =-，则(2,2)m n -= ，所以||m n -== B .4.（2020年河南对口高考）已知向量(2,1)a =- ，(3,4)b =- ，则a 与a b +的夹角为（）A.4πB.3π C.2π D.34π【答案】D【解析】a == (2)31(4)10a b ⋅=-⨯+⨯-=- ，2()5a a b a a b +=+⋅=-，a b +=()cos 2a a b a a bθ+==-+，所以夹角为34π，故选D.5.（2020年河南对口高考）已知向量(1,2)a = ，(3,)b k =- ，a b，则=k .【答案】6-【解析】因为a b，所以1230k ⨯+⨯=，6k =-，故答案为6-.6.（2020年河南对口）已知向量a ，b 满足2a = ，1a b ⋅= ，且a 与b的夹角为60︒，则b 的值为.【答案】1【解析】由题意可知，1cos 60212a b a b b ⋅=⋅︒=⋅= ，解得1b = ，故答案为1.7.（2019年河南对口高考）已知(2,1)A ，(1,3)B -，(3,4)C ，则AB AC ⋅=（）A.4-B.4C.3- D.3【答案】D【解析】(3,2)AB =- ，(1,3)AC = ，31233AB AC ⋅=-⨯+⨯=，故选D.8.（2019年河南对口高考）若向量(1,2)a = ，(3,1)b =- ，则()()a b a b ⋅-=.【答案】(4,1)--【解析】1(3)211a b ⋅=⨯-+⨯=- ，(4,1)a b -= ，所以()()(4,1)a b a b ⋅-=--，故答案为：(4,1)--.9.（2019年河南对口）已知向量a ，b的夹角为60°，1a = ，2b = ，则2a b -= （）A ．1B ．CD ．2【答案】D【解析】∵向量a ，b的夹角为60°，且1a = ，2b = ，∴12cos601a b ⋅=⨯⨯︒= ，∴22a b -= ，故选D ．10.（2018年河南对口高考）下列命题中，正确的是（）A.若→→=b a ，则→→=ba B.若→→=b a ，则→a 与→b 是平行向量C.若→→>b a ，则→→>ba D.若→→≠b a ，则向量→a 与→b 不共线【答案】B【解析】向量相等包含两层含义，一个是方向相同，一个是大小相等，两个向量是不能比较大小的，只有向量的模长可以比较大小，所以应选B.11.（2018年河南对口高考）若向量)1,2(-=→a ，)3,1(=→b ，→→→+=b a c 2，则=→c .【答案】(0,7)【解析】2(2,1)(2,6)(0,7)c a b →→→=+=-+=，故答案为：(0,7).12.（2018年河南对口）已知平面向量()2,1a =，()1,1b =-r ，若a b λ- 与a b + 垂直，则λ=.【答案】2【解析】()()()()()2210a b a b a b a b a a b b λλλλ-⊥+⇒-⋅+=+-⋅-= ，因为()2,1a = ，()1,1b =-r ，所以25a =，22b = ，1a b ⋅= ，所以()5120l l +--=，解得2λ=，故答案为2.13.（2017年河南对口高考）“向量0a b +=”是a b“”=A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件【答案】A【解析】两向量相加为零向量，说明两向量是相反向量，模的大小相等方向相反，所以0a b +=能推出a b =，但a b=推不出0a b +=，故选A.14.（2017年河南对口高考）已知()()1,3,2,1A B AB，则--=.【答案】5【解析】(3,4)AB =-- ，5AB ==，故答案为：5.15.（2017年河南对口）在ABC ∆中，角A ，B ，C 的对边分别为,,a b c ，已知3cos 5A =.(1)若ABC ∆的面积为3，求AB AC的值；(2)设2sin ,1,cos ,cos 22B B m n B ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭ ，且//m n ，求cos C 的值.【答案】(1)92；(2)10【解析】解：(1)因为3cos 5A =，所以4sin 5A =，则12||||sin ||||325ABC S AB AC A AB AC ∆=== ，即15||||2AB AC = ，又3cos 5||||AB ACA AB AC ==，所以92AB AC = .(2)因为//m n ，所以2sin cos cos 22B B B =，即sin cos B B =，所以4B π=，所以cos cos()cos cos sin sin 10C A B A B A B =-+=-+=.16.（2016年河南对口高考）设向量(2,1)AB = ，(1,)AC a = ，且AB AC ⊥，则a 的值是（）A.12B.12-C.2-D.2【答案】D【解析】因为(2,1)AB = ，(1,)AC a = ，且AB AC ⊥ ，所以20AB AC a ⋅=+=，2a =-，故选D.17.（2016年河南对口）已知向量(1,1),(1,3)a b =-=- ，则(2)a a b ⋅+=r r r（）A ．0B ．1C ．1-D ．2【答案】A【解析】由题意，向量(1,1),(1,3)a b =-=- ，可得22,1(1)(1)34a a b =⋅=⨯-+-⨯=-，所以2(2)22240a a b a a b ⋅+=+⋅=⨯-=，故选A .18.（2016年河南对口）已知向量()1,2AB =- ，()2,AC x = ，若AB AC ⊥，则BC =.【解析】()1,2BC AC AB x =-=+ ，AB AC ⊥ ，220AB AC x ∴⋅=-= ，解得：1x =，()1,3BC ∴=，BC ∴= .19.（2015年河南对口高考）若向量()2,1=a ,()1,1-=b ,则2a b +等于（）A．()3,3B．()3,3-C．()3,3-D．()3,3--【答案】D【解析】2(2,4)(1,1)(3,3)a b +=+-=，故选D.20.（2015年河南对口高考）已知向量()0,3=a ，()1,1-=b，则=.【答案】2【解析】3a ==，b == ，3(1)013a b ⋅=⨯-+⨯=-，2cos ,2a b a b a b⋅===-，故答案为：22.21.（2015年河南对口高考）已知()()()0,3,3,2,2,1C B A ，求证：AC AB ⊥.【答案】证明见解析【解析】证明：因为(1,1)AB = ，(2,2)AC =- ，12120AB AC ⋅=⨯-⨯= ，所以AB AC ⊥，即AC AB ⊥.22.（2014年河南对口高考）已知向量(3,1)a - =，(1,2)b -- =，(1,1)c - =，则a b c ++ 模长等于（）A ．5B ．4C ．3D ．2【答案】A【解析】(3,4)a b c ++=-，5a b c ++= ，故选A.23.（2014年河南对口高考）向量a 的模为3，向量b 的模为2，二者的夹角为60，则二者的内积等于.【答案】3【解析】因为3a = ，2b = ，,60a b =︒ ，所以cos ,32cos 603a b a b a b ⋅==⨯︒=，故答案为：3.24.（2014年河南对口高考）下列命题中，正确的是（）A ．若a ∥b ，则a 与b方向相同或相反B ．若a ∥b ，b ∥c ，则a ∥cC ．若两个单位向量互相平行，则这两个单位向量相等D ．若a b = ，b c = ，则a c= 【答案】D【解析】由于零向量的方向是任意的，取0a =，则对于任意向量b ，都有a ∥b ，知A 错；取0b = ，则对于任意向量a ，c 都有a ∥b ，b ∥c ，但得不到a ∥c，知B 错；两个单位向量互相平行，方向可能相反，知C 错；由两向量相等的概念知D 正确，故选D ．25.（2013年河南对口高考）已知向量(3,2)a =- ，(1,1)b =- ，则32a b +等于（）A ．(7,4)-B ．(7,4)C ．(7,4)--D ．(7,4)-【答案】D【解析】32(9,6)(2,2)(7,4)a b +=-+-=-，故选D.26.（2013年河南对口高考）若向量(1,3)a =- 与向量(2,)b m =平行，则m =．【答案】6-【解析】因为向量(1,3)a =- 与向量(2,)b m =平行，所以1230m ⨯+⨯=，6m =-，故答案为：6-.27.（2013年河南对口高考）已知(1,2)a =- ，(2,1)b =- ，证明：4cos ,5a b = ．【答案】证明见解析【解析】证明：a ==，b ==(1)(2)214a b ⋅=-⨯-+⨯= ，所以4cos ,5a ba b a b⋅===，得证.28.（2012年河南对口高考）已知向量(1,2)a = ，(2,1)b =- ，则a ，b之间的位置关系为（）A ．平行B ．不平行也不垂直C ．垂直D ．以上都不对【答案】C【解析】因为(1,2)a = ，(2,1)b =- ，1(2)210a b ⋅=⨯-+⨯= ，所以a b ⊥，故选C.29.（2012年河南对口高考）已知两点()3,4A -和()1,1B ，则AB =.【答案】5【解析】因为()3,4A -和()1,1B ，所以(4,3)AB =-，5AB == ，故答案为：5.30.（2012年河南对口）已知向量a ，b 满足||1a =，||b = ()a a b ⊥- ，则a 与b 的夹角是.【答案】4π【解析】由()a a b ⊥- ，得2()0a a b a a b ⋅-=-⋅= ，所以21a b a ⋅==，所以cos ,2a b a b a b ⋅==⋅，所以,4a b π= ，故答案为4π.。

【最新】高考数学《平面向量》专题解析一、选择题1．在△ABC 中，D 是BC 中点，E 是AD 中点，CE 的延长线交AB 于点,F 则（ ）A ．1162DF AB AC =--u u u r u u u r u u u r B ．1134DF AB AC =--u u u r u u u r u u u rC ．3142DF AB AC =-+u u u r u u u r u u u rD ．1126DF AB AC =--u u u r u u u r u u u r【答案】A 【解析】 【分析】设AB AF λ=u u u r u u u r，由平行四边形法则得出144AE AF AC λ=+u u u r u u u r u u u r ，再根据平面向量共线定理得出得出=3λ，由DF AF AD =-u u u r u u u r u u u r，即可得出答案. 【详解】设AB AF λ=u u u r u u u r ，111124444AE AB A A C A AC D F λ==+=+u u u r u u u u u ur u u u r r u u u r u u u r因为C E F 、、三点共线，则1=144λ+，=3λ所以1111132262DF AF AD AB AB AC AB AC =-=--=--u u u r u u u r u u u r u u u r u u u r u u u r u u ur u u u r故选：A【点睛】本题主要考查了用基底表示向量，属于中档题.2．在ABC V 中，312AB AC ==，D 是AC 的中点，BD u u u r 在AC u u u r方向上的投影为4-，则向量BA u u u r 与AC u u u r的夹角为（ ） A ．45° B ．60°C ．120°D ．150°【答案】C 【解析】 【分析】设BDC α∠=，向量BA u u u r 与AC u u u r 的夹角为θ，BD u u u r 在AC u u u r方向上的投影为cos =4BD α-u u u r，利用线性代换并结合向量夹角公式即可求出夹角．【详解】312AB AC ==，D 是AC 的中点，则4AC =，2AD DC ==， 向量BD u u u r 在AC u u u r方向上的投影为4-， 设BDA α∠=，向量BA u u u r 与AC u u u r的夹角为θ，则cos =4BD α-u u u r，∴()cos ===BD DA AC BA AC BD AC DA ACBA AC BA AC BA AC θ+⋅⋅⋅+⋅⋅⋅⋅u u u r u u u r u u u r u u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u r u u u r u u u r u u u r u u u r()()cos cos180444211===1242BD AC DA AC AB ACα⋅+⋅⨯+-⨯-⨯︒⨯⋅-u u u u u r u u u r u u u u r u u u ru ur r u， 故夹角为120°， 故选：C . 【点睛】本题考查向量的投影，利用数量积求两个向量的夹角，属于中等题.3．若向量a b r r ，的夹角为3π，|2|||a b a b -=+r r r r ，若()a ta b ⊥+r r r ，则实数t =（ ）A ．12-B ．12C ．2D ． 【答案】A 【解析】 【分析】由|2|||a b a b -=+r r r r 两边平方得22b a b =⋅r r r ，结合条件可得b a =r r ，又由()a ta b ⊥+r r r ，可得20t a a b ⋅+⋅=r r r，即可得出答案.【详解】由|2|||a b a b -=+r r r r两边平方得2222442a a b b a a b b -⋅+=+⋅+r r r r r r r r .即22b a b =⋅r r r ，也即22cos 3b a b π=r r r ，所以b a =r r .又由()a ta b ⊥+r r r ，得()0a ta b ⋅+=r r r，即20t a a b ⋅+⋅=r r r .所以2221122ba b t a b⋅=-=-=-r r r r r 故选：A 【点睛】本题考查数量积的运算性质和根据向量垂直求参数的值，属于中档题.4．已知O 是平面上一定点，满足()||cos ||cos AB ACOP OA AB B AC Cλ=++u u u r u u u ru u u r u u u r u u ur u u u r ，[0λ∈，)+∞，则P 的轨迹一定通过ABC ∆的（ ） A ．外心 B ．垂心C ．重心D ．内心【答案】B 【解析】 【分析】可先根据数量积为零得出BC uuu r 与()||cos ||cos ABAC AB B AC Cλ+u u u ru u u ru u ur u u u r 垂直，可得点P 在BC 的高线上，从而得到结论．【详解】Q ()||cos ||cos AB ACOP OA AB B AC Cλ=++u u u r u u u ru u u r u u u r u u ur u u u r ， ∴()||cos ||cos AB ACOP OA AB B AC C λ-=+u u u r u u u ru u u r u u u r u u ur u u u r ， 即()||cos ||cos AB ACAP AB B AC Cλ=+u u u r u u u ru u u r u u ur u u u r ， Q cos BA BC B BA BC ⋅=u u u r u u u r u uu r u u u r ，cos CA CB C CA CB⋅=u u u r u u u r u u u r u u u r ， ∴()0||cos ||cos AB ACBC BC BC AB B AC C⋅+=-+=u u u r u u u ru u u r u u u r u u u r u u ur u u u r ， ∴BC uuu r 与()||cos ||cos AB ACAB B AC Cλ+u u u r u u u ru u ur u u u r 垂直， 即AP BC ⊥uu u r uu u r，∴点P 在BC 的高线上，即P 的轨迹过ABC ∆的垂心.故选：B ． 【点睛】本题重点考查平面向量在几何图形中的应用，熟练掌握平面向量的加减运算法则及其几何意义是解题的关键，考查逻辑思维能力和转化能力，属于常考题.5．在ABC ∆中，若点D 满足3CD DB =u u u r u u u r ，点M 为线段AC 中点，则MD =u u u u r（ ）A ．3144AB AC -u u ur u u u r B ．1136AB AC -u u u r u u u rC ．2133AB AC -u u u r u u u rD ．3144AB AC +u u ur u u u r【答案】A 【解析】 【分析】根据MD MA AB BD =++u u u r u u u u u u r u r u u u r，化简得到答案. 【详解】 ()11312444MD MA AB BD AC AB AC AB AB AC =++=-++-=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u uu u u u r r u u u r .故选：A . 【点睛】本题考查了向量的运算，意在考查学生的计算能力.6．如图，圆O 是等边三角形ABC 的外接圆，点D 为劣弧AC 的中点，则OD =u u u r（ ）A ．2133BA AC +u uu r u u u rB ．2133BA AC -u uu r u u u rC ．1233BA AC +u uu r u u u rD ．4233BA AC +u uu r u u u r【答案】A 【解析】 【分析】连接BO ，易知B ，O ，D 三点共线，设OD 与AC 的交点为E ，列出相应式子得出结论. 【详解】解：连接BO ，易知B ，O ，D 三点共线，设OD 与AC 的交点为E ，则()()221121332333OD BO BE BA BC BA BA AC BA AC ===⨯+=++=+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u uu r u u u r . 故选：A.【点睛】本题考查向量的表示方法，结合几何特点，考查分析能力，属于中档题.7．已知5MN a b =+u u u u r r r ，28NP a b =-+u u u r r r ，3()PQ a b =-u u u r r r ，则（ ）A ．,,M N P 三点共线B ．,,M N Q 三点共线C ．,,N P Q 三点共线D ．,,M P Q 三点共线【答案】B 【解析】 【分析】利用平面向量共线定理进行判断即可. 【详解】因为28NP a b =-+u u u r r r ,3()PQ a b =-u u u r r r所以()2835NQ NP PQ a b a b a b =+=-++-=+u u u r u u u r u u u r r r r r r r ,因为5MN a b =+u u u u r rr ,所以MN NQ =u u u u r u u u r由平面向量共线定理可知,MN u u u u r 与NQ uuur 为共线向量,又因为MN u u u u r 与NQ uuur 有公共点N ,所以,,M N Q 三点共线.故选: B 【点睛】本题考查利用平面向量共线定理判断三点共线;熟练掌握共线定理的内容是求解本题的关键;属于中档题、常考题型.8．在ABC V 中，4AC AD =u u u r u u u r，P 为BD 上一点，若14AP AB AC λ=+u u u r u u u r u u u r ，则实数λ的值（ ）A ．34B ．320C ．316D ．38【答案】C 【解析】 【分析】根据题意，可得出144λ=+u u u r u u u r u u u rAP AB AD ，由于B ，P ，D 三点共线，根据向量共线定理，即可求出λ. 【详解】解：由题知：4AC AD =u u u r u u u r ，14AP AB AC λ=+u u ur u u u r u u u r ，所以144λ=+u u u r u u u r u u u r AP AB AD ，由于B ，P ，D 三点共线，所以1414λ+=， ∴316λ=． 故选：C.【点睛】本题考查平面向量的共线定理以及平面向量基本定理的应用.9．已知ABC V 是边长为1的等边三角形，若对任意实数k ，不等式||1k AB tBC +>u u u r u u u r恒成立，则实数t 的取值范围是（ ）. A ．33,⎛⎫-∞⋃+∞ ⎪ ⎪⎝⎭⎝⎭B ．2323,⎛⎫-∞⋃+∞ ⎪ ⎪⎝⎭⎝⎭C ．23⎫+∞⎪⎪⎝⎭D ．3⎫+∞⎪⎪⎝⎭【答案】B 【解析】 【分析】根据向量的数量积运算，将目标式转化为关于k 的二次不等式恒成立的问题，由0<n ，即可求得结果. 【详解】因为ABC V 是边长为1的等边三角形，所以1cos1202AB BC ⋅=︒=-u u u r u u u r ，由||1k AB tBC +>u u u r u u u r 两边平方得2222()2()1k AB kt AB BC t BC +⋅+>u u u r u u u r u u u r u u u r ，即2210k kt t -+->，构造函数22()1f k k tk t =-+-， 由题意，()22410t t ∆--<=， 解得23t <或23t >. 故选：B. 【点睛】本题考查向量数量积的运算，以及二次不等式恒成立问题求参数范围的问题，属综合中档题.10．在ABC V 中，D 为边AC 上的点，若2133BD BA BC =+u u u r u u u r u u u r ，AD DC λ=u u u v u u u v，则λ=（ ）A ．13B ．12C ．3D ．2【答案】B 【解析】 【分析】根据2133BD BA BC =+u u u v u u u v u u u v ，将,AD DC u u u r u u u r 都用基底()BABC u u u r u u u r ，表示，再根据AD DC λ=u u u v u u u v 求解. 【详解】因为2133BD BA BC =+u u u v u u u v u u u v ，所以1122,+3333AD BD BA BA BC DC BC BD BA BC =-=-+=-=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u uu r u u u r ，因为AD DC λ=u u u v u u u v ，所以λ= 12， 故选：B 【点睛】本题主要考查平面向量的基本定理和共线向量定理，还考查运算求解的能力，属于中档题.11．设x ，y 满足102024x x y x y -≥⎧⎪-≤⎨⎪+≤⎩，向量()2,1a x =r ，()1,b m y =-r ，则满足a b ⊥r r 的实数m的最小值为（ ） A ．125B ．125-C ．32D ．32-【答案】B 【解析】 【分析】先根据平面向量垂直的坐标表示，得2m y x =-，根据约束条件画出可行域，再利用m 的几何意义求最值，只需求出直线2m y x =-过可行域内的点C 时，从而得到m 的最小值即可． 【详解】解：不等式组表示的平面区域如图所示：因为()2,1a x =r ，()1,b m y =-r，由a b ⊥r r得20x m y +-=，∴当直线经过点C 时，m 有最小值，由242x y x y +=⎧⎨=⎩，得8545x y ⎧=⎪⎪⎨⎪=⎪⎩，∴84,55C ⎛⎫ ⎪⎝⎭，∴416122555m y x =-=-=-， 故选：B.【点睛】本题主要考查了平面向量共线（平行）的坐标表示，用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属于中档题．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、求出关键点、定出最优解．12．在ABC V 中，AD AB ⊥，3,BC BD =u u u r u u u r ||1AD =u u u r ，则AC AD ⋅u u u r u u u r的值为（ ）A ．1B ．2C ．3D ．4【答案】C 【解析】 【分析】由题意转化(3)AC AD AB BD AD ⋅=+⋅u u u r u u u r u u u r u u u r u u u r，利用数量积的分配律即得解.【详解】AD AB ⊥Q ，3,BC BD =u u u r u u u r ||1AD =u u u r，()(3)AC AD AB BC AD AB BD AD ∴⋅=+⋅=+⋅u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r2333AB AD BD AD AD =⋅+⋅==u u u r u u u r u u u r u u u r u u u r故选：C 【点睛】本题考查了平面向量基本定理和向量数量积综合，考查了学生综合分析，转化划归，数学运算能力，属于中档题.13．已知四边形ABCD 是平行四边形，点E 为边CD 的中点，则BE =u u u rA ．12AB AD -+u u ur u u u rB ．12AB AD -u u ur u u u rC ．12AB AD +u u u r u u u rD ．12AB AD -u u u r u u u r【答案】A 【解析】 【分析】由平面向量的加法法则运算即可. 【详解】如图，过E 作//,EF BC 由向量加法的平行四边形法则可知1.2BE BF BC AB AD =+=-+u u u v u u u v u u u v u u u v u u u v 故选A. 【点睛】本题考查平面向量的加法法则，属基础题.14．已知数列{a n }的前n 项和为S n ，且a n +1=a n +a (n ∈N *，a 为常数)，若平面内的三个不共线的非零向量OAOB OC u u u r u u u r u u u r，，满足10051006OC a OA a OB =+u u u r u u u r u u u r ，A ，B ，C 三点共线且该直线不过O 点，则S 2010等于（ ） A ．1005 B ．1006C ．2010D ．2012【答案】A 【解析】 【分析】根据a n +1=a n +a ，可判断数列{a n }为等差数列，而根据10051006OC a OA a OB =+u u u r u u u r u u u r，及三点A ，B ，C 共线即可得出a 1+a 2010=1，从而根据等差数列的前n 项和公式即可求出S 2010的值. 【详解】由a n +1=a n +a ，得，a n +1﹣a n =a ； ∴{a n }为等差数列；由10051006OC a OA a OB =+u u u r u u u r u u u r ，所以A ，B ，C 三点共线； ∴a 1005+a 1006=a 1+a 2010=1， ∴S 2010()12010201020101100522a a +⨯===. 故选：A. 【点睛】本题主要考查等差数列的定义，其前n 项和公式以及共线向量定理，还考查运算求解的能力，属于中档题.15．在边长为1的等边三角形ABC 中，点P 是边AB 上一点，且．2BP PA =，则CP CB ⋅=u u u v u u u v（ ） A ．13B ．12C ．23D ．1【答案】C 【解析】 【分析】利用向量的加减法及数乘运算用,CA CB u u u r u u u r 表示CP u u u v，再利用数量积的定义得解．【详解】依据已知作出图形如下：()11213333CP CA AP CA AB CA CB CA CA CB =+=+=+-=+u u u v u u v u u u v u u v u u u v u u v u u u v u u v u u v u u u v .所以221213333CP CB CA CB CB CA CB CB ⎛⎫+=+ ⎪⎝⎭⋅=⋅⋅u u u v u u u v u u v u u u v u u u v u u v u u u v u u u v221211cos 13333π=⨯⨯⨯+⨯= 故选C 【点睛】 本题主要考查了向量的加减法及数乘运算，还考查了数量积的定义，考查转化能力，属于中档题．16．已知向量()()75751515a b ︒︒︒︒==r r cos ,sin ,cos ,sin ，则a b -r r 的值为A ．12B ．1C ．2D ．3【答案】B 【解析】【分析】【详解】 因为11,1,cos75cos15sin 75sin15cos602a b a b ==⋅=︒︒+︒︒=︒=r r r r ，所以||1a b -===r r ，故选B. 点睛：在向量问题中，注意利用22||a a =r ，涉及向量模的计算基本考虑使用此公式，结合数量积的运算法则即可求出.17．已知()4,3a =r ，()5,12b =-r 则向量a r 在b r 方向上的投影为( )A ．165-B ．165C ．1613-D ．1613【答案】C【解析】【分析】 先计算出16a b r r ⋅=-，再求出b r ，代入向量a r 在b r 方向上的投影a b b⋅r r r 可得 【详解】 ()4,3a =r Q ，()5,12b =-r ，4531216a b ⋅=⨯-⨯=-r r ， 则向量a r 在b r 方向上的投影为1613a b b⋅-=r r r ， 故选：C.【点睛】本题考查平面向量的数量积投影的知识点. 若,a b r r 的夹角为θ，向量a r 在b r 方向上的投影为cos a θ⋅r 或a b b⋅r r r 18．已知平面向量,,a b c r r r 满足||||2a b ==r r ，a b ⊥r r ，()()a c b c -⊥-r r r r ，则(a b c ⋅r r r +)的取值范围是( )A ．[0,2]B ．[0,C ．[0,4]D ．[0,8] 【答案】D【解析】【分析】以点O 为原点，OA u u u r ，OB uuu r分别为x 轴，y 轴的正方向建立直角坐标系，根据AC BC ⊥，得到点C 在圆22(1)(1)2x y -+-=，再结合直线与圆的位置关系，即可求解．【详解】 设,,OA a OB b OC c ===u u u r r u u u r r u u u r r， 以点O 为原点，OA u u u r ，OB uuu r 分别为x 轴，y 轴的正方向建立直角坐标系，则(2,0),(0,2)A B ，依题意，得AC BC ⊥，所以点C 在以AB 为直径的圆上运动，设点(,)C x y ，则22(1)(1)2x y -+-=，()22a b c x y +⋅=+r r r ，由圆心到直线22x y t +=的距离d =≤，可得[0,8]t ∈.故选：D ．【点睛】本题主要考查了向量的数量积的坐标运算，以及直线与圆的位置关系的综合应用，着重考查了转化思想，以及推理与运算能力．19．已知,A B 是圆22:16O x y +=的两个动点，524,33AB OC OA OB ==-u u u v u u u v u u u v ，若M 分别是线段AB 的中点，则·OC OM =u u u v u u u u v （ ） A．8+B．8-C ．12 D ．4【答案】C【解析】【分析】【详解】 由题意1122OM OA OB =+u u u u r u u u r u u u r ，则2252115113322632OC OM OA OB OA OB OA OB OA OB ⎛⎫⎛⎫⋅=-⋅+=-+⋅ ⎪ ⎪⎝⎭⎝⎭u u u v u u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v ，又圆的半径为4，4AB =uu u r ，则,OA OB u u u r u u u r 两向量的夹角为π3．则8OA OB ⋅=u u u v u u u v ，2216OA OB ==u u u v u u u v ，所以12OC OM ⋅=u u u r u u u u r ．故本题答案选C ．点睛：本题主要考查平面向量的基本定理.用平面向量的基本定理解决问题的一般思路是:先选择一组基底,并且运用平面向量的基本定理将条件和结论表示成基底的线性组合,在基底未给出的情况下进行向量的运算,合理地选取基底会给解题带来方便.进行向量运算时,要尽可能转化到平行四边形或三角形中.20．已知向量a v ，b v满足a =v ||1b =v ，且2b a +=v v ，则向量a v 与b v 的夹角的余弦值为（ ）A ．2B ．3CD 【答案】D【解析】【分析】 根据平方运算可求得12a b ⋅=r r ，利用cos ,a b a b a b ⋅<>=r r r r r r 求得结果. 【详解】 由题意可知：2222324b a b a b a a b +=+⋅+=+⋅=r r r r r r r r ，解得：12a b ⋅=r rcos ,4a b a b a b ⋅∴<>===r r r r r r 本题正确选项：D【点睛】本题考查向量夹角的求解问题，关键是能够通过平方运算求得向量的数量积.。

专题 15 平面向量的概念、线性运算、平面向量根本定理年 份 题号考 点考 查 内 容2023卷 1 文6平面向量的概念与线性运算主要考查平面向量的线性运算卷 1 理 7平面向量根本定理及其应用 主要考查平面向量的线性运算及平面向量根本定理卷 2 理 13平面向量的概念与线性运算主要考查平面向量共线的充要条件2023卷1文 2平面向量的坐标运算及向量 共线的充要条件主要考查平面向量的坐标与点坐标的关系、平面向量坐 标运算2023卷 2 文 13 平面向量的坐标运算及向量 共线的充要条件主要考查平面向量坐标的线性运算及向量共线的充要 条件卷1理 6 文 7平面向量根本定理及其应用主要考查平面向量的线性运算及平面向量根本定理2023卷 3理 13 文 13 平面向量的坐标运算及向量 共线的充要条件主要考查平面向量的线性运算及向量共线的充要条件2023 卷 2文 3平面向量的坐标运算及向量 共线的充要条件主要考查平面向量坐标运算及模公式考点 47 平面向量的概念与线性运算1．(2023 新课标 I ，文 6)设 D , E , F 分别为∆ABC 的三边 BC , CA , AB 的中点，则 EB + FC =33A. BCB ．（答案）C 1 AD2C ． ADD ． 1 BC2（解析） EB + FC =1 (CB + AB ) + 1 (BC + AC ) = 1( AB + AC ) = AD ，应选 C ． 2 2 22．(2023 福建)在以下向量组中，可以把向量a =(3,2) 表示出来的是A ．e 1 =(0,0),e 2 = (1,2) C ．e 1 =(3,5),e 2 =(6,10) （答案）BB ．e 1 =(-1,2),e 2 =(5,-2) D ．e 1 =(2,-3),e 2 =(-2,3) （解析）对于 A ，C ，D ，都有e 1 ∥ e 2 ，所以只有 B 成立．考点 48 平面向量根本定理及其应用1．(2023 江苏 13)在∆ABC 中， AB = 4 ， AC = 3 ， ∠BAC = 90︒， D 在边 BC 上，延长 AD 到 P ，使得3AP = 9 ，假设 PA = mPB + (2- m )PC ( m 为常数)，则CD 的长度是 ．18 （答案）53 （解析）由向量系数m + ( - m ) = 为常数，结合等和线性质可知 2 2 PA PD= 2 ，1故 PD =2PA = 6 ， AD = PA - PD = 3 = AC ，故∠C = ∠CDA ，故∠CAD =π- 2C ．3AC 3 CD AD在∆ABC 中， cos C = = ；在∆ADC 中，由正弦定理得 = ，BC 5 sin ∠CAD sin Csin(π- 2C ) sin 2C 3 18即CD = ⋅ AD = ⋅ AD = 2 cos C ⋅ AD = 2 ⨯ ⨯ 3 = ．sin C sin C5 52．(2023•新课标Ⅰ，理 6 文 7)在∆ABC 中， AD 为 BC 边上的中线， E 为 AD 的中点，则 EB = ()A ． 3 - 1B ． 13C ． 31D ． 13AB AC4 4（答案）AAB - AC4 4AB + AC4 4AB + AC4 42EB AB AE AB AD =11AB AC （解析）在∆ABC 中， AD 为 BC 边上的中线， E 为 AD 的中点，∴ = - = - 12AB - ⨯ 2 2( AB + AC ) = 3 - 1，应选 A ． 4 43．(2023 新课标Ⅰ，理 7)设 D 为ABC 所在平面内一点 BC = 3CD ，则( )(A) AD = - 1 AB + 4AC (B) AD = 1 AB - 4AC3 3 3 3(C) AD =4 1AB + AC (D) AD =4 1AB - AC 3 33 3（答案）A1114 （解析）由题知 AD = AC + CD = AC + BC = AC + 3 3 ( AC - AB ) = = - AB + 3 3AC ，应选 A ． 4．(2023 广东)设a 是已知的平面向量且a ≠ 0 ，关于向量a 的分解，有如下四个命题：①给定向量b ，总存在向量 c ，使 a = b + c ； ②给定向量b 和c ，总存在实数λ和μ，使a = λb + μc ；③给定单位向量b 和正数μ，总存在单位向量c 和实数λ，使a = λb + μc ；④给定正数λ和μ，总存在单位向量b 和单位向量c ，使a = λb + μc ；上述命题中的向量b ， c 和a 在同一平面内且两两不共线，则真命题的个数是 A ．1B ．2C ．3D ．4（答案）B（解析）利用向量加法的三角形法则，易的①是对的；利用平面向量的根本定理，易的②是对的；以a 的终点作长度为μ的圆，这个圆必须和向量λb 有交点，这个不肯定能满足，③是错的；利用向量加法的三 角形法则，结合三角形两边的和大于第三边，即必须 λb + μc =λ+μ≥ a ，所以④是假命题．综上，此题选 B ．5．(2023 江苏)如图，在同一个平面内，向量OA ， OB ， OC 的模分别为 1，1， ， OA 与OC 的夹角为α ， 且 tan α= 7 ， OB 与 OC 的夹角为 45． 假设 OC = m OA + n OB ( m ， n ∈ R ) ， 则m + n =．（答案）3（解析）由tan α= 7 可得sin α=7 2， cos α=2，由OC = m OA + n OB 得1010⎧ 2 ⎧⎪OC ⋅OA = mOA + nOB ⋅OA ⎪ 2 cos α= m + n c os(α+ 45 ) ⎨ 2 ，即⎨ ，两式相加得，2 cos 45 = m cos(α+ 45 ) + n ⎩OC ⋅OB = mOB ⋅OA + nOB⎩ 2(cos α+ cos 45 ) = (m + n )(1+ cos(α+ 45 )) ，所以2 ⨯2+ 2 ⨯2m + n = 2 cos α+ 2 cos 45 = 10 2 = 3 ，所以 m + n = 3 ． 1+ cos(α+ 45)2 2 7 2 2 1+ ⨯ - ⨯ 10 2 10 2λ6．(2023 北京)向量 a ，b ，c 在正方形网格中的位置如下图，假设c = λa + μb (λ，μ∈R )，则 μ=．（答案）41 （解析） 如图建立坐标系，则 a = (-1,1) ，b = (6, 2) ，c = (-1, 3) ．由c = λa + μb ，可得λ= -2,μ= -，2λ∴ μ= 47．(2023 北京)在△ABC 中，点 M ， N 满足 AM = 2MC ， BN = NC ，假设 MN = x AB + y AC ，则 x =2AB c / /(2a a | a b | ； y = ．1（答案） 2 1 - 61 1 11 1 1 （解析）由 MN = MC + CN = AC + CB = AC + ( AB - AC ) = AB - AC = x AB + y AC ．所3 2 3 2 2 61 1 以 x = ， y = - ．2 6考点 49 平面向量的坐标运算及平面向量共线的充要条件1．(2023•新课标Ⅱ，文 3)已知向量 a = (2, 3) ， b = (3, 2) ，则| a - b |= ( )A ． （答案）AB.2 C ． 5 D ．50（解析） a = (2, 3) ，b = (3, 2) ，∴- b = (2 ，3) - (3 ，2) = (-1 ，1) ，∴ -= ，应选 A ．2．(2023 辽宁)已知点 A (1, 3) ， B (4, -1) ，则与向量 AB 同方向的单位向量为⎛ 34 ⎫⎛ 43 ⎫⎛ - 3 4 ⎫⎛ 4 3 ⎫A ． ，- ⎪B ． ，- ⎪C ． ， ⎪D ． - ， ⎪⎝ 55 ⎭ （答案）A⎝ 55 ⎭ ⎝ 5 5 ⎭⎝ 5 5 ⎭（解析） AB = (3, -4) ，所以| AB |= 5 ，这样同方向的单位向量是 1 = (3 , - 4) ． 5 5 53．(2011 广东)已知向量a =(1，2)， b =(1，0)， c =(3，4)．假设λ为实数， (a + λb )∥c ，则λ=A.14（答案）BB.12C ．1D ．2（解析）a + λb = (1+ λ, 2) ，由(a + λb ) ∥ c ，得6 - 4(1+ λ) = 0 ，解得λ= 124．( 2023•新课标Ⅲ，理 13)已知向量 a = (1, 2) ， b = (2, -2) ， c = (1,λ) ．假设+ b ) ，则λ= ．（答案） 12（解析） 向量 a = (1, 2) ， b = (2, -2) ，∴+ b = (4, 2) ， c = (1,λ) ，+ b ) ， 2a∴ 1 = λ，解得λ= 1．c / /(2a4 2 25．(2023 新课标，文 13) 已知向量 a =(m ，4)，b =(3，−2)，且 a ∥b ，则 m = ．（答案） -6225⎨⎩1（解析） 向量 a ， b 不平行，向量λa + b 与 a + 2b 平行， a + b = t (a + 2b ) = ta + 2tb ，（解析）因为 a ∥b ，所以-2m - 4 ⨯ 3 = 0 ，解得 m = -6 ．6．(2023•新课标Ⅱ，理 13)设向量 a ， b 不平行，向量λ + b 与+ 2b 平行，则实数λ= ．（答案） 12 a a∴λ∴ ⎧λ= t ⎩1 = 2t，解得实数λ= 1 ．27．(2023 江苏)已知向量a = (2,1) ， b = (1, -2) ，假设 m a + n b = (9, -8) ( m , n ∈R)，则 m - n的值为 ．（答案）－3（解析）由题意得： 2m + n = 9, m - 2n = -8 ⇒ m = 2, n = 5, m - n = -3.8．(2023 北京)已知向量a 、b 满足 a = 1 ， b = (2,1) ，且λa + b = 0 (λ∈ R )，则 λ = （答案） ⎧cos θ= - 2（解析）∵| a |= 1，∴可令 a = (cos θ, s in θ) ，∵ λa + b = 0 ，∴⎧λcos θ+ 2 = 0，即⎪λ，解⎨λsin θ+1 = 0⎨⎪sin θ= - 1 ⎩ λ得λ2 = 5 得| λ|=．9．(2023 陕西) 设0 <θ< π，向量a = (sin 2θ，cos θ) ， b (cos θ，1)，假设a ∥b ，则2tan θ= ．1（答案）2（解析）∵ a ∥b ，∴ sin 2θ= cos2θ，∴ 2 sin θcos θ= cos 2θ，∵θ∈π(0, ) 2，∴tan θ= ． 25。