3 三角函数的计算
- 格式:pptx
- 大小:1.76 MB
- 文档页数:10

三角函数关系公式大全一、同角三角函数的基本关系。
1. 平方关系。
- sin^2α+cos^2α = 1- 1+tan^2α=sec^2α(其中secα=(1)/(cosα))- 1 + cot^2α=csc^2α(其中cscα=(1)/(sinα))2. 商数关系。
- tanα=(sinα)/(cosα)- cotα=(cosα)/(sinα)二、诱导公式。
1. 关于α与-α的诱导公式。
- sin(-α)=-sinα- cos(-α)=cosα- tan(-α)=-tanα2. 关于α与π±α的诱导公式。
- sin(π+α)=-sinα- sin(π - α)=sinα- cos(π+α)=-cosα- cos(π-α)=-cosα- tan(π+α)=tanα- tan(π-α)=-tanα3. 关于α与(π)/(2)±α的诱导公式。
- sin((π)/(2)+α)=cosα- sin((π)/(2)-α)=cosα- cos((π)/(2)+α)=-sinα- cos((π)/(2)-α)=sinα- tan((π)/(2)+α)=-cotα- tan((π)/(2)-α)=cotα三、两角和与差的三角函数公式。
1. 两角和的正弦公式。
- sin(A + B)=sin Acos B+cos Asin B2. 两角差的正弦公式。
- sin(A - B)=sin Acos B-cos Asin B3. 两角和的余弦公式。
- cos(A + B)=cos Acos B-sin Asin B4. 两角差的余弦公式。
- cos(A - B)=cos Acos B+sin Asin B5. 两角和的正切公式。
- tan(A + B)=(tan A+tan B)/(1-tan Atan B)6. 两角差的正切公式。
- tan(A - B)=(tan A-tan B)/(1 + tan Atan B)四、二倍角的三角函数公式。


三角函数加减计算公式三角函数的加减计算公式,那可是数学世界里相当重要的一部分啊!咱们先来说说什么是三角函数。
简单来说,三角函数就是描述三角形中边与角之间关系的函数。
比如正弦函数(sin)、余弦函数(cos)和正切函数(tan)等等。
那三角函数的加减计算公式是啥呢?咱们以正弦函数和余弦函数为例哈。
正弦函数的和差公式是:sin(A + B) = sinAcosB + cosAsinB ,sin(A - B) = sinAcosB - cosAsinB 。
余弦函数的和差公式是:cos(A + B) = cosAcosB - sinAsinB ,cos(A - B) = cosAcosB + sinAsinB 。
这些公式看起来挺复杂,但其实只要理解了其中的道理,掌握起来也没那么难。
我给大家讲个事儿吧。
有一次我给学生们讲三角函数的加减公式,有个学生怎么都理解不了。
我就给他举了个例子,说咱们把三角函数想象成两个小伙伴一起合作完成一个任务。
比如说正弦函数 sinA 和余弦函数 cosB 一起完成任务,就像两个人一起搬东西,sinA 出的力是sinAcosB ,cosA 出的力是 cosAsinB ,加在一起就是 sin(A + B) 。
这孩子听完,眼睛一下子亮了,说:“老师,我好像懂了!” 那一刻,我心里那个高兴啊,觉得自己的努力没有白费。
那怎么记住这些公式呢?多做题肯定是少不了的。
通过大量的练习,让这些公式深深地印在脑子里。
还有一个小窍门,就是自己推导几遍公式,这样能更好地理解公式的来龙去脉。
在实际应用中,三角函数的加减公式用处可大了。
比如说在物理学中,计算波的叠加、交流电的合成等等,都离不开这些公式。
在工程学中,设计桥梁、建筑的时候,也需要用到三角函数的知识来计算各种力和角度。
再比如,在解决几何问题的时候,如果知道了一些角的大小,要求另外一些角的函数值,这时候三角函数的加减公式就能派上用场啦。
总之,三角函数的加减计算公式虽然有点复杂,但只要咱们用心去学,多思考,多练习,就一定能掌握好,为咱们解决更多的数学问题打下坚实的基础!希望同学们在学习三角函数加减公式的时候,不要被它们的外表吓到,勇敢地去探索,相信你们一定能够攻克这个难关,在数学的海洋里畅游!。

第一部分三角函数公式tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·积化和差公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·倍角公式:sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2tan(2α)=2tanα/(1-tan^2α)cot(2α)=(cot^2α-1)/(2cotα)sec(2α)=sec^2α/(1-tan^2α)csc(2α)=1/2*secα·cscα·三倍角公式:sin(3α) = 3sinα-4sin^3α= 4sinα·sin(60°+α)sin(60°-α) cos(3α) = 4cos^3α-3cosα= 4cosα·cos(60°+α)cos(60°-α)tan(3α) = (3tanα-tan^3α)/(1-3tan^2α) = tanαtan(π/3+α)tan(π/3-α)cot(3α)=(cot^3α-3cotα)/(3cot^2α-1)·n倍角公式:sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n, 5)cos^(n-5)α·sin^5α-…cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n -4)α·sin^4α-…·半角公式:sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cos α)/sinαcot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1 -cosα)sec(α/2)=±√((2secα/(secα+1))csc(α/2)=±√((2secα/(secα-1))·辅助角公式:Asinα+Bcosα=√(A^2+B^2)sin(α+φ)(tanφ=B/A)Asinα+Bcosα=√(A^2+B^2)cos(α-φ)(tanφ=A/B)·万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2))cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))·降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))·三角和的三角函数:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cos β·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·s inγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tan α·tanβ-tanβ·tanγ-tanγ·tanα)·其它公式1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a /2))^2csc(a)=1/sin(a) sec(a)=1/cos(a)cos30=sin60sin30=cos60·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=[sin(α/2)+cos(α/2)]^21+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/ 2))^2csc(a)=1/sin(a) sec(a)=1/cos(a)cos30=sin60sin30=cos60·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=[sin(α/2)+cos(α/2)]^2[转]洛必达公式+泰勒公式+柯西中值定理+罗尔定理来源:王艺璇的日志洛必达法则洛必达法则(L'Hospital法则),是在一定条件下通过分子分母分别求导再求极限来确定未定式值的方法。

三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB-1tanB tanA + tan(A-B) =tanAtanB1tanB tanA +- cot(A+B) =cotAcotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+ 倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a) 半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin 2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a -cosa+cosb = 2cos2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2b a - tana+tanb=ba b a cos cos )sin(+ 积化和差 sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)] 诱导公式sin(-a) = -sinacos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sinacos(π-a) = -cosasin(π+a) = -sinacos(π+a) = -cosa tgA=tanA =aa cos sin 万能公式 sina=2)2(tan 12tan 2a a + cosa=22)2(tan 1)2(tan 1a a +-tana=2)2(tan 12tan2a a- 其它公式 a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=a b ] a•sin(a)-b•cos(a) =)b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2 其他非重点三角函数 csc(a) =asin 1 sec(a) =acos 1 双曲函数 sinh(a)=2e -e -aa cosh(a)=2e e -aa + tg h(a)=)cosh()sinh(a a 公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)= sinαcos (2kπ+α)= cosαtan (2kπ+α)= tanαcot (2kπ+α)= cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin (π+α)= -sinαcos (π+α)= -cosαtan (π+α)= tanαcot (π+α)= cotα公式三:任意角α与 -α的三角函数值之间的关系:sin (-α)= -sinαcos (-α)= cosαtan (-α)= -tanαcot (-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin (π-α)= sinαcos (π-α)= -cosαtan (π-α)= -tanαcot (π-α)= -cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin (2π-α)= -sinαcos (2π-α)= cosαtan (2π-α)= -tanαcot (2π-α)= -cotα公式六:2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= cosα cos (2π-α)= sinα tan (2π-α)= cotα cot (2π-α)= tanα sin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanα sin (23π-α)= -cosαcos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)2009-07-08 16:13公式表达式乘法与因式分解 a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式 |a+b|≤|a|+|b| |a -b|≤|a|+|b| |a|≤b<=>-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a|一元二次方程的解 -b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系 X1+X2=-b/a X1*X2=c/a 注:韦达定理判别式 b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式 sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R 注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB 注:角B是边a和边c的夹角正切定理:[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h 斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h' 正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l 球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h 圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*r a是圆心角的弧度数r >0 扇形面积公式s=1/2*l*r 锥体体积公式V=1/3*S*H 圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L 注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h 圆柱体V=pi*r2h-----------------------三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差:相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了不知道这样你可以记住伐,实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负.3.三角形中的一些结论:(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1) tan(α+β)=(1+m)/(1-m)tanβ。




三角函数公式本词条由“科普中国”科学百科词条编写与应用工作项目审核。
三角函数是数学中属于初等函数中的超越函数的函数。
它们的本质是任何角的集合与一个比值的集合的变量之间的映射。
通常的三角函数是在平面直角坐标系中定义的。
其定义域为整个实数域。
另一种定义是在直角三角形中,但并不完全。
现代数学把它们描述成无穷数列的极限和微分方程的解,将其定义扩展到复数系。
三角函数公式看似很多、很复杂,但只要掌握了三角函数的本质及内部规律,就会发现三角函数各个公式之间有强大的联系。
而掌握三角函数的内部规律及本质也是学好三角函数的关键所在。
中文名三角函数公式外文名Formulas of trigonometric functions应用学科数学、物理、地理、天文地理等适用领域范围几何,代数变换,数学、物理、地理、天文等目录.1定义式.2函数关系.3诱导公式.4基本公式.▪和差角公式.▪和差化积公式.▪积化和差公式.▪倍角公式.▪半角公式.▪万能公式.▪辅助角公式.5其它公式.▪正弦定理.▪余弦定理.▪降幂公式.▪幂级数.▪泰勒展开式.▪万能公式.▪傅里叶级数定义式编辑锐角三角函数任意角三角函数图形直角三角形任意角三角函数正弦(sin)余弦(cos)正切(tan或tg)余切(cot或ctg)正割(sec)secA=c/b余割(csc)cscA=c/a表格参考资料来源:现代汉语词典[1].函数关系倒数关系:①;②;③商数关系:①;②.平方关系:①②;③诱导公式公式一:设为任意角,终边相同的角的同一三角函数的值相等:公式二:设为任意角,与的三角函数值之间的关系:公式三:任意角与的三角函数值之间的关系:公式四:与的三角函数值之间的关系:公式五:与的三角函数值之间的关系:公式六:及与的三角函数值之间的关系:记背诀窍:奇变偶不变,符号看象限[2].即形如(2k+1)90°±α,则函数名称变为余名函数,正弦变余弦,余弦变正弦,正切变余切,余切变正切。

三角函数的积分计算在数学中,三角函数是一类经典的函数,包括正弦函数、余弦函数、正切函数等。
三角函数的积分计算是数学分析的重要部分,它在许多实际问题的求解中起到了至关重要的作用。
本文将介绍三角函数的积分计算方法,包括基本积分公式、特殊积分公式以及常见的积分例题。
一、基本积分公式1. 正弦函数积分:∫ sin x dx = -cos x + C2. 余弦函数积分:∫ cos x dx = sin x + C3. 正切函数积分:∫ tan x dx = -ln|cos x| + C二、特殊积分公式1. 正弦函数的幂函数积分:∫ sin^2(x) dx = (1/2) x - (1/4) sin(2x) + C2. 余弦函数的幂函数积分:∫ cos^2(x) dx = (1/2) x + (1/4) sin(2x) + C3. 正切函数的幂函数积分:∫ tan^2(x) dx = x - tanx + C4. 正弦函数和余弦函数的积分:∫ sin(x) cos(x) dx = -1/2 cos^2(x) + C5. 正切函数的倒数积分:∫ 1/tan(x) = ln |sin(x)| + C三、常见积分例题1. 计算∫ sin^3(x) cos^4(x) dx:使用三角函数的和差化积公式,将积分化简为∫ sin^3(x) (1-sin^2(x)) cos^2(x) dx,并分别使用换元法和基本积分公式计算,得到最终结果为-(1/4)sin^4(x) + (1/5)sin^6(x) + C。
2. 计算∫ (sin^3(x) + cos^3(x))^2 dx:展开平方后得到二次多项式,再次利用三角函数的和差化积公式,将积分化简为∫ (1+sin^6(x)+2sin^3(x)+cos^6(x)+2cos^3(x)-2sin^3(x)cos^3(x)) dx。
分别使用基本积分公式计算各项,最终结果为 x + (1/7) sin^7(x) + (1/4) cos^4(x) - (1/9) sin^9(x) - (1/5) cos^5(x) + 2/5 C。
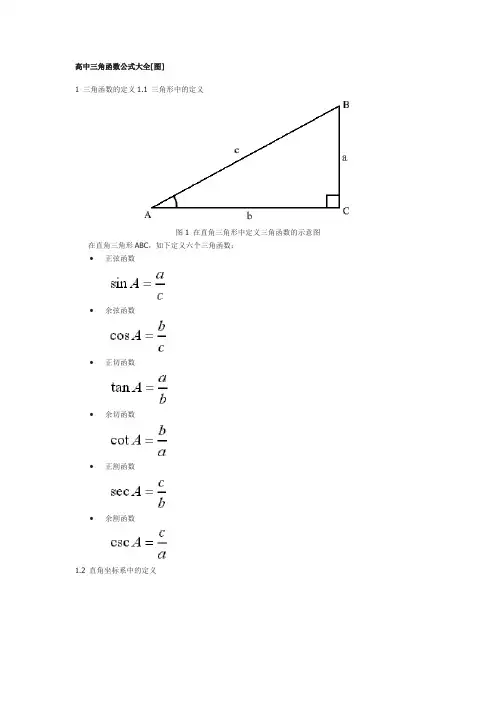
高中三角函数公式大全[图]1 三角函数的定义1.1 三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数:•正弦函数•余弦函数•正切函数•余切函数•正割函数•余割函数1.2 直角坐标系中的定义图2 在直角坐标系中定义三角函数示意图在直角坐标系中,如下定义六个三角函数:•正弦函数r•余弦函数•正切函数•余切函数•正割函数•余割函数2 转化关系2.1 倒数关系2.2 平方关系2 和角公式3 倍角公式、半角公式3.1 倍角公式3.2 半角公式3.3 万能公式4 积化和差、和差化积4.1 积化和差公式证明过程首先,sin(α+β)=sinαcosβ+sinβcosα(已证。
证明过程见《和角公式与差角公式的证明》)因为sin(α+β)=sinαcosβ+sinβcosα(正弦和角公式)则sin(α-β)=sin[α+(-β)]=sinαcos(-β)+sin(-β)cosα=sinαcosβ-sinβcosα于是sin(α-β)=sinαcosβ-sinβcosα(正弦差角公式)将正弦的和角、差角公式相加,得到sin(α+β)+sin(α-β)=2sinαcosβ则sinαcosβ=sin(α+β)/2+sin(α-β)/2(“积化和差公式”之一)同样地,运用诱导公式cosα=sin(π/2-α),有cos(α+β)=sin[π/2-(α+β)]=sin(π/2-α-β)=sin[(π/2-α)+(-β)]=sin(π/2-α)cos(-β)+sin(-β)cos(π/2-α)=cosαcosβ-sinαsinβ于是cos(α+β)=cosαcosβ-sinαsinβ(余弦和角公式)那么cos(α-β)=cos[α+(-β)]=cosαcos(-β)-sinαsin(-β)=cosαcosβ+sinαsinβcos(α-β)=cosαcosβ+sinαsinβ(余弦差角公式)将余弦的和角、差角公式相减,得到cos(α+β)-cos(α-β)=-2sinαsinβ则sinαsinβ=cos(α-β)/2-cos(α+β)/2(“积化和差公式”之二)将余弦的和角、差角公式相加,得到cos(α+β)+cos(α-β)=2cosαcosβ则cosαcosβ=cos(α+β)/2+cos(α-β)/2(“积化和差公式”之三)这就是积化和差公式:sinαcosβ=sin(α+β)/2+sin(α-β)/2sinαsinβ=cos(α-β)/2-cos(α+β)/2cosαcosβ=cos(α+β)/2+cos(α-β)/24.2 和差化积公式部分证明过程:sin(α-β)=sin[α+(-β)]=sinαcos(-β)+sin(-β)cosα=sinαcosβ-sinβcosαcos(α+β)=sin[90-(α+β)]=sin[(90-α)-β]=sin(90-α)cosβ-sinβcos(90-α)=cosαcosβ-sinαs inβcos(α-β)=cos[α+(-β)]=cosαcos(-β)-sinαsin(-β)=cosαcosβ+sinαsinβtan(α+β)=sin(α+β)/cos(α+β)=(sinαcosβ+sinβcosα)/(cosαcosβ-sinαsinβ)=(cosαtanαcosβ+cosβtanβcosα)/(cosαcosβ-cosαtanαcosβtanβ)=(tanα+tanβ)/(1-tanαtanβ)tan(α-β)=tan[α+(-β)]=[tanα+tan(-β)]/[1-tanαtan(-β)]=(tanα-tanβ)/(1+tanαtanβ)诱导公式•sin(-a)=-sin(a)•cos(-a)=cos(a)•sin(pi/2-a)=cos(a)•cos(pi/2-a)=sin(a)•sin(pi/2+a)=cos(a)•cos(pi/2+a)=-sin(a)•sin(pi-a)=sin(a)•cos(pi-a)=-cos(a)•sin(pi+a)=-sin(a)•cos(pi+a)=-cos(a)•tgA=tanA=sinA/cosA两角和与差的三角函数•sin(a+b)=sin(a)cos(b)+cos(α)sin(b)•cos(a+b)=cos(a)cos(b)-sin(a)sin(b)•sin(a-b)=sin(a)cos(b)-cos(a)sin(b)•cos(a-b)=cos(a)cos(b)+sin(a)sin(b)•tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))•tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))三角函数和差化积公式•sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)•sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)•cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)•cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)积化和差公式•sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]•cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]•sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]二倍角公式•sin(2a)=2sin(a)cos(a)•cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)半角公式•sin^2(a/2)=(1-cos(a))/2•cos^2(a/2)=(1+cos(a))/2•tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))万能公式•sin(a)= (2tan(a/2))/(1+tan^2(a/2))•cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))•tan(a)= (2tan(a/2))/(1-tan^2(a/2))其它公式•a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中,tan(c)=b/a]•a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中,tan(c)=a/b]•1+sin(a)=(sin(a/2)+cos(a/2))^2•1-sin(a)=(sin(a/2)-cos(a/2))^2其他非重点三角函数•csc(a)=1/sin(a)•sec(a)=1/cos(a)双曲函数•sinh(a)=(e^a-e^(-a))/2•cosh(a)=(e^a+e^(-a))/2•tgh(a)=sinh(a)/cosh(a)常用公式表(一)1。
三角函数三次方公式
三角函数三次方公式是指将正弦、余弦、正切三角函数的三次方表达式展开后得到的公式。
这些公式在数学和物理学中有着广泛的应用。
1. 正弦三次方公式
sin^3x = (3sinx - sin3x)/4
其中sin3x = 3sinx - 4sin^3x
2. 余弦三次方公式
cos^3x = (cos3x + 3cosx)/4
其中cos3x = 4cos^3x - 3cosx
3. 正切三次方公式
tan^3x = (3tanx - tan3x)/4
其中tan3x = (3tanx - tan^3x)/(1-3tan^2x)
这些公式可以用来简化三角函数的计算,特别是在求解三角函数的积分和导数时非常有用。
同时,它们也是许多数学和物理学问题的解决关键,例如在计算机图形学中,三角函数三次方公式可以用来计算光线的反射和折射角度等问题。
三角函数表格公式大全
sin度数公式:1、sin 30= 1/2,2、sin 45=根号2/2,3、sin 60= 根号3/2。
cos度数公式:1cos 30=根号3/2,2、cos 45=根号2/2,3、cos 60=1/2。
tan度数公式:1、tan 30=根号3/3,2、tan 45=1,3、tan 60=根号3。
1、三角函数是基本初等函数之一,是以角度(数学上最常用弧度制,下同)为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。
也可以等价地用与单位圆有关的各种线段的长度来定义。
2、三角函数在研究三角形和圆等几何形状的性质时有重要作用,也是研究周期性现象的基础数学工具。
在数学分析中,三角函数也被定义为无穷级数或特定微分方程的解,允许它们的取值扩展到任意实数值,甚至是复数值。
3、常见的三角函数包括正弦函数、余弦函数和正切函数。
在航海学、测绘学、工程学等其他学科中,还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。
4、早期对于三角函数的研究可以追溯到古代。
古希腊三角术的奠基人是公元前2世纪的喜帕恰斯。
他按照古巴比伦人的做法,将圆周分为360等份(即圆周的弧度为360度,与现代的弧度制不同)。
对于给定的弧度,他给出了对应的弦的长度数值,这个记法和现代的正弦函数是等价的。
5、喜帕恰斯实际上给出了最早的三角函数数值表。
然而古希腊的三角学基本是球面三角学。
这与古希腊人研究的主体是天文学有关。
梅涅劳斯在他的著作《球面学》中使用了正弦来描述球面的梅涅劳斯定理。
sin3a和cos3a公式
初学三角函数的同学们肯定对于sin3a和cos3a公式感到相当困惑,这两个公式在三角函数中起着重要的作用,因此必须仔细学习和掌握。
下面我们将分别介绍sin3a和cos3a公式。
一、sin3a公式
sin3a是三角函数中的一种,它用于计算三角形中的角度和边长之间的
关系。
对于sin3a公式,公式中包含三角函数sin和三倍角公式,如下
所示:
sin3a=3sin a-4 sin^3 a
其中,sin a表示角度a的正弦值,sin^3 a表示角度a的正弦值的三次方。
sin3a公式的计算结果可以用于计算三角形中的各种角度和边长之
间的关系。
比如,在计算三角形的面积时,可以使用sin3a公式。
二、cos3a公式
cos3a也是三角函数中的一种,它用于计算三角形中的角度和边长之间
的关系。
与sin3a公式类似,cos3a公式也包含三角函数cos和三倍角公式,如下所示:
cos3a=4 cos^3 a-3 cos a
其中,cos a表示角度a的余弦值,cos^3 a表示角度a的余弦值的三次方。
cos3a公式的计算结果可以用于计算三角形中的各种角度和边长之间的关系。
比如,在计算三角形的余弦值时,可以使用cos3a公式。
综上所述,sin3a和cos3a公式在三角函数中起着非常重要的作用,它们可以用于计算三角形中的各种角度和边长之间的关系。
对于初学者来说,记住这两个公式是非常重要的,因为它们将在学习和计算三角函数中经常使用。
三角函数公式大全(很详细)在三角函数的定义方面,可以通过在直角三角形和直角坐标系中定义六个三角函数来理解。
其中包括正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。
转化关系方面,倒数关系和平方关系都是常见的转化方式。
此外,还有和角公式、倍角公式、半角公式和万能公式等。
在积化和差、和差化积方面,可以利用正弦和余弦的和角、差角公式来得到“积化和差公式”。
同样地,余弦的和角、差角公式也可以用来得到相应的公式。
需要注意的是,在文章中有明显的格式错误和段落缺失,需要进行删除和修改。
Cosine of the sum and difference of two angles can be expressed as follows using the product-to-sum identities:cos(α + β) = cosα cosβ - sinα sinβcos(α - β) = cosα cosβ + sinα sinβSimilarly。
sine of the sum and difference of two angles can be expressed as follows:sin(α + β) = sinα cosβ + cosα sinβsin(α - β) = sinα cosβ - cosα sinβThese are known as the sum-to-product identities.Another set of identities that relate the sum and difference of two angles to their sines and cosines are the difference-to-product identities:sinα - sinβ = 2 cos((α + β)/2) sin((α - β)/2)sinα + sinβ = 2 sin((α + β)/2) cos((α - β)/2)cosα - cosβ = -2 sin((α + β)/2) sin((α - β)/2)cosα + cosβ = 2 cos((α + β)/2) cos((α - β)/2)These can be derived using the sum-to-product identities and some algebraic n.There are also several trigonometric identities that involve negative angles or angles that differ by π/2.For example:sin(-a) = -sin(a)cos(-a) = cos(a)sin(π/2 - a) = cos(a)cos(π/2 - a) = sin(a)sin(π/2 + a) = cos(a)cos(π/2 + a) = -sin(a)sin(π - a) = sin(a)cos(π - a) = -cos(a)sin(π + a) = -sin(a)cos(π + a) = -cos(a)Finally。