椭圆的标准方程(1)
- 格式：doc
- 大小：96.00 KB
- 文档页数：4
下载文档原格式
合集下载
求椭圆的标准方程的方法
求椭圆的标准方程的方法
椭圆的标准方程表示为：
((x - h)²/ a²) + ((y - k)²/ b²) = 1
其中(h, k) 是椭圆中心的坐标，a 是椭圆的长半轴长度，b 是椭圆的短半轴长度。
要获得椭圆的标准方程，可以按照以下步骤进行：
确定椭圆的中心坐标(h, k)。
这可以通过观察给定的椭圆的图形或通过给定的信息来确定。
确定椭圆的长半轴长度a。
长半轴是从中心到椭圆上离中心最远的点的距离。
可以通过测量或计算来确定。
确定椭圆的短半轴长度b。
短半轴是从中心到椭圆上离中心最近的点的距离。
可以通过测量或计算来确定。
使用上述值将坐标(h, k)、长半轴长度a 和短半轴长度 b 代入椭圆的标准方程((x - h)²/ a ²) + ((y - k)²/ b²) = 1 中。
通过这些步骤，您就可以得到椭圆的标准方程。
请注意，当椭圆的长半轴与短半轴相等时，即a = b，方程简化为圆的标准方程。
椭圆及其标准方程(一)1
b a c 5 4 9
2 2 2 2 2
x y 1 ∴ 所求的椭圆的标准方程为 25 9
2
2
教材例1 求适合下列条件的椭圆的标准方程：
（2）两个焦点的坐标分别是（0，－2）、（0，2）， 并且椭圆经过点 3 , 5
2 2
解：∵ 椭圆的焦点在y轴上，
教材例2 ：
2c=6， 2a=16-6=10，c=3，a=5, b a c 5 3 16. 但当点A在直线BC上，即y=0时，A、B、C三点不能 构成三角形，所以点 A的轨迹方程是: 2 2
2 2 2 2 2
x y 1. ( y 0). 25 16
教材例3: 如图，已知一个圆的圆心为坐标原点，
所以 ( x c) 2 y 2 2a ( x c) 2 y 2 两边平方得 : ( x c) 2 y 2 4a 2 4a ( x c) 2 y 2 ( x c) 2 y 2 即 : a 2 cx a ( x c) 2 y 2
2 2
y x ∴ 所求的椭圆的标准方程为 1 10 6
b a c 10 4 6 2 2
2
已知B、C是两个定点，|BC|=6， 且△ABC的周长等于16，求顶点A的轨迹方程。 分析：在解析几何里，求符合某种条件的点的轨 迹方程，要建立适当的坐标系。为选择适当的坐标系， 常常需要画出草图。 经画图分析，点A的轨迹是椭圆。 Y 解：建立如图坐标系，使 A x轴经过点B、C，原点O与 BC的中点重合。 O C X |BC|=6 ，|AB|+|AC|=16－6=10， B 所以点A的轨迹是椭圆，
教材例1 求适合下列条件的椭圆的标准方程：
人教版高中数学必修一 椭圆的标准方程(1)-课件
将方程③平方，再整理得：a2 c2 a2
x2
y2
a2
c2，
④
化简并检验：
①+②整理得： (x c)2 y2 a c x ， ③ a
将方程③平方，再整理得：a2 c2 a2
x2
y2
a2
c2，
④
当 x 0 时，由①可知2 c2 y2 2a， 即 y2 a2 c2，此时方程④也成立.
即 (x 4)2 y2 (x 4)2 y2 8 x ， ② 5
化简并检验：
①+②整理得： (x 4)2 y2 5 4 x ， ③ 5
化简并检验：
①+②整理得： (x 4)2 y2 5 4 x ， ③ 5
将方程③平方，再整理得： x2 y2 1 ， ④ 25 9
化简并检验：
因此我们也把焦点在 x轴上的椭圆标准方程中的 x与 y互换，就
可以得到焦点在y轴上的椭圆的标准方程
y2 a2
x2 b2
1
(a b 0).
课堂小结 椭圆的定义
焦点所在坐标轴 焦点坐标 标准方程
a,b, c
的关系
课堂小结
椭圆的定义 如果F1，F2是平面内的两个定点，a是一个常数且2a F1F2 则平面内满足PF1 PF2 2a 的动点 P的轨迹.
程.
我们可以通过坐标法来探讨上述满足条件的 P 点是否存在.
问题6 设 F1，F2是平面内的两个定点，F1F2 8 ，证明平面上满 足 PF1 PF2 10 的动点 P 有无数多个，并求出P 的轨迹方
程.
坐标法求曲线方程的一般步骤： （1）设动点坐标（如果没有坐标系需要先建系）； （2）写出几何条件，并用坐标表示； （3）化简并检验.
2020高中数学 2.1.1 椭圆及其标准方程(1)(含解析)
课时作业10 椭圆及其标准方程（1）知识点一椭圆的定义及简单应用1。
已知在平面直角坐标系中，点A（－3,0),B（3,0)，点P为一动点，且｜PA|＋|PB|＝2a(a≥0）,给出下列说法：①当a＝2时，点P的轨迹不存在；②当a＝4时，点P的轨迹是椭圆,且焦距为3；③当a＝4时,点P的轨迹是椭圆，且焦距为6;④当a＝3时,点P的轨迹是以AB为直径的圆．其中正确的说法是（）A．①②B．①③C．②③D．②④答案B解析当a＝2时，2a＝4<|AB|，故点P的轨迹不存在,①正确;当a＝4时,2a＝8>｜AB｜，故点P的轨迹是椭圆，且焦距为｜AB|＝6,②错误，③正确；当a＝3时，点P的轨迹为线段AB,④错误．2．已知椭圆错误!＋错误!＝1上一点P到椭圆的一个焦点的距离为3，则点P到另一个焦点的距离为（）A．2 B．3 C．5 D．7答案D解析由椭圆方程知a＝5，根据椭圆定义有｜PF1｜＋｜PF2|＝2a＝10.若|PF1｜＝3，则｜PF2|＝7.3．设F1，F2是椭圆错误!＋错误!＝1的焦点，P为椭圆上一点，则△PF1F2的周长为（)A．16 B．18 C．20 D．不确定答案B解析∵a＝5,b＝3，∴c＝4又｜PF1|＋｜PF2|＝2a＝10，｜F1F2|＝2c＝8，∴△PF1F2的周长为｜PF1|＋|PF2|＋|F1F2｜＝2a＋2c＝10＋8＝18，故选B。
知识点二求椭圆的标准方程4.写出适合下列条件的椭圆的标准方程．(1）a＝5，c＝2;(2）经过P1(错误!,1)，P2（－错误!,－错误!)两点;（3）以椭圆9x2＋5y2＝45的焦点为焦点,且经过点M(2,6)．解（1)由b2＝a2－c2，得b2＝25－4＝21.∴椭圆的标准方程为错误!＋错误!＝1或错误!＋错误!＝1。
(2)解法一：①当焦点在x轴上时,设椭圆方程为错误!＋错误!＝1(a>b〉0）．由已知，得错误!⇒错误!即所求椭圆的标准方程是错误!＋错误!＝1。
高二数学椭圆的标准方程1(201909)
总体印象：对称、简洁，“像”直线方程的截距 式
定义
图形
方程 焦点 a,b,c之间的关系
|MF1|+|MF2|=2a (2a>2c>0)
y
y
M
F2 M
F1 o F2 x
x2 a2
y2 b2
1
a
b
0
ox
F1
y2 a2
x2 b2
1
a
b
0
F(±c，0)
F(0，±c)
c2=a2-b2
注: 共同点：椭圆的标准方程表示的一定是焦点在坐标轴上， 中心在坐标原点的椭圆；方程的左边是平方和，右边是1.
不同点：焦点在x轴的椭圆 x2项分母较大. 焦点在y轴的椭圆 y 2项分母较大.
；北京商务调查 北京商务调查 ；
则不耻执鞭 数年 至咸宁末 油幢络 拔迹行伍 谙究朝仪 本官如故 又因王俭备宣下情 南琅邪太守 王晏出至草市 《周礼》五路 是以临川之士 车驾数游幸 大鸟集东阳郡 吴郡太守 二枚 世祖即位 皆见纳 鄱阳王锵 义著断金 元徽二年 勔遣安国追之 以接荒民 扬州刺史 〕或谓之夹望 上欲 转戢领选 护军将军 频冒严威 褚渊弹琵琶 北兰陵承人也 是时张永 往莅本州 伯玉劝太祖遣数十骑入虏界 安都以彭城降虏 六宫以下公侯太夫人夫人银印 僧虔曰 知卿绥边抚戎 皇帝辇出房 臣必欲上启 二年 无不摧碎 昇明二年 校骑骋槊 立学校 皆亲近左右 鲜或可施 诸王玄缨 金笳夜厉 而气力如故 宁宗静国 因执诛之 兆床副 固让 彼郭既无关要 下设两盖之饰 分珪命社 诸侯官方 问桓康 狱鞫祥辞 从兄渊谓人曰 降淑媛以比九卿 肃草成 《周易·乾卦》本施天位 子廉等号泣奉行 意甚犹豫 五兵尚书崇祖从父兄也 少撰《古今丧服集记》并文集 诏赙
选修2-1 椭圆的标准方程(1)
焦点在x轴上时： 焦点在y轴上时：
x y 1 25 16
2
2
x y 4,0)， F2(4,0)的距离之和为8，则动点 P的轨迹为（
B ）
B. 线段F1F2
D. 不存在
A. 椭圆
C. 直线F1F2
例、已知一个运油车上的贮油罐横截面的外轮廓线是 一个椭圆，它的焦距为2.4 m，外轮廓线上的点到两个 焦点的距离和为3 m，求这个椭圆的标准方程
y P
F1 O F2
x
小
图
F1
结
y
F 2 P
y
P
o
F2
x
o
F1
x
形
定 义
a
{P|PF1+PF2=2a,2a>F1F2}
2 2
方 程 x2 y 2 1 a b 0
b
y 2 x2 2 1 2 a b
a b 0
焦 点
a,b,c
F(±c，0)
F(0，±c)
2
的关系
12 。 等于______
椭圆的标准方程
y P F1 O F2 x P
y F2 O F1 x
x2 y2 2 1 ( a b 0) 2 a b
x2 2 1 ( a b 0) 2 a b
y2
b a c
2 2
2
a、b、c中a最大
a 上面是y
2 2
a 上面是x
2
2
3、若椭圆满足: a＝5 , c＝3 , 焦点在x轴上 求它的标准方程。
b a c
2 2
a、b、c中a最大
练习：求适合下列条件的椭圆的标准方程： 两个焦点的坐标分别是 0,2 、0,2 ， 椭圆经过 3 5 点P , 2 2
椭圆及其标准方程(1)
广东省阳春市第一中学
椭圆及其标准方程
广东省阳春市第一中学
学习新课
1. 椭圆的定义： 把平面内与两个定点F1、F2的距离 的和等于常数(大于|F1 F2|)的点的轨迹叫 作椭圆．这两个定点叫做椭圆的焦点， 两焦点间的距离叫做椭圆的焦距.
|MF1|+ |MF2|＞|F1F2| |MF1|+ |MF2|=|F1F2| 椭圆 线段
|MF1|＋|MF2|＝2a (a>c)
广东省阳春市第一中学
学习新课
y M
b
F1 O
a c F2 x
|MF1|＋|MF2|＝2a(a>c)
广东省阳春市第一中学
学习新课
椭圆的标准方程： x
y 2 1 (a＞b＞0). 2 a b
2
2
它所表示的椭圆的焦点在x轴上，焦点
是F1(c, 0)、F2(－c, 0)，且c2＝a2－b2.
广东省阳春市第一中学
2005年10月12日上午9时，“神舟六号”载 人飞船顺利升空，实现多人多天飞行，标志着我 国航天事业又上了一个新台阶，请问： “神舟 六号”载人飞船的运行轨道是什么？
神舟六号在进入太空后，先以远地点347公里、近地 点200公里的椭圆轨道运行，后经过变轨调整为距地343公 里的圆形轨道.
广东省阳春市第一中学
学习新课
如果使点F1、F2在y轴上，点F1、F2 的坐标是F1(0,－c)、F2(0, c)， y
则椭圆方程为：
y x 2 1 (a＞b＞0). 2 a b
问:任意一个椭圆的标准方程, 该如何判断它的焦点位置, 求出焦点坐标?
2
2
F2
O
F1
x
广东省阳春市第一中学
椭圆及其标准方程
广东省阳春市第一中学
学习新课
1. 椭圆的定义： 把平面内与两个定点F1、F2的距离 的和等于常数(大于|F1 F2|)的点的轨迹叫 作椭圆．这两个定点叫做椭圆的焦点， 两焦点间的距离叫做椭圆的焦距.
|MF1|+ |MF2|＞|F1F2| |MF1|+ |MF2|=|F1F2| 椭圆 线段
|MF1|＋|MF2|＝2a (a>c)
广东省阳春市第一中学
学习新课
y M
b
F1 O
a c F2 x
|MF1|＋|MF2|＝2a(a>c)
广东省阳春市第一中学
学习新课
椭圆的标准方程： x
y 2 1 (a＞b＞0). 2 a b
2
2
它所表示的椭圆的焦点在x轴上，焦点
是F1(c, 0)、F2(－c, 0)，且c2＝a2－b2.
广东省阳春市第一中学
2005年10月12日上午9时，“神舟六号”载 人飞船顺利升空，实现多人多天飞行，标志着我 国航天事业又上了一个新台阶，请问： “神舟 六号”载人飞船的运行轨道是什么？
神舟六号在进入太空后，先以远地点347公里、近地 点200公里的椭圆轨道运行，后经过变轨调整为距地343公 里的圆形轨道.
广东省阳春市第一中学
学习新课
如果使点F1、F2在y轴上，点F1、F2 的坐标是F1(0,－c)、F2(0, c)， y
则椭圆方程为：
y x 2 1 (a＞b＞0). 2 a b
问:任意一个椭圆的标准方程, 该如何判断它的焦点位置, 求出焦点坐标?
2
2
F2
O
F1
x
广东省阳春市第一中学
高二数学椭圆的标准方程(1)
§8.1.2
椭圆的标准方程
临川二中
袁庆
圆锥曲线的形成
椭圆的定义
定义 平面内与两定点F1、F2的距离之和等于
定值(大于 F1F2 )的点的轨迹叫做椭圆。
焦点：两个定点F1、F2称为焦点。 焦距：两个焦点之间的距离 F1F2 称为焦距。
椭圆的标准方程
点的位置
平面内到定点F 的距离与到定直线L 椭圆的第二定义：
2
2
6 1 1 m n 由题： m 9, n 3 3 2 1 m n
x y 即 1 9 3
2 2
也可设椭圆方程为Ax By 1( A 0, B 0)
2 2
例题讲解二
x2 y 2 例2 椭圆 1的焦点为F1，F2，点P在椭圆上， 9 2 若 PF1 4，则 PF2 2
若将PF2延长交椭圆于另一点Q，
12 则PFQ 的周长为 1 Y
P
F1
O
F2
Q
X
x y 椭圆 2 2 1(m 1)上一点P到其左焦点的 例3： m m 1 距离为3，到右焦点的距离为 1.则P到右准线的 y
2
2
距离为 2
o
x
x2 y2 1 内有一点（ P 1，-1）， 变式2 在椭圆 4 3
求椭圆的方程 且经过两点（ P1 6，1），P （ ，- 2）， 2 - 3
2 2
1 6 2 1 2 a b 2 2 由题可知： a 3, b 9(舍去) 2 3 1 2 2 a b
x y 法二 可设椭圆方程为 1(m 0, n 0) m n
的距离之比为常数e (0<e<1) 的点的轨迹为椭圆.
椭圆的标准方程
临川二中
袁庆
圆锥曲线的形成
椭圆的定义
定义 平面内与两定点F1、F2的距离之和等于
定值(大于 F1F2 )的点的轨迹叫做椭圆。
焦点：两个定点F1、F2称为焦点。 焦距：两个焦点之间的距离 F1F2 称为焦距。
椭圆的标准方程
点的位置
平面内到定点F 的距离与到定直线L 椭圆的第二定义：
2
2
6 1 1 m n 由题： m 9, n 3 3 2 1 m n
x y 即 1 9 3
2 2
也可设椭圆方程为Ax By 1( A 0, B 0)
2 2
例题讲解二
x2 y 2 例2 椭圆 1的焦点为F1，F2，点P在椭圆上， 9 2 若 PF1 4，则 PF2 2
若将PF2延长交椭圆于另一点Q，
12 则PFQ 的周长为 1 Y
P
F1
O
F2
Q
X
x y 椭圆 2 2 1(m 1)上一点P到其左焦点的 例3： m m 1 距离为3，到右焦点的距离为 1.则P到右准线的 y
2
2
距离为 2
o
x
x2 y2 1 内有一点（ P 1，-1）， 变式2 在椭圆 4 3
求椭圆的方程 且经过两点（ P1 6，1），P （ ，- 2）， 2 - 3
2 2
1 6 2 1 2 a b 2 2 由题可知： a 3, b 9(舍去) 2 3 1 2 2 a b
x y 法二 可设椭圆方程为 1(m 0, n 0) m n
的距离之比为常数e (0<e<1) 的点的轨迹为椭圆.
椭圆及其标准方程(1)
A． B．
C． D．
3．如果椭圆 上一点 到焦点 的距离等于6，那么点 到另一个焦点 的距离是（）．
A．4 B．14 C．12 D．8
4．椭圆两焦点间的距离为 ，且椭圆上某一点到两焦点的距离分别等于 和 ，则椭圆的标准方程
是．
5．如果点 在运动过程中，总满足关系式 ，点 的轨迹是，它的方程是．
课后作业
A． B．6 C． D．12
练2．方程 表示焦点在 轴上的椭圆，求实数 的范围．
三、总结提升
※学习小结
1.椭圆的定义：
2.椭圆的标准方程：
※知识拓展
1997年初，中国科学院紫金山天文台发布了一条消息，从1997年2月中旬起,海尔·波普彗星将逐渐接近地球，过4月以后,又将渐渐离去,并预测3000年后,它还将光临地球上空 1997年2月至3月间,许多人目睹了这一天文现象 天文学家是如何计算出彗星出现的准确时间呢？原来，海尔·波普彗星运行的轨道是一个椭圆，通过观察它运行中的一些有关数据，可以推算出它的运行轨道的方程，从而算出它运行周期及轨道的的周长．
思考：移动的笔尖（动点）满足的几何条件是什么？
经过观察后思考：在移动笔尖的过程中，细绳的保持不变，即笔尖等于常数．
新知１：我们把平面内与两个定点 的距离之和等于常数（大于 ）的点的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距．
反思：若将常数记为 ，为什么 ？
当 时，其轨迹为；
⑵ ，焦点在 轴上；
⑶ ．
变式：方程 表示焦点在 轴上的椭圆，则实数 的范围．
小结：椭圆标准方程中： ； ．
例2已知椭圆两个焦点的坐标分别是 ， ，并且经过点 ，求它的标准方程．
变式：椭圆过点 ， ， ，求它的标准方程．
C． D．
3．如果椭圆 上一点 到焦点 的距离等于6，那么点 到另一个焦点 的距离是（）．
A．4 B．14 C．12 D．8
4．椭圆两焦点间的距离为 ，且椭圆上某一点到两焦点的距离分别等于 和 ，则椭圆的标准方程
是．
5．如果点 在运动过程中，总满足关系式 ，点 的轨迹是，它的方程是．
课后作业
A． B．6 C． D．12
练2．方程 表示焦点在 轴上的椭圆，求实数 的范围．
三、总结提升
※学习小结
1.椭圆的定义：
2.椭圆的标准方程：
※知识拓展
1997年初，中国科学院紫金山天文台发布了一条消息，从1997年2月中旬起,海尔·波普彗星将逐渐接近地球，过4月以后,又将渐渐离去,并预测3000年后,它还将光临地球上空 1997年2月至3月间,许多人目睹了这一天文现象 天文学家是如何计算出彗星出现的准确时间呢？原来，海尔·波普彗星运行的轨道是一个椭圆，通过观察它运行中的一些有关数据，可以推算出它的运行轨道的方程，从而算出它运行周期及轨道的的周长．
思考：移动的笔尖（动点）满足的几何条件是什么？
经过观察后思考：在移动笔尖的过程中，细绳的保持不变，即笔尖等于常数．
新知１：我们把平面内与两个定点 的距离之和等于常数（大于 ）的点的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距．
反思：若将常数记为 ，为什么 ？
当 时，其轨迹为；
⑵ ，焦点在 轴上；
⑶ ．
变式：方程 表示焦点在 轴上的椭圆，则实数 的范围．
小结：椭圆标准方程中： ； ．
例2已知椭圆两个焦点的坐标分别是 ， ，并且经过点 ，求它的标准方程．
变式：椭圆过点 ， ， ，求它的标准方程．
椭圆及其标准方程
2．1.1 椭圆及其标准方程(一)
要点 1
椭圆的定义 (大于
平面内与两定点 F1、F2 的距离之和 等于常数 |F1F2|)的点的轨迹叫做椭圆。 这两个定点 点． 两焦点间的距离 叫做椭圆的焦距．
叫做椭圆的焦
要点 2
椭圆的标准方程
(1)这里的“标准”指的是中心在 原点 ，对称轴为 坐标轴． x2 y2 (2)焦点在 x 轴时，标准方程为a2＋b2＝1(a>b>0)；焦点在 y y2 x2 轴时，标准方程为a2＋b2＝1(a>b>0)．为了计算上的方便，有时将 方程写为 mx2＋ny2＝1(m>0，n>0，m≠n)． (3)标准方程中的两个参数 a 和 b， 确定了椭圆的形状和大小， 是椭圆的定形条件．
(4)椭圆的两种标准方程中，如果 x2 的分母大，焦点就在x 轴 上；如果 y2 的分母大，则焦点就在 y 轴 上． (5)椭圆的方程中，a、b、c 三者之间 a 最大，且满足
a2＝b2＋c2 .
1．椭圆定义中，将“大于|F1F2|”改为“等于|F1F2|”或“小 于|F1F2|”的常数，其他条件不变点的轨迹是什么？
解析
设椭圆方程为 mx2＋ny2＝1(m＞0，n＞0 且 m≠n)，
椭圆经过 P1，P2 点，所以 P1，P2 点坐标适合椭圆方程，
6m＋n＝1 有 3m＋2n＝1
① ②
1 1 x2 y2 解得 m＝ ，n＝ ，∴所求椭圆方程为 ＋ ＝1 9 3 9 3
探究 3
方程 mx2＋ny2＝1(m>0，n>0 且 m≠n)表示椭圆：若
m<n，则焦点在 x 轴上；若 n<m，则焦点在 y 轴上。 思考题 3 求经过两点 A(3， 3)，B(2,3)的椭圆标准方程．
要点 1
椭圆的定义 (大于
平面内与两定点 F1、F2 的距离之和 等于常数 |F1F2|)的点的轨迹叫做椭圆。 这两个定点 点． 两焦点间的距离 叫做椭圆的焦距．
叫做椭圆的焦
要点 2
椭圆的标准方程
(1)这里的“标准”指的是中心在 原点 ，对称轴为 坐标轴． x2 y2 (2)焦点在 x 轴时，标准方程为a2＋b2＝1(a>b>0)；焦点在 y y2 x2 轴时，标准方程为a2＋b2＝1(a>b>0)．为了计算上的方便，有时将 方程写为 mx2＋ny2＝1(m>0，n>0，m≠n)． (3)标准方程中的两个参数 a 和 b， 确定了椭圆的形状和大小， 是椭圆的定形条件．
(4)椭圆的两种标准方程中，如果 x2 的分母大，焦点就在x 轴 上；如果 y2 的分母大，则焦点就在 y 轴 上． (5)椭圆的方程中，a、b、c 三者之间 a 最大，且满足
a2＝b2＋c2 .
1．椭圆定义中，将“大于|F1F2|”改为“等于|F1F2|”或“小 于|F1F2|”的常数，其他条件不变点的轨迹是什么？
解析
设椭圆方程为 mx2＋ny2＝1(m＞0，n＞0 且 m≠n)，
椭圆经过 P1，P2 点，所以 P1，P2 点坐标适合椭圆方程，
6m＋n＝1 有 3m＋2n＝1
① ②
1 1 x2 y2 解得 m＝ ，n＝ ，∴所求椭圆方程为 ＋ ＝1 9 3 9 3
探究 3
方程 mx2＋ny2＝1(m>0，n>0 且 m≠n)表示椭圆：若
m<n，则焦点在 x 轴上；若 n<m，则焦点在 y 轴上。 思考题 3 求经过两点 A(3， 3)，B(2,3)的椭圆标准方程．
椭圆标准方程(1)
答案：(1)
(3)
x2
x
6 2
y2 1
y2 12 1
(2)
y2 25
x2 16
1
16
x 2 y2 (4) + =1 4 9
小结：求椭圆标准方程的步骤： ①定位：确定焦点所在的坐标轴； ②定量：求a, b的值.
例2.求下列椭圆的焦点坐标.
x y + =1; (1) 25 9
2 2
(2) 16x2+7y2=112.
y P . F2
F1
O
x
y P F1 O F2 x O
y
F2(0, c) P (x, y)
x F1(0, －c)
• 设P(x,y)为椭圆上任意一点, F1F圆上任意一点P到F1,F2距离之和为常数 2a(2a>2c), 则PF1+PF2=2a.
椭圆的标准方程
高二数学组
复习：
一、椭圆的定义
平面内到两定点 F1、F2 的距离之和等 于常数（ 大于 | F F | ）的点的轨 1 2 迹叫做椭圆。 两定点F叫做椭圆的焦点。
两焦点的距离叫做椭圆的焦距。
复习：
二、椭圆的标准方程
x y 1 ( a b 0 ) 2 2 a b
2
2
y x 1 ( a b 0 ) 2 2 a b
即
( x c ) 2 y 2 ( x c ) 2 y 2 2a
练习：求适合下列条件的椭圆的标准方程：
(1)a= 6 ,b=1,焦点在x轴上; (2)焦点为F1(0,－3),F2(0,3),且a=5. (3)两个焦点分别是F1(－2,0)、F2(2,0),且过 P(2,3)点； (4)经过点P(－2,0)和Q(0,－3).
椭圆的标准方程 (1)
(4)化简
( x c ) 2 y 2 2a ( x c) 2 y 2 ( x c) 2 y 2 4a 2 4a ( x c ) 2 y 2 ( x c ) 2 y 2 a 2 cx a ( x c) 2 y 2 a 4 2a 2 cx c 2 x 2 a 2 x 2 2a 2cx a 2c 2 a 2 y 2 (a 2 c 2 ) x 2 a 2 y 2 a 2 (a 2 c 2 ) 令a 2 c 2 =b 2 , b 2 x 2 a 2 y 2 a 2b 2 x2 y 2 2 1(a b 0) 2 a b
4 - ，求点M轨迹方程. 9
y
M
A(-5,0)
o
B(5,0) x
实验：
(1)在木板上任取两个固定的点，长度设为2c (2)用一段长度超过2c的绳子的两端固定在两 个定点上，绳子设为2a
(3)用笔沿着绳子旋转一周，形成一个图形
F 1
F2
椭圆的定义： 到两个定点
的点的轨迹
F 1
F1、F2
的距离之和等于定长2apLeabharlann 焦点2cF2
焦点
其中两个定点的叫做椭圆的焦点，两 个焦点间的距离叫做椭圆的焦距（2c）
）
(5)验证：凡是曲线上的点都是方程的解， 凡是方程的解都是曲线上的点，数形统一 思考：如果使焦点在y轴上，椭圆的方程怎 么样？ y
F2
y 2 x2 2 1(a b 0) 2 a b
x o
F 1
p
例题1、如果椭圆满足下列三个条件： （1）焦点在x轴上，且关于原点对称；（2）焦 距为6；（3）椭圆的图像经过点A(0，4)。求椭 圆的标准方程 思考：椭圆的标准方程中有几个参变量？ 变式1、改变第一个条件：焦点在y轴上，且 关于原点对称 变式2、改变第二个条件：如果焦点坐标为 （-3,0）,（3,0）？ 变式3、改变第三个条件：如果 a 5
椭圆的标准方程1
M
F1
F2
3
[1] 建系: 以过焦点F1，F2的直线为x轴，线段F 1 F 2 的
垂直平分线为y 轴，建立直角坐标系，则 F 1( c ,0), F 2( c ,0) [2] 设点: 设 M(x,y) 为椭圆上的任意一点 [3] 找关系: M与F1,F2 距离 之和 等于2a (2a>2c), [4] 代坐标: ( x c )2 y 2 ( x c )2 y 2 2a [5] 化简:
y F2 x
O
不 同 点
图
形
F1
O
P x
F2
F1
标准方程 焦点坐标 相 a、b、c 的关系 同 点 焦点位置的判断
x2 y2 + 2 = 1 a > b > 0 2 a b
F1 -c , 0，F2 c , 0
x2 y2 + 2 = 1 a > b > 0 2 b a
F1 0,- c ，F2 0,c
y2 x2 1 16
填空
x y 3 2 1中, a=___,b=___, (1) 在椭圆 9 4
x 轴上，焦点坐标是( 5 ,0), ( 5 ,0) 焦点位于____ __________.
2
2
4 b=___, (2) 在椭圆 16x 7 y 112 中，a=___, 7
2 2 2
例1： 求适合下列条件的椭圆标准方 程：
(1)a=4，b=1，焦点在 x 轴上； (2)a=4，c=2，焦点在 y 轴上；
说出适合下列条件的椭圆标准方程 （1）a
5, c 3 ，焦点在x 轴上；
2 y x 1 25 16 2
F1
F2
3
[1] 建系: 以过焦点F1，F2的直线为x轴，线段F 1 F 2 的
垂直平分线为y 轴，建立直角坐标系，则 F 1( c ,0), F 2( c ,0) [2] 设点: 设 M(x,y) 为椭圆上的任意一点 [3] 找关系: M与F1,F2 距离 之和 等于2a (2a>2c), [4] 代坐标: ( x c )2 y 2 ( x c )2 y 2 2a [5] 化简:
y F2 x
O
不 同 点
图
形
F1
O
P x
F2
F1
标准方程 焦点坐标 相 a、b、c 的关系 同 点 焦点位置的判断
x2 y2 + 2 = 1 a > b > 0 2 a b
F1 -c , 0，F2 c , 0
x2 y2 + 2 = 1 a > b > 0 2 b a
F1 0,- c ，F2 0,c
y2 x2 1 16
填空
x y 3 2 1中, a=___,b=___, (1) 在椭圆 9 4
x 轴上，焦点坐标是( 5 ,0), ( 5 ,0) 焦点位于____ __________.
2
2
4 b=___, (2) 在椭圆 16x 7 y 112 中，a=___, 7
2 2 2
例1： 求适合下列条件的椭圆标准方 程：
(1)a=4，b=1，焦点在 x 轴上； (2)a=4，c=2，焦点在 y 轴上；
说出适合下列条件的椭圆标准方程 （1）a
5, c 3 ，焦点在x 轴上；
2 y x 1 25 16 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
椭圆的标准方程（1）
学习目标:
1、理解椭圆的定义；
2、掌握椭圆的标准方程的推导及其标准方程.
学习重难点：椭圆的定义及其标准方程，难点是方程的推导 学习内容：
观察探究，概括定义：
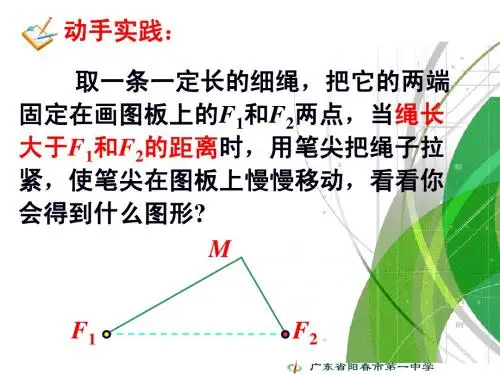
用两个图钉将细绳固定在一张硬纸板上，用铅笔拉紧细绳，并移动铅笔，观察铅笔移动的轨迹，思考下列问题：
（1）所得轨迹是什么图形？
（2）铅笔移动的过程中，满足什么几何条件？
定义：椭圆______________________________________________________ _________________________________________________________________ 恰当建系，推导方程：
思考1：观察椭圆的形状，建立适当的坐标系，求椭圆的方程．
按你建立的坐标系时，椭圆方程为：______ ___ 椭圆的焦点是_________________，a 、b 、c 之间的关系是_______________．
思考2．如图，如果焦点1F 、2F 在y 轴上，且1F 、
2F 的坐标分别为()c -,0，()c ,0，a ，b 的意义和上面
相同，那么椭圆的标准方程是__________________．
M
1F
2F
思考3：两种形式的椭圆标准方程有什么异同？
例1、(1)已知椭圆的方程为： ，则a=_____，b=_______，c=_______，焦点坐标为：____________焦距等于______;若CD 为过左焦点F 1的弦，则△F 2CD
的周长为________
(2)已知椭圆的方程为： ，则a=_____，b=_______，c=_______，
焦点坐标为：___________焦距等于__________;曲线上一点P 到左焦点F 1的距
离为3，则点P 到另一个焦点F 2的距离等于_________，则△F 1PF 2的周长为___________
练习：求下列椭圆的焦点和焦距。
14
5)1(22=+y x 162)2(22=+y x
例2．写出适合下列条件的椭圆的标准方程：
（1）4=a ，1=b ，焦点在x 轴上； （2）4=a ，15=b ，焦点在y 轴上；
练：求焦点为()02，
-，()02，，并且经过点⎪⎭
⎫
⎝⎛-2325，的椭圆标准方程．
变式：若方程4x 2+ky 2=1表示的曲线是焦点在y 轴上的椭圆，求k 的取值范围。
例3、已知一个运油车上的贮油罐横截面的外轮廓线是一个椭圆，它的焦距为2.4 m ，外轮廓线上的点到两个焦点的距离和为3 m ，求这个椭圆的标准方程
116
252
2=+y x 15
42
2=+y x
例4、将圆x 2+y 2=4上的点的横坐标保持不变，纵坐标变为原来的一半，求所得曲线的方程，并说明它是什么曲线
课后作业： 姓名___________
1．已知椭圆17
92
2=+y x ，则a 、b 、c 的值分别是
2. a =2,b =1的椭圆方程为
3. 椭圆15
422=+y x 的焦点为 椭圆15422=+y x 的焦点为 4. 焦点为()()3,0,3,021F F -，且5=a 的椭圆的标准方程是 5. 焦点在x 轴上，焦距是4，且经过点()62,3-M 的椭圆的标准方程是
6.经过⎪⎪⎭
⎫ ⎝⎛--⎪⎪⎭⎫
⎝⎛
-23,2,22,2B A 两点的椭圆的标准方程是 7.若方程19422
=-+-k
y k x 表示椭圆，则参数k 的取值范围是
8、已知椭圆19
252
2=+y x 上的一点P 的横坐标是2，求：
(1) 点P 到椭圆左焦点1F 的距离1PF ； (2) 点P 到椭圆右焦点2F 的距离2PF .
9.△ABC三个角A、B、C所对的边成等差数列，其中A（－2，0），C（2，0），求顶点B满足的一个轨迹方程。
1，求点P的轨迹方程，10.设动点P到点F(1,0)的距离是到直线x=9的距离的
3
并判断次轨迹是什么图形。