数学人教版九年级上册因式分解
- 格式：doc
- 大小：92.50 KB
- 文档页数：5
下载文档原格式
合集下载
人教版数学九年级上册说课稿21.2.3《因式分解法》
人教版数学九年级上册说课稿21.2.3《因式分解法》一. 教材分析《因式分解法》是人教版数学九年级上册第21.2.3节的内容，本节课的主要任务是让学生掌握因式分解的概念、方法和应用。
因式分解是初等数学中的一种重要方法，对于解决代数方程、不等式等问题具有重要意义。
在本节课中，学生将通过学习因式分解的基本概念和方法，能够独立进行简单的因式分解，并能够运用因式分解解决一些实际问题。
二. 学情分析学生在学习本节课之前，已经学习了整式的加减、乘除等基本运算，对于代数概念有一定的了解。
但是，因式分解作为一种独立的解题方法，对学生来说是新的内容，需要通过本节课的学习来掌握。
同时，因式分解需要学生具备一定的逻辑思维能力和转化能力，对于部分学生来说可能存在一定的难度。
三. 说教学目标1.知识与技能目标：学生能够理解因式分解的概念，掌握因式分解的方法，能够独立进行简单的因式分解。
2.过程与方法目标：通过小组合作、讨论交流等方法，培养学生的团队协作能力和解决问题的能力。
3.情感态度与价值观目标：学生能够体验到数学的乐趣，增强对数学学科的兴趣，培养积极的学习态度。
四. 说教学重难点1.教学重点：因式分解的概念和方法。
2.教学难点：因式分解的逻辑思维和转化能力的培养。
五. 说教学方法与手段本节课采用讲授法、小组合作法、案例分析法等多种教学方法，结合多媒体课件、黑板等教学手段，以学生为主体，教师为指导，引导学生主动探索、积极参与，提高学生的学习兴趣和效果。
六. 说教学过程1.导入：通过一个实际问题，引出因式分解的必要性，激发学生的学习兴趣。
2.讲解：讲解因式分解的概念和方法，通过示例让学生理解因式分解的过程。
3.练习：学生独立进行因式分解的练习，教师进行个别指导。
4.小组合作：学生分组进行因式分解的讨论和交流，分享解题经验和方法。
5.总结：教师引导学生总结因式分解的方法和技巧，强化学生对因式分解的理解。
6.作业布置：布置适量的因式分解练习题，巩固所学知识。
九年级上册数学人教版21.2.3 解一元二次方程-因式分解法
初中数学集体备课活页纸
学科
初中数学
主备人
节次
第 周
第 节
课题
21.2.3 解一元二次方程-因式分解法
课时
1
课型
新授课
教学目标
1.能用因式分解法解一些一元二次方程；
2.能根据具体一元二次方程的特征，灵活选择方程的解法。体会解决问题方法的多样性。
教学重点
能用因式分解法解一些一元二次方程.
教学难点
能根据具体一元二次方程的特征，灵活选择方程的解法.
3. 根据“ab=0,则a=0或b=0”,转化为两个一元一次方程.
4.分别解这两个一元一次方程，它们的根就是原方程的根.
第五步：
师友反馈
环节1：师友检测
1.用公式法解下列方程：
环节2：教师评价
一、本节课最佳师友是…
二、
二、课后作业
必做：
选做：
板书设计
教学后记
课 堂 教 学 设 计
教学环节
教学过程
二次备课
第一步：
交流预习
环节1：教师提问
1、什么是一元二次方程
2、一元二次方程的一般形式是什么吗？
3、二次项、一次项、常数项分别是什么？
环节2:师友释疑
问题：根据物理学规律，如果把一个物体从地面以10 m/s的速度竖直上抛，那么物体经过x s离地面的高度(单位：m)为10x－4.9x2.根据上述规律，物体经过多少秒落回地面(结果保留小数点后两位)？
(1)解：设物体经过x s落回地面，这时它离地面的高度为0m，
即10x－4.9x2＝0.
思考：除了配方法或公式法之外，能找到更简单的方法吗？
第二步：
互助探究
环节1:师友探究
学科
初中数学
主备人
节次
第 周
第 节
课题
21.2.3 解一元二次方程-因式分解法
课时
1
课型
新授课
教学目标
1.能用因式分解法解一些一元二次方程；
2.能根据具体一元二次方程的特征，灵活选择方程的解法。体会解决问题方法的多样性。
教学重点
能用因式分解法解一些一元二次方程.
教学难点
能根据具体一元二次方程的特征，灵活选择方程的解法.
3. 根据“ab=0,则a=0或b=0”,转化为两个一元一次方程.
4.分别解这两个一元一次方程，它们的根就是原方程的根.
第五步：
师友反馈
环节1：师友检测
1.用公式法解下列方程：
环节2：教师评价
一、本节课最佳师友是…
二、
二、课后作业
必做：
选做：
板书设计
教学后记
课 堂 教 学 设 计
教学环节
教学过程
二次备课
第一步：
交流预习
环节1：教师提问
1、什么是一元二次方程
2、一元二次方程的一般形式是什么吗？
3、二次项、一次项、常数项分别是什么？
环节2:师友释疑
问题：根据物理学规律，如果把一个物体从地面以10 m/s的速度竖直上抛，那么物体经过x s离地面的高度(单位：m)为10x－4.9x2.根据上述规律，物体经过多少秒落回地面(结果保留小数点后两位)？
(1)解：设物体经过x s落回地面，这时它离地面的高度为0m，
即10x－4.9x2＝0.
思考：除了配方法或公式法之外，能找到更简单的方法吗？
第二步：
互助探究
环节1:师友探究
人教版九年级数学上册：21.2.3 因式分解法 教学设计
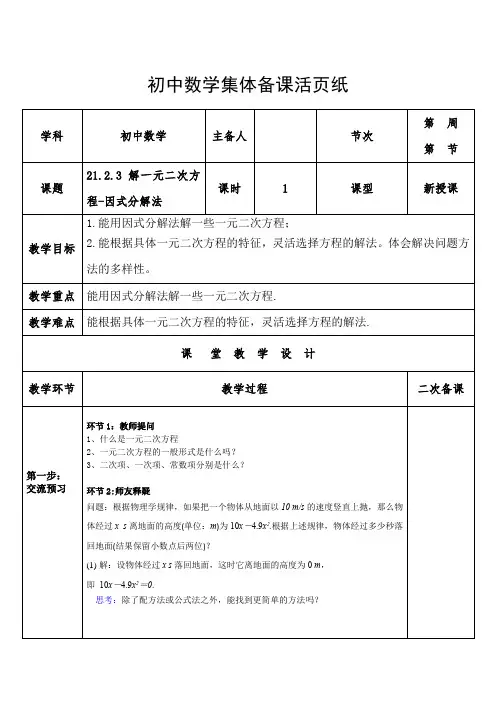
人教版九年级数学上册：21.2.3 因式分解法教学设计一. 教材分析因式分解法是九年级数学上册第21章第2节的一个知识点。
通过学习因式分解法，学生能够理解并掌握因式分解的概念，能够运用因式分解法解决一些实际问题。
本节课的内容包括因式分解的定义、因式分解的方法以及因式分解的应用。
二. 学情分析九年级的学生已经具备了一定的数学基础，对代数运算有一定的了解。
但是，因式分解法是一个较为抽象的概念，学生可能对其理解起来有一定的困难。
因此，在教学过程中，需要引导学生通过实际例子来理解因式分解的概念和方法，并通过练习来巩固所学知识。
三. 教学目标1.理解因式分解的概念，掌握因式分解的方法。
2.能够运用因式分解法解决一些实际问题。
3.培养学生的逻辑思维能力和解决问题的能力。
四. 教学重难点1.因式分解的概念和方法。
2.运用因式分解法解决实际问题。
五. 教学方法采用问题驱动法、案例教学法和小组合作法进行教学。
通过实际例子引导学生理解因式分解的概念和方法，通过案例教学法让学生通过解决实际问题来运用因式分解法，通过小组合作法让学生在小组内进行讨论和交流，共同解决问题。
六. 教学准备1.准备相关的教学案例和练习题。
2.准备教学PPT，包括因式分解的定义、方法和应用的讲解。
七. 教学过程1.导入（5分钟）通过一个实际问题引入因式分解的概念，例如：“已知一个数的平方减去这个数等于10，求这个数。
”引导学生思考如何解决这个问题，从而引出因式分解的概念。
2.呈现（10分钟）通过PPT讲解因式分解的定义和方法，包括提取公因式法、平方差公式法、完全平方公式法等。
通过具体的例子来解释每种方法的运用。
3.操练（10分钟）让学生分组进行练习，每组选择一个因式分解的方法，根据PPT上的例子，自己尝试解决一个问题。
教师巡回指导，解答学生的疑问。
4.巩固（10分钟）让学生独立完成PPT上的练习题，巩固因式分解的方法。
教师选取部分学生的作业进行讲解和分析。
人教版九年级数学上册《因式分解法》课件
分析：该式左右两边含公因式，分析：方程一边以平方形
所以用因式分解法解答较快. 式出现，另一边是常数，
解：变形得 (3x - 5)(x + 5) = 0. 可用直接开平方法.
即 3x - 5 = 0，或 x + 5 = 0. 解：开平方，得
解得
5x + 1 = ±1. 解得 x1 = 0，x2 =
(3) x2 - 12x = 4；
(4) 2x2 − 7x + 3 = 0.
2x 1
x
3
6x x 7x
解：分解因式，得
(2x − 1)(x − 3) = 0，
解得 x1 =
1 2
，x2
=
3.
二 灵活选用适当的方法解方程
例2 用适当的方法解方程：
(1) 3x(x + 5) = 5(x + 5)；
(2) (5x + 1)2 = 1；
x·
×
1
x 5x 4x
解：分解因式，得 (x + 5)(x − 1) = 0， 解得 x1 = −5，x2 = 1．
(3) (x + 3)(x − 1) = 5；
解：整理得 x2 + 2x − 8 = 0，
x4
x 2
2x 4x 2x
分解因式，得 (x + 4)(x − 2) = 0， 解得 x1 = −4，x2 = 2.
(2) (y + 2)(y - 3) = 0； (2) y1 = -2，y2 = 3.
(3) (3x + 6)(2x - 4) = 0； (3) x1 = -2，x2 = 2.
(4) x2 = x.
(4) x1 = 0，x2 = 1.
人教版九年级数学上册21.2.3因式分解解一元二次方程优秀教学案例
3.教师应给予学生充分的指导和支持，引导学生在合作中相互尊重、相互帮助，培养学生的团队精神。
（四）反思与评价
1.教师可以引导学生对学习过程进行反思，让学生总结经验，提高解题能力。
2.教师应采用多元化的评价方式，既注重学生的知识掌握程度，也注重学生的能力发展和情感态度。
3.教师应及时给予学生反馈，鼓励学生的优点，指导学生改进不足，激发学生的学习动力。
3.通过对一元二次方程的因式分解和解题方法的探讨，培养学生分析问题、解决问题的能力。
（三）情感态度与价值观
1.培养学生热爱数学、崇尚科学的情感，激发学生学习数学的兴趣和自信心。
2.使学生认识到数学在实际生活中的重要性，提高学生运用数学知识解决实际问题的意识。
3.培养学生严谨治学、勤奋学习的良好学习习惯，树立学生的团队合作精神。
5.作业小结：教师布置相关的作业题，让学生巩固和应用所学的内容，加深对因式分解解一元二次方程的理解和掌握。教师鼓励学生在完成作业后进行自我检查和反思，及时发现和纠正自己的错误。教师对学生的作业进行及时的批改和反馈，指出学生的优点和不足，指导学生进一步提高。这些作业小结的环节有助于巩固学生所学知识，提高学生的解题能力和学习效果。
2.教师可以提供一些练习题，让学生通过讨论和合作，运用因式分解解一元二次方程的方法解决问题。
3.教师可以引导学生分享彼此的想法和解题过程，促进学生之间的交流和学习。
（四）总结归纳
1.教师可以引导学生总结因式分解解一元二次方程的基本思路和方法，让学生形成系统的知识结构。
2.教师可以强调因式分解解一元二次方程的优势和适用场景，让学生能够根据题目特点选择合适的解题方法。
本节课的教学内容主要包括：了解因式分解解一元二次方程的基本思路，掌握运用因式分解法解一元二次方程的步骤，能灵活运用因式分解法解决实际问题。在教学过程中，我将以案例的形式，引导学生参与课堂，激发学生的学习兴趣，培养学生的合作意识，提高学生的数学素养。
（四）反思与评价
1.教师可以引导学生对学习过程进行反思，让学生总结经验，提高解题能力。
2.教师应采用多元化的评价方式，既注重学生的知识掌握程度，也注重学生的能力发展和情感态度。
3.教师应及时给予学生反馈，鼓励学生的优点，指导学生改进不足，激发学生的学习动力。
3.通过对一元二次方程的因式分解和解题方法的探讨，培养学生分析问题、解决问题的能力。
（三）情感态度与价值观
1.培养学生热爱数学、崇尚科学的情感，激发学生学习数学的兴趣和自信心。
2.使学生认识到数学在实际生活中的重要性，提高学生运用数学知识解决实际问题的意识。
3.培养学生严谨治学、勤奋学习的良好学习习惯，树立学生的团队合作精神。
5.作业小结：教师布置相关的作业题，让学生巩固和应用所学的内容，加深对因式分解解一元二次方程的理解和掌握。教师鼓励学生在完成作业后进行自我检查和反思，及时发现和纠正自己的错误。教师对学生的作业进行及时的批改和反馈，指出学生的优点和不足，指导学生进一步提高。这些作业小结的环节有助于巩固学生所学知识，提高学生的解题能力和学习效果。
2.教师可以提供一些练习题，让学生通过讨论和合作，运用因式分解解一元二次方程的方法解决问题。
3.教师可以引导学生分享彼此的想法和解题过程，促进学生之间的交流和学习。
（四）总结归纳
1.教师可以引导学生总结因式分解解一元二次方程的基本思路和方法，让学生形成系统的知识结构。
2.教师可以强调因式分解解一元二次方程的优势和适用场景，让学生能够根据题目特点选择合适的解题方法。
本节课的教学内容主要包括：了解因式分解解一元二次方程的基本思路，掌握运用因式分解法解一元二次方程的步骤，能灵活运用因式分解法解决实际问题。在教学过程中，我将以案例的形式，引导学生参与课堂，激发学生的学习兴趣，培养学生的合作意识，提高学生的数学素养。
人教版数学九年级上册因式分解法课件
的主要方法有哪些？
一 情境引入
问一问
问题
根据物理学规律，如果把一
个物体从地面以10m/s的速度竖直上
抛，那么物体经过xs离地面的高度
（单位：m)为
10x-4.9 2 .
根据上述规律，物体经过多少秒落
回地面（结果保留小数点后两位）？
设物体经过xs落回地面，这时它离
地面的高度为0m，即
①
10x-4.9 2 =0.
2
2
返回
归一归
师生共同归纳总结：
配方法要先配方，再降次；通过配方法可以推出求根公式，
公式法直接利用求根公式解方程；因式分解法要先将方程一边
化为两个一次因式相乘，另一边为0，再分别使各一次因式等
于0.配方法、公式法适用于所有一元二次方程，因式分解法在
解某些一元二次方程时比较简便，总之，解一元二次方程的基
并被列为芝加哥科学技术博物馆中当今世界88位数学伟
人之一。国际上以华氏命名的数学科研成果有“华氏定
理”、“华氏不等式”、“华一王方法”等。
故事：华罗庚在清华执教期间，为了照料年老多病的公
公，吴筱元留在故乡，挑起家务担子。在以后的日子里，
她不仅操持家务，还帮他抄写论文和书信，接待客人。
几十年来，吴筱元在华罗庚的生活和事业上，起着重要
2.如图，把小圆形场地的半径增加5m
得到大圆形场地，场地面积扩大了一
倍.求小圆形场地的半径.
返回
2.（202X年杭州中考）某网络学习平台202X年的
新注册用户数为100万，202X年的新注册用户数为
169万，设新注册用户数的年平均增长率为x（x＞0
），则x＝
30% （ 用百分数表示）．
返回
一 情境引入
问一问
问题
根据物理学规律，如果把一
个物体从地面以10m/s的速度竖直上
抛，那么物体经过xs离地面的高度
（单位：m)为
10x-4.9 2 .
根据上述规律，物体经过多少秒落
回地面（结果保留小数点后两位）？
设物体经过xs落回地面，这时它离
地面的高度为0m，即
①
10x-4.9 2 =0.
2
2
返回
归一归
师生共同归纳总结：
配方法要先配方，再降次；通过配方法可以推出求根公式，
公式法直接利用求根公式解方程；因式分解法要先将方程一边
化为两个一次因式相乘，另一边为0，再分别使各一次因式等
于0.配方法、公式法适用于所有一元二次方程，因式分解法在
解某些一元二次方程时比较简便，总之，解一元二次方程的基
并被列为芝加哥科学技术博物馆中当今世界88位数学伟
人之一。国际上以华氏命名的数学科研成果有“华氏定
理”、“华氏不等式”、“华一王方法”等。
故事：华罗庚在清华执教期间，为了照料年老多病的公
公，吴筱元留在故乡，挑起家务担子。在以后的日子里，
她不仅操持家务，还帮他抄写论文和书信，接待客人。
几十年来，吴筱元在华罗庚的生活和事业上，起着重要
2.如图，把小圆形场地的半径增加5m
得到大圆形场地，场地面积扩大了一
倍.求小圆形场地的半径.
返回
2.（202X年杭州中考）某网络学习平台202X年的
新注册用户数为100万，202X年的新注册用户数为
169万，设新注册用户数的年平均增长率为x（x＞0
），则x＝
30% （ 用百分数表示）．
返回
数学人教版九年级上册因式分解(提公因式法)
练习
1.解下列方程：
2 2 2 （ 1 ） x x 0 ;(2) x 2 3 x 0 ; ( 3 ) 3 x 6 x 3 ;
2 2 2 ( 4 ) 4 x 121 0 ; ( 5 ) 3 x ( 2 x 1 ) 4 x 2 ; ( 6 ) ( x 4 ) ( 5 2 x ) .
2
2019/1/5
配方法
2 1 0 x 4 . 9 x 0
公式法
2 1 0 x 4 . 9 x 0
2 解： 4 . 9 x 1 0 x 0
100 x0 49 2 2 1 0 0 5 0 5 0 2 x x 0 4 9 4 9 4 9
1. 将方程左边因式分解，右边等于0; 2. 根据“至少有一个因式为零”,转化为两个一 元一次方程. 3. 分别解两个一元一次方程，它们的根就 是原方程的根.
2019/1/5
布置作业
• 教材习题21.2
2019/1/5
( 3x － 2 )( 2x + 1 ) = 0.
有 3x － 2 = 0 或 2x + 1 = 0，
2 1 x1 , x2 . 3 2
2019/1/5
2.把小圆形场地的半径增加5m得到大圆形场地，场地面积增 加了一倍，求小圆形场地的半径． 解：设小圆形场地的半径为r 根据题意 ( r + 5 )2×π=2r2π.
3. 根据“ab=0,则a=0或b=0”,转化为两个一元一次方程. 4. 分别解这两个一元一次方程，它们的根就是原方程的根.
2019/1/5
例3 解下列方程：
xx2 ; 1 x20
2
1 2 3 5 x 2 x x 2 x . 2 4 4 解：（1）因式分解，得 (2)移项、合并同类项，得
因式分解法-人教版九年级数学上册课件
“如果两个因式的积等于零, 2.理论依据是. 那么至少有一个因式等于零”
3.分解因式法解一元二次方程的步骤是:
1.化：化方程为一般形式; 2.分：将方程左边因式分解; 3.转：根据“至少有一个因式为零”,转化为两个一元一次方程 4.解：分别解两个一元一次方程，它们的根就是原方程的根.
合作探究一
下面的解法正确吗？如果不正确，错误在哪？
解方程： x2 7x 6 0得x1 1, x2 6 而x2 - 7x 6 (x -1)(x - 6)
解方程：x2 3x 2 0得x1 1, x2 2而x2 3x 2 (x 1)(x 2)
解方程：3x2
8x
5
0得x1
1,
x2
5 3
而3x2
8x
5
(x
1)(x
5) 3
把下列各式分解因式：
12x2 5x 3
23y2 y 14
能力提升
为解方程(x2－1)2－5(x2－1)＋4＝0，我们可以将x2－1视 为一个整体，然后设x2－1＝y，则y2＝(x2－1)2，原方程化 为y2－5y＋4＝0，解此方程，得y1＝1，y2＝4．
当y＝1时，x2－1＝1，x2＝2，∴x＝± 2
二．用适当方法解下列方程：
1、x2－4x＋3＝0； 2、(x－2)2＝256； 3、x2－3x＋1＝0； 4、(2t＋3)2＝3(2t＋3)； 5、(3－y)2＋y2＝9； 6、 (1 ＋ 2 )x2 － (1 － 2 )x=0
三．用因式分解法解方程x2－kx－16＝0时，得到的 两根均为整数，求k值。
课堂小结
1.用因式分解法解一元二次方程的步骤。 2.解一元二次方程常见的方法有直接开平 方法、公式法、因式分解法、配方法。 每一种方法都有它适合的类型。
3.分解因式法解一元二次方程的步骤是:
1.化：化方程为一般形式; 2.分：将方程左边因式分解; 3.转：根据“至少有一个因式为零”,转化为两个一元一次方程 4.解：分别解两个一元一次方程，它们的根就是原方程的根.
合作探究一
下面的解法正确吗？如果不正确，错误在哪？
解方程： x2 7x 6 0得x1 1, x2 6 而x2 - 7x 6 (x -1)(x - 6)
解方程：x2 3x 2 0得x1 1, x2 2而x2 3x 2 (x 1)(x 2)
解方程：3x2
8x
5
0得x1
1,
x2
5 3
而3x2
8x
5
(x
1)(x
5) 3
把下列各式分解因式：
12x2 5x 3
23y2 y 14
能力提升
为解方程(x2－1)2－5(x2－1)＋4＝0，我们可以将x2－1视 为一个整体，然后设x2－1＝y，则y2＝(x2－1)2，原方程化 为y2－5y＋4＝0，解此方程，得y1＝1，y2＝4．
当y＝1时，x2－1＝1，x2＝2，∴x＝± 2
二．用适当方法解下列方程：
1、x2－4x＋3＝0； 2、(x－2)2＝256； 3、x2－3x＋1＝0； 4、(2t＋3)2＝3(2t＋3)； 5、(3－y)2＋y2＝9； 6、 (1 ＋ 2 )x2 － (1 － 2 )x=0
三．用因式分解法解方程x2－kx－16＝0时，得到的 两根均为整数，求k值。
课堂小结
1.用因式分解法解一元二次方程的步骤。 2.解一元二次方程常见的方法有直接开平 方法、公式法、因式分解法、配方法。 每一种方法都有它适合的类型。
人教版九年级上册数学因式分解法课件
(x-4)2-3(x-4)=0， 因式分解，得 (x-4)(x-4-3)=0，
整理，得 (x-4)(x-7)=0，
于是，得x-4=0或x-7=0， x1=4或x2=7.
活动四 巩固练习
1.三角形两边长分别为2和4,第三边是方程 x2 - 6x+8=0的解，则这个三角形的周长 是 （C） A.8 B.8或10 C.10 D.8和10
第二十一章 一元二次方程 21.2 解一元二次方程 21.2.3 因式分解法
活动一 复习引入
解下列方程.
(1) 2x2+x=0(用配方法)，
x1=0或x2=-
1 2
.
(2) 3x2+6x=0(用公式法).
x1=-2或x2=0.
复习引入
(3) 要使一块矩形场地的长比宽多3 m， 并且面积为28 m2，场地的长和宽各是多少？
设宽为x m，则 x(x+3)=28
长是7 m，宽是4 m (4) 如何设未知数并根据题目的等量关系 列出方程？
复习引入
(5) 所 列 方 程 和 以 前 我 们 学 习 的 方 程 x2+6x+9=2有何联系与区分？
(6) 你能由方程x2+6x+9=2的解联想到怎样 解方程x2+3x-28=0吗？
活动二 实验发现
思考：(1)x(2x+1)=0，(2)3x(x+2)=0.
1 x1 0, x2 2
x1 0, x2 2
问 题 ： (1)你能视察出这两题的特点吗?
(2)你知道方程的解吗？说说你的理由.
实验发现
因式分解法的理论根据是:两个因式的积等于零, 那么这两个因式的值就至少有一个等于零.即：
整理，得 (x-4)(x-7)=0，
于是，得x-4=0或x-7=0， x1=4或x2=7.
活动四 巩固练习
1.三角形两边长分别为2和4,第三边是方程 x2 - 6x+8=0的解，则这个三角形的周长 是 （C） A.8 B.8或10 C.10 D.8和10
第二十一章 一元二次方程 21.2 解一元二次方程 21.2.3 因式分解法
活动一 复习引入
解下列方程.
(1) 2x2+x=0(用配方法)，
x1=0或x2=-
1 2
.
(2) 3x2+6x=0(用公式法).
x1=-2或x2=0.
复习引入
(3) 要使一块矩形场地的长比宽多3 m， 并且面积为28 m2，场地的长和宽各是多少？
设宽为x m，则 x(x+3)=28
长是7 m，宽是4 m (4) 如何设未知数并根据题目的等量关系 列出方程？
复习引入
(5) 所 列 方 程 和 以 前 我 们 学 习 的 方 程 x2+6x+9=2有何联系与区分？
(6) 你能由方程x2+6x+9=2的解联想到怎样 解方程x2+3x-28=0吗？
活动二 实验发现
思考：(1)x(2x+1)=0，(2)3x(x+2)=0.
1 x1 0, x2 2
x1 0, x2 2
问 题 ： (1)你能视察出这两题的特点吗?
(2)你知道方程的解吗？说说你的理由.
实验发现
因式分解法的理论根据是:两个因式的积等于零, 那么这两个因式的值就至少有一个等于零.即：
人教版数学九年级上册第二十一章《因式分解法》课件
分解.
解一元二次方程的方法：
直接开平方法： 直接开平方法就是用直接开平方求解一元二次方程的方法.
用直接开平方法解形如 x m2 nn 0 的方程，
其解为 x n m. 配方法： 把一元二次方程移项之后，在等式两边都加上一次项系数的
一半的平方（配方），使方程一边是完全平方式，另一边是 常数，当此常数是非负数时，直接开平方求解. 公式法： 把一元二次方程化成一般情势，然后计算判别式 Δ=b2-4ac
(2) 3x(x-1)＝2(x-1).
2.如图，把小圆形场地的半径增加 5 m 得到大圆形场地，场地面积扩大了 一倍，求小圆形场地的半径.
3.解方程：2(x-3)=3x(x-3).
4.用因式分解法解下列方程： (1) (x-5) (x-6)=x-5；
(2) 16(x-3)2-25(x-2)2=0.
人教版数学九年级上册
第二十一章 二元一次方程
21.2.3 因式分解法
学习目标
1.能用因式分解法解一些一元二次方程；能根据具体一元 二次方程的特征，灵活选择方程的解法。
2.能根据具体一元二次方程的特征，灵活选择方程的解法， 体会解决问题方法的多样性。
3.在探究因式分解法解方程的过程中体会转化、降次的数 学思想。
解：(1)移项，得 (x-5) (x-6)- (x-5) =0， 因式分解，得 (x-5) (x-6-1)=0， 所以 x-5=0 或 x-6-1=0， 所以 x1=5，x2=7.
5.用因式分解法解下列方程： (1) (x-5) (x-6)=x-5；
(2) 16(x-3)2-25(2 3 )＝0， 于是得x＝0，或x－2 3 ＝0， 解得x1＝0，x2＝2 3. (3)移项，化简，得x2－2x＋1＝0， 因式分解，得(x－1)2＝0， 于是得x－1＝0，即x1＝x2＝1.
解一元二次方程的方法：
直接开平方法： 直接开平方法就是用直接开平方求解一元二次方程的方法.
用直接开平方法解形如 x m2 nn 0 的方程，
其解为 x n m. 配方法： 把一元二次方程移项之后，在等式两边都加上一次项系数的
一半的平方（配方），使方程一边是完全平方式，另一边是 常数，当此常数是非负数时，直接开平方求解. 公式法： 把一元二次方程化成一般情势，然后计算判别式 Δ=b2-4ac
(2) 3x(x-1)＝2(x-1).
2.如图，把小圆形场地的半径增加 5 m 得到大圆形场地，场地面积扩大了 一倍，求小圆形场地的半径.
3.解方程：2(x-3)=3x(x-3).
4.用因式分解法解下列方程： (1) (x-5) (x-6)=x-5；
(2) 16(x-3)2-25(x-2)2=0.
人教版数学九年级上册
第二十一章 二元一次方程
21.2.3 因式分解法
学习目标
1.能用因式分解法解一些一元二次方程；能根据具体一元 二次方程的特征，灵活选择方程的解法。
2.能根据具体一元二次方程的特征，灵活选择方程的解法， 体会解决问题方法的多样性。
3.在探究因式分解法解方程的过程中体会转化、降次的数 学思想。
解：(1)移项，得 (x-5) (x-6)- (x-5) =0， 因式分解，得 (x-5) (x-6-1)=0， 所以 x-5=0 或 x-6-1=0， 所以 x1=5，x2=7.
5.用因式分解法解下列方程： (1) (x-5) (x-6)=x-5；
(2) 16(x-3)2-25(2 3 )＝0， 于是得x＝0，或x－2 3 ＝0， 解得x1＝0，x2＝2 3. (3)移项，化简，得x2－2x＋1＝0， 因式分解，得(x－1)2＝0， 于是得x－1＝0，即x1＝x2＝1.
人教版九年级数学上册《因式分解法》课件
2(x2+2x+1)
根据物理学规律，如果把一个物体从地面以10米/秒的速度竖直上抛， 那么物体经过x秒离地面的高度（单位：米）为
10x-4.9x2
根据上述规律，物体经过多少秒落回地面？
设物体经过x秒落回地面，这时它离地面的高度为____米，则
10x-4.9x2＝0
10x-4.9x2＝0
x(10-4.9x)=0
用因式分解法解下列方程：
（１）x(x-2)+x-2＝0 25x2 2x 1 x2 2x 3
4
4
有公因式 解：
吗？
x 2x 1 0
解：整理得
把方程整理成一般形式
x 2 0 或 x 1 0
x1 2，x2 1
4x2 1 0
2x 12x 1 0
2x 1 0 或 2 x 1 0
x=0 或 x+2＝0
2、方程 x2=4x 的根是__x_1___0__, _x_2____4__
x2-4x＝0 x（x-4）＝0 x＝0 或 x-4＝0
3、解方程：
（1） 3x2-6x＝-3
解： 3x2-6x+3=0 3(x2-2x+1)=0 ∴3(x-1)2=0
x-1=0 x1 x2 1
（2）（x+3)(x-3)=1
人教版 九年级上册第二十一章《一元二次方程》
21.2.3 解一元二次方程 -----因式分解法
1、能用因式分解法解数字系数的一元二次方程；
2、通过因式分解解法对一元二次方程进行求解， 体会降次的思想；
3、体验问题解决方法的多样性，灵活选择最为简 便的解决方法。
回顾旧知
1、什么叫做因式分解？
把一个多项式写成几个因式的乘积的形式叫做因式分解。
根据物理学规律，如果把一个物体从地面以10米/秒的速度竖直上抛， 那么物体经过x秒离地面的高度（单位：米）为
10x-4.9x2
根据上述规律，物体经过多少秒落回地面？
设物体经过x秒落回地面，这时它离地面的高度为____米，则
10x-4.9x2＝0
10x-4.9x2＝0
x(10-4.9x)=0
用因式分解法解下列方程：
（１）x(x-2)+x-2＝0 25x2 2x 1 x2 2x 3
4
4
有公因式 解：
吗？
x 2x 1 0
解：整理得
把方程整理成一般形式
x 2 0 或 x 1 0
x1 2，x2 1
4x2 1 0
2x 12x 1 0
2x 1 0 或 2 x 1 0
x=0 或 x+2＝0
2、方程 x2=4x 的根是__x_1___0__, _x_2____4__
x2-4x＝0 x（x-4）＝0 x＝0 或 x-4＝0
3、解方程：
（1） 3x2-6x＝-3
解： 3x2-6x+3=0 3(x2-2x+1)=0 ∴3(x-1)2=0
x-1=0 x1 x2 1
（2）（x+3)(x-3)=1
人教版 九年级上册第二十一章《一元二次方程》
21.2.3 解一元二次方程 -----因式分解法
1、能用因式分解法解数字系数的一元二次方程；
2、通过因式分解解法对一元二次方程进行求解， 体会降次的思想；
3、体验问题解决方法的多样性，灵活选择最为简 便的解决方法。
回顾旧知
1、什么叫做因式分解？
把一个多项式写成几个因式的乘积的形式叫做因式分解。
人教版数学九年级上册 因式分解法
解：(1)(1－x)2＝3，∴(x－1)2＝3，x－1＝± 3. ∴x1＝1＋ 3，x2＝1－ 3. (2)移项，得x2－6x＝19. 配方，得x2－6x＋(－3)2＝19＋(－3)2.∴(x－3)2＝28. ∴x－3＝±2 7 .∴x1＝3＋2 7 ，x2＝3－2 7 .
探究新知
(3)3x2＝4x＋1;
∴3x＋2＝0 或 12x＋10＝0. ∴x1＝－23，x2＝－56.
链接中考
1.已知x=2是关于x的一元二次方程kx²+（k²﹣2）
x+2k+4=0的一个根，则k的值为 ﹣3 ．
2. 解方程：2（x﹣3）=3x（x﹣3）．
解： 2（x﹣3）=3x（x﹣3），
移项得
2（x﹣3）﹣3x（x﹣3）=0，
10x 4.9x2 0
解： 4.9x2 10x 0
a = 4.9，b =－10，c = 0.
b2－4ac= (－10)2－0=100
x b
b2 4ac 10 10
2a
2 4.9
x1
100 ， 49
x2 0.
探究新知
10x 4.9x2 0
如果a ·b = 0，
因式分解
那么 a = 0或 b = 0.
探究新知 归纳总结
分解因式法解一元二次方程的步骤是:
1. 将方程右边化为等于0的形式； 2. 将方程左边因式分解为A×B； 3. 根据“ab=0,则a=0或b=0”,转化为两个一元一次方程； 4. 分别解这两个一元一次方程，它们的根就是原方程的根.
探究新知
素养考点 1 因式分解法解一元二次方程
例1 解下列方程： （1）x(x-2)+x-2=0
探究新知
(5)5x(x－3)－(x－3)(x＋1)＝0； (6)4(3x＋1)2＝25(x－2)2.
探究新知
(3)3x2＝4x＋1;
∴3x＋2＝0 或 12x＋10＝0. ∴x1＝－23，x2＝－56.
链接中考
1.已知x=2是关于x的一元二次方程kx²+（k²﹣2）
x+2k+4=0的一个根，则k的值为 ﹣3 ．
2. 解方程：2（x﹣3）=3x（x﹣3）．
解： 2（x﹣3）=3x（x﹣3），
移项得
2（x﹣3）﹣3x（x﹣3）=0，
10x 4.9x2 0
解： 4.9x2 10x 0
a = 4.9，b =－10，c = 0.
b2－4ac= (－10)2－0=100
x b
b2 4ac 10 10
2a
2 4.9
x1
100 ， 49
x2 0.
探究新知
10x 4.9x2 0
如果a ·b = 0，
因式分解
那么 a = 0或 b = 0.
探究新知 归纳总结
分解因式法解一元二次方程的步骤是:
1. 将方程右边化为等于0的形式； 2. 将方程左边因式分解为A×B； 3. 根据“ab=0,则a=0或b=0”,转化为两个一元一次方程； 4. 分别解这两个一元一次方程，它们的根就是原方程的根.
探究新知
素养考点 1 因式分解法解一元二次方程
例1 解下列方程： （1）x(x-2)+x-2=0
探究新知
(5)5x(x－3)－(x－3)(x＋1)＝0； (6)4(3x＋1)2＝25(x－2)2.
因式分解法(教学课件)—2025学年人教版数学九年级上册
即
10x－4.9x2.
配方法解方程 10x - 4.9x2 = 0
解： x2 100 x 0， 49
x2
100 49
x
50 49
2
0
50 49
2
x
50 49
2
50 49
2
，
x 50 50，
49 49
x1
100 ， 49
x2 0.
【注意】不能随意在方程两边约去含未知数的代数式， 如 x(x - 1) = x，若约去 x，则会丢失 x = 0这个根．
几种常见的用因式分解法求解的方程：
（1）形如 x2 +bx = 0 的一元二次方程，将左边运用提公因式法因
式分解为 x(x+b) = 0，则 x = 0 或 x+b = 0，即 x1= 0， x2 = -b.
A. x 2
B. x 3
C. x1 2 ， x2 3
D. x1 2 ， x2 3
解析：因为 (x 2)(x 3) 0 ，所以 x 2 0 或 x 3 0 ， 解得 x1 2 ， x2 3 .故选 D.
练习 3 已知某一元二次方程的两根分别为 x1 3 ， x2 4 ，则这个
方程可能为( C )
A. (x 3)(x 4) 0 C. (x 3)(x 4) 0
B. (x 3)(x 4) 0 D. (x 3)(x 4) 0
解析：A、 (x 3)(x 4) 0 ，解得： x1 3 ， x2 4 ，符合题意； B、 (x 3)(x 4) 0 ，解得： x1 3， x2 4 ，不符合题意； C、 (x 3)(x 4) 0 ，解得： x1 3， x2 4 ，不符合题意； D、 (x 3)(x 4) 0 ，解得： x1 3， x2 4 ，不符合题意； 故选：A.
数学人教版九年级上册一元二次方程的解法——因式分解法.2.3 因式分解法
4x2 10.
因式分解，得 ( 2x＋1)( 2x－1 )=0. 2x＋1=0或2x－1=0, 于是得
1 1 x1 , x2 . 2 2
典例精析
例2 用适当的方法解方程： （1）3x（x + 5）= 5（x + 5）； （2）（5x + 1）2 = 1；
分析：该式左右两边可以提取公因式， 分析：方程一边以平方形式出现， 所以用因式分解法解答较快. 另一边是常数，可直接开平方法.
问题1 根据物理学规律，如果把一个物体从地 面以10m/s的速度竖直上抛，那么经过xs物体离 地面的高度(单位：m)为10x-4.9x2.你能根据上
述规律求出物体经过多少秒落回地面吗(精确
到0.01s)? 提示： 设物体经过xs落回地面，这时它离地面
的高度为0，即
10x-4.9x2 =0
配方法解方程10x-4.9x2=0.
解：化为一般式为 x2－2x+1 = 0.
开平方,得
2 7 2 7 x ,x . 解得 x1= 6 2 10 , x2= 6 2 10. 1 2 3 3
x-6 21 0 .
（ -4 ） 2 8 2 7 x . 2 3 3
要点归纳
解法选择基本思路
(1)一般地，当一元二次方程一次项系数为0时（ax2+c=0），
解：化简 (3x -5) (x + 5) = 0. 即 3x - 5 = 0 或 x + 5 = 0.
解：开平方,得 5x + 1 = ±1.
5 x ,x 5. 1 2 3
2 解得, x 1= 0 , x2 = . 5
（3）x2 - 12x = 4 ;
分析：二次项的系数为1,一次项的系
21.21.3 因式分解法 数学人教版九年级上册知识清单+例题讲解+课后练习(含解析)
【类型一：直接利用等式等于 0 求解方程】
1．方程 x(x-6)=0 的解是（ ）
A．x=6
B．x1=0，x2=6
C．x=-6
D．x1=0，x2=-6
2．若关于 x 的一元二次方程的根分别为-5，7，则该方程可以为（ ）
A．（x+5）（x-7）=0 B．（x-5）（x+7）=0 C．（x+5）（x+7）=0 D．（x-5）（x-7）=0
C．24 或
D．
25．已知实数 x 满足（x2﹣2x+1）2+2（x2﹣2x+1）﹣3＝0，那么 x2﹣2x+1 的值为（ ）
A．﹣1 或 3
B．﹣3 或 1
C．3
D．1
26．用换元法解方程
时，如果设 ，那么原方程可变形为（ ）
A．
B．
C．
D．
27．若 2x2+1 与 4x2－2x－5 互为相反数，则 x 为
3．一元二次方程
的根是
【类型二：提公因式解方程】
4．方程（x﹣1）（x+3）＝x﹣1 的根是（ ）
A．x＝1
B．x1＝﹣3，x2＝1 C．x1＝﹣2，x2＝1 D．x1＝﹣3，x2＝0
5．用因式分解法把方程
分解成两个一次方程，正确的是（ ）
A．
B．
C．
D．
6．一元二次方程
的解是 ．
7．解方程:
.
【类型三：十字相乘法解方程】
8．方程 x2+x﹣6＝0 的两个根为（ ）
A．x1＝﹣3，x2＝﹣2
B．x1＝﹣3，x2＝2
C．x1＝﹣2，x2＝3
D．x1＝2，x2＝3
9．如果一个三角形两边的长分别等于一元二次方程
人教版数学九年级上册 因式分解法
+
−
，
=
②2x²-9x+8=0
③4x(2x+1)=3(2x+1) = − ， =
= ， =
④3x²-7x+2=0
=
温馨提示：计算△=b²-4ac，若为平方数，此方程必定可以
因式分解。
②(2x-1)²-x²=0
= ， =
③x²-12x+35=0
= ， =
例题2
下面是小明同学在解一道一元二次的过程，你认为
正确吗？为什么？
解方程： x²=2x
解：方程两边同时除以x
得 x=2
∴方程的解为x=2
易错点：漏解
用合适的方法解一元二次方程
直接开平方法：
可以解ax²=b 型的方程 .
探究因式分解法解一元二次方程
例题1
配方法
解方程
x²−4x=0
解：x²−4x=0
x²-4x+4=4
(x-2)²=4
x-2=±2
x =2±2
∴ =4， =0
因式分解法
由于不是所有的
方程都能因式分
解，这种方法仅
限于能因式分解
的一元二次方程.
解：x²−4x=0
x(x-4)=0
∴ =4， =0
可以发现，上述解法中，使方程化为两个一次式的乘积等于
也可将方程的解代入原
0的形式，再使这两个一次式分别等于0，从而实现降次，
方程来验证是否正确
这种解一元二次方程的方法叫做因式分解法。
练习
1-1
用因式分解法解下列方程
①(x-2)²=3(x-2)
人教版数学九年级上册因式分解法课件
.
5. 用适当方法解下列方程：
（1）(2x+3)2-25=0; 解：化简，得
（2）x2+5x+7=3x+11； 解：化简，得
4x2+12x+9-25=0
x2+2x=4
x2+3x-4=0
x2+2x+1=5
分解因式，得
(x+1)2=5
(x-1)(x+4)=0
x1 5
x1=1, x2=-4来自x1 1 5, x2 1 5
解方程10x-4.9x2=0时，不是用开平方降次，而 是先因式分解，使方程化为两个一次式的乘积等于 0的情势，再使这两个一次式分别等于0，从而实现 降次。这种解一元二次方程的方法叫做因式分解法。
解下列方程： x(x-2)+x-2=0； 解： 分解因式，得 (x-2)(x+1)=0 即 x-2 =0或x+1 =0, x1=2，x2=-1
,
x2=1
因式分解法：方程左边提公因式，得
(5x+4)(x-1)=0
，则x1=
4 5
，x2=1.
课堂小结
因式分解法
通过因式分解 实现降次来解 一元二次方程
提公因式法 公式法
十字相乘法
完全平方公式 平方差公式
解下列方程： (x-2)·(x-3)=0； 解： 由题可得
x-2=0或x-3=0 x1=2, x2=3
4x2－11x=0.
解： 分解因式，得
4
x
x
11 4
0
故x=0或 x 11 0
4
x1=0,x2
11 4
你能归纳出用因式分解法解方一元二次程的一般步骤吗？
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
因式分解复习课教案
山头店镇初级中学范专专
教学目标:
1.知识与技能:掌握运用提公因式法、公式法分解因式,培养学生应用因式分解解决问题的能力.
2.过程与方法:经历探索因式分解方法的过程,培养学生研讨问题的方法,通过猜测、推理、验证、归纳等步骤,得出因式分解的方法.
3.情感态度与价值观:通过因式分解的学习,使学生体会数学美,体会成功的自信和团结合作精神,并体会整体数学思想和转化的数学思想.
教学重、难点:用提公因式法和公式法分解因式.
教具准备:多媒体课件
教学方法:活动探究法
教学过程:
知识详解
知识点1 因式分解的定义
把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.
【说明】 (1)因式分解与整式乘法是相反方向的变形.
例如:
(2)因式分解是恒等变形,因此可以用整式乘法来检验.
怎样把一个多项式分解因式? 一般方法有两个：
知识点2 提公因式法
多项式ma+mb+mc 中的各项都有一个公共的因式m,我们把因式m 叫做这个多项式的公因式.ma+mb+mc=m(a+b+c)就是把ma+mb+mc 分解成两个因式乘积的形式,其中一个因式是各项的公因式m,另一个因式(a+b+c)是ma+mb+mc 除以m 所得的商,像这种分解因式的方法叫做提
公因式法.例如:)1(2-=-x x x x .
探究交流
例1：判断下列各式从左到右哪些是因式分解?
为什么？
(1) )2)(2(422y x y x y x -+=-
(2) xy x y x x 62)3(22
-=+
(3) 22)2(44+=++x x x
(4) 9)3)(3(2-=+-a a a 典例剖析 师生互动
例1 用提公因式法将下列各式因式分解.
（1）
y x y x 231824-； （2）2147ma ma +；
分析:(1)题直接提取公因式分解即可,(2)题首先要适当的变形, 再把b-a 化成-(a-b),然后再提取公因式.
小结 运用提公因式法分解因式时,要注意下列问题:
(1)因式分解的结果每个括号内如有同类项要合并,而且每个括号内不能再分解.
(2)如果出现像(2)小题需统一时,首先统一,尽可能使统一的个数少。
这时注意到(a-b)n=(b-a)n(n 为偶数).
学生做一做 把下列各式分解因式.
(1) (2a+b)(2a-3b)+(2a+5b)(2a+b)
(2) 23)1(2)1(4-+-q q p
知识点3 公式法
(1)平方差公式:2
2b a -=(a+b)(a-b).即两个数的平方差,等于
这两个数的和与这个数的差的积.例如:942-x =(2x+3)(2x-3).
(2)完全平方公式:222)(2b a b ab a ±=+±.即两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
例如:22222)32()3(322)2(9124y x y y x x y xy x -=+∙∙-=+-
探究交流
下列变形是否正确?为什么?
(1)
)3)(3(3x 22y x y x y -+=- (2)
222)32(964y x y xy x -=+-
(3) 22)1(12-=--x x x 例2 把下列各式分解因式.
(1)224)(a b a -+;
(2)2
25101x x +-;
(3)9)(6)(2++-+n m n m .
学生做一做 把下列各式分解因式.
(1)
1)4(2)4(222++-+x x ; (2))1(4)(2-+-+y x y x
综合运用
例3 分解因式.
(1)
x x x +-232; (2) )()(22x y y y x x -+- 分析:本题旨在考查综合运用提公因式法和公式法分解因式. 小结 解因式分解题时,首先考虑是否有公因式,如果有,先提公因式;如果没有公因式是两项,则考虑能否用平方差公式分解因式. 是三项式考虑用完全平方式,最后,直到每一个因式都不能再分解为止.
探索与创新题
例4 若22369y kxy x ++是完全平方式,则k= .
分析:完全平方式是形如:2
22b ab a +±即两数的平方和与这两个数乘积的2倍的和(或差).
学生做一做 若9)3(2+++x k x 是完全平方式,则k= . 课堂小结
用提公因式法和公式法分解因式,会运用因式分解解决计算问题.
各项有"公"先提"公",首项有负常提负,某项提出莫漏"1",括号里面分到"底"。
自我评价 知识巩固
1.若16)3(22+-+x m x 是完全平方式,则m 的值等于( )
A.3
B.-5
C.7.
D.7或-1
2.若)32)(32)(94(81)2(2-++=-x x x x n 则n 的值是( )
A.2
B.4
C.6
D.8
3.分解因式:
=-2294y x . 4.已知x-y=1,xy=2,求32232xy y x y x +-的值.
5.把多项式2
221y xy x -+-分解因式
思考题 分解因式872--x x . p ，q 公式法也是一种方法。