专题六 培优点20 抛物线的焦点弦问题

培优点20 抛物线的焦点弦问题【方法总结】直线与抛物线相交的问题，若直线过抛物线的焦点，可使用焦点弦长公式求弦长，利用焦点弦的特殊结论求解题目．【典例】1 (1)(2020·石家庄模拟)已知F 是抛物线y 2＝2px(p>0)的焦点，过F 的直线与抛物线交于A ，B 两点，AB 的中点为C ，过C 作抛物线准线的垂线交准线于C ′，若CC ′的中点为M(1,4)，则p 等于( ) A ．4 B ．8 C ．4 2 D ．8 2 【答案】 B【解析】 如图，设A(x 1，y 1)，B(x 2，y 2)，∵M(1,4)，∴y 1＋y 2＝8，又C ⎝ ⎛⎭⎪⎫2＋p 2，4，F ⎝ ⎛⎭⎪⎫p 2，0， ∴k AB ＝2，∴直线AB ：y ＝2⎝ ⎛⎭⎪⎫x －p 2， 代入y 2＝2px ， 得y 2－py －p 2＝0， ∴y 1＋y 2＝p ＝8.(2)过抛物线y 2＝4x 的焦点F 的直线l 与抛物线交于A ，B 两点，若|AF|＝2|BF|，则|AB|等于( )A ．4 B.92 C ．5 D ．6【答案】 B【解析】 不妨设点A 在x 轴的上方，如图，设A ，B 在准线上的射影分别为D ，C ，作BE ⊥AD 于点E ，设|BF|＝m ，直线l 的倾斜角为θ， 则|AF|＝2m ，|AB|＝3m ， 由抛物线的定义知|AD|＝|AF|＝2m ，|BC|＝|BF|＝m ， 所以cos θ＝|AE||AB|＝13，所以tan θ＝2 2.则sin 2θ＝8cos 2θ，所以sin 2θ＝89.由y 2＝4x ，知2p ＝4，故利用弦长公式得|AB|＝2p sin 2θ＝92. 【典例】2 已知抛物线C ：y 2＝8x ，P 为C 上位于第一象限的任一点，直线l 与C 相切于点P ，连接PF 并延长交C 于点M ，过P 点作l 的垂线交C 于另一点N ，求△PMN 的面积S 的最小值．【解析】解 由题意知F(2,0)，设P(x 0，y 0)(y 0>0)，M ⎝ ⎛⎭⎪⎫y 218，y 1， N ⎝ ⎛⎭⎪⎫y 228，y 2，切线l 的方程为x －x 0＝t(y －y 0)，则FM →＝⎝ ⎛⎭⎪⎫y 218－2，y 1，FP →＝⎝ ⎛⎭⎪⎫y 208－2，y 0，由M ，F ，P 三点共线，可知FM →∥FP →，即⎝ ⎛⎭⎪⎫y 218－2y 0－⎝ ⎛⎭⎪⎫y 208－2y 1＝0， 因为y 0≠y 1，所以化简可得y 0y 1＝－16.由⎩⎪⎨⎪⎧x －x 0＝t y －y 0，y 2＝8x ，可得y 2－8ty ＋8ty 0－8x 0＝0，因为直线l 与抛物线相切，故Δ＝64t 2－32ty 0＋4y 20＝0，故t ＝y 04.所以直线PN 的方程为y －y 0＝－y 04(x －x 0)，即y 0x ＋4y －4y 0－y 38＝0，所以点M 到直线PN 的距离为d ＝⎪⎪⎪⎪⎪⎪y 21y 08＋4y 1－4y 0－y 308y 20＋16，将y 1＝－16y 0代入可得d ＝⎪⎪⎪⎪⎪⎪32y 0＋4y 0＋y 308y 2＋16＝y 20＋1628|y 0|y 20＋16， 联立⎩⎪⎨⎪⎧y 0x ＋4y －4y 0－y 308＝0，y 2＝8x ，消去x 可得，y 0y 2＋32y －y 30－32y 0＝0，所以y 0＋y 2＝－32y 0，y 2＝－32y 0－y 0，|PN|＝1＋16y 20|y 0－y 2|＝1＋16y 20⎪⎪⎪⎪⎪⎪2y 0＋32y 0＝2y 20＋16y 20＋16y 20，故S ＝12d|PN|＝12×y 20＋1628|y 0|y 20＋16×2y 20＋16y 20＋16y 20＝18⎝ ⎛⎭⎪⎫y 20＋16y 03＝18⎝ ⎛⎭⎪⎫y 0＋16y 03 ≥18⎝⎛⎭⎪⎫2y 0·16y 03＝64，当且仅当y 0＝4时，“＝”成立，此时，△PMN 的面积S 取得最小值，为64. 【方法总结】设AB 是抛物线y 2＝2px(p>0)的一条焦点弦，焦点为F ，A(x 1，y 1)，B(x 2，y 2)，则 (1)x 1x 2＝p 24，y 1y 2＝－p 2.(2)1|AF|＋1|BF|＝2p. (3)|AB|＝2psin 2α(α为弦AB 所在直线的倾斜角)． 【拓展训练】1．设F 为抛物线C ：y 2＝3x 的焦点，过F 且倾斜角为30° 的直线交C 于A ，B 两点，O 为坐标原点，则△OAB 的面积为( ) A.334 B.938 C.6332 D.94【答案】 D【解析】 由已知得焦点为F ⎝ ⎛⎭⎪⎫34，0，因此直线AB 的方程为y ＝33⎝ ⎛⎭⎪⎫x －34，即4x －43y －3＝0.方法一 联立直线方程与抛物线方程，化简得4y 2－123y －9＝0， 故|y A －y B |＝y A ＋y B2－4y A y B ＝6.因此S △OAB ＝12|OF||y A －y B |＝12×34×6＝94.方法二 联立直线方程与抛物线方程得x 2－212x ＋916＝0，故x A ＋x B ＝212.根据抛物线的定义有|AB|＝x A ＋x B ＋p ＝212＋32＝12，同时原点到直线AB 的距离为d ＝|－3|42＋－432＝38， 因此S △OAB ＝12|AB|·d ＝94.2．过抛物线y 2＝2px(p>0)的焦点F 且倾斜角为120° 的直线l 与抛物线在第一、四象限分别交于A ，B 两点，则|AF||BF|的值等于( )A.13B.23C.34D.43 【答案】 A【解析】 记抛物线y 2＝2px 的准线为l ′，如图，作AA 1⊥l ′，BB 1⊥l ′，AC ⊥BB 1，垂足分别是A 1，B 1，C ，则cos ∠ABB 1＝|BC||AB|＝|BB 1|－|AA 1||AF|＋|BF|＝|BF|－|AF||AF|＋|BF|，即cos 60°＝|BF|－|AF||AF|＋|BF|＝12，得|AF||BF|＝13. 3．已知抛物线C ：y 2＝8x 的焦点为F ，点M(－2,2)，过点F 且斜率为k 的直线与C 交于A ，B 两点，若∠AMB ＝90°，则k 等于( )A. 2B.22 C.12D ．2 【答案】 D【解析】 抛物线C ：y 2＝8x 的焦点为F(2,0)， 由题意可知直线AB 的斜率一定存在， 所以设直线方程为y ＝k(x －2)(k ≠0)， 代入抛物线方程可得k 2x 2－(4k 2＋8)x ＋4k 2＝0， 设A(x 1，y 1)，B(x 2，y 2)， 则x 1＋x 2＝4＋8k 2，x 1x 2＝4，所以y 1＋y 2＝8k，y 1y 2＝－16，因为∠AMB ＝90°，所以M A →·M B →＝(x 1＋2，y 1－2)·(x 2＋2，y 2－2)＝16k 2－16k ＋4＝0，解得k ＝2，故选D.4.如图，已知点F(1,0)为抛物线y 2＝2px(p>0)的焦点，过点F 的直线交抛物线于A ，B 两点，点C 在抛物线上，使得△ABC 的重心G 在x 轴上，直线AC 交x 轴于点Q ，且Q 在点F 右侧，记△AFG ，△CQG 的面积为S 1，S 2.(1)求p 的值及抛物线的准线方程； (2)求S 1S 2的最小值及此时点G 的坐标．【解析】解 (1)由题意可得p2＝1，则p ＝2,2p ＝4，抛物线方程为y 2＝4x ，准线方程为x ＝－1. (2)设A(x 1，y 1)，B(x 2，y 2)， 直线AB 的方程为y ＝k(x －1)，k>0， 与抛物线方程y 2＝4x 联立可得， k 2x 2－(2k 2＋4)x ＋k 2＝0， 故x 1＋x 2＝2＋4k 2，x 1x 2＝1，y 1＋y 2＝k(x 1＋x 2－2)＝4k ，y 1y 2＝－4x 1×4x 2＝－4，设C(x 3，y 3)，由重心坐标公式可得， x G ＝x 1＋x 2＋x 33＝13⎝ ⎛⎭⎪⎫2＋4k 2＋x 3， y G ＝y 1＋y 2＋y 33＝13⎝ ⎛⎭⎪⎫4k ＋y 3，令y G ＝0可得，y 3＝－4k ，则x 3＝y 234＝4k 2，即x G ＝13⎝⎛⎭⎪⎫2＋4k 2＋4k 2＝13⎝ ⎛⎭⎪⎫2＋8k 2，由斜率公式可得，k AC ＝y 1－y 3x 1－x 3＝y 1－y 3y 214－y 234＝4y 1＋y 3，直线AC 的方程为y －y 3＝4y 1＋y 3(x －x 3)，令y ＝0，可得x Q ＝x 3＋－y 3y 1＋y 34＝y 234＋－y 3y 1＋y 34＝－y 1y 34，故S 1＝12×(x G －x F )×y 1＝12×⎣⎢⎡⎦⎥⎤13⎝ ⎛⎭⎪⎫2＋8k 2－1×y 1＝y 12×⎝ ⎛⎭⎪⎫83k 2－13，且S 2＝12×(x Q －x G )×(－y 3)＝－y 32⎣⎢⎡⎦⎥⎤－y 1y 34－13⎝ ⎛⎭⎪⎫2＋8k 2， 由y 3＝－4k ，代入上式可得S 2＝2k ⎝ ⎛⎭⎪⎫y 1k －23－83k 2，由y 1＋y 2＝4k ，y 1y 2＝－4可得y 1－4y 1＝4k ，则k ＝4y 1y 21－4，则S 1S 2＝y 12×⎝ ⎛⎭⎪⎫83k 2－132k ⎝ ⎛⎭⎪⎫y 1k －23－83k 2＝2y 21y 21－2y 21－4y 21＋4＝2－4y 21－8＋48y 21－8＋16≥2－42y 21－8×48y 21－8＋16＝1＋32， 当且仅当y 21－8＝48y 21－8，即y 21＝8＋43，y 1＝6＋2时等号成立，此时k ＝4y 1y 21－4＝2，x G＝13⎝⎛⎭⎪⎫2＋8k 2＝2，则点G 的坐标为(2,0)．。

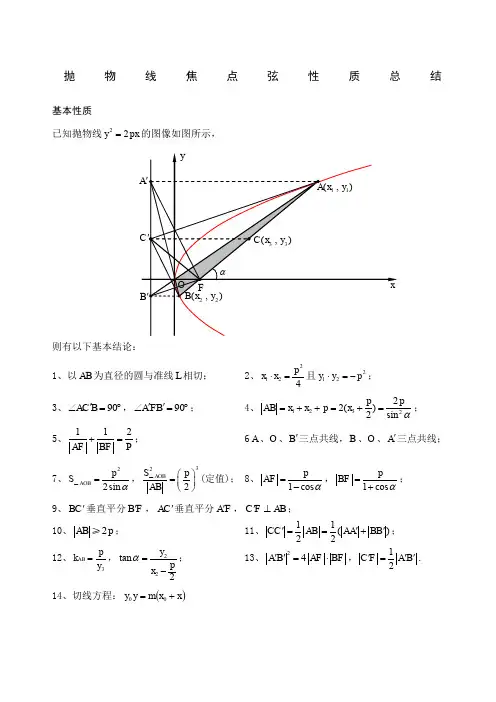
抛物线焦点弦性质总结基本性质 已知抛物线22y px =的图像如图所示，则有以下基本结论：1、以AB 为直径的圆与准线L 相切；2、2124p x x ⋅=且212y y p ⋅=-；3、90AC B '∠=︒，90A FB ''∠=︒；4、123222()2sin p p AB x x p x α=++=+=；5、112AF BF P +=；6A 、O 、B '三点共线，B 、O 、A '三点共线；7、22sin AOB p S α=△，322AOB S p AB ⎛⎫= ⎪⎝⎭△(定值)； 8、1cos p AF α=-，1cos p BF α=+； 9、BC '垂直平分B F '，AC '垂直平分A F '， C F AB '⊥；10、2AB p ≥；11、11()22CC AB AA BB '''==+； 12、3AB p k y =，22tan 2y p x α=-； 13、24A B AF BF ''=⋅，12C F A B '''=. 14、切线方程：()x x m y y +=00性质深究一、焦点弦与切线结论1、过抛物线焦点弦的两端点作抛物线的切线，两切线交点在准线上．特别地，当弦x AB ⊥轴时，则点P 的坐标为,02p ⎛⎫- ⎪⎝⎭． 结论2、切线交点与弦中点连线平行于对称轴结论3、弦AB 不过焦点即切线交点P 不在准线上时，切线交点与弦中点的连线也平行于对称轴．结论4、过抛物线准线上任一点作抛物线的切线，则过两切点的弦必过焦点．特别地，过准线与x 轴的交点作抛物线的切线，则过两切点AB 的弦必过焦点．结论5、过准线上任一点作抛物线的切线，过两切点的弦最短时，即为通径．AB 是抛物线px y 22=（p ＞0）焦点弦，Q 是AB 的中点，l 是抛物线的准线，l AA ⊥1，l BB ⊥1，过A ，B 的切线相交于P ，PQ 与抛物线交于点M ．则有结论6、PA ⊥PB ．结论7、PF ⊥AB ． 结论8、M 平分PQ ． 结论9、PA 平分∠A 1AB ，PB 平分∠B 1BA ．结论102PF =结论11、PAB S ∆2min p =二、非焦点弦与切线 当弦AB 不过焦点，切线交于P 点时，也有与上述结论类似结果：结论12、①p y y x p 221=，221y y y p += 结论13、PA 平分∠A 1AB ，同理PB 平分∠B 1BA ．结论14、PFB PFA ∠=∠结论15、点M 平分PQ结论162=。

抛物线焦点弦的有关结论知识点1：若AB是过抛物线()022>=ppxy的焦点F的弦。

设(),,11yxA()22,yxB，则（1）4221pxx=；（2）221pyy-=证明：如图，（1）若AB的斜率不存在时，依题意,221pxx==4221pxx=∴若AB的斜率存在时，设为,k则⎭⎝⎛-=2:xkyAB()042222222222=++-⇒=⎪⎭⎫⎝⎛-pkpxkxkpxpxk.4221pxx=∴综上：.4221pxx=（2）pyxpyx2,2222211==，,22142221pyypyy±=⇒=∴但22121,0pyyyy-=∴<（2）另证：设2:pmyxAB+=与pxy22=联立，得22122,02pyyppmyy-=∴=--知识点2：若AB是过抛物线()022>=ppxy的焦点F的弦。

设(),,11yxA()22,yxB，则（1）;21pxxAB++=（2）设直线AB的倾斜角为α，则2sin2pAB=证明：（1）由抛物线的定义知,2,221pxBFpxAF+=+=pxxBFAFAB++=+=∴21（2）若,2,9021pxx===则α由（1）知α2sin22ppAB==若pxypxkyAB2,2:,9020=⎪⎭⎫⎝⎛-=≠与设α联立，得()042222222222=++-⇒=⎪⎭⎫⎝⎛-pkpxkxkpxpxk(),22221kkpxx+=+∴()222112kkppxxAB+=++=∴，而αtan=k，()ααα222sin2tantan12ppAB=+=∴知识点3：若AB是过抛物线()022>=ppxy的焦点F的弦，则以AB为直径的圆与抛物线的准线相切。

证明：过点BA、分别向抛物线的准线引垂线，垂足分别为,11BA、过AB中点M向准线引垂线，垂足为,N设以AB为直径的圆的半径为,r.2211rMNMNBBAABFAFABr=∴=+=+==∴以AB为直径的圆与抛物线的准线相切。

（难度3星）1.（2019 •安徽高二期末（文））在平而直角坐标系中，抛物线关于轴对称，顶点为坐标原点，且经过点（2（1）求抛物线的标准方程：（2）过点 3的直线交抛物线于弘"两点，尸点是直线：=一2上任意一点.证明：直线、、的斜率依次成等差数列.【答案】（1）—2 : （2）证明见解析【解析】（1）因为抛物线关于轴对称，可设抛物线为亠2，而点（玄②在抛物线上，从而有另=2X2,得 =故抛物线方程为2=2 ：（2）设点（―）是直线上任意一点，直线交抛物线于“、"两点，所以直线的斜率不等于0,可设直线：= +2交抛物线于（”』）、（？，？），由｛可得：--2 - 2= 0从而有j + 2=2, 1 2= ~~ 2,1 ~ _ 2~= ------- •= ------ 9 =— --1^1 ?+/ 21且在直线上，所以有：1= 丄+Z 2= E+Z-2 —=―：=一'而2 =-，即证得证直线，,+ =2的斜率成等差数列.（难度2星）2. （2020 •河南高二期末（理））已知是抛物线： I （2,）是抛物线上一点，且| |=2（1）求抛物线的方程：（2）直线与抛物线交于，两点，若―'• 一 = -彳（否会过某个泄点若是，求出该立点坐标，若不是，说明理由.【答案】（1）2=4:⑵是，（2,6.【解析】（1）由抛物线的泄义知I | =』+三=2,.・.=2,•••抛物线的方程为：2=4（2）由题意知:可设的方程为：= + ,代入'=4有2— 4 — 4 = 0、（＞。

的焦点,为坐标原点），则直线是设(b 1}>( 9 2)> 则r 2= -4、・・「（宀一么••1 2_ 托 _ 、S・・・•= 广？+ 厂2= 4 =_4 ・•・ =2••• 的方程为 = +Z恒过点（2,0）.所以直线过左点（20・（难度2星）3.（2020 •江西高二期末（文））已知抛物线：亠2（2_ 2=谢圆心.（1）求抛物线Q的标准方程：（2）过抛物线的焦点尸的直线』与抛物线相交于两点，程.■【答案】（1）2=4（2）=2一戒=_2 +2【解析】（1）圆的标准方程为（一庁+ 2*圆心坐标为（20,>0的焦点尸为圆2 +| = £求直线』的方即焦点坐标为 g 则7= I =缩到抛物线的方程亠4（2）设直线的方程为: + /联立抛物线的方程2=4消整理得: 2- {4 2+2) +1=0：.』+ 尸 4 - + 2根据焦点弦的性质可知：| |= ；+ .+ =4 2+4又因为| | = 5 ..4 2+4=M得=±：所以所求直线的方程为：=2 = _2 +2（难度2星）4.（2019 •四川高二期末（文））已知点（一2。

有关抛物线焦点弦问题的探讨过抛物线px y 22=(p>0)的焦点F 作一条直线L 和此抛物线相交于A ),(11y x 、B ),(22y x 两点结论1：p x x AB ++=21p x x px p x BF AF AB ++=+++=+=2121)2()2( 结论2：若直线L 的倾斜角为θ，则弦长θ2sin 2pAB = 证: (1)若2πθ= 时,直线L 的斜率不存在，此时AB 为抛物线的通径,结论得证∴=∴p AB 2(2)若2πθ≠时,设直线L 的方程为：θtan )2(p x y -=即2cot py x +⋅=θ 代入抛物线方程得0cot 222=-⋅-p py y θ由韦达定理θcot 2,21221p y y p y y =+-=由弦长公式得θθθ22212sin 2)cot 1(2cot1pp y y AB =+=-+= 结论3： 过焦点的弦中通径长最小p p2sin 21sin 22≥∴≤θθ ∴AB 的最小值为p 2,即过焦点的弦长中通径长最短.结论4： )(832为定值p AB S oAB =∆()8sin 2sin sin 2221sin 21sin 21sin 21sin 2132220P AB S p p p AB OF BF AF OF AF OF BF OF S S S OAB AF OBF OAB =∴=⋅⋅⋅=⋅⋅=+⋅=⋅⋅+⋅⋅=+=∆∆∆∆θθθθθϑθ结论5： (1) 221p y y -= (2) x 1x 2=42p证44)(,2,22222121222211P P y y x x p y x p y x ==∴== 结论6：以AB 为直径的圆与抛物线的准线相切证：设M 为AB 的中点，过A 点作准线的垂线AA 1， 过B 点作准线的垂线BB 1， 过M 点作准线的垂线MM 1，由梯形的中位线性质和抛物线的定义知 222111AB BFAF BB AA MM =+=+=故结论得证结论7：连接A 1F 、B 1 F 则 A 1F ⊥B 1FFA A FO A FO A F AA OF AA AFA F AA AF AA 11111111//,∠=∠∴∠=∠∴∠=∠∴=同理︒=∠∴∠=∠901111FB A FB B FO B ∴A 1F ⊥B 1 F 结论8：（1）AM 1⊥BM 1 （2）M 1F ⊥AB （3）BF AF FM ⋅=21（4）设AM 1 与A 1F 相交于H ，M 1B 与 FB 1相交于Q 则M 1，Q ，F ，H 四点共圆 （5）2121214M M B M AM =+证：由结论（6）知M 1 在以AB 为直径的圆上∴ AM 1⊥BM 111FB A ∆为直角三角形， M 1 是斜边A 1 B 1 的中点111111111AFA F AA F A M FA M F M M A ∠=∠∠=∠∴=∴︒=∠=∠+∠9011111M AA M FA F AA ︒=∠+∠∴90111FM A AFA∴M 1F ⊥ABBF AF F M ⋅=∴21 AM 1⊥BM 1 F B F A 90111⊥︒=∠∴ 又B AM︒=∠∴90FB A 11 所以M 1，Q ，F,H 四点共圆，22121AB B M AM =+()()()2121211242MM MM BB AABFAF ==+=+=结论9： （1）、A O 、B 1 三点共线 （2）B ，O ，A 1 三点共线（3）设直线AO 与抛物线的准线的交点为B 1，则BB 1平行于X 轴（4）设直线BO 与抛物线的准线的交点为A 1，则AA 1平行于X 轴证：因为p y p y k y p py y x y k oB oA 2212111122,221-=-====，而221p y y -=所以122222oB oA k p y y ppk =-=-=所以三点共线。

《抛物线的焦点弦》专题2019年（ ）月（ ）日 班级 姓名),(),,(.12211y x B y x A ）（ ,,421221221p x x AB p y y p x x ++=-==，pBF AF p S p AB AOB 211,sin 2,sin 2222=+==∆αα）（（3）以AB 为直径的圆与抛物线的准线过抛物线y 2=2px （p ＞0）的焦点F 的直线与抛物线相交于A ，B 两点，自A ，B 向准线作垂线，垂足分别为A ′，B ′，则∠A′FB′=______．【点坐标处理焦点弦问题】1抛物线x y 42=与过焦点的直线交于A ,B 两点，则=∙OB OA2. 过抛物线x y 42=焦点的直线交抛物线于),(),,(2211y x B y x A 两点，如果621=+x x ，那么AB =3.已知抛物线y 2＝4x (p >0)，过其焦点的直线交抛物线于A 、B 两点，若线段AB 的中点的横坐标为2，则AB =4.抛物线x y 42=的焦点做直线交抛物线于A ,B 两点，如果AB =8，O 为坐标原点，则△OAB 的重心的横坐标是【长度与角处理焦点弦问题】1.斜率为1的直线经过抛物线4x y 2=的焦点，与抛物线相交A ，B 两点，求线段AB 的长。

2.过抛物线x y 92=的焦点的弦AB 长为12，则直线AB 倾斜角为3.已知过抛物线()y px p 2=2>0的焦点，斜率为的直线交抛物线于(,)A x y 11和(,)()B x y x x 2112<两点，且AB =9,则抛物线的方程4.过抛物线)0(22>=p px y 的焦点F 作倾斜角为 30的直线交抛物线于A 、B 两点，若线段AB 的长为8，则=p _____________5.过抛物线24y x =的焦点作倾斜角为45的直线l 交抛物线于A ，B 两点，O 为坐标原点，则△OAB 的面积为6.在直角坐标系xoy 中,直线l 过抛物线24y x =的焦F ,且与该抛物线相交于A 、B 两点,其中点A 在x 轴上方,若直线l 的倾斜角为60°,则△OAF 的面积为_______7.设F 为抛物线C:23y x =的焦点，过F 且倾斜角为30°的直线交C 于A,B 两点，O 为坐标原点，则△OAB 的面积为（ ）A. B. C. 6332 D. 94 8.过抛物线2(0)y ax a =>的焦点F 作一直线交抛物线于P Q ，两点，若线段PF 与FQ 的长分别是p q ，，则11p q+=9.过抛物线)0(2>=a ax y 的焦点F 作一直线交抛物线于B A ,两点，若线段BF AF ,的长分别为n m ,，则nm mn +等于10.过抛物线()220y px p =>的焦点F 的直线交抛物线于A,B 两点， 已知3,2AF BF ==，则p 等于 .11.过抛物线24y x ＝的焦点F 的直线交抛物线于A ，B 两点，若｜AF ｜＝5，则｜BF ｜＝12.如图过抛物线y 2＝2px (p ＞0)的焦点的直线l 依次交抛物线及其准线与点A ，B ，C ，若|BC |＝2|BF |，且|AF |＝3，则p=________．13已知直线)0(),2(>-=k x k y 与抛物线C:x y 82=相交A 、B 两点，F 为C 的焦点。