(完整word版)四年级下册奥数题三角形内角和

人教版四年级数学下册第五单元知识点归纳整理第五单元《三角形》一、三角形的认识及特性1、三角形的定义：由3条线段围成的图形（每相邻两条线段的端点相连）叫做三角形。

2、三角形的特点：三角形有3条边、3个角和3个顶点。

3、三角形的底和高：从三角形的一个顶点到它的对边做一条垂线，顶点和垂足之间的线段叫做三角形的高，这条对边叫做三角形的底。

例如：从三角形的一个顶点到它的对边作一条垂线，如图所示：顶点顶点 边AB4、为了表达方便，用字母A、B、C分别表示三角形的三个顶点，上面的三角形可以表示成三角形ABC。

5、三角形的特性：三角形具有稳定性。

6、两点间的距离：两点间所有连线中线段最短，这条线段的长度叫做两点间的距离。

7、三角形三条边的关系：三角形任意两边的和大于第三边。

8、判断3条线段能否围城三角形，只要把较短的两条线段相加的和与最长的线段比较，大于最长的线段就能围成三角形，反之则不能。

二、三角形的分类1、三角形按角分为：锐角三角形、直角三角形和钝角三角形。

①、三个角都是锐角的三角形叫做锐角三角形；②、有一个角是直角的三角形叫做直角三角形；③、有一个角是钝角的三角形叫做钝角三角形。

用集合图形表示为：2、直角三角形的特性：3、三角形按边分为：不等边三角形和等腰三角形（等腰三角形包括等边三角形）用集合图形表示为：直角边直角边4、认识等腰三角形：在等腰三角形中，相等的两条边叫做腰，另一条边叫底；两腰的夹角叫做顶角，两腰与底边的两个夹角底温馨提示：等腰三角形可以是锐角三角形、直角三角形或钝角三角形。

在直角三角形中，如果两条直角边相等，这个直角三角形叫做等腰直角三角形，它的两个底角分别是45°.5、认识等边三角形：三条边相等的三角形叫做等边三角形（也叫正三角形）。

①、等边三角形的特点：3条边都相等，3个角都相等，每个角都是60°。

②、与等腰三角形的关系：等边三角形是特殊的等腰三角形，当等腰三角形的两条腰与底边相等时，这个等腰三角形就是等边三角形。

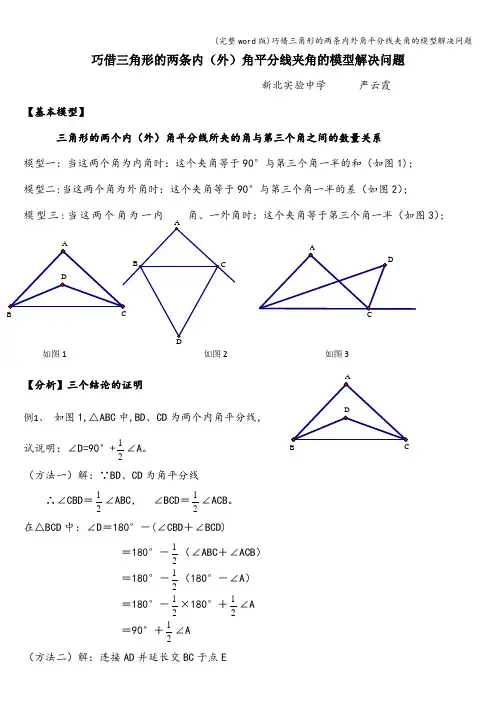
B巧借三角形的两条内（外）角平分线夹角的模型解决问题新北实验中学 严云霞【基本模型】三角形的两个内（外）角平分线所夹的角与第三个角之间的数量关系 模型一：当这两个角为内角时：这个夹角等于90°与第三个角一半的和（如图1)； 模型二:当这两个角为外角时：这个夹角等于90°与第三个角一半的差（如图2）； 模型三:当这两个角为一内角、一外角时：这个夹角等于第三个角一半（如图3）；【分析】三个结论的证明例1、 如图1,△ABC 中,BD 、CD 为两个内角平分线，试说明：∠D=90°+21∠A 。

（方法一）解：∵BD 、CD 为角平分线∴∠CBD ＝21∠ABC ， ∠BCD ＝21∠ACB 。

在△BCD 中：∠D ＝180°－(∠CBD ＋∠BCD)＝180°－21（∠ABC ＋∠ACB ）＝180°－21（180°－∠A ）＝180°－21×180°＋21∠A＝90°＋21∠A（方法二）解：连接AD 并延长交BC 于点EE DCBA解:∵BD 、CD 为角平分线∴∠CBD ＝21∠ABC, ∠BCD ＝21∠ACB 。

∵∠BDE 是△ABD 的外角 ∴∠BDE ＝∠BAD+∠ABD=∠BAD+21∠ABC同理可得∠CDE ＝∠CAD+21∠ACB 又∵∠BDC ＝∠BDE+∠CDE∴∠BDC ＝∠BAD+21∠ABC+∠CAD+21∠ACB＝∠BAC+21（∠ABC+∠ACB ）＝∠BAC+21（180°－∠BAC ）＝90°＋21∠BAC例２、如图,ＢＤ、ＣＤ为△ＡＢＣ的两条外角平分线， 试说明:∠D=90°－21∠A 。

解：∵BD 、CD 为角平分线∴∠CBD=21∠CBE ∠BCD ＝21∠BCF又∵∠CBE 、∠BCD 为△ABC 的外角 ∴∠CBE ＝∠A ＋∠ACB ∠BCF ＝∠A ＋∠ABC∴∠CBE ＋∠BCF ＝∠A ＋∠ACB ＋∠A ＋∠ABC ＝∠A ＋180° 在△BCD 中：∠D ＝180°－（∠CBD ＋∠BCD ） ＝180°－（21∠CBE ＋21∠BCF)＝180°－21（∠CBE ＋∠BCF ）＝180°－21(∠A ＋180°）DCBA＝90°－21∠A【小结】通过对模型1、2的分析和证明，我们还能发现三角形两内角平分线的夹角和两外角平分线的夹角互补，即和为180°。

（完整）小学四年级奥数题100道带答案有解题过程姓名：__________ 班级：__________ 学号：__________1．甲、乙两人同时从相距36千米的A、B两地相向而行，4小时后相遇。

已知甲每小时行5千米，乙每小时行多少千米？解：先根据“速度和=路程÷相遇时间”，求出甲、乙的速度和为36÷4=9（千米/小时）。

再用速度和减去甲的速度，即9-5=4（千米/小时），所以乙每小时行4千米。

2．有一堆苹果，平均分给5个小朋友余2个，平均分给7个小朋友也余2个，这堆苹果最少有多少个？解：先求出5和7的最小公倍数，5×7=35。

再加上余数2，35+2=37（个），所以这堆苹果最少有37个。

3．一个长方形的周长是24厘米，长是宽的2倍，求这个长方形的面积。

解：设宽为x厘米，则长为2x厘米。

根据“长方形周长=（长+宽）×2”，可列出方程：(x+2x)×2=24，3x×2=24，6x=24，x=4。

那么长为2×4=8（厘米），面积=长×宽=8×4=32（平方厘米）。

4．在一个除法算式中，被除数、除数、商和余数的和是100，已知商是8，余数是3，求被除数和除数各是多少？解：设除数为x，则被除数为8x+3。

根据题意可列出方程：(8x+3)+x+8+3=100，9x+14=100，9x=86，x=9.56（此处若考虑除数应为整数，则需要检查题目数据是否有误，但按照题目要求继续计算）。

被除数为8×9.56+3=79.48（同样，此处数据也因除数非整数而带有小数）。

5．小明有一些邮票，他送给小红12张后，还比小红多8张，原来小明比小红多多少张邮票？解：小明送给小红12张后还多8张，那么原来多的数量是12×2+8=32（张）。

6．有一个等差数列：3，8，13，18，…，这个数列的第20项是多少？解：先求公差为8-3=5。

一、教学分析(一) 教材分析：《三角形的内角和》是在学生学习了三角形、长方形等基本图形以及角的度量、三角形的特征、分类的基础上进行教学的，这一部分知识的理解和掌握将为进一步学习几何知识打下坚实的基础。

（二）学情分析通过前面的学习，学生已经初步认识了三角形，并会用工具量角、画角，可以说具备了探索三角形内角和的知识与技能基础。

课前通过了解，已经有不少学生知道了三角形内角和是180°，只是不知道怎样才能得出这个结论，因此学生的生活经验是可利用的教学资源。

学生在这节课上的主要目标是验证三角形的内角和是180°。

（三）教学环境由于班级人数适中，而学校班级均配备电子白板，根据课型需求以及教学内容设计，选择在本班教室进行授课。

二、教学目标（一）知识与技能：理解并掌握三角形的内角和是180°。

（二）过程与方法：通过小组合作、动手操作等活动，经历三角形内角和的探究过程，发展空间观念，并能运用所学知识解决问题。

（三）情感态度与价值观：培养学生科学实验态度，激发学生主动学习数学的兴趣，体验数学学习成功的喜悦。

三、教学重点探索、发现并验证“三角形的内角和是180°”。

四、教学难点能运用不同方法探究三角形内角和，并灵活运用这一发现解决实际问题。

五、教学用具准备多媒体课件、剪刀、量角器、不同类型的三角形、实验报告单。

六、教学流程七、教学过程（一）创境激趣小游戏：猜一猜藏在信封后面的是什么三角形。

你怎么知道的？依次出示：有直角的三角形、有钝角的三角形，有锐角的三角形。

师：我们在猜三角形的时候，看到一个直角，就能断定它一定是直角三角形；看到一个钝角，就能断定他一定是钝角三角形；但只看到一个锐角，就判断不出来是哪种三角形。

看来在一个三角形中，只能有一个直角或一个钝角，那么为什么画不出有两个直角或两个钝角的三角形呢？三角形的这三个角究竟存在什么奥秘呢，今天我们就来一起研究三角形的内角和。

（板书课题）好，上课！【设计意图】创设的不是生活中的情境，而是数学化的情境。

四年级数学下册知识结构总结用字母表示数一、用字母表示数的格式（默写）1、用字母表示数：在含有字母的式子里，数字和字母、字母和字母中间的乘号可以记作“.”，也可以省略不写。

省略时，通常把数字写在字母前面。

如：5×a x×3 a×x x×y×6 1×b 7×7 a×b a×b×c （a—b）÷3写为：5a 3x ax 6xy b 7•7 ab abc a/3－b/3或1/3(a－b)2、求含有字母的式子的值时要注意格式：首先写出字母等于几，再写出含有字母的式子，然后利用脱式计算的形式，将字母换成数再计算即可。

例：超市原有b台彩电，卖出70台后，超市还有彩电（b—70）台。

当b=150台时，超市还有彩电：b—70=150—70=80（台）二、用字母表示数量关系，1、表示路程公式：s=vt；（默写）例：一辆汽车，每小时行驶a千米，上午行驶了4小时，下午行驶了b千米，这辆汽车共行驶了（4a+b）千米。

当a=80 b=200时，这辆汽车行驶了：4a+b=4×80+200=520（千米）。

2、含字母的式子比较大小：如: “< = ˃”2Χ一定（）Χ²。

1）大于2）小于3）等于4）不能确定注意：a²和2a，当a=2时，其值相等；当a≠2时，无法确定。

3、表示面积、周长公式:（默写）正方形的面积公式：s=a•a 或s=a²长方形的面积：S=ab正方形的周长：C=4a长方形的周长：C=2•(a+b) 或c=2(a+b)4、应用类：①某班有女生X人，女生比男生少8人，则某班全体同学的人数是（2X+8）人。

如果X=23时，则某班人数为2x+8=46+8=54（人）②青青林场栽了梧桐树和雪松各X排，已知梧桐树每排12棵，雪松树每排14棵，栽梧桐树和雪松树共计（12+14）X棵。

北师大版小学四年级下册数学单元测试卷（一）班级姓名学号分数、填空题。

（24 分）1、与十分位相邻的两个数位分别是（）和（）。

2、0. 6 里面有（）个0.1 ；0.015 里面有（）0.001 。

3、小数点左边第三位是（）位，右边第二位是（）位。

4、0.48 表示把 1 平均分成（）份，取其中的（）份, 改写成分数是（）5、5.24 里面有（）个一，（）个0.1 和（）个0.01276、27写成小数是（），0.05 写成分数是（）。

1007、由二个千，三个一和四个百分之一组成的数是（）。

8、一个数十位上和百分位上都是8，其余各位上都是0，这个数写作（）。

9、在□内填上适当的分数或小数。

10、6 厘米=（）分米80 克=（）千克5 元 4 角=（）元7 米6 分米=（）米。

11、在○里填上“ <”、“>”或“ =”6.25 ○ 6.250 4.989 ○ 4.8989 0.99 元○1 元 2 米24 厘米○ 2.2412、小华在计算29.28 减一位小数时，把小数点丢了，结果为17.28 ，正确结果应是（）、判断题。

（对的在括号里打“√” ，错的打“×”。

）（10分）1、0.001 读作零点零一。

（）2、小数都比整数小。

（）3、在小数点末尾添上“ 0”或者去掉“ 0”，小数的大小不变。

（）4、在0.5 与0.7 之间的小数只有一个。

（）5、两位小数加上两位小数，结果一定是四位小数三、选择题。

（把正确的答案的序号填在括号里。

）（10 分）1、小数部分的最高位是（）位。

A、千分位 B 、百分位 C 、十分位2、下面各数中比 1 小的数有（）。

A、0.99 B 、0.109 C 、 1.03、和 2.05 大小相等的小数是（）。

A、20.05 B 、2.050 C 、 2.504、把 4 改写成以百分之一为单位的小数是（）。

A、0.04 B 、0.40 C 、4.005、、由4个百，5 个一，7 个十分之一和6个百分之一组成的数是（）A、405.76 B 、45.76 C 、450.76四、计算题。

三角形内角和、外角练习题规律方法指导1．三角形内角和为180°，三角形三个外角的和是360°,这是在做题时题设不用加以说明的已知条件；在三个角中已知其中两个角的度数便能求第三个角的大小.2．在一个三角形中最多只能有一个钝角或者一个直角，最少有两个锐角.3．三角形内角和定理和三角形外角的性质是求角度数及有关的推理论证时经常使用的理论依据．外角的性质应用：①证明一个角等于另两个角的和；②作为中间关系式证明两角相等；③证明角的不等关系.4．利用作辅助线求解问题，会使问题变得简便.经典例题透析类型一：三角形内角和定理的应用1．已知一个三角形三个内角度数的比是1：5：6，则其最大内角的度数为（）A．60° B．75° C．90° D．120°举一反三：【变式1】在△ABC中，∠A=55°，∠B比∠C大25°，则∠B的度数为（）A．50° B．75°C．100° D．125°【变式2】三角形中至少有一个角不小于________度。

类型二：利用三角形外角性质证明角不等2．如图所示，已知CE是△ABC外角∠ACD的平分线，CE交BA延长线于点E。

求证：∠BAC ＞∠B。

举一反三：【变式】如图所示，用“＜”把∠1、∠2、∠A联系起来________。

类型三：三角形内角和定理与外角性质的综合应用3．如图，求∠A+∠B+∠C+∠D+∠E的度数.举一反三：【变式】如图所示，五角星ABCDE中，试说明∠A+∠B+∠C+∠D+∠E=180°。

类型四：与角平分线相关的综合问题4．如图9，△ABC中，∠ABC、∠ACB的平分线相交于点Ｄ．（1）若∠ABC＝70°，∠ACB＝50°，则∠BDC＝________；（2）若∠ABC＋∠ACB＝120°，则∠BDC＝________；（3）若∠A＝60°，则∠BDC＝________；（4）若∠A＝100°，则∠BDC＝________；（5）若∠A＝n°，则∠BDC＝________．举一反三：【变式1】如图10，BE是∠ABD的平分线，CF是∠ACD的平分线，BE 与CF交于G，若∠BDC= 140°，∠BGC=110°，求∠A的大小.80【变式2】如图11, △ABC的两个外角的平分线相交于点D，如果∠A＝50°，求∠D.【变式3】如图12，在△ABC中，AE是角平分线，且∠B=52°，∠C=78°，则∠AEB的度数是_____.【变式4】（2009北京四中期末）如图所示，△ABC的外角∠CBD、∠BCE的平分线相交于点F，若∠A=68°，求∠F的度数。

上课日期： 上课时间： 教师姓名：知识点一：格点面积 一、正方形格点问题在一张纸上，先画出一些水平直线和一些竖直直线，并使任意两条相邻的平行线的距离都相等(通常规定是1个单位)，这样在纸上就形成了一个方格网，其中的每个交点就叫做一个格点．在方格网中，以格点为顶点画出的多边形叫做格点多边形，例如，右图中的乡村小屋图形就是一个格点多边形．那么，格点多边形的面积如何计算？它与格点数目有没有关系？如果有，这两者之间的关系能否用计算公式来表达？下面就让我们一起来探讨这些问题吧！用N 表示多边形内部格点，L 表示多边形周界上的格点，S 表示多边形面积，请同学们分析前几个例题的格点数．我们能发现如下规律：12LS N =+-．这个规律就是毕克定理．二、 三角形格点问题1、定义：所谓三角形格点多边形是指：每相邻三点成“∵”或“∴”，所形成的三角形都是等边三角形．规定它的面积为1，以这样的点为顶点画出的多边形为三角形格点多边形．2、公式：关于三角形格点多边形的面积同样有它的计算公式：如果用S 表示面积，N 表示图形内包含的格点数，L 表示图形周界上的格点数，那么有22S N L =⨯+-，就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2．知识点二：图形剪拼巧求面积知识框架毕克定理若一个格点多边形内部有N 个格点，它的边界上有L 个格点，则它的面积为12LS N =+-．本讲中很多类型的题目还要求同学们去动手尝试．通过本讲知识的学习，让同学们了解不同图形的分割、拼合、剪拼的方法，锻炼同学们的平面想象能力以及增强学生的动手操作能力．（1）把一个几何图形按某种要求分成几个图形，就叫做图形的分割．（2）反过来，按一定的要求也可以把几个图形拼成一个完美的图形，就叫做图形的拼合．（3）将一个或者多个图形先分割开，再拼成一种指定的图形，则叫做图形的剪拼．我们在图形的分割、拼合和剪拼的过程中，都要结合所提供的图形特点来思考．（1）如果把一个图形分割成若干个大小、形状相等的部分，那么就要想办法找图形的对称点，把图形先分少，再分多．（2）图形中，如果有数量方面的要求，可以先从数量入手，找出平分后每块上所含数量的多少，再结合数量来分割图形．（3）如果是要把几个图形拼合成一个大图形，要特别注意每条边的长度，把相等的边长拼合在一起，先拼少的，再拼多的．（4）如果是剪拼图形，要抓住“剪、拼前后图形的面积相等”这个关键，根据已知条件和图形的特点，通过分析推理和必要的计算，确定剪拼的方法．一、解题关键：分割其实就是运用特殊的三角形（等角直角三角形、等边三角形等）、正方形、等边图形的特殊性质进行分割而得，所以分割的关键是利用了特殊图形的关系解题。

四年级下册数学《三角形内角和》教案3篇The teaching plan of the sum of the inner angles of a triangle四年级下册数学《三角形内角和》教案3篇前言：数学是研究数量、结构、变化、空间以及信息等概念的一门学科，从某种角度看属于形式科学的一种，在人类历史发展和社会生活中，数学发挥着不可替代的作用，是学习和研究现代科学技术必不可少的基本工具。

本教案根据数学课程标准的要求和教学对象的特点，将教学诸要素有序安排，确定合适的教学方案的设想和计划、并以启迪发展学生智力为根本目的。

便于学习和使用，本文档下载后内容可按需编辑修改及打印。

本文简要目录如下：【下载该文档后使用Word打开，按住键盘Ctrl键且鼠标单击目录内容即可跳转到对应篇章】1、篇章1：四年级下册数学《三角形内角和》教案2、篇章2：四年级下册数学《三角形内角和》教案3、篇章3：四年级下册数学《三角形内角和》教案篇章1:四年级下册数学《三角形内角和》教案【教学内容】：人教版义务教育课程标准试验教科书数学四年级下册第67页。

【设计理念】遵循由特殊到一般的规律进行探究活动是这节课设计的主要特点之一。

《数学课程标准》指出，让学生学习有价值的数学，让学生带着问题、带着自己的思想、自己的思维进入数学课堂，对于学生的数学学习有着重要作用。

因此，我尝试着将数学文本、课外预习、课堂教学三方有机整合，在质疑、解疑、释疑中展开教学，培养学生提出问题、分析问题和解决问题的探究能力。

【教材分析】三角形的内角和是三角形的一个重要特征。

本课是安排在学习三角形的概念及分类之后进行的，它是学生以后学习多边形的内角和及解决其它实际问题的基础。

学生在掌握知识方面：已经掌握了三角形的分类，比较熟悉平角等有关知识；能力方面：经过三年多的学习，已具备了初步的动手操作能力和主动探究能力以及合作学习的习惯。

因此，教材很重视知识的探索与发现，安排了一系列的实验操作活动。

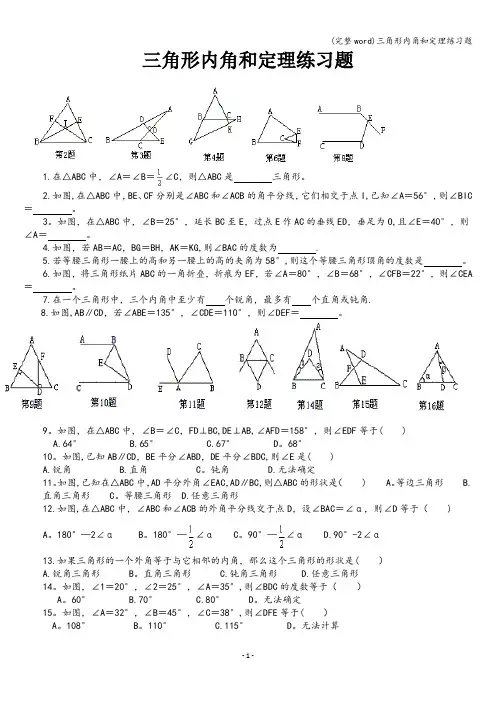
三角形内角和定理练习题1.在△ABC中，∠A＝∠B＝∠C，则△ABC是三角形。

2.如图,在△ABC中，BE、CF分别是∠ABC和∠ACB的角平分线，它们相交于点I,已知∠A＝56°，则∠BIC ＝。

3。

如图，在△ABC中，∠B＝25°，延长BC至E，过点E作AC的垂线ED，垂足为O,且∠E＝40°，则∠A＝。

4.如图，若AB＝AC，BG＝BH，AK＝KG,则∠BAC的度数为.5.若等腰三角形一腰上的高和另一腰上的高的夹角为58°,则这个等腰三角形顶角的度数是。

6.如图，将三角形纸片ABC的一角折叠，折痕为EF，若∠A＝80°，∠B＝68°，∠CFB＝22°，则∠CEA ＝。

7.在一个三角形中，三个内角中至少有个锐角，最多有个直角或钝角.8.如图,AB∥CD，若∠ABE＝135°，∠CDE＝110°，则∠DEF＝。

9。

如图，在△ABC中，∠B＝∠C，FD⊥BC,DE⊥AB,∠AFD＝158°，则∠EDF等于( )A.64°B.65°C.67°D。

68°10。

如图,已知AB∥CD，BE平分∠ABD，DE平分∠BDC,则∠E是( )A.锐角B.直角C。

钝角 D.无法确定11。

如图,已知在△ABC中，AD平分外角∠EAC，AD∥BC,则△ABC的形状是（) A。

等边三角形 B.直角三角形C。

等腰三角形 D.任意三角形12.如图,在△ABC中，∠ABC和∠ACB的外角平分线交于点D，设∠BAC＝∠α，则∠D等于（)A。

180°—2∠α B。

180°—∠αC。

90°—∠α D.90°-2∠α13.如果三角形的一个外角等于与它相邻的内角，那么这个三角形的形状是( ）A.锐角三角形B。

直角三角形 C.钝角三角形 D.任意三角形14。

如图，∠1＝20°，∠2＝25°，∠A＝35°,则∠BDC的度数等于（）A。