振动力学(倪振华)练习题
- 格式:doc
- 大小:15.76 MB
- 文档页数:140



1.转动惯量为J 的圆盘由三段抗扭刚度分别为1k 、2k 和3k 的轴约束,如图所示。
求系统的固有频率。
解:系统的动能为 221•=θJ T2k 和3k 相当于串联,则 32θθθ+= 3322θθk k =联立以上两式得 θθ3232k k k +=θθ3223k k k +=系统的势能为 ()[]223322221323232121212121θθθθk k k k k k k k k k U +++=++=利用θωθn =•和U T =可得 ()()3232132n k k J k k k k k +++=ω2.面积为S ,质量为m 的薄板连接于弹簧下端,在粘性流体中振动,如图所示。
作用于薄板的阻尼力为νμS F d 2=,S 2为薄板总面积,ν为速度。
若测得薄板无阻尼自由振动的周期为0T ,在粘性流体中自由振动的周期为d T 。
求系数μ。
解:平面在液体中上下振动时:02=++•••kx x S x m μ dn d n T T m k πξωωπω2-1,220====kS m S m S n n 222,22μξωμξξωμ==⇒= kS k 222--1μξ=2020220-2-22T T T ST mk S k T T T T d dd πμμ=⇒=3.如图所示均匀刚性杆质量为1m ,求系统的频率方程。
解:先求刚度矩阵。
令0x 1,==θ得:22212111a k b k a a k b b k k +=⋅+⋅=b k 221-k =令1,0==x θ得:a k k 212-=222-k k =则刚度矩阵为:⎥⎦⎤⎢⎣⎡+=2222221--k ak a k a k b k K再求质量矩阵。
令0,1==••••x θ ,得:0,31212111==m a m m令1,0==••••x θ,得:22212,0m m m ==则质量矩阵为: ⎥⎥⎦⎤⎢⎢⎣⎡=2210031m a m M故频率方程为: 0-2=M K ω4.在图所示系统中,已知m 和k 。

![《振动力学》习题集[含答案]](https://uimg.taocdn.com/bf1e364afad6195f302ba63b.webp)
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得:()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得:()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解:系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。

2振动力学》习题集(含答案)质量为 m 的质点由长度为 l 、质量为 m 1 的均质细杆约束在铅锤平面内作微幅摆动,如 图所示。
求系统的固有频率。
解: 系统的动能为:1 2 1 2 T m xl I x22 其中 I 为杆关于铰点的转动惯量:利用xnx 和T U 可得:3 2m m 1 g2 3m m 1 lml 1dxx 2l m 1x 2dxlm 1l31则有:系统的势能为:1 2 2 1 2 2ml x m 1l x 2 611 2 2 3m m 1 l x6U mgl 1 cosxm 1g cosx 1 2mglx14m 1glx1 2m4m 1 glx 2图质量为m、半径为R的均质柱体在水平面上作无滑动的微幅滚动,在两根弹性刚度系数为k 的水平弹簧,如图所示。
求系统的固有频率。
CA=a的A 点系有解:如图,令为柱体的转角,则系统的动能和势能分别为:利用1212 1 2 23T I B mR2mR2 2mR2B2241222U2k Ra2 k R a24k R a 23mR2R 3m图U 可得:n J k 2 k 3转动惯量为 J 的圆盘由三段抗扭刚度分别为 k 1 , k 2 和 k 3 的轴约束,如图所示。
求系统的固有频率。
k 2解:系统的动能为:12J 2k 2和 k 3相当于串联,则有:以上两式联立可得:系统的势能为:k 2k 3 k 1 k 2 k 3k 1 3,k 2k 2k 3k 3k 2k 2 k 3利用U 12k 1k 2 2212k 3 k 1 k 2 k 3 k 2k 3 2k 2 k 3n 和T U 可得:在图所示的系统中,已知 k i i 1,2,3 , m, a 和b ,横杆质量不计。
求固有频率。
答案图解:对 m 进行受力分析可得:质量 m 1在倾角为 的光滑斜面上从高 h 处滑下无反弹碰撞质量 m 2 ,如图所示。
确定mg k 3x 3 ,即 x 3mgk 3如图可得:F 1 mgb F 2 x 1, x 2k 1a b k 1k 2mga a b k 2x 0 x 1 x x 1a x 2 x 1ab a 2k 1 2b 2k 2 mga b 2 k 1k 2 x 则等效弹簧刚度为:x 0 x 3a 2k 1b 2 k 2 a b 2k 1k 21mgk 0mg2b k 1k 2k3a 2k 1k 3b 2k 2k 3 a b 2 k 1k 2则固有频率为:nk 1k 2k 3 a b 2 2 2 2 m k 1k 2 a b k 3 k 1a k 2bx 2mg系统由此产生的自由振动。

《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。

《振动力学》习题集(含答案)质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图所示。
求系统的固有频率。
图解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图所示。
求系统的固有频率。
图解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn = 和U T =可得:()mkR a R mR a R k n 343422+=+=ω转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图所示。
求系统的固有频率。
图解:系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn = 和U T =可得:()()3232132k k J k k k k k n +++=ω在图所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。

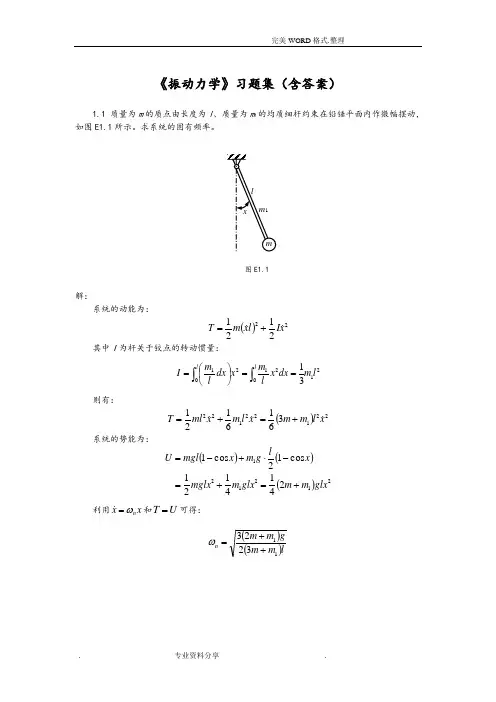
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解:系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
振动力学考题集[]1、四个振动系统中,自由度为无限大的是()。
A. 单摆;B. 质量-弹簧;C. 匀质弹性杆;D. 无质量弹性梁;2、两个分别为c1、c2的阻尼原件,并连后其等效阻尼是()。
A. c1+c2;B. c1c2/(c1+c2);C. c1-c2;D. c2-c1;3、()的振动系统存在为0的固有频率。
A. 有未约束自由度;B. 自由度大于0;C. 自由度大于1;D. 自由度无限多;4、多自由度振动系统中,质量矩阵元素的量纲应该是()。
A. 相同的,且都是质量;B. 相同的,且都是转动惯量;C. 相同的,且都是密度;D. 可以是不同的;5、等幅简谐激励的单自由度弹簧-小阻尼-质量振动系统,激励频率()固有频率时,稳态位移响应幅值最大。
A. 等于;B. 稍大于;C. 稍小于;D. 为0;6、自由度为n的振动系统,且没有重合的固有频率,其固有频率的数目(A )。
A. 为n;B. 为1;C. 大于n;D. 小于n;7、无阻尼振动系统两个不同的振型u(r)和u(s),u(r)T Mu(s)的值一定()。
A. 大于0;B. 等于0;C. 小于0;D. 不能确定;8、无阻尼振动系统的某振型u(r),u(r)T Ku(r)的值一定()。
A. 大于0;B. 等于0;C. 小于0;D. 不能确定;9、如果简谐激励力作用在无约束振动系统的某集中质量上,当激励频率为无限大时,该集中质量的稳态位移响应一定()。
A. 大于0;B. 等于0;C. 为无穷大;D. 为一常数值;10、相邻固有频率之间的间隔呈近似无限等差数列的振动系统是()。
A. 杆的纵向振动;B. 弦的横向振动;C. 一般无限多自由度系统;D. 梁的横向振动;11、两个刚度分别为k1、k2串连的弹簧,其等效刚度是()。
A. k1+k2;B. k1k2/(k1+k2);C. k1-k2;D. k2-k1;12、无阻尼振动系统两个不同的振型u(r)和u(s),u(r)T Ku(s)的值一定()。