华东理工大学概率论 卷积公式补充例子

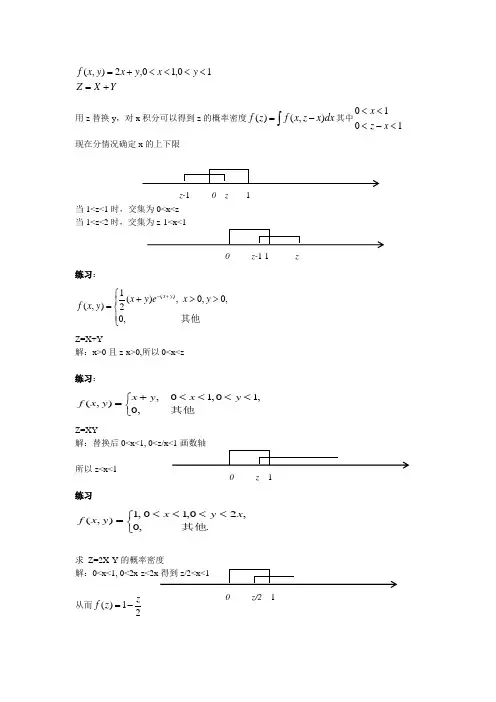
YX Z y x y x y x f +=<<<<+=10,10,2),( 用z 替换y ，对x 积分可以得到z 的概率密度()(,)f z f x z x dx =-⎰其中1010<-<<<x z x 现在分情况确定x 的上下限当1<z<1时，交集为0<x<z当1<z<2时，交集为z-1<x<1练习： ⎪⎩⎪⎨⎧>>+=+-其他 ,0,0,0 ,)(21),()(y x e y x y x f y xZ=X+Y解：x>0且z-x>0,所以0<x<z练习：, 01,01,(,)0, x y x y f x y +<<<<⎧=⎨⎩其他Z=XY解：替换后0<x<1, 0<z/x<1画数轴所以z<x<1练习 .,20,10,0,1),(其他x y x y x f <<<<⎩⎨⎧=求 Z=2X-Y 的概率密度解：0<x<1, 0<2x-z<2x 得到z/2<x<1从而21)(z z f -=z-1 0 z 1 0 z-1 1 z0 z 10 z/2 1教材例题：x>0, 0<y<20求Z=X+Y解：x>0, 0<z-x<20,如果z<20，交集0<x<z如果z>20，交集z-20<x<z教材练习：0<x<1,0<y<2Z=X+Y解：换掉y ，得到0<x<1, 0<z-x<2以下分类讨论0<z<2时，交集0<x<z如果1<z<2，交集0<x<1如果2<z<3，交集z-2<x<1确定了每种情况的上下限，使用卷积公式即可求出具体的概率密度函数参考资料：概率论第3章.百度文库.光昌国概率论与数理统计(14).百度文库.刘春华00概率论、数理统计与随机过程 第三章 张帼奋主编z-20 0 z 0 z-20 z z-2 0 z 1 z-2 0 1 z 0 z-2 1 z。

卷积公式的例子
卷积公式的应用非常广泛，以下是5个具体的例子：
1. 丢骰子：有两枚骰子，求两枚骰子点数加起来为4的概率。

可以把它写成卷积的形式：(f∗g)(4)=∑m=13f(4−m)g(m)。

2. 做馒头：假设馒头的生产速度是f(t)，腐败函数为g(t)，那么一天后生产出来的馒头总量就是f(t)和g(t)的卷积，即馒头生产出来之后，会随时间不断腐败。

3. 信号处理：如果一个系统对输入信号的响应是g(t)，那么在t=0时刻有一个输入，这个输入将随时间按g(t)的规律衰减，这也是卷积的应用。

4. 图像处理：在图像处理中，卷积常常用来进行滤波操作。

比如，有一个滤波器h，和一幅图像f，那么滤波后的图像g就是f和h的卷积。

5. 物理学：在物理学中，卷积被用来描述两个函数之间的关系。

例如，如果一个力在时间上作用于一个物体，那么该物体在时间上的位移就是该力和单位冲激响应的卷积。

东华理⼯⼤学概率论期末考试试卷总结版东华理⼯⼤学《概率论与数理统计》考试试卷（A1）（A ）)(x F 取值为(0,)+∞ （B ）)(x F 为单调递减（C ）0 F(x)1≤≤ (D) F(x)1≤3、设~[2,4]X U ，当122<4x x <<时，=<<)(21x X x p （） (A)122x - （B ）224x - (C ) 244x - (D) 212x x - 4、设总体X 的数学期望为µ，⽅差为2σ，),(21X X 是X 的⼀个样本，则在下述的４个估计量中，最优的是（）。

(A) 11241?55X X µ=+ (B) 2127188X X µ=+ (C) 31211?42X X µ=+ (D) 41211?32X X µ=+ 5、设(X,Y)为连续型随机向量,其联合密度为),(y x f ,两个边缘密度分别为()X f x 与()Y f y ,则下式中错误的是( ). (A) ()X EX xf x dx +∞-∞=(B) ?+∞∞-+∞∞-=dxdy y x xf EX ),((C) ()22()X Y EY y f x f y dy +∞+∞-∞-∞=(D) ()(,)E XY xyf x y dxdy +∞+∞6、已知~(2,1)X N -，~(3,1)Y N ，且,X Y 相互独⽴,记28,~Z X Y Z =-+则( ).(A))5,0(N (B))12,0(N (C))54,0(N (D))2,1(-N 7、在0H 为原假设，1H 为备择假设的假设检验中，则称（）为犯第⼀类错误．0000(A)(B)H H H H 为真，接受不真，接受 0101(C)(D)H H H H 为真,接受不真,接受⼀．填空题：（本⼤题共7⼩题，每⼩题3分，共21分）1．设A 、B 为随机事件，P （A ）=0.6，P （A-B ）=0.3，则P （|B A ）= 。

概率公式整理 A uQ = Q I.随机事件及其概率吸收律：AU0=A A 5人〃)=4 = A/In0 = 04n(4u/^) = 4A-B = AB = A-(AB)反演律：AuB = A B AB = A<j B P(A) = 1-P(A) P(B-A) = P(B)-P(AB) U A =A AA A =U Ar=l r=l f=l i=l 若 AuB => P[B -A) = P(B) - P(A) 2. 概率的定义及其计算： 对任意两个事件人B,有 加法公式:对任意两个事件有P(A uB) = P(A) + P(B) - P(AB) P(CjA)述P(AJ-工P(AC)+ E) + - + (-1)"'1P(A,A 2 • • • A n ) /«1 r=l lii<j<n l<i<j<kin 3. 条件概率 P(B | A)= 些凹 乘法公式 P(AB) = P(A)P(B\A)(P(A) > 0) P(4) P( A"…人)"(A )P (爲 ⑷…P(九I A A …A” J (P(A,2 …心)>0) 全概率公式 P(A) = £ P(AB,) = 2 P(BJ P(A I fi,) Bayes 公式 P(B k \ A)= “仲i=l P(4)P(AuB)<P(A) + P(B) =P (城)P(4| 以)r=l略hl 血-iz 甘4旷 ◎十"拓“饴 PS <X<b) = P(X< h)-P(X< a) 随机变山及其分布分布函数计畀— =F (b) — F (a) 离散型随机变量(1) 0 - I 分布P(X =k) = p A (l-p)' \ k = 0y l 二项分布 〃(〃,/?)若 P(4)=" P(X=k) = C"(l_p 严,"0,1,k k k 2 才 * Possion 定理 lim/zp,, =2>0 有 >!^CnPn(l ~Pn) =e 万 "0,12 …4. 5. ⑵ n — (3) Poisson 分布 P(久) P(X=R) =小一，k=o,12•… k\6.连续型随机变量(1) 均匀分布b-a (X ,ci<x<bF(g其他 x-a⑵指数分布 £(2) /(X)=0, x>0 具他 09 1 一严 x<() ,x>0 ⑶止态分布N(〃，cr2)] r"-")2 -oo<x<+oo F(x) = /—— f e 2a ：d/ 2a 2 1 _ 匚 i x d (p(x) = -J=-e 3 -oo<x<-Foo 0(x) = -^=J l e 7dz -oo<x <+<x> 二维随机变显(X,Y)的分布函数 F(x,y)=「[' f(i h v)dvclu J_8 J 一8 边缘分布函数与边缘密度函数(x) = j' j^*5f(u y v)dvdu f x (x) = ^f\x,v)dv人(y)=L*7V(0J)—标准正态分布 7 •多维随机变昴及具分布 />(y)= P f f(u.v)dudvJ ・8 er —oo&连续型二维随机变量 (1)区域G 上的均匀分布，=U,V)eG0, 其他(2)二维正态分布.( — “J，一 2 P/(^y)= ------------- xer 」2勿0 2寸1 _ P ・ —OQ < X < -H» OO < y < +009.二维随机变竝的条件分布f (x, y) = f x (x)/r j x (y|x) X 的 R 阶中心矩 E((X-E(X))*) X 的 方差 E((X-E(X))2) = D(X)X,Y 的k + l 阶混合原点矩 E(X k Y l) X.Y 的k + l 阶混合中心矩 E((X-E(X)r(Y-£(Y))‘) X 9Y 的二阶混合原点矩 E(XY) X 9Y 的二阶混介中心矩 X"的协方差E((X-E(X))(y-E(r)))'(x-E(x))(y-E(y))、< J D (X )莎百 丿X 的方差 D(X) = E((X ・E(X))2) AXX) = £(X 2)-£C(X) 协方差 cov(x,y)=E ((X - E(x))(y 一E(r)))=E(XY)-E(X)E(Y) = ±^(D(X±Y)-D(X)-D(Y))相关系数C ：组合数 中心n, n>h m>0, n. m^N.⑴排列数公式= yi(n-lXw- 2)---(n -m + 1)=出=?2! = ?2(«-1\^- 2)・・・2 1(2)组合数公式AW>0 =fy(y)f x \Y (x\y)A(y)>o+8fx (x) = L /(x, y)dy = L £|y (彳 y)齐(y)〃y A(y)= J m /(^ y)^ = L 环(妝)人(兀皿二 f(x,y) fx\Y(^fy(y) =AW 「E(X)= [ ^xf(x)dx J —8x 的k 阶绝对原点矩E (I x r)如④)=册-屉如凹10.随机变量的数字特征 数学期望E(X) =工5 “1随机变虽函数的数学期望X 的k 阶原点矩E(X k)A(y)Ard)fx(x) 4«oX#的相关系数cov(XV)4D (X)/D (Y)1.排列数(MI <M )V C：（3）组合数性质:一””（心）册亦等（5 c； +C；A +C；“ +・・・ + C；。

概率论与数理统计基本公式第一部分 概率论基本公式1、)(;A B A B A AB A B A B A -⋃=⋃-==--2、对偶率:.----⋃=⋂⋂=⋃B A B A B A B A ；3、概率性率：)()();()()(),()()(B P A P B P A P B A P A B AB P A P B A P ≥-=-⊂-=-时有：特别，)()()(212121A P A P A A P A A +=⋃为不相容事件，则、有限可加：)()()()(AB P B P A P B A P -+=⋃对任意两个事件有：4、古典概型222n 2!)(n ,22)-n 2)!n 2(22nC n A P C A n n n ==！，则自成一双为：！！（解：分堆法：每堆自成一双鞋的概率只，事件堆，每堆为只，分为双鞋总共例： 5、条件概率称为无条件概率。

的条件概率，条件下，事件称为在事件)(,)()()|(B P B A A P AB P A B P =B)|P(B)P(A P(AB) A)|P(A)P(B P(AB)==乘法公式：)|()()(i i A B P A P B P i∑=全概率公式：)|()()|()()()()|(jj ji i i A B P A P A B P A P B P B A P B A P i ∑==贝叶斯公式：例:有三个罐子,1号装有2红1黑共3个球,2号装有3红1黑4个球,3号装有2红2黑4个球，某人随机从其中一罐，再从该罐中任取一个球，（1)求取得红球的概率;（2)如果取得是红球,那么是从第一个罐中取出的概率为多少？.348.0)()()|()|()2(.639.0)(31)()()(.21)|(;43)|(;32)|()|()()(}{3,2,1i }{)1(111321321i i 321≈=≈∴==========∑A P B P B A P A B P A P B P B P B P B A P B A P B A P A B P A P B P B B B A i B ii 由贝叶斯公式：，，依题意，有：由全概率公式是一个完备事件、、，由题知取得是红球。

概率论中的卷积公式是描述两个随机变量和的概率分布的公式。

下面是卷积公式的推导过程：假设有两个随机变量X和Y，它们的概率密度函数分别为f(x)和g(y)。

我们想要求得X和Y的和Z的概率密度函数。

首先，我们定义Z = X + Y。

我们可以使用累积分布函数（CDF）来推导卷积公式。

首先，我们考虑Z小于等于z的情况，即P(Z ≤ z)。

根据定义，这可以表示为：P(Z ≤ z) = P(X + Y ≤ z)对于给定的z，我们可以将Y的取值范围从负无穷到正无穷进行分割。

假设Y = y时，X需要满足X ≤ z - y才能使得X + Y ≤ z。

因此，我们可以将上式写为积分形式：P(Z ≤ z) = ∫[负无穷到正无穷] P(X ≤ z - y)g(y)dy根据X的分布函数F(x) = P(X ≤ x)，上式可以进一步写为：P(Z ≤ z) = ∫[负无穷到正无穷] F(z - y)g(y)dy为了得到Z的概率密度函数，我们需要对上式进行求导。

我们对z求导得到：f_Z(z) = d/dz ∫[负无穷到正无穷] F(z - y)g(y)dy根据导数的性质，我们可以将求导操作移到积分符号内部，得到：f_Z(z) = ∫[负无穷到正无穷] d/dz [F(z - y)]g(y)dy根据导数的链式法则，我们有 d/dz [F(z - y)] = f(z - y)。

代入上式，得到：f_Z(z) = ∫[负无穷到正无穷] f(z - y)g(y)dy最终，我们得到了卷积公式：f_Z(z) = (f * g)(z)其中，(f * g)(z)表示函数f和g的卷积，也可以写为f(z)和g(z)的卷积。

以上是卷积公式的推导过程，它在概率论中有广泛的应用，用于计算随机变量和的概率分布。

第一章 随机事件和概率⎪⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧-+→⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧Ω→贝努利概型贝叶斯公式/)(独立性全概公式和乘法公式条件概率减法加法五大公式几何概型古典概型随机事件样本空间基本事件随机试验BC C B C B C B A P A E ω第二章 随机变量及其分布⎭⎬⎫⎩⎨⎧-→⎭⎬⎫⎩⎨⎧≤<→⎭⎬⎫⎩⎨⎧)()()()(a F b F A P b X a A X 随机事件随机变量基本事件ωω第三章 二维随机变量及其分布⎪⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=+=⎭⎬⎫⎩⎨⎧→⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧→分布分布分布三大统计分布函数分布正态分布均匀分布常见二维分布独立性条件分布边缘分布连续型分布密度离散型分布律联合分布F t X X X Z Y X Z Y X n 221),,min(max,),(χξ第四章 随机变量的数字特征⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧→切比雪夫不等式矩方差期望一维随机变量⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧→协方差矩阵相关系数协方差方差期望二维随机变量第五章 大数定律和中心极限定理⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧→辛钦大数定律伯努利大数定律切比雪夫大数定律大数定律⎭⎬⎫⎩⎨⎧→棣莫弗－拉普拉斯定理列维－林德伯格定理中心极限定理二项定理 泊松定理第六章 数理统计的基本概念正态总体下的四大分布统计量样本函数样本个体总体数理统计的基本概念→⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧第七章 参数估计{}⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧→⎭⎬⎫⎩⎨⎧单正态总体的区间估计区间估计一致性有效性无偏性估计量的评选标准极大似然估计矩估计点估计从样本推断总体第八章 假设检验单正态总体的假设检验两类错误基本步骤基本思想假设检验的基本概念→⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧。

华东理工大学概率论答案-9-10华东理工大学概率论与数理统计作业簿（第四册）学 院 ____________专 业 ____________班 级 ____________ 学 号 ____________姓 名 ____________任课教师____________第九次作业一． 填空题1. 设X 服从泊松分布，若26EX =，则(1)P X >= 213e --。

解 222~(),6()X P E X D X E X λλλ==+=+故 2λ=. (1)1(1)1(0)(1)P X P X P X P X >=-≤=-=-= 2221213e e e---=--=-. 2.设随机变量~(,)B n p ξ，已知 2.4, 1.44E D ξξ==，则参数n= 6 ，p = 0.4 。

解 2.4,6,1.44,0.4.E np n D npq p ξξ===⎧⎧⇒⎨⎨===⎩⎩3. 某保险公司的某人寿保险险种有1000人投保，每个人在一年内死亡的概率为0.005，且每个人在一年内是否死亡是相互独立的，欲求在未来一年内这1000个投保人死亡人数不超过10人的概率。

用Excel 的BINOMDIST 函数计算。

BINOMDIST （10 , 1000, 0.005, TRUE ）= 0.986531_。

4. 运载火箭运行中进入其仪器仓的粒子数服从参数为4的泊松分布，用Excel 的POISSON 函数求进入仪器舱的粒子数大于10的概率。

POISSON （10 , 4 ，TRUE ）=0.9972, 所求概率p =_0.0028_。

5. ~(4)P ξ，由切比雪夫不等式有(|4|6)P ξ-<≥__8/9___。

二． 选择题1. 在相同条件下独立的进行3次射击，每次射击击中目标的概率为23，则至少击中一次的概率为 （ D ）A. 274B. 2712C. 2719D. 2726三．计算题1. 设随机变量ξ的密度函数是1cos ,0()220,x x p x π⎧≤≤⎪=⎨⎪⎩其它 对ξ独立的随机观察4次，η表示观察值大于3π的次数，求 （1）η的概率分布（分布律）， （2）E D ηη和。