《算法设计与分析》递归算法典型例题
- 格式:pdf
- 大小:179.71 KB
- 文档页数:7

递归算法及经典例题详解
1.什么是递归
递归简单来说就是在运行过程中不断调用自己,直到碰到终止条件,返回结果的过程。
递归可以看作两个过程,分别是递和归。
递就是原问题把要计算的结果传给子问题;归则是子问题求出结果后,把结果层层返回原问题的过程。
下面设一个需要经过三次递归的问题,为大家详细看一下递归的过程:当然,现实中我们遇到递归问题是不会按照图中一样一步一步想下来,主要还是要掌握递归的思想,找到每个问题中的规律。
2.什么时候使用递归
递归算法无外乎就是以下三点:1.大问题可以拆分为若干小问题2.原问题与子问题除数据规模不同,求解思路完全相同3.存在递归终止条件
而在实际面对递归问题时,我们还需要考虑第四点:
当不满足终止条件时,要如何缩小函数值并让其进入
下一层循环中
3.递归的实际运用(阶层计算)
了解了大概的思路,现在就要开始实战了。
下面我们来看一道经典例题:
求N的阶层。
首先按照思路分析是否可以使用递归算法:
1.N!可以拆分为(N-1)!*N
2.(N-1)!与N!只有数字规模不同,求解思路相同
3.当N=1时,结果为1,递归终止
满足条件,可以递归:
publicstaticintFactorial(int num){if(num==1){return num;}return num*Factorial(num-1);}
而最后的return,便是第四步,缩小参数num的值,让递归进入下一层。
一般来说,第四步往往是最难的,需要弄清该如何缩
小范围,如何操作返回的数值,这一步只能通过不断
地练习提高了(当然如果你知道问题的数学规律也是
可以试出来的)。

算法设计与分析习题答案算法设计与分析是计算机科学中一个重要的领域,它涉及到算法的创建、优化以及评估。
以下是一些典型的算法设计与分析习题及其答案。
习题1:二分查找算法问题描述:给定一个已排序的整数数组,编写一个函数来查找一个目标值是否存在于数组中。
答案:二分查找算法的基本思想是将数组分成两半,比较中间元素与目标值的大小,如果目标值等于中间元素,则查找成功;如果目标值小于中间元素,则在左半部分继续查找;如果目标值大于中间元素,则在右半部分继续查找。
这个过程会不断重复,直到找到目标值或搜索范围为空。
```pythondef binary_search(arr, target):low, high = 0, len(arr) - 1while low <= high:mid = (low + high) // 2if arr[mid] == target:return Trueelif arr[mid] < target:low = mid + 1else:high = mid - 1return False```习题2:归并排序算法问题描述:给定一个无序数组,使用归并排序算法对其进行排序。
答案:归并排序是一种分治算法,它将数组分成两半,分别对这两半进行排序,然后将排序好的两半合并成一个有序数组。
```pythondef merge_sort(arr):if len(arr) > 1:mid = len(arr) // 2left_half = arr[:mid]right_half = arr[mid:]merge_sort(left_half)merge_sort(right_half)i = j = k = 0while i < len(left_half) and j < len(right_half): if left_half[i] < right_half[j]:arr[k] = left_half[i]i += 1else:arr[k] = right_half[j]j += 1k += 1while i < len(left_half):arr[k] = left_half[i]i += 1k += 1while j < len(right_half):arr[k] = right_half[j]j += 1k += 1arr = [38, 27, 43, 3, 9, 82, 10]merge_sort(arr)print("Sorted array is:", arr)```习题3:动态规划求解最长公共子序列问题问题描述:给定两个序列,找到它们的最长公共子序列。

算法设计与分析基础习题1.15..证明等式gcd(m,n)=gcd(n,m mod n)对每一对正整数m,n都成立.Hint:根据除法的定义不难证明:●如果d整除u和v, 那么d一定能整除u±v;●如果d整除u,那么d也能够整除u的任何整数倍ku.对于任意一对正整数m,n,若d能整除m和n,那么d一定能整除n和r=m mod n=m-qn;显然,若d能整除n和r,也一定能整除m=r+qn和n。
数对(m,n)和(n,r)具有相同的公约数的有限非空集,其中也包括了最大公约数。
故gcd(m,n)=gcd(n,r)6.对于第一个数小于第二个数的一对数字,欧几里得算法将会如何处理?该算法在处理这种输入的过程中,上述情况最多会发生几次?Hint:对于任何形如0<=m<n的一对数字,Euclid算法在第一次叠代时交换m和n, 即gcd(m,n)=gcd(n,m)并且这种交换处理只发生一次.7.a.对于所有1≤m,n≤10的输入, Euclid算法最少要做几次除法?(1次)b. 对于所有1≤m,n≤10的输入, Euclid算法最多要做几次除法?(5次)gcd(5,8)习题1.21.(农夫过河)P—农夫W—狼G—山羊C—白菜2.(过桥问题)1,2,5,10---分别代表4个人, f—手电筒4. 对于任意实系数a,b,c, 某个算法能求方程ax^2+bx+c=0的实根,写出上述算法的伪代码(可以假设sqrt(x)是求平方根的函数)算法Quadratic(a,b,c)//求方程ax^2+bx+c=0的实根的算法//输入:实系数a,b,c//输出:实根或者无解信息If a≠0D←b*b-4*a*cIf D>0temp←2*ax1←(-b+sqrt(D))/tempx2←(-b-sqrt(D))/tempreturn x1,x2else if D=0 return –b/(2*a)else return “no real roots”else //a=0if b≠0 return –c/belse //a=b=0if c=0 return “no real numbers”else return “no real roots”5.描述将十进制整数表达为二进制整数的标准算法a.用文字描述b.用伪代码描述解答:a.将十进制整数转换为二进制整数的算法输入:一个正整数n输出:正整数n相应的二进制数第一步:用n除以2,余数赋给Ki(i=0,1,2...),商赋给n第二步:如果n=0,则到第三步,否则重复第一步第三步:将Ki按照i从高到低的顺序输出b.伪代码算法DectoBin(n)//将十进制整数n转换为二进制整数的算法//输入:正整数n//输出:该正整数相应的二进制数,该数存放于数组Bin[1...n]中i=1while n!=0 do {Bin[i]=n%2;n=(int)n/2;i++;}while i!=0 do{print Bin[i];i--;}9.考虑下面这个算法,它求的是数组中大小相差最小的两个元素的差.(算法略) 对这个算法做尽可能多的改进.算法MinDistance(A[0..n-1])//输入:数组A[0..n-1]//输出:the smallest distance d between two of its elements习题1.31.考虑这样一个排序算法,该算法对于待排序的数组中的每一个元素,计算比它小的元素个数,然后利用这个信息,将各个元素放到有序数组的相应位置上去.a.应用该算法对列表‖60,35,81,98,14,47‖排序b.该算法稳定吗?c.该算法在位吗?解:a. 该算法对列表‖60,35,81,98,14,47‖排序的过程如下所示:b.该算法不稳定.比如对列表‖2,2*‖排序c.该算法不在位.额外空间for S and Count[] 4.(古老的七桥问题)习题1.41.请分别描述一下应该如何实现下列对数组的操作,使得操作时间不依赖数组的长度. a.删除数组的第i 个元素(1<=i<=n)b.删除有序数组的第i 个元素(依然有序) hints:a. Replace the i th element with the last element and decrease the array size of 1b. Replace the ith element with a special symbol that cannot be a value of the array ’s element(e.g., 0 for an array of positive numbers ) to mark the i th position is empty. (―lazy deletion ‖)第2章 习题2.17.对下列断言进行证明:(如果是错误的,请举例) a. 如果t(n )∈O(g(n),则g(n)∈Ω(t(n)) b.α>0时,Θ(αg(n))= Θ(g(n)) 解:a. 这个断言是正确的。


《递归算法题目》
同学们,今天咱们来聊聊递归算法题目。
啥是递归算法呢?简单说,就是一个函数自己调用自己。
听起来有点绕,对吧?别担心,咱们通过例子来理解。
比如说,计算阶乘。
咱们要算 5 的阶乘,也就是5! 。
正常算法是
5×4×3×2×1 ,那用递归算法呢,就是这样:先定义一个函数,假设叫factorial ,如果要算n 的阶乘,当n 等于0 或者 1 时,结果就是 1 ;如果n 大于 1 ,那结果就是n 乘以factorial(n - 1) 。
再比如,计算斐波那契数列。
这个数列前两个数是0 和 1 ,从第三个数开始,每个数都是前两个数的和。
用递归算法,咱们也能搞定。
那为啥要学递归算法呢?因为它能让一些复杂的问题变得简单。
就像走迷宫,有时候直接往前走找不到出口,但是退一步,换个角度,可能就柳暗花明啦。
不过,递归算法也有它的小麻烦。
要是不小心,可能会陷入无限循环,就像在一个圈圈里一直转,出不来啦。
那怎么才能做好递归算法的题目呢?首先,得把问题分析清楚,搞明白啥时候该停止递归。
然后,要仔细设计递归的条件和步骤。
同学们,递归算法就像一把神奇的钥匙,能打开很多难题的大门。
只要咱们多练习,多思考,就一定能掌握它,让它为咱们的编程之路助力!
加油吧,同学们,相信你们都能搞定递归算法题目!。

递归的经典例子
1. 算数学题的时候啊,像计算一个数的阶乘,这就是一个递归的经典例子呀!比如说计算 5 的阶乘,不就是 5 乘以 4 的阶乘嘛,而 4 的阶乘又等于 4 乘以 3 的阶乘,依次类推,这多有意思啊!
2. 还有走迷宫呢,你想想,当你在迷宫里遇到岔口,你选择一条路走,然后又遇到岔口,又继续选择,这不就跟递归很像嘛!你不断地进入更小的问题去探索,直到找到出口,这难道不是很神奇吗?
3. 画树也可以用递归呀!先画一个树干,然后树干上又分出树枝,每个树枝又可以当作新的树干去继续分树枝,这不就跟递归的过程一样嘛,哇塞,这样就能画出一棵复杂又漂亮的树啦!
4. 你知道汉诺塔游戏不?那就是典型的递归例子哟!要把盘子从一个柱子移到另一个柱子,不就得不断地用递归的方法去解决嘛,天啊,真是好烧脑又好有趣!
5. 再来说说我们电脑里的文件系统,那也是递归的体现呀!文件夹里有子文件夹,子文件夹里还有子文件夹,就这么一层层下去,像不像递归在大展身手呢?
6. 回忆一下我们看电影的时候,很多故事里不是也有类似递归的情节嘛!主角解决一个问题又引出新的问题,然后一直这么循环,这也可以说是一种故事里的递归呀,多有意思的发现呀!
总之,递归在生活中无处不在,它就像一把神奇的钥匙,能打开很多复杂问题的大门,给我们带来惊喜和挑战!。
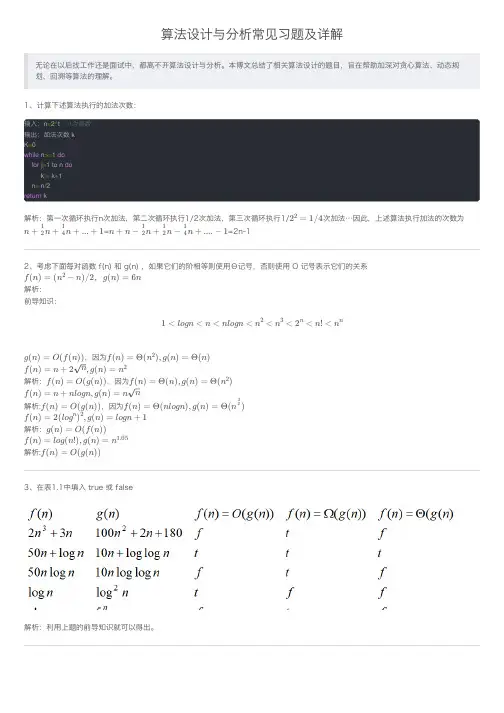
算法设计与分析常见习题及详解⽆论在以后找⼯作还是⾯试中,都离不开算法设计与分析。
本博⽂总结了相关算法设计的题⽬,旨在帮助加深对贪⼼算法、动态规划、回溯等算法的理解。
1、计算下述算法执⾏的加法次数:输⼊:n =2^t //t 为整数输出:加法次数 k K =0while n >=1 do for j =1 to n do k := k +1 n = n /2return k解析:第⼀次循环执⾏n次加法,第⼆次循环执⾏1/2次加法,第三次循环执⾏1/次加法…因此,上述算法执⾏加法的次数为==2n-12、考虑下⾯每对函数 f(n) 和 g(n) ,如果它们的阶相等则使⽤Θ记号,否则使⽤ O 记号表⽰它们的关系解析:前导知识:,因为解析:,因为解析:,因为解析:解析:3、在表1.1中填⼊ true 或 false解析:利⽤上题的前导知识就可以得出。
2=21/4n +n +21n +41...+1n +n −n +21n −21n +41....−1f (n )=(n −2n )/2,g (n )=6n1<logn <n <nlogn <n <2n <32<n n !<n ng (n )=O (f (n ))f (n )=Θ(n ),g (n )=2Θ(n )f (n )=n +2,g (n )=n n 2f (n )=O (g (n ))f (n )=Θ(n ),g (n )=Θ(n )2f (n )=n +nlogn ,g (n )=n nf (n )=O (g (n ))f (n )=Θ(nlogn ),g (n )=Θ(n )23f (n )=2(log ),g (n )=n 2logn +1g (n )=O (f (n ))f (n )=log (n !),g (n )=n 1.05f (n )=O (g (n ))4、对于下⾯每个函数 f(n),⽤f(n) =Θ(g(n))的形式,其中g(n)要尽可能简洁,然后按阶递增序排列它们(最后⼀列)解析:最后⼀个⽤到了调和公式:按阶递增的顺序排列:、、、、、、、、、(n −2)!=Θ((n −2)!)5log (n +100)=10Θ(logn )2=2n Θ(4)n 0.001n +43n +31=Θ(n )4(lnn )=2Θ(ln n )2+3n logn =Θ()3n 3=n Θ(3)n log (n !)=Θ(nlogn )log (n )=n +1Θ(nlogn )1++21....+=n1Θ(logn )=∑k =1nk 1logn +O (1)1++21....+n 15log (n +100)10(lnn )2+3n logn log (n !)log (n )n +10.001n +43n +313n 22n (n −2)!5、求解递推⽅程前导知识:主定理前导知识:递归树:例⼦:递归树是⼀棵节点带权的⼆叉树,初始递归树只有⼀个结点,标记为权重W(n),然后不断进⾏迭代,最后直到树种不再含有权为函数的结点为⽌,然后将树根结点到树叶节点的全部权值加起来,即为算法的复杂度。

1、实验内容递归求n的二次方各项的系数。
2、程序设计代码如下:#include"stdio.h"void coeff(int a[],int n)if(n==1)a[1]=1;a[2]=1;elsecoeff(a,n-1);a[n+1]=1;for(int i=n;i>=2;i=i-1)a[i]=a[i]+a[i-1];a[1]=1;void main()int a[100],i,n;printf("输入n的值:");scanf("%d",&n);coeff(a,n);for(i=1;i<=n+1;i++)printf(" %d ",a[i]);printf("\n");1、实验内容写出计算ackerman函数ack(m,n)的递归计算函数。
2、程序设计代码如下:#include "stdio.h"int ack(int m,int n)if(m==0)return n+1;else if(n==0)return ack(m-1,1);elsereturn ack(m-1,ack(m,m-1));void main()int m,n,z;printf("input m and n:");scanf("%d %d",&m,&n);if(m<0 && n<0)printf("error input!");elsez=ack(m,n);printf("%d\n",z);第四章例15 求数列的最大子段和给定n个元素的整数列(可能为负整数)a1,a2,…..,an。
求形如:ai,ai+1,……aj i,j=1,…..,n,i<=j的子段,使其和为最大。

《算法设计与分析》一、 排序和查找是经常遇到的问题。
按照要求完成以下各题:(1)对数组A={15,29,135,18,32,1,27,25,5},用快速排序方法将其排成递减序。
解:(1)第一步:15 29 135 18 32 1 27 25 5 第二步:29 135 18 32 27 25 15 1 5第三步:135 32 29 18 27 25 15 5 1 第四步:135 32 29 27 25 18 15 5 1(2)请描述递减数组进行二分搜索的基本思想,并给出非递归算法。
解:基本思想:首先将待搜索元素v 与数组的中间元素2n A ⎡⎤⎢⎥⎣⎦进行比较,如果2n v A ⎡⎤>⎢⎥⎣⎦,则在前半部分元素中搜索v ;若2n v A ⎡⎤=⎢⎥⎣⎦,则搜索成功;否则在后半部分数组中搜索v 。
非递归算法:输入:递减数组A[left:right],待搜索元素v 。
输出:v 在A 中的位置pos ,或者不在A 中的消息(-1)。
步骤:int BinarySearch(int A[],int left,int right,int v) {int mid;while (left<=right) {mid=int((left+right)/2); if (v==A[mid]) return mid;else if (v>A[mid]) right=mid-1; else left=mid+1; }return -1; }(3)给出上述算法的递归算法。
解:输入:递减数组A[left:right],待搜索元素v 。
输出:v 在A 中的位置pos ,或者不在A 中的消息(-1)。
步骤:【3分】int BinarySearch(int A[],int left,int right,int v) {int mid;if (left<=right){mid=int((left+right)/2); if (v==A[mid]) return mid;else if (v>A[mid]) return BinarySearch(A,left,mid-1,v); else return BinarySearch(A,mid+1,right,v); } elsereturn -1;}(4)使用上述算法对(1)所得到的结果搜索如下元素,并给出搜索过程:18,31,135。

递归经典题目
递归是一种常用的算法技术,它可以用来解决许多经典问题。
以下是一些经典的递归问题:
1. 斐波那契数列:这是一个经典的递归问题,其中每个数字是前两个数字的和。
例如,斐波那契数列的前几个数字是 0、1、1、2、3、5、8、13、21 等。
2. 阶乘函数:这是一个计算一个数的阶乘的递归函数。
例如,5 的阶乘是 5 4 3 2 1 = 120。
3. 汉诺塔问题:这是一个经典的递归问题,其中有一些盘子需要从一根柱子移动到另一根柱子,每次只能移动一个盘子,并且不能将一个较大的盘子放在较小的盘子上面。
4. 二分搜索:这是一个在排序数组中查找特定元素的递归算法。
它首先将数组分成两半,然后根据目标值与中间元素的比较结果,选择另一半继续搜索。
5. 回溯算法:这是一种通过递归搜索所有可能解的算法,通常用于解决约束满足问题。
例如,排列组合问题、八皇后问题等。
6. 分治算法:这是一种将问题分解为更小的子问题,然后递归地解决这些子问题的算法。
例如,归并排序和快速排序等。
7. 动态规划:这是一种使用递归和备忘录(或称为记忆化)的方法,用于解决具有重叠子问题和最优子结构的问题。
例如,背包问题和最短路径问题等。
这些经典的递归问题涵盖了不同的应用领域和算法类型,可以通过学习和解决这些问题来提高自己的编程和算法技能。

算法递归典型例题实验一:递归策略运用练习三、实验项目1.运用递归策略设计算法实现下述题目的求解过程。
题目列表如下:(1)运动会开了N天,一共发出金牌M枚。
第一天发金牌1枚加剩下的七分之一枚,第二天发金牌2枚加剩下的七分之一枚,第3天发金牌3枚加剩下的七分之一枚,以后每天都照此办理。
到了第N天刚好还有金牌N枚,到此金牌全部发完。
编程求N和M。
(2)国王分财产。
某国王临终前给儿子们分财产。
他把财产分为若干份,然后给第一个儿子一份,再加上剩余财产的1/10;给第二个儿子两份,再加上剩余财产的1/10;……;给第i个儿子i份,再加上剩余财产的1/10。
每个儿子都窃窃自喜。
以为得到了父王的偏爱,孰不知国王是“一碗水端平”的。
请用程序回答,老国王共有几个儿子?财产共分成了多少份?源程序:(3)出售金鱼问题:第一次卖出全部金鱼的一半加二分之一条金鱼;第二次卖出乘余金鱼的三分之一加三分之一条金鱼;第三次卖出剩余金鱼的四分之一加四分之一条金鱼;第四次卖出剩余金鱼的五分之一加五分之一条金鱼;现在还剩下11条金鱼,在出售金鱼时不能把金鱼切开或者有任何破损的。
问这鱼缸里原有多少条金鱼?(4)某路公共汽车,总共有八站,从一号站发轩时车上已有n位乘客,到了第二站先下一半乘客,再上来了六位乘客;到了第三站也先下一半乘客,再上来了五位乘客,以后每到一站都先下车上已有的一半乘客,再上来了乘客比前一站少一个……,到了终点站车上还有乘客六人,问发车时车上的乘客有多少?(5)猴子吃桃。
有一群猴子摘来了一批桃子,猴王规定每天只准吃一半加一只(即第二天吃剩下的一半加一只,以此类推),第九天正好吃完,问猴子们摘来了多少桃子?(6)小华读书。
第一天读了全书的一半加二页,第二天读了剩下的一半加二页,以后天天如此……,第六天读完了最后的三页,问全书有多少页?(7)日本著名数学游戏专家中村义作教授提出这样一个问题:父亲将2520个桔子分给六个儿子。
算法递归典型例题实验一:递归策略运用练习三、实验项目1运用递归策略设计算法实现下述题目的求解过程。
题目列表如下:(1)运动会开了N天,一共发岀金牌M枚。
第一天发金牌1枚加剩下的七分之一枚,第二天发金牌2枚加剩下的七分之一枚,第3天发金牌3枚加剩下的七分之一枚,以后每天都照此办理。
到了第N天刚好还有金牌N枚,到此金牌全部发完。
编程求(2)国王分财产。
某国王临终前给儿子们分财产。
他把财产分为若干份,然后给第一个儿子一份,再加上剩余财产的1/10;给第二个儿子两份,再加上剩余财产的1/10 ;……;给第i个儿子i份,再加上剩余财产的1/10。
每个儿子都窃窃自喜。
以为得到了父王的偏爱,孰不知国王是“一碗水端平”的。
请用程序回答,老国王共有几个儿子?财产共分成了多少份?源程序:(3)岀售金鱼问题:第一次卖岀全部金鱼的一半加二分之一条金鱼;第二次卖岀乘余金鱼的三分之一加三分之一条金鱼;第三次卖岀剩余金鱼的四分之一加四分之一条金鱼;第四次卖岀剩余金鱼的五分之一加五分之一条金鱼;现在还剩下11条金鱼,在岀售金鱼时不能把金鱼切开或者有任何破损的。
问这鱼缸里原有多少条金鱼?(4)某路公共汽车,总共有八站,从一号站发轩时车上已有n位乘客,到了第二站先下一半乘客,再上来了六位乘客;到了第三站也先下一半乘客,再上来了五位乘客,以后每到一站都先下车上已有的一半乘客,再上来了乘客比前一站少一个……,到了终点站车上还有乘客六人,问发车时车上的乘客有多少?(5)猴子吃桃。
有一群猴子摘来了一批桃子,猴王规定每天只准吃一半加一只(即第二天吃剩下的一半加一只,以此类推) ,第九天正好吃完,问猴子们摘来了多少桃子?(6)小华读书。
第一天读了全书的一半加二页,第二天读了剩下的一半加二页,以后天天如此……,第六天读完了最后的三页,问全书有多少页?(7)日本著名数学游戏专家中村义作教授提岀这样一个问题:父亲将2520个桔子分给六个儿子。
分完后父亲说:“老大将分给你的桔子的1/8给老二;老二拿到后连同原先的桔子分1/7 给老三;老三拿到后连同原先的桔子分1/6给老四;老四拿到后连同原先的桔子分1/5给老五;老五拿到后连同原先的桔子分1/4给老六;老六拿到后连同原先的桔子分1/3给老大”。
习 题 解 析第1章1. 解析:算法主要是指求解问题的方法。
计算机中的算法是求解问题的方法在计算机上的实现。
2. 解析:算法的五大特征是确定性、有穷性、输入、输出和可行性。
3. 解析:计算n ⎢⎥⎣⎦的算法,其中n 是正整数。
可以取循环变量i 的值从1开始,算i 的平方,取平方值最接近且小于或者等于n 的i 即可。
4. 解析:可以使用反证法,设i=gcd(m, n)=gcd(n, m mod n),则设m=a*i ,n=b*i ,且a 与b 互质,这时m mod n=(a-x*b )*i ,只需要证明b 和a-x*b 互质,假设二者不互质,可以推出a 与b 不互质,因此可以得到证明。
5. 解析:自然语言描述:十进制整数转换为二进制整数采用“除2取余,逆序排列”法。
具体做法是:用2整除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为0时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
流程图:如图*.1开始输入n长度len=(logn/log2)len>=0Y输出(n>>len)&1)len=len-1N结束图*.1 十进制整数转换成二进制整数流程图6. 解析:a.如果线性表是数组,则可以进行随机查找。
由于有序,因此可以进行折半查找,这样可以在最少的比较次数下完成查找。
b.如果线性表是链表,虽然有序,则只能进行顺序查找,从链表头部开始进行比较,当发现当前节点的值大于待查找元素值,则查找失败。
7. 解析:本题主要是举例让大家了解算法的精确性。
过程中不能有含糊不清或者二义性的步骤。
大家根据可行的方式总结一下阅读一本书的过程即可。
8. 解析:数据结构中介绍的字典是一种抽象数据结构,由一组键值对组成,各个键值对的键各不相同,程序可以将新的键值对添加到字典中,或者基于键进行查找、更新或删除等操作。
【算法分析】递归算法的⼏个经典例⼦例⼀:整数划分问题 将正整数n表⽰成⼀系列正整数之和:n=n1+n2+…+nk,其中n1≥n2≥…≥nk≥1,k≥1。
正整数n的这种表⽰称为正整数n的划分。
求正整数n的不同划分个数。
例如:正整数6有如下11种不同的划分:6;5+1;4+2,4+1+1;3+3,3+2+1,3+1+1+1;2+2+2,2+2+1+1,2+1+1+1+1;1+1+1+1+1+1在本例中,如果设p(n)为正整数n的划分数,则难以找到递归关系,因此考虑增加⼀个⾃变量:将最⼤加数n1不⼤于m的划分个数记作q(n,m)。
下⾯对可能出现的四种情况进⾏分析:① m=1: 当m等于1时,对n的划分只可能1+1+1+……+1这⼀种情况。
②m>n时: 当m⼤于n时,由于划分中不可能出现负数,所以{n1, n2, n2,… , nk}(n = n1+n2+n3+……+nk)只可能出现⼩于等于n的整数。
故有q(n, m)=q(n, n)⑤m=n时: 当m等于n时,包含n⾃⾝的划分和没有n的划分两个部分。
⽽包含n⾃⾝的划分只有⼀种情况,故有有q(n, n)=1+q(n,n-1)④m<n时: n的m划分有包含m和不包含m两个部分。
其中包含m的部分⽤集合可表⽰为{m, {x1, x2, x3, 4,…, xk}}(其中x1+x2+……+xk=n-m)【详解见图1】,这部分的划分数为q(n-m, m);⽽不包含m的划分中,最⼤值不能为m,故划分数就等于q(n, m)。
所以在m<n时整数n的划分数为:q(n, m)=q(n, m-1)+q(n-m, m)。
【图1:ipad坏了,⼀时找不到纸,后⾯再补吧。
】递归求整数划分:1int q(int n, int m){2if(m==1){3return1;4 }5else if(m>n){6return q(n,n);7 }8else if(m==n){9return q(n,n-1)+1;10 }11else if(m<n){12return q(n-m, m)+q(n,m-1);13 }14 }。
递归算法经典题目递归算法是一种非常强大的编程技术,它能够解决一些复杂的问题,将它们分解为更小的子问题。
以下是一些经典的递归算法题目:1. 斐波那契数列:这是一个经典的递归问题,斐波那契数列中的每个数字都是前两个数字的和。
例如,0, 1, 1, 2, 3, 5, 8, 13, 21... 编写一个函数来计算斐波那契数列中的第n个数字。
2. 阶乘:阶乘是一个数的所有小于及等于该数的正整数的乘积。
例如,5的阶乘(记作5!)是5 4 3 2 1 = 120。
编写一个函数来计算一个数的阶乘。
3. 二分搜索:二分搜索是一种在排序数组中查找特定元素的搜索算法。
编写一个函数,该函数使用二分搜索在给定的排序数组中查找特定的元素。
4. 回溯算法:回溯算法用于解决决策问题,例如八皇后问题。
在这个问题中,我们需要在一个8x8棋盘上放置8个皇后,使得任何两个皇后都不在同一行、同一列或同一对角线上。
编写一个使用回溯算法解决八皇后问题的函数。
5. 合并排序:合并排序是一种分治算法,它将一个大的列表分成两个较小的子列表,对子列表进行排序,然后将它们合并成一个已排序的列表。
编写一个使用递归实现合并排序的函数。
6. 快速排序:快速排序也是一种分治算法,它选择一个"基准"元素,然后将所有比基准小的元素放在其左边,所有比基准大的元素放在其右边。
然后对左右两个子列表进行快速排序。
编写一个使用递归实现快速排序的函数。
7. 深度优先搜索(DFS):这是一种用于遍历或搜索树或图的算法。
这个算法会尽可能深地搜索树的分支。
当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。
这一过程一直进行到已发现从源节点可达的所有节点为止。
如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
编写一个使用递归实现深度优先搜索的函数。
这些题目都可以帮助你理解和应用递归算法。