相似多边形的定义

第八讲 相似多边形与相似三角形一、新知探索与考点剖析考点一：相似多边形例1．下面各组中的两个图形，形状相同的图形是（ ）例2．（1）以下五个命题：①所有的正方形都相似； ②所有的矩形都相似；③所有的菱形都相似； ④所有的三角形都相似； ⑤所有的等腰直角三角形都相似； ⑥所有的正五边形都相似．其中正确的命题有______________________．（2）已知四边形ABCD 与四边形A ′B ′C ′D ′相似,相似比为4:3，①若∠A ′=65°,则∠A=___________； ②A ′B ′=6 cm,则 AB=___________；③若四边形ABCD 周长为64cm,则四边形A ′D ′、B ′C ′的周长为______________．例3．E 、F 分别是矩形ABCD 的边AD 、BC 的中点，若矩形ABCD ∽矩形EABF ，（1） 求长方形ABCD 长AD 与宽CD 的比； （2） 当AB=1时，求矩形ABCD 的面积. ◎变式提升训练◎1. 如图，已知四边形ABCD ∽A ’B ’C ’D ’, 则x= ，y= ， = ．考点二：相似三角形例4. 如图，ΔABC 与ΔADB 中，∠ABC=∠ADB=90°，AC=5cm ，AB=4cm ，如果图中的两个直角三角形相似，求AD 的长.◎变式提升训练◎1． 如图，点C 、D 在线段AB 上，且ΔPCD 是等边三角形.当ΔAPB ∽ΔACP 时，则∠APB=_________.2.如图，已知点D 在AC 上，且△ABD ∽△ACB ，AB=2，AD=1，求CD 的长.3.如图，在矩形ABCD 中，点E F 、分别在边AD DC 、上，A B ED E F △∽△，692AB AE DE ===，，，求EF 的长．C第1题第2题第3题二、易错点、考点强化提升例6.如图，在梯形ABCD 中，AD ∥BC ，M 为AB 上一点，MN ∥BC 交CD 于N.若AD=2，BC=8，M 点在何处时，MN 所分梯形AMND 与梯形MBCN 相似？◎变式提升训练◎如图，在△ABC 中，已知∠ACB=900，过C 作1CD AB ⊥于1D ，过点1D 作12D D BC ⊥于2D 过2D 作23D D AB ⊥于3D ，这样继续下去.（1）判断图中的这些三角形的形状都相同吗？（2）若∠B=30°，AC=1，求线段1n n D D +(n 为正整数)的长度.◎素质能力测试◎一、选择题：1．梯形ABCD 中，AD ∥BC ，AD=a ，BC=b ，EF ∥AD 交AB 、CD 于E 、F ，且梯形AEFD 与梯形EBCF 相似，则EF 等于（ ）．A ．abB ．2b a +C ．222b a + D ．不能确定2. 如图,AB 是斜靠在墙上的长梯,梯脚B 距墙脚1.6m,梯上点D 距墙1.4m, BD 长0.55m,且△ADE ∽△ABC,则梯子的长AB=( ) A.3.85m B.4.00m C.4.40m D.4.50m3. 如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使⊿ABC ∽⊿CAD, 只要CD 等于( )A.c b 2B.a b 2C.c abD.ca 213A DC M N B4. 一个钢筋三角架三 长分别为20cm,50cm,60cm,现要再做一个与其相似的钢筋三角架,而只有长为30cm 和50cm 的两根钢筋,要求以其中的一根为一边,从另一根截下两段(允许有余料)作为另两边,则不同的截法有( )A.一种B.两种C.三种D.四种二、填空题1．两个相似多边形的相似比是81，则这两个多边形的对应对角线的比是________．2．在菱形ABCD 和菱形A ′B ′C ′D ′中，∠A =∠A ′=60°，若AB ∶A ′B ′=1∶3， 则BD ∶A ′C ′=____________．三、解答题1．在一矩形ABCD 的花坛与花坛四周修筑小路，使得相对两条小路的宽均相等.如果花坛AB=20米，AD=30米，试问小路的宽x 与y 的比值为多少时，能使使小路四周所围成的矩形A ′B ′C ′D ′与矩形ABCD 相似？请说明理由.2．如图，梯形ABCD 中，AD ∥BC ，E 是AB 上的一点，EF ∥BC ，并且EF 将梯形ABCD 分成的两个梯形AEFD 、EBCF 相似，若AD=4，BC=9，求AE ∶EB ．——相似多边形与相似三角形 姓名：______一、选择题：1．下列图形中一定相似的是（ ）A ．有一个角相等的两个平行四边形B ．有一个角相等的两个等腰梯形C ．有一个角相等的两个菱形D ．有一组邻边对应成比例的两平行四边形 2．下列结论不正确的是（ ）． A ．所有的矩形都相似 B ．所有的正方形都相似C ．所有的等腰直角三角形都相似D ．所有的正八边形都相似3．五边形ABCDE ∽五边形A ′B ′C ′D ′E ′，若对应边AB 与A ′B ′的长分别为50厘米 和40厘米，则五边形A ′B ′C ′D ′E ′与五边形ABCDE 的相似比是（ ）． A ．5∶4 B．4∶5 C ．5∶25 D ．25∶54．若△ABC ∽△DEF,它们的周长分别为6 cm 和8 cm ，那么下式中一定成立的是（ ）． A ．3AB=4DE B ．4AC=3DEC ．3∠A=4∠D D ．4（AB+BC+AC ）=3（DE+EF+DF ）5．某学生利用树影测松树的高度，他在某一时刻测得1．5米长的竹竿影长0．9米，但当他马上测松树高度时，因松树靠近一幢高楼，影子不是全部在地面上，有一部分影子落在墙上，他测得留在地面部分的影长是2．4米，留在墙上部分的影高是1.5米，则松树的高度为_____米．二、解答题1．已知：△ABC 三边的比为1∶2∶3，△A ′B ′C ′∽△ABC ，且△A ′B ′C ′的最大边长为15 cm ，求△A ′B ′C ′的周长．2.已知ABC A B C '''△∽△,△ABC 2，A B C '''△的两边长分别为1A B C '''△的第三边长.3. 如图，分别取等边三角形ABC 各边的中点D 、E 、F ，得△DEF ．若△ABC 的边长为a ． （1）△DEF 与△ABC 相似吗？如果相似，相似比是多少？（2）分别求出这两个三角形的面积．（3）这两个三角形的面积比与边长之比有什么关系吗？。

一、知识点分析与例题讲解一、相似多边形的性质知识点1：相似多边形边、角的性质根据相似多边形的定义，可知当两个多边形相似时，它们的对应角相等，对应边对应成比例，其比叫做相似多边形的相似比。

知识点2：相似多边形的周长、面积的性质相似多边形的周长比等于相似比，面积比等于相似比的平方。

由于从多边形的一个顶点出发，可引出（n －3）条对角线，这（n －3）条对角线将多边形分成了（n －2）个三角形，所以相似多边形具有与相似三角形相类似的性质，诸如相似多边形的周长比等于相似比，面积比等于相似比的平方。

例1、已知图中的两个四边形相似，找出图中的成比例线段，并用比例式表示。

例2、如图，在平行四边形ABCD 中，延长AB 到E ，使12BE AB =，延长CD 到F ，使,DF DC EF =交BC 于G ，交AD 于H ，则BEG ∆的周长与CFG ∆的周长的比为_________。

例3、如图，在梯形ABCD 中，E BC AD ,//是AB 上一点，BC EF //，并且EF 将梯形ABCD分成的两个梯形AEFD 、EBCF 相似，若9,4==BC AD ，求EB AE :。

二、位似图形知识点1位似三角形与为似多边形如果两个三角形不仅是相似三角形，而且每组对应点所在的直线都经过同一个点，那么两个三角形叫做位似三角形，它们的相似比又称为位似比，这个点叫做位似中心。

同样，如果两个多边形不仅是相似多边形，而且每组对应点所在的直线都经过同一个点，那么两个多边形叫做位似多边形，它们的相似比又称为位似比，这个点叫做位似中心。

利用多边形的位似可以将一个三角形或多边形缩小或放大。

知识点2位似变换与位似图形若两个几何图形F 与F ’相似，而且对应点连线交于同一点O ，则称F 与F ’关于点O 位似，O 叫做位似中心。

把一个几何图形变换成与之位似的图形,叫做位似变换。

知识点3位似多边形的画法1、连接位似中心与多边形各顶点；2、延长各连线，使得延长线与连线之比为位似比；3、按顺序连接所得各点。

初中-数学-打印版
什么是相似多边形？
什么是相似多边形？
难易度：★★★
关键词：相似图形的性质
答案：
多边形的边数相同，各角对应相等，各边对应成比例叫相似多边形。

即把握两个关键各角对应相等，各边对应成比例。

【举一反三】
典例：两个多边形相似的条件是（）
A．对应角相等 B．对应边相等
C．对应角相等，对应边相等 D．对应角相等，对应边成比例
思路导引：一般来讲，解决本题要把握相似多边形的概念，即把握两个关键各角对应相等，各边对应成比例。

标准答案：D
初中-数学-打印版。

第四章图形的相似3 相似多边形教学目标教学反思1.了解相似多边形的定义，掌握相似多边形的性质.2.在探索相似多边形的性质时掌握类比的方法.3.体会相似多边形与相似三角形的区别与联系.教学重难点重点：相似多边形的判定.难点：两个多边形相似性质的简单应用.教学过程导入新课教师用多媒体出示几个图形，让学生找出形状相同的图形，并连线.然后教师提出问题形状相同的两个图形有什么样的关系？由这一问题来引入本节课要研究的课题.探究新知一、预习新知下图中的两个多边形分别是幻灯片上的多边形ABCDEF和银幕上的多边形A1B1C1D1E1F1.它们的形状相同吗？教学反思师：它们的形状相同吗？生：六边形ABCDEF和六边形A1B1C1D1E1F1形状相同.师：在上面的两个多边形中，是否有相等的内角？设法验证你的猜测.生：∠A与∠A1，∠B与∠B1，∠C与∠C1，∠D与∠D1，∠E与∠E1，∠F与∠F1分别对应相等.师：这样的角我们称为对应角，在上面的两个多边形中，夹相等内角的两边是否成比例？生：通过测量AB与A1B1，BC与B1C1，CD与C1D1，DE与D1E1，EF与E1F1，F A与F1A1的比相等.师：这样的边我们称为对应边.师：从上面的讨论结果来看，大家能否猜到相似多边形的定义呢？生：可以，各角分别相等、各边成比例的两个多边形叫做相似多边形.师：相似怎样表示呢？请同学们认真看书.生：六边形ABCDEF和六边形A1B1C1D1E1F1相似，记作六边形ABCDEF∽六边形A1B1C1D1E1F1.师：相似多边形对应边的比叫做相似比，一般用字母k表示，“∽”读作“相似于”.在记两个多边形相似时，需要注意什么？生：要把表示对应顶点的字母写在对应的位置上.二、合作探究观察下面两组图形.（1）（2）师：（1）中的两个图形相似吗？生：（1）中的两个图形不相似.师：为什么？教学反思生：虽然这两个图形的对应边成比例，但是对应角不相等，所以这两个图形不相似.师：（2）中的两个图形相似吗？生：也不相似.师：这又是为什么呢？生：虽然这两个图形的对应角相等，但是对应边不成比例，所以这两个图形不相似.教师补充：两个多边形不相似，它们的对应角可能相等，如上面的（2）；两个多边形不相似，它们的对应边可能成比例，如上面的（1）.师：任意两个等边三角形相似吗？生：相似，因为它们的对应角都为60°，对应边成比例.师：任意两个正方形呢？生：也是相似的师：那任意两个正n边形呢？生：两个正n边形的对应角相等，对应边成比例，所以它们都是相似的.师：任意两个菱形相似吗？生：不一定相似师：为什么？生：虽然对应边成比例，但是菱形对应角不一定相等，所以不一定相似.巩固练习在矩形ABCD中，AB＝4，BC＝3，下列四个矩形中与矩形ABCD相似的是()答案：A典型例题【例1】如图，四边形ABCD与四边形A′B′C′D′相似，求∠A的度数与x 的值．【问题探索】此题考查相似多边形的性质，如何用相似多边形的性质求∠A 的度数与x 的值？【解】由相似图形的性质，知∠A ＝∠A ′＝107°，4x ＝52，x ＝85.【总结】相似多边形的对应边成比例，对应角相等． 【例2】在宽为20 m ，长为30 m 的矩形花坛四周修筑小路．(1)如果四周的小路的宽均相等，都是x ，如图1，那么小路四周所围成的矩形A ′B ′C ′D ′和矩形ABCD 相似吗？请说明理由；(2)如果相对着的两条小路的宽均相等，宽度分别为x ，y ，如图2，试问小路的宽x 与y 的比值为多少时，能使得小路四周所围成的矩形A′B ′C ′D ′和矩形ABCD 相似？请说明理由．图1 图2【问题探索】判断两个矩形是否相似要从边出发，求小路的宽x 与y的比值，要运用相似图形的性质．【解】(1)如果四周的小路的宽均相等，那么小路四周所围成的矩形A ′B ′C ′D ′和矩形ABCD 不相似．理由：设四周的小路的宽为x m.30230x +＝1515x +，20220x +＝1010x+. ∵ 30230x +20220x+≠， ∴ 小路四周所围成的矩形A ′B ′C ′D ′和矩形ABCD 不相似． (2)∵ 当20220y +＝30230x+时，小路四周所围成的矩形A ′B ′C ′D ′和矩形ABCD 相似，解得xy＝32， 教学反思∴路的宽x与y的比值为3∶2时，能使小路四周所围成的矩形A′B′C′D′和矩形ABCD相似．【总结】相似多边形的对应边成比例，对应角相等，两个边数相同的多边形，如果各边对应边成比例，各角对应相等，那么它们就相似．课堂练习1.放大镜中的多边形与原多边形的关系是()A．形状不同，大小不同B．形状相同，大小相同C．形状相同，大小不同D．形状不同，大小相同2.给出下列命题：①所有的正方形都相似；①所有的矩形都相似；①所有的三角形都相似；①所有的等腰直角三角形都相似；①所有的正五边形都相似.其中，正确命题为()A.①①①B.①①①C.①①①D.①①①3.若△ABC①△A′B′C′，且AB︰A′B′=1∶2，则△ABC与△A′B′C′相似比是，△A′B′C′与△ABC的相似比是．4.如图，ABCD∽AEFB，且AB＝3 cm，BC＝6 cm.求AE的长.参考答案1.C2.C3.1224.解：∵ABCD∽AEFB，∴ABAE =BCEF.又∵AB＝3 cm，BC＝6 cm，EF＝AB＝3 cm，∴AE＝3×36=32.课堂小结(学生总结，老师点评)1.相似多边形的定义2.相似多边形的性质3.相似比的定义布置作业习题4.4第1题、第2题板书设计第四章图形的相似3 相似多边形1.相似多边形：各角分别相等、各边成比例的两个多边形叫做相似多边形.2.相似比：相似多边形对应边的比叫做相似比.。

《相似多边形和图形的位似》汇报人：日期:•相似多边形的基本概念•相似多边形的判定方法•图形的位似变换目录•相似多边形与位似变换的关系•相似多边形和位似变换的应用举例•总结与展望01相似多边形的基本概念如果两个多边形的对应角相等，则它们是相似的。

对应角相等如果两个多边形的对应边成比例，则它们是相似的。

对应边成比例对应边成比例相似多边形的对应边成比例。

面积比等于相似比的平方相似多边形的面积比等于相似比的平方。

对应角相等相似多边形的对应角相等。

等边三角形矩形三边都相等的三角形。

四个角都是直角的四边形。

等腰三角形等腰梯形正方形两边相等的三角形，其中两边为腰，另一边为底。

有一组对边平行且另一组对边相等的四边形。

四边相等且四个角都是直角的四边形。

02相似多边形的判定方法平行线的性质是判定定理的基础，通过平行线的性质可以推导出相似多边形的判定定理。

平行线性质相似三角形的判定相似多边形的定义首先证明两个三角形相似，再利用相似三角形的性质推导出两个多边形相似。

根据相似多边形的定义，如果两个多边形的对应角相等，则它们相似。

030201判定定理可以应用于实际问题中，例如在建筑设计、工程绘图等领域中，需要利用相似多边形的性质进行计算和设计。

判定定理也可以应用于数学问题中，例如在几何证明、代数运算等领域中，可以利用相似多边形的性质进行证明和计算。

数学问题中的应用实际问题中的应用首先根据相似三角形的性质，证明两个三角形相似；然后利用相似三角形的性质，推导出两个多边形相似。

证明过程具体证明过程需要使用到平行线的性质、相似三角形的性质等知识点，通过逻辑推理和数学运算来证明判定定理的正确性。

03图形的位似变换如果一个图形经过某种变换后，其形状和大小保持不变，但各对应点间的相对位置关系发生了改变，那么这种变换称为位似变换。

定义位似变换保持了图形间的相对位置关系，但改变了图形的形状和大小。

位似变换的特性位似变换保持了图形间的相对位置关系，即图形中的点在变换后仍然保持它们之间的相对位置不变。

平行线分线段成比例及相似多边形讲义【知识点拨】知识点一：图形的相似形状相同的图形叫做相似图形。

（1）两个图形相似，其中一个图形可以看作由另一个图形放大或缩小得到；（2）全等的图形可以看成是一种特殊的相似，即不仅形状相同，大小也相同；（3）判断两个图形是否相似，就是看两个图形是不是形状相同，与其他因素无关。

知识点一：图形的相似形状相同的图形叫做相似图形。

（1）两个图形相似，其中一个图形可以看作由另一个图形放大或缩小得到；（2）全等的图形可以看成是一种特殊的相似，即不仅形状相同，大小也相同；（3）判断两个图形是否相似，就是看两个图形是不是形状相同，与其他因素无关。

例1、下列命题正确的是（ ）A、相似多边形是全等多边形B、不全等的多边形不是相似多边形C、全等多边形是相似多边形D、不相似的多边形可能是全等多边形（变式）1、下列说法中正确的是（ ）A、 两个三角形不全等，那么它们也不相似B、两个三角形不相似，那么它们也不全等C、两个相似三角形一定不全等D、两个全等三角形一定不相似例2、观察下面的图形，如图形状相同的有 。

2、视力表对我们来说并不陌生．如图是视力表的一部分，其中开口向上的两个“E”之间的变换是（ ）A、平移B、旋转C、对称D、相似知识点二、相似多边形1、相似多边形的定义：对应角相等、对应边成比例的两个多边形叫做相似多边形．相似多边形对应边的比叫做它们的相似比．2、相似多边形的性质： 相似多边形的对应角相等，对应边成比例．性质：相似多边形的周长之比等于相似比；相似多边形的面积之比等于相似比的平方．考点：相似多边形1、一个多边形的边长分别是2、3、4、5、6，另一个和它相似的多边形的最短边长为6，则这个多边形的最长边为 。

2、两个相似六边形的周长分别是l1，l2，面积分别是S1，S2，若 l1：l2=2︰3，S2-S1 =30，则S1= ______，S2=_____.3.如图中的两个梯形相似，求出未知边x、y、z的长度和α、β的大小．4、△ABC的三边长分别为、、2，△DEF的两边长分别为1和，如果△ABC∽△DEF，那么△DEF的第三边长为（ ）A、 B、2 C、 D、5、一个多边形的边长分别是4 cm、5 cm、6 cm、4 cm、5cm，和它相似的一个多边形最长边为8 cm，那么这个多边形的周长是（ ）A、12 cmB、18 cmC、32 cmD、48 cm6、Rt△ABC的两条直角边分别为3 cm、4 cm，与它相似的Rt△A'B'C'的斜边为20 cm，那么Rt△A'B'C'的周长为（ ）A、48 cmB、28 cmC、12 cmD、10 cm7、如果一个矩形对折后和原来的矩形相似，则此矩形的长边与短边之比为（ ）A、2：1B、4：11C、：1D、1.5：18、两个相似三角形的对应高的比为1：，其中小三角形的最长边为10 cm，那么另一个三角形的最长边为________。

3相似多边形●归纳导入下列每组图形形状相同吗？每组图形中边与角分别有什么关系？【归纳】相似多边形的定义：各角分别__相等__各边__成比例__的两个多边形叫做相似多边形．【教学与建议】教学：通过图形的比较，归纳相似多边形所具备的共同特征，导入相似多边形的定义．建议：强调相似多边形定义的两个关键点：一是各角分别相等；二是各边成比例．●类比导入色彩斑斓的世界中有许多形状相同的图形，这些图形的形状相同，大小不等，我们称之为相似图形．今天，老师就带领同学们来了解相似王国里的一个伟大家族——相似多边形(板书课题)．【教学与建议】教学：收集相似图形的信息，体会相似图形在生活中的实际意义，自然引出课题——相似多边形．建议：让学生口答图片的异同，教师补充．命题角度1利用相似多边形的定义判断相似多边形具备的两个关键点：①各角分别相等；②各边分别成比例．【例1】(1)已知矩形ABCD中，AB＝4，BC＝3，下列四个矩形中与矩形ABCD相似的是(A)A B C D(2)下列各组图形中相似的有__①②__．(填序号)①放大镜下放大后的图象和原来的事物；②幻灯片的底片与投影在屏幕上的画面；③天空中两片白云的照片．命题角度2利用相似多边形的性质计算利用相似多边形的性质进行计算的关键是找准对应边和对应角．【例2】(1)一个五边形的边长分别为2，3，4，5，6，另一个和它相似的五边形的最大边长为24，则这个五边形的最短边长为(B)A．6 B．8 C．10 D．12(2)在四边形ABCD与四边形A′B′C′D′中，AB＝3，BC＝5，∠D＝50°，A′B′＝6，要使四边形ABCD∽四边形A′B′C′D′，则B′C′＝__10__，∠D′＝__50°__．高效课堂教学设计1．掌握相似多边形和相似比的概念．2．利用定义判断两个多边形是否相似．3．掌握相似多边形的性质，能根据相似比进行相关的计算．▲重点相似多边形的定义和性质．▲难点如何判断两个多边形是否相似．◆活动1创设情境导入新课(课件)观察以下三组图形，每一组图形的对应边、对应角有什么关系呢？（1）（2）（3）◆活动2 实践探究 交流新知 【探究1】相似多边形的概念和性质 教师展示课件(播放动画)在这两个多边形中，是否有相等的内角？夹相等内角的两边是否成比例？ 归纳：1.各角分别相等、各边成比例的两个多边形叫做相似多边形． 2．相似用“∽”表示，读作“相似于”．例如，在上图中，六边形ABCDEF 与六边形A 1B 1C 1D 1E 1F 1相似，记作六边形ABCDEF ∽六边形A 1B 1C 1D 1E 1F 1.在记两个多边形相似时，要把表示对应顶点的字母写在对应的位置上．3．相似多边形对应边的比叫做相似比．例如，五边形ABCDE ∽五边形A 1B 2C 1D 1E 1，对应边的比AB A 1B 1 ＝BCB 1C 1＝CD C 1D 1 ＝DE D 1E 1 ＝EA E 1A 1 ＝45 ，因此五边形ABCDE 与五边形A 1B 1C 1D 1E 1的相似比为k 1＝45，五边形A 1B 1C 1D 1E 1与五边形ABCDE 的相似比为k 2＝54.讨论：下面每组图形形状相同，它们的对应角有怎样的关系？对应边呢？ (1)正三角形ABC 与正三角形DEF ； (2)正方形ABCD 与正方形EFGH .（1） （2）归纳：相似多边形的对应边成比例，对应角相等． 【探究2】相似多边形的判定 1．想一想：(1)任意两个等边三角形相似吗？任意两个正方形呢？任意两个正n 边形呢？ (2)任意两个菱形相似吗？2．观察下面两组图形，提出问题(多媒体展示)： 图①中的两个图形相似吗？为什么？ 图②中的两个图形呢？与同伴交流．图① 图②如果两个多边形不相似，那么它们的各角可能对应相等吗？它们的各边可能对应成比例吗？ 归纳：相似多边形必须同时具备两点：对应角相等、对应边成比例． ◆活动3 开放训练 应用举例例1 一块长3 m 、宽1.5 m 的矩形黑板如图所示，镶在其外围的木质边框宽7.5 cm.边框的内外边缘所成的矩形相似吗？为什么？(让学生先判断，分组讨论，再通过计算验证自己的判断)【方法指导】对应边成比例的两个矩形相似．解：不相似．理由如下：内边缘矩形长3 m ，宽1.5 m ，外边缘所成的矩形长为3＋0.075×2＝3.15(m)，宽为 1.5＋0.075×2＝1.65(m).∴边框的内外边缘所成的矩形的长之比为33.15 ＝2021 ，宽之比为1.51.65 ＝1011 .∵2021≠1011，∴边框的内外边缘所成的矩形不相似． 例2 如图，四边形ABCD ∽四边形A ′B ′C ′D ′，则∠1＝__70°__，AD ＝__28__．【方法指导】根据相似多边形对应边之比相等，对应角相等可得．解：四边形ABCD ∽四边形A ′B ′C ′D ′，则∠1＝∠B ＝70°，A ′D ′AD ＝D ′C ′DC .即21AD ＝1824，解得AD ＝28.◆活动4 随堂练习1．如果六边形ABCDEF ∽六边形A ′B ′C ′D ′E ′F ′，∠B ＝75°，则∠B ′的度数是(C) A ．15° B ．25° C ．75° D ．105°2．△ABC ∽A ′B ′C ′，相似比为35 ，且AC ＝3，BC ＝4，AB ＝5，则A ′C ′＝__5__，__B ′C ′__＝__203__，A ′B ′＝__253__，∠C ′＝__90°__．3．课本P 87随堂练习T 1.解：(1)相似．理由如下：∵32 ＝4.53 ＝1.5，且矩形的每个内角均为90°，∴该组两个矩形相似；(2)不相似．理由如下：∵22.5 ≠36，∴该组两个矩形不相似．◆活动5 课堂小结与作业学生活动：这节课你的主要收获是什么？还有什么疑惑？教学说明：相似多边形的概念及性质的运用中，通过观察、类比提高数学思维． 作业：课本P 88随堂练习T 2，P 88习题4.4中的T 1、T 2、T 3.本节课设置大量的图片，体现数学来源于生活．通过折纸操作、观察、猜想，探索出相似多边形的概念，让学生切身感受到自己是学习的主人，为学生今后获取知识、探索发现和创造打下良好的基础．。

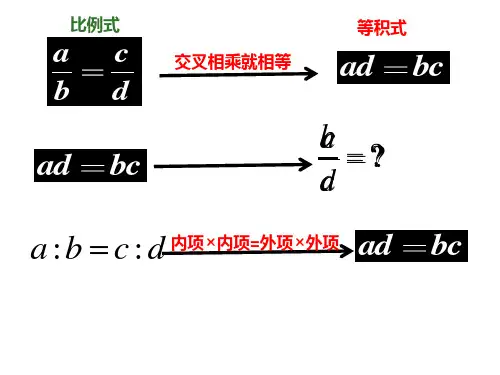
3.3相似多边形（第1课时）知识点一：相似多边形的有关概念各角对应相等，各边对应成比例的两个多边形叫做相似多边形。

△ABC 与△A B C '''相似，记作△ABC ∽△A B C '''。

【例1】下列语句中，正确的有 。

①两个菱形一定是相似图形；②两个矩形一定是相似图形；③两个正方形一定是相似图形；④两个等边三角形一定是相似图形。

【例2】四边形ABCD 的四边长分别为2、3、4、5，与其相似的四边形1111A B C D 的最大边长为15，那么四边形1111A B C D 的最小边长为多少？知识点二：相似多边形的性质及判定相似多边形的对应角相等，对应边成比例。

【例3】已知四边形ABCD ∽四边形A B C D ''''，∠A ＝∠A '＝90°，∠B ＝∠B '＝100°，∠C ＝70°，且20AB =，10A B ''=，10BC =，12C D ''=，16AD =，试求C '∠，D ∠，D '∠，CD ，B C ''，A D ''的值。

，各角对应相等，各边对应成比例的两个多边形是相似多边形。

【例4】如右图，有一矩形草地ABCD ，长BC 为20 m,宽AB 为10 m ，它的外围有1 m 等宽的小路。

问里外两个矩形相似吗？A B C D '''' （填“一定”或“不一定”3、如右图，矩形ABCD 的边长AB ＝矩形ABCD 与矩形A B C D ''''相似吗？并说明理由。

草地A D B C A 'B 'C 'D '。

几何中的平行四边形和相似多边形一、平行四边形的定义和性质1.平行四边形是四边形的一种，具有以下性质：a.对边平行且相等；b.对角相等；c.对边上的高相等；d.对角线互相平分。

二、相似多边形的定义和性质1.相似多边形是指形状相同但大小不一定相同的多边形，具有以下性质：a.对应角相等；b.对应边成比例；c.对应边上的高成比例；d.面积的比等于对应边的比的平方。

三、平行四边形的判定1.两组对边分别平行的四边形是平行四边形；2.一组对边平行且相等的四边形是平行四边形；3.对角线互相平分的四边形是平行四边形。

四、相似多边形的判定1.两组对应角相等的多边形是相似多边形；2.两组对应边成比例的多边形是相似多边形；3.对应角相等且对应边成比例的多边形是相似多边形。

五、平行四边形的应用1.求解平行四边形的面积；2.证明平行四边形的性质；3.解决实际问题中的平行四边形，如平面几何中的最大面积等。

六、相似多边形的应用1.求解相似多边形的面积比；2.证明相似多边形的性质；3.解决实际问题中的相似多边形，如比例尺的应用等。

七、平行四边形和相似多边形的关系1.所有平行四边形都是相似多边形，但相似多边形不一定是平行四边形；2.平行四边形的对边平行且相等是相似多边形对应边成比例的特殊情况；3.相似多边形的对应角相等是平行四边形对角相等的特殊情况。

4.平行四边形和相似多边形是几何中的重要概念，掌握它们的定义、性质和判定方法是解决相关问题的关键；5.平行四边形和相似多边形的性质和判定方法在实际问题中有着广泛的应用，要灵活运用；6.平行四边形和相似多边形的关系要理解清楚，有助于解决更复杂的几何问题。

习题及方法：1.习题：判断下列四边形中，哪些是平行四边形？a.两组对边分别平行的四边形；b.一组对边平行且相等的四边形；c.对角线互相平分的四边形；d.所有角都相等的四边形。

方法：根据平行四边形的定义和性质进行判断。

答案：a、b、c是平行四边形。