下载文档原格式
第十九届全国青少年信息学奥林匹克联赛初赛提高组C++语言试题竞赛时间：2013 年10 月13 日14:30~16:30选手注意：✍试题纸共有12 页，答题纸共有2 页，满分100 分。
请在答题纸上作答，写在试题纸上的一律无效。
✍不得使用任何电子设备（如计算器、手机、电子词典等）或查阅任何书籍资料。
一、单项选择题（共15 题，每题1.5 分，共计22.5 分；每题有且仅有一个正确选项）1. 一个32 位整型变量占用（）个字节。
A. 4B. 8C. 32D. 1282. 二进制数11.01 在十进制下是（）。
A. 3.25B. 4.125C. 6.25D. 11.1253. 下面的故事与（）算法有着异曲同工之妙。
从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：?从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：‘从前有座山，山里有座庙，庙里有个老和尚给小和尚讲故事....’?A. 枚举B. 递归C. 贪心D. 分治4. 1948 年，（）将热力学中的熵引入信息通信领域，标志着信息论研究的开端。
A. 冯·诺伊曼（John von Neumann）B. 图灵（Alan Turing）C. 欧拉（Leonhard Euler）D. 克劳德·香农（Claude Shannon）5. 已知一棵二叉树有2013 个节点，则其中至多有（）个节点有2 个子节点。
A. 1006B. 1007C. 1023D. 10246. 在一个无向图中，如果任意两点之间都存在路径相连，则称其为连通图。
右图是一个有5 个顶点、8 条边的连通图。
若要使它不再是连通图，至少要删去其中的（）条边。
A. 2B. 3C. 4D. 57. 斐波那契数列的定义如下：F1 = 1, F2 = 1, F n = F n – 1 + F n – 2 (n ≥ 3)。
如果用下面的函数计算斐波那契数列的第n 项，则其时间复杂度为（）。
衢州市第十七届(中国电信杯)青少年信息学(计算机)竞赛初赛试题(高中组PASCAL语言)1、CPU的英文全称（）。
A．Central Processing Unit B．Contral Processing UnitC．Command Processing Unit A．Chip Processing Unit2、光盘上记录数据位0，是用（）表示的。
A．平坦部分 B．凹坑部分 C．边沿部分 D．平坦和凹坑两部分3．DES是一种（）。
A．网络服务 B．数据压缩标准 C．网络协议 D．密码体制4．表示存储的容最时，经常碰到K，M，G，T等字母，它们部表示一个具体的数值，其中T 代表（）A．210 B．220 C．230 D．240DES是一套基于DirectShow核心框架的编程接口。
DES的出现，简化了视频编辑任务，弥补了DirectShow对于媒体文件非线性编辑支持的先天性不足。
但是，就技术本身而言，DES 并没有超越DirectShow Filter架构，而只是DirectShow Filter的一种增强应用5．网页中可以插入的动画格式有（）。
A．dwg B．gif C．bmp D．jpg6、在同—张软盘上（）。
A．允许同一子目录中的两个文件同名，也允许不同子目录中的两个文件同名B．不允许同一子目录中的两个文件同名，但允许不同子目录中的两个文件同名C．允许同一子目录中的两个文件同名，但不允许不同子目录中的两个文件同名D．不允许同一子目录中的两个文件同名，也不允许不同子目录中的两个文件同名7．微机内的存储器的地址是以（）编址的。
A．二进制位 B．字长 C．字节 D．微处理器的型号8．在24*24点阵的字库中，汉字“一”与“编”的字模占用字节数分别是（）。
A．32、32 B．32、72 C．72、72 D．72、329．因特网目前所使刚的IP协议地址长度是32位二进数（4字节），新一代IP协议IPv6所规定的地址长度为（）。
第十二届全国信息学奥林匹克分区联赛（NOIP2006）复赛试题（提高组竞赛用时：3小时）关于竞赛中不同语言使用限制的说明一．关于使用Pascal语言与编译结果的说明1．对于Pascal语言的程序，当使用IDE和fpc编译结果不一致时，以fpc的编译结果为准。
2．允许使用数学库(uses math子句)，以及ansistring。
但不允许使用编译开关（最后测试时pascal的范围检查开关默认关闭：{$R-,Q-,S-}），也不支持与优化相关的选项。
二．关于C++语言中模板使用的限制说明1．允许使用的部分：标准容器中的布尔集合，迭代器，串，流。
相关的头文件：<bitset > <iterator > <string > <iostream >2．禁止使用的部分：序列：vector，list，deque序列适配器：stack, queue, priority_queue 关联容器：map, multimap, set, multiset 拟容器：valarray 散列容器：hash_map, hash_set, hash_multimap, hash_multiset 所有的标准库算法相关头文件：<vector > <list > <deque > <stack > <map > <set > <algorithm >1．能量项链(energy.pas/c/cpp)【问题描述】在Mars星球上，每个Mars人都随身佩带着一串能量项链。
在项链上有N颗能量珠。
能量珠是一颗有头标记与尾标记的珠子，这些标记对应着某个正整数。
并且，对于相邻的两颗珠子，前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样，通过吸盘（吸盘是Mars人吸收能量的一种器官）的作用，这两颗珠子才能聚合成一颗珠子，同时释放出可以被吸盘吸收的能量。
NOI’ 95“同创杯”全国青少年信息学（计算机）奥林匹克竞赛分区联赛复赛试题（高中组）（上机编程，完成时间：210 分钟）<1>编码问题：设有一个数组A:ARRAY[0..N-1] OF INTEGER；数组中存放的元素为0～N-1 之间的整数，且A[i]≠ A[j]（当i≠ j时）。
例如： N=6 时，有：此时，数组 A 的编码定义如下：A[0] 的编码为0；A[i] 的编码为：在A[0] ，A[1]∴上面数组 A 的编码为：A= （ 4，3， 0， 5，1， 2），， A[i-1] 中比 A[i] 的值小的个数（B= （0， 0，0，3，1， 2）i=1 ，2，， N-1 ）程序要求解决以下问题：①给出数组 A 后，求出其编码。
②给出数组 A 的编码后，求出 A 中的原数据。
<2> 灯的排列问题：设在一排上有 N 个格子（ N≤ 20），若在格子中放置有不同颜色的灯，每种灯的个数记为 N 1， N2， N k（ k 表示不同颜色灯的个数）。
放灯时要遵守下列规则：①同一种颜色的灯不能分开；②不同颜色的灯之间至少要有一个空位置。
例如： N=8 （格子数）R=2 （红灯数）B=3 （蓝灯数）放置的方法有：R-B 顺序R R B B BR R B B BR R B B BR R B B BR R B B BR R B B BB-R顺序B B B BBBBBBBBBBBBBBR RRRBRRRRRRRR放置的总数为12 种。
数据输入的方式为：NP1（颜色，为一个字母）P2N1（灯的数量）N2Q（结束标记， Q 本身不是灯的颜色）程序要求：求出一种顺序的排列方案及排列总数。
<3> 设有一个四层的积木块，1～ 4 层积木块的数量依次为：5， 6，7， 8如下图所示放置：815851691423414326其中，给出第三层与第四层所标示的数字，并已知第三层的数据是由第四层的数据计算出来的。
全国青少年信息学奥林匹克联赛初赛提高组C++语言试题竞赛时间：2013年10月13日14:30~16:30选手注意：试题纸共有12页，答题纸共有2页，满分100分。
请在答题纸上作答，写在试题纸上的一律无效。
不得使用任何电子设备（如计算器、手机、电子词典等）或查阅任何书籍资料。
一、单项选择题（共15题，每题1.5分，共计22.5分；每题有且仅有一个正确选项）1.一个32位整型变量占用（）个字节。
A.4 B.8 C.32 D.1282.二进制数11.01在十进制下是（）。
A.3.25 B.4.125 C.6.25D.11.1253.下面的故事与（）算法有着异曲同工之妙。
从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：?从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：‘从前有座山，山里有座庙，庙里有个老和尚给小和尚讲故事....’?A.枚举B.递归C.贪心D.分治4.1948年，（）将热力学中的熵引入信息通信领域，标志着信息论研究的开端。
A.冯·诺伊曼（John von Neumann）B.图灵（Alan Turing）C.欧拉（Leonhard Euler）D.克劳德·香农（Claude Shannon）5.已知一棵二叉树有2013个节点，则其中至多有（）个节点有2个子节点。
A.1006B.1007C.1023D.10246.在一个无向图中，如果任意两点之间都存在路径相连，则称其为连通图。
右图是一个有5个顶点、8条边的连通图。
若要使它不再是连通图，至少要删去其中的（）条边。
A.2B.3C.4D.57.斐波那契数列的定义如下：F1=1,F2=1,Fn=Fn–1+Fn–2(n≥3)。
如果用下面的函数计算斐波那契数列的第n项，则其时间复杂度为（）。
int F(int n){if(n<=2)return 1;elsereturn F(n-1)+F(n-2);}A.O(1)B.O(n)C.O(n2)D.O(F n)8.二叉查找树具有如下性质：每个节点的值都大于其左子树上所有节点的值、小于其右子树上所有节点的值。
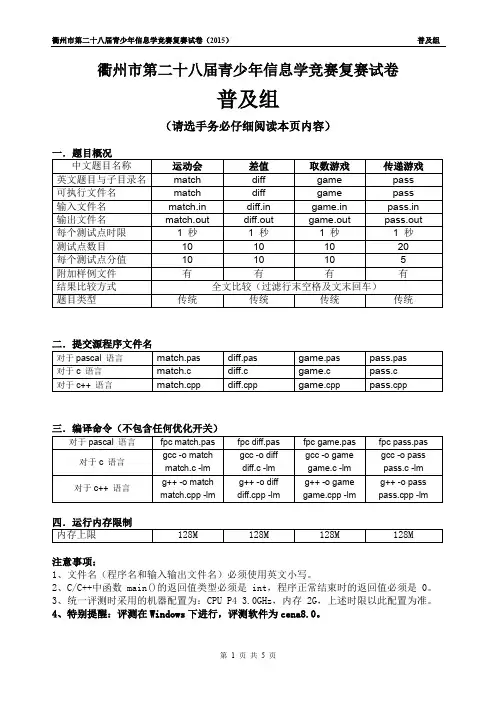
衢州市第二十八届青少年信息学竞赛复赛试卷普及组（请选手务必仔细阅读本页内容）二．提交源程序文件名三．编译命令（不包含任何优化开关）注意事项：1、文件名（程序名和输入输出文件名）必须使用英文小写。
2、C/C++中函数 main()的返回值类型必须是 int，程序正常结束时的返回值必须是 0。
3、统一评测时采用的机器配置为：CPU P4 3.0GHz，内存 2G，上述时限以此配置为准。
4、特别提醒：评测在Windows下进行，评测软件为cena8.0。
运动会(match.pas/c/cpp)【问题描述】梦幻城市每年为全市初中生兴办一次运动会。
为促使各校同学之间的交流，采用特别的分队方式：每一个学校的同学，必须被均匀分散到各队，使得每一队中该校的人数皆相同。
为增加比赛的竞争性，希望分成越多队越好。
你的任务是给定参赛的学校数以及各校的人数，确定最多可以分成的队数。
【输入格式】第一行一个正整数N，代表学校的个数。
接下来N行，每行一个正整数，分别代表这N 个学校的人数。
【输出格式】输出共一行一个正整数，为最多可分成的队数。
【输入样例1】3121620【输出样例1】4【输入样例2】4400200150625【输出样例2】25【数据规模】对于100%的数据：1≤N≤500；每个学校的人数最多为10,000；差值(diff.pas/c/cpp)【问题描述】有一个长度为N 的序列A，现求使其(A1-A2)+(A2-A3)+...+(A N-1-A N)结果最大的一种排列，若有多种排列满足此条件，输出字典序最小的那种。
序列B 的字典序比序列C 小，当且仅当存在i(i<N) 满足B i<C i，且对于每个j(0<j<i)都有B j=C j。
【输入格式】第一行一个整数N，表示序列的长度。
第二行N 个整数表示序列A，第i个整数为A i，每两个整数之间用一个空格隔开。
输出共一行N 个整数，即所求的排列，每两个整数之间用一个空格隔开，行末不要有多余空格。
第二十届全国青少年信息学奥林匹克比赛初赛提升组 C 语言试题一、单项选择题（每题 1.5 分，共 22.5 分）。
1.以下哪个是面向对象的高级语言 ( ).A. 汇编语言B. C++C. FORTRAND. Basic2.1TB 代表的字节数目是 ( ).A.2的 10次方B.2的 20次方C. 2的 30次方D.2的 40 次方3. 二进制数 00100100 和 00010101的和是 ( ).A. 00101000B. 001010100C. 01000101D. 001110014.TCP协议属于哪一层协议 ( ).A. 应用层B. 传输层C. 网络层D. 数据链路层5. 以下几个 32 位 IP 地点中，书写错误的选项是().6.在无向图中，所有定点的度数之和是边数的( )倍 .B.1C.2D.47.对长度位 n 的有序单链表，若检索每个元素的概率相等，则次序检索到表中任一元素的均匀检索长度为 ( ).A. n/2B. (n+1)/2C. (n-1)/2D. n/48.编译器的主要功能是 ( ).A.将一种高级语言翻译成另一种高级语言B.将源程序翻译成指令C.将初级语言翻译成高级语言D.将源程序从头组合9.二进制数 111.101 所对应的十进制数是 ( ).A. 5.625B. 5.5C. 6.125D. 7.62510.如有变量int a, float x, y, 且 a=7, x=2.5, y=4.7, 则表达式x+a%3*(int)(x+y)%2/4 的值大概是().A. 2.500000B. 2.750000C. 3.500000D. 0.00000011. 有以下构造体说明和变量定义，如下图，指针p、q、 r 分别指向一个链表中的三个续结点。
struct node {data next data next data next int data;struct node *next;↑ p↑ q↑ r} *p,*q,*r;现要将 q 和 r 所指结点的先后地点互换，同时要保持链表的连续，以下程序段中错误的选项是().A.q->next = r ->next; p -> next = r; r ->next = q;B.p->next = r; q->next = r->next; r ->next = q;C.q->next = r ->next; r ->next = q; p->next = r;D.r->next = q; q ->next = r ->next; p ->next = r;12.同时查找2n 个数中的最大值和最小值，最少比较次数为( ).A. 3(n-2)/2B. 4n-2C. 3n-2D. 2n-213.设 G 是有 6 个结点的完整图，要获得一颗生成树，需要从G中删去 ()条边 .A.6B.9C.10D.1514.以下时间复杂度不是 O(n2)的排序方法是 ( ).A. 插入排序B. 合并排序C. 冒泡排序D. 选择排序15. 以下程序实现了找第二小元素的算法。
2002年全国青少年信息学〔计算机〕奥林匹克分区联赛复赛提高组试题解题报告题一均分纸牌〔存盘名NOIPG1〕[问题描述]有N堆纸牌，编号分别为1，2，…,N。
每堆上有假设干张，但纸牌总数必为N 的倍数。
可以在任一堆上取假设干张纸牌，然后移动。
移牌规那么为：在编号为1堆上取的纸牌，只能移到编号为2的堆上；在编号为N的堆上取的纸牌，只能移到编号为N-1的堆上；其他堆上取的纸牌，可以移到相邻左边或右边的堆上。
现在要求找出一种移动方法，用最少的移动次数使每堆上纸牌数都一样多。
例如N=4，4堆纸牌数分别为：①9②8③17④6移动3次可达到目的：从③取4张牌放到④〔981310〕->从③取3张牌放到②〔9111010〕->从②取1张牌放到①〔10101010〕。
[输入]：键盘输入文件名。
文件格式：N〔N堆纸牌，1<=N<=100〕A1A2…An〔N堆纸牌，每堆纸牌初始数，l<=Ai<=10000〕[输出]：输出至屏幕。
格式为：所有堆均达到相等时的最少移动次数。
‘[输入输出样例]a.in：498176屏慕显示：3分析：如果你想到把每堆牌的张数减去平均张数，题目就变成移动正数，加到负数中，使大家都变成0，那就意味着成功了一半！拿例题来说，平均张数为10,原张数9，8，17，6，变为-1，-2，7，-4，其中没有为0的数，我们从左边出发：要使第1堆的牌数-1变为0，只须将-1张牌移到它的右边〔第2堆〕-2中；结果是-1变为0，-2变为-3，各堆牌张数变为0，-3，7，-4；同理：要使第2堆变为0，只需将-3移到它的右边〔第3堆〕中去，各堆牌张数变为0，0，4，-4；要使第3堆变为0，只需将第3堆中的4移到它的右边〔第4堆〕中去，结果为0，0，0，0，完成任务。
每移动1次牌，步数加1。
也许你要问，负数张牌怎么移，不违反题意吗？其实从第i堆移动-m张牌到第i+1堆，等价于从第i+1堆移动m张牌到第i堆，步数是一样的。
衢州市第二十七届青少年信息学竞赛复赛试卷
提高组
（请选手务必仔细阅读本页内容）
二．提交源程序文件名
三．编译命令（不包含任何优化开关）
注意事项：
1、文件名（程序名和输入输出文件名）必须使用英文小写。
2、C/C++中函数 main()的返回值类型必须是 int，程序正常结束时的返回值必须是 0。
3、统一评测时采用的机器配置为：CPU P4 3.0GHz，内存 2G，上述时限以此配置为准。
4、特别提醒：评测在Windows下进行，评测软件为cena8.0。
修补管道
(pipe.pas/c/cpp)
【题目描述】
大陆被分成n*m 的格子，两个城市M 和Z 之间的天然气通过管道相连，管道有以下几种形态：
天然气从城市M 运送到城市Z ，管道是双向的，且对于Block +,天然气必须在两个方向都有流动。
如图：
现在有一个格子的管道消失了，你的任务就是找到这个格子以及管道的类型。
【输入格式】
第一行两个数n,m ，中间用一个空格隔开；以下 n 行，每行m 个字符。
'.'表示空格，'|'，'-'，'+'，'1'，'2'，'3'，'4'表示管道的类型。
M 、Z 表示起点和终点。
数据保证只有一个管道口和M 、Z 相邻，这个管道设计中没有废弃管道（也就是说所有管道都必须使用),数据保证答案存在且唯一。
【输出格式】
一行，前两个数表示管道位置，后一个字符表示管道类型。
即（行，列，管道类型），中间用一个空格隔开。
【数据规模】
对于100%的数据：1≤n,m ≤25；
【样例输入1】 3 7 ....... .M-.-Z. .......
【样例输出1】 2 4 -
【样例输入2】 3 5 ..1-M 1-+.. Z.23.
【样例输出2】 2 4 4
跳跃
(jump.pas/c/cpp)
【题目描述】
跳跃是笨笨的天性,当然跳需要消耗能量，每跳1米就会消耗1点能量，如果笨笨有很多能量就能跳很高。
笨笨为了收集能量，来到百亩森林的一个神秘地方。
在这里，笨笨的正上方每100米处就有一个能量球（也就是这些能量球位于海拔100，200，300……米处），每个能量球所能提供的能量是不同的，一共有N个能量球（也就是最后一个能量球在N×100米处）。
笨笨为了想收集能量，想跳着吃完所有的能量球。
笨笨可以自由控制他每次跳的高度，接着他跳起把这个高度以下的能量球都吃了，他便能获得能量球内的能量，接着吃到的能量球消失。
当然笨笨的跳跃技能还不够高，还不会二级跳，所以不能因新吃到的能量而变化此次跳跃的高度，并且每次跳完都会掉下来，回到地面。
问笨笨若要吃完所有的能量球，最多还能保留多少能量。
【输入格式】
输入文件第1行包含两个正整数N，M，表示了能量球的个数和笨笨的初始能量。
第2行包含N个非负整数，从左到右第I个数字依次从下向上描述了位于I×100米位置能量球包含的能量，每2个整数之间用1个空格隔开。
【输出格式】
输出文件仅包括一个非负整数，为笨笨吃完所有能量球后最多保留的能量。
【样例输入】
3 200
200 200 200
【样例输出】
400
【样例说明】
第1次跳100米，得到200能量，消耗100能量，所以落地后拥有300能量。
第2次跳300米，吃到剩下的第2棵能量球，消耗拥有的300能量，得到400能量。
若第1次跳200米，第2次跳300米，最后剩余300能量。
【数据规模】
对于10%的数据：有N≤10；
对于20%的数据：有N≤100；
对于40%的数据：有N≤1,000；
对于70%的数据：有N≤100,000；
对于100%的数据：有N≤2,000,000；
保证对于所有数据，笨笨都能吃到所有的能量球，并且能量球包含的能量之和不超过231-1。
叠箱子
(box.pas/c/cpp)
【题目描述】
笨笨有N 个重量为1的无盖空箱子，每个箱子有长和宽，那么长宽小的箱子就可以放进长宽大的箱子里。
现在笨笨要通过把箱子放进其他箱子中来制造一个最重的箱子，请你告诉笨笨一个箱子最多能有多少重。
假设箱子i 的长为A i ，宽为B i 。
那么箱子i 能放进箱子j 的条件就是A i <A j 而且B i <B j （如果A i <B j
而且B i <A j ，那么箱子j 是不能放进箱子i 的）。
箱子i 、j 不能同时放进箱子k 中；但是如果箱子i 放进箱子j ，箱子j 又放进箱子k 是可以的。
【输入格式】
第一行1个整数N ，表示箱子个数。
之后N 行，每行2个整数A i 、B i ，表示箱子的长宽。
【输出格式】
一个整数，表示最重的箱子的重量。
【数据规模】
对于10%的数据: 1≤N ≤10； 对于40%的数据: 1≤N ≤1,000；
对于100%的数据: 1≤N ≤500,000； 0≤A i ,B i ≤1,000,000；
神奇的项链
(fett.pas/c/cpp)
【题目描述】
笨笨有一条神奇的项链，为什么说它神奇呢？因为它有两个性质：
1. 神奇的项链可以拉成一条线，线上依次是N 个珠子，每个珠子有一个能量值E i ；
2. 除了第一个和最后一个珠子，其他珠子都满足E i =(E i-1+E i+1)/2+D i 。
【样例输入1】 4 9 10 10 9 1 8 0 0
【样例输出1】 3
【样例输入2】 7 1 2 2 4 2 5 3 3 4 5 5 4 6 5
【样例输出2】 4
由于这条项链很长，我们只能知道其两端珠子的能量值。
并且我们知道每个珠子的D i 是多少。
请聪明的你求出这N 个珠子的能量值分别是多少。
【输入格式】
第一行三个整数N 、E 1、E N ，表示珠子个数N ，第一个珠子和第N 个珠子的能量值。
第二行N-2个整数，表示第2个珠子到第N-1个珠子的D i 。
【输出格式】
输出仅一行，N 个整数，表示1到N 个这N 个珠子各自的能量值E i 。
每2个整数之间用1个空格隔开；请放心，数据保证对于任意珠子满足(E i-1+E i+1)Mod 2=0；
【数据规模】
对于40%的数据: 1<N ≤100；
对于70%的数据: 1<N ≤5,000，所有数据（包括计算中的）不超过109； 对于100%的数据: 1<N ≤500,000； |E 1|、|E N |≤1015；|D i |≤104；
Ships
(ships.pas/c/cpp)
【题目描述】
告诉你一个n*n 的正方形。
正方形里只有0和1。
问你由1组成的不同大小的极大4连通块（有公共边）分别有多少。
【输入格式】
第一行一个整数n 表示正方形的大小（左上角为(1,1))。
接下来n 行，每行有一些用','分隔的区间，表示在该行上哪些区间值为1。
以';'结束。
对于每个区间的描述，如果区间的大小为1，那么仅用一个数字表示。
如果区间大小大于1，那么用"st-en"描述。
st 为区间开始的列号。
en 为区间结束的列号。
-为分隔符。
【输出格式】
输出含有若干行。
你应该按照连通块的大小降序输出。
对于每一行，你需要输出两个整数a ，b ，分别表示连通块的大小和这种大小的连通块的个数，a,b 之间用1个空格隔开。
【样例输入2】 10 1 29
0 2 -3 5 1 4 2 -1
【样例输出2】
1 13 25 33 47 51 53 47 37 29
【样例输入1】 4 1 4 0 0
【样例输出1】 1 2 3 4
【样例输入】
12
2-4,7,9;
1,4,11-12;
1,4,10,12;
1,4-8,10-12;
1,8;
1,3-6,8,10-12;
1,3,5-6,8,11;
1,8,10-12;
1-8;
;
2;
2-4,7-10,12;
【样例输出】
29 1
7 3
4 2
1 3
【数据规模】
保证只有不超过1,000个连通块。
保证每个连通块大小不超过1,000；
对于30%的数据：1≤n≤2,000；
对于100%的数据：1≤n≤30,000；。
