数学模型课程设计-中国人口增长预测

中国人口增长猜测模型随着时间的推移，人口数量的变化对于一个国家的进步和社会经济的稳定至关重要。

在中国这样人口浩繁的国家，准确地猜测人口的增长是制定各种政策和规划的基础。

为了更好地满足人民的需求并提供适当的资源，许多探究者和政府部门一直致力于开发和改进中国的人口增长猜测模型。

人口增长猜测是一项复杂的任务，因为涉及到多个变量和互相之间的干系。

为了更好地理解中国人口增长模型，我们将从几个重要的方面入手进行分析。

起首，人口自然增长率是一个重要的参考指标。

自然增长率是指在没有移民和移民的状况下，人口数量因诞生和死亡而增长的程度。

中国的人口自然增长率一直保持在较高水平，这在一定程度上反映了人口结构的变化和诞生率的变化。

通过分析历史数据和趋势，我们可以计算出过去几年甚至几十年的自然增长率，并将其作为人口增长模型的参考指标。

其次，男女比例也是人口增长猜测的重要因素之一。

在过去的几十年里，中国一直面临着男女比例失衡的问题，男性人口相对过多。

这种不平衡的状况在人口增长模型中需要得到充分的思量，因为它直接影响到将来人口的调整和平衡。

除此之外，人口迁移的影响也不行轻忽。

城市化进程加快，许多农村人口涌向城市寻求更好的生活和就业机会。

这种人口迁移对人口增长模型产生了直接的影响，特殊是对城市人口的增长速度和浓度产生了重要的影响。

最后，经济进步也与人口增长密切相关。

经济的快速进步会增进人口的增长，因为更多的人可以获得更好的生活条件和医疗保健。

然而，在人口增长模型中，也需要思量到经济进步对资源分配和环境压力的影响，以确保人口的增长是可持续的。

基于以上几个方面的因素和变量，探究者们提出了许多不同的人口增长猜测模型。

其中一种常用的模型是基于历史数据建立的趋势模型。

通过对历史数据的分析，我们可以发现一些规律和趋势，并将其应用于将来的猜测。

这种猜测方法相对简易，但有时会受到外界因素的干扰。

另一种常用的猜测模型是基于数学和统计分析的模型，如人口增长速度模型和人口结构模型。

数学建模之中国人口增长的预测和人口结构的简析随着社会经济的发展，人口增长一直是一个备受关注的问题。

数学建模是研究人口增长和人口结构的重要方法之一、本文将对中国人口增长的预测和人口结构进行简析，并利用数学建模方法进行预测分析。

首先，中国人口增长的情况是众所周知的。

随着中国的经济快速发展，人民生活水平的提高，医疗水平的提高以及计划生育政策的实施，中国的人口增长率逐渐放缓。

根据国家统计数据，自2024年以来，中国的总人口增长率一直在下降，其中在2024年总人口为14亿人，增长率仅为0.35%。

根据这一趋势，可以推断出未来的人口增长率可能会进一步下降。

在进行人口增长预测时，可以运用数学建模方法中的指数增长模型。

指数增长模型是描述人口增长的一种常用方法，其基本形式为：N(t)=N0*e^(r*t)其中，N(t)表示时间t时刻的人口数量，N0表示初始人口数量，r表示人口增长率，e表示自然对数的底数。

利用指数增长模型可以对未来的人口增长进行预测。

但要注意的是，由于人口增长受到多种因素的影响，例如政策调整、经济发展、文化变迁等，所以对于人口的精确预测是一项复杂而困难的任务。

因此，在进行人口预测时，应结合实际情况，综合考虑人口增长的多个因素。

另外，人口结构是指人口在不同年龄段的分布情况。

人口结构反映了一个地区或国家的经济、社会、教育等方面的发展状况。

中国的人口结构表现为老龄化趋势和少子化现象。

根据国家统计数据，中国的老龄化人口比例逐年提高，同时生育率呈下降趋势。

这种人口结构的变化将对中国的社会、经济等多个方面产生深远的影响。

为了分析人口结构的变化，可以利用数学建模中的人口金字塔。

人口金字塔以年龄为横轴，人口数量为纵轴，通过金字塔的形状和比例来反映人口的结构情况。

通过观察人口金字塔的变化，可以了解人口的年龄分布情况，判断人口的变化趋势，为相关政策和规划提供依据。

总之，中国人口增长的预测和人口结构的分析是一个复杂的问题，数学建模可以提供一种客观、科学的方法来分析这些问题。

中国人口增长预测数学建模引言中国作为世界上人口最多的国家之一，人口增长一直是一个备受关注的问题。

人口数量的增长对于国家的经济、社会、环境等方面都有着重要的影响。

因此，预测中国人口的增长趋势对于未来的发展规划具有重要意义。

本文将介绍一种基于数学建模的方法，用于预测中国人口的增长情况。

方法数据收集为了进行人口增长预测的数学建模，我们需要收集一系列历史人口数据。

这些数据可以从各种统计年鉴、人口普查、政府发布的数据等渠道获取。

通常，我们需要收集的数据包括中国的总人口数量、出生率、死亡率、迁入率和迁出率等。

建立数学模型基于收集到的数据，我们可以建立一个数学模型来描述中国人口的增长情况。

常用的数学模型包括指数增长模型、Logistic增长模型等。

在本文中，我们以Logistic增长模型为例。

Logistic增长模型基于以下假设： 1. 人口增长率与当前人口数量成正比； 2. 当人口数量接近一定的上限时，人口增长率会逐渐减小。

Logistic增长模型的公式可以表示为：dP/dt = r*P*(1-P/K)其中，P表示人口数量，t表示时间，r表示人口增长率，K表示人口的上限。

参数估计为了应用Logistic增长模型进行人口预测，我们需要估计模型中的参数。

参数估计可以通过拟合历史数据来完成。

常用的参数估计方法包括最小二乘法、最大似然估计等。

模型验证一旦完成参数估计，我们可以使用模型预测未来的人口变化情况。

为了验证模型的准确性，我们可以将预测结果与实际观测数据进行比较。

如果预测结果与实际观测数据较为接近，说明模型具有较好的预测能力。

预测未来人口增长利用建立的数学模型和参数估计，我们可以进行未来人口增长的预测。

通过不同的假设和参数值，我们可以探讨不同因素对人口增长的影响。

例如，我们可以考虑不同的出生率和死亡率情况下的人口增长，或者研究不同人口政策下的人口增长趋势。

结论本文介绍了一种基于数学建模的方法，用于预测中国人口的增长情况。

中国人口增长预测本题是一个人口发展预测的问题。

人口发展与一般种群增长一样，是由自然增长率决定的。

然而，人类个体是一种社会的个体，所以人口发展有自己的特点。

想到人口的迁移，性别比例，城镇化等。

同时，人口发展受政策的影响，例如计划生育；也要受到人们意识的影响，像生育意识等。

但是从社会层面上看，生育意识在整个社会上体现为妇女的生育模式，进而可以特别地去考虑。

思考方法：首先，数据的处理。

在经过EXCEL分析和验证后，适当修正题中的个别有误数据后，利用有效数据进行建模求解，在此过程中，我们提取出死亡率、生育率等感念，且把人的一生按年龄分为青年期、衰老期等阶段。

这是求解人口增长模型的必要过程和方法。

其次，模型建立。

和一般的预测模型一样，本模型也是个预测模型，所以考虑到用题目所给的五年的信息，来推测今后几十年的人口的总数和结构情况。

对此，我们选用差分方程模型和数据参数拟合等方法。

同时，将死亡率与出生率分开分别计算和拟合，通过五年的实际数据拟合出相应函数的参数，再利用此函数进行评估和预测。

最后，利用已有信息以及上述所求出的对应函数和方程，对中短期与长期进行估计和预测，进而得出人口结构、人口比例、人口数量等一系列的相关数据。

以下是解答过程：1.数据说明：x：表示最大的年龄；mi=1,2,3,4,5,6 其中1表示市男性，2表示市女性，3表示镇男性，4表示镇女性，5表示乡男性，6表示乡女性；A ：表示婴儿性别比例矩阵；* ：表示点乘；P(x,t)：表示t时刻年龄为x的人口数量；ibir(x,t)：表示t时刻年龄为x的出生率；i)(,i dea x t：表示t时刻年龄为x的死亡率；)(i t k：表示t时刻婴儿的死亡率；tra(x,t)：表示t时刻年龄为x的人口迁出率；i2.假设条件1. 假设国内社会环境稳定，无异常大量死亡或出生情况发生，人口比例，人口总数不会出现突变状况； 2. 假设只存在乡向城镇迁出，不存在其他迁移方式，且不同年龄段迁移率相同； 3. 假设不考虑国家之间的迁入与迁出，把中国内部看为一个封闭的模型； 4. 对于90岁以上的人都按照90岁处理； 5. 假设只存在乡向城镇迁出，不存在其他迁移方式，且不同年龄段迁出率相同，按照0.6%均匀增长。

基于logistic模型对中国未来人口的预测分析随着全球人口的快速增长，人口问题已成为各国政府和学术界关注的焦点。

中国作为世界人口最多的国家之一，其人口增长趋势对全球的影响巨大。

对中国未来人口的预测分析至关重要。

本文将采用logistic模型对中国未来人口的增长趋势进行预测分析，希望可以为未来的人口政策制定提供一定的参考。

一、中国人口的现状中国是世界上人口最多的国家，目前的总人口数量已经超过了13亿。

在过去几十年里，中国经历了人口快速增长的阶段，但随着经济发展和社会进步，人口增长速度逐渐放缓。

根据中国国家统计局的数据，近年来中国人口增长率呈现出逐渐减小的趋势，但总人口数量仍在持续增加。

二、logistic模型的概念logistic模型是一种常用于生物学、经济学和人口学等领域的数学模型，用于描述一个事物的增长曲线。

这种曲线呈现出一种S形状，其特点是在开始的阶段增长较快，在后期逐渐趋于稳定。

这种模型可以用来预测未来的增长趋势，对于人口预测分析具有一定的优势。

为了对中国未来人口的增长趋势进行预测分析，我们可以采用logistic模型来建立一个数学模型。

我们需要收集中国过去几十年的人口数据，包括总人口数量、出生率、死亡率等信息。

然后，我们可以利用这些数据来拟合logistic模型，从而得出一个能够描述中国人口增长趋势的数学公式。

在建立logistic模型的过程中，需要注意的是，我们需要对数据进行适当的处理和修正，避免受到外部因素的干扰。

要考虑到中国的人口政策对人口增长的影响，以及经济发展和社会进步对出生率和死亡率的影响等。

只有在进行了充分的数据分析和处理之后，我们才能够得到一个能够准确反映中国人口增长趋势的logistic模型。

我们可以得知未来中国人口的增长速度将会逐渐减缓。

随着中国人口政策的调整和经济社会的发展，出生率和死亡率都将会受到一定的影响，从而导致人口增长速度的变化。

我们还可以得出中国人口规模的未来预测。

中国人口增长的预测和人口结构的简析摘要本文根据过去数十年的人口数据，通过建立不同的数学模型，对中国人口的增长进行了短期和中长期的预测。

模型一：从中国统计年鉴—2008，查找得到2000-2007年的人口数据，然后用灰色模型进行人口的短期（2008-2017）预测。

这里，我们采用两种算法进行人口总数的预测。

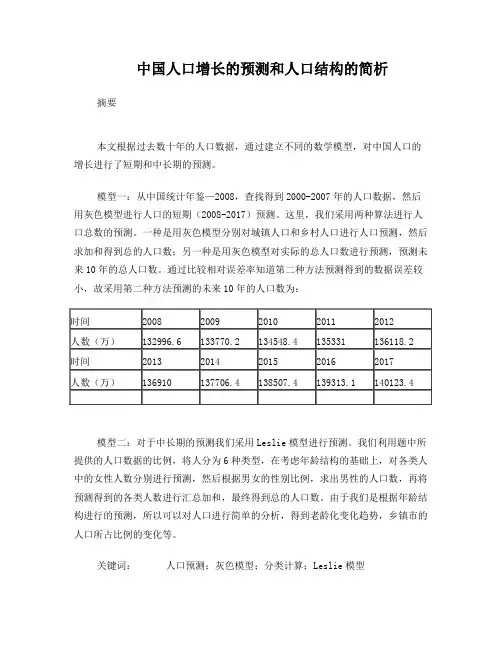
一种是用灰色模型分别对城镇人口和乡村人口进行人口预测，然后求加和得到总的人口数；另一种是用灰色模型对实际的总人口数进行预测，预测未来10年的总人口数。

通过比较相对误差率知道第二种方法预测得到的数据误差较小，故采用第二种方法预测的未来10年的人口数为：模型二：对于中长期的预测我们采用Leslie模型进行预测。

我们利用题中所提供的人口数据的比例，将人分为6种类型，在考虑年龄结构的基础上，对各类人中的女性人数分别进行预测，然后根据男女的性别比例，求出男性的人口数，再将预测得到的各类人数进行汇总加和，最终得到总的人口数。

由于我们是根据年龄结构进行的预测，所以可以对人口进行简单的分析，得到老龄化变化趋势，乡镇市的人口所占比例的变化等。

关键词：人口预测；灰色模型；分类计算；Leslie模型一、模型假设模型一的假设：1、不考虑国际迁移，认为国家内部迁移不改变人口总量；2、不考虑自然灾害、疾病等因素对人口数量的影响；3、文中短期预测到2017年4、大面积自然灾害、疾病的发生以及人们的生育观念等因素会对当年的生育率和人口数量产生影响，认为这些因素在预测误差允许的范围内．模型二的假设：1、每一年龄组的女性在每一个时间段内有相同的生育率和死亡率；2、在预测的时间段内男女的性别比例保持现状不变；3、不考虑人口的迁入和迁出；4、不考虑空间等自然因素的影响，不考虑自然灾害对人口数量的影响。

二、问题分析中国是一个人口大国，随着经济的不断发展，生产力达到较高的水平，现在的问题已不是仅仅满足个人的需要，而是要考虑社会的需要。

中国未富先老，对经济的发展产生很大的影响。

中国人口增长预测模型摘要本文针对我国人口增长中出现的新特点，建立了两个符合实际情况的预测模型，对中国人口增长的中短期和长期趋势做出预测。

模型一：建立时间序列分析法中的ARMA 模型, 对中国人口总数进行预测。

根据处理后的数据的自相关函数和偏相关函数的拖尾性，估计出ARMA 的参数p和q，并对估计的参数进行检验和调节，最终确定参数，建立出ARMA(p ,q)模型。

用此模型预测出2020 年和2030 年的人口分别为138135.3 万人和143352.6 万人。

模型二：建立阻滞增长模型，把出生率和死亡率考虑进去，对人口进行预测，并用Matlab软件编程进行求解。

通过此模型预测出2020年和2030年的人口分别为142108.3万人和146768.4万人，并且人口在2036年左右达到峰值。

模型三：建立人口发展方程，模型一需要的原始数据少，操作简单，适合于中短期预测，但长期预测效果不佳；模型二和模型三综合考虑了各因素，对中短期和长期均有较好的预测效果，但所需数据量大，操作较为复杂。

关键字时间序列模型Eviews 人口发展模型微分方程1.问题重述近年来中国的人口发展出现了一些新的特点，例如，老龄化进程加速、出生人口性别比持续升高，以及乡村人口城镇化等因素，这些都影响着中国人口的增长。

关于中国人口问题已有多方面的研究，并积累了大量数据资料。

试从中国的实际情况和人口增长的上述特点出发，参考相关数据资料，建立中国人口增长的数学模型，并由此对中国人口增长的中短期和长期趋势做出预测；并指出模型中的优点与不足之处。

2.问题的分析一个国家人口的变化和随时间的发展过程，是由很多因素决定的，社会制度、自然环境、生活水平、科学文化水平、战争、自然灾害和移民等等，都能严重地影响社会人口的发展过程。

要预测人口发展的总趋势，首先要预测的是人口总数。

在当代中国社会，环境稳定，如果没有大规模传染病和战争等的影响，每年的死亡率应该相对稳定，出生率也一直在国家政策的控制中，所以人口总数的预测可以看成一个平稳序列的预测，这样我们考虑用时间序列来进行预测。

中国人口增长预测摘要本文从中国人口的实际情况和人口增长的特点出发，根据题目和中国统计年鉴中的相关数据，建立了两个关于中国人口增长的数学模型，并对中国人口做出了分析和预测。

模型一：利用中国统计年鉴中 2000—2005 年人口的数据，运用灰色理论的基本原理建立 GM(1,1) 模型。

该模型利用离散数据列进行生态处理，建立动态的微分方程，对我国近5年、10年、20年的总人口分别进行了预测。

又根据中国人口城乡分布不同且总趋势也不同的特点，把全国人口分为城市人口、城镇人口、乡村人口三部分分别进行灰色预测。

结果表明，该模型较好的反映并预测中国人口短中期和长期的变化情况。

模型二：按人口年龄结构特征，将人口分为幼年（0—14岁）男女、中年（15—49岁）男女、老年（50岁以上）男女。

各年龄段的人口变化是由出生率、死亡率和转化为其他年龄段的转化人数决定的。

根据各年龄段人口数量变化特点，对各年龄段转化人数引入转化因子，改进马尔萨斯模型，附带出生率、死亡率、生育率、出生性别比率等约束条件，建立了新的具有年龄结构的人口增长模型。

结合我国人口的特点，运用已知数据和利用微分方程的数值解，预测出男性和女性幼年、中年、老年的人口数量。

可反映中国不同年龄结构的人口分布情况。

关键词：灰色预测；小误差频率；微分方程组；人口模型；转移因子一．问题重述中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。

因此人口预测的科学性、准确性是至关重要的。

英国人口学家马尔萨斯的人口指数增长模型和荷兰生物学家的Logistic模型都是经典的人口预测模型。

但是，影响中国人口的因素较多，人口结构较复杂，这些模型对人口预测很粗略，甚至是不准确的。

因此，我们要根据我国具体的人口结构现状（如老龄化进程加速）、人口的分布现状（如乡村人口城镇化）、人口比率现状（如出生人口性别比持续升高）等特点，来较准确、较具体地对中国人口进行预测，建立人口增长的数学模型，由此对中国人口中短期和长期增长趋势做出预测。

关键字：人口数平衡点方程模型运动预测曲线稳定增长人口一题目：请在人口增长的简单模型的基础上。

" （1）找到现有的描述人口增长，与控制人口增长的模型；" （2）深入分析现有的数学模型，并通过计算机进行仿真验证；" （3）选择一个你们认为较好的数学模型，并应用该模型对未来20年的某一地区或国家的人口作出有关预测；" （4）就人口增长模型给报刊写一篇文章，对控制人口的策略进行论述。

二摘要：本次建模是依照已知普查数据，利用Logistic模型，对中国人口的增长进行预测。

首先假设人口增长符合Logistic模型，即引入常数，用来表示自然环境条件所能容许的最大人口数。

并假设净增长率为，即净增长率随着人口数N（t）增长而减小，当N(t) 时，净增长率趋于零。

按照这个假设，。

用参数＝3.0,r=0.0386, =1908, =14.5。

画出N=N(t)的图像，作为人口增长模型的一种近似。

做微分方程解的定性分析，求出N=N(t)的驻点和拐点，按照函数作图方法列出定性分析表，作出相轨迹的运动图。

当初始人口<时，方程的解单调递增到地趋向，这意味着如果使用Logistic模型描述人口增长，则人口发展地总趋势是渐增到最大人口数，因此可作为人口的预测值，也称谓平衡点。

用导数做稳定分析，为判断平衡点是否为稳定，可在平面上绘制f(x)的图象，然后像函数绘图那样，用导数进行定性分析，通过图看出人口数N(t)按时间是递增的，当人口数未达到饱和状态的时候，将逐渐地趋向，这意味着是稳定的平衡点。

按该模型，未来人口的数量将随着时间的演化，从初始状态出发达到极限状态，这样就给出了人口的未来预测。

三问题的提出1． Malthus模型英国统计学家Malthus（1766－1834）发现人口增长率是一个常数。

设t时刻人口为N（t），因为人口总数很大，可近似把N（t）当作连续变量处理。

Malthus的假设是：在人口的自然增长过程中，净相对增长率（出生率减去死亡率）是常数，即单位时间内人口的增长量与人口总数成正比。

中国人口增长预测模型中国是全球人口最多的国家之一，人口增长对社会经济发展和资源分配产生重大影响。

因此，准确预测中国的人口增长对于政府决策和社会规划至关重要。

本文将介绍一个基于趋势分析和数学模型的中国人口增长预测模型。

首先，分析历史数据是了解人口增长趋势的关键。

我们可以通过查阅官方统计数据来获得中国过去几十年的人口数量。

这些数据可以反映出不同年代的人口变化情况。

通过对这些数据进行趋势分析，我们可以更好地了解人口增长的规律。

其次，我们可以使用数学模型来预测未来的人口增长。

常用的人口增长模型包括线性增长模型、指数增长模型和Logistic增长模型。

线性增长模型假设人口每年以相同的速度增长，而指数增长模型则假设人口增长的速度与当前的人口数量成正比。

Logistic增长模型则考虑到了环境容量的限制，即人口增长速度会随着人口密度的增大而减缓。

在选择模型时，我们需要考虑人口增长的影响因素。

例如，出生率、死亡率和迁徙率等因素都会对人口增长产生影响。

因此，在构建预测模型时，我们需要综合考虑这些因素，并基于历史数据进行参数估计。

在模型构建完成后，我们可以利用计算机软件进行模拟和预测。

这些软件可以根据历史数据和模型参数，预测未来的人口数量和变化趋势。

通过不断调整模型参数，我们可以提高预测准确度，从而使我们的预测结果更具有可信度。

然而，人口增长预测也存在一定的不确定性。

例如，社会政策的改变、科技进步和自然灾害等都可能对人口增长产生重大影响。

因此，我们在使用预测模型时应该意识到这些不确定性，并将其考虑在内。

此外，随着社会的发展和科技的进步，我们可以探索更加精细化的人口增长预测模型。

例如，可以考虑区域差异和人口组成的变化，利用更多的经济、社会和环境因素来对人口增长进行建模。

这样的模型可以更好地适应中国复杂多变的人口情况。

综上所述，中国人口增长预测模型是一种重要工具，可以帮助我们了解和预测中国人口的发展趋势。

通过分析历史数据、构建数学模型并利用计算机软件进行模拟和预测，我们可以提高预测的准确性，并为政府决策和社会规划提供有力的支持。

中国人口增长预测数学建模引言中国作为世界人口最多的国家之一，人口增长一直是一个备受关注的话题。

为了能够合理规划和管理资源，预测中国人口的增长趋势对决策者来说至关重要。

本文将运用数学建模的方法，通过分析历史数据，来预测中国人口的增长。

数据收集与处理为了进行人口增长预测，首先需要收集和处理相关的数据。

我们可以通过查阅统计年鉴、人口普查数据等公开的数据来获取所需信息。

然后，需要对数据进行清洗和整理，以便进行后续的分析和建模工作。

人口增长模型选择人口增长涉及到多个因素的复杂影响，如出生率、死亡率、迁移率等。

为了能够对中国人口的增长进行模型化，我们需要选择适合的数学模型。

常用的人口增长模型有Malthusian模型、Logistic模型等。

在选择模型时，需要考虑模型的适用性和可解释性。

Malthusian模型Malthusian模型是由英国经济学家Malthus提出的，他认为人口增长是按指数规律进行的。

该模型是基于以下假设：1.出生率和死亡率是恒定的；2.人口的增长率与人口规模成正比。

Malthusian模型的数学表达式为：$$ \\frac{{dP}}{{dt}} = rP $$其中，P为人口规模，P为时间，P为每个个体的平均增长率。

根据该模型，人口规模以指数形式增长。

Logistic模型Logistic模型是在Malthusian模型的基础上发展起来的，它考虑到了环境资源的有限性对人口增长的限制。

Logistic模型的数学表达式为：$$ \\frac{{dP}}{{dt}} = rP(1 - \\frac{{P}}{{K}}) $$其中，P为人口规模，P为时间，P为每个个体的平均增长率，P为环境资源的极限容量。

该模型认为人口规模在达到环境资源的极限容量时，增长率将逐渐减小。

变量的估计和参数的拟合在建立模型之后，需要对模型进行参数估计和拟合。

可以利用历史数据来对模型中的参数进行估计，并通过优化算法来拟合模型与实际数据的拟合度。

中国人口增长的预测和人口的结构分析摘要本文是在已知国家政策和人口数据的前提下对未来人口的发展进行预测和评估，选择了两种模型分别对人口发展的短期和长期进行预测。

模型一中我们在人口阻滞增长模型logistic模型的基础上进行改进，弥补了logistic原始模型仅仅能表示环境对人口发展趋势影响的缺陷，加入了社会因素的影响作为改进，保证了logistic改进模型的有效性和短期预测的正确性。

多次运用拟合的方法（非线性单元拟合，线性多元拟合）对数据进行整合，得到的改进模型对短期预测具有极高的准确性，证明了我们的修正方式与模型改进具有一定的正确性。

模型二中我们分别考虑了城、乡、镇人口的发展情况，利用不同年龄段存活率和死亡率的不同，采用迭代的方式也就是Leslie矩阵的方式对人口发展进行预测，迭代的方式不同于拟合，具有逐步递进的准确性，在参数正确的前提下，能够保证每一年得到的人口都有正确性，同时我们分男女两方面来考虑模型，不仅仅用静态的男女比例来估算人口总数，具有更高的准确性。

然而Leslie模型涉及的参数较多，如果采用动态模型的方式，计算量过大，我们首先用均值的方式对模型进行简化，同样得到迭代矩阵后的人口数值，发展趋势与预测相同，能够很好的预测中国人口的长期发展，同时，由于Leslie矩阵涉及多个参数，所以我们用最终的结果来表征老龄化程度，城乡比，抚养比等多个评价社会发展的参数，得到了较好的估计值，使模型在估算人口的基础上得到了推广和应用。

通过logistic改进模型和Leslie模型我们分别对中国人口发展进行短期和中长期预测，均能得到很好的效果，说明了我们的模型在适用范围内的准确性和实用性。

关键词：人口发展预测；logistic模型改进；参数拟合；Leslie迭代模型；一、问题重述中国是世界上人口最多的发展中国家, 人口问题始终是制约我国发展的关键因素之一，人口众多、资源相对不足、环境承载能力较弱是中国现阶段的基本国情,短时间内难以改变。

中国人口增长预测模型摘 要人口问题是当今世界上最令人关注的问题之一。

本文针对中国现阶段的国情及人口调查数据建立了四个模型，分别对中国短中期和长期的人口增长进行了预测和分析。

首先，我们假设每年的人口增长率不变，为一常数k 。

根据统计所得的1994～2005年的人口数据，我们建立了模型I (指数增长模型)，对2006～2010年的全国总人口进行了预测(见表2)，并求出了误差率%04758.1＝λ，对模型做了检验。

()()()⎪⎩⎪⎨⎧≤≤=>=10000t t t P t P k kP dt dP(I ) 由于模型I 预测误差率太大，于是建立了模型II (灰色预测模型)对短期人口增长进行预测(见表3)，并计算出平均误差率%01204.0=λ，预测效果很好。

()()()()()()()()()[]at a e a u P e t P t P t P---=-+=+/1111ˆ0110 (II ) 为了对中国人口增长进行长期预测，我们改进了模型I ，即取消了人口增长率固定不变的假设，改设增长率()P k 是人口P 的线性函数，建立了模型I I I (阻滞增长模型)，计算得出误差率%13.0＝λ。

利用该模型对2006～2120年的中国人口进行了预测(见表4)，发现115年(2120年)之后中国人口趋近最大值亿344.15。

()()()⎪⎩⎪⎨⎧≤≤=>⎪⎪⎭⎫⎝⎛-=10000001t t t P t P k P P P k dt dP m (I I I ) 以上三个模型都只考虑了人口总数和总的增长率，不涉及年龄结构及性别比例。

在人口预测中人口年龄结构也是十分重要的，因为不同年龄人的生育率和死亡率有很大的差别，即使两个国家或地区目前人口总数一样，如果它们年龄结构状况不同，则两者的发展将大不一样。

为了更准确地预测人口增长情况，我们考虑了年龄性别等因素，建立了模型V I 。

()()()()()()⎪⎩⎪⎨⎧-+=-+=-+=+---t U t F P P t U t F P P t U t F P P P P P P t t t t t t t t t t 333,13222,12111,11321＋＝ (V I ) 其中t P 为第t 年全国总人口，1t P 、2t P 、3t P 分别为第t 年城市、镇、乡的总人口；()t F 1，()t F 2，()t F 3分别为第t 年城市、镇、乡的新生人口总数；()t U 1，()t U 2，()t U 3分别为第t 年城市、镇、乡的死亡人口总数。

中国人口增长预测数学模型
中国人口增长可以用人口增长率来描述。

人口增长率是指一个国家的出生率、死亡率和移民率产生的净人口变化的比率。

一般来说，一个国家的人口增长率越高，其人口增长速度越快，反之亦然。

由于中国的出生率和死亡率一直在变化，因此需要建立一个数学模型来预测中国的人口增长。

常见的模型有以下几种：
1. 指数模型
指数模型假设人口增长率是一个恒定值，因此未来的人口数量可以通过不断累乘现有人口数量和人口增长率来预测。

这种模型适用于人口增长迅速的情况，但并不适用于中国的情况，因为中国的人口增长率不是恒定的。

2. Logistic 模型
Logistic 模型假设人口增长率随着人口数量的变化而变化，即当人口数量增加到某一点时，人口增长率会逐渐降低。

这种模型适用于人口数量增长迅速的情况，适用于中国的情况。

3. 随机游走模型
随机游走模型假设人口增长率是一个随机变量，可以根据历史发展趋势来预测未来的变化。

这种模型适用于人口数量变化不规律的情况，但对于中国这样的大国而言，其复杂性较高，难以建立准确的模型。

总之，预测中国的人口增长需要考虑许多因素，例如出生率、死亡率、移民率等等，而且这些因素也会受到其它因素的干扰，例如经济、社会政治等因素。

因此，建立准确的模型需要大量的数据和正确的假设。

中国人口增长预测模型一、问题分析中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。

建立中国人口预测模型具有重要意义，预测未来人口发展状况的主要有三个依据：第一,根据现有人口的数量、性别、年龄构成、出生率、死亡率、迁移率等预测未来人口数量的变动；第二，根据过去某一时期内人口增长的速度或绝对数，预测未来人口发展状况；第三，根据影响人口总数变动的因素进行人口预测，下面从这三个依据出发建立中国人口增长模型。

二、模型假设人口数量和结构变化的因素不外乎出生、死亡和迁移，由于我们预测的是全国的人口，国际的迁入迁出对全国人口的影响不大，所以我们的模型只考虑了自然的出生和死亡，对迁入及迁出因素忽略不计。

三、模型的建立模型（一）修正指数模型与阻滞增长模型1、修正指数模型修正指数曲线的人口趋势模型，依据历年人口记录数据来预测未来人口发展状况，修正指数曲线是一种具有增长极限的曲线，该模型的形式为：y（t）= K + ta b式中：K, a , b 均为待估参数，由表达式可见,当时间很大时, K 为增长上限或下限。

修正指数曲线模型的特点是一阶差分的环比为一个常数，根据这一特点，当某一时间序列的一阶差分的环比近似为一常数时，可以用该模型来进行预测。

至于模型中参数估计的问题,可以分为两种情况讨论：第一种情况：根据经验，当增长上限K已知时，可以先将模型线性化，再用最小二乘法来估计其余两个未知参数a 和b。

对于模型：y（t）= K +ta b( K > 0，a < 0，0 <b < 1)进行变换，并取对数可以将模型变为ln( K – y（t）)= ln( - a) + tlnb令Y= ln( K – y（t）)， A = ln( - a)， B = lnb，则原模型转换为直线模型：Y= A + tB，再代回求解得：a = - A e，b = B e第二种情况：当K，a，b 均未知时，模型无法线性化，因此不能用最小二乘估计参数，但此时可以用三和法或是三点法估计参数。

如何预测中国人口增长——胡海滔、纪从威、张新干一．问题的提出中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。

根据已有数据，运用数学建模的方法，对中国人口做出分析和预测是一个重要问题。

根据中国1982~1998年的人口统计数据，取1982年为起始（t=0），1982年的人口101654万人，人口自然增长率为14%，以36亿作为我国人口的容纳量，试建立一个较好的人口数学模型并给出相应的算法和程序，并与实际人口进行比较。

二．模型假设(1)x(t)表示t时刻我国人口总数，我们将x(t)看成t的连续函数；(2)对一个国家而言，迁入和迁出人数相对很少，故略去迁移对人口变化的影响，即人口数量变化仅与出生率和死亡率有关；(3)每一社会成员的死亡与生育水平相同，即人口死亡率与出生率之差与人口总数成正比。

三．符号说明t:统计总人口数量的时间；()t x：t时间的总人口数；X：初始时候的总人口数，即1982年的总人口数；r：人口自然增长率；x：自然资源和环境条件所能容纳的最大人口数量。

m四．模型建立模型：指数增长模型（马尔萨斯模型）1.模型建立：记t 时刻的人口为()t x ,当考察一个国家的人口时，()t x 为一个很大的整数。

利用微积分这一数学工具，将()t x 视为连续、可微函数。

记初始时刻（t=0）的人口为0X 。

假设人口增长率为常数r ，即单位时间内()t x 的增量等于r 乘以()t x .考虑到t 到t t ∆+时间内人口的增量，显然有：t t rx t x t t x ∆=-∆+)()()( （1）令0→t ，得到()t x 满足微分方程rx dtdx= ， 0)0(x x = 于是X （t ）满足微分方程：⎪⎩⎪⎨⎧==0)0()()(X x t rx dtt dx （2） 2.模型求解：解得微分方程（2）得：X （t ）=0X )(0t t r e - （3）表明：∞→t 时，)0(>∞→r x t1982年人口自然增长率r 为14‰，1016540=X为了能对比Malthus 模型计算的长期值和实际值，取1982~2005年数据：根据Malthus模型，用Matlab计算1982~2005各年的人口总数，程序：t=[1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005]; t0=1982;x=10.1654*exp(0.014*(t-t0));xformat short计算结果：x =Columns 1 through 1410.1654 10.3087 10.4541 10.6014 10.750910.9025 11.0562 11.2121 11.3701 11.5304 11.693011.8578 12.0250 12.1946Columns 15 through 2412.3665 12.5408 12.7176 12.8969 13.078813.2632 13.4501 13.6398 13.8321 14.0271用Matlab软件将计算值与实际人口总数进行对比：程序：t=[1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998];x=[101654 103008 104357 105851 107507 109300 111026 112704 114333 115823 117171 115817 119850 121121 122389 123626 124810];plot(t,x);hold ony=[101654 103087 104541 106014 107509 109025 110562 112121 113701 115304 116930 118578 120250 121946 123665 125408 125408];plot(t,y,'r*');legend('实际值','预测值');hold offxlabel('年份');ylabel('总人口数');title('模型计算值与实际值对比');grid;19801985199019952000200511.051.11.151.21.251.31.351.41.455年份总人口数模型计算值与实际值对比3.结果分析从1982年起在较短的一段时间内（1982~1995）用Malthus 模型计算的值与实际人口总数很接近，相对误差均在1%以下。

中国人口增长预测摘要: 中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。

根据已有数据，运用数学建模的方法，对中国人口做出分析和预测是一个重要问题。

对此，我们建立了短期与长期两种预测人口增长的模型，并对附录中城镇乡的人口演变趋势做拟合与分析。

本文的建模过程选用了1996年到2005年的人口数据。

短期人口预测用曲线的直接拟合，分析出人口的增长趋势。

人口的出生率与死亡率均符合指数函数bt=+，利y ae c用logistic模型求出人口最大上限x，据此拟合人口增长的指数函数x（t），预测m2006-2011年的人口数量。

长期预测中，建立灰色动态模型GM（1,1）预测中国人口长期增长趋势。

在解系数的过程中运用了最小二乘法，得出预测人口数据的方程)0(ˆx，并预测2011年到2015年的人口数量。

在对中国总人口进行短期和中长期的总体预测后，我们从附件中提取出城、镇、乡三地人口、男女出生性别比、老龄人口比率等相关数据，对中国未来城、镇、乡三地人口比例、男女出生性别比、妇女生育率、老龄人口比率等影响人口发展的主要因素做趋势预测，从而达到了对中国人口全方位的预测。

关键词: 曲线拟合、灰色动态模型、最小二乘法、自然增长率一、问题的重述中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。

根据已有数据，运用数学建模的方法，对中国人口做出分析和预测是一个重要问题。

近年来中国的人口发展出现了一些新的特点，例如，老龄化进程加速、出生人口性别比持续升高，以及乡村人口城镇化等因素，这些都影响着中国人口的增长。

2007年初发布的《国家人口发展战略研究报告》还做出了进一步的分析。

关于中国人口问题已有多方面的研究，并积累了大量数据资料。

附录2就是从《中国人口统计年鉴》上收集到的部分数据。

试从中国的实际情况和人口增长的上述特点出发，建立中国人口增长的数学模型，并由此对中国人口增长的中短期和长期趋势做出预测。

二、符号说明nianfen 年份chusheng 出生率bata0 估计的参数值nlinfit 非线性拟合函数1y出生率函数2y死亡率函数mx人口上限t 时间x（t）人口增长函数X(0)中国各年人口总数X(1) X(0)的一次累加序列Z(1) X(1)的紧邻均值生成数列-a 发展系数b 灰色作用量)0(ˆx人口预测值c 均方差k∆相对误差三、模型的假设1.假设人口迁入迁出对问题产生的影响可以忽略；2.忽略社会环境、自然、经济、文化水平的对人口的影响；3.长期预测中，不考虑出生率、死亡率等因素的影响。

资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载数学建模中国人口增长预测地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容2013高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》（以下简称为“竞赛章程和参赛规则”，可从全国大学生数学建模竞赛网站下载）。

我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛章程和参赛规则的，如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛章程和参赛规则，以保证竞赛的公正、公平性。

如有违反竞赛章程和参赛规则的行为，我们将受到严肃处理。

我们授权全国大学生数学建模竞赛组委会，可将我们的论文以任何形式进行公开展示（包括进行网上公示，在书籍、期刊和其他媒体进行正式或非正式发表等）。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）： A我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：参赛队员 (打印并签名) ：1.2.3.指导教师或指导教师组负责人 (打印并签名)：日期：年月赛区评阅编号（由赛区组委会评阅前进行编号）：2013高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：赛区评阅记录（可供赛区评阅时使用）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：摘要本文主要内容是结合中国近几年的人口实际情况，我们从拟合和递推两种方向考虑建立了两个模型，对中国未来人口的变化趋势做出了预测。