理论力学动力学测试

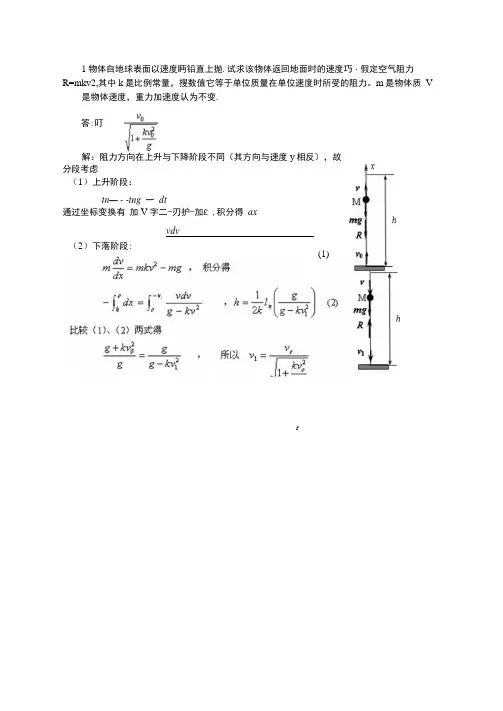
1物体自地球表面以速度眄铅直上抛.试求该物体返回地面时的速度巧・假定空气阻力R=mkv2,其中k是比例常量，搜数值它等于单位质量在单位速度时所受的阻力。

m是物体质V 是物体速度，重力加速度认为不变.答:叮解：阻力方向在上升与下降阶段不同（其方向与速度y相反），故分段考虑（1）上升阶段：tn— - -tng一dt通过坐标变换有加V字二-刃护-加£ ,积分得axvdv（2）下落阶段:(1)g2.静止中心0以引力F=k2mr吸弓I质量是m的质点M,其中k是比例常量，r=OM是点M的矢径.运动开始时OMo=b,初速度时呵并与阪成夹角求质点M的运动方程。

x = b cos 处 + —cosasin ktky = —sinasin^k解：取坐标如图，质点M在任意位貳将fna = F 沿x、y轴投彫，得mx = 一F cos<p= -k2fnrcos （p= -Qmxfny = 一Fsin cp= -k2fnr sin (p= -k^my艮卩x+k2x = 0 , y+^2y = 0徽分方程得通解为：x = s coskt+c2 sin kt求导得x = -kc x sin kt + kc2 coskt , y = -kc3 sin kt + kc^ cos kt (2)已知初始条件f=0 z 妒b z /o=0，x0 = v0 sin a ,代入方程（1），（2）得点M的运动方程为v =—cosax = 2?cos Ar/ +—kcos ar sin kt -I sin asin kt y =c3 cos kt + c^ sin kt (1)九=v0 sin a3单摆M 的悬线长/,摆重G 支点B 具有水平向左的均加速度a.如将摆在&=0处静止 释啟，试确定悬线的张力T （表示成&的函数）.解：质点的相对徴分方程为 ma r = mg+f +©投影到法线方向由式(2)得T = Gsin3 + —acos0 + — v 2g 0T = G 3 sin + 3 — cos — 2 —\ g S )答・ T - G(3sin3-cos^- 2-) g g投影到切线方向= T-Gsin^-0e cosB g !(2)由式（1）得 妙=gcos^-usin 0分离变量并积分|*V Xiv = \ f geos^10- [ asm Odd v 2 = 2"gsin &+ocos&-a 1(3)将式（3）代入上式代入式（2）得dt dt积分得4.水平面内弯成任意形状的细管以匀角速度G 绕点0转动.光滑小球M 在管內可自由 运动.设初瞬时小球在吆处，OMo=©相对初速^v o =0,求小球相对速度大小冬与极径r的关系。

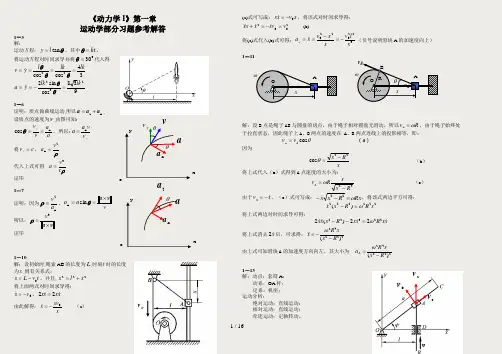
《动力学I 》第一章 运动学部分习题参考解答1－3 解：运动方程：θtan l y =，其中kt =θ。

将运动方程对时间求导并将030=θ代入得34cos cos 22lklk l yv ====θθθ938cos sin 2232lk lk y a =-==θθ1－6证明：质点做曲线运动,所以n t a a a +=, 设质点的速度为v ,由图可知:a a v v yn cos ==θ，所以: yv va a n =将c v y =，ρ2n v a =代入上式可得 ρc v a 3=证毕 1－7证明：因为n2a v =ρ，v a a v a ⨯==θsin n所以：va ⨯=3vρ证毕1－10解：设初始时,绳索AB 的长度为L ,时刻t 时的长度 为s ,则有关系式：t v L s 0-=，并且 222x l s +=将上面两式对时间求导得： 0v s-= ，x x s s 22= 由此解得：xsv x-= （a ） (a)式可写成：s v xx 0-= ，将该式对时间求导得： 2002v v s x x x =-=+ (b)将(a)式代入(b)式可得：3220220xlv x x v x a x -=-==（负号说明滑块A 的加速度向上）1－11解：设B 点是绳子AB 与圆盘的切点，由于绳子相对圆盘无滑动，所以R v B ω=，由于绳子始终处于拉直状态，因此绳子上A 、B 两点的速度在 A 、B 两点连线上的投影相等，即： θcos A B v v = （a ） 因为xR x 22cos -=θ （b ） 将上式代入（a ）式得到A 点速度的大小为： 22Rx x Rv A -=ω （c ）由于xv A -=，（c ）式可写成：Rx R x x ω=--22 ，将该式两边平方可得： 222222)(x R R x xω=- 将上式两边对时间求导可得：x x R x x R x xx 2232222)(2ω=-- 将上式消去x2后，可求得：22242)(R x xR x --=ω由上式可知滑块A 的加速度方向向左，其大小为 22242)(R x xR a A -=ω1－13解：动点：套筒A ；动系：OA 杆； 定系：机座； 运动分析：绝对运动：直线运动； 相对运动：直线运动； 牵连运动：定轴转动。

理论力学试题及答案一、选择题（每题2分，共20分）1. 牛顿第一定律描述的是：A. 物体在受力时的运动状态B. 物体在不受力时的运动状态C. 物体在受力时的加速度D. 物体在受力时的位移答案：B2. 根据牛顿第二定律，物体的加速度与作用力和物体质量的关系是：A. 加速度与作用力成正比，与质量成反比B. 加速度与作用力成反比，与质量成正比C. 加速度与作用力成正比，与质量成正比D. 加速度与作用力成反比，与质量成反比答案：A3. 以下哪个不是刚体的运动特性？A. 刚体的质心保持静止或匀速直线运动B. 刚体的各部分相对位置不变C. 刚体的各部分速度相同D. 刚体的各部分加速度相同答案：C4. 角动量守恒定律适用于：A. 只有重力作用的系统B. 只有内力作用的系统C. 外力矩为零的系统D. 外力为零的系统答案：C5. 以下哪个是能量守恒定律的表述？A. 一个封闭系统的总动能是恒定的B. 一个封闭系统的总势能是恒定的C. 一个封闭系统的总能量是恒定的D. 一个封闭系统的总动量是恒定的答案：C二、简答题（每题10分，共20分）6. 简述牛顿第三定律的内容及其在实际中的应用。

答案：牛顿第三定律，又称作用与反作用定律，表述为：对于两个相互作用的物体，它们之间的作用力和反作用力总是大小相等、方向相反。

在实际应用中，例如在推门时，门对人的作用力和人对门的作用力大小相等，方向相反。

7. 描述什么是简谐振动，并给出一个生活中的例子。

答案：简谐振动是一种周期性振动，其回复力与位移成正比，且总是指向平衡位置。

生活中的例子包括弹簧振子，当弹簧被拉伸或压缩后释放，它会在原始平衡位置附近做周期性的往复运动。

三、计算题（每题15分，共30分）8. 一个质量为m的物体，从静止开始，沿着一个斜面下滑，斜面的倾角为θ。

如果斜面的摩擦系数为μ，求物体下滑的加速度。

答案：首先，物体受到重力mg的作用，分解为沿斜面方向的分力mg sinθ和垂直斜面方向的分力mg cosθ。

《理论力学》习题三答案一、单项选择题（本大题共30小题，每小题2分，共60分）1. 求解质点动力学问题时，质点的初始条件是用来（ C ）。

A 、分析力的变化规律； B 、建立质点运动微分方程； C 、确定积分常数； D 、分离积分变量。

2. 在图1所示圆锥摆中，球M 的质量为m ，绳长l ，若α角保持不变，则小球的法向加速度为（ C ）。

A 、αsin g ；B 、αcos g ；C 、αtan g ；D 、αtan gc 。

3. 已知某点的运动方程为2bt a S +=（S 以米计,t 以秒计，a 、b 为常数），则点的轨迹为（ C ）。

A 、是直线；B 、是曲线；C 、不能确定；D 、抛物线。

4. 如图2所示距地面H 的质点M ，具有水平初速度0v，则该质点落地时的水平距离l 与（ B ）成正比。

A 、H ； B、H ； C 、2H ；D 、3H 。

5. 一质量为m 的小球和地面碰撞，开始瞬时的速度为1v ，碰撞结束瞬时的速度为2v（如图3），若v v v ==21，则碰撞前后质点动量的变化值为（ A ）。

A 、mv ；B 、mv 2 ；C 、mv 3；D 、 0。

6. 一动点作平面曲线运动，若其速率不变，则其速度矢量与加速度矢量（ B ）。

A 、平行； B 、垂直； C 、夹角随时间变化； D 、不能确定。

7. 三棱柱重P ，放在光滑的水平面上，重Q 的匀质圆柱体静止释放后沿斜面作纯滚动，则系统在运动过程中（ A ）。

A 、沿水平方向动量守恒，机械能守恒；B 、动量守恒，机械能守恒；C 、沿水平方向动量守恒，机械能不守恒；D 、均不守恒。

图1图2图38. 动点M 沿其轨迹运动时，下列几种情况中，正确的应该是（ A ）。

A 、若始终有a v⊥，则必有v 的大小等于常量； B 、若始终有a v ⊥，则点M 必作匀速圆周运动；C 、若某瞬时有v ∥a，则点M 的轨迹必为直线；D 、若某瞬时有a 的大小为零，且点M 作曲线运动，则此时速度必等于零。

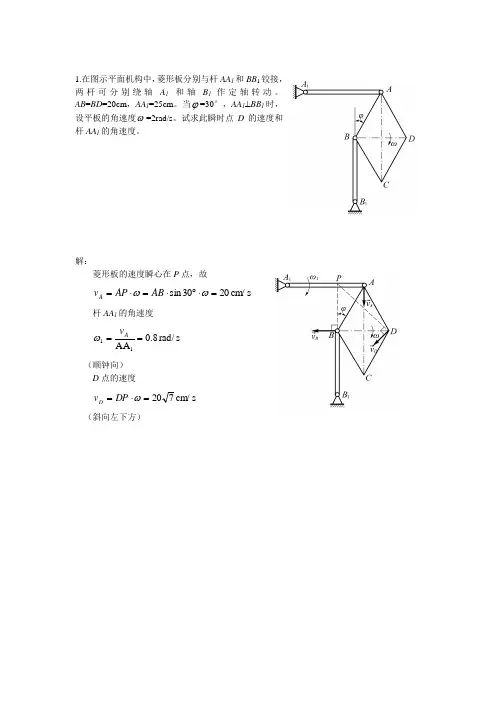
1.在图示平面机构中，菱形板分别与杆AA 1和BB 1铰接，两杆可分别绕轴A 1 和轴B 1作定轴转动。

AB =BD =20cm ，AA 1=25cm 。

当ϕ=30°，AA 1⊥BB 1时，设平板的角速度ω=2rad/s 。

试求此瞬时点D 的速度和杆AA 1的角速度。

解：菱形板的速度瞬心在P 点，故s cm /2030sin =⋅︒⋅=⋅=ωωAB AP v A杆AA 1的角速度 s rad/8.0AA 11==Av ω（顺钟向）D 点的速度s cm/720=⋅=ωDP v D（斜向左下方）2.等腰三角形平板ABC 的腰长AB =BC ＝5 cm ，AC =6 cm ，端点A 和端点B 分别在水平面上和斜面上运动。

斜面与铅垂线之间的夹角ϕ＝⎪⎭⎫ ⎝⎛43arctan 。

在图示位置时，AC 边铅垂，平板的角速度ω＝4 rad/s ，角加速度α＝5 rad/s 2。

试求该瞬时A ，B 和C 三点的加速度的大小。

解：平板取A 为基点 t n BA BA A B a a a a +==式中2n ωAB a BA =，αAB a BA =tBC ： ()()ϕθϕθϕ---+=cos sin cos 0t n BA BA A a a a故 2cm /s 1.2=A ay ： ϕϕϕcos sin cos t n BA BA B a a a --=-故 2cm/s 85=B a取A 为基点 t n CA CA A C a a a a ++=式中 2n ωAC a CA =，αAC a CA =tx ：2t cm/s 9.27=+-=CA A C a a a xy ： 2n cm/s 96-=-=CA C a a y 2cm/s 100=C a3.在图示平面机构中，已知：杆OA 以匀角速度0ω绕定轴O 转动，OA =AC =r ，O 1B =2r ， β=30°。

在图示位置时，OA ，CB 水平，O 1B ，AC 铅垂。

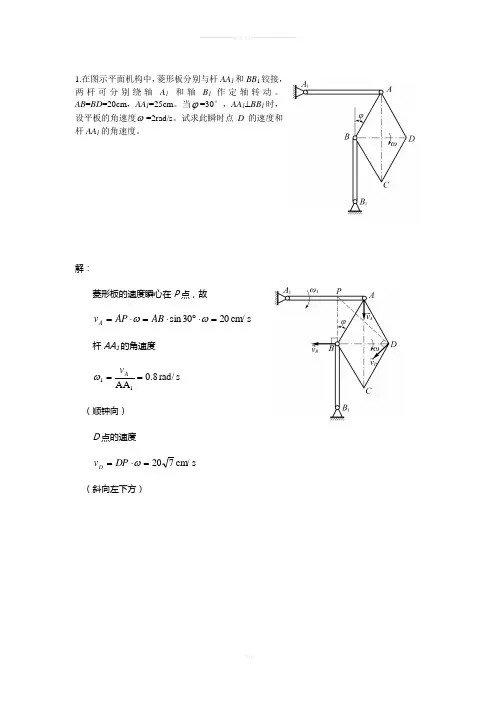
1.在图示平面机构中，菱形板分别与杆AA 1和BB 1铰接，两杆可分别绕轴A 1 和轴B 1作定轴转动。

AB =BD =20cm ，AA 1=25cm 。

当ϕ=30°，AA 1⊥BB 1时，设平板的角速度ω=2rad/s 。

试求此瞬时点D 的速度和杆AA 1的角速度。

解： 菱形板的速度瞬心在P 点，故s cm /2030sin =⋅︒⋅=⋅=ωωAB AP v A杆AA 1的角速度s rad/8.0AA 11==Av ω（顺钟向）D 点的速度s cm/720=⋅=ωDP v D（斜向左下方）2.等腰三角形平板ABC 的腰长AB =BC ＝5 cm ，AC =6 cm ，端点A 和端点B 分别在水平面上和斜面上运动。

斜面与铅垂线之间的夹角＝⎪⎭⎫ ⎝⎛43arctan 。

在图示位置时，AC 边铅垂，平板的角速度＝4 rad/s ，角加速度＝5 rad/s 2。

试求该瞬时A ，B 和C 三点的加速度的大小。

解：平板取A 为基点t n BA BA A B a a a a +==式中2n ωAB a BA =，αAB a BA =tBC ：()()ϕθϕθϕ---+=cos sin cos 0tn BA BA A a a a故 2cm /s 1.2=A ay ： ϕϕϕcos sin cos tn BA BAB a a a --=- 故 2cm/s 85=B a取A 为基点 tn CA CA A C a a a a++=式中2n ωAC a CA =，αAC a CA =tx ：2tcm/s 9.27=+-=CA A C a a a xy ： 2ncm/s 96-=-=CA C a a y2cm/s 100=C a3.在图示平面机构中，已知：杆OA 以匀角速度0ω绕定轴O 转动，OA =AC =r ，O 1B =2r ，=30°。

在图示位置时，OA ，CB 水平，O 1B ，AC 铅垂。

《理论⼒学》模拟试卷《理论⼒学》模拟试卷（⼀）⼀、判断题1、⽤⼒的平⾏四边形法则，将⼀已知⼒分解为F1和F2两个分⼒，要得到唯⼀解答，必须具备：已知F1和F2两⼒的⼤⼩；或已知F1和F2两⼒的⽅向；或已知F1或F2中任⼀个⼒的⼤⼩和⽅向。

()2、某⼒在⼀轴上的投影与该⼒沿该坐标轴的分⼒其⼤⼩相等，故投影就是分⼒。

( )3、图⽰结构在计算过程中，根据⼒线可传性原理，将⼒P由A点传⾄B点，其作⽤效果不变。

()4、作⽤在任何物体上的两个⼒，只要⼤⼩相等，⽅向相反，作⽤线相同，就⼀定平衡。

( )⼆、选择题1、图⽰四个⼒四边形中，表⽰⼒⽮R是F1、F2和F3的合⼒图形是()2、图⽰⼒F1、F2、F3和F4分别在坐标轴X上的投影的计算式为( )A.X1=-F1cosα1B.X2=-F1cosα2C.X3=-F1cosα3D.X4=-F1cosα43、固定铰⽀座约束反⼒()A.可以⽤任意两个相互垂直的通过铰⼼的⼒表⽰B.可以⽤任意⼀个⼤⼩和⽅向未知的通过铰⼼的⼒表⽰C.其反⼒的⽅向在标定时可以任意假设D.其反⼒的⽅向在标定时不可以任意假设4、⼒对物体作⽤效果，可使物体()A.产⽣运动B.产⽣内⼒C.产⽣变形D.运动状态发⽣改变和产⽣变形5、作⽤在刚体上的⼆⼒平衡条件是( )A.⼤⼩相等、⽅向相反、作⽤线相同、作⽤在两个相互作⽤物体上B.⼤⼩相等、⽅向相反、作⽤线相同、作⽤在同⼀刚体上C.⼤⼩相等、⽅向相同、作⽤线相同、作⽤在同⼀刚体上D.⼤⼩相等、⽅向相反、作⽤点相同三、填空题1、合⼒投影定理是指合⼒在任⼀轴上的投影，等于各___________在同⼀轴上投影的_____________。

2、图⽰(a)(b)(c)三种荷载作⽤下，梁AB的⽀座反⼒为：a图____________________b图______________________c图____________________四、分析与计算题1、图⽰结构的各构件⾃重不计，AB放置于光滑CD上，试画出AB，CD和整体的受⼒图。

适用标准文案一、是非题1.只需知道作用在质点上的力，那么质点在任一刹时的运动状态就完整确立了。

（错）2.在惯性参照系中，无论初始条件怎样变化，只需质点不受力的作用，则该质点应保持静止或等速直线运动状态。

（对）3.作用于质点上的力越大，质点运动的速度越高。

（错）4.牛顿定律合用于随意参照系。

（错）5.一个质点只需运动，就必定受有力的作用，并且运动的方向就是它受力的方向。

（错）6.圆盘在圆滑的水平面上平动，其质心作等速直线运动。

若在此圆盘平面上作用一力偶，则今后圆盘质心的运动状态是变速直线运动。

（错）7.若系统的总动量为零，则系统中每个质点的动量必为零。

（错）8.质系动量关于时间的变化率，只与作用于系统的外力相关，而与内力没关。

（对）9.刚体在一组力作用下运动，只需各个力的大小和方向不变，无论各力的作用点如何变化，刚体质心的加快度的大小和方向不变。

（对）10.冲量的量纲与动量的量纲同样。

（对）11.平动刚体各点的动量对一轴的动量矩之和能够用质心对该轴的动量矩表示。

（对）12.质点系关于随意动点的动量矩对时间的导数，等于作用于质点系的全部外力关于同一点的矩的矢量和。

（错）13.因为质点系的动量为p m v C，所以质点系对O 点的动量矩为L O M O m v C。

（错）14.质点系的内力不可以改变质点系的动量与动量矩。

（对）15.刚体的质量是刚体平动时惯性大小的胸怀，刚体对某轴的转动惯量则是刚体绕该轴转动时惯性大小的胸怀。

（对）16.机械能守恒定理是，当质点系不受外力作用时，则动能与势能之和等于零。

（错）17.系统内力所做功之代数和总为零。

（错）18.假如某质点系的动能很大，则该质点系的动量也很大。

（错）19.在使用动静法时，凡是运动着的质点都应加上惯性力。

（错）20.平移刚体惯性力系可简化为一个协力，该协力必定作用在刚体的质心上。

（对）21.拥有垂直于转轴的质量对称面的转动刚体，其惯性力系可简化为一个经过转轴的力和一个力偶，此中力偶的矩等于对转轴的转动惯量与刚体角加快度的乘积，转向与角加快度相反。

1、作用在同一刚体上的两个力，若有，则该二力是一对平衡的力。

2、力可以沿着作用线移动而不改变它对物体的运动效应。

3、三力平衡定理指出：三力汇交于一点，则这三个力必然互相平衡。

4、约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。

5、两端用光滑铰链连接的构件是二力构件。

6、用解析法求平面汇交力系的合力时，若选用不同的直角坐标系，则所求得的合力不同。

7、若平面汇交力系构成首尾相接、封闭的力多边形，则合力必然为零。

8、平面汇交力系平衡时，力多边形各力应首尾相接，但在作图时力的顺序可以不同。

9、一个力在任意轴上的投影的大小一定小于或等于该力的模，而沿该轴的分力的大小则可能大于该力的模。

10、平面汇交力系的主矢就是该力系之合力。

11、摩擦力的方向总是与物体的运动方向相反。

（）12、约束力的方向与该约束所能阻碍的位移方向相反。

（）13、作用于刚体上的力的三要素是力的大小、方向和作用点。

（）14、如果作用于一个物体上的三力汇交于一点，则此三力必平衡。

（）15、平面任意力系简化的最终结果为一个力。

（）16、力对于一点的矩不因力沿其作用线移动而改变。

（）17、空间平行力系独立的平衡方程数为6个。

（）18、加速度d vd t的大小为ddvt。

（）19、相对加速度a r与相对速度v r的关系为a r=d vrd t（）20、已知质点的质量和作用于质点的力，质点的运动规律就完全确定。

（）21、质点系中各质点都处于静止时，质点系的动量为零。

于是可知如果质点系的动量为零，则质点系中各质点必都静止。

（）22、质点系的质量与其质心速度的乘积等于质点系的动量。

（）23、根据力的平移定理，可以将一个力分解成一个力和一个力偶。

反之，一个力和一个力偶肯定能合成为一个力。

（）24、摩擦力的方向总是与物体的运动方向相反。

（）25、牵连运动是指动点相对于定参考系的运动。

（ ） 26、质点系的质量与其质心速度的乘积等于质点系的动量。

《动力学 I 》第一章运动学部分习题参考解答1-3 解:运动方程:θtan l y =,其中kt =θ。

将运动方程对时间求导并将 030=θ代入得34cos cos 22lk lk l y v ====θθθ98cos sin 2232lk lk y a =-==θθ1-6证明:质点做曲线运动 , 所以 n t a a a +=, 设质点的速度为 v , 由图可知 : a a vv y n cos ==θ,所以 : yv va a n = 将c v y =, ρ2n va =代入上式可得ρc v a 3=证毕 1-7证明:因为 n2a v=ρ, va a v a ⨯==θsin n所以:va ⨯=3v ρ证毕1-10解:设初始时 , 绳索 AB 的长度为 L , 时刻 t 时的长度为 s , 则有关系式: t v L s 0-=,并且 222x l s +=将上面两式对时间求导得:0v s-= , x x s s 22= 由此解得:xsv x-= (a (a式可写成:s v x x 0-= ,将该式对时间求导得: 2002v v s x x x=-=+ (b 将 (a式代入 (b式可得:3220220xlv x x v x a x -=-==(负号说明滑块 A 的加速度向上1-11解:设 B 点是绳子 AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上 A 、 B 两点的速度在 A、 B 两点连线上的投影相等,即: θcos A B v v = (a 因为xR x 22cos -=θ (b 将上式代入(a 式得到 A 点速度的大小为: 22Rx x Rv A -=ω (c由于 x v A -=, (c 式可写成:Rx R x xω=--22 ,将该式两边平方可得: 222222 (x R R x x ω=- 将上式两边对时间求导可得:x x R x x R x xx 2232222 (2ω=-- 将上式消去 x 2后,可求得:22242(R x xR x--=ω由上式可知滑块 A 的加速度方向向左,其大小为 2 2242(R x xR a A -=ω1-13解:动点:套筒 A ;动系:OA 杆; 定系:机座; 运动分析:绝对运动:直线运动; 相对运动:直线运动; 牵连运动:定轴转动。

理论力学部分第一章 静力学基础一、是非题1．力有两种作用效果，即力可以使物体的运动状态发生变化，也可以使物体发生变形。

（ ）2．两端用光滑铰链连接的构件是二力构件。

（ ）3．作用在一个刚体上的任意两个力成平衡的必要与充分条件是：两个力的作用线相同，大小相等，方向相反。

（ ）4．作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。

（ ）5．三力平衡定理指出：三力汇交于一点，则这三个力必然互相平衡。

（ ）6．约束反力的方向总是与约束所能阻止的被约束物体的运动方向一致的。

（ ）二、选择题1．若作用在A 点的两个大小不等的力1F 和2F ，沿同一直线但方向相反。

则其合力可以表示为 。

① 1F －2F ；② 2F －1F ；③ 1F ＋2F ；2．三力平衡定理是 。

① 共面不平行的三个力互相平衡必汇交于一点；② 共面三力若平衡，必汇交于一点；③ 三力汇交于一点，则这三个力必互相平衡。

3．在下述原理、法则、定理中，只适用于刚体的有 。

① 二力平衡原理； ② 力的平行四边形法则；③ 加减平衡力系原理； ④ 力的可传性原理；⑤ 作用与反作用定理。

4．图示系统只受F 作用而平衡。

欲使A 支座约束力的作用线与AB 成30︒角，则斜面的倾角应为________。

① 0︒； ② 30︒；③ 45︒； ④ 60︒。

5．二力A F 、B F 作用在刚体上且0=+B A F F ，则此刚体________。

①一定平衡； ② 一定不平衡；③ 平衡与否不能判断。

三、填空题1．二力平衡和作用反作用定律中的两个力，都是等值、反向、共线的，所不同的是。

2．已知力F沿直线AB作用，其中一个分力的作用与AB成30°角，若欲使另一个分力的大小在所有分力中为最小，则此二分力间的夹角为度。

3．作用在刚体上的两个力等效的条件是。

4．在平面约束中，由约束本身的性质就可以确定约束力方位的约束有，可以确定约束力方向的约束有，方向不能确定的约束有（各写出两种约束）。

理论力学习题-质点动力学基本方程.(总9页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--104第9章 质点动力学基本方程一、是非题(正确的在括号内打“√”、错误的打“×”)1. 凡是适合于牛顿三定律的坐标系称为惯性参考系。

( √ )2. 一质点仅受重力作用在空间运动时，一定是直线运动。

( × )3. 两个质量相同的物体，若所受的力完全相同，则其运动规律也相同。

( × )4. 质点的运动不仅与其所受的力有关，而且还和运动的初始条件有关。

( √ )5. 凡运动的质点一定受力的作用。

( × )6. 质点的运动方向与作用于质点上的合力方向相同。

( × )二、填空题1．质点是指大小可以忽略不计，但具有一定质量的物体。

2．质点动力学的基本方程是∑=i m F a ，写成自然坐标投影形式为∑=τF dt s d m22∑=nFv m ρ2∑=b F 0。

、 、1053．质点保持其原有运动状态不变的属性称为惯性。

4．质量为m 的质点沿直线运动，其运动规律为0ln(1)v t x b b=+，其中0v 为初速度，b 为常数。

则作用于质点上的力=F 2020()mbv b v t -+。

5．飞机以匀速v 在铅直平面内沿半径为r 的大圆弧飞行。

飞行员体重为P ，则飞行员对座椅的最大压力为2(1)vP gr+。

三、选择题1．如图所示，质量为m 的物块A 放在升降机上， 当升降机以加速度a 向上运动时，物块对地板的压力等于( B )。

(A) mg(B) )(a g m +(C) )(a g m -(D) 02．如图所示一质量弹簧系统，已知物块的质量为m ，弹簧的刚度系数为c ，静伸长量为s δ，原长为0l ，若以弹簧未伸长的下端为坐标原点，则物块的运动微分方程可写成( B )。

(A) 0=+x m cx(B) 0)(=-+s x mcxδ (C) g x m cx s =-+)(δ (D) 0)(=++s x mcxδ 3．在介质中上抛一质量为m 的小球，已知小球所受阻力R kv =-，坐标选择如图所示，试写出上升段与下降段小球的运动微分方程，上升段( A )，下降段( A )。

第三篇动力学一、选择题(每题２分,共20分)1。

在铅直面内得一块圆板上刻有三道直槽AO,BO,CO,三个质量相等得小球M1,M2,M3在重力作用下自静止开始同时从Ａ,B,C三点分别沿各槽运动,不计摩擦,则___＿_＿__到达O 点、(A)Ｍ１小球先; (B)M2小球先; (C)M3小球先; (D)三球同时。

题1 题2 题32、质量分别为m1=m,m2=2m得两个小球M1,M２用长为L而重量不计得刚杆相连。

现将M1置于光滑水平面上,且M1M２与水平面成角。

则当无初速释放,M2球落地时,M1球移动得水平距离为___＿_＿_＿＿＿＿＿。

(Ａ);ﻩﻩ(B);ﻩﻩ(C);ﻩﻩ(D)0。

3、质量为m,长为b得匀质杆OＡ,以匀角速度ω绕O轴转动。

图示位置时,杆得动量及对O 轴得动量矩得大小为_＿______。

(Ａ),; (B),;(C),;ﻩ(D),。

4.在＿__＿_情况下,跨过滑轮得绳子两边张力相等,即Ｆ1=F2(不计轴承处摩擦)。

(A)滑轮保持静止或以匀速转动或滑轮质量不计;(B)滑轮保持静止或滑轮质量沿轮缘均匀分布;(C)滑轮保持静止或滑轮质量均匀分布;(D)滑轮质量均匀分布。

题4 题５5.均质杆长L,重P,均质圆盘直径Ｄ=L,亦重P,均放置在铅垂平面内,并可绕O轴转动。

初始时杆轴线与圆盘直径均处于水平位置,而后无初速释放,则在达到图示位置瞬时,杆得角速度ω1___＿＿___圆盘得角速度ω2。

(A)大于;ﻩ(B)小于; (C)等于;ﻩ(D)小于或等于。

６.均质杆AＢ,长L,质量m,沿墙面下滑,已知A端速度,B端高度ｈ,ＡB对过杆端A,质心C,瞬心I得水平轴得转动惯量分别为JＡ,J C,J I,则图示瞬时杆得动能为____＿_____、(A); (B); (C);(D)题６题7 题8７.已知均质杆长L,质量为m,端点B得速度为,则AB杆得动能为＿__＿__＿____。

(A);ﻩﻩ(B);ﻩ(C); (D)8、质量为ｍ1得均质杆OA,一端铰接在质量为ｍ2得均质圆盘中心,另一端放在水平面上,圆盘在地面上作纯滚动。

第一章静力学基础一． 填空题1．理论力学的任务是研究物体作 机械运动 的规律2．平衡是指 （相对于地球）静止或作匀速直线运动 . 3．力是物体之间 相互的机械 作用，这种作用使物体的 运动 或 形状 发生改变。

4．刚体是受力作用而 不变形 的物体。

5．刚体受到两个力作用而平衡的充分必要条件是 此两力等值、反向、共线 。

6．对刚体而言，力的三要素是大小、方向、作用线。

7．对刚体而言，力是 物体位移 矢量。

第二章 平面汇交力系和平面力偶系一、填空题1．平面汇交力系平衡的几何条件是 力多边形自行封闭 。

2．同一平面内两力偶的等效条件是 两力偶矩矢量相等 。

3．研究平面汇交力系时, 采用两种方法, 即 几何法 和 分析法 。

4．一个力F在某轴上的分力是 量、投影是 量。

5．力偶使刚体转动的效果和 矩心位置 无关，完全由 力偶矩 决定。

6．力偶可在作用平面内任意 移动 ，也可向平行平面 移动 。

三、计算题1．不计杆重，求图示结构中AB 、AC 两杆所受的力。

第三章 一、填空题1．平面任意力系平衡的充要条件为：该力系的主矢 和 主矩 同时为零。

2．平面平行力系独立的平衡方程有 3 个，可解 3 个未知量的问题。

3．作用在刚体上A 点的力,F可以等效平移到刚体上任意点B ，但必须附加一个力偶，此附加力偶的矩等于 。

4．平面任意力系向一点简化，需要将力系中的各力 简化 到作用面内选定的一点上，该点称为 简化中心 。

三、计算题1．求图示简支梁A 、B 处的约束力。

)(2/7,)(2/9),(4↓=↑=→=qa qa qa FFFBAyAXCABθKN50mKN /20m4m2A BC第四章 空间力系一、填空题1．空间力偶系的独立平衡方程有 3 个。

2．在空间任意力系的简化结果中，当主矢主矩互相 定位时，称为力螺旋。

3．空间任意力系平衡的充分必要条件是：该力系的主矢和主矩分别为零。

4．空间任意力系有 3 个独立的平衡方程。

第三篇 动力学一、选择题（每题2分，共20分）1．在铅直面内的一块圆板上刻有三道直槽AO ，BO ，CO ，三个质量相等的小球M 1，M 2，M 3在重力作用下自静止开始同时从A ，B ，C 三点分别沿各槽运动，不计摩擦，则________到达O 点。

（A ）M 1小球先； （B ）M 2小球先； （C ）M 3小球先； （D ）三球同时。

题1 题2 题32．质量分别为m 1=m ，m 2=2m 的两个小球M 1，M 2用长为L 而重量不计的刚杆相连。

现将M 1置于光滑水平面上，且M 1M 2与水平面成︒60角。

则当无初速释放，M 2球落地时，M 1球移动的水平距离为____________。

（A ）3L； （B ）4L； （C ）6L； （D ）0。

3．质量为m ，长为b 的匀质杆OA ，以匀角速度ω绕O 轴转动。

图示位置时，杆的动量及对O 轴的动量矩的大小为________。

（A ）2ωmb p =，122ωmb L O =； （B ）0=p ，122ωmb L O =；（C ）2ωmb p =，22ωmb L O =； （D ）2ωmb p =，32ωmb L O =。

4．在_____情况下，跨过滑轮的绳子两边张力相等，即F 1=F 2（不计轴承处摩擦）。

（A ）滑轮保持静止或以匀速转动或滑轮质量不计； （B ）滑轮保持静止或滑轮质量沿轮缘均匀分布； （C ）滑轮保持静止或滑轮质量均匀分布； （D ）滑轮质量均匀分布。

题4 题55．均质杆长L ，重P ，均质圆盘直径D =L ，亦重P ，均放置在铅垂平面内，并可绕O 轴转动。

初始时杆轴线和圆盘直径均处于水平位置，而后无初速释放，则在达到图示位置瞬时，杆的角速度ω1________圆盘的角速度ω2。

（A ）大于； （B ）小于； （C ）等于； （D ）小于或等于。

6．均质杆AB ，长L ，质量m ，沿墙面下滑，已知A 端速度v，B 端高度h ，AB 对过杆端A ，质心C ，瞬心I 的水平轴的转动惯量分别为J A ，J C ，J I ，则图示瞬时杆的动能为__________。