线性规划与投资组合的论文
- 格式：pdf
- 大小：458.08 KB
- 文档页数：18
下载文档原格式
合集下载
基于整数线性规划和混合整数线性规划的投资组合优化
1引言线性规划是用来寻求变量处于线性关系时的有效方法，在项目选择、投资组合优化、季节收益预测等问题中有多种应用。
整数规划与线性规划非常相似，但它要求所有或部分变量是整数。
某些情况下，整数规划更可取，如二元变量的管理决策。
部分决策变量为整数的模型，称为混合整数规划。
本文将会研究整数线性规划在投资组合优化中的应用。
模型A ，即整数线性规划（ILP ）模型可以看作NP 完全问题中的0-1背包问题，通过模型A 找出可选入投资组合的股票。
另一个模型是混合整数线性规划（MILP ），这里使用的是有限资产平均绝对偏差（LAMAD ）模型的演变来确定投资所选股票的确切数量，分配最合适的权重，以达到风险最小化、回报最大化的效果。
本文采用3种算法求解：分支剪界算法、动态规划算法和贪心算法。
分支剪界算法用CPLEX 12.6实现，动态规划算法和贪心算法在Eclipse 标准4.4平台上，用Java 语言实现，所采用的股票信息和数据由NASDAQ 和yahoo finance 网站获取。
2算法介绍以下介绍的算法都可以归属于启发法的范畴。
启发法是指不以找到问题的最佳或最确切的解决方案为目标的技术，而是找到一个足够可信的解决方案的方法。
直觉判断、刻板印象和常识都属于这个“范畴”。
它非常适用于在计算或搜索过于详尽和不实际的情况下，通过心理捷径来加快得到满意解决方案的过程，以减轻作出决策的认知负担。
它有常见的几种策略：第一种是将问题的目标状态进行切分，然后通过实现子目标逐渐实现总的目的；第二种是从最终目标状态逆向去寻找达到这个状态的途径；第三种是逐步收缩初始状态和目标状态的距离的方法。
元启发式是指导搜索过程的策略或上层方法论，元启发式的目标是有效地探索搜索空间，以找到最接近的最优解。
启发式依赖于问题，用于确定特定问题的“足够好”的解决方案，而元启发式就像一种设计模式，可以应用于更广泛的问题。
启发式方法特别适用于混合整数规划，因为混合整数规划太大而无法求解最优，而线性规划较为松弛，可以在合理的时间内求解。
高校投资组合课设论文。
《数学建模》课程设计学号：201317201姓名：马雪摘要根据投资项目分析，本题主要研究最优投资组合问题，要以合理的方案，计算每种项目获得的最大利润，使资金安排最优化，同时也是一个线性规划问题。
按照求最大值的要求，以五年后拥有的资金总额为目标函数，以资金的金额限制为约束条件，建立线性模型，运用Matlab软件对模型进行求解，得到比较理想的结果：（1）第一年年初对项目A投资61.5163万元，对项目D投资38.4837万元，第二年年初对项目A投资10.7927万元，对项目C投资30.0000万元，第三年年初对项目A投资16.8370万元，对项目B投资40.0000万元，对项目D 投资13.9068万元，第四年年初对项目A投资27.1528万元，第五年年初对项目D投资19.3626万元。
（2）第一年年初对项目A投资63.0712万元，对项目D投资36.9288万元，第二年年初对项目A投资9.1446万元，对项目C投资30.0000万元，第三年年初对项目A投资13.5076万元，对项目B投资40.0000万元，对项目D 投资11.0242万元，第四年年初对项目A投资22.2019万元，第五年年初对项目D投资15.5337万元。
问题重述：A组1、生产计划高校现有一笔资金100万元，现有4个投资项目可供投资。
项目A：从第一年到底四年年初需要投资，并于次年年末回收本利115%。
项目B：从第三年年初需要投资，并于第5年末才回收本利135%，但是规定最大投资总额不超过40万元。
项目C：从第二年年初需要投资，并于第5年末才回收本利145%，但是规定最大投资总额不超过30万元。
项目D：五年内每年年初可以买公债，并于当年年末归还，并可获得6%的利息。
(1)试为该校确定投资方案，使得第5年末他拥有的资金本利总额最大。
（2）该校在第3年有个校庆，学校准备拿出8万元来筹办，又应该如何安排投资方案，使得第5年末他拥有的资金本利总额最大。
风险投资组合的线性规划模型(优秀论文)
1998年A题风险投资组合的线性规划模型1摘要对市场上的多种风险资产和一种无风险资产（存银行）进行组合投资策略的设计需要考虑两个目标：总体收益尽可能大和总体风险尽可能小，而这两个目标在一定意义上是对立的。
本文给出组合投资方案设计的一个线性规划模型。
主要思路是通过线性加权综合两个设计目标；假设在投资规模相当大的基础上，将交易费函数近似线性化；通过决策变量的选取化解风险函数的非线性。
模型的最大优点是：计算过程稳定性好，速度快。
我们对各种加权因子，求得了最优化决策方案，从而得到问题的有效投资曲线。
根据有效投资曲线，投资者可以由自己的主观偏好，直观地选择自己的投资方向。
最后通过非线性规划，说明线性规划的结果对于交易费收取的阈值有一定的容忍度。
一. 问题的提出在风险市场的投资问题中，风险与收益始终是一对矛盾。
一般来说想要追求高收益，风险也大; 若想风险小，收益也会相应减少。
研究表明，大部分的投资者具有以下的行为偏好：对于收益来说，总是越多越好；从风险的角度来说，大部分人都属于风险回避者。
我们可以通过选取适当的组合投资方案，在取得良好收益的同时使总体风险减少。
设某公司有一笔数额相当大的资金，投资购买若干种风险资产或存银行生息。
风险资产收益高但风险大，存银行生息无风险但收益低。
公司财务人员对多种资产进行了评估，估算出在这一时期内各种资产的平均收益率和风险损失率，并考虑购买时需付一定的交易费（不买当然无须付费，购买额不超过阈值时，交易费按阈值计算）。
现在需要设计一种投资组合方案，以利用好这笔资金使得净收益尽可能大，而总风险尽可能小。
二. 模型的基本假设及符号说明(一)基本假设H1: 只考虑给定时间内的收益和风险，且银行存款利率在给定时间内保持不变;H2: 公司用于投资的资金数额相当大，且无贷款或透支;H3: 各种资产投资风险相互独立。
H4: 总体风险可用所投资的资产中最大的一个风险来度量。
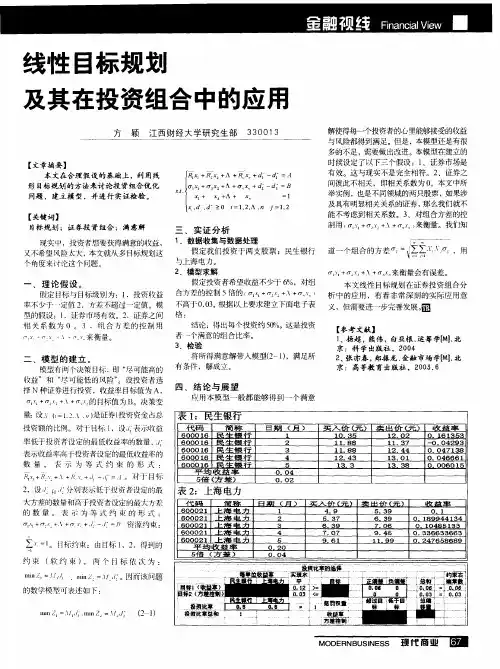
(二)符号说明S i: 第i种资产(i=1，2，...，n，n+1)，其中S n+1表示存入银行;r i : S i的平均收益率;q i : S i的风险损失率;p i : S i的交易费率;1本文发表于《数学的实践与认识》1999. No1. p39-42.u i : S i 购买额阈值;M: 资金总额;X i: 投资S i 占总额的比重(不含交易费) ， 以下简称投资; Y i: 投资S i 的交易费占总额的比重， 以下简称交易费; f 1: 净收益; f 2: 总体风险; λ: 权因子;三. 模型的建立(一) 基本模型我们的目标是对各种资产投资以后，不仅收益尽可能大，同时总体风险还要尽可能小。
线性目标规划及其在投资组合中的应用
目标 规 划 ；证 券投 资 组合 ；满 意 解
Ｒ Ｘ ＋Ｒ１ １ ＋Ｒ １ ｌ１ ｘ ＋ ｘ ＋ｄ １
１ ＋ 盯２ ‘ ２＋ ＋ 盯 ｒ＋ Ａ ｊ
ｄ ：＝Ａ
＝
Ｂ １
…
１＋
２ ＋Ａ ＋
． ｉ
ｘ ， ． ｄ ｄ
０ ｆ １ ２ Ａ ｎ ／＝１２ ＝ ，，
现 实 中 ．投 资者想 要获 得满意 的收 益 ， １ 数据收集与数据处理 Ｙ ∑ ，用 假 定我 们 投 资 于两 支 股 票 民生银行 道一个组合的方差 １ ． 又不希望 风险 太大 ， 本文就 从 多 目标规 划这 与上 海 电力 。 个角度 来讨论 这 个问题 。 ２ 、模 型 求解 十 ＋、 （ 来 衡量 会有误 差 。 ：： ＋『 假 定投 资者希 望收 益 不少于 ６ ％，对组 理论假 设 。 本 文线 性 目标 规 划在 证 券投 资 组 合分 ， ， ． ，＼ 假定 目标与 日标 级 别为 ：１ ．投 资收益 合方差 的控 制 ５倍的 ｆ ＋ ＋ ＋ Ｙ １ 析 中的 应 用 ，有 着 非 常深 刻 的 实 际应 用意 ．３ 根据 队 上 求建立 下面 电子表 要 率 不少于 ・ 值 ２ 定 ．方差 不超过 一定值 。模 不高 于 ００ 。 义， 但需要进一步完善发展。 固 型 的假 设 ：１ 券 市场有 效。２ ． ．证 券之 间 格 ： 结论 ：得 出每 个投 资约 ５％。这 是投 资 ０ 相 关 系数 为 ｏ 。３ ．组 合方 差 的 控 制 用 【 参考文献】 者 一 个满 意 的组 合比率 。 ： ＋ １ 一 Ｙ来 衡量 。 ｌ 、 １ 扬超 ， 熊伟，白亚根 ． 运筹学【】北 Ｍ。 ３ 、检 验 京 ：科 学 出版 社 ，２ ０ ０４ 将 所得 满意解 带 入模型 （一１，满 足所 ２ ） ２ 张亦春， 、 郑振龙 ． 融市场学［Ｉ北 金 Ｍ。 二 、模型的 建立 。 京 ：高 等教 育 出版 社 ，２ ０ ． ０３６ 模 型有 两 个决 策 口标 ，即 “ 尽可 能高的 有 条件 ，解 成立 。
Ｒ Ｘ ＋Ｒ１ １ ＋Ｒ １ ｌ１ ｘ ＋ ｘ ＋ｄ １
１ ＋ 盯２ ‘ ２＋ ＋ 盯 ｒ＋ Ａ ｊ
ｄ ：＝Ａ
＝
Ｂ １
…
１＋
２ ＋Ａ ＋
． ｉ
ｘ ， ． ｄ ｄ
０ ｆ １ ２ Ａ ｎ ／＝１２ ＝ ，，
现 实 中 ．投 资者想 要获 得满意 的收 益 ， １ 数据收集与数据处理 Ｙ ∑ ，用 假 定我 们 投 资 于两 支 股 票 民生银行 道一个组合的方差 １ ． 又不希望 风险 太大 ， 本文就 从 多 目标规 划这 与上 海 电力 。 个角度 来讨论 这 个问题 。 ２ 、模 型 求解 十 ＋、 （ 来 衡量 会有误 差 。 ：： ＋『 假 定投 资者希 望收 益 不少于 ６ ％，对组 理论假 设 。 本 文线 性 目标 规 划在 证 券投 资 组 合分 ， ， ． ，＼ 假定 目标与 日标 级 别为 ：１ ．投 资收益 合方差 的控 制 ５倍的 ｆ ＋ ＋ ＋ Ｙ １ 析 中的 应 用 ，有 着 非 常深 刻 的 实 际应 用意 ．３ 根据 队 上 求建立 下面 电子表 要 率 不少于 ・ 值 ２ 定 ．方差 不超过 一定值 。模 不高 于 ００ 。 义， 但需要进一步完善发展。 固 型 的假 设 ：１ 券 市场有 效。２ ． ．证 券之 间 格 ： 结论 ：得 出每 个投 资约 ５％。这 是投 资 ０ 相 关 系数 为 ｏ 。３ ．组 合方 差 的 控 制 用 【 参考文献】 者 一 个满 意 的组 合比率 。 ： ＋ １ 一 Ｙ来 衡量 。 ｌ 、 １ 扬超 ， 熊伟，白亚根 ． 运筹学【】北 Ｍ。 ３ 、检 验 京 ：科 学 出版 社 ，２ ０ ０４ 将 所得 满意解 带 入模型 （一１，满 足所 ２ ） ２ 张亦春， 、 郑振龙 ． 融市场学［Ｉ北 金 Ｍ。 二 、模型的 建立 。 京 ：高 等教 育 出版 社 ，２ ０ ． ０３６ 模 型有 两 个决 策 口标 ，即 “ 尽可 能高的 有 条件 ，解 成立 。
线性规划论文
线性规划论文在运筹学和数学中，线性规划（Linear Programming，简称LP）是一种用于最大化或最小化线性函数的方法，同时满足一组线性约束条件的数学优化问题。
线性规划模型广泛应用于多个领域，包括经济学、管理科学、工程设计等。
线性规划的基本形式可以描述为：最大化（或最小化）目标函数：Z = c1x1 + c2x2 + ... + cnxn在约束条件下：a11x1 + a12x2 + ... + a1nxn ≤ b1a21x1 + a22x2 + ... + a2nxn ≤ b2...am1x1 + am2x2 + ... + amnxn ≤ bm其中，Z是目标函数的值，c1、c2、...、cn是目标函数的系数，x1、x2、...、xn是决策变量，a11、a12、...、amn 是约束条件的系数，b1、b2、...、bm是约束条件的右侧常数。
线性规划的求解过程可以使用各种算法，包括单纯形法、内点法、分枝界限法等。
这些算法可以在有限的步骤内找到最优解或确定问题无解。
线性规划论文可以探讨和研究以下方面：1. 线性规划在不同领域的应用：例如，在物流和供应链管理中，线性规划可以用于优化物流路径和资源分配问题。
在生产调度中，线性规划可以用于优化生产流程和资源利用率。
在投资组合优化中，线性规划可以用于确定最佳的资产配置方案。
2. 线性规划算法的改进和优化：线性规划算法的效率和准确性是论文可以研究的重点。
可以尝试改进现有算法，提出新的求解方法，或设计特定领域的定制算法。
3. 线性规划的扩展：线性规划的基本形式可以通过引入非线性约束、整数约束或混合整数约束来扩展。
这些扩展可以增加问题的复杂性，但也可以更好地适应实际情况。
4. 线性规划与其他优化方法的比较：线性规划与其他优化方法（如非线性规划、动态规划等）的比较可以探讨各种方法的优缺点，并确定在不同情况下的最佳选择。
5. 线性规划的理论和应用研究：除了具体问题的求解，线性规划的理论研究也是论文的重要组成部分。
数学建模论文-组合投资问题1
组合投资问题的研究摘要本文研究了投资的风险和收益问题，建立了投资的单目标和多目标决策模型，并将多目标决策问题转化为单目标的决策模型，采用线性规划问题求解以解决公司的投资组合问题。
利用线性规划和灰色预测模型对公司五年投资过程中的投资的收益和风险分别进行了评估预测，求出了在不同的投资环境下第五年末的最大利润数值。
针对问题一：本文以第五年所得总金额为目标函数，应用线性规划理论建立了单目标优化模型，并运用Lingo软件求得第五年所得总金额的最大值：374140.5万，则第五年的最大利润：174140.5万。
针对问题二：本文分别对独立投资和同时投资这两种情况进行分析，对题中表2和表3进行了处理，算出来各项目每一年的到期利润率，分别以到期利润率的时间响应函数和标准差为目标函数建立了模型，运用灰色系统理论对上述两种投资方式近五年的各项目到期利润率进行预测，通过Matlab软件求得了两种不同投资方式的近五年各项目到期利润率预测结果（具体数据见表7.2和表7.3）和各项目标准差（具体数据见表7.5和7.6），并对预测结果进行了级比偏差检验，检验结果显示此时预测结果精度较高。
针对问题三：本文综合考虑了独立投资和同时投资这两种情况，同样以第五年的所得总金额为目标函数，并建立了单目标优化模型，通过Lingo软件求得第五年所得总金额的最优值：558422.0万，则第五年的最大利润358422.0万。
针对问题四：以题三中标准差最大值表示投资最大风险损失率，为此分别以第五年最大总金额和最小风险损失费为目标函数建立了多目标线性优化目标函数，比运用Lingo软件求得：当8.0s时，可得第五年总金额最大值：569975万,=则第五年的最大利润369975万。
针对问题五：假设一部分资金存入银行获取利息，并向银行贷款进行其他项目投资，然后根据题四方法和思想，运用Lingo软件求得：当3.0s时，可得第=五年总金额最大值：79582.4万,则第五年的最大利润59582.4万。
投资项目策划组合选择论文
投资项目组合选择摘要投资项目组合问题，是现实世界中普遍存在的一个问题。
首先，我们通过认真分析问题，把它转化为了一个线性规划问题，利用数学知识找出其决策变量、约束条件、目标函数，并建立了相应的数学模型（模型一）。
其次，我们分不利用MATLAB软件、LINGO软件编写了相应的MATLAB程序、LINGO程序，并发觉利用两个软件所求得的目标函数值相同，但最优解并不相同。
再次，为了验证结果的正确性，我们建立了另一个模型——模型二，并利用MATLAB软件和LINGO软件分不对它求解，发觉模型一和模型二的LINGO求解的最优解相同，而MATLAB求解的最优解仍不相同。
通过对问题和模型的分析，我们得出两个模型均正确的结论，另外，利用运筹学的知识知问题有无穷多个最优解。
最后，我们对实验结果进行了分析，对模型的灵敏度（即鲁棒性）进行了分析，还对模型进行了评价和推广。
关键词：投资组合；线性规划；MATLAB；LINGO；鲁棒性(灵敏度)THE CHOOSES OF PORTFOLIO PROJECTABSTRACTInvestment combinatorial problems in the real world, is a widespread problem. First, we through careful analysis problem, convert it to a linear programming problem, using mathematical knowledge to find its decision variables and constraints,the objective function, and establishes the mathematical model (model one). Secondly, we were using the software MATLAB, software LINGO writted the corresponding MATLAB program, the corresponding LINGO program, and found the two results for the objective function values are the same, but the optimal solution is not the same. Again, in order to verify the correctness ofthe results, we establish another model(model two), and using software MATLAB and LINGO the two softwares to solve it, respectively.And the optimal solution calculated by LINGO software of two models is same,but the optimal solution calculated by MATLAB software of two models is not the same. Through the analysis of the problem and models, we draw two models are correct conclusion. In addition, using knowledge of operation research know that the problem has multiple optimal solutions. Finally, we analyses experimental results of model, the sensitivity (robustness), and analyses the model evaluation and promotion.Key words: Portfolioformation; Linear program; The software of MATLAB; The software of LINGO; robustness (sensitiveness)目录1 问题的提出 (1)2 问题的分析 (1)3 问题假设 (3)4 符号讲明 (3)5 建立模型一 (4)6 模型一的求解 (4)7 模型验证 (7)7.1模型一的LINGO求解验证 . (7)7.2 建立模型二 (9)7.3 模型二的求解 (9)7.4 对比结果并分析 (11)8 结果分析 (12)8．1灵敏度分析 (13)8．2结果分析 (14)9 模型的推广与改进.. (14)参考文献 (16)附录.......................................................... ..171 问题的提出某投资者有50万元可用于长期投资，可供选择的投资项目包括购买国库券、购买公司债券等。
线性规划在风险资产投资组合中的应用
线性规划在风险资产投资组合中的应用作者：张立山张晓红来源：《职业时空》2008年第04期一、问题的提出假设市场上有n种资产（如股票，债券）供投资者选择，第i种资产记为Si（i=1，2，，，n），某投资机构有数目为M的一笔资金可用作一个时期的投资。
经分析评估，估算出这一时期购买Si的平均收益率为ri，并预测出购买Si的风险损失率为σi，且购买Si需支付交易费，费率为Si。
考虑到投资种类越是独立和分散，总的风险就越小，不妨假设用这笔资金购买的资产总体风险可用所投资的产品中风险最大的产品的风险来度量。
另外假设同期银行的存款（设为S0）利率是r0，且既无风险又无费率（σ0=0，p0=0）。
已知n=4的相关数据如表1所示。
现在的最优化问题是为该投资机构设计一种风险投资组合方案，使得总体收益尽可能大，而总体风险尽可能小。
二、模型的构建假设资金M中比例为αi的部分被用来购买资产Si，则购买资产Si的资金为M*αi，购买资产Si的花费为M*αi*pi，从而购买资产Si的最后净收益为：三、投资组合的有效边界最简单的方法是采用计算机进行随机模拟的方法，得出不同种类风险资产的投资组合及有效边界。
首先，可以通过代入法观察收益与风险，即E与-Q的关系；然后设定i，即用来投资的资产种类，用计算机随机模拟的方法对αi取随机数，经过数千次代入计算后得出E，-Q的数值；在以E为纵坐标，Q为横坐标的坐标系上表示的图形就是投资者可能选择的投资组合集合，其中，同一风险水平上收益最高的投资组合连线就是投资者的有效边界。
四、最优投资组合的确定在有效边界曲线上，每个点代表一个投资组合，具有不同的风险水平和相应的收益水平，风险越高，收益越大。
那么投资者如何选择投资组合呢？马科维茨投资组合理论引入了无差异曲线，代表投资者的风险偏好。
无差异曲线是在坐标系中凸向原点的不相交的曲线簇。
曲线上的点无差异，距离原点越远，效用值越高。
代表某一投资者偏好的无差异曲线与有效边界的切点就是投资者的最优投资组合。
线性规划的应用
线性规划的应用1. 引言线性规划是一种优化问题的数学建模工具，广泛应用于经济、工程、运输、资源分配等领域。
本文将探讨线性规划在生产计划、供应链管理和投资组合优化中的应用。
2. 生产计划中的线性规划应用生产计划是企业核心业务之一，通过合理的生产计划可以提高生产效率和降低成本。
线性规划可以匡助企业确定最佳的生产计划，以满足市场需求并最大化利润。
例如，假设一家创造公司有多个产品需要生产，每一个产品的生产成本、销售价格和市场需求量都不同。
通过线性规划模型，可以确定每一个产品的生产数量，以最大化总利润。
3. 供应链管理中的线性规划应用供应链管理是企业与供应商、生产商和分销商之间协调和优化物流和信息流的过程。
线性规划可以用于优化供应链中的物流和库存管理。
例如，一家零售公司需要决定每一个仓库的库存水平和重新补充货物的频率，以最大程度地满足顾客需求并最小化库存成本。
通过线性规划模型，可以确定最佳的库存水平和补货策略。
4. 投资组合优化中的线性规划应用投资组合优化是金融领域中的一个重要问题，即如何选择一组资产以最大化收益并控制风险。
线性规划可以用于确定最佳的投资组合权重。
例如，一个投资者有多个可选的资产，每一个资产有不同的预期收益率和风险。
通过线性规划模型，可以确定每一个资产的权重，以最大化整体投资组合的预期收益并控制风险。
5. 结论线性规划是一种强大的数学工具，可以应用于各种优化问题中。
本文讨论了线性规划在生产计划、供应链管理和投资组合优化中的应用。
通过合理的模型建立和求解，可以匡助企业和个人做出最佳决策，提高效益和竞争力。
基于线性规划在证券投资组合模型中的应用
基于线性规划在证券投资组合模型中的应用作者：杨静冯乐乐张庆樊灿来源：《山东青年》2014年第12期摘要：证券投资组合是指投资者根据风险程度和收益情况下，参照以前的证券投资规律，选择一种低风险的投资策略。
由此马科维茨的“均值-方差组合模型”则显得备受欢迎。
然而，事实并非如此，“均值-方差组合模型”在计算上并不被人们认可，所以不能大范围的推广，在实际生活中的应用少之又少。
为了解决这个问题，本文在分析了马科维茨模型后，提出了一种新的证券投资组合模型，即“基于线性规划的投资组合模型”。
该模型通过建立与求解证券投资组合中风险最小化线性规划模型及收益最大化线性规划模型，以求寻找一种更加优化的证券投资组合，做出正确的投资策略。
关键词：线性规划;证券投资;马科维茨;收益;风险一、绪论1、文献概述马科维茨（Markowitz）于1952年提出投资组合理论，开创了金融数理分析的先河，是现代经济学的一个不可或缺的理论基础。
在马科维茨的投资组合模型中，数学期望代表着预期收益，方差代表着风险，协方差代表着资产之间的相互关系。
投资组合的数学期望为投资组合中所有资产收益的加权平均数，而资产组合的方差为各资产方方差及其协方差的加权平均[1]。
利用马科维茨模型确定最小方差投资组合，首先要得到构成投河组合的单个资产的收益、风险及资产之间的相互关系，然后，计算投资组合的收益和风险。
基于此，方可根据投资者投资决策的基本准则确定来最小方差投资组合。
基于马科维茨投资组合的基本思想，我们不难知道在资产完全不相关的情况下，投资组合的风险会随着资产数量的增加而趋于无穷小，甚至可变为零。
而在现实生活中，资产完全不相关或完全相关的情况并不多见，其中大部分都处于不完全相关状态，所以资产之间的协方差就成了投资组合方差的决定因素，而协方差是不能依靠投资组合的多元化来降低的。
2、提出问题在进行证券投资时，投资者必须确保在获得一定的收益时使得风险降到最低，或在可接受的风险水平下使得获得利益达到最大[2]。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
m a x ( 或 m i n ) z ( c1 x1 c 2 x 2 c n x n ) ） b1 a 1 1 x1 a 1 2 x 2 a 1 n x n ( 或 ， ） b2 a 2 1 x1 a 2 2 x 2 a 2 n x n ( 或 ， s .t . a x a x a x (或 ， ） bm m2 2 mn n m1 1 x1 , , x n 0
二、线性规划问题的数学模型
通常称现实世界中人们关心，研究的实际对象为原型。模型是将某一部分信 息简缩，提炼而构造的原型替代物。数学模型则是对现实世界的一个特定对象， 为达到一定目的， 根据内在规律做出必要的简化假设，并运用适当数学工具得到 的一个数学结构。 线性规划问题的数学模型包含三个组成要素： （1） 决策粗变量， 只决策者为实现规划目标采取的方案，措施，是问题中要确定的未知量； （2）目 标函数，指问题要达到的目的要求，表示为决策变量的函数； （3）约束条件，指 决策变量取值时受到的各种可用资源的限制，表示为含决策变量的等式或不等 式。如果在规划问题的数学模型中，决策变量为可控的连续变量，目标函数和约 束条件都是线性的，这类模型称为线性规划问题的数学模型。 一般线性规划问题的数学模型可表示为以下几种形式：
1
பைடு நூலகம்
1，投资组合与线性规划
投资指货币转化为资本的过程。 投资可分为实物投资、 资本投资和证券投资。 前者是以货币投入企业， 通过生产经营活动取得一定利润。后者是以货币购买企 业发行的股票和公司债券， 间接参与企业的利润分配。投资者把资金按一定比例 分别投资于不同种类的项目或有价证券或同一种类有价证券的多个品种上， 这种 分散的投资方式就是投资组合。通过投资组合可以分散风险，即“不能把鸡蛋放 在一个篮子里” ，这是证券投资基金成立的意义之一,市场持续震荡，风险凸显。 在选择基金理财投资时， 秉承“一堆鸡蛋多个篮子”的理念，优选基金做投资组 合，更助你抗风险。基金组合应结合自身所处生命周期，承受风险能力与投资期 限而投资多只各类型基金，均衡风险管理，增强投资的稳定性，使基金投资在各 个阶段都能获得较好的收益，而不能简单地将股票基金累计相加。那么，投资人 应如何选择基金作为自己的投资组合呢？要想让自己的投资得到最大的收益就 应遵循线性规划。 线性规划是运筹学的一个最基本的分支，它已成为帮助各级管 理人员进行决策的一种十分重要的工具。传统的管理只注重定性分析，已远远不 能适应当今社会发展的需要。 现代化管理要求采用定性分析和定量分析相结合的 方法，一切管理工作要力求做到定量化，最优化，于是就产生了各种各样的管理 优化技术。 线性规划在世界上各个工业化国家已经得到了极为广泛的应用，为那 些国家的公司， 企业节省了成千上万的资金，那么线性规划主要有那些方法来解 决实际问题。
Linear programming mathematical model was developed to describe the actual problems in mathematical form, it reflects the actual problem between the number of laws of nature. As a result of portfolio practical problems are often more complicated, to establish the linear programming mathematical model, to a question should be analysed seriously, seize the most essential factors, using simple mathematical formula to describe, to establish the mathematical model which is simple and can correctly reflect the essence of the problem. From the real problems in the establishment of mathematical models of general According to the influence factors to achieve the purpose of finding the decision variables, then the decision variables and to achieve the objective function of the relationship between the objective function was determined by the decision variables, restrictive conditions to determine the decision variables are the constraint conditions. When we get the mathematical model of objective function is a linear function, constraint condition for linear equations or inequalities that this mathematical model for linear programming model and using the software solution, can be of limited resources reasonable allocation and combination, so as to achieve the best economic benefit. This paper consists of the following three parts : the first part introduces the initial portfolio and linear programming contact; the second part introduces the mathematical model of linear programming; the third part introduces linear programming to solve portfolio optimization problems. Keywords：Linear programming; simplex method; investment portfolio;
关键词：线性规划；单纯形法；投资组合；
摘要部分去掉第一段，增加本文关于投资组合的 一般线性规划模型、动态模型、整数规划模型的介绍 及其解法、结论的简要概括。 修改后，要对全文认真、仔细地研读，发现错误， 及时改正，然后可以打印了。并要对文中的例题及其 解法，包括计算机程序熟练掌握，准备答辩。
I
Abstract
引
言
随着经济全球化的不断发展，企业面临更加激烈的市场竞争。企业必须不断 提高盈利水平，增强其获利的能力，在成本、生产、运输、销售等环节中提高效 率，形成企业的核心竞争力，才能在激烈的市场竞争中立于不败之地。在各类经 济活动中， 经常遇到这样的问题： 在生产条件不变的情况下， 如何通过统筹安排， 改进生产组织或计划，合理安排人力、物力资源，组织生产过程，使总的经济效 益最好。 这样的问题常常可以化成或近似地化成所谓的“线性规划”问题。线性 规划是应用分析、量化的方法，对经济管理系统中的人、财、物等有限资源进行 统筹安排，为决策者提供有依据的最优方案，以实现有效管理。利用线性规划我 们可以解决很多问题。如：在不违反一定资源限制下，组织安排生产，获得最好 的经济效益（产量最多、利润最大、效用最高） 。也可以在满足一定需求条件下， 进行合理配置，使成本最小。同时还可以在任务或目标确定后，统筹兼顾，合理 安排，用最少的资源（如资金、设备、原材料、人工、时间等）去完成任务。下 面我们简单的介绍线性规划与投资组合的关系并运用线性规划解决一些投资组 合中的实际问题。
II
目
引
录
言............................................................................................................................1
1、投资组合与线性规划................................................................ 错误！未定义书签。 2、线性规划问题的数学模型......................................................................................2 3、投资组合中的优化问题..........................................................................................3 3.1 一般线性规划解决投资组合中的优化问题...................................................4 3.1.1 投资组合问题.........................................................................................4 3.1.2 最佳广告投放方案...............................................................................6 3.2 投资组合中的动态规划问题..........................................................................8 3.3 投资组合中的整数规划问题.........................................................................10 结论.................................................................................................. 错误！未定义书签。 参考文献......................................................................................................................13