弹性力学3应变分析

15
1.1.3 应变的概念
(a) x方向的线应变
(b) y方向的线应变
(c) xy面内的剪应变
图 1-3 单元体应变的几何描述
在图1-3(a)中，单元体在x方向上有一个的伸长量。微分单元 体棱边的相对变化量就是x方向上的正应变。即
x
u x x
y
u y x
（1.9）
u y y
ux y
相应地，y轴方向的正应变为： x-y 平面内的剪应变：
tan 1
（1.10）
; tan 2
（1.11）
16
1.1.3 应变的概念
因此，剪应变 xy 为
xy
u x 1 2 x y u y
（1.12）
应变分量的矩阵型式
x xy ij yx y zx yy
2 2 Tn n n 2

m A
B T
G
P A

n
o
y
图1-1 物体内任意点处的应力
（1.6）
12
1.1.2 应力的概念 应力状态
在物体内的同一点处，不同方向截面上的应力是不同的。只有 同时给出过该点截面的外法向方向，才能确定物体内该点处此截面 上应力的大小和方向，才能表示这一点的应力状态。
x' ' y z'
=
0 1 0 cos 0 sin
0 x1 sin y1 cos z1
（b）
将第一式代入上式，可得
x ' 1 0 0 cos sin 0 x ' y y 0 cos sin = sin cos 0 z' z 0 sin cos 0 0 1

§3.1 应变状态11
• 三个刚性转动分量及6个应变分量合在一起，才全 面反映了物体变形
xyz x y z xy yz zx
B
B’’ 刚性转动
B’’’
B’
变形
A 刚性平动 A`
§3.1 应变状态12
• 工程应变： ln l0
l0
变形后长度 原始长度
不适用于大变形
• 自然应变/对数应变：
在塑性变形较大时，用-曲线不能真正代表加载和变形的状态。
x y z
• ——弹性体一点的体积改变量
• 引入体积应变有助于简化公式。
• 大于零表示体积膨胀，小于零体积压缩。
• 注意：土力学中塑性体应变符号约定相反。
§3.2 主应变与应变主方向8
应变Lode参数: 为表征偏量应变张量的形式，引入应变Lode参数：
22 3 1 3
1
(1.66)
如果两种应变状态με 相等，表明它们所对应的应变莫尔圆 相似，也即偏应变张量的形式相同。
Vz y
;
zx
Vz x
Vx z
;
§3.3 应变率张量 2
小变形情况下，应变速率分量与应变分量间存在如下关系:
x
Vx x
du x dt
d dt
u x
x
u x
y
Vy y
dv y dt
d v
dt
y
y
v y
z
Vz z
z
dw dt
d w dt z
z
w z
线应变速率
j
Vj,i )
(1.56)
§3.3 主应变与应变主方向 4
由于时间度量的绝对值对塑性规律没有影响，因

系，即 σx = Eεx 这就是虎克定律。 应力
（Hooke‘s Law）
Y
弹塑性范围
弹性范围
斜率, E
应变
工程上，一般将应变与应力间的关系表示为
xE 1xyz yE 1yzx
xy
1
G
xy
yz
1
G
yz
zE 1zxy
zx
1
G
zx
称它们为物理方程（广义虎克定律）。
x 1 E 1 1 2 x 1 y 1 z
1
0
对 1 0
称
1
2
对于平面应变问题的弹性矩阵，只须在上式
中，以 E
1 2
代E，
1
代μ即可。
小结
则有
uu vv ww (在 u 上)
用矩阵形式表示为：
uu (在 u 上)
小结
弹性力学基本方程的一般形式为
回顾
平衡微分方程 σb0 (在 内)
几何方程 物理方程
ε tu σDε
(在 内) (在 内)
边界条件
nσt
(在 t 上)
uu
(在 u 上)
其中 t u ， 为弹性体的完整边界。
§2-3 平面应变和平面应力问题
平面应变问题
位移：按平面应变的定义，三个方向的位移函数是
uux,y vv(x,y) w0
应变：由几何方程应变-位移关系，得
x
u x
1x,
y,
y
v y
3x,
y,
xy yz
u y
v x
2x,
v w0 z y
y
z
w0, z
zx
u z

通过监测土木工程结构的振动、变形等响应信息，识别结构的损 伤位置和程度，评估结构的安全性。
加固与改造设计
根据安全性评估结果，对土木工程结构进行加固与改造设计，提 高结构的承载能力和安全性。
05
弹性应变数值模拟与仿真技术
有限元法基本原理及软件实现过程
有限元法基本原理
将连续体离散化为有限个单元，通过单元节点相互连接，形 成单元刚度矩阵和整体刚度矩阵，进而求解弹性力学问题。
跨学科交叉融合创新点挖掘
力学与材料科学
深入研究材料在弹性应变过程中的力学行为和失效机制，为新型弹性应变材料的研发提供 理论指导。
电子信息与计算机科学
将电子信息技术和计算机科学技术应用于弹性应变领域，推动智能化测量技术和自动化测 试系统的发展。
生物医学工程
借鉴生物医学工程中的仿生学原理和方法，研发具有生物相容性和生物活性的新型弹性应 变材料。
动力学特性
考虑航空航天器在飞行过程中的动力学特性，如 振动、冲击等，确保结构在复杂环境下的稳定性 和可靠性。
热弹性效应
针对航空航天器在极端温度环境下的热弹性效应 ，进行结构优化设计，降低热应力对结构的影响 。
汽车零部件疲劳寿命预测方法
应力-寿命曲线
通过实验测定汽车零部件在不同应力水平下的疲劳寿命，绘制应力 -寿命曲线，预测零部件的疲劳寿命。
陶瓷材料一般具有较低的弹性，但 在某些特定条件下，如高温或高压 下，其弹性形变能力会发生变化。
橡胶材料
橡胶材料具有显著的弹性和可恢复 性，其弹性形变能力主要来源于分 子链的卷曲和拉伸。
复合材料弹性应变机制
基体与增强相相互作用
界面效应
复合材料中基体与增强相之间的相互作用 对其弹性应变行为具有重要影响。

应力定义为：单位面积上所受的内力，是在面力或 体力作用下，物体内部假想面上单位面积上的一对 大小相等、方向相反的力，是作用在该面上力的大 小的度量。
应力也称为胁强(力的强度)：应力并不是一个 “力”，因为它的量纲不是力而是单位面积上的力。
应力的方向与作用力的方向相反。
6
2.1 应力分析
16
2、非均匀变形 用物体内部变形 单元体（应变椭 圆）表示非均匀 变形 ——褶皱
17
2.2.3 应变分类
应变---当弹性体受到应力作用后，将发生体积和形 状的变化，即应变。



体积形变----指物体只发生体积变化而无形状变化的 应变。它是受正应力作用的结果。 形状形变-----物体只发生形状的变化。它是剪切应力 作用的结果。 理论力学是研究物体的整体运动。把物体作为一种刚 体，在外力作用下只能产生整体平移和转动。 弹性力学不仅要考虑物体的整体运动，而且要研究物 体内部各质点的相对运动，相对运动是产生应变的必 要条件。
设N为M 邻近点，其向径 为 r dr 。受力后N点位移 到 N ，它的位移向量记 为 u(r dr) 。 N点对M点的相对位移是
z
N (x+dx,y+dy,z+dz)
dr
M （x,y,z)
u (r )
u( r )
u (r dr)
N
u(r dr) u(r)
dx 1。由 （1-9） ds
u e e xx x
同理可求得沿y和z轴上单位长度得伸长值
e e yy
e e zz
v y w z
28
（2）切应变：变形体不仅在三个坐标方向上有相对伸长(或 压缩)，而且还会产生旋转，即夹角也会发生变化。(见下图) 假设两个正交线元素 MN和MP。受力后， 相对位移分别是du1 和du2。假设： dx=|MN|=|dr1| dy=|MP|=|dr2| MN、MP的相对位移 du1和du2对可由（11）式求出。

σ x τ xy τ xz σ xx σ xy σ xz τ xy σ y τ yz 或σ xy σ yy σ yz τ z τ yz σ z σ xz σ yz σ zz
写法： 采用张量下标记号的应力写法 写法： 把坐标轴x、 、 分别 把坐标轴 、y、z分别 表示， 用x1、x2、x3表示， 或简记为x 或简记为 j (j=1,2,3),
s j = σ j −σm, ( j = 1,2,3)
应力偏张量也有三个不变量： 应力偏张量也有三个不变量：
(3 −13)
J1 = s1 + s2 + s3 = σ1 +σ2 +σ3 −3σM = 0 1 2 2 2 J2 = −(s1s2 + s2s3 + s3s1) = (s1 + s2 + s3 ) 2 J3 = s1s2s3
3
偏张量的第二不变量 J2 有关。 有关。
四、等效应力 1.定义： 定义： 定义 相等的两个应力状态的力学效应相同， 如果假定 J2相等的两个应力状态的力学效应相同，那么
对一般应力状态可以定义： 对一般应力状态可以定义：
σ ≡ 3J2 =
1 2
(σ1 −σ2 )2 + (σ2 −σ3 )2 + (σ3 −σ1)2
三、等斜面上的应力 等斜面：通过某点做平面 ，该平面的法线与三个应力主轴
夹角相等 坐标轴与三个应力主轴一致， 设在这一点取 x1, x2 , x3 坐标轴与三个应力主轴一致， σ 3 则等斜面法线的三个方向余弦为
l1 = l2 = l3 =1/ 3
(3 − 20)
八面体面： 八面体面：
满足（3-20）式的面共有八个，构成 满足（ 20）式的面共有八个， 一个八面体，如图所示。 一个八面体，如图所示。 等斜面常也被叫做八面体面。 等斜面常也被叫做八面体面。 若八面体面上的应力向量用F 表示，则按（ 若八面体面上的应力向量用F8表示，则按（3-3）式有 1 2 2 2 2 2 2 2 F = (σ1l1) + (σ2l2 ) + (σ3l3) = (σ1 +σ2 +σ3 ) (3− 21) 8 3

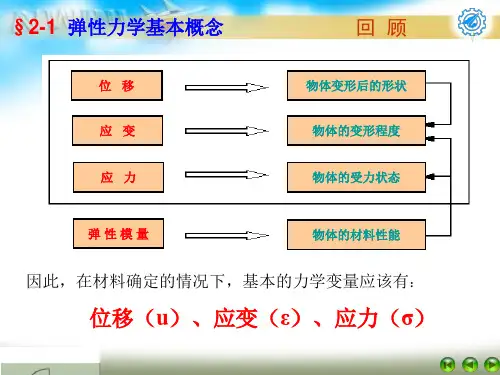
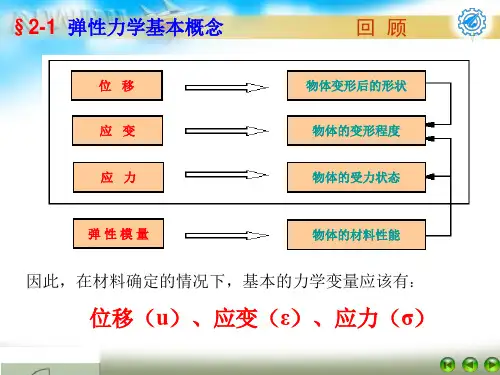
试说明弹性力学中应力,应变,位移三者之间的关系.
应变,就是物体受到外力而产生的局部或全部物理状态变化的现象。

如面团,轻微压一下再松手 ,面团可以恢复原状,如弹簧,在-定拉力或压下,弹簧长度发生变化，去掉这个力, 弹簧恢复原状。

但是,如果这个大了,团不能恢复原状,弹簧也同样不能恢复原状。

应变=单位度伸或缩短量。

励=单位面积所用力。

按照你说的应变与位移,应该与弹簧或具有弹性的物体有关。

这样来说，弹簧的应变就能够计算到位移。

虎克定律。

在工程和机械中，许多结构或构件属于这一类问
题。如直的堤坝和隧道；圆柱形长管受到内水
（油）压力作用；圆柱形长辊轴受到垂直于纵轴
的均匀压力等，均可近似的视为平面应变问题。
y
y
o z
y
o z
y
o
x
o
x
平面应变问题
还有一种情况，当构件的纵向尺寸不很大 但两端面被刚性光滑面固定，不能发生纵向位 移时，若其他条件与上面所述相同，也属于平 面应变问题。 通常，只要是长的等直柱体或板，受到垂直于 其纵轴而且沿长度方向无变化的载荷作用时， 都可以简化为平面应变问题。下面是这种情况 下的应力、应变以及弹性力学的基本方程式。
各个方向上具有相同特性； (4) 线性弹性假定：物体的变形与外来作用力的关系是线性的，
外力去除后，物体可恢复原状； (5) 小变形假定：物体变形远小于物体的几何尺寸。
以上基本假定将作为问题简化的出发点。
§2-2 弹性力学基本方程
回顾
b’ a’
b
zx zx
xz
a
xy
c
zy zy
c’ yz yz
xz
d
研究的基本技巧
采用微小体积元dxdydz 的分析方法（针对任意 变形体）
dz
dy
dx
弹性体的基本假设
回顾
为突出所处理的问题的实质，并使问题简单化和抽 象化，在弹性力学中，特提出以下几个基本假定。
(1) 物质连续性假定：物质无空隙，可用连续函数来描述； (2) 物质均匀性假定：物体内各个位置的物质具有相同特性； (3) 物质(力学)特性各向同性假定：物体内同一位置的物质在
yx
xy
yx
d’
a’

5
数学弹性力学的典型问题主要有一般性理论、柱体扭转和弯曲、 数学弹性力学的典型问题 主要有 一般性理论 、 柱体扭转和弯曲 、 主要有一般性理论 平面问题、变截面轴扭转，回转体轴对称变形等方面 平面问题、变截面轴扭转，回转体轴对称变形等方面。 等方面。 在近代，经典的弹性理论得到了新的发展。例如， 在近代 ， 经典的弹性理论得到了新的发展 。 例如 ， 把切应力的成 对性发展为极性物质弹性力学；把协调方程(保证物体变形后连续，各 对性发展为极性物质弹性力学；把协调方程(保证物体变形后连续， 应变分量必须满足的关系)发展为非协调弹性力学；推广胡克定律， 应变分量必须满足的关系)发展为非协调弹性力学；推广胡克定律，除 机械运动本身外，还考虑其他运动形式和各种材科的物理方程称为本 机械运动本身外 ， 还考虑其他运动形式和各种材科的物理方程称为 本 构方程。对于弹性体的某一点的本构方程， 构方程 。 对于弹性体的某一点的本构方程 ， 除考虑该点本身外还要考 虑弹性体其他点对该点的影响，发展为非局部弹性力学等。 虑弹性体其他点对该点的影响，发展为非局部弹性力学等。 但是，由于课程所限， 但是 ， 由于课程所限 ， 我们在以下几节里仅对弹性体力学作简单 的介绍，为振动部分和波动部分作准备。 的介绍，为振动部分和波动部分作准备。
6
§8.1 弹性体力学－－弹性体的应力和应变简介 弹性体力学－－ －－弹性体的应力和应变简介
弹性体有四种形变 拉伸压缩、剪切、扭转和弯曲。其实， 弹性体有四种形变：拉伸压缩、剪切、扭转和弯曲。其实，最基本的形 四种形变： 变只有两种 拉伸压缩和剪切形变； 两种： 变只有两种：拉伸压缩和剪切形变；扭转和弯曲可以看作是由两种基本形变 的组成。 的组成。
Fn ∆l =Y S l0
其中：Y 称为杨氏模量，反映材料对于拉伸或压缩变形的抵抗能力。 杨氏模量， 其中： 称为杨氏模量 反映材料对于拉伸或压缩变形的抵抗能力。

在弹性力学平面应力问题和平面应变问题中，有限差分法常用于求解偏微 分方程，特别是对于规则的网格划分，计算效率较高。
有限差分法的精度取决于差分格式的选择和网格的划分，同时需要注意数 值稳定性和计算精度的问题。
边界元法
边界元法是一种基于边界积 分方程的数值分析方法，通 过将微分方程转化为边界积
分方程来求解。
变形特点
应用领域
在平面应力问题中，变形主要发生在作用 面上，而在平面应变问题中，变形可以发 生在整个结构中。
平面应力问题在桥梁、建筑和机械等领域 有广泛应用，而平面应变问题在岩土、地 质和材料等领域有广泛应用。
06
结论与展望
结论总结
平面应力问题和平面应变问题在弹性力学中具有重要地位，它们是描述物体在应力作用下的变形和应 力分布的基础。
弹性模量表示材料在受力作用下的刚度，是衡量材料抵 抗弹性变形能力的重要参数。
剪切模量表示材料在剪切力作用下的刚度，与弹性模量 和泊松比有关。
03
平面应变问题
应变状态分析
平面应变条件
应变分量中，只有$varepsilon_{x}$ 、$varepsilon_{y}$和 $gamma_{xy}$不为零，其余分量为 零。
有限元法在弹性力学平面应力问题和平面应变问题中广泛 应用，因为它能够处理复杂的几何形状和边界条件，且计 算精度高。
有限元法的实现需要建立离散化的模型、选择合适的单元 类型和求解算法，并进行数值稳定性和误差分析。
有限差分法
有限差分法是一种基于差分原理的数值分析方法，通过将微分方程转化为 差分方程来求解。
薄板弯曲问题
考虑一个矩形薄板，受到一对相距较远的集中力作用，使板发生弯曲。根据平面应力问题，可以分析 板的应力分布、中性面位置以及挠度等。

弹性力学网络课程第一章绪论内容介绍知识点弹性力学的特点弹性力学的基本假设弹性力学的发展弹性力学的任务弹性力学的研究方法内容介绍：一. 内容介绍本章作为弹性力学课程的引言，主要介绍课程的研究对象、基本分析方法和特点；课程分析的基本假设和课程学习的意义以及历史和发展。

弹性力学的研究对象是完全弹性体，因此分析从微分单元体入手，基本方程为偏微分方程。

偏微分方程边值问题在数学上求解困难，使得弹性力学的基本任务是研究弹性体由于外力载荷或者温度改变，物体内部所产生的位移、变形和应力分布等，为解决工程结构的强度，刚度和稳定性问题作准备，但是并不直接作强度和刚度分析。

本章介绍弹性力学分析的基本假设。

弹性力学分析中，必须根据已知物理量，例如外力、结构几何形状和约束条件等，通过静力平衡、几何变形和本构关系等，推导和确定基本未知量，位移、应变和应力等与已知物理量的关系。

由于工程实际问题的复杂性是由多方面因素构成的，如果不分主次地考虑所有因素，问题是十分复杂的，数学推导将困难重重，以至于不可能求解。

课程分析中使用张量符号描述物理量和基本方程。

目前，有关弹性力学的文献和工程资料都是使用张量符号的。

如果你没有学习过张量概念，请进入附录一学习，或者查阅参考资料。

二. 重点1.课程的研究对象；2.基本分析方法和特点；3.弹性力学的基本假设；4.课程的学习意义；5.弹性力学的发展。

特点：弹性力学，又称弹性理论。

作为固体力学学科的一个分支，弹性力学的基本任务是研究弹性体由于外力载荷或者温度改变，物体内部所产生的位移、变形和应力分布等，为解决工程结构的强度，刚度和稳定性问题作准备，但是并不直接作强度和刚度分析。

构件承载能力分析是固体力学的基本任务，但是对于不同的学科分支，研究对象和方法是不同的。

弹性力学的研究对象是完全弹性体，包括构件、板和三维弹性体，比材料力学和结构力学的研究范围更为广泛。

弹性是变形固体的基本属性，而“完全弹性”是对弹性体变形的抽象。

弹性力学知识点总结弹性力学是力学的一个重要分支，研究固体物体的变形和回复过程。

在本文中，将对弹性力学的几个重要概念和原理进行总结和介绍。

1. 弹性模量弹性模量是衡量固体物体抵抗形变的能力的物理量。

根据胡克定律，弹性模量E可以通过应力σ和应变ε的比值得到：E = σ/ε。

其中，应力表示受力物体单位面积上的力的大小，应变表示物体在应力作用下产生的形变程度。

2. 胡克定律胡克定律是弹性力学的基本原理，描述了理想弹性体在弹性应变范围内的力学行为。

根据胡克定律，应变与应力成正比。

即ε = σ/E，其中E为杨氏模量。

3. 杨氏模量杨氏模量是衡量固体材料抗拉性能的物理量，表示固体在单位面积上受到的拉力与单位长度的伸长量之比。

杨氏模量的定义为：E =F/AΔL/L0，其中F为受力物体的拉力，A为受力物体的横截面积，ΔL为拉伸后的长度增量，L0为原始长度。

4. 泊松比泊松比是衡量固体材料体积收缩性的物理量。

泊松比定义为物体在一轴方向上受力引起的形变量与垂直方向上的形变量之比。

公式表示为：μ = -εlateral/εaxial。

5. 应力-应变关系弹性力学中的应力-应变关系描述了材料在受力作用下的力学行为。

对于弹性材料，应力与应变成线性关系，即应力和应变成比例。

6. 弹性极限弹性极限是指固体材料可以弹性变形的最大程度。

超过弹性极限后，材料将会发生塑性变形。

7. 弹性势能弹性势能是指物体在形变后能够恢复到初始状态的能力。

弹性势能可以通过应变能来表示，其大小等于物体在受力作用下形变所储存的能量。

8. 弹性波传播弹性波是在固体中传播的一种机械波。

根据介质的不同，弹性波可以分为纵波和横波。

9. 斯内尔定律斯内尔定律描述了弹性力学体系中应力与应变之间的关系。

根据斯内尔定律，弹性变形是由应力和应变之间的线性关系所描述的。

10. 压力容器设计弹性力学在压力容器设计中起着重要作用。

根据弹性力学的原理，可以计算压力容器在不同压力下的变形情况，从而设计出满足安全要求的容器结构。

跨学科融合
弹性力学与材料科学、计算科学、生物学等学科的交叉融合，为解决 复杂工程问题提供了新的思路和方法。
数值模拟与计算
随着计算机技术的进步，数值模拟和计算在弹性力学领域的应用越来 越广泛，能够更精确地模拟和预测材料的力学行为。
多尺度分析
从微观到宏观的多尺度分析方法，能够更好地理解材料的微观结构和 宏观性能之间的关系。
它们简化了问题的复杂性，使得 弹性力学成为一种实用的工程工 具。
02
基本假设的局限性
03
限制条件的考虑
在某些情况下，这些假设可能不 成立，例如在处理非均匀、非各 项同性或大变形问题时。
在应用弹性力学时，必须考虑这 些限制条件，以确保结果的准确 性和可靠性。
06 弹性力学的发展趋势和未 来研究方向
弹性力学的发展趋势
非线性力学
随着工程结构的复杂性和非线性特征的增加，非线性力学的研究越来 越受到重视，为解决复杂工程问题提供了新的理论和方法。
未来研究方向
新材料和新结构的力学行为
智能材料的力学行为
研究新型材料和复杂结构的力学行为，探 索其性能优化和设计方法。
研究智能材料的响应机制和调控方法，探 索其在传感器、驱动器和自适应结构等领 域的应用。
生物医学中的弹性力学问题
研究生物组织的力学行为和生理功能，探 索其在生物医学工程和再生医学等领域的 应用。
环境与可持续发展的弹性力学问 题
研究环境因素对材料和结构的影响，探索 其在环保和可持续发展等领域的应用。
THANKS FOR WATCHING
感谢您的观看
材料力学性能的测试
材料弹性模量的测定
通过实验测定材料的弹性模量，可以了解材料的力学性能，为工程设计和材料选择提供依据。

弹性力学中的应变与应力关系弹性力学是物理学中的一个重要分支，主要研究物质体积和形状在外力作用下所发生的变化及其原因。

具体来说，就是通过研究应力（反映外力作用效果的物理量）和应变（反映物质形状和体积改变的物理量）之间的关系，来理解和解释物质的弹性行为。

本文将详细阐述应力和应变在弹性力学中的相关内容。

首先，我们需要明确应力和应变的概念，以便更好地理解二者之间的关系。

应力是弹性力学研究的基本物理量，它可以反映物质内部的力的大小和方向。

根据力的分布特点和作用方式，可以将应力分为正应力和剪应力等类型。

与此同时，应变是描述物体位形变化的物理量，它可以反映物体形状和体积的变化情况。

在弹性力学中，应力和应变之间的基本关系通常用应力--应变法则或哈肋定律来描述。

具体来说，对于同一物体，存在一个比例系数（即弹性模量），当其应力不超过一定值（即弹性限度）时，应力和应变之间达到正比关系，即应力等于弹性模量乘以应变。

这就是典型的线性弹性行为。

当然，应力和应变的关系并不总是线性的。

当物体受到的应力超过一定值后，应变可能导致物体的永久性形变，这就涉及到弹性物质的塑性行为。

塑性行为是弹性力学的另一个重要研究方向，对于理解材料的力学行为有着特别重要的意义。

在实际应用中，不同的应力类型和物质性质可能会引起不同的应变特性。

因此，为了更具体、精确地描述和理解应力和应变之间的关系，出现了多种理论和模型，如弹塑性理论、粘弹性理论、破坏理论等。

这些理论和模型都在一定程度上解释了应力和应变之间的复杂关系，并为理解和控制各种物质的弹性行为提供了重要的理论工具。

总的来说，弹性力学中的应力与应变关系是一个复杂而重要的主题，只有深入理解和掌握应力与应变的特性，才能准确地分析和预测物质在受力情况下的弹性行为。

而对于这些知识的理解和应用，在工程技术、材料科学等领域有着广泛的应用前景。

弹性力学中的应变能和位移能弹性力学是研究固体物体在外力作用下产生的形变和应力分布的一门学科。

在弹性力学中，应变能和位移能是两个重要的概念，它们在分析物体的弹性行为和能量转化过程中起着关键的作用。

应变能是指物体在外力作用下发生形变时所储存的能量。

当外力作用结束后，物体会恢复到原始形状，而储存的应变能也会被释放出来。

应变能的大小与物体的形变程度有关，一般来说，形变越大，应变能也越大。

应变能可以通过应变能密度来表示，即单位体积内的应变能。

应变能密度与物体的体积有关，体积越大，应变能密度也越大。

应变能密度可以用来计算物体在外力作用下的弹性势能，它是弹性力学中的一个重要参数。

位移能是指物体在外力作用下产生的位移所储存的能量。

当外力作用结束后，物体会恢复到原始位置，而储存的位移能也会被释放出来。

位移能的大小与物体的位移程度有关，一般来说，位移越大，位移能也越大。

位移能可以通过位移能密度来表示，即单位体积内的位移能。

位移能密度与物体的体积有关，体积越大，位移能密度也越大。

位移能密度可以用来计算物体在外力作用下的弹性势能，它也是弹性力学中的一个重要参数。

应变能和位移能在弹性力学中具有相似的性质和计算方法，但它们所描述的物理现象略有不同。

应变能主要描述了物体的形变过程，而位移能主要描述了物体的位移过程。

在实际应用中，应变能和位移能常常同时存在，相互转化。

例如，当一个物体被拉伸时，它的形变能会转化为位移能，而当物体恢复到原始形状时，位移能会再次转化为形变能。

这种能量的转化过程是弹性力学中的一个基本原理。

应变能和位移能在工程和科学领域中有广泛的应用。

在结构设计中，通过计算物体的应变能和位移能，可以评估结构的稳定性和安全性。

在材料研究中，通过研究物体的应变能和位移能，可以了解材料的弹性性质和破坏机制。

在地震学中，通过研究地震波的传播和物体的应变能和位移能，可以预测地震的破坏程度和影响范围。

总之，应变能和位移能是弹性力学中重要的概念，它们在分析物体的弹性行为和能量转化过程中起着关键的作用。

弹性力学公式总结弹性力学是研究物体在受力后的形变与应变关系的力学分支。

在弹性力学中，常使用一些公式来描述物体的力学性质。

下面是一些弹性力学中常用的公式：1. 应变（strain）公式：应变是物体在受力后发生的形变相对于初始状态的比例。

应变可以分为线性应变和剪切应变两种类型。

线性应变公式：ε=ΔL/L其中，ε表示线性应变，ΔL表示长度变化，L表示初始长度。

剪切应变公式：γ=Δθ其中，γ表示剪切应变，Δθ表示切变角度的变化。

2. 应力（stress）公式：应力是物体表面上的内力，是由外力作用于物体上的单位面积所产生的力。

法向应力公式：σ=F/A其中，σ表示法向应力，F表示受力，A表示作用面积。

切向应力公式：τ=F/A其中，τ表示切向应力，F表示受力，A表示作用面积。

3.长度变形公式：受力作用下，物体的长度会发生变化，有两种类型：拉伸和压缩。

拉伸变形公式：ΔL=FL/AE其中，ΔL表示长度变化，F表示受力，L表示初始长度，A表示截面积，E表示弹性模量。

压缩变形公式：ΔL=-FL/AE4.钢材弹性模量公式：钢材弹性模量是衡量材料抵抗外力而形变的能力指标。

E=σ/ε其中，E表示弹性模量，σ表示法向应力，ε表示线性应变。

5.线性弹性体系恢复力公式：恢复力是物体受到外力作用后恢复到初始状态所产生的力。

F=kΔx其中，F表示恢复力，k表示弹性系数，Δx表示位移。

6.钢丝绳伸长公式：钢丝绳在受拉伸力作用下会发生伸长。

ΔL=FL/EA其中，ΔL表示伸长长度，F表示受力，L表示初始长度，A表示截面积，E表示钢丝绳的弹性模量。

7.矩形梁弯曲公式：在作用力下，矩形梁会发生弯曲。

M = -EI(d^2y / dx^2)其中，M表示弯曲力矩，E表示杨氏模量，I表示截面惯性矩，y表示梁的纵轴位移，x表示位置。

这些公式是弹性力学中的一些基本公式，用于描述物体在受力后的形变与应变关系，以及恢复力、弯曲等力学性质。

掌握这些公式对于深入理解和研究弹性力学具有重要意义。

x y z
ui
ui x j
dx j
开 v v dx v dy v dz
即
x y z
为：w w dx w dy w dz
x y z
金属塑性成形原理
二、应变及其分量
应变：表示变形大小的物理量
应变
相对应变（条件应变、名义应变、工程应变）— 仅适用于小变形 真实应变（对数应变）— 适用于大变形
则 B的位移分量为A的位移分量加上各方向的位移增量。即：
ui ui ui
ui 为B点相对于A的位移增量
位移增量各方向的偏导与微分之积。按泰勒级数展开、略去二阶以上的
高阶微量，得：
ui
ui
ui
ui
ui x j
（ ui为 u, v, w ；xj为 x, y, z）
展
u u dx u dy u dz
ry
P1
A1
与PC所夹的直角发生了改变。
棱边PA的线应变为 r1 rx r
o
P
rx
A
x
rx
rx
金属塑性成形原理
PA在x轴方向上的线应变为
棱边 PA 向y轴方向偏转的角度为axy
棱边 PC向x轴方向偏转的角度为ayx 两棱边的夹角减小了axy+ ayx （ axy≠ ayx ）
C点在垂直于PC方向偏移了δrt
Є ln l ln 12 0.1823 l0 10
l l0 12 10 0.2
l0
10
误差：9.7%
Є ln l ln 15 0.4054 l0 10
l l0 15 10 0.5
l0
10
误差：23.3%
金属塑性成形原理
2. 相对应变及其分量