几类特殊类型函数的积分

1.1:(y)解: 变形为1 J(x, y) - P 2(x)q 1(y)(x -1)(y -1)运用积分因子方法求解几种特殊类型微分方程方小，数学与计算机科学学院摘 要：针对满足某些条件的微分方程，着重研究如何直接地、有效地求出其积 分因子的方法,从而方便快捷地求出其通解•引言：方程取形式M(x,y)dx • N(x,y)dy =0时的求解问题教材中主要介绍了五 种类型的初等解法，实际上作为基础的还是恰当微分方程，其他类型均可借助积分因子化为这种类型，掌握一些特殊类型的积分因子求法及部分特殊结构微分方 程的积分因子的求法，从而大提高解微分方程的效率和可操作性•一.几种特殊类型结构的微分方程 M(x,y)dx ，N(x,y)dy = 0的积分因子 的求法1 •常见一阶微分方程几种运用积分因子转化成恰当微分方程 可分离变量方程= f (x) ( y)很容易求得积分因子为■-dx求(xy - x)dx (xy x - y -1)dy = 0 的积分因子x(y -1)dx (x -1)(y 1)dy = 0积分因子为方程两边乘以上积分因子得:dy = 0 x-1y -1两边积分得原方程的通解为x y ln(x T)( y T)2 二 C1 .2 线性微分方程—g(x)「g(x ),设f(x ,y )及三连续'试证方程d y _f(x ,y g o 为线性微分方程它有仅依赖于x 的积分因子• 证明：设方程dy - f (x, y)dx =0是线性微分方程.即存在g(x), h(x)使得f(x, y)二 yg(x) h(x)这样M 二-f (x, y)二-yg(x) -h(x), N = 1, .:M :N.:y；xN所以，方程具有积分因子C-g(x)dx.二=e这即证明了方程有仅依赖于x 的积分因子.例2 :解方程:(ycosx-ysinx)dx (ysinx xc°sx)dy = 0解： • .M = ycosx - xsinx, N = ysinx xcosx:N ：:M=y于是积分因子为ydy yu =e 二e•••通解为e y (xcosx ysinx-sinx)=C” __n-(n -J p(x)dx)1.3 伯努利微分方程方程的积分因子是'=y e证明: 设伯努利方程为改写为dy _ p(x)ydx _ q(x) y n dx 二 0,乘以y』得y 』dy - p(x)y 1』dx _q(x)dx = 01 _n 1 _od(y )一(1 一 n)p(x)y dx —(1 - n)q(x)dx = 0,再乘以_(1』)p(x)dxe41』)p(x)dxe(1 - n)q(x)dx 二 0,_(1_n) p(x)dx」 dx ] = 0.少=p( x) y q( x)y ndx p( )y q( )y 5式0,1)11-(1-n) fp(x)dx [d(y )-(1 - n)p(x)y dx]-e1 _n _(1 _n [ p ( s) dxd[y e]—d[ .(1 - n)q(x)e这是全微分方程，因此所求积分因子是■— 」n_]p(x)dx)y e例 求3 • y 二(cosx —sinx) y 2的积分因子及通解 dx解：积分因子/、.np(x )dx/ 菽(x, y) = y ey e原方程两边同乘以 y °e ，并化为对称式为y 2e"dy y °e*dx = (cosx -sin x)e»dx凑微分为：d( —e^y J) = d(e 亠 sin x)两边同时求积分得：e^si nx e "^y = C1.4齐次微分方程M(x,y)dx • N(x,y)dy =0当xM • yN = 0时有积分因子(・N) xxM N - MNex-xN(xM yN)2由于方程是齐次的，我们不妨设 M(x, y)和N(x, y)是m 次齐次函数，则有.:M:x;:M*x匕cN 冰* y = m • M 与—*x — * y = m * N ex cy由上:M :N :N :M yNyMxMxNcycyexex从而得到：因此方程 M (x, y)dx N (x, y)dy =0当xM ■ yN = 0时有积分因子-1xM yNxM yN证明由于切(x,y) = ^<jN(x,yr^^xM +yN xM +yN则有.:MNN(xM yN) - M (x N y )；：(」M) _ ：：y jy ；:y訶一 (xM yN)2MNyN MN - yM * —dycy-(xM +yN)2J同理，例(y 2「3x 2)dy 2x y d x 0yy 2 -0 1 y 3-0 1 N(y)P(x)解此为齐次方程，故有积分因子J =1 (Px Qy) =1 (2x 2y y 3 _3x 2y) =1 (y 3 _x 2y)乘以积分因子，原方程化为■2222』 32[2x (y -x )]dx [(y -3x ) (y -xy)]dy = O这是一个全微分方程，它的通解为x 2x dx 0 2 2 0y - x2 2 2In y -In(y -x ) In y = C 其中C 为常数2、具有特殊结构的一阶微分方程 M (x, y)dx • N(x, y)dy = 0的积分因子的求法 2.1 方程 M (x)N(y)dx P(x)Q(y) =0有积分因子：显然,直接验证可得= 1旷 N(y)P(x)为上式的积分因子..f (x)dx • ■ (y)dy若(：：P).(：y) -(：Q) (：：X )二 Qf (x) -P “y)」「I-是方程的积分因子解：因为(：：P).(：：y) -(9) (；:x)2=6y x (2x 6y ) =(x 6y 2) 2(3y x)2 21 2 2一(x6xy)(-—)-(3y xy)(——)xy1 = Q(-—)-P()x y故有积分因子dx1 2xy于是原u[f(u)-gL )]dx g(」)d —0(1)(3 x 1 y)dx -(x y 1 2) 6)dy 二 0 (3 x)dx-6dy [(1 y) dx -(x y 2)dy] = 0这是一个全微分方程，积分得出通解为3ln x - 6y x y = C或 3yln x - 6y 2 x =cy2.2 设函数f(u),g(u)连续、可微且, 则方程yf(xy)dx - xg(xy)dy =0有积分因子:xy[f (xy)-g(xy)]证明:令沁二」,则原方程可化为，但对于一个较复杂的方程，往往不容易直接求得它的积分因(xy[ f (xy) -g(xy)]子•(1)式两边同乘以fT 齐得显然(2)为恰当方程，故(1)有积分因子 」[f(」)_g(」)]”因而原方程有积分因子dxg(Jdu = 01 2x故有积分因子■' - 1 2 2 2 2{xy[(x 2y 21) -(x 2y 2 一1)]}1乘上 —得2xy^xy 2dx 丄 dx -x 2ydy 2 2x 22（xy 2dx x 2ydy ） 2（空-包）=0x y二.针对满足某些条件的微分方程，运用积分因子方法求出通解但是如果把它的左端分成几组，比如分成两组：（M 1dx N 1dy ） （M 2dx N 2dy ） =0（3）后,可分别求得各组的积分因子 叫和^,也就是如果有J 1/l 2使SM 1 叫 N j dy 二J2M 2 」2N 2dy 二 d 」2于是借助于7,常可求得Mdx • NdY =0的积分因子.为了说明这一点，先注意 下一事实•如果「是Mdx • NdY =0的一个积分因子，且 ％」Ndy 二d ，,则」^1）也是Mdx • NdY =0的积分因子.此处 C 1）是，的任一连续函数. 事实上」3） Mdx "_ （」）Ndy 二（」）（」Mdx 订：Ndy ）二（Jd 」 其中①表示©的一个原函数•据此知,对于任意的函数 V ）及7（\）、2：：（」2）都分别是⑶的第一组和第 二组的积分因子.函数有着广泛选择的可能性.若能选择：：使亠=U 1 C\）「f ）则卩就既是（3）的第一组也是第二组的积分因子.因而也就是Mdx • NdY =0的积分因子.3y 2 x例:解方程：( 3x )dx - (1 )dy =0x y解:原方程改写为3(上dx dy) (3x2—)dy = 0x y显然丄i 二x,鋼=xy,丄2 二y,丄2 二x‘ y为使x \xy)二y (x3y),只须取丫")二"2,「(")= J于是求得原方程的一个积分因子：」二x (xy)二y (x3y)二x3y2而以之乘方程的两端，便得2 2 ^52、，，32 6x y 3x y )dx (x y x y)dy = 0于是/ \3 z 3 2P(x, y) = 0 (x2y3 +3x5y2)dx= —+ —(取c = 0) •••通解为(xy)3 . (x3y)2结论1 :设u(x, y)是方程M (x, y)dx N(x,y)dy =0的积分因子，从而求得可微方程U(x,y)使dU =亠(Mdx • Ndy) /(x,y)=曲(U )时」i(x,y)也是方程的积分因子,其中：(t)是t的可微函数.结论2:设u (x, y) , U2(x, y)是方程M (x, y)dx N(x, y)dy = 0的两个积分因子，且 F =常-2数，则匚1二C (任意常数)是方程的通解•^2结论3:假设当方程M(x,y)dx ・N(x,y)dy=O为齐次方程时，且为恰当方程，则它的通解可表示为xM (x, y)dx ■ yN(x, y)dy =c (c为任意常数).参考文献(顶格、宋体、小四号加粗)：[1] 刘广珠.高中生考试焦虑成因分析[J].陕西师大学报(哲社版)，1995,24( 1): 161-164.(参考文献序号在文中采用右上标注的方式，用数字加方括号表示，如[1]，[2]，…，序号应连续。

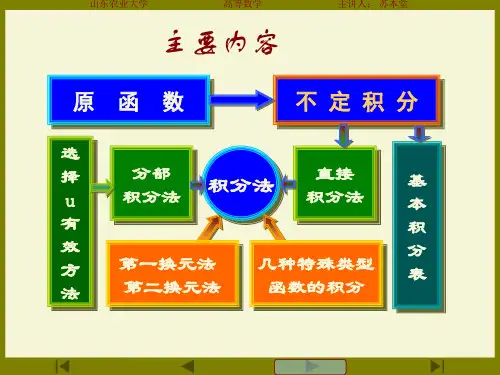
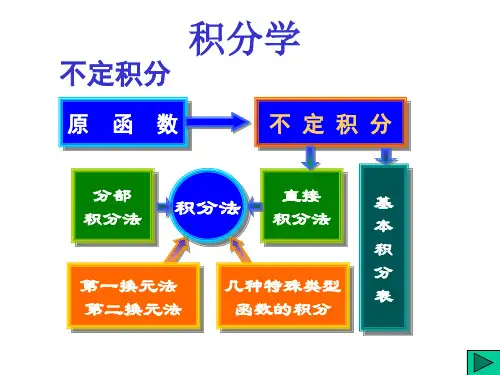
几种特殊类型函数的积分一、有理函数的不定积分1.化有理函数为简单函数两个多项式的商所表示的函数)(x R 称为有理函数，即mm m m m nn n n n b x b x b x b x b a x a x a x a x a x Q x P x R ++++++++++==------122110122110)()()( （1） 其中n 和m 是非负整数；n a a a a ,,,,210 及m b b b b ,,,,210 都是实数，并且0,000≠≠b a ．当（1）式的分子多项式的次数n 小于其分母多项式的次数m ，即m n <时，称为有理真分式；当m n ≥时，称为有理假分式．对于任一假分式，我们总可以利用多项式的除法，将它化为一个多项式和一个真分式之和的形式．例如12)1(112224+++-=+++x x x x x x ． 多项式的积分容易求得，下面只讨论真分式的积分问题．设有理函数（1）式中m n <，如果多项式)(x Q 在实数围能分解成一次因式和二次质因式的乘积：μλβα)()()()()(220s rx x q px x b x a x b x Q ++++--= ．其中s r q p b a ,,,,,,, 为实数；042<-q p ，…，042<-s r ；,,,βα μλ,, 为正整数，那末根据代数理论可知，真分式)()(x Q x P 总可以分解成如下部分分式之和，即βααα)()()()()(1121b x B a x A a x A a x A x Q x P -++-++-+-=-λββ)()(21112q px x N x M b x B b x B ++++-++-+-μλλλ)()(21121222s rx x S x R q px x N x M q px x N x M ++++++++++++++-srx x S x R s rx x S x R +++++++++-21222)(μμμ ． （2） 其中i i i i i i S R N M B A ,,,,,,, 都是待定常数，并且这样分解时，这些常数是唯一的．可见在实数围，任何有理真分式都可以分解成下面四类简单分式之和： （1）a x A - ， （2）k a x A )(- （k 是正整数，2≥k ）， （3）qpx x B Ax +++2（042<-q p ）， （4）kq px x B Ax )(2+++ （k 是正整数，04,22<-≥q p k ）．2. 有理函数的不定积分求有理函数的不定积分归结为求四类简单分式的积分．下面讨论这四类简单分式的积分．（1）C a x A a x d ax A dx a x A +-=--=-⎰⎰ln )(1，（2）C a x k A a x d a x A dx a x A k k k+-⋅--=--=---⎰⎰1)(11)()()(， （3）dx qpx x B Ax ⎰+++2（042<-q p ）． 将分母配方得)4()2(222p q p x q px x -++=++，作变量代换2px u +=，则du dx p u x =-=,2；由于04,0422>-<-p q q p ，记224a p q =-，于是 du a u B pu A dx p q p x B Ax dx qpx x B Ax ⎰⎰⎰++-=-+++=+++22222)2()4()2( du au ApB du a u Au ⎰⎰+-++=22222C au a Ap B a u A +-++=arctan 2)ln(222 C pq p x p q Ap B q px x A +-+--+++=22242arctan 42)ln(2．（4）dx q px x B Ax k⎰+++)(2 (04,22<-≥q p k )．作变量代换2px u +=，并记224a p q =-，于是⎰⎰⎰+-++=+++du a u ApB du a u Au dx q px x B Ax k k k )(2)()(22222． 其中第一个积分C a u k A a u d a u A du a u Au k k k ++⋅--=++=+--⎰⎰122222222)(1)1(2)()(2)(． 第二个积分可通过建立递推公式求得．记 ⎰+=kk a u du I )(22 利用分部积分法有⎰⎰++++=+=12222222)(2)()(k kk k a u du u k a u u a u du I du a u a a u k a u u k k ⎰++-+++=12222222)()(2)(122222)(+-++=k k kkI a kI a u u ．整理得 k k k I ka k a u u k a I 22221212)(21-++⋅=+． 于是可得递推公式]2232)()1(21[111222----++⋅-=k k k I k k a u u k a I ． （3）利用（3）式，逐步递推，最后可归结为不定积分C a u aa u du I +=+=⎰arctan 1221． 最后由2px u +=全部换回原积分变量，即可求出不定积分⎰+++dx q px x B Ax k )(2． 例1 求⎰++-dx x x x 22)32(1． 解⎰⎰++-+=++-dx x x dx x x x 2222]2)1[(21)32(1 ⎰⎰+-++=2222)2(2)2(1u du du u u x u]2212121[212)2(21222⎰+++⋅⨯⨯-+-=u du u u uC u u u +-++-=2arctan 221)2(212`C x x x x ++-+++-=21arctan 221)32(222．例2 求dx x x ⎰-2)1(1． 解 因为2)1(1-x x 可分解为1)1()1(122-+-+=-x C x B x A x x ． 其中A ，B ，C 为待定系数．可以用两种方法求出待定系数．第一种方法：两端去掉分母后，得)1()1(12-++-=x Cx Bx x A ． （4）即 A x C A B x C A +--++=)2()(12由于（4）式是恒等式，等式两端2x 和x 的系数及常数项必须分别相等，于是有⎪⎩⎪⎨⎧==--=+1020A C A B C A ， 从而解得 1=A ，1=B ，1-=C ．第二种方法：在恒等式（4）中，代入特殊的x 值，从而求出待定系数．如令0=x ，得1=A ；令1=x ，得1=B ；把A ，B 的值代入（4）式，并令2=x ，得C 2211++=，即1-=C ．于是⎰⎰---+=-dx x x x dx x x )11)1(11()1(122 ⎰⎰⎰---+=dx x dx x dx x 11)1(112C x x x +----=1ln 11ln ． 例3 求⎰+-+dx x x x 22)1)(1(22． 解 因为1)1(1)1)(1(2222222++++++-=+-+x E Dx x C Bx x A x x x ， 两端去分母得)1)(1)(()1)(()1(22222+-++-+++=+x x E Dx x C Bx x A x234)2()()(x B E D A x D E x D A +-++-++=)()(C E A x C B E D --++-+-+．两端比较系数得 ⎪⎪⎪⎩⎪⎪⎪⎨⎧=--=+-+-=+-+=-=+220200C E A C B ED BE D A D E D A ，解方程组得1=A ，2-=B ，0=C ，1-=D ，1-=E ，故dx x x x x x dx x x x )11)1(211()1)(1(2222222⎰⎰++-+--=+-+ dx x x dx x x dx x ⎰⎰⎰++-+--=11)1(211222C x x x x +-+-++-=arctan )1ln(21111ln 22 C x x x x +-+++-=arctan 1111ln22． 例4 求⎰+-+dx x x x 6532． 解 因为32)3)(2(36532-+-=--+=+-+x B x A x x x x x x ，两端去分母得 )2()3(3-+-=+x B x A x ． 令2=x ，得5-=A ；令3=x ，得6=B ．于是Cx x dx x x dx x x x +---=---=+-+⎰⎰2ln 53ln 6)2536(6532C x x +--=56)2()3(ln ． 从理论上讲，多项式)(x Q 总可以在实数围分解成一次因式和二次质因式的乘积，从而把有理函数)()(x Q x P 分解为多项式与四类简单分式之和，而简单分式都可以积出．所以，任何有理函数的原函数都是初等函数．但我们同时也应该注意到，在具体使用此方法时会遇到困难．首先，用待定系数法求待定系数时，计算比较繁琐；其次，当分母的次数比较高时，因式分解相当困难．因此，在解题时要灵活使用各种方法．例5 求dx x x x x x ⎰+++++12232． 解dx x dx x dx x x x x dx x x x x x ⎰⎰⎰⎰+++=+++++=+++++1111)1)(1()1()1(12222232C x x +++=arctan 1ln ．例6 求dx x x x x ⎰+-+-)54)(44(122 ．解 dx x x x x x x x x dx x x x x ⎰⎰+-+-+--+-=+-+-)54)(44()44()54()54)(44(1222222dx x x dx x x ⎰⎰+--+-=54144122 ⎰⎰-+----=)2(1)2(1)2()2(122x d x x d xC x x +----=)2arctan(21．例7 求dx x ⎰+114． 解⎰⎰⎰+--++=+dx x x dx x x dx x 112111211142424dx x x x dx x x x ⎰⎰+--++=2222221112111121 )1(2)1(121)1(2)1(12122xx d xx x x d x x +-+--+-=⎰⎰C x x x x x x ++++---=1212ln 24121arctan 221222．二、三角函数有理式的积分由三角函数和常数经过有限次四则运算所构成的函数称为三角函数有理式．因为所有三角函数都可以表示为x sin 和x cos 的有理函数，所以，下面只讨论)cos ,(sin x x R 型函数的不定积分．由三角学知道，x sin 和x cos 都可以用2tan x 的有理式表示，因此，作变量代换2tan x u =，则222122tan12tan22sec 2tan22cos 2sin 2sin u u x xx x x x x +=+===, 22222222112tan 12tan 12sec 2tan 12sin 2cos cos u u x xx x x x x +-=+-=-=-=． 又由u x arctan 2=，得du u dx 212+=，于是 ⎰⎰++-+=du u u u u u R dx x x R 222212)11,12()cos ,(sin ． 由此可见，在任何情况下，变换2tan x u =都可以把积分dx x x R )cos ,(sin ⎰有理化．所以，称变换2tan x u =为万能代换．例8 求dx xx ⎰++cos sin 11． 解 设2tan x u =，则du u du u u u u u dx x x ⎰⎰⎰+=+⋅+-+++=++1112111211cos sin 112222C xC u ++=++=2tan1ln 1ln ． 例9 求dx xx ⎰-+cos 1sin 1．解 设2tan x u =，则du u u u u du u u u u u dx xx ⎰⎰⎰+++=+⋅+--++=-+)1(2)1(12111121cos 1sin 12222222du u u du u ⎰⎰++=)1(2122du u u u u du u ⎰⎰+-++=)1()1(212222⎰⎰⎰+-+=du u u du u du u 2212121C u u u ++-+-=)1ln(ln 212 C x x x +--=)2ln(sec 2cot 2tan ln 22．虽然利用代换2tan x u =可以把三角函数有理式的积分化为有理函数的积分，但是，经代换后得出的有理函数积分一般比较麻烦．因此，这种代换不一定是最简捷的代换．例10 求dx xx ⎰+sin 1sin ． 解 dx x x x dx xx x dx x x ⎰⎰⎰-=--=+222cos sin sin sin 1)sin 1(sin sin 1sin dx xx dx x x ⎰⎰--=222cos cos 1cos sin ⎰⎰⎰+--=dx dx x x d x 22cos 1cos cos 1C x x x ++-=tan cos 1． 例11 求dx x ⎰+2cos 311． 解x d x dx x x dx xtan 4tan 13sec sec cos 3112222⎰⎰⎰+=+=+ C x +=)2tan arctan(21．三、简单无理函数的积分（一）),(nb ax x R +型函数的积分),(u x R 表示x 和u 两个变量的有理式．其中a ，b 为常数．对于这种类型函数的积分，作变量代换u b ax n=+，则a b u x n -=，du anu dx n 1-=，于是 du a nuu a b u R dx b ax x R n n n 1),(),(-⋅-=+⎰⎰ ． （5）（5）式右端是一个有理函数的积分．例12 求⎰++dx x 3211． 解 令u x =+32，则23-=u x ，du u dx 23=，于是⎰⎰⎰++-=+=++du u u du u u dx x 111313211223 C u u u du u u +++-=++-=⎰)1ln 2(3)111(32C x x x +++++-+=333221ln 323)2(23．例13 求dx xx ⎰+31．解 为了同时去掉被积函数中的两个根式，取3和2的最小公倍数6，并作变量代换u x =6，则6u x =，du u dx 56=，23u x =，3u x =，于是du u u du u u dx xx⎰⎰⎰+=+=+1616128283u d uu u u ⎰++-+-=)111(62246 C u u u u u ++-+-=arctan 6625676357 C x x x x x x ++-+-=66656arctan 6625676．（二）),(ndcx b ax x R ++型函数的积分 这里),(u x R 仍然表示x 和u 两个变量的有理式．其中d c b a ,,,为常数．对于这种类型函数的不定积分，作变量代换u d cx b ax n=++，则nn cu a b du x --=，du cu a bc ad nu dx n n 21)()(--=-，于是du cu a bc ad nu u cu a b du R dx d cx b ax x R n n n nn21)()(),(),(--⋅--=++-⎰⎰． （6） （6）式右端是一个有理函数的积分．例14 求dx xx x ⎰+11． 解 令u x x =+1, 则112-=u x ，du u u dx 22)1(2--=，于是 duu u du u u du u u u u dx x x x ⎰⎰⎰⎰-+--=--=--⋅-=+111212)1(2)1(112222222C u u u du u ++---=-+-=⎰11ln 2)111(22C u u u +--++-=1ln )1ln(222 C x x xx x++++++-=ln )11ln(212．例15 求dx x x ⎰-+342)1()1(1．解 ⎰⎰+--+=-+dx x x x x dx x x 334211)1)(1(1)1()1(1，令ux x =+-311，则311u x x =+-，3311u u x -+=，du u u dx 232)1(6-=， 于是du u dx x x x dx x x ⎰⎰⎰=+--=-+23234212311)1(1)1()1(1C x x C u +-+-=+-=3112323．。