固体物理学5能带理论
- 格式:doc
- 大小:800.55 KB
- 文档页数:18






能带理论(Energy band theory)的概念摘要: 本文运用能带理论就晶体中的电子行为作一些讨论, 以期对能带理论的概念更细致的把握。
关键词: 能带理论能带理论的概念能带理论(Energy band theory)是研究晶体(包括金属、绝缘体和半导体的晶体)中电子的状态及其运动的一种重要的近似理论。
它把晶体中每个电子的运动看成是独立的在一个等效势场中的运动,即是单电子近似的理论;对于晶体中的价电子而言,等效势场包括原子核的势场、其他价电子的平均势场和考虑电子波函数反对称而带来的交换作用, 是一种晶体周期性的势场。
能带理论认为晶体中的电子是在整个晶体内运动的共有化电子, 并且共有化电子是在晶体周期性的势场中运动。
1、电子的共有化运动我们先来讨论电子的共有化运动。
我们知道,由于原子核对电子的静电引力,使得电子只能围绕原子核在一定的轨道上运动。
由于电子在空间运动的范围受到限制,电子在能量上就呈现出不连续的状态, 电子的能量只能取彼此分立的一系列可能值——能级。
晶体是由大量的原子在空间有规则地周期性地排列而成的。
相邻原子间距只有几个埃的能量级,例如,硅的原子间距为4.2 埃。
因此,晶体中的原子状态和孤立原子中的电子状态不同,特别是外层电子的状态会有显著的变化。
原子中的电子分列在内外层电子轨道上, 每一层轨道对应于确定的能量。
当原子间相互接近形成晶体时,不同原子的内外层个电子轨道之间就有一定的交迭,相邻原子最外层轨道上交迭最多,内层轨道交迭较少。
图一图二当原子组成晶体后,由于电子轨道间的交迭,电子不再完全局限于某一个原子中,他可以由一个原子转移到相邻的原子上去,而且可以从相邻的原子再转移到更远的原子上去,以致任何一个电子可以在整个晶体中从一个原子转移到另一个原子,而不再专属于哪一个原子所有,这就是晶体中电子共有化运动。
应该注意到,不同原子的相似轨道才有相近的能量,电子只能在相似轨道上进行转移。
因此, 产生共有化运动是由于不同原子的相似轨道间的交迭而引起的。

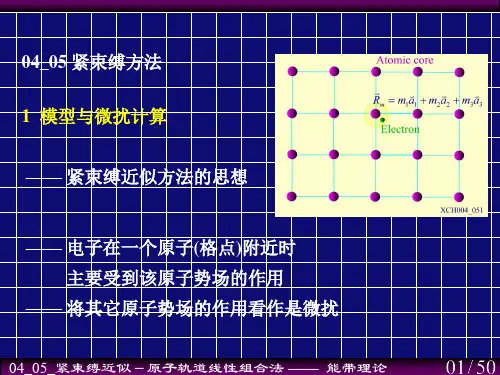

第六章 能带理论 (习题参考答案)1. 一矩形晶格,原胞长10a 210m-=⨯,10b410m-=⨯(1)画出倒格子图(2)以广延图和简约图两种形式,画出第一布里渊区和第二布里渊区(3)画出自由电子的费米面(设每个原胞有2个电子)解:(1)因为a =a i=20A i b =b j=40A j倒格子基矢为12a iA*=, 014bj A*=以a *b *为基矢构成的倒格子如图。
由图可见,矩形晶格的倒格子也是矩形格子。
(2)取任一倒格子点O作为原点,由原点以及最近邻点A i,次近邻点B i的连线的中垂线可以围成第一,第二布里渊区,上图这就是布里渊区的广延图。
如采用简约形式,将第二区移入第一区,我们得到下图。
(3) 设晶体中共有N个原胞,计及自旋后,在简约布里渊区中便有2N个状态。
简约布里渊区的面积21()8A a bA ***-=⨯=而状态密度22()16()N g K N A A*==当每个原胞中有2个电子时,晶体电子总数为 22()216Fk FN g k kdk N k ππ=⨯=⎰所以1/211111()0.2()210()8F k A m π---=≈=⨯这就是费米圆的半径。
费米圆如下图所示2. 已知一维晶体的电子能带可写成()2271cos cos 2,88E k ka ka m a ⎛⎫=-+⎪⎝⎭式中a 是晶格常数。
试求: (i )能带的宽度;(ii )电子在波矢k 状态时的速度; (iii )能带底部和顶部电子的有效质量。
()()()()()()()()22222m in 2m ax 22m ax m in 22222m in 71cos cos 2,8811cos 24400,2;221sin 24sin 404k i E k ka ka m a ka m a k E k E am a E E E m am aii v E kv ka ka m aiii E k kk E E mπ⎛⎫=-+⎪⎝⎭⎡⎤=--⎢⎥⎣⎦====∆=-=∴=∇∴=--==+解:当时,当时,能带的宽度为:在能带底部,将在附近用泰勒级数展开,可得:()()()22m in 22m ax 22m ax 220342203k E mm m E k k E E k mk E mm m ππδδδ****=+∴===-=+∴=-在能带顶部,将在附近用泰勒级数展开,令k=+k 可得:aa3. 试证明:如果只计及最近邻的相互作用,用紧束缚方法导出的简单立方晶体中S 态电子的能带为()2cos 2cos 2cos 2s x y z E k E A J ak ak ak πππ⎡⎤=--++⎣⎦并求能带的宽度。
第五章固体的能带理论1.布洛赫电子论作了哪些基本近似?它与金属自由电子论相比有哪些改进?解:布洛赫电子论作了3条基本假设,即①绝热近似,认为离子实固定在其瞬时位置上,可把电子的运动与离子实的运动分开来处理;②单电子近似,认为一个电子在离子实和其它电子所形成的势场中运动;③周期场近似,假设所有电子及离子实产生的场都具有晶格周期性。
布洛赫电子论相比于金属自由电子论,考虑了电子和离子实之间的相互作用,也考虑了电子与电子的相互作用。
2.周期场对能带形成是必要条件吗?解:周期场对能带的形成是必要条件,这是由于在周期场中运动的电子的波函数是一个周期性调幅的平面波,即是一个布洛赫波。
由此使能量本征值也称为波矢的周期函数,从而形成了一系列的能带。
3.一个能带有N个准连续能级的物理原因是什么?解:这是由于晶体中含有的总原胞数N通常都是很大的,所以k的取值是十分密集的,相应的能级也同样十分密集,因而便形成了准连续的能级。
4.禁带形成的原因如何?您能否用一物理图像来描述?解:对于在倒格矢K中垂面及其附近的波矢k,即布里渊区界面附近的波矢k,由于h采用简并微扰计算,致使能级间产生排斥作用,从而使)E函数在布里渊区界面处“断开”,(k即发生突变,从而产生了禁带。
5.近自由电子模型与紧束缚模型各有何特点?它们有相同之处?解:所谓近自由电子模型就是认为电子接近于自由电子状态的情况,而紧束缚模型则认为电子在一个原子附近时,将主要受到该原子场的作用,把其它原子场的作用看成微扰作用。
这两种模型的相同之处是:选取一个适当的具有正交性和完备性的布洛赫波形式的函数集,然后将电子的波函数在所选取的函数集中展开,其展开式中有一组特定的展开系数,将展开后的电子的波函数代入薛定谔方程,利用函数集中各基函数间的正交性,可以得到一组各展开系数满足的久期方程。
这个久期方程组是一组齐次方程组,由齐次方程组有解条件可求出电子能量的本征值,由此便揭示出了系统中电子的能带结构。

固体能带理论(学号:1120120332 姓名:马英 )摘要:固体能带理论是凝聚态物理学的重要组成部分,在密度泛函理论基础上,对固体能带理论70年来的发展作简单的论述和分析,并阐述固体能带计算各种方法的物理原理及共典型应用。
关键词:固体、半导体、金属、单电子、准粒子、离子、晶体、应力一、自由电子模型在这个模型中,电子与电子,晶格与电子之间的相互作用被忽略.也可以这样说晶格对电子的影响视为平均势场索米菲理论:自由电子模型+费米狄拉克分布 解释: 1.电子气热容量 2.电子发射3.电子气的顺磁与逆磁效应 二、3个重要近似和周期性势场 绝热近似:由于原子核质量比电子的质量大得多,电子的运动速度远大于原子核的运动速度,即原子核的运动跟不上电子的运动。
所以在考虑电子的运动时,认为原子实不动。
单电子近似::一个电子在离子实和其它电子所形成的势场中运动。
又称hartree-Fock 自洽场近似。
周期场近似:原子实和电子所形成的势场是周期性的。
周期性势场 :单电子近似的结果:周期性势场(周期为一个晶格常数)。
3. Bloch 波(1)Bloch 定理:在周期性势场中运动的电子,气波函数由如形式 :其中u 具有晶格的周期性,即(2)Bloch 波的性质a.波函数不具有晶体周期性,而(k 为实数时)电子分布几率具有晶格的周期性b.当k 为虚数,描写电子的表面态,k =is(s>0)(S 小于0时无意义.)c. 周期边界条件:)()(r u e r rk i⋅=ϕ)()(332211a n a n a n r u r u+++=)()(x u e x ika=ϕ222|)(||)(||)(|x u a x x =+=ϕϕ)()(x u e x sx-=ϕ)()(x Na x ϕϕ=+)()(ˆ)(x e x TNa x ikNaϕϕϕ==+)()(a x x n K k k +=+ϕϕd. 波矢相差倒格矢整数倍的Bloch 波等效.因此把波矢限制在第一布区内.且第一布区内的分立波矢数为晶体原胞数N 可容纳的电子数为2N.三、单电子近似下电子的能量状态. 电子满足的薛定谔方程:在克龙尼克—潘纳模型下:周期运动中的离子许可能级形成能带.能带之间存在不许可能量范围称为禁带,且禁带位于布区边界. 关于能带的讨论:1.在原理布区边界的区域内, 电子的能量可粗略的视为自由电子的能量.2.在布区边界上,电子能量不连续,出现禁带,禁带的宽度为:3.在同一能带中,能量最大的地方称为带顶,能量最小的地方称为带底,能量最大值与最小值之差称为能带宽度.带底附近能量曲线是一开口向上的小抛物线,带顶附近,能量曲线是一开口向下的小抛物线.4.能量是k 的周期函数,周期为倒格子矢量.5.能量曲线的三种表示方法:(1)第一布区图 (2)扩展区图 (3)周期区图6.E 为k 的多值函数,以视区别 表示第s 个能带的能量,而k 表示在第一布区中取值. 7.每个能带可容纳2N 个电子,第一布区分立k 的数目为N. 考虑自旋2N.)()()()()())(2(22x u e x V na x V x E x x V m ikx ==+=+∇-ψψψ其中: a -b -0c a 0V cb a +=禁带a πa π232V 22V 12V m k E 222 =|2|g l l V E =禁带a πa π232V 22V 12V )(k E s ⎪⎪⎪⎪⎭⎫ ⎝⎛=N Na a ππ22四、费米面的构造费米面是电子的占据态与非占据态之间的分界面.晶体(特别是导体)的许多性质决定于费米面附近电子的行为.因此费米面的形状十分重要。
能带理论是研究固体中电子运动规律的一种近似理论。
固体由原子组成,原子又包括原子实和最外层电子,它们均处于不断的运动状态。
为使问题简化,首先假定固体中的原子实固定不动,并按一定规律作周期性排列,然后进一步认为每个电子都是在固定的原子实周期势场及其他电子的平均势场中运动,这就把整个问题简化成单电子问题。
能带理论就属这种单电子近似理论,它首先由F.布洛赫和L.-N.布里渊在解决金属的导电性问题时提出.能带和能带隙具体的计算方法有自由电子近似法、紧束缚近似法、正交化平面波法和原胞法等。
前两种方法以量子力学的微扰理论作为基础,只分别适用于原子实对电子的束缚很弱和很强的两种极端情形;后两种方法则适用于较一般的情形,应用较广。
能级(Enegy Level):在孤立原子中,原子核外的电子按照一定的壳层排列,每一壳层容纳一定数量的电子。
每个壳层上的电子具有分立的能量值,也就是电子按能级分布。
为简明起见,在表示能量高低的图上,用一条条高低不同的水平线表示电子的能级,此图称为电子能级图。
能带(Enegy Band):晶体中大量的原子集合在一起,而且原子之间距离很近,以硅为例,每立方厘米的体积内有5×1022个原子,原子之间的最短距离为0.235nm。
致使离原子核较远的壳层发生交叠,壳层交叠使电子不再局限于某个原子上,有可能转移到相邻原子的相似壳层上去,也可能从相邻原子运动到更远的原子壳层上去,这种现象称为电子的共有化。
从而使本来处于同一能量状态的电子产生微小的能量差异,与此相对应的能级扩展为能带。
禁带(Forbidden Band):允许被电子占据的能带称为允许带,允许带之间的范围是不允许电子占据的,此范围称为禁带。
原子壳层中的内层允许带总是被电子先占满,然后再占据能量更高的外面一层的允许带。
被电子占满的允许带称为满带,每一个能级上都没有电子的能带称为空带。
价带(Valence Band):原子中最外层的电子称为价电子,与价电子能级相对应的能带称为价带。
5.2恒定电场磁场作用下布洛赫电子的运动 1 恒定电场作用下布洛赫电子的运动 恒定电场中布洛赫电子在k 空间的振荡以一维晶体为例讨论在恒定电场中布洛赫电子的运动。
设电场力F = - qE ( E 为电场强度 ) 沿x 轴正方向,根据F dtdk = (5.2.1)布洛赫电子在k 空间作匀速运动,在准经典运动中,布洛赫电子没有足够的能量从一个能带跃迁到另一个能带,只能保持在同一个能带中运动。
由于布洛赫电子的能量E (k ) 是k 空间的周期函数,布洛赫电子在k 空间作匀速运动时,它的能量沿E (k ) 函数曲线周期性变化。
若用约化布里渊区表示,当电子运动到布里渊区边界 (k = π/a ) 时,由于k = -π/a 与k = π/a 相差倒格矢 2π/a ,实际描述同一个量子态,因此布洛赫电子从k = π/a 运动出简约区,实际上同时从k = -π/a 运动进入简约区,布洛赫电子在k 空间作来回循环运动。
恒定电场中布洛赫电子在r 空间的振荡布洛赫电子在k 空间作来回循环运动,能量随时间作周期性变化,由于布洛赫电子的速度是能量E (k ) 对k 的一阶导数,有效质量的倒数是能量E (k ) 对k 的二阶导数,表现在其在r 空间的运动速度和有效质量也随时间作周期性变化。
布洛赫电子速度的周期性变化,意味着它在r 空间的振荡。
有外电场时,布洛赫电子的能量附加有静电势能,沿x 轴正方向下降,能带发生倾斜。
设开始时,一能带底部电子在电场力作用下运动到能带顶部,遇到了能隙,相当于存在有一势垒,在准经典运动中,电子局限在同一能带中运动,遇到势垒后将全部被反射回来,速度改变方向,布洛赫电子由能带顶部返回能带底部,这就是布洛赫电子在r 空间的振荡。
布洛赫电子在运动过程中将要不断受到声子、杂质和缺陷的散射,相邻两次散射之间的平均时间间隔称为电子的平均自由运动时间,用τ表示,如果τ很小,布洛赫电子来不及完成振荡运动就被散射了,τ的典型值为10-13秒,布洛赫电子在k 空间振荡的圆频率为:qEa qE a =⎪⎪⎭⎫ ⎝⎛=-122ππω (5.2.2)观测到布洛赫电子在k 空间振荡的条件为1>>ωτ (5.2.3) 如果取a = 3 Å,需要电场强度E 大于2 ⨯ 105 V -cm -1。
第五章 晶体中的电子能带理论电子在固体中的运动问题处理第一步简化 —— 绝热近似:离子实质量比电子大,离子运动速度慢,讨论电子问题,认为离子是固定在瞬时位置上第二步简化 —— 单电子近似:每个电子是在固定的离子势场以及其它电子的平均场中运动第三步简化 —— 所有离子势场和其它电子的平均场是周期性势场 复杂的多体问题转化为周期场中的单电子运动问题5-1 布洛赫波函数一、布洛赫定理 1.晶格的周期性势场(1)在晶体中每点势能为各个原子实在该点所产生的势能之和;(2)每一点势能主要决定于与核较近的几个原子实(因为势能与距离成反比); (3)理想晶体中原子排列具有周期性,晶体内部的势场具有周期性;(4)电子的影响:电子均匀分布于晶体中,其作用相当于在晶格势场中附加了一个均匀的势场,而不影响晶体势场的周期性。
电子在一个具有晶格周期性的势场中运动()()n R r V r V+=其中n R 为任意格点的位矢。
()ψψ E r V m =⎥⎦⎤⎢⎣⎡+∇-222 2. 布洛赫定理当势场具有晶格周期性时,波动方程的解具有如下性质:),(e )(r R r nR k i nψψ⋅=+其中k 为电子波矢,332211n a n a n a n R++=是格矢。
根据布洛赫定理波函数写成如下形式:()()r u r k r k i k⋅=e ψ ()()n k kR r u r u +=在晶格周期性势场中运动的电子的波函数是按晶格周期调幅的平面波。
具有此形式的波函数称为布洛赫波函数。
3.证明布洛赫定理(1)引入平移对称算符)(n R T(2)说明: 0]ˆ,ˆ[=H T(3) λψψ=Tˆ nR k i n R ⋅=e )(λ(1)平移对称算符)(n R T)()()(n n R r f r f R T +=)2()()()()(2n n n n R r f R r f R T r f R T+=+= )()()(n n l R l r f r f R T +=)(ˆ)()()(r H r r V r f ,,可以是ψ (2) 0]ˆ,ˆ[=H T)(2ˆ22r V mH +∇-= ),()(n R r V r V += 在直角坐标系中:)()(22222222n R r zy x r +∇=∂∂+∂∂+∂∂=∇233222222112)()()(a n z a n y a n x +∂∂++∂∂++∂∂= 晶体中单电子哈密顿量Hˆ具有晶格周期性。
)(ˆ)(ˆn R r H r H +=)()(ˆ)()(ˆ)(ˆn n n R r R r H r r H R T ++=ψψ 0]ˆ,ˆ[=H T平移对称操作算符与哈密顿算符是对易的。
由于对易的算符有共同的本征函数,所以如果波函数)(rψ是Hˆ的本征函数,那么 )(r ψ也一定是算符)(ˆn R T 的本征函数。
(3) λψψ=Tˆ nR k i n R ⋅=e )(λ,则有对应的本征值为设)()(ˆn n R R T λ )()()()()(ˆr R R r r R T n n n ψλψψ=+=根据平移特点)(ˆ)(ˆ)(ˆ)(ˆ)(ˆ332211332211a n T a n T a n T a n a n a n T R T n =++=[][][]321)(ˆ)(ˆ)(ˆ321n n n a T a T a T =可得到[][][])()()()()()()()(ˆ321321r a a a r R r R T n n n n n ψλλλψλψ==即[][][]321)()()()(321n n n n a a a Rλλλλ=?)()()(321=a a aλλλ、、,321321个原胞、、方向各有、、设晶体在N N N a a a由周期性边界条件⎪⎩⎪⎨⎧+=+=+=)()()()()()(332211a N r r a N r r a N r rψψψψψψ根据上式可得到()[])()()()()(ˆ111111r a N r r a r a N T N ψψψλψ=+== []1)(11=N a λ 11π21e )(N l i a =λ同理可得:,e )(22π22N l i a = λ 33π23e )(N l i a = λ这样)(ˆn R T 的本征值取下列形式 )π(2333222111e )(N ln N l n N l n i n R ++=λ引入矢量 333222111N bl N b l N b l k++=式中321b b b 、、为晶格三个倒格基矢,由于ij j i b a δπ2=⋅ , nR k i n R ⋅=e )(λ晶体中的电子的波函数所满足的方程)(e )(r R r nR k i nψψ⋅=+再证明布洛赫波函数具有如下形式:()()r u r k r ki k⋅=e ψ()()n k kR r u r u +=可以看出平面波rk i ⋅e能满足上式。
因此矢量k具有波矢的意义。
当波矢增加一个倒格矢h K ,平面波rK k i h ⋅+)(e也满足上式。
因此电子的波函数一般是这些平面波的线性叠加∑∑⋅⋅⋅++=+=hr K i h r k i hr K k i h k h hK k a K k a r )e (e )e ()()(ψ ∑⋅+=h r K i h k h K k a r u )e ()(设则上式化为 )(e )(r u r k r k i k⋅=ψ)()(r u R r u kn k=+ 即晶体中电子的波函数是按晶格周期调幅的平面波。
)(e )(r R r nR k i nψψ⋅=+22)()(r R r k n kψψ=+可以认为电子在整个晶体中自由运动。
布洛赫函数的平面波因子描述晶体中电子的共有化运动,而周期函数的因子描述电子在原胞中运动,这取决于原胞中电子的势场。
5.1.2 k的取值和范围个原胞,、、方向各有、、设晶体在321321N N N a a a由周期性边界条件 ⎪⎩⎪⎨⎧+=+=+=)()()()()()(332211a N r r a N r r a N r r k kk k k kψψψψψψ)()(11r a N r k kψψ=+())(e )(1111r u a N r k a N r k i k+⋅=+ψ)(e e 11r u k r k i a N k i⋅⋅= )(r k ψ 1e=⋅jj a N k i333222111N b l N b l N b l k++=332211b b b τττ++=,π2ij j j b a δ=⋅j j j l N =τ (其中lj 为任意整数),jj j N l =τ 只能取一些分立的值。
整数时,当+='jj ττ ,'n K k k k+=换成相当于波矢 )()(r r hKk k+=ψψ k 态和h K k +态是同一电子态,而同一电子态对应同一个能量,故)()(h K k E k E +=为使本征函数和本征值一一对应,即使电子的波矢与本征值)(k E一一对应起来,必须把波矢k 的值限制在一个倒格子原胞区间内,通常取:)3,2,1(,22=≤<-i b k b ii i——简约布里渊区(第一布里渊区)在简约布里渊区内,电子的波矢数目等于晶体的原胞数目N =N 1N 2N 3。
在波矢空间内,由于N 的数目很大,波矢点的分布是准连续的。
一个波矢对应的体积为:C V N N N b N b N b 33*332211π)2(Ωπ)2(Ω)(===⨯⋅一个波矢代表点对应的体积为:CV 3π)2(电子的波矢密度为:3π)2(cV 简约布里渊区的波矢数目N N =Ω⋅Ω33)2()2(ππ5-2 近自由电子近似模型:假定周期场起伏较小,而电子的平均动能比其势能的绝对值大得多。
作为零级近似,用势能的平均值V 0代替V (x ),把周期性起伏V (x )-V 0作为微扰来处理。
1.势场)()(x V a x V =+(a 为晶格常量)ikxnn V x V e )(∑= ⎰--=22d )e (1aa ikx n x x V a V,e )()(a x ik nn V a x V +∑=+ ,1e =ika n ak π2=即 V V V V V x V nx ainn nx ainn ∆+=+==∑∑0π20π2e'e)(⎰-=220)d (1aa x x V a V 是势能的平均值其中 我们取V 0=0。
由于势能是实数,可得关系式:*n n V V =- 2.零级近似解)()()(d d 2222x E x x V x m k k k ψψ=⎥⎦⎤⎢⎣⎡+- 按照微扰理论,哈密顿量写成 ,ˆˆˆ0H H H '+= 02220d d 2ˆV x m H +-= 式中 ∑=∆='nnx a i n V V H π2e 'ˆ )()()(ˆ0000x x E x H kk k ψψ= m k E k2220= 晶格长度Na L e Lx ikx k ==,1)(0ψ零级近似下的解与自由电子波函数相同。
按量子力学微扰理论,电子的能量可写成⋅⋅⋅+++=⋅⋅⋅⋅+++=)()()()(210210x x x x E E E E kk k k k k k k ψψψψ计入微扰后本征值的一级和二级修正为:∑-∆=∆=''002'21k k kkkEE k V k E k V k E ,波函数的一级修正为 000'1'''k kk kk EE k V k ψψ∑-∆=[]0d )(00*1=-=⎰x V x V E k kk ψψ可以证明:=∆k V k '⎪⎩⎪⎨⎧=-=其他情况当,0π2,)(''n a k k V k x V k n ∑''-∆+=k k k k E E k V k E E 002'0∑⎥⎦⎤⎢⎣⎡+-+=n n n a k k m V m k 222222)π2(22 ∑-∆+='''000'0')()(kk k k k k E E kV k x x ψψψ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡--+=∑-nnxa i n ikx n a k k m V L 222π2*)π2(2e '1e 1 )(e x u k ikx = 上式右端第一部分波矢为k 的前进平面波,第二部分为电子在行进过程中遭受到起伏势场的散射作用所产生的散射波。
当前进波波矢k 远离n π/a 时,第二部分的贡献很小,波函数主要由前进平面波决定,此时电子的行为与自由电子近似。