培优专题7-菱形、矩形、正方形和梯形(含答案)

一、选择题1.（2016山东东营，10，3分）如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，分析下列四个结论：①△AEF∽△CAB；②CF=2AF；③DF=DC；④tan∠A．4个B．3个C．2个D．1个【答案】B【逐步提示】本题考查矩形的性质，相似三角形的判定与性质，平行四边形的判定与性质，锐角三角函数的定义等．综上所述，①②③正确，而无法判断④正确，故选B．【解后反思】【一题多解】③取BC的中点M，连接DM，FM，∴FM=CM．∵E是AD的中点，∴DE=BM，又∵DE∥BM，∴四边形BMDE是平行四边形，∴DM∥BE，∴DM⊥CF，∴DM是线段CF的垂直平分线，∴DF=DC．【关键词】矩形的性质；相似三角形的判定与性质；平行四边形的判定与性质；锐角三角函数的定义2.（2016山东泰安，23，3分）如图，矩形ABCD中，已知AB＝6，BC＝8，BD的垂直平分线交AD于点E，交BC于点F，则△BOF的面积为．【逐步提示】本题考查了矩形的性质、勾股定理、相似三角形的判定与性质，解题的关键是相似三角形面积比等于相似比的平方的性质的应用．与因为已知AB ＝6，BC ＝8，所以可以求出△BDC 的面积，因为EF 垂直平分BD ，可知∠BOF ＝90°，所以△BOF 与△BCD 相似．利用勾股定理可以求出BD 的长，也就知道了OB 的长度，根据相似三角形面积比等于相似比的平方，可以计算出△BOF 的面积．【详细解答】解：∵四边形ABCD 是矩形，∴AB ＝CD ＝6，∠C ＝90°，∵BC ＝8，∴由勾股定理得10BD ，168242BCD S ∆⨯⨯＝＝，∵EF 垂直平分BD ，∴∠BOF ＝90°，152OB BD ＝＝．∵∠OBF ＝∠DBC ，∠BOF ＝∠C＝90°，∴△BOF ∽△BCD ，∴222525864BOF BCD S OB S BC ∆∆⎛⎫ ⎪⎝⎭＝＝＝，∴257524648BOF S ∆⨯＝＝．【解后反思】由于所求的△BOF 是直角三角形，所以有的同学可能直接用12S OB OF ∆⨯⨯＝来计算三角形的面积，这样解决起来就很繁琐．实际上本题是考查相似三角形的性质：两个相似三角形面积的比等于相似比的平方．所以认真审题，理清脉络很关键．【关键词】矩形的性质；勾股定理；垂直平分线；相似三角形的性质．3. （ 2016山东省枣庄市，9，3分）如图，四边形ABCD 是菱形，AC ＝8，DB ＝6，DH ⊥AB 于H ，则DH 等于（ ） A ．245 B ．125C ．5D ．4【答案】A ．【逐步提示】本题考查了菱形的性质，及面积公式，解题的关键是灵活运用菱形的性质．根据菱形对角线互相垂直且平分，求出菱形的边长，再利用菱形的面积公式即可求出高线DH ． 【详细解答】解：设AC 、BD 交于点O ．∵四边形ABCD 是菱形，∴AO ＝12AC ＝4，BO ＝12DB ＝3，∠AOB ＝90°，∴AB5，∵S 菱形ABCD ＝12AC ²DB ＝AB ²DH ，∴DH ＝12AC BD AB ⋅＝18625⨯⨯＝245，OAEDBFC第23题图ABDCH故选择A . 【解后反思】本题考查了菱形的性质及面积公式．菱形的性质：①菱形的四条边相等；②菱形的对角线互相垂直平分，且每一条对角线平分一组对角；③S 菱形ABCD ＝12AC ²DB ＝底³高．本题在解答时，还可以利用△BDH ∽△BAO ，BD DHBA AO=求解． 【关键词】 勾股定理；菱形的性质；菱形的面积；4. （2016山东淄博，8，4分）如图，正方形ABCD 的边长为10， AG =CH =8，BG =DH =6，连接GH . 则线段GH 的长为（ ）A.C.145D. 10－【答案】B【逐步提示】本题考查正方形，勾股定理及逆定理的知识，解题关键是能灵活添加辅助线，将问题转化为已知问题解决. 延长BG 交CH 于点E ，根据正方形的性质证明ABG ≌△CDH≌△BCE ，可得GE =BE ﹣BG =2、HE =CH ﹣CE =2、∠HEG =90°，由勾股定理可得GH 的长． 【详细解答】解：法一：如图，延长BG 交CH 于点E ，∵AG =CH =8，BG =DH =6，AB =CD =10，∴△ABG ≌△CDH （SSS ）. ∵22AG BG +=2286+=210=2AB ，∴△ABG 是直角三角形，∠AGB =90°. 同理△DHC 是直角三角形，∠DHC =90°. ∵∠1=∠5，∠2=∠6，∠AGB =∠CHD =90°， ∴∠1+∠2=90°，∠5+∠6=90°， 又∵∠2+∠3=90°，∠4+∠5=90°， ∴∠1=∠3=∠5，∠2=∠4=∠6，∵AB =BC ，∴△ABG ≌△BCE （ASA ）.∴BE =AG =8，CE =BG =6，∠BEC =∠AGB =90°.ABDCHO∴GE =BE －BG =8－6=2. 同理可得HE =2GE .在RT △GHE 中，GH故选择B. 法二：过点G 作EF ⊥AB 于点EF ，过点H 作HF ∥AB .∵22AG BG +=2286+=210=2AB ，∴△ABG 是直角三角形，∠AGB =90°. 同理△DHC 是直角三角形，∠DHC =90°. ∴EG =6810⨯=4.8. ∴GF =10－2³4.8=0.4. ∵BE =6610⨯=3.6，∴HF =10－2³3.6=2.8. ∴HG故选择B.【解后反思】添加辅助线，构造直角三角形求解是解题关键. 【关键词】正方形，勾股定理及逆定理5. (2016天津，10，3分)如图，把一张矩形纸片ABCD 沿对角线AC 折叠，点B 的对应点为B ′，AB ′与DC 相交于点E ，则下列结论正确的是()A ．∠DAB′=∠CAB ′ B ．∠ACD=∠B′CDC ．AD =AE D ． AE =CE 【答案】D【逐步提示】本题是一道有关折叠的问题，应根据折叠的性质求解．根据折叠得到△ABC 与△AB′C 全等，得到∠BAC =∠B′AC ,然后利用矩形的性质将∠ACE 转化到∠CAB′.【解析】根据折叠得到△ABC ≌△AB ′C ，∴=BAC B AC '∠∠，又∵AB ∥CD ，∴∠BAC =∠DCA ，∴∠EAC =∠DCA ，∴EA =E C.故选择D .【解后反思】折叠问题是属于轴对称变换，折叠后图形的形状和大小不变，三角形折叠后得到的三角形与原三角形全等，对应边和对应角相等.【关键词】折叠问题；等腰三角形；全等三角形(2016浙江宁波，12，4分)如图是一个由 5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S 1 ,另两张直角三角形纸片的面积都为 S 2,中间一张正方形纸片的面积为S 3,则这个平行四边形的面积一定可以表示为( )E FA. 4S 1B. 4S 2C. 4S 2+ S 3D. 3S 1+ 4S 3【答案】A【逐步提示】本题考查了平行四边形性质、直角三角形性质、整式的加减运算，解题的关键是引入字母找出S 1 、S 2、S 3 之间的关系.设等腰直角三角形纸片的直角边长为a, 中间一张正方形纸片的边长为m,从而可以表示出面积为S 2的直角三角形纸片两条直角边长，进而得出S 1 、S 2、S 3 之间的关系.【解析】设等腰直角三角形纸片的直角边长为a, 中间一张正方形纸片的边长为m,则2112S a =，23S m =，∴22213111()()()(2)222S a m a m a m S S =-+=-=-, 即31222S S S =-，∴这个平行四边形的面积=123121212222(22)4S S S S S S S S ++=++-=，故选择A . 【解后反思】此类问题常常通过引入字母，再结合图形把所求的面积具体化，找出三个面积之间的等量关系，就可以求得问题的解.【关键词】等腰三角形与直角三角形；平行四边形；平方差公式；整式的加减6.(2016浙江舟山，9，3分)如图，矩形ABCD 中，AD =2，AB =3，过点A ．C 作相距为2的平行线段AE 、CF ，分别交CD ．AB 于点E 、F ，则DE 的长是( )A ． 5B ．136C ．1D ．56【答案】D【逐步提示】本题考查了矩形、平行四边形、全等三角形的性质与判定，解题的关键是用DE 的代数式表示AE 的长度. 过点F 作FH ⊥AE ，交AE 于点H ，根据平行线间的距离的概念，得FH =2=AD .设DE =x .先说明四边形AECF 为平行四边形，由矩形、平行四边形的性质可得DE =BF =x ，即F A =3－x .再证△ADE ≌△FHA ，得AE =F A =3－x ，然后在Rt △ADE 中利用勾股定理构造关于x 的方程，解方程求出x 的值，即得DE 的长.【解析】设DE=x.过点F 作FH ⊥AE ，交AE 于点H ，∵AE 、CF 是平行线段，∴FH=2=AD ，AE ∥CF.∵四边形ABCD 是矩形，∴AB ∥CD ，AB=CD ，∴.四边形AECF 为平行四边形，∴AF=CE ，∴DE=BF=x ，即FA=3－x. 在矩形ABCD 中，∠BAD=∠D=90°，∴∠D=∠AHF=90°，∠DAE=AFH ，∴△ADE ≌△FHA ，∴AE=FA=3－x.因此在Rt △ADE 中，由“AD 2+DE 2=AE 2”得“22+x 2=(3－x)2”，解得x=56，即DE=56，故选择D .【解后反思】本题较综合地考查了部分特殊四边形的性质与判定，全等三角形的识别与性质等知识，设DE=x后，利用上述知识，用x的代数式表示AE的长度是解答本题的关键，再结合勾股定理，利用方程求解，充分体现了方程思想在求解几何图形相关问题的重要功能.【关键词】矩形的性质；平行四边形的判定；全等三角形的识别与性质；勾股定理；方程思想.7.（2016四川省广安市，8，3分）下列说法：①三角形的三条高一定都在三角形内；②有一个角是直角的四边形是矩形；③有一组邻边相等的平行四边形是菱形；④两边及一角对应相等的两个三角形全等；⑤一组对边平行，另一组对边相等的四边形是平行四边形．其中正确的个数有（）A．1个B．2个C．3个D．4个【答案】A【逐步提示】本题考查了三角形的中线、高线、角平分线的概念，矩形的判定，菱形的判定，全等三角形的判定，平行四边形的判定等，解题的关键是掌握这些概念、定理等．因为直角三角形与钝角三角形的三条高不都在三角形内，故①错；至少有三个角是直角的四边形是才是矩形，故②错；③是菱形的定义，正确；满足④的条件时有可能形成“边边角”的情况，故错误；等腰梯形满足“一组对边平行，另一组对边相等”，但它不是平行四边形，故⑤错误．【详细解答】解：只有③正确，故选择A.【解后反思】要理解三角形“三线”的概念，掌握三角形、平行四边形、矩形、菱形的判定方法，这是正确解题的基础．能画图举反例，以排除不符合条件情形，也是解这类题的基本功，要多思考，勤积累．类似的问题还有：判断下列说法是否正确：（1）一组对边相等且一组对角相等的四边形是平行四边形.解：错误．如图1，作△ABC，使AB＝AC，在BC上取一点D（D点不与B、C重合且BD≠CD），连接AD.再以A为顶点，AD为一边，作∠EAD，使∠EAD＝∠ADC，且AE＝DC，连接DE.由上述画图方法，可知△ADC≌△DAE（SAS）.所以DE＝AC＝AB，∠AED＝∠C＝∠B.即四边形ABCD有一组对边相等（DE＝AB）、一组对角相等（∠AED＝∠B），但却不是平行四边形（另一组对边AE和BD不平行也不相等）.（2）一组对边相等，且一条对角线平分另一条对角线的四边形是平行四边形.解：错误．如图2，画两条相交直线，交点为O，在其中一条直线上截取OA＝OC，分别过A、C两点向另一条直线作垂线，垂足分别为E、F.在线段OF上取一点D（D点不与O、F重合），连接CD.再在线段OE的延长线上取一点B ，使EB ＝FD ，连接AB .由上述画图方法，易知△COF ≌△AOE （AAS ），则CF ＝AE ，由“SAS ”可判定△CFD ≌△AEB ，则CD ＝AB .连接AD 、BC ，则四边形ABCD 满足条件，却不是平行四边形.（3）一组对角相等，且连接这一组对角的顶点的对角线被另一条对角线平分的四边形是平行四边形.解：错误．如图，画一个“筝形”ABCD ，其中AB ＝AD ，BC ＝DC 且AO ≠OC ，则该“筝形”满足条件，但它不是平行四边形.【关键词】 中线、高线、角平分线；矩形的判定；菱形的判定；全等三角形的判定；平行四边形的判定 8. （ 2016四川泸州，10，3分）如图，矩形ABCD 的边长AD=3,AB=2,E 为AB 的中点，F 在边BC 上，且BF=2FC ，AF 分别与DE 、DB 相交于点M ，N ，则MN 的长为（ ）A.5B.204D.5【答案】B ，9 （ 2016四川省绵阳市，11，3分）如图，点E ，点F 分别在菱形ABCD 的边AB ，AD 上，且AE ＝DF ，BF 交DE 于点G ，延长BF 交CD 的延长线于H ，若AF DF ＝2，则HFBG的值为 ········ （ ） A ．23 B ．712C ．12D ．512【答案】B ．【逐步提示】本题考查了相似三角形的判定和性质．由菱形ABCD 知AB ∥CD ，AD ∥BC ，可知图中存在多个相似三角形中的基本图形：“A ”型“与”X “型．由基本图形得HF FB ＝DF AF ＝12，所以HF ＝13HB ①．类似地，HD ＝12AB ，又BE ＝23AB ，所以HD BE ＝34．由基本图形得BG HG ＝BE HD ＝43，所以BG ＝47HB ②，由①②可求HFBG的比值． 【详细解答】解：设菱形ABCD 的边长为3a ．因为四边形ABCD 是菱形，AFDF＝2，AE ＝DF ，所以AE ＝DF ＝a ，AF ＝BE ＝2a ，AB ∥CD，所以HF FB ＝HD AB ＝DF AF ＝12，所以HD ＝12AB ＝32a ，HF ＝13HB ．因为AB ∥CD ，所以BG HG ＝BE HD ＝232a a＝43，所以BG ＝47HB ．所以HF BG ＝1347HBHB 712，故答案为B ．【解后反思】（1）求线段的比通常利用平行线或相似三角形得到比例线段，然后再进行转化得到所求两线段的比．（2）遇到平行线，要联想到以下两个常用的基本图形（“A ”型“与”X “型）．【关键词】菱形的性质；相似三角形的判定；转化思想．E CDFGHAB10（2016四川南充，8，3分）如图，对折矩形纸片ABCD，使AB与DC重合得到折痕EF，将纸片展平，再一次折叠，使点D落到EF上G点处，并使折痕经过点A，展平纸片后∠DAG的大小为（）A．30°B．45°C．60°D．75°【答案】C【逐步提示】本题主要考查了翻折变换的性质以及平行线的性质，正确得出∠2=∠4是解题关键．直接利用翻折变换的性质以及直角三角形的性质得出∠2=∠4，再利用平行线的性质得出∠1=∠2=∠3，进而得出答案．【详细解答】解：如图所示：由题意可得：∠1=∠2，AN=MN，∠MGA=90°，则NG=12AM，故AN=NG，则∠2=∠4，∵EF∥AB，∴∠4=∠3，∴∠1=∠2=∠3=13×90°=30°，∴∠DAG=60°．故选择C．【解后反思】本题还可以采用如下方法求解。

中考数学二轮专题复习-矩形、菱形及正方形一、单选题1．下列四边形中，对角线互相垂直平分的是（）A．平行四边形、菱形B．矩形、菱形C．矩形、正方形D．菱形、正方形2．下列测量方案中，能确定四边形门框为矩形的是（）A．测量对角线是否互相平分B．测量两组对边是否分别相等C．测量对角线是否相等D．测量对角线交点到四个顶点的距离是否都相等3．如图，菱形的对角线、相交于点，过点作于点，连接，若，，则菱形的面积为（）A．B．C．D．4．如图，有甲、乙、丙三个矩形，其中相似的是（）A．甲与丙B．甲与乙C．乙与丙D．三个矩形都不相似5．如图，在菱形ABCD中，DE⊥AB，cosA＝，AE＝3，则tan∠DBE的值是（）A．B．2C．D．6．如图，在菱形ABCD中，对角线AC与BD交于点O，E是边AB的中点，连结OE.若菱形ABCD的面积为24，AC＝8，则OE的长为（）A．B．3C．D．57．如图，在正方形ABCD中，E是边BC上一点，且BE：CE＝1：3，DE交AC于点F，若DE＝10，则CF等于()A．B．C．D．8．如图，矩形中，对角线交于点O，，则矩形的面积是（）A．2B．C．D．89．如图，将长、宽分别为6cm，cm的长方形纸片分别沿AB，AC折叠，点M，N恰好重合于点P．若∠α＝60°，则折叠后的图案（阴影部分）面积为（）A．cm2 B．（36）cm2C．cm2D．cm210．如图所示，反比例函数的图象经过矩形OABC的边AB的中点，则矩形OABC的面积为（）A．2B．4C．5D．811．如图，在菱形ABCD中，AB=4，∠B=60°，AE⊥BC，AF⊥CD ，垂足分别为点E，F，连结EF，则△AEF 的面积是（）A．B．C．D．12．如图，四边形ABCD是正方形，BE⊥EF，DF⊥EF，BE=2.5dm，DF=4dm，那么EF的长为（）A．6.5dm B．6dm C．5.5dm D．4dm13．将一矩形纸片ABCD沿CE折叠，B点恰好落在AD边上的F处，若，则的值为（）A．B．C．D．14．正方形ABCD的边长为8，M在DC上，且DM＝2，N是AC上的一动点，DN＋MN的最小值为（）A．6B．8C．10D．915．如图，在矩形ABCD中，对角线、BD交于C，，垂足为E，，那么的面积是（）A．B．C．D．16．如图，在Rt△ABC中，∠ACB＝90°，以其三边为边向外作正方形，过点C作CI⊥HJ于点I，交AB于K，在图形的外部作矩形MNPQ，使点D，E，G和H，J都落在矩形的边上.已知矩形BJIK的面积为1，正方形ACDE的面积为4，则为（）A．B．C．D．17．如图，正方形的边长为a，点E在边上运动（不与点A，B重合），，点F在射线上，且与相交于点G，连接．则下列结论：①，② 的周长为 ，③；④当 时，G 是线段 的中点，其中正确的结论是（ ）A ．①②③B ．①④C ．①③④D ．①②③④ 18．如图，菱形ABCD 的边长为4，E 、F 分别是AB 、AD 上的点，AC 与EF 相交于点G ，若， ，则FG 的长为（ ）A ．B ．2C ．3D ．419．如图，在△ABC 中，∠ACB ＝90°，以△ABC 的各边为边分别作正方形BAHI ，正方形BCFG 与正方形CADE ，延长BG ，FG 分别交AD ，DE 于点K ，J ，连结DH ，IJ.图中两块阴影部分面积分别记为S 1，S 2.若S 1：S 2＝1：4，S 四边形边BAHE ＝18，则四边形MBNJ 的面积为（ ）A．5B．6C．8D．920．如图，在Rt△ABC中，∠CBA＝60°，斜边AB＝10，分别以△ABC的三边长为边在AB上方作正方形，S1，S2，S3，S4，S5分别表示对应阴影部分的面积，则S1+S2+S3+S4+S5＝（）A．50B．50C．100D．100二、填空题21．在四边形ABCD中，对角线AC，BD交于点O，OA=OC=OB=OD，添加一个条件使四边形ABCD是正方形，那么所添加的条件可以是(写出一个即可)22．如图，分别以Rt△ABC三边构造三个正方形，面积分别为S1，S2，S3，若S1=15，S3=39，则S2=.23．如图，在平面直角坐标系中，点A1（1，0）、A2（3，0）、A3（6，0）、A4（10，0）、……，以A1A2为对角线作第一个正方形A1C1A2B1，以A2A3为对角线作第二个正方形A2C2A3B2，以A3A4，为对角线作第三个正方形A3C3A4B3，……，顶点B1，B2，B3……都在第一象限，按照此规律依次下去，则点Bn的坐标为.24．如图，菱形ABCD的对角线，BD相交于点，，，以AB为直径作一个半圆，则图中阴影部分的面积为.25．如图，在矩形ABCD中，AB＝8，AD＝10，AD，AB，BC分别与⊙O相切于E，F，G三点，过D作⊙O的切线交BC于点M，切点为N，则DM的长为.26．建党100周年主题活动中，702班浔浔设计了如图1的“红色徽章”其设计原理是：如图2，在边长为的正方形四周分别放置四个边长为的小正方形，构造了一个大正方形，并画出阴影部分图形，形成了“红色徽章”的图标.现将阴影部分图形面积记作，每一个边长为的小正方形面积记作，若，则的值是.27．如图，正方形ABCD的边长为4，P是边CD上的一动点，EF⊥BP交BP于G，且EF平分正方形ABCD的面积，则线段GC的最小值是.28．正方形ABCD的边长为4，点E是BC边上的一动点，连结AE，过点B作BF⊥AE于点F，以BF为边作正方形FBHG，当点E从B运动到C时，求CF的最短距离为；线段HG扫过的面积为29．如图，在矩形ABCD中，AB＝4，BC＝3，将△BCD沿射线BD平移长度a（a＞0）得到△B'C'D'，连接AB'，AD'，则当△AB'D'是直角三角形时，a的长为.30．如图，矩形ABCD中，AB＝20，AD＝15，P，Q分别是AB，AD边上的动点，PQ＝16，以PQ 为直径的⊙O与BD交于点M，N，则MN的最大值为．三、计算题31．如图，在中，，D为的中点，，，连接交于点O.（1）证明：四边形为菱形；（2）若，，求菱形的高.32．如图，已知在矩形ABCD中，AB=6，BC=2，点E，F分别在边CD，AB上，且DE=BF.（1）求证:四边形AFCE是平行四边形；（2）若□AFCE是菱形，求菱形AFCE的边长.四、解答题33．如图，在四边形ABCD中，E，F，G，H分别是AB，BD，CD，AC的中点，AD＝BC，求证：四边形EFGH是菱形．34．如图，矩形ABCD中，BC=4，将矩形ABCD绕点C顺时针旋转得到矩形A′B′C′D′，此时点B′恰好落在边AD上．连接B′B，若∠AB′B=75°，求旋转角及AB长．35．如图，△ABC中，点D是边AC的中点，过D作直线PQ∥BC，∠BCA的平分线交直线PQ于点E，点G是△ABC的边BC延长线上的点，∠ACG的平分线交直线PQ于点F．求证：四边形AECF是矩形．36．在几何探究问题中，经常需要通过作辅助线（如，连接两点，过某点作垂线，作延长线，作平行线等等）把分散的条件相对集中，以达到解决问题的目的.（1）（探究发现）如图1，点E，F分别在正方形ABCD的边BC，CD上，，连接EF.通过探究，可发现BE，EF，DF之间的数量关系为（直接写出结果）.（2）（验证猜想）同学们讨论得出下列三种证明思路（如图1）：思路一：过点A作，交CD的延长线于点G.思路二：过点A作，并截取，连接DG.思路三：延长CD至点G，使，连接AG.请选择你喜欢的一种思路证明（探究发现）中的结论.（3）（迁移应用）如图2，点E，F分别在正方形ABCD的边BC，CD上，且，，设，试用含的代数式表示DF的长.37．在平面直角坐标系中，O为原点，点A（6，0），点B在y轴的正半轴上，∠ABO＝30°．矩形CODE的顶点D，E，C分别在OA，AB，OB上，OD＝2．（Ⅰ）如图①，求点E的坐标；（Ⅱ）将矩形CODE沿x轴向右平移，得到矩形C′O′D′E′，点C，O，D，E的对应点分别为C′，O′，D′，E′．设OO′＝t，矩形C′O′D′E′与△ABO重叠部分的面积为S．①如图②，当矩形C′O′D′E′与△ABO重叠部分为五边形时，C′E′，E′D′分别与AB相交于点M，F，试用含有t的式子表示S，并直接写出t的取值范围；②当≤S≤5 时，求t的取值范围（直接写出结果即可）．38．阅读下面的例题及点拨，并解决问题：例题：如图①，在等边中，是边上一点(不含端点)，是的外角的平分线上一点，且.求证：.点拨：如图②，作，与的延长线相交于点，得等边，连接.易证：，可得；又，则，可得；由，进一步可得又因为，所以，即：.问题：如图③，在正方形中，是边上一点(不含端点)，是正方形的外角的平分线上一点，且.求证：.五、综合题39．将绕点A按逆时针方向旋转度，并使各边长变为原来的n倍，得，如图①，我们将这种变换记为.（1）如图①，对作变换得，则；直线与直线所夹的锐角为度；（2）如图②，中，，对作变换得，使点B、C、在同一直线上，且四边形为矩形，求和n的值；（3）如图③，中，，对作变换得，使点B、C、在同一直线上，且四边形为平行四边形，求和n的值. 40．如图（1）如图1，正方形ABCD与调研直角△AEF有公共顶点A，∠EAF＝90°，连接BE、DF，将△AEF绕点A旋转，在旋转过程中，直线BE、DF相交所成的角为β，则＝；β＝；（2）如图2，矩形ABCD与Rt△AEF有公共顶点A，∠EAF＝90°，且AD＝2AB，AF＝2AE，连接BE、DF，将Rt△AEF绕点A旋转，在旋转过程中，直线BE、DF相交所成的角为β，请求出的值及β的度数，并结合图2进行说明；（3）若平行四边形ABCD与△AEF有公共项点A，且∠BAD＝∠EAF＝α(0°＜α＜180°)，AD＝kAB，AF＝kAE(k≠0)，将△AEF绕点A旋转，在旋转过程中，直线BE、DF相交所成的锐角的度数为β，则：①＝；②请直接写出α和β之间的关系式．答案解析部分【解析】【解答】解：∵平行四边形对角线互相平分，菱形对角线互相垂直平分，矩形对角线互相平分且相等，正方形对角线互相垂直平分且相等，∴A、B、C不符合题意，D符合题意.故答案为：D.【分析】根据平行四边形对角线互相平分，菱形对角线互相垂直平分，矩形对角线互相平分且相等，正方形对角线互相垂直平分且相等，即可得出答案.【解析】【解答】解：A、∵对角线互相平分的四边形是平行四边形，而对角线互相平分且相等的四边形才是矩形，∴选项A不符合题意；B、∵两组对边分别相等是平行四边形，∴选项B不符合题意；C、∵对角线互相平分且相等的四边形才是矩形，∴对角线相等的四边形不是矩形，∴选项C不符合题意；D、∵对角线交点到四个顶点的距离都相等，∴对角线互相平分且相等，∵对角线互相平分且相等的四边形是矩形，∴选项D符合题意.故答案为：D.【分析】利用对角线互相平分且相等的四边形是矩形，可作出判断.【解析】【解答】解：∵四边形ABCD是菱形，∴OA=OC，OB=OD，AC⊥BD，∵DH⊥AB，∴∠BHD=90°，∴BD=2OH，∵OH=2，∴BD=4，∵OA=3，∴AC=6，∴菱形ABCD的面积．故答案为：A．【分析】根据菱形的性质和直角三角形斜边上的中线定理求出对角线的长即可求出菱形的面积。

矩形、菱形与正方形专题训练(含答案)班级________姓名________成绩________一、选择题(每小题3分，共30分)1．如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE＝2，DE＝6，∠EFB＝60°，则矩形ABCD的面积是( )A．12 B．24 C．12 3 D．16 3第1题图第2题图第3题图第4题图2．如图，菱形ABCD中，∠B＝60°，AB＝4，则以AC为边长的正方形ACEF的周长为( ) A．14 B．15 C．16 D．173．如图，将矩形ABCD沿对角线BD折叠，使点C与点C′重合．若AB＝2，则C′D的长为( ) A．1 B．2 C．3 D．44．如图，在△ABC中，AC＝BC，点D，E分别是边AB，AC的中点．将△ADE绕点E旋转180°得△CFE，则四边形ADCF一定是( )A．矩形B．菱形C．正方形D．梯形5．由菱形的两条对角线的交点向各边引垂线，以各垂足为顶点的四边形是( )A．平行四边形B．矩形C．菱形D．正方形6．如图，▱ABCD的周长为16 cm，AC，BD相交于点O，OE⊥AC交AD于点E，则△DCE的周长为( )A．4 cm B．6 cm C．8 cm D．10 cm第6题图第9题图第10题图7．菱形的周长为8 cm，高为1 cm，则菱形两邻角度数比为( )A．3∶1 B．4∶1 C．5∶1 D．6∶18．用两块完全相同的直角三角形拼下列图形：①平行四边形，②矩形，③菱形，④正方形，⑤等腰三角形，⑥等边三角形，一定能拼成的图形是( )A．①④⑤B．②⑤⑥C．①②③D．①②⑤9．如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S1，S2，则S1＋S2的值为( )A．16 B．17 C．18 D．1910．如图，F为正方形ABCD的边AD上一点，CE⊥CF交AB的延长线于点E，若正方形ABCD 的面积为64，△CEF的面积为50，则△CBE的面积为( )A．20 B．24 C．25 D．26二、填空题(每小题3分，共24分)11．如图所示，在菱形ABCD中，∠ADC＝72°，AD的垂直平分线交对角线BD于点P，垂足为点E，连结CP，则∠CPB＝____度．第11题图第12题图第14题图第15题图12．如图，四边形ABCD的两条对角线AC，BD互相垂直，A1，B1，C1，D1分别是四边形ABCD 各边中点，如果AC＝8，BD＝10，则四边形A1B1C1D1的面积为___．13．矩形的对角线相交成的角中，有一个角是60°，这个角所对的边长为20 cm，则其对角线长为____________-_，矩形的面积为_______________．14．如图，四边形ABCD是菱形，对角线AC和BD相交于点O，AC＝4 cm，BD＝8 cm，则这个菱形的面积是____cm2.15．如图，矩形ABCD中，点E，F分别是AB，CD的中点，连结DE和BF，分别取DE，BF的中点M，N，连结AM，CN，MN，若AB＝22，BC＝23，则图中阴影部分的面积为____________．,第16题图第17题第18题图16．如图，▱ABCD的对角线相交于点O，请你添加一个条件______________，使▱ABCD是矩形．17．如图，正方形ABCD中，对角线AC，BD交于点O，E点在BC上，EG⊥OB，EF⊥OC，垂足分别为点G，F，AC＝10，则EG＋EF＝____．18．如图，在平面直角坐标系中，矩形OABC的顶点A，C的坐标分别为(10，0)，(0，4)，点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为_______________________________．三、解答题(共66分)19．(6分)如图，已知矩形ABCD中，E是AD上一点，F是AB上一点，EF⊥EC且EF＝EC，DE ＝4 cm，矩形ABCD的周长为32 cm，求AE的长．20．(8分)如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，连结BM，DN.(1)求证：四边形BMDN是菱形；(2)若AB＝4，AD＝8，求MD的长．21．(8分)如图所示，矩形ABCD中，AE⊥BD于点E，∠DAE∶∠BAE＝3∶1，求∠BAE和∠EAO 的度数．22．(10分)如图，已知菱形ABCD中，AB＝AC，E，F分别是BC，AD的中点，连结AE，CF.(1)证明：四边形AECF是矩形；(2)若AB＝8，求菱形ABCD的面积．23．(12分)如图，已知四边形ABCD是平行四边形，DE⊥AB，DF⊥BC，垂足分别是点E，F，并且DE＝DF，求证：(1)△ADE≌△CDF；(2)四边形ABCD是菱形．24．(10分)在四边形ABCD中，AB＝CD，M，N，P，Q分别是AD，BC，BD，AC的中点，求证：MN与PQ互相垂直平分．参考答案一、选择题(每小题3分，共30分)1．如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE＝2，DE＝6，∠EFB＝60°，则矩形ABCD的面积是( D )A．12 B．24 C．12 D．16第1题图第2题图第3题图第4题图2．如图，菱形ABCD中，∠B＝60°，AB＝4，则以AC为边长的正方形ACEF的周长为( C ) A．14 B．15 C．16 D．173．如图，将矩形ABCD沿对角线BD折叠，使点C与点C′重合．若AB＝2，则C′D的长为( B ) A．1 B．2 C．3 D．44．如图，在△ABC中，AC＝BC，点D，E分别是边AB，AC的中点．将△ADE绕点E旋转180°得△CFE，则四边形ADCF一定是( A )A．矩形B．菱形C．正方形D．梯形5．由菱形的两条对角线的交点向各边引垂线，以各垂足为顶点的四边形是( B )A．平行四边形B．矩形C．菱形D．正方形6．如图，▱ABCD的周长为16 cm，AC，BD相交于点O，OE⊥AC交AD于点E，则△DCE的周长为( C )A．4 cm B．6 cm C．8 cm D．10 cm第6题图第9题图第10题图7．菱形的周长为8 cm，高为1 cm，则菱形两邻角度数比为( C )A．3∶1 B．4∶1 C．5∶1 D．6∶18．用两块完全相同的直角三角形拼下列图形：①平行四边形，②矩形，③菱形，④正方形，⑤等腰三角形，⑥等边三角形，一定能拼成的图形是( D )A．①④⑤B．②⑤⑥C．①②③D．①②⑤9．如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S1，S2，则S1＋S2的值为( B )A．16 B．17 C．18 D．1910．如图，F为正方形ABCD的边AD上一点，CE⊥CF交AB的延长线于点E，若正方形ABCD 的面积为64，△CEF的面积为50，则△CBE的面积为( B )A．20 B．24 C．25 D．26二、填空题(每小题3分，共24分)11．如图所示，在菱形ABCD中，∠ADC＝72°，AD的垂直平分线交对角线BD于点P，垂足为点E，连结CP，则∠CPB＝__72__度．第11题图第12题图第14题图第15题图12．如图，四边形ABCD的两条对角线AC，BD互相垂直，A1，B1，C1，D1分别是四边形ABCD 各边中点，如果AC＝8，BD＝10，则四边形A1B1C1D1的面积为__20__．13．矩形的对角线相交成的角中，有一个角是60°，这个角所对的边长为20 cm，则其对角线长为__40_cm__，矩形的面积为__400_cm2__．14．如图，四边形ABCD是菱形，对角线AC和BD相交于点O，AC＝4 cm，BD＝8 cm，则这个菱形的面积是__16__cm2.15．如图，矩形ABCD中，点E，F分别是AB，CD的中点，连结DE和BF，分别取DE，BF的中点M，N，连结AM，CN，MN，若AB＝2，BC＝2，则图中阴影部分的面积为__2__．,第16题图第17题第18题图16．如图，▱ABCD的对角线相交于点O，请你添加一个条件__AO＝BO(答案不唯一)__，使▱ABCD 是矩形．17．如图，正方形ABCD中，对角线AC，BD交于点O，E点在BC上，EG⊥OB，EF⊥OC，垂足分别为点G，F，AC＝10，则EG＋EF＝__5__．18．如图，在平面直角坐标系中，矩形OABC的顶点A，C的坐标分别为(10，0)，(0，4)，点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为__(8，4)，(3，4)或(2，4)__．三、解答题(共66分)19．(6分)如图，已知矩形ABCD中，E是AD上一点，F是AB上一点，EF⊥EC且EF＝EC，DE ＝4 cm，矩形ABCD的周长为32 cm，求AE的长．解：∵∠AFE ＋∠AEF ＝∠AEF ＋∠CED ＝90°，∴∠AFE ＝∠DEC .又∵∠A ＝∠D ＝90°，EF ＝EC ，∴△AEF ≌△DCE ，∴AE ＝CD .设AE ＝x ，则CD ＝x ，∴AD ＋CD ＝21×32，即x ＋4＋x ＝16，∴x ＝6.即AE ＝6 cm20．(8分)如图，在矩形ABCD 中，对角线BD 的垂直平分线MN 与AD 相交于点M ，与BD 相交于点O ，与BC 相交于点N ，连结BM ，DN .(1)求证：四边形BMDN 是菱形；(2)若AB ＝4，AD ＝8，求MD 的长．解：(1)∵MN 是BD 的垂直平分线，∴BO ＝DO ，∠BON ＝∠DOM ＝90°.∵四边形ABCD 是矩形，∴AD ∥BC ，∴∠BNO ＝∠DMO ，∴△BON ≌△DOM (AAS )，∴OM ＝ON .∵OB ＝OD ，∴四边形BMDN 是平行四边形．∵MN ⊥BD ，∴▱BMDN 是菱形(2)设MD ＝x ，则MB ＝x ，MA ＝8－x ，在Rt △ABM 中，∵BM 2＝AM 2＋AB 2，∴x 2＝(8－x )2＋42，解得x ＝5.∴MD 的长为521．(8分)如图所示，矩形ABCD 中，AE ⊥BD 于点E ，∠DAE ∶∠BAE ＝3∶1，求∠BAE 和∠EAO 的度数．解：提示：由∠DAE ∶∠BAE ＝3∶1，求出∠BAE ＝22.5°，而∠ABD ＝90°－∠BAE ＝90°－22.5°＝67.5°，∵∠BAO ＝∠ABD ＝67.5°，∴∠EAO ＝∠BAO －∠BAE ＝67.5°－22.5°＝45°22．(10分)如图，已知菱形ABCD 中，AB ＝AC ，E ，F 分别是BC ，AD 的中点，连结AE ，CF .(1)证明：四边形AECF 是矩形；(2)若AB ＝8，求菱形ABCD 的面积．解：(1)∵四边形ABCD 是菱形，∴AB ＝BC ，又∵AB ＝AC ，∴△ABC 是等边三角形．∵E 是BC 的中点，∴AE ⊥BC (等边三角形三线合一)，∠AEC ＝90°.同理，CF ⊥AD .∵E ，F 分别是BC ，AD 的中点，∴AF ＝21AD ，EC ＝21BC .∵四边形ABCD 是菱形，∴AD 綊BC ，∴AF 綊EC ，∴四边形AECF 是平行四边形(一组对边平行且相等的四边形是平行四边形)．又∵∠AEC ＝90°，∴四边形AECF 是矩形(有一个角是直角的平行四边形是矩形)(2)在Rt △ABE 中，∵AE ＝＝4，∴S 菱形ABCD ＝8×4＝3223．(12分)如图，已知四边形ABCD 是平行四边形，DE ⊥AB ，DF ⊥BC ，垂足分别是点E ，F ，并且DE ＝DF ，求证：(1)△ADE ≌△CDF ；(2)四边形ABCD 是菱形．解：证明：(1)∵四边形ABCD 是平行四边形，∴∠A ＝∠C ，又∵DE ＝DF ，DE ⊥AB ，DF ⊥BC ，∴∠DEA ＝∠DFC ＝90°，∴△ADE ≌△CDF (AAS ) (2)由(1)知AD ＝DC ，又∵四边形ABCD 是平行四边形，∴四边形ABCD 是菱形24．(10分)在四边形ABCD 中，AB ＝CD ，M ，N ，P ，Q 分别是AD ，BC ，BD ，AC 的中点，求证：MN 与PQ 互相垂直平分．解：证明：连结MP ，NQ ，PN ，MQ ，∵PM 綊21AB ，同理NQ 綊21AB ，∴PM 綊NQ ，∴四边形MPNQ 为平行四边形，又∵PN 綊21CD ，而CD ＝AB ，∴PN ＝PM ，∴四边形MPNQ 为菱形，∴MN 与PQ 互相垂直平分。

中考数学专题训练：矩形、菱形、正方形（附参考答案）1．下列命题正确的是( )A ．正方形的对角线相等且互相平分B ．对角互补的四边形是平行四边形C ．矩形的对角线互相垂直D ．一组邻边相等的四边形是菱形2．如图，D ，E ，F 分别是△ABC 各边的中点，则以下说法错误的是( )A ．△BDE 和△DCF 的面积相等B ．四边形AEDF 是平行四边形C ．若AB ＝BC ，则四边形AEDF 是菱形D ．若∠A ＝90°，则四边形AEDF 是矩形3．如图，在正方形ABCD 中，E ，F 分别是AB ，BC 的中点，CE ，DF 交于点G ，连接AG .下列结论：①CE ＝DF ；②CE ⊥DF ；③∠AGE ＝∠CDF .其中正确的结论是( )A ．①②B ．①③C ．②③D ．①②③4．如图，平行四边形ABCD 的对角线AC ，BD 相交于点O ，E 为BC 的中点，连接EO 并延长交AD 于点F ，∠ABC ＝60°，BC ＝2AB .下列结论：①AB ⊥AC ；②AD ＝4OE ；③四边形AECF 是菱形；④S △BOE ＝14S △ABC .其中正确结论的个数是( )A ．4B ．3C ．2D ．15．如图，在矩形ABCD中，AB＝6 cm，BC＝9 cm，点E，F分别在边AB，BC上，AE＝2 cm，BD，EF交于点G.若G是EF的中点，则BG的长为______cm.6．如图，在菱形ABCD中，AC，BD为菱形的对角线，∠DBC＝60°，BD＝10，点F为BC的中点，则EF的长为_____．7．已知四边形ABCD是正方形，点E在边DA的延长线上，连接CE交AB于点G，过点B作BM⊥CE，垂足为点M，BM的延长线交AD于点F，交CD的延长线于点H.(1)如图1，求证：CE＝BH；(2)如图2，若AE＝AB，连接CF，在不添加任何辅助线情况下，请直接写出图2中的四个三角形(△AEG除外)，使写出的每个三角形都与△AEG全等．8．如图，在菱形ABCD中，E，F，G，H分别是AB，BC，CD，AD上的点，且BE ＝BF＝CG＝AH.若菱形的面积等于24，BD＝8，则EF＋GH＝_____．9．如图，在矩形ABCD中，点E在DC上，DE＝BE，AC与BD相交于点O，BE与AC相交于点F.(1)若BE平分∠CBD，求证：BF⊥AC；(2)找出图中与△OBF相似的三角形，并说明理由；(3)若OF＝3，EF＝2，求DE的长度．10．(1)如图1，在矩形ABCD中，点E，F分别在边DC，BC上，AE⊥DF，垂足为点G.求证：△ADE∽△DCF.【问题解决】(2)如图2，在正方形ABCD中，点E，F分别在边DC，BC上，AE＝DF，延长BC 到点H，使CH＝DE，连接DH.求证：∠ADF＝∠H.【类比迁移】(3)如图3，在菱形ABCD中，点E，F分别在边DC，BC上，AE＝DF＝11，DE＝8，∠AED＝60°，求CF的长．参考答案1．A 2．C 3．A 4．D5．√13 6．5 7．(1)证明略 (2)略8．6解析：如图，连接AC ，交BD 于点O ，∵四边形ABCD 是菱形，BD ＝8，∴AB ＝BC ＝AD ＝CD ，AC ⊥BD ，AO ＝OC ＝12AC ，BO ＝OD ＝12BD ＝4. ∵S 菱形ABCD ＝12AC ·BD ＝24，∴AC ＝6，∴AO ＝3，∴AB ＝√AO 2+BO 2＝5＝AD .∵BE ＝BF ＝CG ＝AH ，∴AE ＝CF ＝DH ＝DG ，∴BE AE ＝BF CF ，∴EF ∥AC .同理可得GH ∥AC ，设BE ＝BF ＝CG ＝AH ＝a ，则有DH ＝5－a ，∵EF ∥AC ，∴△BEF ∽△BAC ，∴BE AB ＝EF AC ，即a 5＝EF 6，∴EF ＝65a ，同理可得DH DA ＝GH CA ，即5−a 5＝GH 6，∴GH ＝6－65a ，∴EF ＋GH ＝6.9．(1)证明略(2)与△OBF相似的三角形有△ECF，△BAF，理由略(3)DE＝3＋√1910．(1)证明：∵四边形ABCD是矩形，∴∠C＝∠ADE＝90°，∴∠CDF＋∠DFC＝90°.∵AE⊥DF，∴∠DGE＝90°，∴∠CDF＋∠AED＝90°，∴∠AED＝∠DFC，∴△ADE∽△DCF.(2)证明：∵四边形ABCD是正方形，∴AD＝DC，AD∥BC，∠ADE＝∠DCF＝90°.∵AE＝DF，∴Rt△ADE≌Rt△DCF(HL)，∴DE＝CF.∵CH＝DE，∴CF＝CH.∵点H在BC的延长线上，∴∠DCH＝∠DCF＝90°.又∵DC＝DC，∴△DCF≌△DCH(SAS)，∴∠DFC＝∠H.∵AD∥BC，∴∠ADF＝∠DFC，∴∠ADF＝∠H.(3)解：如图3，延长BC至点G，使CG＝DE＝8，连接DG，∵四边形ABCD是菱形，∴AD＝DC，AD∥BC，∴∠ADE＝∠DCG，∴△ADE≌△DCG(SAS)，∴∠DGC＝∠AED＝60°，AE＝DG. ∵AE＝DF，∴DG＝DF，∴△DFG是等边三角形，∴FG＝DF＝11.∵CF＋CG＝FG，∴CF＝FG－CG＝11－8＝3，即CF的长为3.。

矩形、菱形、正方形重点与难点：矩形、菱形、正方形的性质与判定定理。

一、知识点（1）矩形：有一个角是直角的平行四边形；菱形：有一组邻边相等的平行四边形；正方形：有一个角是直角并且有一组邻边相等的平行四边形。

（注：矩形、菱形、正方形的定义既是性质又是判定）（2）矩形的性质：矩形的四个角都是直角；矩形的对角线相等；矩形是轴对称图形菱形的性质：菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；正方形的性质：正方形既是矩形又是菱形，它具有矩形和菱形的全部性质；（3）矩形的判定：有三个角是直角的平行四边形是矩形；对角线相等的平行四边形是矩形；菱形的判定：四边都相等的四边形是菱形；对角线互相垂直的平行四边形是菱形；正方形的判定：先判定是矩形，再判定是菱形；或者先判定是菱形，再判定是矩形。

（4）直角三角形斜边上的中线等于斜边的一半；菱形的面积等于对角线乘积的半二、例题：例1、如图，矩形ABCD中，E为AD上一点，EF⊥CE交AB于F，若DE=2，矩形的周长为16，且CE=EF，求AE的长。

解：∵矩形ABCD∴∠A=∠D=90°（矩形的四个角都是直角）∴∠AEF+∠AFE=90°∵CE⊥EF∴∠AEF+∠DEC=90°∴∠AFE=∠DEC（等角的余角相等）在△AEF和△DCE中B CE D AF⎪⎩⎪⎨⎧=∠=∠∠=∠CE EF DCE AEF D A ∴△AEF ≌ △DCE（AAS ）∴AE=DC（全等三角形的对应边相等） ∴2×（AE+DE+CD ）=16 即AE=3。

例2、如图，E 是菱形ABCD 边AD 的中点，EF⊥AC 于H ，交CB 的延长线于F ，交AB 于G ，求证：AB 与EF 互相平分。

证明：∵菱形ABCD∴AC 平分∠BAD（菱形的对角线平分对角）AD 平行且等于AB （菱形四条边都相等，平行四边形的对边互相平行） ∠GAE=∠GBF，∠GFB=∠GEA（两直线平行，内错角相等）在△AEH 和△AGH 中⎪⎩⎪⎨⎧∠=∠=∠=∠EHA GHA AH AH EAHGAH ∴△AEH ≌ △AGH（ASA ） ∴AE=AG ∵AE=21AD ∴AG=21AD=21AB 即AG=AB 在△AEG 和△BFG 中⎪⎩⎪⎨⎧=∠=∠∠=∠GB GA GBF GEA FBG EAG ∴△AEG ≌ △BFG（AAS ） ∴AG=BG，EG=FGABCDEFGH例3、如图，以正方形ABCD 的DC 边为一边向外作一个等边三角形，①求证：△ABE 是等腰三角形；②求∠BAE 的度数。

菱形、矩形、正方形、梯形能力提升专题训练一． 选择题1、如图1，菱形ABCD 中，∠B ＝60°，AB ＝2㎝，E 、F 分别是BC 、CD 的中点，连结AE 、EF 、AF ，则△AEF的周长为（ ）A ．32㎝B ．33㎝C ．34㎝D ．3㎝2、如图2,等腰梯形ABCD 中，AB ∥DC ，AD=BC=8，AB=10，CD=6，则梯形ABCD 的面积是（ ）. A 、1516 B 、516 C 、1532 D 、 1716图23、如图3，正方形ABCD 的三边中点E 、F 、G 。

连ED 交AF 于M,GC 交DE 于N, 下列结论 ①GM ⊥CM , ②CD=CM ,③四边形MFCG 为等腰梯形。

④∠CMD=∠AGM 其中正确的有（ ）A ①②③B ①②④C ①③④D ①②③④4、如图5，在等腰梯形ABCD 中，AD ∥BC ，对角线AC ⊥BD 于点O ，AE ⊥BC ，DF ⊥BC ，垂足分别为E 、F ，AD ＝4，BC ＝8，则AE ＋EF 等于（ ）A ．9B ．10C ．11D ．12图55、如图6，在等腰梯形ABCD 中，AB ∥CD ， 对角线AC ⊥BC ，∠B ＝60º，BC ＝2cm ，则梯形ABCD 的面积为（ ）A ．33cm2 B ．6 cm2 C ．36cm2 D ．12 cm26、如图，在等腰梯形ABCD 中，DC ∥AB ，对角线AC 与BD 交于点O ，BE ⊥AB 交AC 的延长线于E ，EF ∥BD 交AD 的延长线于F ，下列结论：①OB=OE ；②∠AEF=2∠BAC ；③AD=DF ；④A ．1个B ．2个C ．3个D ．4个7．如图，正方形ABCD 的边长为8，M 在DC 上，且DM=2，N 是AC 上一动点，则DN+MN 的最小值为（ ）．图ABCD EFA CBD图6GN MFE DCBA图3 FEOCAB DD C BA E GF A ．8 B ．82 C ．217 D ．108．（2011重庆中考）如图，正方形ABCD 中，AB ＝6，点E 在边CD 上，且CD ＝3DE 。

一、性质1、下列性中.矩形具有而质平行四边形不一定具有的是（）A 、对边相等B 、对角相等C 、对角线相等D 、对边平行2 .在矩形ABCD 中.NAOD=130°.则NACB=__3 .已知矩形的一条对角线长是8cm.两条对角线的一个交角为60°.则矩形的周长为4 .矩形ABCD 被两条对角线分成四个小三角形.如果四个小三角形的周长的和是86cm.对角线是13cm.那么矩形的周长是5 .如图所示.矩形ABCD 中.AE ，BD 于E.Nk BAE=30°.BE=1cm.那么DE 的长为 6、直角三角形斜边上的高与中线分别是5cm 和6cm.则它的面积为7、已知.在Rt△ABC 中出口为斜边AC 上的中线.若NA=35°.那么NDBC 二。

8、如图.矩形ABCD 中.AC 与8口交于。

点.BELAC 于E.CFLBD 于F.求证：BE=CF. 9 .如口图.△ABC 中.NACB=90度.点D 、E 分别为AC 、AB 矩形的习题精选AB的中点.点F在BC延长线上.且/CDF=NA.求证：四边形DECF是平行四边形；10.已知：如图.在aABC中.NBACW90°NABC=2NC.AD±AC.交BC或CB的延长线D。

试说明：DC=2AB.11、在4ABC中.NC=90O.AC=BC.AD=BD.PE^AC于点E.PFLBC于点F。

求证：DE=DF二、判定1、下列检查一个门框是否为矩形的方法中正确的是（C）A.测量两条对角线.是否相等B.测量两条对角线.是否互相平分他用曲尺测量门框的三个角.是否都是直角口.用曲尺测量对角线.是否互相垂直2、平行四边形ABCD.E是CD的中点.4人8£是等边三角形.求证：四边形ABCD是矩形3、在平行四边形ABCD中.对角线AC、BD相交于O.EF过点O.且AF，BC. 求证：四边形AFCE是矩形4、平行四边形ABCD中.对角线AC、8口相交于点。

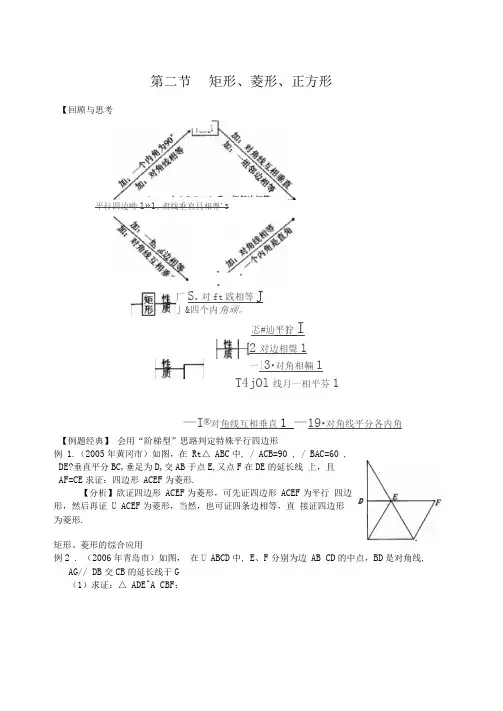
第二节 矩形、菱形、正方形厂S.对ft 践相等J」&四个内角顽。

忑#辿平狞I2对边相聲1 一|3•对角相輛1 T4jOl 线月一相平芬1—I®对角线互相垂直1 —19•对角线平分各内角【例题经典】 会用“阶梯型”思路判定特殊平行四边形例 1.（2005年黄冈市）如图，在 Rt △ ABC 中, / ACB=90 , / BAC=60 , DE?垂直平分BC,垂足为D,交AB 于点E ,又点F 在DE 的延长线 上，且AF=CE 求证：四边形 ACEF 为菱形.【分析】欲证四边形 ACEF 为菱形，可先证四边形 ACEF 为平行 四边形，然后再证 U ACEF 为菱形，当然，也可证四条边相等，直 接证四边形为菱形.矩形、菱形的综合应用例2 . （2006年青岛市）如图， 在U ABCD 中, E 、F 分别为边 AB CD 的中点，BD 是对角线,AG// DB 交CB 的延长线于G （1）求证：△ ADE^A CBF ；【回顾与思考】 平行四边呦1»1,肃线垂直且相尊'3 D(2 )若四边形BEDF 是菱形，则四边形 AGBD 是什么特殊四边形？并证明你的结论. 【解析】(1 )•••四边形ABCD 是平行四边形 •••/ 1=/ C, AD=CB AB=CD• •点E 、F 分别是AB CD 的中点，1 1 ••• AE=——AB, CF=——CD22••• AE=CF•••△ ADE^A CBF(2 )当四边形BEDF 是菱形时，四边形 AGBD 是矩形. •••四边形ABCD 是平行四边形， ••• AD// BC. • AG// BD,•••四边形AGBD 是平行四边形. •••四边形BEDF 是菱形， ••• DE=BE •/ AE=BE••• AE=BE=DE•••/ 1=/ 2,/ 3=/ 4 .• / 1+/ 2+/ 3+/ 4=180°, ••• 2 / 2+2/ 3=180° .•••/ 2+/ 3=90° . 即/ ADB=90 , •••四边形AGBD 是矩形.会解决与特殊平行四边形有关的动手操作问题 例3. （2005年吉林省）如图，在矩形纸片ABCD 中, AB=3%/3 , 落在AB 边上的点P 处，点D 落在点Q 处，AD 与PQ 相交于点 （1 ）求BE 、QF 的长.（2）求四边形PEFH 的面积.【分析】折叠型试题是近年中考试题的热点，要想解好此类题，考生必须有想像力, 抓住折叠的角与边不发生变化，必要时需要考生剪一个四边形实际折叠一下帮助理解.【考点精练】 一、基础训练1如图1,在菱形 ABCD 中，已知AB=10, AC=16那么菱形 ABCD 勺面积为 ________________ . 2. （2006年黄冈市）如图2,将边长为8cm 的正方形ABCD 勺四边沿直线L 向右滚动（不滑 动），当正方形滚动两周时，正方形的顶点 A 所经过的路线的长是 __________ cmBC=6, H,/ 沿EF 折叠后，点CBPE=30.M) GO D...1S C （£＞） 5 C（3）3 .用两个全等的直角三角形拼下列图形：①平行四边形；②矩形；③菱形；④正方形；⑤等腰三角形；⑥等边三角形；一定可以拼成的是_______________ （只填序号）. 4•如图3,点E、F是菱形ABCD勺边BC CD上的点，请你添加一个条件（？不得另外添加辅助线和字母），使AE=AF你添加的条件是___________________ .5. （2006年烟台市）如图4,先将一矩形ABCD置于直角坐标系中，使点A与坐标系的原点重合，边AB AD分别落在x轴、y轴上（如图①所示），？再将此矩形在坐标平面内按逆时针方向绕原点旋转30。

第二节矩形、菱形、正方形1. 矩形(1)定义：有一个角是直角的平行四边形叫做矩形．(2)性质：①边：对边平行且相等；②角：四个角都是直角；③对角线：对角线互相平分且相等；④对称性：矩形是中心对称图形，也是轴对称‘图形．(3)判定：①有一个角是直角的平行四边形是矩形；②对角线相等的平行四边形是矩形；③有三个角是直角的四边形是矩形．2.菱形(1)定义：有一组邻边相等的平行四边形叫做菱形．(2)性质：①边：对边平行且四边相等；②角：邻角互补，对角相等；③对角线：对角线互相垂直平分且每条对角线平分一组对角；④对称性：菱形是中心对称图形，也是轴对称图形；⑤菱形的面积等于底乘以高，或者等于对角线乘积的一半．(3)菱形的判定：①一组邻边相等的平行四边形是菱形；②对角线互相垂直的平行四边形是菱形；③四边相等的四边形是菱形．3．正方形(1)定义：有一组邻边相等，并且有一个角是直角的平行四边形叫做正方形．(2)性质：①边：对边平行，四条边都相等；②角：四个角都是直角；③对角线：两条对角线互相垂直平分且相等，每条对角线平分一组对角：④对称性：正方形是中心对称图形，也是轴对称图形． (3)判定：①有一组邻边相等的矩形是正方形；②有一个角是直角的菱形是正方形；③定义：有一组邻边相等，并且有一个角是直角的平行四边形叫做正方形． 4. 直角三角形斜边中线线等于斜边一半 5. 对角线互相垂直的四边形的性质 ①面积是对角线乘积的一半：,21S BD AC ABCD ⋅=四边形如图8-2-1所示， ②对边平方和相等：,2222AD BC CD AB +=+如图8-2-1所示．1. 平行四边形和特殊平行四边形的区别与联系(1)矩形的特殊性：①对角线相等②四个角均为ο90(2)菱形的特殊性：①对角线互相垂直且平分对角②四条边相等2．对称性矩形、菱形、正方形除了有平行四边形中心对称的性质，还有特殊的 轴对称性3．矩形中会得到两个直角三角形的性质 (1)直角三角形斜边中线等于斜边一半 (2)直角三角形中ο30所对边为斜边一半．4．区别菱形和筝形均为轴对称图形，但筝形四条边两两相等，菱形四条边都相等． 5．正方形具有中心对称性和 轴对称性例1．（山东菏泽中考）在OABCD 中，,4,3==BC AB 当口ABCD 的面积最大时，下列结论正确的有( );5=AC ①;180ο=∠+∠C A ②;BD AC ⊥③.BD AC =④①②③.A ①②④.B ②③④.C ①③④.D128--检测1.如图8-2-2所示，平行四边形ABCD 中，DQ CN BN AQ ,,,分别是,DAB ∠CDA BCD ABC ∠∠∠,,的平分线，AQ 与BN 交于P ，CN 与DQ 交于M ，证明：四边形PQMN 是矩形．例2.(新疆中考)如图8-2-3所示．口ABCD 中．,60,1,2ο=∠==ADC AD AB 将□ABCD 沿过点A 的直线l 折叠，使点D 落到AB 边上的点D 处，折痕交CD 边于点E.(1)求证：四边形BCED 是菱形；(2)若点P 是直线L 上的一个动点，请计算PB PD +的最小值，228-- 328-- 428--检测2.（哈尔滨中考）如图8-2-4所示，在菱形ABCD 中．,120ο=∠BAD 点E ，F 分别在边AB 、BC 上，△BEF 与△GEF 关于直线EF 对称，点B 的对称点是点G ．且点G 在边AD 上，若,26,=⊥AB AC EG 则FG 的长为 例3．（四川雅安中考）如图8-2-5所示，正方形ABCD 中，点E ，F 分别在BC ，CD 上，△AEF 是等边三角形，连接AC 交EF 于G ，下列结论：,DF BE =①,15ο=∠DAF ②③AC 垂直平分EF ．+BE ④,FF DF =⋅=∆∆ABE CEF S 2S ⑤其中正确结论有( )A.2个 B ．3个 C ．4个 D ．5个528-- 628--检测3.（云南昆明中考）如图8-2-6所示，在正方形ABCD 中，AC 为对角线，E 为AB 上一点，过点E 作,//AD EF与AC 、DC 分别交于点G ，F ，H 为CG 的中点，连接.,,,FH DH FH DE 下列结论：;DF EG =①;180ο=∠+∠ADH AEH ②;DHC EHF ∆≅∆③④若,32=AB AE 则,S 13S 3DHC EDH ∆∆=其中结论正确的有( )A ．1个B ．2个C ．3个D ．4个第二节 矩形、菱形、正方形（建议用时：30分钟）实战演练1．如图8-2-1所示，在一个3×3方格纸上，若以格点（即小正方形的顶点）为顶点画正方形，在该3×3方格纸上最多可画出的正方形的个数是( )A ．13个B ．14个C ．18个D ．20个2．如图8-2-2所示，在矩形ABCD 中，M ，N 分别是AD ，DC 边的中点，AN 与MC 交于P 点，若,33ο+∠=∠NBC MCB 那么∠MPA 的大小是( )ο33.A ο66.B ο45.C ο78.D128-- 228-- 328--3．（广东深圳中考）如图8-2-3所示，,90,ο=∠=ACB CA CB 点D 在边BC 上（与B ，C 不重合），四边形ADEF 为正方形，过点F 作,CA FG ⊥交CA 的延长线于点G ，连接FB ，交DE 于点Q ，给出以下结论：;FG AC =①;2:1S :S .C =∆BFG FAB 四边形②.ABF ABC ∠=∠③其中正确的个数是( )0.A 1.B 2.C 3.D4．如图8-2-4所示，过正方形ABCD 的顶点B 作,//CA BE 且作AC AE =又,//AE CF 则下列等式成立的是( )AEB BCF A ∠=∠21. AEB BCF B ∠=∠31..51.CAE BCF C ∠=∠ BFC BCF D ∠=∠. 5．如图8-2-5所示，在正方形ABCD 中，点E 是BC 边的中点，如果,5=DE 那么四边形ABED 的面积是428-- 528-- 628--6．如图8-2-6所示，四边形ABCD 为正方形，AB 为边向正方形外作等边三角形ABE ，CE 与DB 相交于点F ，则=∠AFD 度． 7．如图8-2-7所示，点P 在正方形ABCD 外，APB PB ∆=,10的面积为BPC ∆,60的面积为30．则正方形ABCD 的面积为 8．（广东广州中考）如图8-2-8所示，正方形ABCD 的边长为1，AC ，BD 是对角线．将△DCB 绕着点D 顺时针旋转ο45得到△DGH ，HG 交AB 于点E ．连接DE 交AC 于点F ．连接FG ．则下列结论：①四边形AEGF 是菱形；;GED AED ∆≅∆②;5.112ο=∠DFG ③.5.1=+FG BC ④其中正确的结论是（ ）728-- 828--9．（江苏南通中考）如图8-2-9所示，将DABCD 的边AB 延长到点E ，使,AB BE =连接DE ，交边BC 于点F. (1)求证：;CDF BEF ∆≅∆ (2)连接BD ，CE ，若.2A BFD ∠=∠ 求证：四边形BECD 是矩形．928--10.如图8-2 - 10所示，E 是正方形ABCD 中AD 边上的中点，BD 与CE 交于点F. AF 与BE 交于点G.请你根据图形判断AF 与BE 的位置具有什么关系？并给予证明．1028--11．如图8 -2 - 11所示，菱形ABCD 的对角线AC 与BD 交于点0，延长BA 到E ，使=AE ,21AB 连接OE ，延长DE交CA 的延长线于F.求证：DF OE 21=1128--12．（北京通州二模）如图8 -2 -12所示，在菱形ABCD 中，,60ο=∠ADC 点F 为CD 上任意一点（不与C ，D 重合），过点F 作CD 的垂线，交BD 于点E ，连接AE. (1)①依题意补全图8 -2 -12；②线段EF ，CF ，AE 之间的等量关系是(2)在图8-2 - 12中将△DEF 绕点D 逆时针旋转，当点C E F ,,在一条直线上时（如图8-2 -13所示），线段EF ，CE ．AE 之间的等量关系是写出判断线段EF ，CE ，AE 之间的等量关系的思路（可以不写出证明过程）1228-- 1328--拓展创新13.（四川内江中考）如图8-2 -14所示，菱形ABCD 的两条对角线分别为6和8，M ，N 分别是边BC ．CD 的中点，P是对角线BD 上一点，则PM+ PN 的最小值为 ．14218-- 1528--拓展1．如图8 -2 -15所示，在菱形ABCD 中，E a AB ,4=在BC 上，=∠=BAD a BE ,2P ,120ο点在BD 上，则PC PE +的最小值为拓展2．在边长为12的正方形ABCD 中，点P O N M ,,,分别在边DA CD BC AB ,,,上，如果,3,AP DP BM AM ==则OP NO MN ++的最小值是极限挑战14.（江苏竞赛）如图8-2 -16所示，正方形ABCD 中，E ．F 分别是BC ．CD 边上的点，AE ，AF BF DE ,,把正方形分成8小块，各小块的面积分别为,S ,,S ,S 821Λ试比较3S 与872S S S ++的大小，并说明理由．1628--答案。

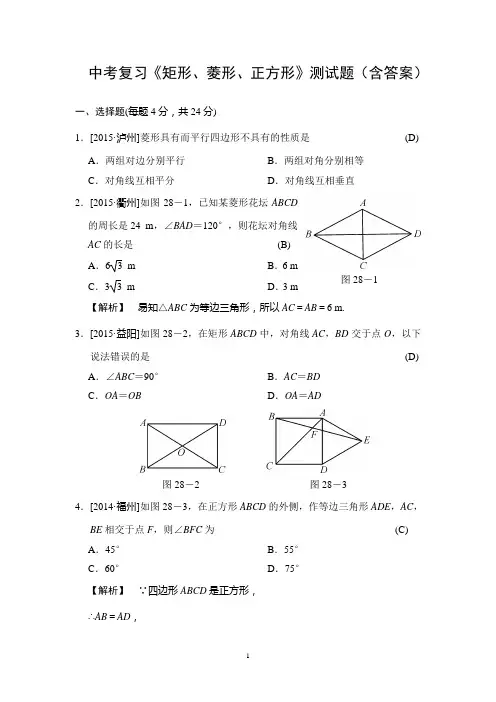
中考复习《矩形、菱形、正方形》测试题（含答案）一、选择题(每题4分，共24分)1．[2015·泸州]菱形具有而平行四边形不具有的性质是(D) A．两组对边分别平行B．两组对角分别相等C．对角线互相平分D．对角线互相垂直2．[2015·衢州]如图28－1，已知某菱形花坛ABCD的周长是24 m，∠BAD＝120°，则花坛对角线AC的长是(B)A．6 3 m B．6 m图28－1 C．3 3 m D．3 m【解析】易知△ABC为等边三角形，所以AC＝AB＝6 m.3．[2015·益阳]如图28－2，在矩形ABCD中，对角线AC，BD交于点O，以下说法错误的是(D) A．∠ABC＝90°B．AC＝BDC．OA＝OB D．OA＝AD图28－2 图28－34．[2014·福州]如图28－3，在正方形ABCD的外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为(C) A．45°B．55°C．60°D．75°【解析】∵四边形ABCD是正方形，∴AB＝AD，又∵△ADE 是等边三角形， ∴AE ＝AD ＝DE ，∠DAE ＝60°， ∴AB ＝AE ，∴∠ABE ＝∠AEB ，∠BAE ＝90°＋60°＝150°， ∴∠ABE ＝(180°－150°)÷2＝15°， 又∵∠BAC ＝45°， ∴∠BFC ＝45°＋15°＝60°.5．[2015·临沂]如图28－4，四边形ABCD 为平行四边形，延长AD 到E ，使DE ＝AD ，连结EB ，EC ，DB .添加一个条件，不能使四边形DBCE 成为矩形的是 (B) A ．AB ＝BEB ．BE ⊥DCC ．∠ADB ＝90°D ．CE ⊥DE【解析】 因为四边形ABCD 为平行四边形，所以AD 綊BC ，因为DE ＝AD ，所以DE 綊BC所以四边形EDBC 为平行四边形，A ．假若AB ＝BE ，因为AB ＝BE ，AD ＝DE ，BD ＝BD ，所以△ADB ≌△EDB ，所以∠BDE ＝90°，所以四边形EDBC 为矩形； B ．假若BE ⊥DC ，可得四边形EDBC 为菱形；C ．假若∠ADB ＝90°，所以∠EDB ＝90°，所以四边形EDBC 为矩形；D ．假若CE ⊥DE ，所以∠DEC ＝90°，所以四边形EDBC 为矩形，故选B. 6．[2015·日照]小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件①AB ＝BC ，②∠ABC ＝90°，③AC ＝BD ，④AC ⊥BD 中选两个作为补充条件，使▱ABCD 成为正方形(如图28－5)现有下列四种选法，你图28－4图28－5认为其中错误的是(B)A．①②B．②③C．①③D．②④【解析】此题考查正方形的判定，即在▱ABCD的基础上，需要再同时具备矩形和菱形的特征．①是菱形的特征；②是矩形的特征；③是矩形的特征，④是菱形的特征．而B中都是矩形的特征，故选B.二、填空题(每题4分，共20分)7．[2015·铜仁]已知一个菱形的两条对角线长分别为6 cm和8 cm，则这个菱形的面积为__24__cm2.8．[2014·衡阳]如图28－6，在矩形ABCD中，∠BOC＝120°，AB＝5，则BD的长为__10__．9．[2015·上海]已知E是正方形ABCD的对角线AC上一点，图28－6 AE＝AD，过点E作AC的垂线，交边CD于点F，那么∠F AD＝__22.5__度．10．[2014·淄博]已知▱ABCD，对角线AC，BD相交于点O，请你添加一个适当的条件，使▱ABCD成为一个菱形．你添加的条件是__AB＝BC或AC⊥BD等__．11．[2014·资阳]如图28－7，在边长为4的正方形ABCD中，E是AB边上的一点，且AE＝3，点Q为对角线AC上的动点，则△BEQ周长的最小值为__6__．图28－7【解析】如答图，连结BD，DE，∵四边形ABCD是正方形，∴点B与点D关于直线AC对称，∴DE的长即为BQ＋QE的最小值，∵DE＝BQ＋QE＝5，∴△BEQ周长的最小值＝DE＋BE＝5＋1＝6.三、解答题(共20分)12．(10分)[2015·安顺]如图28－8，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于图28－8F.(1)求证：AE＝DF；(2)若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．证明：(1)∵DE∥AC，DF∥AB，∴四边形AEDF是平行四边形，∴AE＝DF；(2)若AD平分∠BAC，四边形AEDF是菱形，理由如下：∵DE∥AC，DF∥AB，∴四边形AEDF是平行四边形，∵AD平分∠BAC，∴∠EAD＝∠F AD，∵AE∥DF，∴∠EAD＝ADF，∠DAF＝∠FDA，∴AF＝DF，∴平行四边形AEDF为菱形．13．(10分)[2015·青岛]已知：如图28－9，在△ABC中，AB ＝AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为E.(1)求证：△ABD≌△CAE；图28－9(2)连结DE ，线段DE 与AB 之间有怎样的位置和数量关系？请证明你的结论． 解：(1)证明：∵AB ＝AC ，AD 是BC 边上的中线， ∴AD ⊥BC ，BD ＝CD . ∵AE ∥BC ，CE ⊥AE ， ∴四边形ADCE 是矩形， ∴AD ＝CE .在Rt △ABD 与Rt △CAE 中， ⎩⎪⎨⎪⎧AD ＝CE ，AB ＝CA ，∴△ABD ≌△CAE (HL )；(2)DE ∥AB ，DE ＝AB .证明如下： 如答图所示，∵四边形ADCE 是矩形， ∴AE ＝CD ＝BD ，AE ∥BD ， ∴四边形ABDE 是平行四边形， ∴DE ∥AB ，DE ＝AB .14．(10分)[2014·扬州]如图28－10，已知Rt △ABC ，∠ABC ＝90°，先把△ABC 绕点B 顺时针旋转90°后至△DBE ，再把△ABC 沿射线AB 平移至△FEG ，DE ，FG 相交于点H .(1)判断线段DE ，FG 的位置关系，并说明理由； (2)连结CG ，求证：四边形CBEG 是正方形． 解：(1)DE ⊥FG ，理由如下：由题意得∠A ＝∠EDB ＝∠GFE ，∠ABC ＝∠DBE ＝90°，第13题答图图28－10∴∠BDE＋∠BED＝90°.∴∠GFE＋∠BED＝90°，∴∠FHE＝90°，即DE⊥FG；(2)证明：∵△ABC沿射线AB平移至△FEG，∴CB∥GE，CB＝GE.∴四边形CBEG是平行四边形．∵∠ABC＝∠GEF＝90°，∴四边形CBEG是矩形．∵BC＝BE，∴四边形CBEG是正方形．15．(10分)[2015·南京]如图28－11，AB∥CD，点E，F分别在AB，CD上，连结EF，∠AEF，∠CFE的平分线交于点G，∠BEF，∠DFE的平分线交于点H.(1)求证：四边形EGFH是矩形；(2)小明在完成(1)的证明后继续进行了探索，过G作MN∥EF，分别交AB，CD于点M，N，过H作PQ∥EF，分别交AB，CD交于点P，Q，得到四边形MNQP.此时，他猜想四边形MNQP是菱形，请在下列框图中补全他的证明思路．小明的证明思路由AB∥CD，MN∥EF，易证四边形MNQP是平行四边形，要证▱MNQP是菱形，只要证MN＝NQ.由已知条件__FG平分∠CFE__，MN∥EF，可证NG＝NF，故只要证GM＝FQ，即证△MEG≌△QFH，易证__GE＝FH__，__∠GME ＝∠FQH__.故只要证∠MGE＝∠QFH.易证∠MGE＝∠GEF，∠QFH＝∠EFH，__∠GEF＝∠EFH__，即可得证．图28－11解：(1)证明：∵EH平分∠BEF.∴∠FEH＝12∠BEF，∵FH平分∠DFE，∴∠EFH＝12∠DFE，∵AB∥CD，∴∠BEF＋∠DFE＝180°，∴∠FEH＋∠EFH＝12(∠BEF＋∠DFE)＝12×180°＝90°，又∵∠FEH＋∠EFH＋∠EHF＝180°，∴∠EHF＝180°－(∠FEH＋∠EFH)＝180°－90°＝90°，同理可证，∠EGF＝90°，∵EG平分∠AEF，∴∠FEG＝12∠AEF，∵EH平分∠BEF，∴∠FEH＝12∠BEF，∵点A，E，B在同一条直线上．∴∠AEB＝180°，即∠AEF＋∠BEF＝180°.∴∠FEG＋∠FEH＝12(∠AEF＋∠BEF)＝12×180°＝90°，即∠GEH＝90°.∴四边形EGFH是矩形；(2)本题答案不唯一，下列解法供参考．例如，FG平分∠CFE；GE＝FH；∠GME ＝∠FQH；∠GEF＝∠EFH.16．(6分)[2015·资阳]若顺次连结四边形ABCD四边的中点，得到的图形是一个矩形，则四边形ABCD一定是(D) A．矩形B．菱形C．对角线相等的四边形D．对角线互相垂直的四边形17．(10分)如图28－12，在菱形ABCD中，边长为10，∠A＝60°.顺次连结菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；…；按此规律继续下去，则四边形A2B2C2D2的周长是__20__；四边形A2 016B2 016C2 016D2 016的周长是__521 005__．图28－12。

特殊的平行四边形——矩形、菱形、正方形专题培优、能力提升复习讲义中考考点梳理一、矩形1、矩形的概念有一个角是直角的平行四边形叫做矩形。

2、矩形的性质（1）具有平行四边形的一切性质（2）矩形的四个角都是直角（3）矩形的对角线相等（4）矩形是轴对称图形3、矩形的判定（1）定义：有一个角是直角的平行四边形是矩形（2）定理1：有三个角是直角的四边形是矩形（3）定理2：对角线相等的平行四边形是矩形4、矩形的面积：S矩形=长×宽=ab二、菱形1、菱形的概念有一组邻边相等的平行四边形叫做菱形。

2、菱形的性质（1）具有平行四边形的一切性质（2）菱形的四条边相等（3）菱形的对角线互相垂直，并且每一条对角线平分一组对角（4）菱形是轴对称图形3、菱形的判定（1）定义：有一组邻边相等的平行四边形是菱形（2）定理1：四边都相等的四边形是菱形（3）定理2：对角线互相垂直的平行四边形是菱形4、菱形的面积：S菱形=底边长×高=两条对角线乘积的一半三、正方形1、正方形的概念有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。

2、正方形的性质（1）具有平行四边形、矩形、菱形的一切性质（2）正方形的四个角都是直角，四条边都相等（3）正方形的两条对角线相等，并且互相垂直平分，每一条对角线平分一组对角（4）正方形是轴对称图形，有4条对称轴（5）正方形的一条对角线把正方形分成两个全等的等腰直角三角形，两条对角线把正方形分成四个全等的小等腰直角三角形（6）正方形的一条对角线上的一点到另一条对角线的两端点的距离相等。

3、正方形的判定（1）判定一个四边形是正方形的主要依据是定义，途径有两种：先证它是矩形，再证有一组邻边相等。

先证它是菱形，再证有一个角是直角。

（2）判定一个四边形为正方形的一般顺序如下：第一步：先证明它是平行四边形；第二步：再证明它是菱形（或矩形）；第三步：最后证明它是矩形（或菱形）4、正方形的面积： 设正方形边长为a ，对角线长为b ，S 正方形=222b a 中考典例精选考点典例一、矩形的性质与判定【例1】如图，矩形ABCD 的对角线AC 、BD 相交于点O ,若AB ＝AO ， 求∠ABD 的度数.图6A B 【答案】∠ABD =60°.【解析】考点：矩形的性质；等边三角形的判定及性质.【点睛】此题考查了等边三角形的判定与性质，矩形的性质，熟练掌握等边三角形的判定与性质是解本题的关键．【举一反三】1.已知：如图，在矩形ABCD中，点E在边AB上，点F在边BC上，且BE=CF，EF⊥DF，求证：BF=CD．【答案】详见解析.【解析】试题分析：由四边形ABCD为矩形，得到四个角为直角，再由EF与FD垂直，利用平角定义得到一对角互余，利用同角的余角相等得到一对角相等，利用ASA得到△BEF≌△CFD，利用全等三角形对应边相等即可得证．考点：矩形的性质；全等三角形的判定与性质．2. 如图，将矩形ABCD 沿GH 对折，点C 落在Q 处，点D 落在E 处，EQ 与BC 相交于F ．若AD=8cm ，AB=6cm ，AE=4cm ．则△EBF 的周长是 cm ．【答案】8.【解析】试题分析：BE=AB-AE=2.设AH=x ，则DH=AD ﹣AH=8﹣x ，在Rt △AEH 中，∠EAH=90°，AE=4，AH=x ，EH=DH=8﹣x ，∴EH 2=AE 2+AH 2，即（8﹣x ）2=42+x 2，解得：x=3．∴AH=3，EH=5.∴C △AEH =12.∵∠BFE+∠BEF=90°，∠BEF+∠AEH=90°，∴∠BFE=∠AEH ．又∵∠EAH=∠FBE=90°，∴△EBF ∽△HAE ，∴32==∆∆AH BE C C HAE EFB ． ∴C △EBF =23=C △HAE =8．考点：1折叠问题；2勾股定理；3相似三角形.考点典例二、菱形的性质与判定【例2】如图，在▱ABCD中，已知AD＞AB．（1）实践与操作：作∠BAD的平分线交BC于点E，在AD上截取AF=AB，连接EF；（要求：尺规作图，保留作图痕迹，不写作法）（2）猜想并证明：猜想四边形ABEF的形状，并给予证明．【答案】(1)详见解析；（2）四边形ABEF是菱形，理由详见解析.【解析】（2）四边形ABEF是菱形；理由如下：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠DAE=∠AEB，∵AE平分∠BAD，∴∠BAE=∠DAE，∴∠BAE=∠AEB，∴BE=AB，由（1）得：AF=AB，∴BE=AF，又∵BE ∥AF ，∴四边形ABEF 是平行四边形，∵AF=AB ，∴四边形ABEF 是菱形．考点：角平分线的画法；平行四边形的性质；菱形的判定.【点睛】本题考查了平行四边形的性质，菱形的判定，熟记各性质与平行四边形和菱形的判定方法是解题的关键．在利用菱形计算或证明时，应充分利用菱形的性质，如“菱形的四条边都相等”“菱形的对角线互相垂直且平分，并且每一组对角线平分一组对角”等.对于菱形的判定，若可证出四边形为平行四边形，则可证一组邻边相等或对角线互相垂直；若相等的边较多，则可证四条边都相等.【举一反三】1. 如图，四边形ABCD 是菱形，8=AC ，6=DB ，AB DH ⊥于H ，则DH 等于A ．524 B ．512 C ．5 D ．4【答案】A.【解析】 考点：菱形的性质.2. 如图，菱形ABCD 的边AB=8，∠B=60°，P 是AB 上一点，BP=3，Q 是CD 边上一动点，将梯形APQD 沿直线PQ 折叠，A 的对应点为A ′，当CA ′的长度最小时，CQ 的长为（ ）A. 5B. 7C. 8D. 213 CD H【答案】B．【解析】考点：菱形的性质；轴对称（折叠）；等边三角形的判定和性质；最值问题．考点典例三、正方形的性质与判定【例3】如图，在四边形ABCD中，AB＝BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N.(1)求证：∠ADB＝∠CDB；(2)若∠ADC＝90°，求证：四边形MPND是正方形．【答案】证明见解析.【解析】考点：正方形的判定；全等三角形的判定与性质．【点睛】本题考查了全等三角形的判定和性质、角平分线的性质、矩形的判定和性质以及正方形的判定，解题的关键是熟记各种几何图形的性质和判定．正方形是特殊的矩形又是特殊的菱形，具有矩形和菱形的所有性质.证明一个四边形是正方形，可以先判定为矩形，再证邻边相等或对角线互相垂直；或先判定为菱形，再证有一个角是直角或对角线相等.【举一反三】1.如图，正方形ABCD的边长为10，AG=CH=8，BG=DH=6，连接GH，则线段GH的长为（）A．B．2 C．D．10﹣5【答案】B.【解析】考点：正方形的性质；全等三角形的判定及性质；勾股定理.考点典例四、特殊平行四边形综合题【例4】如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE ⊥BC，交直线MN于E，垂足为F，连接CD，BE.(1)求证：CE＝AD；(2)当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由；(3)若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．【答案】（1）证明见解析；（2）四边形BECD是菱形，（3）当∠A=45°时，四边形BECD是正方形．理由见解析.【解析】（3）当∠A=45°时，四边形BECD是正方形，理由是：考点：正方形的判定；平行四边形的判定与性质；菱形的判定．【点睛】本题考查了正方形的判定、平行四边形的性质和判定，菱形的判定，直角三角形的性质的应用，主要考查学生运用定理进行推理的能力． 【举一反三】如图，正方形ABCD 的边长为1,AC 、BD 是对角线，将△DCB 绕点D 顺时针旋转450得到△DGH ， HG 交AB 于点E ，连接DE 交AC 于点F ，连接FG ，则下列结论：①四边形AEGF 是菱形 ②△AED ≌△GED③∠DFG ＝112.5︒ ④BC ＋FG ＝1.5其中正确的结论是 .（填写所有正确结论的序号）图5F EH G BA【答案】①②③. 【解析】试题分析：由旋转的性质可得HD=BD=2 ∴HA=12-考点：旋转的性质；全等三角形的判定及性质；菱形的判定.课后巩固、提高自测小练习一、选择题1．关于ABCD的叙述，正确的是（）A．若AB⊥BC ABCD是菱形B．若AC⊥BD ABCD是正方形C．若AC=BD，则ABCD是矩形D．若AB=AD ABCD是正方形【答案】C.【解析】试题分析：根据矩形的判定可得A、C项应是矩形；根据菱形的判定可得B、D项应是菱形,故答案选C.考点：矩形、菱形的判定.2. 下列说法正确的是（）A．对角线互相垂直的四边形是菱形B．矩形的对角线互相垂直C．一组对边平行的四边形是平行四边形D．四边相等的四边形是菱形【答案】D.【解析】考点：1菱形的判定；2矩形的性质；3平行四边形的判定.3．如图，在周长为12的菱形ABCD中，AE=1，AF=2，若P为对角线BD上一动点，则EP+FP的最小值为（）A．1 B．2 C．3 D．4【答案】C.【解析】试题分析：作F点关于BD的对称点F′，则PF=PF′，连接EF′交BD于点P．此时，EP+FP的值最小，值为EF′．∵四边形ABCD为菱形，∴AB=BC=CD=DA=3，AB∥CD，∵AF=2，AE=1，∴DF=AE=1，∴四边形AEF′D是平行四边形，∴EF′=AD=3．∴EP+FP的最小值为3．故选：C．考点：1轴对称；2菱形.4.如图，在▱ABCD中，对角线AC与BD交于点O，若增加一个条件，使▱ABCD成为菱形，下列给出的条件不正确的是（ ）A ．AB =AD B ．AC ⊥BD C ．AC =BD D ．∠BAC =∠DAC 【答案】C ． 【解析】考点：菱形的判定；平行四边形的性质．5. 如图，正方形ABCD 中，AB =6，点E 在边CD 上，且CE =2DE ．将△ADE 沿AE 对折至△AFE ，延长EF 交边BC 于点G ，连结AG 、CF ．下列结论：①△ABG ≌△AFG ；②BG =GC ；③EG =DE +BG ；④AG ∥CF ；⑤S △FGC =3.6．其中正确结论的个数是（ ）A ．2B ．3C ．4D ．5 【答案】D ． 【解析】试题分析：∵正方形ABCD 的边长为6，CE =2DE ，∴DE =2，EC =4，∵把△ADE 沿AE 折叠使△ADE 落在△AFE 的位置，∴AF =AD =6，EF =ED =2，∠AFE =∠D =90°，∠FAE =∠DAE ，在Rt △ABG 和Rt △AFG 中，∵AB =AF ，AG =AG ，∴Rt △ABG ≌Rt △AFG （HL ），∴GB =GF ，∠BAG =∠FAG ，∴∠GAE =∠FAE +∠FAG =12∠BAD =45°，所以①正确； 设BG =x ，则GF =x ，C =BC ﹣BG =6﹣x ，在Rt △CGE 中，GE =x +2，EC =4，CG =6﹣x ，∵222CG CE GE +=，∴222(6)4(2)x x-+=+，解得x=3，∴BG=3，CG=6﹣3=3，∴BG=CG，所以②正确；∵EF=ED，GB=GF，∴GE=GF+EF=BG+DE，所以③正确；∵GF=GC，∴∠GFC=∠GCF，又∵Rt△ABG≌Rt△AFG，∴∠AGB=∠AGF，而∠BGF=∠GFC+∠GCF，∴∠AGB+∠AGF=∠GFC+∠GCF，∴∠AGB=∠GCF，∴CF∥AG，所以④正确；过F作FH⊥DC．∵BC⊥DH，∴FH∥GC，∴△EFH∽△EGC，∴EH EFGC EG=，EF=DE=2，GF=3，∴EG=5，∴△EFH∽△EGC，∴相似比为：EH EFGC EG==25，∴S△FGC=S△GCE﹣S△FEC=12×3×4﹣12×4×（25×3）=3.6，所以⑤正确．故正确的有①②③④⑤，故选D．考点：翻折变换（折叠问题）；全等三角形的判定与性质；正方形的性质．6.小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形，她对折了（）A．1次B．2次C．3次D．4次【答案】B．【解析】考点：翻折变换（折叠问题）．7.菱形具有而一般平行四边形不具有的性质是（）A．对边相等B．对角相等C．对角线互相平分D．对角线互相垂直【答案】D．【解析】考点：菱形的性质；平行四边形的性质．8.如图，将△ABC沿BC方向平移得到△DCE，连接AD，下列条件能够判定四边形ACED为菱形的是（）A．AB=BC B．AC=BC C．∠B=60°D．∠ACB=60°【答案】B．【解析】试题分析：∵将△ABC沿BC方向平移得到△DCE，∴AB//CD，∴四边形ABCD为平行四边形，当AC=BC时，平行四边形ACED是菱形．故选B．考点：菱形的判定；平移的性质．二、填空题1.如图，四边形ABCD是轴对称图形，且直线AC是对称轴，AB∥CD，则下列结论：①AC⊥BD；②AD∥BC；③四边形ABCD是菱形；④△ABD≌△CDB．其中正确的是（只填写序号）【答案】①②③④.【解析】考点：1菱形的性质和判定；2轴对称；3平行线的性质.2. 如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE⊥BD，垂足为点E，若∠EAC=2∠CAD，则∠BAE=度．【答案】22.5°．【解析】试题分析：已知四边形ABCD是矩形，由矩形的性质可得AC=BD，OA=OC，OB=OD，即可得OA=OB═OC，由等腰三角形的性质可得∠OAC=∠ODA，∠OAB=∠OBA，即可得∠AOE=∠OAC+∠OCA=2∠OAC，再由∠EAC=2∠CAD，可得∠EAO=∠AOE，因AE⊥BD，可得∠AEO=90°，所以∠AOE=45°，所以∠OAB=∠OBA=67.5°，即∠BAE=∠OAB ﹣∠OAE=22.5°．考点：矩形的性质；等腰三角形的性质．3. 如图，边长为1的正方形ABCD的对角线AC、BD相交于点O．有直角∠MPN，使直角顶点P与点O重合，直角边PM、PN分别与OA、OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是．（1）EF=OE；（2）S四边形OEBF：S正方形ABCD=1：4；（3）BE+BF=OA；（4）在旋转过程中，当△BEF与△COF的面积之和最大时，AE=；（5）OG•BD=AE2+CF2．【答案】（1），（2），（3），（5）．【解析】1（2）∵S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=S正方形ABCD，4∴S四边形OEBF：S正方形ABCD=1：4；故正确；（3）∴BE+BF=BF+CF=BC=2OA；故正确；（5）∵∠EOG=∠BOE，∠OEG=∠OBE=45°，∴△OEG∽△OBE，∴OE：OB=OG：OE，∴OG•OB=OE2，∵OB=12BD，OE=22EF，∴OG•BD=EF2，∵在△BEF中，EF2=BE2+BF2，∴EF2=AE2+CF2，∴OG•BD=AE2+CF2．故正确．考点：四边形综合题．4.如图，已知菱形ABCD的两条对角线长分别为AC=8和BD=6，那么，菱形ABCD的面积为．【答案】24． 【解析】试题分析：根据菱形面积等于两条对角线的长度的乘积的一半即可得，菱形的面积=21×6×8=24. 考点：菱形的性质．5．将矩形ABCD 纸片按如图所示的方式折叠，EF ，EG 为折痕，试问∠AEF +∠BEG = ．【答案】90°． 【解析】考点：翻折变换（折叠问题）．6. 如图，四边形OABC 为矩形，点A ，C 分别在x 轴和y 轴上，连接AC ，点B 的坐标为（4，3），∠CAO 的平分线与y 轴相交于点D ，则点D 的坐标为 ．【答案】（0，43）．【解析】考点：矩形的性质；坐标与图形性质．三、解答题1.如图，矩形ABCD中，延长AB至E，延长CD至F，BE=DF，连接EF，与BC、AD分别相交于P、Q两点．（1）求证：C P=AQ；（2）若BP=1，PQ=22，∠AEF=45°，求矩形ABCD的面积．【答案】（1）证明见解析；（2）8．【解析】考点：矩形的性质；全等三角形的判定与性质．2.如图，点P在矩形ABCD的对角线AC上，且不与点A，C重合，过点P分别作边AB，AD的平行线，交两组对边于点E，F和G，H．（1）求证：△PHC≌△CFP；（2）证明四边形PEDH和四边形PFBG都是矩形，并直接写出它们面积之间的关系．【答案】（1）证明见解析；（2）证明见解析，面积相等．【解析】试题分析：（1）由矩形的性质得出对边平行，再根据平行线的性质得出相等的角，结合全等三角形的判定定理AAS即可得出△PHC≌△CFP；（2）由矩形的性质找出∠D=∠B=90°，再结合对边互相平行即可证出四边形PEDH和四边形PFBG都是矩形，通过角的正切值，在直角三角形中表示出直角边的关系，利用矩形的面积公式即可得出两矩形面积相等．考点：矩形的判定与性质；全等三角形的判定与性质．3.如图，四边形ABCD是正方形，点E是BC的中点，∠AEF=90°，EF交正方形外角的平分线CF于F．求证：A E=EF．【答案】证明见解析．【解析】试题分析：先取AB的中点H，连接EH，根据∠AE F=90°和ABCD是正方形，得出∠1=∠2，再根据E是BC 的中点，H是AB的中点，得出BH=BE，AH=CE，最后根据CF是∠DCG的角平分线，得出∠AHE=∠ECF=135°，从而证出△AHE≌△ECF，即可得出AE=EF．试题解析：取AB的中点H，连接EH．∵∠AEF=90°，∴∠2+∠AEB=90°，∵四边形ABCD是正方形，∴∠1+∠AEB=90°，∴∠1=∠2，∵E是BC的中点，H是AB的中点，∴BH=BE，AH=CE，∴∠BHE=45°，∵CF是∠DCG的角平分线，∴∠FCG=45°，∴∠AHE=∠ECF=135°，在△AHE和△ECF中，∵∠1=∠2，AH=EC，∠AHE=∠ECF，∴△AHE≌△ECF（ASA），∴AE=EF．考点：正方形的性质；全等三角形的判定与性质．4. 如图，△ABC≌△ABD，点E在边AB上，CE∥BD，连接DE．求证：（1）∠CEB=∠CBE；（2）四边形BCED是菱形．【答案】详见解析.【解析】∵CE∥BD，∴四边形CEDB是平行四边形，∵BC=BD，∴四边形CEDB是菱形．考点：全等三角形的性质；菱形的判定．。

矩形、菱形与正方形一、选择题1．矩形具有而菱形不具有的性质是（）A．两组对边分别平行 B．对角线相等C．对角线互相平分D．两组对角分别相等2．如图，在△ABC中，AC=BC，点D、E分别是边AB、AC的中点，将△ADE绕点E旋转180°得△CFE，则四边形ADCF一定是（）A．矩形 B．菱形 C．正方形D．梯形3．如图，在矩形ABCD中，AD=2AB，点M、N分别在边AD、BC上，连接BM、DN．若四边形MBND是菱形，则等于（）A．B．C．D．4．如图，四边形ABCD是菱形，对角线AC=8cm，BD=6cm，DH⊥AB于点H，且DH与AC交于G，则GH=（）A． cm B． cm C． cm D． cm5．如图所示，E、F分别是正方形ABCD的边CD，AD上的点，且CE=DF，AE，BF相交于点O，下列结论①AE=BF；②AE⊥BF；③AO=OE；④S△AOB=S四边形DEOF中，错误的有（）A．1个B．2个C．3个D．4个二、填空题6．若菱形的两条对角线分别为2和3，则此菱形的面积是．7．在矩形ABCD中，对角线AC、BD相交于点O，若∠AOB=60°，AC=10，则AB= ．8．如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°＜α＜90°），若∠1=110°，则∠α= ．9．如图，在正方形ABCD中，E是AB上一点，BE=2，AE=3BE，P是AC上一动点，则PB+PE的最小值是．10．如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD上，下列结论：①CE=CF；②∠AEB=75°；③BE+DF=EF；④S正方形ABCD=2+．其中正确的序号是（把你认为正确的都填上）．三、解答题（共40分）11．如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．（1）线段BD与CD有什么数量关系，并说明理由；（2）当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．12．如图，在△ABC中，D、E分别是AB、AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF．（1）求证：四边形BCFE是菱形；（2）若CE=4，∠BCF=120°，求菱形BCFE的面积．13．如图1，在正方形ABCD中，E、F分别是边AD、DC上的点，且AF⊥BE．（1）求证：AF=BE；（2）如图2，在正方形ABCD中，M、N、P、Q分别是边AB、BC、CD、DA上的点，且MP⊥NQ．MP与NQ是否相等？并说明理由．14．如图，在边长为3的正方形ABCD中，点E是BC边上的点，BE=1，∠AEP=90°，且EP交正方形外角的平分线CP于点P，交边CD于点F，（1）的值为；（2）求证：AE=EP；（3）在AB边上是否存在点M，使得四边形DMEP是平行四边形？若存在，请给予证明；若不存在，请说明理由．矩形、菱形与正方形参考答案与试题解析一、选择题1．矩形具有而菱形不具有的性质是（）A．两组对边分别平行 B．对角线相等C．对角线互相平分D．两组对角分别相等【考点】矩形的性质；菱形的性质．【分析】根据矩形与菱形的性质对各选项分析判断后利用排除法求解．【解答】解：A、矩形与菱形的两组对边都分别平行，故本选项错误；B、矩形的对角线相等，菱形的对角线不相等，故本选项正确；C、矩形与菱形的对角线都互相平分，故本选项错误；D、矩形与菱形的两组对角都分别相等，故本选项错误．故选B．【点评】本题考查了矩形的性质，菱形的性质，熟记两图形的性质是解题的关键．2．如图，在△ABC中，AC=BC，点D、E分别是边AB、AC的中点，将△ADE绕点E旋转180°得△CFE，则四边形ADCF一定是（）A．矩形 B．菱形 C．正方形D．梯形【考点】旋转的性质；矩形的判定．【分析】根据旋转的性质可得AE=CE，DE=EF，再根据对角线互相平分的四边形是平行四边形判断出四边形ADCF是平行四边形，然后利用等腰三角形三线合一的性质求出∠ADC=90°，再利用有一个角是直角的平行四边形是矩形解答．【解答】解：∵△ADE绕点E旋转180°得△CFE，∴AE=CE，DE=EF，∴四边形ADCF是平行四边形，∵AC=BC，点D是边AB的中点，∴∠ADC=90°，∴四边形ADCF是矩形．故选：A．【点评】本题考查了旋转的性质，矩形的判定，主要利用了对角线互相平分的四边形是平行四边形，有一个角是直角的平行四边形是矩形的判定方法，熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键．3．如图，在矩形ABCD中，AD=2AB，点M、N分别在边AD、BC上，连接BM、DN．若四边形MBND是菱形，则等于（）A．B．C．D．【考点】勾股定理；菱形的性质；矩形的性质．【分析】首先由菱形的四条边都相等与矩形的四个角是直角，即可得到直角△ABM中三边的关系．【解答】解：∵四边形MBND是菱形，∴MD=MB．∵四边形ABCD是矩形，∴∠A=90°．设AB=x，AM=y，则MB=2x﹣y，（x、y均为正数）．在Rt△ABM中，AB2+AM2=BM2，即x2+y2=（2x﹣y）2，解得x=y，∴MD=MB=2x﹣y=y，∴==．故选：C．【点评】此题考查了菱形与矩形的性质，以及直角三角形中的勾股定理．解此题的关键是注意数形结合思想与方程思想的应用．4．如图，四边形ABCD是菱形，对角线AC=8cm，BD=6cm，DH⊥AB于点H，且DH与AC交于G，则GH=（）A． cm B． cm C． cm D． cm【考点】菱形的性质；勾股定理；解直角三角形．【分析】先求出菱形的边长，然后利用面积的两种表示方法求出DH，在Rt△DHB中求出BH，然后得出AH，利用tan∠HAG的值，可得出GH的值．【解答】解：∵四边形ABCD是菱形，对角线AC=8cm，BD=6cm，∴AO=4cm，BO=3cm，在Rt△AOB中，AB==5cm，∵BD×AC=AB×DH，∴DH=cm，在Rt△DHB中，BH==cm，则AH=AB﹣BH=cm，∵tan∠HAG===，∴GH=AH=cm．故选：B．【点评】本题考查了菱形的性质、解直角三角形及三角函数值的知识，注意菱形的面积等于对角线乘积的一半，也等于底乘高．5．如图所示，E、F分别是正方形ABCD的边CD，AD上的点，且CE=DF，AE，BF相交于点O，下列结论①AE=BF；②AE⊥BF；③AO=OE；④S△AOB=S四边形DEOF中，错误的有（）A．1个B．2个C．3个D．4个【考点】正方形的性质．【分析】根据四边形ABCD是正方形及CE=DF，可证出△ADE≌△BAF，则得到：①AE=BF，以及△ADE 和△BAF的面积相等，得到；④S△AOB=S四边形DEOF；可以证出∠ABO+∠BAO=90°，则②AE⊥BF一定成立．错误的结论是：③AO=OE．【解答】解：∵四边形ABCD是正方形，∴CD=AD∵CE=DF∴DE=AF∴△ADE≌△BAF∴AE=BF（故①正确），S△ADE=S△BAF，∠DEA=∠AFB，∠EAD=∠FBA∵S△AOB=S△BAF﹣S△AOF，S四边形DEOF=S△ADE﹣S△AOF，∴S△AOB=S四边形DEOF（故④正确），∵∠ABF+∠AFB=∠DAE+∠D EA=90°∴∠AFB+∠EAF=90°∴AE⊥BF一定成立（故②正确）．假设AO=OE，∵AE⊥BF（已证），∴AB=BE（线段垂直平分线上的点到线段两端点的距离相等），∵在Rt△BCE中，BE＞BC，∴AB＞BC，这与正方形的边长AB=BC相矛盾，∴，假设不成立，AO≠OE（故③错误）；故错误的只有一个．故选：A．【点评】本题考查了正方形的四条边都相等，每一个角都是直角的性质，全等三角形的判定与性质，综合题但难度不大，求出△ADE≌△BAF是解题的关键，也是本题的突破口．二、填空题6．若菱形的两条对角线分别为2和3，则此菱形的面积是 3 ．【考点】菱形的性质．【分析】菱形的面积是对角线乘积的一半，由此可得出结果即可．【解答】解：由题意，知：S菱形=×2×3=3，故答案为：3．【点评】本题考查了菱形的面积两种求法：（1）利用底乘以相应底上的高；（2）利用菱形的特殊性，菱形面积=×两条对角线的乘积；具体用哪种方法要看已知条件来选择．7．在矩形ABCD中，对角线AC、BD相交于点O，若∠AOB=60°，AC=10，则AB= 5 ．【考点】含30度角的直角三角形；矩形的性质．【分析】根据矩形的性质，可以得到△AOB是等边三角形，则可以求得OA的长，进而求得AB的长．【解答】解：∵四边形ABCD是矩形，∴OA=OB又∵∠AOB=60°∴△AOB是等边三角形．∴AB=OA=AC=5，故答案是：5．【点评】本题考查了矩形的性质，正确理解△AOB是等边三角形是关键．8．如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°＜α＜90°），若∠1=110°，则∠α= 20°．【考点】旋转的性质；矩形的性质．【分析】根据矩形的性质得∠B=∠D=∠BAD=90°，根据旋转的性质得∠D′=∠D=90°，∠4=α，利用对顶角相等得到∠1=∠2=110°，再根据四边形的内角和为360°可计算出∠3=70°，然后利用互余即可得到∠α的度数．【解答】解：如图，∵四边形ABCD为矩形，∴∠B=∠D=∠BAD=90°，∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′D′，∴∠D′=∠D=90°，∠4=α，∵∠1=∠2=110°，∴∠3=360°﹣90°﹣90°﹣110°=70°，∴∠4=90°﹣70°=20°，∴∠α=20°．故答案为：20°．【点评】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了矩形的性质．9．如图，在正方形ABCD中，E是AB上一点，BE=2，AE=3BE，P是AC上一动点，则PB+PE的最小值是10 ．【考点】轴对称﹣最短路线问题；正方形的性质．【分析】由正方形性质的得出B、D关于AC对称，根据两点之间线段最短可知，连接DE，交AC于P，连接BP，则此时PB+PE的值最小，进而利用勾股定理求出即可．【解答】解：如图，连接DE，交AC于P，连接BP，则此时PB+PE的值最小．∵四边形ABCD是正方形，∴B、D关于AC对称，∴PB=PD，∴PB+PE=PD+PE=DE．∵BE=2，AE=3BE，∴AE=6，AB=8，∴DE==10，故PB+PE的最小值是10．故答案为：10．【点评】本题考查了轴对称﹣最短路线问题，正方形的性质，解此题通常是利用两点之间，线段最短的性质得出．10．如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD上，下列结论：①CE=CF；②∠AEB=75°；③BE+DF=EF；④S正方形ABCD=2+．其中正确的序号是①②④（把你认为正确的都填上）．【考点】正方形的性质；全等三角形的判定与性质；等边三角形的性质．【专题】压轴题．【分析】根据三角形的全等的知识可以判断①的正误；根据角角之间的数量关系，以及三角形内角和为180°判断②的正误；根据线段垂直平分线的知识可以判断③的正误，利用解三角形求正方形的面积等知识可以判断④的正误．【解答】解：∵四边形ABCD是正方形，∴AB=AD，∵△AEF是等边三角形，∴AE=AF，在Rt△ABE和Rt△ADF中，，∴Rt△ABE≌Rt△ADF（HL），∴BE=DF，∵BC=DC，∴BC﹣BE=CD﹣DF，∴CE=CF，∴①说法正确；∵CE=CF，∴△ECF是等腰直角三角形，∴∠CEF=45°，∵∠AEF=60°，∴∠AEB=75°，∴②说法正确；如图，连接AC，交EF于G点，∴AC⊥EF，且AC平分EF，∵∠CAF≠∠DAF，∴DF≠FG，∴BE+DF≠EF，∴③说法错误；∵EF=2，∴CE=CF=，设正方形的边长为a，在Rt△ADF中，AD2+DF2=AF2，即a2+（a﹣）2=4，解得a=，则a2=2+，S正方形ABCD=2+，④说法正确，故答案为：①②④．【点评】本题主要考查正方形的性质的知识点，解答本题的关键是熟练掌握全等三角形的证明以及辅助线的正确作法，此题难度不大，但是有一点麻烦．三、解答题（共40分）11．如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．（1）线段BD与CD有什么数量关系，并说明理由；（2）当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．【考点】矩形的判定；全等三角形的判定与性质．【专题】证明题．【分析】（1）根据两直线平行，内错角相等求出∠AFE=∠DCE，然后利用“角角边”证明△AEF和△DEC全等，根据全等三角形对应边相等可得AF=CD，再利用等量代换即可得证；（2）先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形，再根据一个角是直角的平行四边形是矩形，可知∠ADB=90°，由等腰三角形三线合一的性质可知必须是AB=AC．【解答】解：（1）BD=CD．理由如下：依题意得AF∥BC，∴∠AFE=∠DCE，∵E是AD的中点，∴AE=DE，在△AEF和△DEC中，，∴△AEF≌△DEC（AAS），∴AF=CD，∵AF=BD，∴BD=CD；（2）当△ABC满足：AB=AC时，四边形AFBD是矩形．理由如下：∵AF∥BD，AF=BD，∴四边形AFBD是平行四边形，∵AB=AC，BD=CD（三线合一），∴∠ADB=90°，∴▱AFBD是矩形．【点评】本题考查了矩形的判定，全等三角形的判定与性质，平行四边形的判定，是基础题，明确有一个角是直角的平行四边形是矩形是解本题的关键．12．如图，在△ABC中，D、E分别是AB、AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF．（1）求证：四边形BCFE是菱形；（2）若CE=4，∠BCF=120°，求菱形BCFE的面积．【考点】菱形的判定与性质；三角形中位线定理．【分析】从所给的条件可知，DE是△ABC中位线，所以DE∥BC且2DE=BC，所以BC和EF平行且相等，所以四边形BCFE是平行四边形，又因为BE=FE，所以是菱形；∠BCF是120°，所以∠EBC为60°，所以菱形的边长也为4，求出菱形的高面积就可求．【解答】（1）证明：∵D、E分别是AB、AC的中点，∴DE∥BC且2DE=BC，又∵BE=2DE，EF=BE，∴EF=BC，EF∥BC，∴四边形BCFE是平行四边形，又∵BE=FE，∴四边形BCFE是菱形；（2）解：∵∠BCF=120°，∴∠EBC=60°，∴△EBC是等边三角形，∴菱形的边长为4，高为2，∴菱形的面积为4×2=8．【点评】本题考查菱形的判定和性质以及三角形中位线定理，以及菱形的面积的计算等知识点．13．如图1，在正方形ABCD中，E、F分别是边AD、DC上的点，且AF⊥BE．（1）求证：AF=BE；（2）如图2，在正方形ABCD中，M、N、P、Q分别是边AB、BC、CD、DA上的点，且MP⊥NQ．MP与NQ是否相等？并说明理由．【考点】正方形的性质；全等三角形的判定与性质．【专题】证明题．【分析】（1）根据正方形的性质可得AB=AD，∠BAE=∠D=90°，再根据同角的余角相等求出∠ABE=∠DAF，然后利用“角边角”证明△ABE和△DAF全等，再根据全等三角形的证明即可；（2）过点A作AF∥MP交CD于F，过点B作BE∥NQ交AD于E，然后与（1）相同．【解答】（1）证明：在正方形ABCD中，AB=AD，∠BAE=∠D=90°，∴∠DAF+∠BAF=90°，∵AF⊥BE，∴∠ABE+∠BAF=90°，∴∠ABE=∠DAF，∵在△ABE和△DAF中，，∴△ABE≌△DAF（ASA），∴AF=BE；（2）解：MP与NQ相等．理由如下：如图，过点A作AF∥MP交CD于F，过点B作BE∥NQ交AD于E，∵AB∥CD，AD∥BC，∴四边形AMPF与四边形BNQE是平行四边形，∴AF=PM，BE=NQ，∵在正方形ABCD中，AB=AD，∠BAE=∠D=90°，∴∠DAF+∠BAF=90°，∵AF⊥BE，∴∠ABE+∠BAF=90°，∴∠ABE=∠DAF，∵在△ABE和△DAF中，，∴△ABE≌△DAF（ASA），∴AF=BE；∴MP=NQ．【点评】本题考查了正方形的性质，全等三角形的判定与性质，主要利用了正方形的四条边都相等，每一个角都是直角的性质，同角的余角相等的性质，利用三角形全等证明相等的边是常用的方法之一，要熟练掌握并灵活运用．14．如图，在边长为3的正方形ABCD中，点E是BC边上的点，BE=1，∠AEP=90°，且EP交正方形外角的平分线CP于点P，交边CD于点F，（1）的值为；（2）求证：AE=EP；（3）在AB边上是否存在点M，使得四边形DMEP是平行四边形？若存在，请给予证明；若不存在，请说明理由．【考点】正方形的性质；全等三角形的判定与性质；平行四边形的判定．【分析】（1）由正方形的性质可得：∠B=∠C=90°，由同角的余角相等，可证得：∠BAE=∠CEF，根据同角的正弦值相等即可解答；（2）在BA边上截取BK=BE，连接KE，根据角角之间的关系得到∠AKE=∠ECP，由AB=CB，BK=BE，得AK=EC，结合∠KAE=∠CEP，证明△AKE≌△ECP，于是结论得出；（3）作DM⊥AE于AB交于点M，连接ME、DP，易得出DM∥EP，由已知条件证明△ADM≌△BAE，进而证明MD=EP，四边形DMEP是平行四边形即可证出．【解答】（1）解：∵四边形ABCD是正方形，∴∠B=∠D，∵∠AEP=90°，∴∠BAE=∠FEC，在Rt△ABE中，AE==，∵sin∠BAE==sin∠FEC=，∴=，解法二：由上得∠BAE=∠FEC，∵∠BAE=∠FEC，∠B=∠DCB，∴△ABE∽△ECF，∴=，（2）证明：在BA边上截取BK=BE，连接KE，∵∠B=90°，BK=BE，∴∠BKE=45°，∴∠AKE=135°，∵CP平分外角，∴∠DCP=45°，∴∠ECP=135°，∴∠AKE=∠ECP，∵AB=CB，BK=BE，∴AB﹣BK=BC﹣BE，即：AK=EC，由第一问得∠KAE=∠CEP，∵在△AKE和△ECP中，，∴△AKE≌△ECP（ASA），∴AE=EP；（3）答：存在．证明：作DM⊥AE交AB于点M，则有：DM∥EP，连接ME、DP，∵在△ADM与△BAE中，，∴△ADM≌△BAE（ASA），∴MD=AE，∵AE=EP，∴MD=EP，∴MD EP，∴四边形DMEP为平行四边形．【点评】此题考查了相似三角形的判定与性质，全等三角形的判定与性质以及正方形的性质等知识．此题综合性很强，图形比较复杂，解题的关键是注意数形结合思想的应用与辅助线的准确选择．。

人教版九年级数学中考矩形、菱形、正方形专项练习基础达标一、选择题1.(2018江苏淮安)如图,菱形ABCD 的对角线AC ,BD 的长分别为6和8,则这个菱形的周长是( )A.20B.24C.40D.48,AO=12AC=3,BO=12BD=4,且AO ⊥BO ,则AB=√AA 2+AA 2=5, 故这个菱形的周长L=4AB=20. 故选A.2.(2017四川广安)下列说法:①四边相等的四边形一定是菱形②顺次连接矩形各边中点形成的四边形一定是正方形 ③对角线相等的四边形一定是矩形④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分其中正确的有( )个. A.4 B.3C.2D.13.(2017四川眉山)如图,EF 过▱ABCD 对角线的交点O ,交AD 于点E ,交BC 于点F ,若▱ABCD 的周长为18,OE=1.5,则四边形EFCD 的周长为( ) A.14 B.13C.12D.104.(2018贵州遵义)如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为()A.10B.12C.16D.18PM⊥AD于点M,交BC于点N.则四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,×2×8=8,∴S△DFP=S△PBE=12∴S阴影=8+8=16,故选C.5.(2017山东枣庄)如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=A(x<0)的图象经过顶点B,则k的值为()AA.-12B.-27C.-32D.-366.(2018江苏无锡)如图,已知点E是矩形ABCD的对角线AC上的一动点,正方形EFGH的顶点G,H都在边AD上,若AB=3,BC=4,则tan ∠AFE的值()A.等于37B.等于√33C.等于34D.随点E位置的变化而变化EF∥AD,∴∠AFE=∠FAG,△AEH∽△ACD,∴AAAA =AAAA=34.设EH=3x,AH=4x,∴HG=GF=3x,∴tan∠AFE=tan∠FAG=AA AA =3A3A+4A=37.故选A.二、填空题7.(2018湖南株洲)如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长度为..5四边形ABCD是矩形,∴AC=BD=10,BO=DO=12BD,∴OD=12BD=5,∵点P,Q分别是AO,AD的中点,∴PQ是△AOD的中位线,∴PQ=12DO=2.5.8.(2018广东广州)如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点D在y轴上,则点C的坐标是.-5,4)菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点D在y轴上,∴AB=5,∴AD=5,∴由勾股定理知:OD=√AA2-AA2=√52-32=4,∴点C的坐标是(-5,4).9.(2018湖北武汉)以正方形ABCD的边AD为边作等边三角形ADE,则∠BEC的度数是.150°1,图1∵四边形ABCD为正方形,△ADE为等边三角形,∴AB=BC=CD=AD=AE=DE,∠BAD=∠ABC=∠BCD=∠ADC=90°,∠AED=∠ADE=∠DAE=60°,∴∠BAE=∠CDE=150°,又AB=AE,DC=DE,∴∠AEB=∠CED=15°,则∠BEC=∠AED-∠AEB-∠CED=30°.如图2,图2∵△ADE是等边三角形,∴AD=DE,∵四边形ABCD是正方形,∴AD=DC,∴DE=DC,∴∠CED=∠ECD,∴∠CDE=∠ADC-∠ADE=90°-60°=30°,∴∠CED=∠ECD=1(180°-30°)=75°,同理∠BEA=∠ABE=75°,2∴∠BEC=360°-75°×2-60°=150°.三、解答题10.如图,在菱形ABCD 中,对角线AC 与BD 交于点O.过点C 作BD 的平行线,过点D 作AC 的平行线,两直线相交于点E.(1)求证:四边形OCED 是矩形;(2)若CE=1,DE=2,则ABCD 的面积是多少?四边形ABCD 是菱形,∴AC ⊥BD , ∴∠COD=90°. ∵CE ∥OD ,DE ∥OC ,∴四边形OCED 是平行四边形,又∠COD=90°,∴平行四边形OCED 是矩形.(1)知,平行四边形OCED 是矩形,则CE=OD=1,DE=OC=2.∵四边形ABCD 是菱形, ∴AC=2OC=4,BD=2OD=2, ∴菱形ABCD 的面积为12AC ·BD=12×4×2=4. 能力提升一、选择题1.下列说法中,正确的个数为( )①对顶角相等;②两直线平行,同旁内角相等; ③对角线互相垂直的四边形为菱形;④对角线互相垂直平分且相等的四边形为正方形.A.1B.2C.3D.4对顶角相等,故①正确;②两直线平行,同旁内角互补,故②错误;③对角线互相垂直且平分的四边形为菱形,故③错误; ④对角线互相垂直平分且相等的四边形为正方形,故④正确,故选B .2.(2018山东枣庄)如图,在矩形ABCD 中,点E 是边BC 的中点,AE ⊥BD ,垂足为F ,则tan ∠BDE 的值是( )A.√24B.14C.13D.√23四边形ABCD 是矩形,∴AD=BC ,AD ∥BC , ∵点E 是边BC 的中点, ∴BE=12BC=12AD , ∴△BEF ∽△DAF , ∴AA AA =AA AA =12, ∴EF=12AF , ∴EF=13AE ,∵点E 是边BC 的中点, ∴由矩形的对称性得:AE=DE , ∴EF=13DE ,设EF=x ,则DE=3x , ∴DF=√AA 2-AA 2=2√2x , ∴tan ∠BDE=AAAA =2√2A =√24.故选A.3.如图,在Rt △ABC 中,∠C=90°,AC=BC=6cm,点P 从点A 出发,沿AB 方向以每秒√2 cm 的速度向终点B 运动;同时,动点Q 从点B 出发沿BC 方向以每秒1 cm 的速度向终点C 运动,将△PQC 沿BC 翻折,点P 的对应点为点P'.设Q 点运动的时间为t s,若四边形QPCP'为菱形,则t 的值为( )A.√2B.2C.2√2D.3PP',交BC于N点,过P作PM⊥AC,垂足为M.若运动t s时四边形QPCP'为菱形,则PQ=PC,PN⊥BC,四边形PMCN为矩形,BQ=t,AP=√2t,PM=NC=t,∴QC=2t,∴BC=BQ+QC=t+2t=3t=6cm,∴t=2,故选B.4.(2018河南)如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1 cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为()图1图2A.√5B.2D.2√5C.52D作DE⊥BC于点E由题图2可知,点F由点A到点D用时为a s,△FBC的面积为a cm2.∴AD=a.DE·AD=a.∴12∴DE=2.当点F从D到B时,用√5s,∴BD=√5.Rt△DBE中,BE=√AA2-AA2=√(√5)2-22=1,∵ABCD是菱形,∴EC=a-1,DC=a.Rt△DEC中,a2=22+(a-1)2,.解得a=52故选C.5.(2017广东)如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是()A.①③B.②③C.①④D.②④二、填空题6.(2018山东潍坊)如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x 轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C'D'的位置,B'C'与CD相交于点M,则点M的坐标为.)-1,√33,连接AM ,∵将边长为1的正方形ABCD 绕点A 逆时针旋转30°得到正方形AB'C'D', ∴AD=AB'=1,∠BAB'=30°, ∴∠B'AD=60°,在Rt △ADM 和Rt △AB'M 中,∵{AA =AA ',AA =AA ,∴Rt △ADM ≌Rt △AB'M (HL), ∴∠DAM=∠B'AM=12∠B'AD=30°, ∴DM=AD tan ∠DAM=1×√33=√33, ∴点M 的坐标为(-1,√33).三、解答题 7.如图所示,在△ABC 中,点O 是AC 边上的一个动点,过O 作直线MN ∥BC ,设MN 交∠ACB 的平分线于点E ,交∠ACB 的外角平分线于点F.(1)求证:OE=OF ;(2)当点O 运动到何处时,四边形AECF 是矩形?并证明你的结论.MN ∥BC ,∴∠OEC=∠BCE.又∠OCE=∠BCE ,∴∠OEC=∠OCE ,∴OE=OC.同理可证OF=OC ,∴OE=OF.O 运动到AC 中点时,四边形AECF 是矩形.证明:∵CE ,CF 分别是∠ACB 的内,外角平分线.∴∠OCE+∠OCF=12(∠ACB+∠ACD )=12×180°=90°,即∠ECF=90°,又∵OE=OF ,∴当O 点运动到AC 中点时,OA=OC ,四边形AECF 是矩形.8.(2018贵州遵义)如图,正方形ABCD的对角线交于点O,点E,F分别在AB,BC上(AE<BE),且∠EOF=90°,OE,DA的延长线交于点M,OF,AB的延长线交于点N,连接MN.(1)求证:OM=ON;(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.四边形ABCD是正方形,∴OA=OB,∠DAO=45°,∠OBA=45°,∴∠OAM=∠OBN=135°,∵∠EOF=90°,∠AOB=90°,∴∠AOM=∠BON,∴△OAM≌△OBN(ASA),∴OM=ON.,过点O作OH⊥AD于点H,∵正方形的边长为4,∴OH=HA=2,∵E为OM的中点,∴HM=4,则OM=√22+42=2√5,由(1)知OM=ON,∴MN=√2OM=2√10.。

第十六讲平行四边形、矩形、菱形、正方形培优竞赛辅导一【知识点精析】背一背：平行四边形、矩形、菱形、正方形的性质及判定（各有几条）填一填：二、基础达标训练：（1）两条对角线的四边形是平行四边形；（2）两条对角线的四边形是矩形；（3）两条对角线的四边形是菱形；（4）两条对角线的四边形是正方形；（5）两条对角线的平行四边形是矩形；（6）两条对角线的平行四边形是菱形；（7）两条对角线的平行四边形是正方形；（8）两条对角线的矩形是正方形；（9）两条对角线的菱形是正方形。

三、易错题精选选择题1、菱形的两条对角线的长分别是10和24，则这个菱形的周长是（）A． 24 B． 52 C． 10 D． 342、下列命题中，假命题是（）。

A、四个内角都相等的四边形是矩形B、四条边都相等的平行四边形是正方形C、既是菱形又是矩形的四边形是正方形D、对角线互相垂直的平行四边形是菱形3、下列各句判定矩形的说法（1）对角线相等的四边形是矩形；（2）对角线互相平分且相等的四边形是矩形；（3）有一个角是直角的四边形是矩形；（4）有四个角是直角的四边形是矩形；（5）四个角都相等的四边形是矩形；（6）对角线相等，且有一个角是直角的四边形是矩形；是正确有几个（）A． 2个B． 3个C． 4个D． 5个4、用两个全等的直角三角形拼下列图形：（1）平行四边形（不包含菱形、矩形、正方形）；（2）矩形；（3）菱形；（4）正方形；（5）等腰三角形，一定可以拼成的图形是（）A．（1）（2）（5）B．（2）（3）（5）C．（1）（4）（5）D．（1）（2）（3）5、如图，在△ABC中，∠ACB=90°，AC=2，BC=1，点A、C分别在x轴、y轴上，当点A在x轴运动时，点C随之在y轴上运动，在运动过程中，点B到原点O的最大距离为（）．D．3 A．B．C．1+6、如图所示，E、F分别是正方形ABCD的边CD，AD上的点，且CE=DF，AE，BF相交于点O，下列结论①AE=BF；②AE⊥BF；③AO=OE；④S△AOB=S四边形DEOF中，错误的有（）A． 1个B． 2个C． 3个D． 4个7、如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE，AE⊥EF，AE=EF，现有如下结论：①BE=GE；②△AGE≌△ECF；③∠FCD=45°；④GE=FC；其中，正确的结论有（）A．1个B．2个C． 3 D．4个8、如图，在正方形ABCD中，AB=4，E为CD上一动点，AE交BD于F，过F作FH⊥AE于H，过H作GH⊥BD于G，下列有四个结论：①AF=FH，②∠HAE=45°，③BD=2FG，④△BGH是等腰直角三角形，其中正确的结论有（）A. ①②③B. ②③④C. ①③④D. ①②③④．5题图6题图7题图8题图填空题1、已知直角三角形两条边的长分别为8和6，则斜边上的中线为_________．2、矩形ABCD的两条对角线相交于点O，∠AOB=60°，AB=1，则矩形的面积等于_________．3、菱形ABCD的对角线AC=6cm，BD=4cm，以AC为边作正方形ACEF，则BF长为_________．4、在矩形ABCD中，AD=5，AB=4，点E，F在直线AD上，且四边形BCFE为菱形．若线段EF的中点为点M，则线段AM的长为_________．5、如图，一块长为a米，宽为b米的矩形土地被踩出两条小路（过A，B间任意一点作AD的平行线，被每条小路截得的线段长都是2米）．若小路①，②的面积分别为S1，S2，则S1，S2的大小关系是s1_s2．6、如图，直线l是矩形ABCD的一条对称轴，点P是直线l上一点，且使得△PAB和△PBC均为等腰三角形，则满足条件的点P共有_________个．7、如图，把一个矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在A′的位置上．若OB=，，求点A′的坐标为_________．5题图6题图7题图8题图8、如图，菱形ABCD的边长为2，∠DAB=60°，E为BC的中点，在对角线AC上存在一点P，使△PBE的周长最小，则△PBE的周长的最小值为．9、如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系、已知OA=3，OC=2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处，若在y轴上存在点P，且满足FE=FP，则P点坐标为_________．10、如图，在矩形ABCD中，AB=5，BC=7，点E为BC上一动点，把△ABE沿AE折叠，当点B的对应点B′落在∠ADC的角平分线上时，则点B′到BC的距离为（）A．1或2 B．2或3 C． 3或4 D．4或511、如图，直线y=﹣3x+3与x轴交于点B，与y轴交于点A，以线段AB为边，在第一象限内作正方形ABCD，点C落在双曲线y=（k≠0）上，将正方形ABCD沿x轴负方向平移a个单位长度，使点D恰好落在双曲线y=（k≠0）上的点D1处，则a=_______．FDA EB C9题图10题图11题图例1图四、经典例题精讲例1以△ABC的边AB、AC为边作等边△ABD和等边△ACE，四边形ADFE是平行四边形．（1）当∠BAC等于时，四边形ADFE是矩形；当∠BAC等于时，平行四边形ADFE不存在；（2）当△ABC分别满足什么条件时，平行四边形ADFE是菱形、正方形．变式题组如图，在菱形ABCD中，M，N分别是边AB，BC的中点，MP⊥AB交边CD于点P，连接NM，NP．（1）若∠B=60°，这时点P与点C重合，则∠NMP=度；（2）求证：NM=NP；（3）当△NPC为等腰三角形时，求∠B的度数．变式题组如图1，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合)，以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：（1）①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系；②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度 ，得到如图2、如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断．例2、如图，在直角梯形ABCD中，AB∥CD，∠BCD=Rt∠，AB=AD=10cm，BC=8cm．点P从点A出发，以每秒3cm 的速度沿折线ABCD方向运动，点Q从点D出发，以每秒2cm的速度沿线段DC方向向点C运动．已知动点P、Q同时发，当点Q运动到点C时，P、Q运动停止，设运动时间为t．（1）求CD的长；（2）当四边形PBQD为平行四边形时，求t的值及四边形PBQD的周长；（3）在点P、点Q的运动过程中，是否存在某一时刻，使得△BPQ的面积为20cm2？若存在，请求出所有满足条件的t的值；若不存在，请说明理由．培优竞赛升级检测Ａ ＦＣＤＢＥ 第2题图第5题图 1、下列命题中，真命题是（ ）Ａ两条对角线互相垂直且相等的四边形是正方形 Ｂ．两条对角线互相垂直的四边形是菱形 Ｃ．两条对角线相等的四边形是矩形 Ｄ．两条对角线互相平分的四边形是平行四边形 2、如图在ABC △中，点D 、E 、F 分别在边AB 、BC 、CA 上，且DE CA ∥，DF BA ∥．下列四种说法： ①四边形AEDF 是平行四边形；②如果90BAC ∠=，那么四边形AEDF 是矩形；③如果AD 平分BAC ∠，那么四边形AEDF 是菱形；④如果AD BC ⊥且AB AC =，那么四边形AEDF 是菱形.其中，正确的有 .（只填写序号）3、如图，在△ABC 中，点D 是BC 的中点，点E 、F 分别是线段AD 及其延长线上，且DE=DF ，给出下列条件：①BE ⊥EC ；②BF ∥EC ；③AB=AC ，从中选择一个条件使四边形BECF 是菱形，并给出证明，你选择的条件是 （只填写序号）．3题图 4题图4、如图，在矩形ABCD 中，AB =5，BC =4，E 、F 分别是AB 、AD 的中点.动点R 从点B 出发，沿B→C →D →F 方向运动至点F 处停止．设点R 运动的路程为x ，EFR △的面积为y ，当y 取到最大值时，点R 应运动到( ) A ．BC 的中点处 B ．C 点处C ．CD 的中点处D ．D 点处5、如图，在矩形ABCD 中，AD ＝6，AB ＝4，点E 、G 、H 、F 分别在AB 、BC 、CD 、AD 上，且AF ＝CG ＝2，BE ＝DH ＝1，点P 是直线EF 、GH 之间任意一点，连结PE 、PF 、PG 、PH ，则△PEF 和△PGH 的面积和等于 .6、如图1，在△ABC 和△EDC 中，AC=CE=CB=CD ；∠ACB=∠DCE=90°，AB 与CE 交于F ，ED 与AB ，BC ，分别交于M ，H ．（1）求证：CF=CH ；（2）如图2，△ABC 不动，将△EDC 绕点C 旋转到∠BCE=45°时，试判断四边形ACDM 是什么四边形？并证明你的结论．7、在正方形ABCD 中，点P 是CD 边上一动点，连接P A ，分别过点B 、D 作BE ⊥P A 、DF ⊥P A ，垂足分别为E 、F ，如图①．(1)请探究BE 、DF 、EF 这三条线段的长度具有怎样的数量关系？若点P 在AB C DP EF ADB C P E F AP F EB C D图① 图② 图③ DC 的延长线上，如图②，那么这三条线段的长度之间又具有怎样的数量关系？若点P 在CD 的延长线上呢，如图③，请分别直接写出结论；(2)就(1)中的三个结论选择一个加以证明．8、如图1，若四边形ABCD 、四边形GFED 都是正方形，显然图中有AG ＝CE ，AG ⊥CE ．⑴当正方形GFED 绕D 旋转到如图2的位置时，AG ＝CE 是否成立？若成立，请给出证明；若不成立，请说 明理由；⑵当正方形GFED 绕D 旋转到如图3的位置时，延长CE 交AG 于H 交，于AD 于M ．①求证：AG 丄CH ；②当AD ＝4，DG 2CH 的长．第十六讲 平行四边形、矩形、菱形、正方形培优竞赛辅导答案一【知识点精析】背一背：平行四边形、矩形、菱形、正方形的性质及判定（各有几条） 填一填：二、基础达标训练：（1）两条对角线互相平分的四边形是平行四边形；（2）两条对角线相等且互相平分的四边形是矩形；（3）两条对角线互相垂直平分的四边形是菱形；（4）两条对角线相等且互相垂直平分的四边形是正方形；（5）两条对角线相等的平行四边形是矩形；（6）两条对角线互相垂直的平行四边形是菱形；（7）两条对角线相等且互相垂直的平行四边形是正方形；（8）两条对角线互相垂直的矩形是正方形；（9）两条对角线相等的菱形是正方形。

2012年全国各地中考数学压轴题专集答案七、平行四边形、矩形、菱形、正方形、梯形 1．（天津）已知一个矩形纸片OACB ，将该纸片放置在平面直角坐标系中，点A （11，0），点B （0，6），点P 为BC 边上的动点（点P 不与点B 、C 重合），经过点O 、P 折叠该纸片，得点B ′ 和折痕OP ．设BP ＝t ．（Ⅰ）如图①，当∠BOP ＝30°时，求点P 的坐标；（Ⅱ）如图②，经过点P 再次折叠纸片，使点C 落在直线PB ′ 上，得点C ′ 和折痕PQ ，若AQ ＝m ，试用含有t 的式子表示m ；（Ⅲ）在（Ⅱ）的条件下，当点C ′ 恰好落在边OA 上时，求点P 的坐标（直接写出结果即可）．解：（Ⅰ）根据题意，∠OBP ＝90°，OB ＝6 在Rt △OB P 中，由∠BOP ＝30°，BP ＝t ，得OP ＝2t 根据勾股定理，OP 2＝OB 2＋BP 2即(2t)2＝6 2＋t 2，解得t ＝23（t ＝－23舍去）． ∴点P 的坐标为（23，6）（Ⅱ）∵△OB ′P 、△QC ′P 分别是由△OBP 、△QCP 折叠得到的 ∴△OB ′P ≌△OBP ，△QC ′P ≌△QCP ∴∠OPB ′＝∠OPB ，∠QPC ′＝∠QPC∵∠OPB ′＋∠OPB ＋∠QPC ′＋∠QPC ＝180°，∴∠OPB ＋∠QPC ＝90° ∵∠BOP ＋∠OPB ＝90°，∴∠BOP ＝∠CPQ又∠OBP ＝∠C ＝90°，∴△OBP ∽△PCQ ，∴OBPC＝BPCQ由题设BP ＝t ，AQ ＝m ，BC ＝11，AC ＝6，则PC ＝11－t ，CQ ＝6－m ∴611－t＝t6－m，∴m ＝1 6 t 2－ 116t ＋6（0＜t＜11） （Ⅲ）点P 的坐标为（11－13 3 ，6）或（11＋13 3，6）提示：过点P 作PH ⊥OA 于H易证△PC ′H ∽△C ′QA ，∴PHAC ′＝PC ′C ′Q∵PC ′＝PC ＝11－t ，PH ＝OB ＝6，AQ ＝m ，C ′Q ＝CQ ＝6－m∴AC ′＝C ′Q 2－AQ 2＝36－12m∴636－12m＝11－t6－m图② 图①∵611－t＝t6－m，即6t ＝11－t6－m∴636－12m＝6t，∴36－12m ＝t2，即12m ＝36－t2又m ＝16 t2－11 6t ＋6，即12m ＝2t2－22t ＋72 ∴2t2－22t ＋72＝36－t2，即3t2－22t ＋36＝0解得：t ＝11±133∴点P 的坐标为（11－133，6）或（11＋133，6）2．（天津模拟）如图，在梯形ABCO 中，A （0，2），B （4，2），点C 为x 轴正半轴上一动点，M 为线段BC 中点．（1）设C （x ，0），S △AOM＝y ，求y 与x 的函数关系式；（2）如果以线段AO 为直径的⊙D 和以BC 为直径的⊙M 外切，求点C 的坐标；（2）连接OB 交线段AM 于N ，如果以A 、N 、B 为顶点的三角形与△OMC 相似，求直线CN 的解析式．解：（1）取OA 中点D ，连接DM则DM ＝1 2 (AB ＋OC)＝1 2 (4＋x )＝ 12x ＋2∴y ＝1 2 OA ·DM ＝ 1 2 ×2×( 1 2 x ＋2 )＝ 12x ＋2 即y ＝ 12x ＋2（2）设⊙M 的半径为r ，⊙M 与AB 交于点E ，连接CE 则∠BEC ＝90°，OC ＝AE ＝x ，BE ＝4－x ，CE ＝2 在Rt △BCE 中，(4－x)2＋22＝(2r)2①又DM ＝1＋r ＝x ＋42② 由①、②解得x ＝43∴点C 的坐标为（43，0）（3）延长AM 交x 轴于点F则△CMF ≌△BMA ，∴CF ＝AB ＝4，OF ＝x ＋4∵AB ∥OF ，△ANB ∽△FNO ，∴ANNF＝ABOF＝4x ＋4∴AN ＝4x ＋8AF ＝4x ＋822＋(x ＋4)2＝4x ＋8x2＋8x ＋20∵DM ⊥OA ，AD ＝OD ，∴AM ＝OM ∴∠DAM ＝∠DOM ，∴∠BAN ＝∠MOC ①若ABAN＝OMOC，则△ABN ∽△OMC 于是44x ＋8x2＋8x ＋20＝(x ＋4 2)2＋12x整理得：x2＋8x －20＝0，解得：x 1＝－10（舍去），x 2＝2 ∴C （2，0），F （6，0）可得直线AF 的解析式为y ＝－1 3x ＋2，直线OB 的解析式为y ＝1 2x由⎩⎨⎧y ＝－ 1 3x ＋2y ＝ 1 2x 解得⎩⎨⎧x ＝125y ＝65∴N （12 5，65）设直线CN 的解析式为y ＝kx ＋b ，则： ⎩⎪⎨⎪⎧12 5k ＋b ＝6 52k ＋b ＝0解得⎩⎪⎨⎪⎧k ＝3b ＝－6∴直线CN 的解析式为y ＝3x －6②若 AB AN ＝ OCOM，则△ABN ∽△OCM于是44x ＋8x2＋8x ＋20＝x(x ＋42)2＋12整理得：x ＋8＝2x ，解得：x ＝8 ∴C （8，0），F （12，0）可得直线AF 的解析式为y ＝－1 6x ＋2，直线OB 的解析式为y ＝1 2x由⎩⎨⎧y ＝－ 16x ＋2y ＝ 1 2x解得⎩⎪⎨⎪⎧x ＝3y ＝3 2∴N （3，32）设直线CN 的解析式为y ＝k ′x ＋b ′，则： ⎩⎪⎨⎪⎧3k ′＋b ′＝3 28k ′＋b ′＝0 解得⎩⎨⎧k ′＝－310b ′＝12 5∴直线CN 的解析式为y ＝－310x ＋1253．（上海模拟）在矩形ABCD 中，AB ＝4，BC ＝3，E 是AB 边上一点（与A 、B 不重合），EF ⊥CE 交AD 于点F ，过点E 作∠AEH ＝∠BEC ，交射线FD 于点H ，交射线CD 于点N ． （1）如图1，当点H 与点F 重合时，求BE 的长；（2）如图2，当点H 在线段FD 上时，设BE ＝x ，DN ＝y ，求y 与x之间的函数关系式，并写出自变量x 的取值范围；（3）连接AC ，当△FHE 与△AEC 相似时，求线段DN 的长．解：（1）∵EF ⊥EC ，∴∠AEF ＋∠BEC ＝90° ∵∠AEH ＝∠BEC ，∴∠BEC ＝45° ∵∠B ＝90°，∴BE ＝BC ∵BC ＝3，∴BE ＝3（2）过点E 作EG ⊥CN ，垂足为点G ∴BE ＝CG∵AB ∥CN ，∴∠AEH ＝∠N ，∠BEC ＝∠ECN ∵∠AEH ＝∠BEC ，∴∠N ＝∠ECN ，∴EN ＝EC ∴CN ＝2CG ＝2BE∵BE ＝x ，DN ＝y ，CD ＝AB ＝4 ∴y ＝2x －4（2≤x≤3） （3）∵∠A ＝90°，∴∠AFE ＋∠AEF ＝90° ∵EF ⊥EC ，∴∠AEF ＋∠BEC ＝90° ∴∠AFE ＝∠BEC ，∴∠HFE ＝∠AEC 当△FHE 与△AEC 相似时 ①若∠FHE ＝∠EAC∵∠BAD ＝∠B ，∠AEH ＝∠BEC∴∠FHE ＝∠ECB ，∴∠EAC ＝∠ECB∴tan ∠EAC ＝tan ∠ECB ，∴BCAB＝BEBC∴34＝BE3，∴BE ＝94，∴DN ＝12②若∠FHE ＝∠ECA ，作EG ⊥CN 于G ，交AC 于O ∵EN ＝EC ，EG ⊥CN ，∴∠1＝∠2∵AH ∥EG ，∴∠FHE ＝∠1，∴∠FHE ＝∠2 ∴∠2＝∠ECA ，∴OE ＝OC设OE ＝OC ＝3k ，则AE ＝4k ，AO ＝5k ∴AO ＋OC ＝8k ＝5，∴k ＝58∴AE ＝52，BE ＝32，∴CN ＝3，∴DN ＝1综上所述：线段DN 的长为12或1 4．（上海模拟）已知在梯形ABCD 中，AB ∥DC ，AD ＝2DE ，CE ＝2BE ，∠ADE ＝∠ECD ，DE ＝CE ＝4． （1）如图1，求证：DE ∥CB ；A EBN DC 图1F (H )A B EN DCF H图2A EBF备用图A BH N CDF E1 2A BHCDFENGOA BEN DCF H G（2）如图2，点F 是线段EB 上一动点（不与E 重合），连接CF 并延长交DE 的延长线于点G ，设EF ＝x ，DG ＝y ，求y 与x 的函数关系式；（3）点P 是线段AE 上一动点（不与E 重合），连接CP 交DE 于点Q ，当△PQE 是等腰三角形时，求AP 的长．（1）证明：∵AB ∥DC ，∴∠CEB ＝∠ECD ∵∠ADE ＝∠ECD ，∴∠ADE ＝∠CEB ∵AD ＝2DE ，CE ＝2BE ，∴ADDE＝CEBE∴△ADE ∽△CEB ，∴∠AED ＝∠B∴DE ∥CB（2）解：∵AB ∥DC ，DE ∥CB∴四边形DEBC 是平行四边形，∴DE ＝BC ∵DE ＝CE ＝4，∴BC ＝4 ∵CE ＝2BE ，∴BE ＝2 ∵DG ∥CB ，∴ EGBC＝EFBF即y －44＝x2－x∴y ＝82－x（0＜x ＜2）（3）解：①当PE ＝QE 时 ∵PE ∥DC ，∴DCEP＝DQEQ∴DC ＝DQ∵四边形DEBC 是平行四边形，∴DC ＝BE ＝2 ∴DQ ＝2∵△ADE ∽△CEB ，DE ＝CE ＝CB ＝4，BE ＝2 ∴AE ＝AD ＝8∴PE ＝QE ＝DE －DQ ＝4－2＝2 ∴AP ＝8－2＝6CA D EB 图2F G C A D E B 图1 CA D E B备用图 CA D E BQP②当PE＝PQ时则∠PQE＝∠PEQ∵AE＝AD，∴∠ADE＝∠PEQ∴∠PQE＝∠ADE，∴AD∥PC∴四边形APCD是平行四边形∴AP＝DC＝2③当PQ＝EQ时则∠QPE＝∠QEP＝∠CBE＝∠CEB此时点P与点E重合，△PQE不存在综上所述，当△PQE是等腰三角形时，AP的长为6或25．（上海模拟）如图，在梯形ABCD中，AB∥DC，∠D＝90°，AB＝3，DC＝6，BC＝5．点E是边DC上任意一点，点F在边AB的延长线上，且AE＝AF，连接EF，与边BC相交于点G．（1）设BF＝x，DE＝y，求y关于x的函数关系式，并确定自变量x的取值范围；（2）当四边形BECF是平行四边形时，求BF的长；（3）当点E在边DC上移动时，△BFG能否成为等腰三角形？如果能，求BF的长；如果不能，请说明理由．解：（1）∵AB∥DC，∠D＝90°，AB＝3，DC＝6，BC＝5∴AD＝4在Rt△ADE中，AD2＋DE2＝AE2∵BF＝x，∴AF＝AB＋BF＝3＋x∵AE＝AF＝3＋x，DE＝y，∴42＋y2＝(3＋x)2∴y＝x2＋6x－7当E与D重合时，y＝0，则x＝AD－AB＝1当E与C重合时，AC＝AD2＋DC2＝213，x＝213－3∴1≤x≤213－3（2）∵BF∥EC，∴若四边形BECF是平行四边形，只需BF＝EC∴x＝6－x2＋6x－7，解得x＝43 18即BF的长为43 18（3）①若BF＝BG，则∠BGF＝∠BFG＝∠AEF∴BG∥AE，∴BFAB＝FGEG∵AB∥CD，∴BFEC＝FGEGA BD C备用图A BD CEFGCADE BQP∴BFAB＝BFEC，∴EC ＝AB ＝3，DE ＝DC －EC ＝3 ∵AD ＝4，∴AE ＝AF ＝5，∴BF ＝AF －AB ＝2②若BG ＝FG ，过G 作AD 的平行线，分别交BF 、EC 于点M 、N 则MN ⊥AB ，四边形ADNM 是矩形 ∴AM ＝DN ，BM ＝12BF ＝1 2x ∵BG ＝FG ，AB ∥DC ，∴EG ＝CG∴EN ＝1 2 EC ＝ 1 2 ( DC －DE )＝ 1 2 ( 6－y )＝3－ 12y∴3＋12x ＝y ＋3－12y ，∴x ＝y ∴x ＝x2＋6x －7，解得x ＝76，即BF ＝76③若BF ＝FG ，过F 作FH ⊥BG 于H ，过E 作EK ⊥GC 于K 则BG ＝2BH ＝2BF ·cos ∠FBG ＝2BF ·cos ∠C ＝2x ·3 5＝65x∴GC ＝5－65x ∵BF ＝FG ，∴∠FBG ＝∠FGB ＝∠EGC ∵AB ∥DC ，∴∠FBG ＝∠C ∴∠EGC ＝∠C ，∴EC ＝EG ∴KC ＝12GC ＝5 2 － 3 5x ∵cos ∠C ＝KC EC ＝ 3 5 ，∴KC ＝ 35EC∴5 2－3 5x ＝3 5 (6－x2＋6x －7 )，解得x ＝373 84当x ＝373 84时，5 2－3 5x ＝5 2 － 3 5 ×373 84 ＝－ 23140＜0 ∴x ＝37384不合题意，应舍去 综上所述，△BFG 能成为等腰三角形，BF 的长为2或766．（上海模拟）有一张矩形纸片ABCD ，已知AB ＝2，AD ＝5，把这张纸片折叠，使点A 落在边BC 上的点E 处，折痕为MN （MN 交AB 于M ，交AD 于N ）． （1）如图1，当BE ＝2时，求AM 的长；（2）当点E 在BC 上运动时，设BE ＝x ，AN ＝y ，求y 关于x 的函数关系式，并确定函数的定义域； （4）连接DE ，是否存在这样的点E ，使△AME 与△DNE 相似？若存在，求出此时BE 的长，若不存在，请说明理由．A B DCE FG HK A B DCE FGM NA B D C 备用图 A B D C N E M 图1 A B DC 备用图解：（1）设BM ＝a ，∵AB ＝2，∴ME ＝AM ＝2－a 在Rt △BME 中，BM 2＋BE 2＝ME 2∴a2＋2＝(2－a)2，∴a ＝1 2∴AM ＝32（2）设BM ＝a ，∵BE ＝x ，∴a2＋x2＝(2－a)2∴a ＝4－x2 4，∴AM ＝2－ 4－x2 4 ＝4＋x24延长NM 交CB 延长线于点F∵∠F ＝∠ANM ＝∠ENM ，∴EF ＝EN ＝AN ＝y ∴BF ＝y －x∵△BFM ∽△ANM ，∴BFAN＝BMAM∴y －xy＝4－x244＋x2 4，∴y ＝4＋x22x由⎩⎪⎨⎪⎧0＜x≤20＜ 4＋x2 2x≤5 解得5－ 21≤x≤2 ∴函数的定义域为5－21≤x≤2 （3）存在∵y ＝4＋x22x≥242x ·x2＝2≥x ，即AN≥BE ∴∠DNE ≥90° 又∵∠AME ≥90°，AM ＝ME∴若△AME ∽△DNE ，则DN ＝EN ∴∠NDE ＝∠NED∵AM ＝ME ，∴∠MAE ＝∠MEA ∵AD ∥BC ，∴∠NDE ＝∠DEC∴∠BAE ＝∠DEC ，∴△ABE ∽△ECD ∴ABEC＝BECD，∴25－x＝x2解得x 1＝4（舍去），x 2＝1 ∴BE ＝1∴存在点E ，使△AME 与△DNE 相似，此时BE 的长为1 7．（上海模拟）如图，在边长为6的正方形ABCD 的两侧作正方形BEFG 和正方形DMNK ，恰好使得N 、A 、F 三点在一直线上，连接MF 交线段AD 于点P ，连接NP ，设正方形BEFG 的边长为x ，正方形DMNK 的边长为y ．（1）求y 关于x 的函数关系式及自变量x 的取值范围； （2）当△NPF 的面积为32时，求x 的值； （3）以P 为圆心，AP 为半径的圆能否与以G 为圆心，GF 为半径的圆相切？如果能，请求出x 的值，如果不能，请说明理由． N KG CE DF A B PMA BDCN EM FA BDCN EM解：（1）∵正方形BEFG、正方形DMNK、正方形ABCD ∴∠E＝∠F＝90O，AE∥MC，MC∥NK∴AE∥NK，∴∠KNA＝∠EAF∴△KNA∽△EAF，∴NKEA＝KAEF，即yx＋6＝y－6x∴y＝x＋6（0＜x≤6）（2）由（1）知NK＝AE，∴AN＝AF∵正方形DMNK，∴AP∥NM，∴FPPM＝AFAN＝1∴FP＝PM，∴S△MNP＝S△NPF＝32∴S正方形DMNK＝2S△MNP＝64∴y＝8，∴x＝2（3）连接PG，延长FG交AD于点H，则GH⊥AD易知：AP＝y2，AH＝x，PH＝y2－x，HG＝6；PG＝AP＋GF＝y2＋x①当两圆外切时在Rt△GHP中，PH2＋HG2＝PG2，即(y2－x)2＋62＝(y2＋x)2解得：x＝－3－33（舍去）或x＝－3＋3 3 ②当两圆内切时在Rt△GHP中，PH2＋HG2＝PG2，即(y2－x)2＋62＝(y2－x)2方程无解所以，当x＝33－3时，两圆相切8．（上海模拟）已知：正方形ABCD的边长为1，射线AE与射线BC交于点E，射线AF与射线CD交于点F，∠EAF＝45°，连接EF．（1）如图1，当点E在线段BC上时，试猜想线段EF、BE、DF有怎样的数量关系？并证明你的猜想；（2）设BE＝x，DF＝y，当点E在线段BC上运动时（不包括点B、C），求y关于x的函数解析式，并指出x的取值范围；（3）当点E在射线BC上运动时（不含端点B），点F在射线CD上运动．试判断以E为圆心，以BE为半径的⊙E和以F为圆心，以FD为半径的⊙F之间的位置关系；（4）如图2，当点E在BC的延长线上时，设AE与CD交于点G．问：△EGF与△EF A能否相似？若能相似，求出BE的长，若不可能相似，请说明理由．A BDCEF图1ABDC EFG图2（1）猜想：EF＝BE＋DF证明：将△ADF绕点A顺时针旋转90°，得△ABF′，易知点F′、B、E在同一直线上（如.图1）∵AF′＝AF∠F′AE＝∠1＋∠3＝∠2＋∠3＝90°－45°＝45°＝∠EAF又AE＝AE，∴△AF′E≌△AFE∴EF＝F′E＝BE＋BF＝BE＋DF（2）在Rt△EFC中，EC2＋FC2＝EF2∵EC＝1－x，FC＝1－y，EF＝x＋y∴(1－x)2＋(1－y)2＝(x＋y)2∴y＝1－x1＋x（0＜x＜1）（3）①当点E在点B、C之间时，由（1）知EF＝BE＋DF，故此时⊙E与⊙F外切；②当点E在点C时，DF＝0，⊙F不存在.③当点E在BC延长线上时，将△ADF绕点A顺时针旋转90°，得△ABF′（如图2）则AF′＝AF，∠1＝∠2，BF′＝DF，∠F′AF＝90°∴∠F′AE＝∠EAF＝45°又AE＝AE，∴△AF′E≌△AFE∴EF＝EF′＝BE－BF′＝BE－DF∴此时⊙E与⊙F内切综上所述，当点E在线段BC上时，⊙E与⊙F外切；当点E在BC延长线上时，⊙E与⊙F内切（4）△EGF与△EF A能够相似，只要当∠EFG＝∠EAF＝45°即可此时CE＝CF设BE＝x，DF＝y，由（3）知EF＝x－y在Rt△CFE中，CE2＋CF2＝EF2∴(x－1)2＋(1＋y)2＝(x－y)2∴y＝x－1x＋1（x＞1）由CE＝CF，得x－1＝1＋y，即x－1＝1＋x－1 x＋1化简得x2－2x－1＝0，解得x1＝1－2（舍去），x2＝1＋ 2∴△EGF与△EF A能够相似，此时BE的长为1＋ 29．（上海模拟）如图，在等腰梯形ABCD中，AD∥BC，AB＝CD＝2，AD＝1，连接BD，作∠EBC＝∠ABD，交边CD于E．（1）设BC＝x，CE＝y，求y关于x的函数关系式，并写出函数的定义域；（2）当BE⊥CD时，求BC的长；（3）当△BDE是等腰三角形时，求BC的长．解：（1）延长AD、BE交于点F∵DF∥BC，∴∠F＝∠EBC，∠EDF＝∠ECB∴△DEF∽△CEB，∴DFBC＝DECEABDC EFG图2F′12DBACEABDCEF图1F′12即DFx ＝2－yy ，∴DF ＝x (2－y)y∵∠F ＝∠EBC ，∠EBC ＝∠ABD ，∴∠F ＝∠ABD 又∠A ＝∠A ，∴△ABF ∽△ADB ∴AFAB＝ABAD，即AF2 ＝21，∴AF ＝4 ∵AD ＋DF ＝AF ，∴1＋x (2－y)y＝4 ∴y ＝2xx ＋3（0＜x ＜5且x ≠1） （2）当BE ⊥CD 时，过D 作DG ⊥BC 于G 则△DGC ∽△BEC ，∴ DCGC＝BCCE即212(x －1)＝x2xx ＋3，解得x ＝23－1（舍去负值） ∴此时BC 的长为23－1（3）∵∠DBE ＜∠ABC ＝∠C ＜∠DEB ，∴DB ＞DE ①当BD ＝BE 时 ∵△ABF ∽△ADB ，∴BFBD＝ABAD＝21∴BF ＝2BD ＝2BE ，∴BE ＝EF ∴△DEF ∽△CEB ，∴CE ＝DE ＝12CD ＝1 即2xx ＋3＝1，解得x ＝3 ②当BE ＝DE 时，则∠BDE ＝∠DBE ∴∠BEC ＝2∠DBE 过D 作DH ⊥BC 于H则∠C ＝∠ABC ＝∠ABD ＋∠DBE ＋∠EBC ＝2∠EBC ＋∠DBE 在△BEC 中，∠BEC ＋∠EBC ＋∠C ＝180° ∴2∠DBE ＋∠EBC ＋2∠EBC ＋∠DBE ＝180° ∴DBE ＋∠EBC ＝60°，即∠DBC ＝60° ∵HC ＝12 (x －1)，∴BH ＝x －12 (x －1)＝12(x ＋1)∴DH ＝3BH ＝32(x ＋1) 在Rt △DHC 中，DH 2＋HC 2＝DC 2∴34 (x ＋1)2＋14 (x －1)2＝4，解得x ＝13－1 2∴当△BDE 是等腰三角形时，BC 的长为3或13－1210．（重庆）已知：如图，在直角梯形ABCD 中，AD ∥BC ，∠B ＝90°，AD ＝2，BC ＝6，AB ＝3．E 为BC 边上一点，以BE 为边作正方形BEFG ，使正方形BEFG 和梯形ABCD 在BC 的同侧． （1）当正方形的顶点F 恰好落在对角线AC 上时，求BE 的长；D B A CEFDB A CEG D BA CEFDBA CEH（2）将（1）问中的正方形BEFG 沿BC 向右平移，记平移中的正方形BEFG 为正方形B ′EFG ，当点E 与点C 重合时停止平移．设平移的距离为t ，正方形B ′EFG 的边EF 与AC 交于点M ，连接B ′D ，B ′M ，DM ．是否存在这样的t ，使△B ′DM 是直角三角形？若存在，求出t 的值；若不存在，请说明理由；（3）在（2）问的平移过程中，设正方形B ′EFG 与△ADC 重叠部分的面积为S ，请直接写出S 与t 之间的函数关系式以及自变量t 的取值范围．解：（1）如图①，设正方形BEFG 的边长为x 则BE ＝FG ＝BG ＝x∵AB ＝3，BC ＝6，∴AG ＝AB －BG ＝3－x ∵GF ∥BE ，∴△AGF ∽△ABC ∴AGAB＝GFBC，即3－x3 ＝x6解得x ＝2，即BE ＝2（2）存在满足条件的t ，理由如下： 如图②，过D 作DH ⊥BC 于点H 则BH ＝AD ＝2，DH ＝AB ＝3由题意得：BB ′＝HE ＝t ，HB ′＝|t －2|，EC ＝4－t在Rt △B ′ME 中，B ′M 2＝B ′E 2＋ME 2＝22＋(2－1 2 t )2＝ 1 4t2－2t ＋8∵EF ∥AB ，∴△MEC ∽△ABC ∴MEAB＝ECBC，即ME3 ＝4－t6 ，∴ME ＝2－12t 在Rt △DHB ′ 中，B ′D 2＝DH 2＋B ′H 2＝32＋(t －2)2＝t2－4t ＋13 过M 作MN ⊥DH 于点N则MN ＝HE ＝t ，NH ＝ME ＝2－12t∴DN ＝DH －NH ＝3－(2－1 2 t )＝ 12t ＋1在Rt △DMN 中，DM 2＝DN 2＋MN 2＝5 4t2＋t ＋1（ⅰ）若∠DB ′M ＝90°，则DM 2＝B ′M 2＋B ′D 2即 5 4t2＋t ＋1＝(1 4 t 2－2t ＋8 )＋( t 2－4t ＋13 )，解得t ＝20 7（ⅱ）若∠B ′MD ＝90°，则B ′D 2＝B ′M 2＋DM 2即t2－4t ＋13＝( 1 4 t 2－2t ＋8 )＋( 5 4t 2＋t ＋1 )，解得t 1＝－3＋ 17，t 2＝－3－17∵0≤t≤4，∴t ＝－3＋17（ⅲ）若∠B ′DM ＝90°，则B ′M 2＝B ′D 2＋DM 2B ACD BA CD备用图B A CD 图①EFGBACD 图②EFGHB ′ M N即14t2－2t＋8＝(t2－4t＋13)＋(54t2＋t＋1)，此方程无解综上所述，当t＝207或－3＋17时，△B′DM是直角三角形（3）当0≤t≤43时，S＝14t2当43≤t≤2时，S＝－18t2＋t－23当2≤t≤103时，S＝－38t2＋2t－53当103≤t≤4时，S＝－12t＋52提示：当点F落在CD上时，如图③FE＝2，EC＝4－t，DH＝3，HC＝4由△FEC∽△DHC，得FEEC＝DHHC即24－t＝34，∴t＝43当点G落在AC上时，点G也在DH上（即DH与AC的交点）t＝2当点G落在CD上时，如图④GB′＝2，B′C＝6－t由△GB′C∽△DHC，得G′BB′C＝DHHC即26－t＝34，∴t＝103当点E与点C重合时，t＝4①当0≤t≤43时，如图⑤∵MF＝t，FN＝1 2t∴S＝S△FMN＝12·t·12t＝14t2②当43≤t≤2时，如图⑥∵PF＝t－43，FQ＝34PF＝34t－1∴S△FPQ＝12(t－43)(34t－1)＝38t2－t＋23∴S＝S△FMN－S△FPQ＝14t2－(38t2－t＋23)＝－18t2＋t－23③当2≤t≤103时，如图⑦∵B′M＝12B′C＝12(6－t)＝3－12t图⑤B图⑥图⑦BACD图③EFGB′HBACD图④EFGB′H∴GM＝2－(3－12t)＝12t－1∴S梯形GMNF＝12(12t－1＋12t)×2＝t－1∴S＝S梯形GMNF－S△FPQ＝(t－1)－(38t2－t＋23)＝－38t2＋2t－53④当103≤t≤4时，如图⑧∵PB′＝34B′C＝34(6－t)＝92－34t∴GP＝2－(92－34t)＝34t－52∴S梯形GPQF＝12(34t－52＋34t－1)×2＝32t－72∴S＝S梯形GMNF－S梯形GPQF＝(t－1)－(32t－72)＝－12t＋5211．（浙江金华、丽水）如图，在直角梯形ABCD中，∠A＝90°，∠B＝120°，AD＝3，AB＝6．在底边AB上取点E，在射线DC上取点F，使得∠DEF＝120°．（1）当点E是AB的中点时，求线段DF的长；（2）若射线EF经过点C，求AE的长；（3）设AE＝x，CF＝y，求y关于x的函数关系式，并写出自变量x的取值范围．解：（1）过E作EG⊥DF于H，则EG＝A D＝ 3∵E是AB的中点，AB＝6，∴DG＝3，∴∠DEG＝60°∵∠DEF＝120°，∴∠FEG＝∠DEG＝60°∴GF＝3，∴DF＝6（2）过B作BG⊥DC于G，则四边形ABGD是矩形∴BG＝AD＝ 3∵AB∥DC，∠ABC＝120°，∴∠BCD＝60°∴BC＝BGcos60°＝2在AB上截取AH＝1，连接DH则DH＝2，∠AHD＝60°，∴∠DHE＝120°∴∠1＋∠2＝60°∵∠DEC＝120°，∴∠2＋∠3＝60°∴∠1＝∠3又∠DHE＝∠EBC＝120°，∴△DHE∽△EBC，∴HEBC＝DHEB设AE＝x，则HE＝x－1，EB＝6－x∴x－12＝26－x，解得x1＝2，x2＝5∴若射线EF经过点C，则AE的长是2或5（3）①当点F在线段DC上时过F作FG∥BC交AB于G，在AB上截取AH＝1，连接DH DACBEFDACBE(F)HDACBE(F)GH12 3DACBEFGDACBEFGH图⑧则DH＝2，∠AHD＝60°，∠DHE＝120°，BG＝CF＝y，EG＝6－x－y，GF＝BC＝2由（2）知△DHE∽△EGF，∴HEGF＝DHEG，即x－12＝26－x－y∴y＝(x－2)(x－5)1－x（2≤x≤5）②当点F在DC的延长线上时过F作FG∥BC交AB的延长线于G，在AB上截取AH＝1，连接DH由△DHE∽△EGF，得x－12＝26－x＋y∴y＝(x－2)(x－5)x－1（1＜x＜2或5＜x＜6）12．（浙江嘉兴、舟山）将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，即如图①，∠BAB′＝θ，AB′AB＝B′C′BC＝AC′AC＝n，我们将这种变换记为[θ，n]．（1）如图①，对△ABC作变换[60°，3]得△AB′C′，则S△AB′C′:S△ABC＝_________；直线BC与直线B′C′所夹的锐角为_________度；（2）如图②，△ABC中，∠BAC＝30°，∠ACB＝90°，对△ABC作变换[θ，n]得△AB′C′，使点B、C、C′在同一直线上，且四边形ABB′C′为矩形，求θ和n的值；（3）如图③，△ABC中，AB＝AC，∠BAC＝36°，BC＝1，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB′C′为平行四边形，求θ和n的值．解：（1）3；60（2）∵四边形ABB′C′是矩形，∴∠BAC′＝90°∴θ＝∠CAC′＝∠BAC′－∠BAC＝90°－30°＝60°在Rt△ABB′是中，∠ABB′＝90°，∠BAB′＝60°∴n＝AB′AB＝2（3）∵四边形ABB′C′是平行四边形，∴AC′∥BB′又∵∠BAC＝36°，∴θ＝∠CAC′＝∠ACB＝72°∴∠C′AB′＝∠AB′B＝∠BAC＝36°，而∠B＝∠B ∴△ABC∽△B′BA，∴AB2＝1·(1＋AB)∴AB＝1±5 2∵AB＞0，n＝B′C′BC＝1＋52B AC′（图①）C′ BACB′（图②）C′BAC B′（图③）C′DACBEFGHDACBEFGH13．（浙江某校自主招生）如图，矩形ABOD 中，AB ＝6，AD ＝8，M 是边AD 上的点，且AM :MD ＝1 :3．点E 从点A 出发，沿AB 运动到点B 停止．连接EM 并延长交射线OD 于点F ，过M 作EF 的垂线交射线BO 于点G ，连接EG 、FG ．（1）设AE ＝t 时，△EFG 的面积为S ，求S 关于t 的函数关系式，并写出自变量t 的取值范围； （2）若P 是MG 的中点，在E 点运动的整个过程中，点P 到x 轴的距离是否为定值？请说明理由； （3）请直接写出E 点运动的整个过程中点P解：（1）当点E 与点A 重合时，t ＝0 S ＝S △ABD＝12×8×6＝24当点E 与点A 重合时，0＜t≤6在矩形ABOD 中，∠A ＝∠ADO ＝90° ∴∠MDF ＝90°，∴∠A ＝∠MDF∵∠AME ＝∠DMF ，∴△AME ∽△DMF∴AMMD＝MEMF＝13∵AD ＝8，∴AM ＝2在Rt △AME 中，AE ＝t ，AM ＝2，∴ME ＝4＋t2∴EF ＝4ME ＝44＋t2过M 作MN ⊥BO 于N ，则∠MNG ＝90°，∠AMN ＝90° MN ＝AB ＝6＝3AM ，∴∠AME ＋∠EMN ＝90° ∵∠EMG ＝90°，∴∠NMG ＋∠EMN ＝90° ∴∠AME ＝NMG ，∴△AME ∽△NMG∴MEMG＝AMMN＝13，∴MG ＝3ME ＝34＋t2∴S ＝12EF ·MG ＝12×44＋t2×34＋t2＝24＋6t2（2）过P 作PH ⊥BO 于H ，则PH ∥MN ∵P 是MG 的中点，∴PH ＝12MN ＝3 ∴点P 到x 轴的距离是定值3 （3）点P 的运动路线的长为9提示：由（2）知，在E 点运动的整个过程中，点P 到x 轴的距离是定值3 所以点P 的运动路线是一条平行于BG 的线段分别作出E 与A 重合、E 与B 重合时P 点的位置P 1、P 2，则P 1P 2即为P 点运动路线的长 在Rt △BMG 2中，∵MG 1⊥BG 2，∴∠G 1MG 2＝∠MBG 1 ∴tan ∠G 1MG 2＝tan ∠MBG 1＝3，∴G 1G 2＝3MG 1＝18∵P1P2是△MG1G2的中位线，∴P1P2＝12G1G2＝9即点P的运动路线的长为914．（浙江模拟）如图1，在平面直角坐标系中，矩形OABC的顶点A、C的坐标分别为A（5，0），C（0，3）．射线y＝kx交折线A－B－C于点P，点A关于OP的对称点为A′．（1）当点A′恰好在CB边上时，求CA′的长及k的值；（2）若经过O、A、A′三点的抛物线恰好以A′为顶点，求k的值及该抛物线的解析式；（3）如图2，当点P在AB边上，点A′在CB上方时，连接A′O、A′P分别交CB边于点E、F．是否存在实数k使△A′EF≌△BPF？若存在，求出k值；若不存在，说明理由；（4）以OP为直径作⊙M，则⊙M与矩形OABC最多有_________个公共点，直接写出公共点个数最多时k的取值范围．12．解：（1）当点A′恰好在CB边上时，连接A′O、A′P，如图1∵OA′＝OA＝5，OC＝3∴CA′＝OA′2－OC2＝52－32＝4∴A′B＝CB－CA′＝5－4＝1设P A＝x，则A′P＝P A＝x，BP＝3－x在Rt△A′PB中，A′B2＋BP2＝A′P2∴12＋(3－x)2＝x2，解得x＝53，∴P（5，53）∴k＝y Px P＝13（2）连接A′O、A′P、A′A，设A′A交射线OP于点D，如图2 则OP垂直平分A′A∵经过O、A、A′三点的抛物线恰好以A′为顶点∴由抛物线的对称性可知A′O＝A′A＝2A′D∴∠A′OD＝30°，∴∠AOD＝∠A′OD＝30°∴P A＝33OA＝533，∴P（5，533）∴k＝y Px P＝33可得∠A′OA＝60°，∴△A′OA是等边三角形∴点A′的坐标为（52，532）设抛物线的解析式为为y＝a(x－52)2＋532把O（0，0）代入上式，得0＝a(0－52)2＋532解得a＝23 5∴抛物线的解析式为为y＝－235(x－52)2＋532（3）假设存在实数k，使△A′EF≌△BPF，如图3 ∵∠A′＝∠B＝90°，∠A′FE＝∠BFP∴A′E＝BP，A′F＝BF设A′E＝BP＝a，A′F＝BF＝b则A′P＝P A＝3－a，EF＝PF＝3－a－b，OE＝5－a CE＝5－(3－a－b)－b＝2＋a在Rt△OCE中，OC2＋CE2＝OE2∴32＋(2＋a)2＝(5－a)2，解得a＝6 7∴P A＝3－67＝157，∴P（5，157）∴k＝y Px P＝37（4）以OP为直径的⊙M与矩形OABC最多有6个公共点提示：∵∠OAP＝90°∴当点P在AB边上时，⊙M经过O、A、P三点，如图4∵∠COP＜90°，∴⊙M必与OC边交于另一点又∵⊙M与BC边最多有2个公共点∴⊙M与矩形OABC最多有6个公共点当点P在BC边上时，情况亦然①当⊙M与BC边相切于点D时，连接DM并延长交OA于E，如图5 则MD⊥BC，∴DE∥AB∥OC，∴DE＝OC＝3∵M是OP的中点，∴E是OA的中点∴ME＝12P A设P A＝x，则ME＝12x，DM＝12OP＝12x2＋52∵DM＋ME＝DE，∴12x2＋52＋12x＝3解得x＝1112，∴P（5，1112）∴k＝y Px P＝1160②当⊙M与AB边相切于点E时，连接EM并延长交OC于D，如图6设CP＝x，则DM＝12x，ME＝12OP＝12x2＋32∵DM＋ME＝DE，∴12x＋12x2＋32＝5解得x＝9120，∴P（9120，3）图4图5∴k＝y Px P＝6091又∵当点P与点B重合时，⊙M经过O、A、B、C四点，此时k＝3 5∴当⊙M与矩形OABC有6个公共点时，k的取值范围是：1160＜k＜6091且k≠3515．（浙江模拟）如图，点A的坐标为（0，－4），点B为x轴上一动点，以线段AB为边作正方形ABCD （按逆时针方向标记），正方形ABCD随着点B的运动而相应变动．点E为y轴的正半轴与正方形ABCD 某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．（1）当t＝3时，求点C的坐标；（2）当t＞0时，求m与t之间的函数关系式；（3）是否存在t，使点M（－2，2）落在正方形ABCD的边上？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．解：（1）过点C作CF⊥x轴于F则△CFB≌△BOA，得CF＝BO＝3，FB＝OA＝4∴点C的坐标为（－1，3）（2）当0＜t≤4时，点E为y轴的正半轴与BC边的交点，如图1易证△BOE∽△AOB，得OEOB＝OBOA即mt＝t4，∴m＝14t2当t＞4时，点E为y轴的正半轴与CD边的交点，如图2易证△EDA∽△AOB，得DAOB＝EAAB而DA＝AB，∴AB2＝OB·EA即42＋t2＝t(m＋4)，∴m＝t＋16t－4（3）存在当t≤0时∵正方形ABCD位于x轴的下方（含x轴），∴此时不存在当0＜t≤4时①若点M在BC边上，有t2＝4t＋2解得t＝2或t＝－4（舍去）②若点M在CD边上，有t－24＝2－(4－t)t解得t＝2或t＝4 当t＞4时图1图2①若点M在CD边上，有t＋16t－4－24＝2t解得t＝2（舍去）或t＝4（舍去）②若点M在AD边上，有2－16t4＝2t解得t＝12综上所述：存在，符合条件的t的值为2、4、1216．（浙江模拟）如图，直角梯形OABC的直角顶点C在x轴上，C（82，0），∠AOC＝45°，AB＝52，点D是AB边上的一点，且AD:BD＝2:3．有一45°角的顶点E在x轴上运动，角的一边过点D，角的另一边与直线OA交于点F，连接DF．（1）求点D的坐标；（2）若点E在x轴正半轴上运动，设CE＝x，OF＝y，求y与x的函数关系式；（3）在点E的运动过程中，是否存在某一时刻，使得△DEF成为等腰三角形？若存在，请求出所有符合条件的点F的坐标；若不存在，请说明理由．解：（1）作AG⊥OC于G，DH⊥OC于H，如图1∵∠AOC＝45°，∴AG＝OG＝OC－AB＝82－52＝3 2∵AB＝52，AD:BD＝2:3，∴AD＝2 2∴OH＝32＋22＝5 2∴D（52，32）（2）①当点E在线段OC上时，如图1连接DC，则HC＝OC－OH＝82－52＝3 2∴HC＝DH＝32，∴CD＝6，∠DCH＝45°∴∠EDC＋∠DEC＝135°∵∠DEF＝45°，∴∠FEO＋∠DEC＝135°∴∠FEO＝∠EDC，又∠EOF＝∠DCE＝45°∴△OEF∽△CDE，∴OFOE＝CECD，即y82－x＝x6∴y＝－16x2＋423x②当点E在OC延长线上时，如图2∵∠AOC＝∠DCO＝45°，∴∠EOF＝∠DCE ∠CDE＋∠CED＝45°∵∠DEF＝45°，∴∠CED＋∠OEF＝45°备用图∴∠OEF ＝∠CDE ，∴△OEF ∽△CDE∴OFOE＝CECD，即y82＋x＝x6∴y ＝1 6 x 2＋ 42 3x（3）①当点E 在线段OC 上时i ）若EF ＝ED ，如图3，则△OEF ≌△CDE ∴OE ＝CD ＝6，CE ＝82－6，∴OF ＝CE ＝82－6 ∴F （8－32，8－32）ii ）若DF ＝DE ，如图4，则∠EDF ＝90° 作FM ⊥AB 于M ，EN ⊥AB 于N则△DFM ≌△EDN ，∴DM ＝EN ＝32，∴M （22，32） ∴F （22，22）iii ）若DF ＝EF ，如图5，则∠DFE ＝90°作FN ⊥OC 于N ，交直线AB 于M ，则△FNE ≌△DMF ∴FN ＝DM设ON ＝x ，则FN ＝x ，MF ＝32－x ，DM ＝52－x ∴x ＝52－x ，∴x ＝522∴F （522，522）②当点E 在OC 延长线上时，如图2 ∵∠DEF ＝45°，∠DFE ＜45°，∠EDF ＞90° ∴△DEF 不可能是等腰三角形③当点E 在CO 延长线上时，如图6 ∵∠DEF ＝135°，∴只能EF ＝ED ，此时△OEF ≌△CDE∴OE ＝CD ＝6，CE ＝82＋6，∴OF ＝CE ＝82＋6 ∴F （－8－32，－8－32）综上所述，存在4个时刻使得△DEF 成为等腰三角形，点F 的坐标为：F 1（8－32，8－32），F 2（22，22），F 3（522，522），F 4（－8－32，－8－32）17．（浙江模拟）如图，在平面直角坐标系中，直角梯形OABC 的顶点A 、B 的坐标分别是（5，0），（3，2），点D 在线段OA 上，BD ＝BA ，点Q 是线段BD 上一个动点，点P 的坐标是（0，3），设直线PQ 的解析式为y ＝kx ＋b ．（1）求k 的取值范围；图6（2）当k 是取值范围内的最大整数时，若抛物线y ＝ax2－5ax 的顶点在直线PQ 、OA 、AB 、BC 围成的四边形内部，求a 的取值范围． 解：（1）∵直线y ＝kx ＋b 经过P （0，3），∴b ＝3 ∴直线PQ 的解析式为y ＝kx ＋3 ∵A （5，0），B （3，2），BD ＝BA ，∴D （1，0） 设线段BD 的解析式为y ＝mx ＋n （1≤x≤3）∴⎩⎪⎨⎪⎧3m ＋n ＝2m ＋n ＝0 解得⎩⎪⎨⎪⎧m ＝1n ＝－1 ∴线段BD 的解析式为y ＝x －1（1≤x≤3）依题意，得⎩⎪⎨⎪⎧m ＝1y ＝kx ＋3 解得x ＝4 1－k∵1≤x≤3，∴1≤41－k≤3解得－3≤k≤－13（2）∵－3≤k≤－13，且k 为最大整数，∴k ＝－1 则直线PQ 的解析式为y ＝－x ＋3∵抛物线y ＝ax2－5ax 的顶点坐标是（5 2，－25 4a ），对称轴为x ＝5 2解方程组⎩⎪⎨⎪⎧y ＝－x ＋3x ＝52得⎩⎨⎧x ＝52y ＝1 2即直线PQ 与抛物线对称轴的交点坐标为（5 2，12）∴12＜－25 4a ＜2，解得－ 8 25 ＜ a ＜－2 2518．（浙江模拟）如图，矩形ABCD 中，AB ＝1，BC ＝3，将矩形ABCD 绕中心O 顺时针旋转90°得到矩形A ′B ′C ′D ′（1）求点A 在旋转过程中所走过的路径的长；（2）求矩形ABCD 在旋转过程中所扫过的面积；（3）若点P 为线段BC 上一点，且使得∠APA ′＝60°，则满足条件的点P 有几个？请你选择一个点P 求△APA ′ 的面积． 解：（1）易知点A 的路径是以O 为圆心、以OA 长为半径、圆心角为90°的一段圆弧∵AB ＝1，BC ＝3，∴AC ＝2，OA ＝1∴点A 在旋转过程中所走过的路径的长为：π×1×90 180＝π2（2）如图，将矩形ABCD 绕它的对称中心O 旋转90°，扫过的面积是图中阴影部分的面积 ∵AB ＝1，A ′D ′＝BC ＝3，∴A ′G ＝DG ＝BE ＝C ′E ＝3－12∵AB ＝1，AD ＝ 3∴∠ADB ＝∠DBC ＝30°，∠OFC ＝∠A ′C ′D ′＝∠BDC ＝60° ∴∠A ′OD ＝∠BOC ′＝30°∴S 阴影＝S ⊙O－2(S 扇形BOD－2 S △BOE)＝S ⊙O－2 S 扇形BOD ＋4 S △BOE)＝π×12－2×π×12×30 360＋4×12 ×3－1 2 ×1 2＝56 π＋3－1 2（cm 2） （3）满足条件的点P 有2个 提示：在BC 上取点P 1，使BP 1＝33则∠AP 1B ＝60°，P 1H ＝3－3 3 －3－1 2＝3 6 ＋12A ′H ＝3－3－1 2＝3＋12∴tan ∠A ′P 1H ＝A ′HP 1H＝3，∴∠A ′P 1H ＝60° ∴∠AP 1A ′＝60°在BC 上取点P 2，使P 2H ＝A ′G ＝3－12则△A ′P 2H ≌△AA ′G ，∴A ′P 2＝A ′A ＝A ′H 2＋P 2H 2＝ 2BP 2＝3＋1 2 －3－12＝1＝AB ，∴AP 2＝ 2 ∴AP 2＝A ′P 2＝A ′A ，∴△AP 2A ′ 是等边三角形 ∴∠AP 2A ′＝60°又∵△AP 2A ′ 的外接圆与BC 最多有2个交点 ∴满足条件的点P 有2个 若求△AP 1A ′ 的面积∵S 梯形ABHA ′＝1 2 ×(1＋3＋1 2)× 3＋1 2 ＝3 2 ＋ 34 ，S △ABP 1 ＝ 1 2 ×1× 3 3 ＝36S △A ′P 1H＝1 2 ×(3 6＋1 2)× 3＋1 2 ＝3 6 ＋14∴S △AP 1A ′＝S 梯形ABHA ′－S △ABP 1－S △A ′P 1H＝36＋12若求△AP 2A ′ 的面积则S △AP 2A ′＝1 2 ×2×3 2 ×2＝32DB AC C ′D ′A ′B ′ E P 1P 2 H G19．（江苏连云港）已知梯形ABCD ，AD ∥BC ，AB ⊥BC ，AD ＝1，AB ＝2，BC ＝3．问题1：如图1，P 为AB 边上一点，以PD ，PC 为边作平行四边形PCQD ．请问对角线PQ ，DC 的长能否相等，为什么？问题2：如图2，若P 为AB 边上任意一点，以PD ，PC 为边作平行四边形PCQD ．请问对角线PQ 的长是否存在最小值？如果存在，请求出最小值；如果不存在，请说明理由． 问题3：若P 为AB 边上任意一点，延长PD 到E ，使DE ＝PD ，再以PE ，PC 为边作平行四边形PCQE ．请探究对角线PQ 的长是否也存在最小值？如果存在，请求出最小值；如果不存在，请说明理由． 问题4：如图3，若P 为DC 边上任意一点，延长P A 到E ，使AE ＝nP A （n 为常数），以PE ，PB 为边作平行四边形PBQE ．请探究对角线PQ 的长是否也存在最小值？如果存在，请直接写．．．出．最小值；如果不存在，请说明理由．解：问题1：如图1，∵四边形PCQD 是平行四边形若对角线PQ 、DC 相等，则四边形PCQD 是矩形，∴∠DPC ＝90° ∵AD ＝1，AB ＝2，BC ＝3，∴DC ＝2 2 设PB ＝x ，则AP ＝2－x在Rt △DPC 中，PD 2＋PC 2＝DC 2，即x 2＋32＋(2－x)2＋1＝8化简得x 2－2x ＋3＝0，∵△＝(－2)2－4×1×3＝－8＜0，∴方程无解∴对角线PQ 与DC 不可能相等问题2：如图2，在平行四边形PCQD 中，设对角线PQ 与DC 相交于点G 则G 是DC 的中点过点Q 作QH ⊥BC ，交BC 的延长线于H ∵AD ∥BC ，∴∠ADC ＝∠DCH即∠ADP ＋∠PDG ＝∠DCQ ＋∠QCH∵PD ∥CQ ，∴∠PDC ＝∠DCQ ，∴∠ADP ＝∠QCH 又∵PD ＝CQ ，∴Rt △ADP ≌Rt △HCQ ，∴AD ＝HC∵AD ＝1，BC ＝3，∴BH ＝4∴当PQ ⊥AB 时，PQ 的长最小，即为4 问题3：如图3，设PQ 与DC 相交于点G ∵PE ∥CQ ，PD ＝DE ，∴DGGC＝PDCQ＝12∴G 是DC 上一定点作QH ⊥BC ，交BC 的延长线于H同理可证∠ADP ＝∠QCH ，∴Rt △ADP ∽Rt △HCQ ∴ADCH＝PDCQ＝12，∴CH ＝2，∴BH ＝BC ＋CH ＝3＋2＝5 ∴当PQ ⊥AB 时，PQ 的长最小，即为5 问题4：存在最小值，最小值为22(n ＋4) 提示：如图4，设PQ 与AB 相交于点GB PA D C Q图（2） B PA D C Q 图（1） BPA DCQ 图（3）EB PA DCQ 图（1）B PA DCQ图（2）GHBP ADCQ图（3）GHE∵PE ∥BQ ，AE ＝nP A ，∴AGBG＝P ABQ＝1n ＋1∴G 是AB 上一定点作QH ∥DC ，交CB 的延长线于H ，作CK ⊥CD ，交QH 的延长线于K ∵AD ∥BC ，AB ⊥BC ，∴∠ADP ＝∠BHQ ∠P AD ＋∠P AG ＝∠QBH ＋∠QBG ＝90°，∠P AG ＝∠QBG ∴∠P AD ＝∠QBH ，∴△ADP ∽△BHQ ，∴ADBH＝P ABQ＝1n ＋1∴BH ＝n ＋1，∴CH ＝BC ＋BH ＝3＋n ＋1＝n ＋4过点D 作DM ⊥BC 于M ，则四边形ABMD 是矩形 ∴BM ＝AD ＝1，DM ＝AB ＝2 ∴MC ＝BC －BM ＝3－1＝2＝DM ∴∠DCM ＝45°，∴∠HCK ＝45° ∴CK ＝CH ·co s 45°＝22(n ＋4) ∴当PQ ⊥CD 时，PQ 的长最小，最小值为22(n ＋4) 20．（江苏常州）已知，在矩形ABCD 中，AB ＝4，BC ＝2，点M 为边BC 的中点，点P 为边CD 上的动点（点P 异于C ，D 两点）．连接PM ，过点P 作PM 的垂线与射线DA 相交于点E （如图）．设CP ＝x ，DE ＝y ．（1）写出y 与x 之间的关系式________________；（2）若点E 与点A 重合，则x 的值为________________；（3）是否存在点P ，使得点D 关于直线PE 的对称点D ′ 落在边AB 上？若存在，求x 的值；若不存在，请说明理由．解：（1）y ＝－x2＋4x （0＜x＜4） （2）x ＝2± 2（3）经探究得：当0＜x≤2－2 或2＋2≤x＜4时，点E 在边AD 上当2－2＜x ＜2＋2时，点E 在DA 的延长线上①当0＜x ≤2－2 或2＋2≤x＜4时假设存在点P ，使得点D 关于直线PE 的对称点D ′ 落在边AB 上设直线DD ′ 交直线PE 于点H ，连接PD ′、D ′M ，延长PM 交AB 的延长线于点F∵D 与D ′ 关于直线PE 对称，∴PE ⊥DD ′，PD ＝PD ′∵PF ⊥PE ，∴DD ′∥PF 又∵AB ∥CD ，∴四边形DD ′FP 为平行四边形∴PD ＝PD ′＝D ′F ＝4－x.∵M 为边BC 的中点，∴D ′M ⊥PF∴∠CBA ＝90°，∴△D ′MB ∽△MBF ，∴ BM D ′B＝BFBM易得BF ＝PC ，∴(4－2x)x ＝1，解得x ＝2±22BPA D C E M （备用图）B P A DC E M BP A D CQ图（4）EGMHKB PADC EM D FH B P A D CEM D ′ FH。

矩形、菱形与正方形专题训练（含答案）班级_________ 姓名 __________ 成绩 ___________、选择题（每小题3分，共30分）1.如图，把矩形ABCD 沿EF 翻折，点B 恰好落在AD 边的B 处，若AE = 2, DE = 6, / EFB = 60 ° 则矩形ABCD 的面积是（ ）A . 12B . 24C . 12 .'3D . 16 .'3第1题图 第2题图 第3题图 第4题图2 . 如图，菱形ABCD 中，/ B = 60 ° AB = 4,则以AC 为边长的正方形 ACEF 的周长为（） A . 14 B . 15C . 16D . 173. 如图， 将矩形 ABCD 沿对角线 BD 折叠，使点 C 与点 C 重合.若AB = 2，则CD 的长为（） A. 1 B . 2C . 3D . 44. 如图， 在厶ABC 中，AC =BC , 占 八D ,E 分别是边AB , ,AC 的中点. 将厶 ADE 绕点E 旋转180 得厶CFE ，则四边形 ADCF •宀曰疋是 ( )A.矩形 B . 菱形 C . 正方形 D .梯形5•由菱形的两条对角线的交点向各边引垂线，以各垂足为顶点的四边形是（ ）6.如图，?ABCD 的周长为16 cm , AC , BD 相交于点 O , 0E 丄AC 交AD 于点 丘，则厶DCE 的周 长为（）A •平行四边形B •矩形C •菱形D .正方形A . 4 cmB . 6 cmC .第6题图 第9题图7•菱形的周长为 8 cm ,高为1 cm ,则菱形两邻角度数比为BC10 cmA F DE&用两块完全相同的直角三角形拼下列图形：①平行四边形，②矩形，③菱形，④正方形，⑤等腰三角形，⑥等边三角形，一定能拼成的图形是（）A .①④⑤B .②⑤⑥C .①②③D .①②⑤9. 如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S i, S2,则S i + S2的值为（）A . 16B . 17 C. 18 D . 1910. 如图，F为正方形ABCD的边AD上一点，CE丄CF交AB的延长线于点E,若正方形ABCD 的面积为64,A CEF的面积为50,则厶CBE的面积为（）A . 20B . 24C . 25D . 26二、填空题（每小题3分，共24分）11. 如图所示，在菱形ABCD中，/ ADC = 72 ° AD的垂直平分线交对角线BD于点P,垂足为点E,连结CP,则/ CPB = _______ 度.1)第11题图第12题图第14题图第15题图12 .如图，四边形ABCD的两条对角线AC, BD互相垂直，A1, B1, C1, D1分别是四边形ABCD 各边中点，如果AC= 8, BD = 10,则四边形A1B1C1D1的面积为—.13 .矩形的对角线相交成的角中，有一个角是60°这个角所对的边长为20 cm,则其对角线长为___________ -_,矩形的面积为__________________ .14 .如图，四边形ABCD是菱形，对角线AC和BD相交于点O, AC = 4 cm, BD = 8 cm,则这个菱形的面积是_____ c m2.AC , BD 交于点 O , E 点在BC 上，EG 丄OB , EF 丄OC ,垂足，使?ABCD 是矩形.17 .如图，正方形 ABCD 中，对角线第18题图15 .如图，矩形 ABCD 中，点E , F 分别是 AB , CD 的中点，连结 DE 和BF ，分别取 DE , BF 的 中点M , N ,连结AM , CN , MN ,若AB = 2 2, BC = 2 '3,则图中阴影部分的面积为，第16题O ,请你添加一个条件16 .如图,分别为点G , F, AC= 10,则EG + EF = ______ .18. 如图，在平面直角坐标系中，矩形OABC的顶点A, C的坐标分别为(10, 0), (0, 4),点D是OA的中点，点P在BC上运动，当△ ODP是腰长为5的等腰三角形时，点P的坐标为三、解答题(共66分)19. (6分)如图，已知矩形ABCD中，E是AD上一点，F是AB上一点，EF丄EC且EF = EC, DE =4 cm，矩形ABCD的周长为32 cm,求AE的长.20. (8分)如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O,与BC相交于点N,连结BM , DN.(1)求证：四边形BMDN是菱形；⑵若AB= 4, AD = 8,求MD的长.21 . （8 分）如图所示，矩形ABCD 中，AE丄BD 于点E,/ DAE :/ BAE = 3 : 1，求/ BAE 和/ EAO 的度数.22. （10分）如图，已知菱形 ABCD 中，AB = AC , E , F 分别是BC , AD 的中点，连结 AE , CF. （1）证明：四边形 AECF 是矩形； ⑵若AB = 8,求菱形 ABCD 的面积.参考答案一、选择题（每小题3分，共30分）1.如图，把矩形ABCD 沿EF 翻折，点B 恰好落在AD 边的B 处，若AE = 2, DE = 6, / EFB = 60 ° 则矩形ABCD 的面积是（D ） A . 12B . 24C . 12D . 164 / 9DE 丄AB , DF 丄BC ,垂足分另U 是点 E , F ，并且DE = DF ，求证： (1)△ ADECDF ; (2)四边形 ABCD 是菱形.24. (10分)在四边形 ABCD 中，AB = CD , M , N , P , Q 分别是AD , BC , BD , AC 的中点，求证:MN 与PQ 互相垂直平分.23. （12分）如图，已知四边形 ABCD 是平行四边形,6.如图，？ABCD 的周长为16 cm , AC , BD 相交于点 O , 0E 丄AC 交AD 于点 丘，则厶DCE 的周 长为（C ）7.菱形的周长为 8 cm ,高为1 cm ,则菱形两邻角度数比为 （C ） A . 3 : 1B . 4 : 1C . 5 : 1D . 6 : 1&用两块完全相同的直角三角形拼下列图形：①平行四边形，②矩形，③菱形，④正方形，⑤等 腰三角形，⑥等边三角形，一定能拼成的图形是 （D ）A .①④⑤B .②⑤⑥C .①②③D .①②⑤9.如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为 S 1, S 2,则S 1 +S 2的值为（B ） A . 16B . 17C . 18D . 19的面积为64,^ CEF 的面积为50,则厶CBE 的面积为（B）2 . 如图，菱形ABCD 中，/ B = 60 ° AB = 4,则以AC 为边长的正方形 ACEF 的周长为（C ） A . 14 B . 15C . 16D . 173. 如图， 将矩形 ABCD 沿对角线 BD 折叠，使点 C 与点 C 重合.若AB = 2，贝U CD 的长为（B ） A . 1 B . 2C . 3D . 44. 如图，在厶ABC 中，AC =BC , 点D , E 分别是边AB , ,AC 的中点. 将厶 ADE 绕点E 旋转180 得厶CFE ，则四边形 ADCF •宀曰(A )定是A.矩形 B . 菱形C .正方形D .梯形A •平行四边形B •矩形C •菱形D .正方形 A . 4 cmB . 6 cmC .第6题图10 .如图, F 为正方形 ABCD 的边AD 上一点, CE 丄CF 交AB 的延长线于点 E ,若正方形 ABCD第4题图第1题图 第2题图 第3题图 5•由菱形的两条对角线的交点向各边引垂线，以各垂足为顶点的四边形是 （B BC第9题图10 cm二、填空题(每小题3分，共24分)11.如图所示，在菱形 ABCD 中，/ ADC = 72 ° AD 的垂直平分线交对角线 BD 于点P ,垂足为点 E ,连结 CP ,则/ CPB =72 度.第11题图 第12题图 第14题图 第15题图12. 如图，四边形 ABCD 的两条对角线 AC , BD 互相垂直，A 1, B 1, C 1, D 1分别是四边形 ABCD 各边中点，如果 AC = 8, BD = 10,则四边形 A 1B 1C 1D 1的面积为 _20_. 13. 矩形的对角线相交成的角中，有一个角是 _40 cm ，矩形的面积为_400 cm 2 .14. 如图，四边形 ABCD 是菱形，对角线 AC 和BD 相交于点O , AC= 4 cm , BD = 8 cm ,则这个菱形的面积是_16 cm 2.15. 如图，矩形 ABCD 中，点E , F 分别是 AB , CD 的中点，连结 DE 和BF ，分别取 DE , BF 的是矩形. 17.如图，正方形 ABCD 中，对角线 AC , BD 交于点O , E 点在BC 上, EG 丄OB , EF 丄OC ,垂足 分别为点 G , F , AC = 10,则 EG + EF = 5 . 18.如图，在平面直角坐标系中，矩形 OABC 的顶点A , C 的坐标分别为(10, 0), (0, 4),点D 是 OA 的中点，点P 在BC 上运动，当△ ODP 是腰长为5的等腰三角形时，点 P 的坐标为 _(8, 4), (3, 4)或(2, 4)_. 三、解答题(共66分)19. (6分)如图，已知矩形 ABCD 中，E 是AD 上一点，F 是AB 上一点，EF 丄EC 且EF = EC , DE =4 cm ，矩形ABCD 的周长为32 cm ，求AE 的长.B . 24C . 25D . 2660°这个角所对的边长为 20 cm ,则其对角线长为中点M , N ,连结AM , CN , MN ，若，第16题图16.如图, ?ABCD 的对角线相交于点 O ,请你添加一个条件AO = BO (答案不唯一)，使?ABCD第17题AB = 2, BC = 2，则图中阴影部分的面积为2解：I/ AFE + / AEF = / AEF + / CED = 90° /•/ AFE = / DEC . 又•••/ A = / D = 90° EF = EC ,•••△ AEF◎△ DCE AE = CD.1设 AE = x ，贝U CD = x , • AD + CD = 2x32，即 x + 4 + x = 16, •- x = 6.即卩 AE = 6 cm⑴求证：四边形 BMDN 是菱形； ⑵若AB = 4, AD = 8,求MD 的长.解：(1) •/ MN 是 BD 的垂直平分线，• BO = DO , / BON =/ DOM = 90° •••四边形 ABCD 是矩形，• AD // BC ，• / BNO = / DMO , • △ BON ◎△ DOM (AAS), • OM = ON.v OB = OD , •四边形 BMDN 是平行四边形.•/ MN 丄BD , • ?BMDN 是菱形(2)设 MD = x ，贝U MB = x , MA = 8-x ，在 Rt △ ABM 中，T BM 2= AM 2+ AB 2, • x 2= (8- x)2 + 42,解得 x = 5.「. MD 的长为 521 . （8 分）如图所示，矩形 ABCD 中，AE 丄 BD 于点 E ，/ DAE :/ BAE = 3 : 1，求/ BAE 和/ EAO 的度数.解：提示：由 / DAE :/ BAE = 3 ： 1 ,求出 / BAE = 22.5 ° 而/ABD = 90°— / BAE = 90° — 22.5° = 67.5°•••/ BAO = / ABD = 67.5 ° •••/ EAO = Z BAO — / BAE = 67.5。