2012美国数学竞赛AMC8名师制作优质教学资料

2010年第26届AMC 81. 某国中共有戴老师、刘老师与杨老师等三位数学老师。

戴老师的班有11位学生、刘老师的 班有9位学生、杨老师的班有8位学生参加了今年的AMC 8竞试。

试问这个国中共有几位学 生参加了今年的AMC 8竞试？ (A) 26 (B) 27 (C) 28 (D) 29 (E) 30 。

2. 如果对于任意的正整数a 、b ，规定a ＊b =ba ba +⨯，则5＊10=？ (A)103 (B) 1 (C) 2 (D) 310 (E) 50 。

月 月 月 月 月 月 月 月 月 月＄5 ＄＄＄3. 下图显示今年前十个月5加仑汽油的价格。

试问 最高价格比最低价格多出的金额是最低价格的百 分之多少？(A) 50 (B) 62 (C) 70 (D) 89 (E) 100 。

4. 试问2, 3, 0, 3, 1, 4, 0, 3这些数的平均数、中位数与众数(即出现最多次的数)的和是多少？ (注：将给定的一组数由小排到大，最中间的数或最中间两数的平均值称为中位数。

) (A) 6.5 (B) 7 (C) 7.5 (D) 8.5 (E) 9 。

5. 小莉要换掉一个吊在天花板下方10公分处的电灯泡，天花板距离地面2.4公尺，小莉身高 1.5公尺，手伸起可摸到她头顶上46公分处，如果她站在凳子上，恰可摸到电灯泡，试问这 个凳子的高度是多少公分？ (A) 32 (B) 34 (C) 36 (D) 38 (E) 40 。

6. 试问下列哪一种图形有最多条的对称轴？(A) 正三角形 (B) 非正方形的菱形 (C) 非正方形的矩形 (D) 等腰梯形 (E) 正方形 。

7. 如果只使用1美分、5美分、10美分与25美分的硬币，阿福至少需要有几个硬币才能支付 任何少于1美元的钱数？ (1美元=100美分) (A) 6 (B) 10 (C) 15 (D) 25 (E) 99 。

8. 当小美在一条笔直的公路上骑脚踏车时，她看见小忠在她前面21公里处与她同方向溜冰。

2019 AMC 8 Problems Problem 1Ike and Mike go into a sandwich shop with a total of to spend. Sandwiches cost each and soft drinks cost each. Ike and Mikeplan to buy as many sandwiches as they can and use the remaining money to buy soft drinks. Counting both soft drinks and sandwiches, how many items will they buy?Solution 1We maximize the number of sandwiches Mike and Ike can buy by finding the lowest multiple of that is less than This number isTherefore, they can buy sandwiches for They spend the remaining money on soft drinks, so they buy soft drinks. Combining the items, Mike and Ike buy soft drinks.The answer isProblem 2Three identical rectangles are put together to form rectangle , as shown in the figure below. Given that the length of the shorter side of each of the smaller rectangles is 5 feet, what is the area in square feet ofrectangle ?Solution 1We know that the length of the shorter side of the 3 identical rectangles are all 5 so we can use that by seeing that the longer side of the right rectangle is the same as 2 of the shorter sides of the other 2 left rectangles. This meansthat which is the longer side of the right rectangle, and because all the rectangles are congruent, we see that each of the rectangles have a longer side of 10 and a shorter side of 5. Now the bigger rectangle has a shorter length of 10(because the shorter side of the bigger rectangle is the bigger side of the shorter rectangle, which is 10) and so the bigger side of the bigger rectangle is the bigger side of the smaller rectangle + the smaller side of the smaller rectangle, which is . Thus, the area is forchoice ~~Saksham27Solution 2Using the diagram we find that the larger side of the small rectangle is 2 times the length of the smaller side. Therefore the longer side is . So the area of the identical rectangles is . We have 3 identical rectangles that form the large rectangle. Therefore the area of the large rectangleis . ~~fath2012Solution 3We see that if the short sides are 5, the long side has tobe because the long side is equal to the 2 short sides and because the rectangles are congruent. If that is to be, then the long side of the BIG rectangle(rectangle ) is because long side +short side of the small rectangle is . The short side ofrectangle is because it is the long side of the short rectangle. Multiplying and together gets us which is .~~mathboy282Problem 3Which of the following is the correct order of thefractions and from least to greatest?Solution 1Consider subtracting 1 from each of the fractions. Our new fractions would then be and . Since , it follows that the answeris-will3145Solution 2We take a commondenominator:Since it follows that the answeris .-xMidnightFirex~ dolphin7 - I took your idea and made it an explanation.Solution 3When and , . Hence, the answeris . ~ ryjsThis is also similar to Problem 20 on the AMC 2012.Problem 4Quadrilateral is a rhombus with perimeter meters. The length of diagonal is meters. What is the area in square meters ofrhombus ?Solution 1A rhombus has sides of equal length. Because the perimeter of the rhombusis , each side is . In a rhombus, diagonals are perpendicular and bisect each other, which means = = .Consider one of the right triangles:= , and = . Using Pythagorean theorem, we findthat = .Thus the values of the two diagonals are = and = . The area of a rhombus is = = =~phoenixfireSolution 2 (Heron's)Since a rhombus has sides ofequal length, . In triangle ABC, and . Using Heron's formula, we have. Simplifying, wehave so. ~~RWhiteProblem 5A tortoise challenges a hare to a race. The hare eagerly agrees and quickly runs ahead, leaving the slow-moving tortoise behind. Confident that he will win, the hare stops to take a nap. Meanwhile, the tortoise walks at a slow steady pace for the entire race. The hare awakes and runs to the finish line, only to find the tortoise already there. Which of the following graphs matches the description of the race, showing the distance traveled by the two animals over time from start to finish?Solution 1 (Using the answer choices)First, the tortoise walks at a constant rate, ruling out Second, when thehare is resting, the distance will stay the same, ruling out and . Third, the tortoise wins the race, meaning that the non-constant one should go off thegraph last, ruling out . Therefore, the answer is the only one left.Problem 6There are grid points (uniformly spaced) in the square shown in the diagram below, including the points on the edges. Point is in the center of the square. Given that point is randomly chosen among the other points, what is theprobability that the line is a line of symmetry for the square?Solution 1Lines of symmetry go through point , and there are directions the lines could go, and there are dots ateach direction.. ~heeeeeheeeeeeeProblem 7Shauna takes five tests, each worth a maximum of points. Her scores on the first three tests are , , and . In order to average for all five tests, what is the lowest score she could earn on one of the other two tests?Solution 1We should notice that we can turn the information we are given into a linear equation and just solve for our set variables. I'll use the variables and for thescores on the last two tests.We can now cross multiply to get rid of thedenominator. Now that we have this equation, we will assign as the lowest score of the two other tests, andso: Now we know that the lowest score on the two othertests is .~ aopsavSolution 2Right now, she scored and points, with a total of points. She wants her average to be for her tests so she needs to score points in total. She needs to score a total of points in her tests. So the minimum score she can get is when one of her scores is . So the least possible score she can get is . ~heeeeeeeheeeeeeNote: You can verify that is the right answer because it is the lowest answer out of the 5. Since it is possible to get 48, we are guaranteed that that is the right answer. ~~ gorefeebuddieSolution 3We can compare each of the scores with the averageof : , , , ;So the last one has to be (since all the differences have to sum to ), which corresponds to .Problem 8Gilda has a bag of marbles. She gives of them to her friend Pedro. Then Gilda gives of what is left to another friend, Ebony. Finally, Gildagives of what is now left in the bag to her brother Jimmy. What percentage of her original bag of marbles does Gilda have left for herself?Solution 1After Gilda gives % of the marbles to Pedro, she has % of the marbles left. If she then gives % of what's left to Ebony, she has = % of what she had at the beginning. Finally, she gives % of what's left to herbrother, so she has . of what she had in the beginning left.~heeeeeeeheeeeeeSolution 2Suppose Gilda has 100 marbles.Then she gives Pedro 20% of 100 = 20, she remains with 80 marbles.Out of 80 marbles she gives 10% of 80 = 8 to Ebony.Thus she remains with 72 marbles.Then she gives 25% of 72 = 18 to Jimmy, finally leaving her with 54.And =54%=~phoenixfireSolution 3 (Only if you have no time, do this method)Since she gave away 20% and 10% of what is left and then another 25% of what is actually left, we can do 20+10+25 or 55%. But it is actually going to be a bit more than 55% because 10% of what is left is not 10% of the total amount. Sothe only option that is greater than 100% - 55% is . ~~ gorefeebuddie Problem 9Alex and Felicia each have cats as pets. Alex buys cat food in cylindrical cans that are cm in diameter and cm high. Felicia buys cat food in cylindrical cans that are cm in diameter and cm high. What is the ratio of the volume one of Alex's cans to the volume one of Felicia's cans?Solution 1Using the formula for the volume of a cylinder, we get Alex, , and Felicia, . We can quickly notice that cancels out on both sides, and thatAlex's volume is of Felicia's leaving as the answer.~aopsavSolution 2Using the formula for the volume of a cylinder, we get that the volume of Alex's can is , and that the volume of Felicia's can is . Nowwe divide the volume of Alex's can by the volume of Felicia's can, so we get , which is ~~SmileKat32Solution 3The ratio of the numbers is . Looking closely at the formula , we see that the will cancel, meaning that the ratio of them willbeProblem 10The diagram shows the number of students at soccer practice each weekday during last week. After computing the mean and median values, Coach discovers that there were actually participants on Wednesday. Which of the followingstatements describes the change in the mean and median after the correction ismade?The mean increases by and the median does not change.The mean increases by and the median increases by .The mean increases by and the median increases by .The mean increases by and the median increases by .The mean increases by and the median increases by .Solution 1On Monday, people come. On Tuesday, people come. On Wednesday, people come. On Thursday, people come. Finally, onFriday, people come. , so themean is . The median is . The coach figures out that actually people come on Wednesday. The new mean is , while the new median is . The median and mean bothchange, so the answer is Another way to compute the change in mean is to notice that the sum increased by with the correction. So the average increased by .Problem 11The eighth grade class at Lincoln Middle School has students. Each student takes a math class or a foreign language class or both. There are eighth graders taking a math class, and there are eight graders taking a foreign language class. How many eighth graders take only a math class and not a foreign language class?Solution 1Let be the number of students taking both a math and a foreign language class.By P-I-E, we get = .Solving gives us .But we want the number of students taking only a math class.Which is .~phoenixfireSolution 2We have people taking classes. However we over-countedthe number of people who take both classes. If we subtract the original amount of people who take classes we get that people took the two classes. To find the amount of people who took only math class web subtract the people who didn'ttake only one math class, so we get -fath2012Solution 3We're basically just finding the number of students not taking a foreign languagesince all the rest would be taking only math.Problem12The faces of a cube are painted in six different colors: red , white ,green , brown , aqua , and purple . Three views of the cube are shown below. What is the color of the face opposite the aqua face?Solution 1is on the top, and is on the side, and is on the right side. That means that (image ) is on the left side. From the third image, you knowthat must be on the bottom since is sideways. That leaves us with the back, so the back must be . The front is opposite of the back, so the answeris .~heeeeeeeheeeeeSolution 2Looking closely we can see that all faces are connected with except for . Thus the answer is .Problem 13A palindrome is a number that has the same value when read from left to right or from right to left. (For example 12321 is a palindrome.) Let be the least three-digit integer which is not a palindrome but which is the sum of three distinct two-digit palindromes. What is the sum of the digits of ?SolutionNote that the only positive 2-digit palindromes are multiples of 11,namely . Since is the sum of 2-digit palindromes, is necessarily a multiple of 11. The smallest 3-digit multiple of 11 which is not a palindrome is 110, so is a candidate solution. We must check that 110 can be written as the sum of three distinct 2-digit palindromes; this sufficesas . Then , and the sum of the digits of is .Problem 14Isabella has coupons that can be redeemed for free ice cream cones at Pete's Sweet Treats. In order to make the coupons last, she decides that she will redeem one every days until she has used them all. She knows that Pete's is closed on Sundays, but as she circles the dates on her calendar, she realizes that no circled date falls on a Sunday. On what day of the week does Isabella redeem her first coupon?Solution 1Let to denote a day where one coupon is redeemed and the day when the second coupon is redeemed.If she starts on a she redeems her next coupon on .to .Thus is incorrect.If she starts on a she redeems her next coupon on .to .to .to .Thus is incorrect.If she starts on a she redeems her next couponon .to .to .to .to .And on she redeems her last coupon.No sunday occured thus is correct.Checking for the other options,If she starts on a she redeems her next coupon on . Thus is incorrect.If she starts on a she redeems her next coupon on .to .to .Checking for the other options gave us negative results, thus the answeris .~phoenixfireSolution 2LetWhich clearly indicates if you start form a you will not geta .Any other starting value may lead to a .Which means our answer is .~phoenixfireSolution 3Like Solution 2, let the days of the week be numbers. and arecoprime, so continuously adding to a number will cycle throughall numbers from to . If a string of 6 numbers in this cycle does not contain , then if you minus 3 from the first number of this cycle, it will always be . So, theanswer is . ~~SmileKat32Solution 4Since Sunday is the only day that has not been counted yet. We can just add the 3 days as it will become . ~~ gorefeebuddie Note: This only works when 7 and 3 are relatively prime.Problem 15On a beach people are wearing sunglasses and people are wearing caps. Some people are wearing both sunglasses and caps. If one of the people wearing a cap is selected at random, the probability that this person is is alsowearing sunglasses is . If instead, someone wearing sunglasses is selected at random, what is the probability that this person is also wearing acap?Solution 1The number of people wearing caps and sunglasses is . So then 14 people out of the 50 people wearing sunglasses also havecaps. ~heeeeeeheeeeeeProblem 16Qiang drives miles at an average speed of miles per hour. How many additional miles will he have to drive at miles per hour to average miles per hour for the entire trip?Solution 1(answer options)The only option that is easily divisible by is . Which gives 2 hours of travel. And by the formulaAnd =ThusBoth are equal and thus our answer is~phoenixfireSolution 2Note that the average speed is simply the total distance over the total time. Let the number of additional miles he has to drive be Therefore, the total distanceis and the total time (in hours) is We canset up the following equation: Simplifying the equation, we get Solving the equation yields so ouranswer is .~twinemmaSolution 3If he travels miles at a speed of miles per hour, he travels for 30 min. Average rate is total distance over total timeso , where d is the distance left to travel and t is the time to travel that distance. solve for to get . you also know that he has to travel miles per hour for some time, so plug that in for d to get and andsince , the answer is . Problem 17What is the value of theproductSolution 1We rewrite:The middle terms cancel, leaving us with~phoenixfireSolution 2If you calculate the first few values of the equation, all of the values tend to , but are not equal to it. The answer closest to but not equal to itis .~heeeeeeeheeeeeSolution 3Rewriting the numerator and the denominator, we get . We can simplify by canceling 99! on both sides, leaving us with: Werewrite as and cancel , which gets . Answer B. Problem 18The faces of each of two fair dice are numbered , , , , , and . When the two dice are tossed, what is the probability that their sum will be an even number?Solution 1The approach to this problem: There are two cases in which the sum can be an even number: both numbers are even and both numbers are odd. This results in only one case where the sum of the numbers are odd (one odd and one even in any order) . We can solve for how many ways the numbers add up to an odd number and subtract the answer from .How to solve the problem: The probability of getting an odd number firstis . In order to make the sum odd, we must select an even number next. The probability of getting an even number is . Now we multiply the twofractions: . However, this is not the answer because we could pick an even number first then an odd number. The equation is the same except backward and by the Communitive Property of Multiplication, the equations are itdoes not matter is the equation is backward or not. Thus we do . This is the probability of getting an odd number. In order to get the probability ofgetting an even number we do- ViratKohli2018 (VK18)Solution 2We have a die with evens and odds on both dies. For the sum to be even, the rolls must consist of odds or evens.Ways to roll odds (Case ): The total number of ways to roll oddsis , as there are choices for the first odd on the first rolland choices for the second odd on the second roll.Ways to roll evens (Case ): Similarly, we have ways toroll evens.Totally, we have ways to roll dies.Therefore the answer is , or .~A1337h4x0rSolution 3 (Complementary Counting)We count the ways to get an odd. If the sum is odd, then we must have an evenand an odd. The probability of an even is , and the probability of an odd is . We have to multiply by because the even and odd can be in any order. Thisgets us , so the answer is . - juliankuang Solution 4To get an even, you must get either 2 odds or 2 evens. The probability of getting 2 odds is . The probability of getting 2 evens is . If you add them together, you get =Problem 19In a tournament there are six teams that play each other twice. A teamearns points for a win, point for a draw, and points for a loss. After all the games have been played it turns out that the top three teams earned the same number of total points. What is the greatest possible number of total points for each of the top three teams?Solution 1After fully understanding the problem, we immediately know that the three top teams, say team , team , and team , must beat the other threeteams , , . Therefore, ,, must eachobtain points. However, they play against each teamtwice, for a total of points against , , and . For gamesbetween , , , we have 2 cases. In both cases, there is an equality of points between , , and .Case 1: A team ties the two other teams. For a tie, we have 1 point, so wehave points (they play twice). Therefore, this case brings a total of points.Case 2: A team beats one team while losing to another. This gives equality, as each team wins once and loses once as well. For a win, we have points, so a team gets points if they each win a game and lose a game. Thiscase brings a total of points.Therefore, we use Case 2 since it brings the greater amount of points, or , so the answer is .~A1337h4x0rNote that case 2 can be easily seen to be better as follows. Let be the number of points gets, be the number of points gets, and be the number of points gets. Since , to maximize , we can just maximize . But in each match, if one team wins then the total sum increases by points, whereas if they tie, the total sum increasesby points. So it is best if there are the fewest ties possible.Solution 2(1st match(3) + 2nd match(1)) * number of teams(6) = 24, .Explanation: So after reading the problem we see that there are 6 teams and each team versus each other twice. This means one of the two matches has to be a win, so 3 points so far. Now if we say that the team won again and make it 6 points, that would mean that team would be dominating the leader-board and the problem says that all the top 3 people have the same score. So that means the maximum amount of points we could get is 1 so that each team gets the same amount of matches won & drawn so that adds up to 4. 4 * the number of teams(6)= 24 so the answer isProblem 20How many different real numbers satisfy the equationSolutionWe have that if and only if .If , then , giving 2 solutions.If , then , giving 2 more solutions. All four of these solutions work, so the answer is . Further,the equation is a quartic in , so by the Fundamental Theorem of Algebra, there can be at most four real solutions.Problem 21What is the area of the triangle formed by the lines , , and ?Solution 1You need to first find the coordinates where the graphs intersect. ,and intersect at . , and intersect at . and intersect at . Usingthe Shoelace Theorem you get ==.~heeeeeeheeeeeSolution 2Graphing the lines, we can see that the height of the triangle is 4, and the base is 8. Using the formula for the area of a triangle, we get which is equalto . ~SmileKat32Problem 22A store increased the original price of a shirt by a certain percent and then lowered the new price by the same amount. Given that the resulting pricewas of the original price, by what percent was the price increased and decreased?Solution 1Suppose the fraction of discount is . Thatmeans ; so ,and , obtaining . Therefore, the price was increased and decreased by %, or .Solution 2(Answer options)Let the price be 100 and then trying for each option leads to .-phoenixfireSolution 3Let x be the discount. We can also work in reverse such as ()= .Thus = . Solving for givesus . But has to be positive. Thus = .Problem 23After Euclid High School's last basketball game, it was determined that of theteam's points were scored by Alexa and were scored by Brittany. Chelsea scored points. None of the other team members scored more than points What was the total number of points scored by the other team members?Solution 1Since and are integers, wehave . We see that the number of points scored by the other team members is less than or equal to and greater than or equal to . We let the total number of points be and the total number of points scored by the other team members, which meansthat, which means . The only value of that satisfies all conditions listed is , so . - juliankuang (lol im smart.) Solution 2Starting from the above equation where is the total number of points scored and is the number of points scored by the remaining 7 team members, we can simplify to obtain the Diophantineequation , or . Since is necessarily divisible by 28, let where and divide by 28 to obtain . Then it is easy to see () is the only candidate, giving . -scrabbler94Solution 3Fakesolve: We first start by setting the total number of points as ,since . However, we see that this does not work since we surpass the number of points just with the information given(). Next, we assume that the total number of points scored is . With this, we have that Alexa, Brittany, and Chelseascore: , and thus, the other seven players would have scored a total of (We see that this workssince we could have of them score points, and the other of themscore point) -aops5234Problem 24In triangle , point divides side sothat . Let be the midpoint of and let be thepoint of intersection of line and line . Given that the areaof is , what is the area of ?Solution 1Draw on such that is parallel to . That makestriangles and congruentsince . so .Since ( and ,so ), the altitude of triangle is equal to of the altitude of . The area of is , so the areaof ~heeeeeeeheeeee Solution 2 (Mass Points)First, when we see the problem, we see ratios, and we see that this triangle basically has no special properties (right, has medians, etc.) and this screams mass points at us.First, we assign a mass of to point . We figure out that has a massof since . Then, by adding , we get thatpoint has a mass of . By equality, point has a mass of also.Now, we add for point and for point .Now, is a common base for triangles and , so we figure out that the ratios of the areas is the ratios of the heights whichis . So, 's area is one third the area of , and weknow the area of is the area of since they have the same heights but different bases.So we get the area of as -BrudderNote: We can also find the ratios of the areas using the reciprocal of the product of the mass points of over the product of the mass pointsof which is which also yields -BrudderSolution 3is equal to . The area oftriangle is equal to because it is equal to on half of the area of triangle , which is equal to one third of the area of triangle , which is . The area of triangle is the sum of the areas oftriangles and , which is respectively and . So, is equal to =, so the area of triangle is . That minus the area of triangle is . ~~SmileKat32Solution 4 (Similar Triangles)Extend to such that asshown:Then and .Since , triangle has four times the area oftriangle . Since , we get .Since is also , we have becausetriangles and have the same height and same areas and so their bases must be the congruent. Thus triangle has twice the side lengths and therefore four times the area of triangle ,giving .(Credit to MP8148 for the idea)Solution 5 (Area Ratios)As before we figure out the areas labeled in the diagram. Then we notethat Solving gives . (Credit to scrabbler94 for the idea)Solution 6 (Coordinate Bashing)Let be a right triangle, andLetThe line can be described with the equationThe line can be described withSolving, we get andNow we can find-Trex4daysSolution 7Let =(the median divides the area of the triangle into two equal parts)Construction: Draw a circumcircle around with as is diameter. Extend to such that it meets the circle at . Draw line .(Since is cyclic)But is common in both with an area of 60.So, .\therefore (SAS Congruency Theorem).In , let be the median of .Which meansRotate to meet at and at . will fit exactlyin (both are radii of the circle). From the above solutions, .is a radius and is half of it implies = .Which meansThus~phoenixfire & flamewavelightSolution 8Using the ratio of and , we find the area of is and the areaof is . Also using the fact that is the midpoint of , we know . Let be a point such is parellel to . We immediatley know that by . Using that we can conclude has ratio .Using , we get . Therefore using the fact that is in , the area hasratio and we know hasarea so is . - fath2012Solution 9Labeling the areas in the diagram, we have:so .So our answer is . ~~RWhiteSolution 10 (Menelaus's Theorem)By Menelaus's Theorem on triangle , wehaveTherefore,Solution 11 (Graph Paper)Note: If graph paper isunavailable, this solution can still be used by constructing a small grid on a sheet of blank paper.As triangle is loosely defined, we can arrange its points such that the diagram fits nicely on a coordinate plane. By doing so, we can construct it on graph paper and be able to visually determine the relative sizes of the triangles. As point splits line segment in a ratio, we draw as avertical line segment units long. Point is thus unit belowpoint and units above point . By definition, Point splits linesegment in a ratio, so we draw units long directly leftof and draw directly between and , unit away from both.We then draw line segments and . We can easily tell thattriangle occupies square units of space. Constructing line and drawing at the intersection of and , we can easily see thattriangle forms a right triangle occupying of a square unit of space.。

amc教材中文
AMC（American Mathematics Competition）是美国数学竞赛的缩写，其教材主要有《Art of Problem Solving》和《First Steps for Math Olympians》等。

《Art of Problem Solving》第1卷和第2卷适用于AMC系列所有考试，不仅可以帮助学生掌握数学考点，更重要的是开拓思维，将数学思维应用到生活中，从而解决实际问题。

《First Steps for Math Olympians》一书是特别针对AMC全球数学竞赛考试所作，该书籍把AMC考试中的考点和知识点一一进行说明分析，通过图示和例题讲解让学生更好掌握与巩固，深受美国学生的喜爱与好评。

AMC教材难度较高，涵盖几何、代数、数论、微积分等一系列基础数学知识，因此适合对数学有浓厚兴趣的学生使用。

同时，这些教材按照程度深浅分入门、进阶提高、竞赛准备三个大类，遵循从概念、原理讲起，阐述清楚一个概念后，配有例题讲解，例题讲解之后布置一些难度由浅入深的习题。

如果需要中文版本的AMC教材，可以尝试在网上寻找相关的翻译版本或者联系AMC官方机构获取更多帮助。

美国数学竞赛AMC8 -- 2017年真题解析（英文解析+中文解析）Problem 1Answer: ASolution:We compute each expression individually according to the order of operations. We get A is 10, B is 8, C is 9, D is 9, E is 0.中文解析：A: 10; B : 8; C : 9; D: 9; E: 0. 最大值是A。

Problem 2Answer: ESolution:Let x be the total amount of votes casted. From the chart, Brenda received 30% of the votes and had 36 votes. We can express this relationship as 30% x=36. Solving for x, we get x=120.中文解析：Brenda占30% ，是36票，则三个人共收到投票：36/30%=120. 答案是E。

Problem 3Answer: CSolution:Since 2*2=4, 4*4=16，8*8=64，Thus，expression is sqrt(16*（8*2）)=8.中文解析：根号4是2. 8*2=16, 根号16是4. 16*4=64，根号64是8. 答案是C。

Problem 4Answer: DSolution:We can approximate 7,928m564 to 8,000,000. We can approximate 0.000315 to 0.0003. Multiplying the two yields 2400.中文解析：7，928，564可以近似于8，000，000. 因此，0.000315*8，000，000=315*8=2520. 近似于2400. 答案是D。

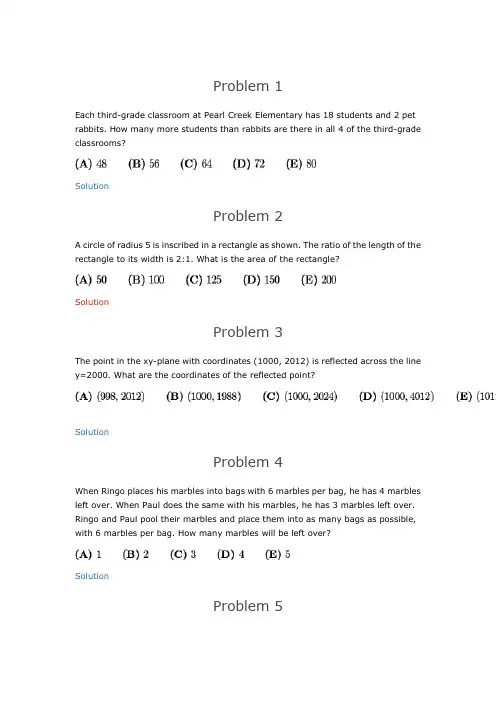
Problem 1Each third-grade classroom at Pearl Creek Elementary has 18 students and 2 pet rabbits. How many more students than rabbits are there in all 4 of the third-grade classrooms?SolutionProblem 2A circle of radius 5 is inscribed in a rectangle as shown. The ratio of the length of the rectangle to its width is 2:1. What is the area of the rectangle?SolutionProblem 3The point in the xy-plane with coordinates (1000, 2012) is reflected across the line y=2000. What are the coordinates of the reflected point?SolutionProblem 4When Ringo places his marbles into bags with 6 marbles per bag, he has 4 marbles left over. When Paul does the same with his marbles, he has 3 marbles left over. Ringo and Paul pool their marbles and place them into as many bags as possible, with 6 marbles per bag. How many marbles will be left over?SolutionProblem 5Anna enjoys dinner at a restaurant in Washington, D.C., where the sales tax on meals is 10%. She leaves a 15% tip on the price of her meal before the sales tax is added, and the tax is calculated on the pre-tip amount. She spends a total of 27.50 dollars for dinner. What is the cost of her dinner without tax or tip in dollars?SolutionProblem 6In order to estimate the value of x-y where x and y are real numbers with x > y > 0, Xiaoli rounded x up by a small amount, rounded y down by the same amount, and then subtracted her rounded values. Which of the following statements is necessarily correct?A) Her estimate is larger than x-y B) Her estimate is smaller than x-y C) Her estimate equals x-y D) Her estimate equals y - x E) Her estimate is 0SolutionProblem 7For a science project, Sammy observed a chipmunk and a squirrel stashing acorns in holes. The chipmunk hid 3 acorns in each of the holes it dug. The squirrel hid 4 acorns in each of the holes it dug. They each hid the same number of acorns, although the squirrel needed 4 fewer holes. How many acorns did the chipmunk hide?SolutionProblem 8What is the sum of all integer solutions to ?SolutionProblem 9Two integers have a sum of 26. When two more integers are added to the first two integers the sum is 41. Finally when two more integers are added to the sum of the previous four integers the sum is 57. What is the minimum number of even integers among the 6 integers?SolutionProblem 10How many ordered pairs of positive integers (M,N) satisfy the equation =SolutionProblem 11A dessert chef prepares the dessert for every day of a week starting with Sunday. The dessert each day is either cake, pie, ice cream, or pudding. The same dessert may not be served two days in a row. There must be cake on Friday because of a birthday. How many different dessert menus for the week are possible?SolutionProblem 12Point B is due east of point A. Point C is due north of point B. The distance betweenpoints A and C is , and = 45 degrees. Point D is 20 meters due Northof point C. The distance AD is between which two integers?SolutionProblem 13It takes Clea 60 seconds to walk down an escalator when it is not operating, and only 24 seconds to walk down the escalator when it is operating. How many seconds does it take Clea to ride down the operating escalator when she just stands on it?SolutionProblem 14Two equilateral triangles are contained in square whose side length is . The bases of these triangles are the opposite side of the square, and their intersection is a rhombus. What is the area of the rhombus?SolutionProblem 15In a round-robin tournament with 6 teams, each team plays one game against each other team, and each game results in one team winning and one team losing. At the end of the tournament, the teams are ranked by the number of games won. What is the maximum number of teams that could be tied for the most wins at the end on the tournament?SolutionProblem 16Three circles with radius 2 are mutually tangent. What is the total area of the circles and the region bounded by them, as shown in the figure?SolutionProblem 17Jesse cuts a circular paper disk of radius 12 along two radii to form two sectors, the smaller having a central angle of 120 degrees. He makes two circular cones, using each sector to form the lateral surface of a cone. What is the ratio of the volume of the smaller cone to that of the larger?SolutionProblem 18Suppose that one of every 500 people in a certain population has a particular disease, which displays no symptoms. A blood test is available for screening for this disease. For a person who has this disease, the test always turns out positive. For aperson who does not have the disease, however, there is a false positive rate--inother words, for such people, of the time the test will turn out negative, butof the time the test will turn out positive and will incorrectly indicate that the person has the disease. Let be the probability that a person who is chosen at random from this population and gets a positive test result actually has the disease. Which of the following is closest to ?SolutionProblem 19In rectangle , , , and is the midpoint of . Segmentis extended 2 units beyond to point , and is the intersection of and. What is the area of ?SolutionProblem 20Bernardo and Silvia play the following game. An integer between 0 and 999, inclusive, is selected and given to Bernardo. Whenever Bernardo receives a number, he doubles it and passes the result to Silvia. Whenever Silvia receives a number, she adds 50 to it and passes the result to Bernardo. The winner is the last person who produces a number less than 1000. Let be the smallest initial number that resultsin a win for Bernardo. What is the sum of the digits of ?SolutionProblem 21Four distinct points are arranged on a plane so that the segments connecting them have lengths , , , , , and . What is the ratio of to ?SolutionProblem 22Let be a list of the first 10 positive integers such that for eacheither or or both appear somewhere before in the list. How many such lists are there?SolutionProblem 23A solid tetrahedron is sliced off a wooden unit cube by a plane passing through two nonadjacent vertices on one face and one vertex on the opposite face not adjacent to either of the first two vertices. The tetrahedron is discarded and the remaining portion of the cube is placed on a table with the cut surface face down. What is the height of this object?SolutionProblem 23A solid tetrahedron is sliced off a wooden unit cube by a plane passing through two nonadjacent vertices on one face and one vertex on the opposite face not adjacent to either of the first two vertices. The tetrahedron is discarded and the remaining portion of the cube is placed on a table with the cut surface face down. What is the height of this object?SolutionProblem 24Amy, Beth, and Jo listen to four different songs and discuss which ones they like. No song is liked by all three. Furthermore, for each of the three pairs of the girls, there is at least one song liked by those girls but disliked by the third. In how many different ways is this possible?SolutionProblem 25A bug travels from to along the segments in the hexagonal lattice picturedbelow. The segments marked with an arrow can be traveled only in the direction of the arrow, and the bug never travels the same segment more than once. How many different paths are there?Retrieved from"/Wiki/index.php/2012_AMC_10B_Problems"。

AMC美国数学竞赛AMCB试题及答案解析A M C美国数学竞赛A M C B试题及答案解析 The latest revision on November 22, 20202003 AMC 10B1、Which of the following is the same as2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al’s pills cost a total of for the two weeks. How much does one green pill cost3、The sum of 5 consecutive even integers is less than the sum of the rst consecutive odd counting numbers. What is the smallest of the even integers4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the gure. She plants one flower per square foot in each region. Asters cost 1 each, begonias each, cannas 2 each, dahlias each, and Easter lilies 3 each. What is the least possible cost, in dollars, for hergarden5、Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches to make sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a “-inch” television screen is closest, in inches, to which ofthe following7、The symbolism denotes the largest integer not exceeding . For example. , and . Compute.8、The second and fourth terms of a geometric sequence are and . Which of the following is a possible first term9、Find the value of that satisfies the equation10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increased11、A line with slope intersects a line with slope at the point. What is the distance between the -intercepts of these two lines12、Al, Betty, and Clare split among them to be invested in different ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubled their money, whereas Al has managed to lose . What was Al’s origin al portion.13、Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of is14、Given that , where both and are positive integers, find the smallest possible value for .15、There are players in a singles tennis tournament. The tournament is single elimination, meaning that a player who losesa match is eliminated. In the first round, the strongest players are given a bye, and the remaining players are paired off to play. After each round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played is16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the year.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly ll the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone’s height to its radius18、What is the largest integer that is a divisor offor all positive even integers19、Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles20、In rectangle , and . Points and are onso that and . Lines and intersect at . Find the area of .21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardlessof the color you pulled out. What is the probability that all beadsin the bag are red after three such replacements22、A clock chimes once at minutes past each hour and chimes on the hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at 11:15 AM on February , , on what date will the chime occur23、A regular octagon has an area of one square unit.What is the area of the rectangle24、The rst four terms in an arithmetic sequence are , , , and , in that order. What is the fth term25、How many distinct four-digit numbers are divisible by and haveas their last two digits。

美国数学竞赛AMC8 -- 2018年真题解析（英文解析+中文解析）Problem 1Answer: ASolution:You can just do 289/20 and round your answer to get 14.中文解析:比例是1:20 ,真实建筑是289feet,因此复制品的高度是: 289/20约等于14feet. 答案是A. Problem 2Answer: DSolution:By adding up the numbers in each of the 6 parentheses, wehave:(2/1)*(3/2)*(4/3)*(5/4)*(6/5)*(7/6) . Using telescoping, most of the terms cancel out diagonally. We are left with 7 .中文解析:=(2/1)*(3/2)*(4/3)*(5/4)*(6/5)*(7/6)=7/1=7. 答案是D.Problem 3Answer: DSolution:The five numbers which cause people to leave the circle are 7, 14, 17, 21,27. The most straightforward way to do this would be to draw out the circle with the people, and cross off people as you count. The last one standing is Dan.中文解析:依次离开圆圈的数字分别是7, 14, 17, 21, 27,... 直接把A, B, C, D, E 按圆形排列, 依次数, 划掉出局的, 最后剩下的是D. 答案是D.Problem 4Answer: CSolution:We count 3*3=9 unit squares in the middle, and 4 small triangles each with an area of 1. Thus, the answer is 9+4=13.中文解析:这个12边形围起来的小正方形共有9个,其面积是9*1=9. 小三角形有8个,其面积是8*0.5=4. 因此面积一共是9+4=13. 答案是C.Problem 5Answer: ESolution:We can rewrite the given expression as1+(3-2)+(5-4)+...+(2017-2016)+(2019-2018)=1+1+1+ (1)The number of 1s is the same as the number of terms in 1,3,5,7, ……2017, 2019. Thus the answer is 1010.中文解析:把上式按下面的规则用小括号括起来:=1+(3-2)+(5-4)+(7-6)+...+(2017-2016)+(2019-2018)=1+1+1+1+...+1+1.除了第一个1外,还有: 2018/2=1009个1. 因此和是1010. 答案是E.Problem 6Answer: CSolution:Since Anh spends half an hour to drive 10 miles on the coastal road, his speed is 10/0.5=20 mph. His speed on the highway then is 20*3=60 mph. He drives 50 miles, so he drives for 5/6 hours, which is equal to 50 minutes. The total amount of minutes spent on his trip is 30+50=80 minutes.中文解析:海滨道路上花费的时间是30分钟(0.5小时),路程是10英里,因此速度是: 10/0.5=20 . 则高速路的速度是3*20=60 mph. 高速路的距离是50mile, 则时间是50/60=5/6 小时=50分钟. 答案是A.Problem 7Answer: BSolution:We use the property that the digits of a number must sum to a multiple of 9 if it are divisible by 9. This means u=7. Since we are looking for the remainder when divided by 8, we can ignore the thousands. The remainder when 187 is divided by 8 is 3.中文解析:因为这个数能被9整除,因此 2+0+1+8+U 是9的倍数,因此u=7. 20187除以8的余数只需要看后三位187除以3的余数. 余数是3. 答案是B.Problem 8Answer: CSolution:The mean, or average number of days is the total number of days divided by the number of students. The total number of days is (1*1+2*3+3*2+4*6+5*8+6*4+7*2)=109. The total number of students is 1+3+2+6+8+3+2=25. Hence, 109/25=4.36.中文解析:有1个学生锻炼了1天, 3个学生锻炼了2天, 2个学生锻炼了3天, ....平均值是: (1+3*2+2*3+6*4+8*5+3*6+2*7)/(1+3+2+6+8+3+2)=109/25=4.36 答案是C. Problem 9Answer: BSolution:He will place （12*2）+（14*2）=52 tiles around the border. For the inner part of the room, we have 10*14=140 square feet. Each tile takes up 4 square feet, so he will use 140/4=35 tiles for the inner part of the room. Thus, the answer is 52+35=87.中文解析:1-foot 的正方形需要: 16*2+10*2=52块.中间剩下的面积是: 14*10=140. 2-foot的瓷砖的面积是2*2=4. 需要140/4=35块瓷砖.共需要: 52+35=87块瓷砖. 答案是B.Problem 10Answer: CSolution:The sum of the reciprocals is 1/1 + 1/2 +1/4=7/4. Their average is 7/12. Taking the reciprocal of this gives 12/7.中文解析:harmonic mean是先计算这组数的倒数的算数平均值,然后再求倒数. 1/1, 1/2, 1/4 的算数平均值是: 7/12. 其倒数是12/7. 因此harmonic mean是12/7. 答案是C.Problem 11Answer: CSolution:The total number of ways is C(6,2)=15, if we treat Abby and Bridget as a pair and distinguishable and forget the others. The total number of ways they are adjacent = 4 (for the rows) + 3 (for the columns) Therefore, P(Abby and Bridget sitting adjacent) is 7/15.中文解析:第一步安排A的座位, 第二步安排B的座位.A的座位可能位于4个角落之一,也可能位于两个中间位置之一. ,分两种情况.第一种, A的座位位于4个角落之一的可能性是4/6, 下一步安排B的座位, B和A相邻的可能性有: 2/5.第二种, A的座位唯一两个中间位置之一的可能性是2/6, 下一步安排B的座位, B和A相邻的可能性有: 3/5.综合起来: 4/6*2/5 + 2/6 * 3/5 =7/15. 答案是C.Problem 12Answer: BSolution:We see that every 35 minutes the clock passes, the watch passes 30 minutes. That means that the clock is 7/6 as fast the watch, so when the car clock passes 7 hours, the watch has passed 6 hours, meaning that the time would be 6:00.中文解析:当实际时间过了30分钟时(从12:00 到12: 30), 她的汽车表的时间过了35分钟. 其比值时30:35=6:7. 当汽车表显示7个小时时, 根据比例关系,实际时间应该是6点. 答案是B. Problem 13Answer: ASolution:Say Lalia gets a value of x on her first 4 tests, and a value of y on her last test. Thus, 4x+y=410.The value y has to be greater than 82, because otherwise she would receive the same score on her last test. Additionally, the greatest value for y is 98 (as y=100 would give x as a decimal), so therefore the greatest value y can be is 98. As a result, only 4 numbers work, 86, 90, 94, 98.中文解析:假设前4次考试的分数都是x, 最后一次考试的分数是y, 则4x+y=82*5. 即4x=410-y.其中x,y都是正整数, 82<y<=100. 并且410-y必须是4的倍数.y最大可以是98, 因此每次减4,y依次可以是98, 94, 90, 86. 共4种可能性. 答案是A. Problem 14Answer: DSolution:120=2*2*2*3*5. For the greatest five-digit number , 120=8*5*3*1*1. Thus, n is 85311. The sum of each digits is 8+5+3+1+1=18.中文解析:120=2*2*2*3*5. 为了这个5位数最大,首先让万位数上的数字最大, 120可以写成8*5*3*1*1. 因此这个5位数是85311. 其各位数字之和是: 8+5+3+1+1=18. 答案是D.Problem 15Answer: DSolution:Let the radius of the large circle be R. Then the radii of the smaller circles are R/2. The areas of the circles are directly proportional to the square of the radii, so the ratio of the area of the small circle to the large one is 1/4. This means the combined area of the 2 smaller circles is half of the larger circle, and therefore the shaded region is equal to the combined area of the 2 smaller circles, which is 1.中文解析:两个小圆面积合起来是1, 那么一个小圆的面积是0.5. 大圆的半径是小圆的半径的2倍,因此大圆的面积是小圆面积的4倍,大圆的面积是0.5*4=2. 阴影部分的面积是: 2-1=1. 答案是D.Problem 16Answer: CSolution:Since the Arabic books and Spanish books have to be kept together, we can treat them both as just one book. That means we're trying to find the number of ways you can arrange one Arabic book, one Spanish book, and three German books, which is just 5 factorial. Now we multiply this product by 2! because there are 2 factorial ways to arrange just the Arabic books, and 4! ways to arrange just the Spanish books. Multiplying all these together, we have 5!*2!*4!=5760.中文解析：用捆绑法，把2本Arabic 书看做一个整体， 4本Spanish书看做一个整体。

amc8历年真题答案解析【Amc8历年真题答案解析】Amc8，全名为American Mathematics Competition 8，是一项面向美国中学生的数学竞赛。

每年11月份举行的Amc8竞赛，旨在通过一系列挑战性的数学问题，培养学生的数学思维能力、创造力和解决问题的能力。

以下是Amc8历年真题的答案解析。

一、2000年真题：1. 答案：C解析：问题要求选择一个在100和999之间的正整数，满足各个数字的平方和等于该数本身。

首先明确数字的范围是100到999，因此只需要考虑三位数。

假设一个三位数为$abc$，那么它满足条件$a^2+b^2+c^2=abc$。

考虑到$a,b,c$的范围在1到9之间，可以通过穷举法逐个尝试。

当$a=2$时，$b=5$和$c=1$，满足条件$2^2+5^2+1^2=251$，因此答案为C。

2. 答案：D解析：问题给出了一个小测试，Tom回答7道题目，其中4道题回答正确。

考虑到每道问题只有两个选择（正确或错误），因此回答7道题目的所有可能性为$2^7=128$。

在这些可能性中，只有一种情况Tom回答了4道题目正确，因此答案为D。

3. 答案：A解析：问题给出了一个图形，包含了一系列长方形。

我们需要计算图形中所有（不重叠）长方形的个数。

首先考虑长方形最小边长为1的情况，可以在图形中找到4个这样的长方形。

然后考虑最小边长为2的情况，可以找到3个长方形。

以此类推，最小边长为3、4、5的情况下，分别可以找到2个、1个、0个长方形。

因此，总共可以找到的长方形个数为$4+3+2+1=10$，答案为A。

4. 答案：C解析：问题给出了一个5乘5的正方形网格，要求从左上角走到右下角，只能向右或向下移动，且不能重复经过同一格。

我们需要计算从左上角到右下角有几条路径。

可以发现，从左上角到右下角，一共需要移动4次向右，4次向下。

因此可以将问题转化为在8个移动中选择4个向右，即$C_8^4=\frac{8!}{4!4!}=70$，答案为C。