简单函数优化的遗传算法C语言程序

基于C语言的遗传算法应用研究介绍遗传算法是一种受生物学启发的优化算法，通过模拟进化过程来寻找最优解。

它被广泛应用于解决各种复杂问题，如组合优化、函数优化、机器学习等领域。

在本文中，我们将讨论基于C语言的遗传算法的应用研究。

遗传算法的原理遗传算法的原理是基于自然选择和遗传机制。

它模拟了生物进化过程中的选择、复制和变异等操作。

算法通过对一个种群进行迭代操作来逐步优化解的质量，直到找到全局最优解或最优近似解。

遗传算法主要包含以下几个关键步骤： 1. 初始化种群：随机生成一组个体作为初始种群。

2. 评估适应度：根据问题的定义，对每个个体计算适应度值。

3.选择操作：根据适应度值选择优秀的个体作为父代。

4. 交叉操作：通过交叉操作，将父代的基因进行混合，生成新的子代。

5. 变异操作：对子代进行变异，引入新的基因信息。

6. 更新种群：用新的个体替代原来的个体，形成新的种群。

7. 终止条件：根据预先设定的终止条件，决定算法是否结束。

C语言在遗传算法中的应用C语言作为一种通用的高级编程语言，具有高效、灵活和可移植的特点，非常适合在遗传算法中实现。

以下是C语言在遗传算法中的几个关键应用。

种群表示C语言可以使用数组或结构体等数据结构来表示遗传算法的种群。

每个个体可以用一个固定长度的二进制串或其他数据类型来表示。

C语言提供了强大的数组操作功能，使得种群的处理和操作更加简便和高效。

适应度函数C语言可以定义适应度函数来评估每个个体的适应度值。

适应度函数根据问题的特定要求来计算一个个体的适应度值，作为选择操作的依据。

C语言提供了丰富的数学函数库，使得适应度函数的计算更加方便。

选择操作C语言可以使用多种选择算法来选择优秀的个体作为父代。

例如，可以使用轮盘赌选择、锦标赛选择等方法来实现选择操作。

C语言提供了条件语句和随机数生成等功能，使得选择操作的实现简单而灵活。

交叉操作C语言可以通过交叉操作将父代的基因混合，生成新的子代。

一个简单实用的遗传算法c程序（转载）c++ 2009-07-28 23:09:03 阅读418 评论0 字号：大中小这是一个非常简单的遗传算法源代码，是由Denis Cormier (North Carolina State University)开发的，Sita S.Raghavan (University of North Carolina at Charlotte)修正。

代码保证尽可能少，实际上也不必查错。

对一特定的应用修正此代码，用户只需改变常数的定义并且定义“评价函数”即可。

注意代码的设计是求最大值，其中的目标函数只能取正值；且函数值和个体的适应值之间没有区别。

该系统使用比率选择、精华模型、单点杂交和均匀变异。

如果用Gaussian变异替换均匀变异，可能得到更好的效果。

代码没有任何图形，甚至也没有屏幕输出，主要是保证在平台之间的高可移植性。

读者可以从,目录coe/evol 中的文件prog.c中获得。

要求输入的文件应该命名为‘gadata.txt’；系统产生的输出文件为‘galog.txt’。

输入的文件由几行组成：数目对应于变量数。

且每一行提供次序——对应于变量的上下界。

如第一行为第一个变量提供上下界，第二行为第二个变量提供上下界，等等。

/**************************************************************************//* This is a simple genetic algorithm implementation where the *//* evaluation function takes positive values only and the *//* fitness of an individual is the same as the value of the *//* objective function *//**************************************************************************/#include <stdio.h>#include <stdlib.h>#include <math.h>/* Change any of these parameters to match your needs */#define POPSIZE 50 /* population size */#define MAXGENS 1000 /* max. number of generations */#define NVARS 3 /* no. of problem variables */#define PXOVER 0.8 /* probability of crossover */#define PMUTATION 0.15 /* probability of mutation */#define TRUE 1#define FALSE 0int generation; /* current generation no. */int cur_best; /* best individual */FILE *galog; /* an output file */struct genotype /* genotype (GT), a member of the population */{double gene[NVARS]; /* a string of variables一个变量字符串*/ double fitness; /* GT's fitness适应度*/double upper[NVARS]; /* GT's variables upper bound 变量的上限*/ double lower[NVARS]; /* GT's variables lower bound变量的下限*/ double rfitness; /* relative fitness 相对适应度*/double cfitness; /* cumulative fitness 累计适应度*/};struct genotype population[POPSIZE+1]; /* population */struct genotype newpopulation[POPSIZE+1]; /* new population; *//* replaces the *//* old generation */ /* Declaration of procedures used by this genetic algorithm */void initialize(void);double randval(double, double);void evaluate(void);void keep_the_best(void);void elitist(void);void select(void);void crossover(void);void Xover(int,int);void swap(double *, double *);void mutate(void);void report(void);/***************************************************************//* Initialization function: Initializes the values of genes *//* within the variables bounds. It also initializes (to zero) *//* all fitness values for each member of the population. It *//* reads upper and lower bounds of each variable from the */ /* input file `gadata.txt'. It randomly generates values *//* between these bounds for each gene of each genotype in the *//* population. The format of the input file `gadata.txt' is *//* var1_lower_bound var1_upper bound */ /* var2_lower_bound var2_upper bound ... */ /***************************************************************/void initialize(void){FILE *infile;int i, j;double lbound, ubound;if ((infile = fopen("gadata.txt","r"))==NULL){fprintf(galog,"\nCannot open input file!\n");exit(1);}/* initialize variables within the bounds */for (i = 0; i < NVARS; i++){fscanf(infile, "%lf",&lbound);fscanf(infile, "%lf",&ubound);for (j = 0; j < POPSIZE; j++){population[j].fitness = 0;population[j].rfitness = 0;population[j].cfitness = 0;population[j].lower[i] = lbound;population[j].upper[i]= ubound;population[j].gene[i] = randval(population[j].lower[i],population[j].upper[i]);}}fclose(infile);}/***********************************************************//* Random value generator: Generates a value within bounds */ /***********************************************************/double randval(double low, double high){double val;val = ((double)(rand()%1000)/1000.0)*(high - low) + low;return(val);}/*************************************************************//* Evaluation function: This takes a user defined function. *//* Each time this is changed, the code has to be recompiled. */ /* The current function is: x[1]^2-x[1]*x[2]+x[3] *//*************************************************************/void evaluate(void){int mem;int i;double x[NVARS+1];for (mem = 0; mem < POPSIZE; mem++){for (i = 0; i < NVARS; i++)x[i+1] = population[mem].gene[i];population[mem].fitness = (x[1]*x[1]) - (x[1]*x[2]) + x[3];}}/***************************************************************//* Keep_the_best function: This function keeps track of the */ /* best member of the population. Note that the last entry in */ /* the array Population holds a copy of the best individual *//***************************************************************/void keep_the_best(){int mem;int i;cur_best = 0; /* stores the index of the best individual */for (mem = 0; mem < POPSIZE; mem++){if (population[mem].fitness > population[POPSIZE].fitness){cur_best = mem;population[POPSIZE].fitness = population[mem].fitness;}}/* once the best member in the population is found, copy the genes */ for (i = 0; i < NVARS; i++)population[POPSIZE].gene[i] = population[cur_best].gene[i]; }/****************************************************************//* Elitist function: The best member of the previous generation *//* is stored as the last in the array. If the best member of *//* the current generation is worse then the best member of the *//* previous generation, the latter one would replace the worst *//* member of the current population */ /****************************************************************/void elitist(){int i;double best, worst; /* best and worst fitness values */int best_mem, worst_mem; /* indexes of the best and worst member */ best = population[0].fitness;worst = population[0].fitness;for (i = 0; i < POPSIZE - 1; ++i){if(population[i].fitness > population[i+1].fitness){if (population[i].fitness >= best){best = population[i].fitness;best_mem = i;}if (population[i+1].fitness <= worst){worst = population[i+1].fitness;worst_mem = i + 1;}}else{if (population[i].fitness <= worst){worst = population[i].fitness;worst_mem = i;}if (population[i+1].fitness >= best){best = population[i+1].fitness;best_mem = i + 1;}}}/* if best individual from the new population is better than */ /* the best individual from the previous population, then *//* copy the best from the new population; else replace the *//* worst individual from the current population with the *//* best one from the previous generation */if (best >= population[POPSIZE].fitness){for (i = 0; i < NVARS; i++)population[POPSIZE].gene[i] = population[best_mem].gene[i];population[POPSIZE].fitness = population[best_mem].fitness;}else{for (i = 0; i < NVARS; i++)population[worst_mem].gene[i] = population[POPSIZE].gene[i];population[worst_mem].fitness = population[POPSIZE].fitness;}}/**************************************************************//* Selection function: Standard proportional selection for *//* maximization problems incorporating elitist model - makes *//* sure that the best member survives *//**************************************************************/void select(void){int mem, i, j, k;double sum = 0;double p;/* find total fitness of the population */for (mem = 0; mem < POPSIZE; mem++){sum += population[mem].fitness;}/* calculate relative fitness */for (mem = 0; mem < POPSIZE; mem++){population[mem].rfitness = population[mem].fitness/sum;}population[0].cfitness = population[0].rfitness;/* calculate cumulative fitness */for (mem = 1; mem < POPSIZE; mem++){population[mem].cfitness = population[mem-1].cfitness +population[mem].rfitness;}/* finally select survivors using cumulative fitness. */for (i = 0; i < POPSIZE; i++){p = rand()%1000/1000.0;if (p < population[0].cfitness)newpopulation[i] = population[0];else{for (j = 0; j < POPSIZE;j++)if (p >= population[j].cfitness &&p<population[j+1].cfitness)newpopulation[i] = population[j+1];}}/* once a new population is created, copy it back */for (i = 0; i < POPSIZE; i++)population[i] = newpopulation[i];}/***************************************************************//* Crossover selection: selects two parents that take part in *//* the crossover. Implements a single point crossover */ /***************************************************************/void crossover(void){int i, mem, one;int first = 0; /* count of the number of members chosen */ double x;for (mem = 0; mem < POPSIZE; ++mem){x = rand()%1000/1000.0;if (x < PXOVER){++first;if (first % 2 == 0)Xover(one, mem);elseone = mem;}}}/**************************************************************//* Crossover: performs crossover of the two selected parents. *//**************************************************************/void Xover(int one, int two){int i;int point; /* crossover point *//* select crossover point */if(NVARS > 1){if(NVARS == 2)point = 1;elsepoint = (rand() % (NVARS - 1)) + 1;for (i = 0; i < point; i++)swap(&population[one].gene[i], &population[two].gene[i]);}}/*************************************************************//* Swap: A swap procedure that helps in swapping 2 variables */ /*************************************************************/void swap(double *x, double *y){double temp;temp = *x;*x = *y;*y = temp;}/**************************************************************//* Mutation: Random uniform mutation. A variable selected for *//* mutation is replaced by a random value between lower and */ /* upper bounds of this variable */ /**************************************************************/void mutate(void){int i, j;double lbound, hbound;double x;for (i = 0; i < POPSIZE; i++)for (j = 0; j < NVARS; j++){x = rand()%1000/1000.0;if (x < PMUTATION){/* find the bounds on the variable to be mutated */lbound = population[i].lower[j];hbound = population[i].upper[j];population[i].gene[j] = randval(lbound, hbound);}}}/***************************************************************//* Report function: Reports progress of the simulation. Data *//* dumped into the output file are separated by commas */ /***************************************************************/void report(void){int i;double best_val; /* best population fitness */double avg; /* avg population fitness */double stddev; /* std. deviation of population fitness */ double sum_square; /* sum of square for std. calc */ double square_sum; /* square of sum for std. calc */ double sum; /* total population fitness */sum = 0.0;sum_square = 0.0;for (i = 0; i < POPSIZE; i++){sum += population[i].fitness;sum_square += population[i].fitness * population[i].fitness;}avg = sum/(double)POPSIZE;square_sum = avg * avg * POPSIZE;stddev = sqrt((sum_square - square_sum)/(POPSIZE - 1));best_val = population[POPSIZE].fitness;fprintf(galog, "\n%5d, %6.3f, %6.3f, %6.3f \n\n", generation,best_val, avg, stddev); }/**************************************************************//* Main function: Each generation involves selecting the best *//* members, performing crossover & mutation and then */ /* evaluating the resulting population, until the terminating *//* condition is satisfied */ /**************************************************************/void main(void){int i;if ((galog = fopen("galog.txt","w"))==NULL){exit(1);}generation = 0;fprintf(galog, "\n generation best average standard \n"); fprintf(galog, " number value fitness deviation \n"); initialize();evaluate();keep_the_best();while(generation<MAXGENS){generation++;select();crossover();mutate();report();evaluate();elitist();}fprintf(galog,"\n\n Simulation completed\n");fprintf(galog,"\n Best member: \n");for (i = 0; i < NVARS; i++){fprintf (galog,"\n var(%d) = %3.3f",i,population[POPSIZE].gene[i]);}fprintf(galog,"\n\n Best fitness = %3.3f",population[POPSIZE].fitness);fclose(galog);printf("Success\n");}/***************************************************************/链接库文件？这个简单一般的第三方库文件有2种提供方式1.lib静态库，这样必须在工程设置里面添加。

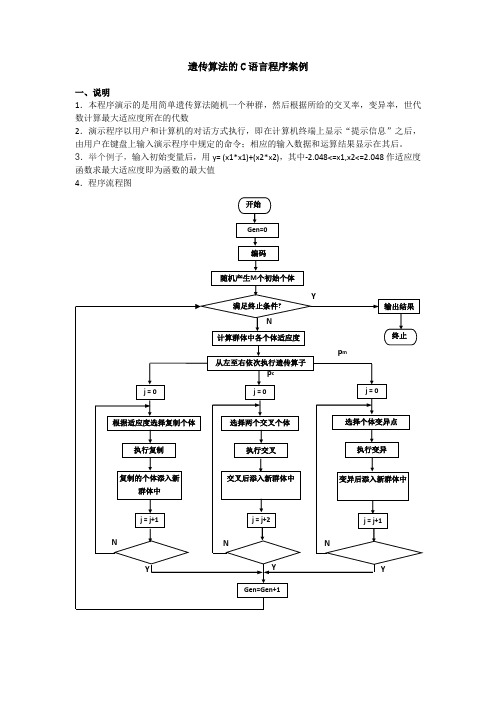
遗传算法的C语言程序案例一、说明1．本程序演示的是用简单遗传算法随机一个种群，然后根据所给的交叉率，变异率，世代数计算最大适应度所在的代数2．演示程序以用户和计算机的对话方式执行，即在计算机终端上显示“提示信息”之后，由用户在键盘上输入演示程序中规定的命令；相应的输入数据和运算结果显示在其后。

3．举个例子，输入初始变量后，用y= (x1*x1)+(x2*x2)，其中-2.048<=x1,x2<=2.048作适应度函数求最大适应度即为函数的最大值4．程序流程图5．类型定义int popsize; //种群大小int maxgeneration; //最大世代数double pc; //交叉率double pm; //变异率struct individual{char chrom[chromlength+1];double value;double fitness; //适应度};int generation; //世代数int best_index;int worst_index;struct individual bestindividual; //最佳个体struct individual worstindividual; //最差个体struct individual currentbest;struct individual population[POPSIZE];3．函数声明void generateinitialpopulation();void generatenextpopulation();void evaluatepopulation();long decodechromosome(char *,int,int);void calculateobjectvalue();void calculatefitnessvalue();void findbestandworstindividual();void performevolution();void selectoperator();void crossoveroperator();void mutationoperator();void input();void outputtextreport();6．程序的各函数的简单算法说明如下：（1）．void generateinitialpopulation ()和void input ()初始化种群和遗传算法参数。

遗传算法的C语⾔实现（⼆）-----以求解TSP问题为例上⼀次我们使⽤遗传算法求解了⼀个较为复杂的多元⾮线性函数的极值问题，也基本了解了遗传算法的实现基本步骤。

这⼀次，我再以经典的TSP问题为例，更加深⼊地说明遗传算法中选择、交叉、变异等核⼼步骤的实现。

⽽且这⼀次解决的是离散型问题，上⼀次解决的是连续型问题，刚好形成对照。

⾸先介绍⼀下TSP问题。

TSP(traveling salesman problem,旅⾏商问题)是典型的NP完全问题，即其最坏情况下的时间复杂度随着问题规模的增⼤按指数⽅式增长，到⽬前为⽌还没有找到⼀个多项式时间的有效算法。

TSP问题可以描述为：已知n个城市之间的相互距离，某⼀旅⾏商从某⼀个城市出发，访问每个城市⼀次且仅⼀次，最后回到出发的城市，如何安排才能使其所⾛的路线最短。

换⾔之，就是寻找⼀条遍历n个城市的路径，或者说搜索⾃然⼦集X={1,2,...,n}(X的元素表⽰对n个城市的编号)的⼀个排列P(X)={V1,V2,....,Vn},使得Td=∑d(V i,V i+1)+d(V n,V1)取最⼩值，其中,d(V i,V i+1)表⽰城市V i到V i+1的距离。

TSP问题不仅仅是旅⾏商问题，其他许多NP完全问题也可以归结为TSP问题，如邮路问题，装配线上的螺母问题和产品的⽣产安排问题等等，也使得TSP问题的求解具有更加⼴泛的实际意义。

再来说针对TSP问题使⽤遗传算法的步骤。

（1）编码问题：由于这是⼀个离散型的问题，我们采⽤整数编码的⽅式，⽤1~n来表⽰n个城市，1~n的任意⼀个排列就构成了问题的⼀个解。

可以知道，对于n个城市的TSP问题，⼀共有n!种不同的路线。

(2)种群初始化：对于N个个体的种群，随机给出N个问题的解（相当于是染⾊体）作为初始种群。

这⾥具体采⽤的⽅法是：1,2，...,n作为第⼀个个体，然后2,3，..n分别与1交换位置得到n-1个解，从2开始，3,4,...,n分别与2交换位置得到n-2个解，依次类推。

C语言人工智能算法实现神经网络和遗传算法人工智能（Artificial Intelligence）是当今科技领域中备受关注的热门话题，而C语言作为一种广泛应用的编程语言，也可以用于实现人工智能算法。

本文将详细介绍如何用C语言来实现神经网络和遗传算法，以展示其在人工智能领域的应用。

1. 神经网络神经网络是一种模仿人脑的学习和决策过程的计算模型。

它由多个神经元组成的层级结构构成，每个神经元接收来自上一层神经元输出的信号，并根据一定的权重和激活函数来计算输出。

下图展示了一个简单的神经网络结构：[图1：神经网络结构图]为了实现一个神经网络，我们需要在C语言中定义神经网络的结构体，并实现前馈传播和反向传播算法。

首先，我们需要定义神经网络的层级结构，可以使用数组或链表来表达。

每个神经元需要存储权重、偏差和激活函数等信息。

我们可以使用结构体来表示神经元的属性，例如：```Ctypedef struct Neuron {double* weights; // 权重数组double bias; // 偏差double output; // 输出} Neuron;```然后，定义神经网络的结构体：```Ctypedef struct NeuralNetwork {int numLayers; // 层数int* layerSizes; // 每层神经元数量的数组Neuron** layers; // 神经元层级的数组} NeuralNetwork;```接下来，我们需要实现神经网络的前馈传播算法。

前馈传播算法用于将输入数据从输入层传递到输出层，并计算网络的输出。

算法的伪代码如下所示：```Cfor each layer in network {for each neuron in layer {calculate neuron's weighted sum of inputs;apply activation function to obtain neuron's output;}}```最后，需要实现神经网络的反向传播算法，用于根据期望输出来调整网络的权重和偏差。

实验一 遗传算法解决函数优化问题一、实验目的1.掌握遗传算法的基本原理和步骤。

2. 复习VB 、VC 的基本概念、基本语法和编程方法，并熟练使用VB 或VC 编写遗传算法程序。

二、实验内容1. 上机编写程序，解决以下函数优化问题：()1021min 100i i i f x x =⎛⎫=≤ ⎪⎝⎭∑X2. 调试程序。

3. 根据实验结果，撰写实验报告。

三、实验原理遗传算法是一类随机优化算法，但它不是简单的随机比较搜索，而是通过对染色体的评价和对染色体中基因的作用，有效地利用已有信息来指导搜索有希望改善优化质量的状态。

标准遗传算法流程图如下图所示，主要步骤可描述如下： ① 随机产生一组初始个体构成初始种群。

② 计算每一个体的适配值（fitness value ，也称为适应度）。

适应度值是对染色体(个体)进行评价的一种指标，是GA 进行优化所用的主要信息，它与个体的目标值存在一种对应关系。

③ 判断算法收敛准则是否满足，若满足，则输出搜索结果；否则执行以下步骤。

④ 根据适应度值大小以一定方式执行复制操作（也称为选择操作）。

⑤ 按交叉概率p c 执行交叉操作。

⑥ 按变异概率p m 执行变异操作。

⑦ 返回步骤②。

图1.1 标准遗传算法流程图四、程序代码#include <stdio.h>#include <math.h>#include <stdlib.h>#include<time.h>#define byte unsigned char#define step 200 //步长#define MAX 50#define N 10 //随机数个数#define Pc 0.74 //被选择到下一代的概率,个数=Pc*N，小于N 下一代数=上一代，不用处理#define Pt 0.25 //交叉的概率,个数=Pt*N 舍，小于N 0~(n2+1)随机数，之后部分开始交叉#define Pm 0.01 //变异的概率,个数=Pm*N*n2 入，小于N 0~(N*(n2+1))随机数/(n2+1)=个体,0~(N*(n2+1))随机数%(n2+1)=该个体基因位置#define n2 15//2的15次方,共16位#define next_t (int)(Pt*N)//交叉个数#define next_m (int)(Pm*N+1)//变异个数向后约等于#define e 0.001//次数限制阈值/*int N=10; //随机数个数float Pc=0.74; //被选择到下一代的概率,个数=Pc*N，小于N 下一代数=上一代，不用处理float Pt=0.25; //交叉的概率,个数=Pt*N 舍，小于N 0~(n2+1)随机数，之后部分开始交叉float Pm=0.01; //变异的概率,个数=Pm*N*n2 入，小于N 0~(N*(n2+1))随机数/(n2+1)=个体,0~(N*(n2+1))随机数%(n2+1)=该个体基因位置*/bytebitary[N][n2+1],bitary0[N][n2+1];//二进制int src1[N];float ShowType(int a);//表现型void BinNum(int a);//二进制位数n2 float fit_func(float a);//适应度void DecToBin (int src,int num);//十进制转二进制void BinToDec (void);//十进制转二进制int selectT(float a,float b[10]);//选择交叉个体int selectM(float a,float b[10]);//选择变异个体void main(void){//范围是[-100,100]*************************** intsrc[N],i=0,j=0,k=0,count=0;//十进制float show[N];//表现型float fit[N],sumfit=0;//适应度float pcopy[N];//优胜劣汰，遗传到下一代的概率fit[i]/总和(fit[i]) float pacc[N];//pcopy[i]累加概率值float prand[N];//随机产生N个0~1的下一代概率int iselect;//根据概率选择到的个体序号int new_select[N];//根据概率选择到的个体int new_T[next_t],new_M[next_m];float min,min1;printf("随机数(原始母体),表现型, 适配值\n");srand( (unsigned)time(NULL) );for(i=0;i<N;i++){src[i]=rand()%32768;//rand()%201-100===>-100~100的十进制随机数随时间递增show[i]=ShowType(src[i]);//转化成表现型fit[i]=fit_func(show[i]);//计算各个适配值(适应度)sumfit=sumfit+fit[i]; //种群的适应度总和printf("%5d, %f, %f\n",src[i],s how[i],fit[i]);}printf("\n第%d代适配总值\n%f\n",count,sumfit);//第0代count++;min=sumfit;printf("\n遗传到下一代的概率\n");for(i=0;i<N;i++){pcopy[i]=fit[i]/sumfit;printf("%f, ",pcopy[i]);}// 求选择(被复制)的累加概率,用于轮盘赌产生随机数区域，选择下一代个体printf("\n遗传到下一代的累加概率\n");pacc[0]=pcopy[0];for(i=1;i<N;i++){pacc[i]=pacc[i-1]+pcopy[i];printf("%f, ",pacc[i]);}//每个src[N]都随机取其中一个pcopy，取得的值pcopy[i]跟pcopy概率大小有关//模拟轮盘赌方式选择新一代printf("\n\n新产生的第%d代,表现型, 适配值\n",count);srand( (unsigned)time(NULL) );for(i=0;i<N;i++){prand[i]=(float)( (rand()%101)*0.01 );//0~1的十进制小数，精确到0.01iselect=selectT(prand[i],pacc);new_select[i]=src[iselect];//产生的新一代,十进制show[i]=ShowType(new_select[i]);/ /转化成表现型fit[i]=fit_func(show[i]);DecToBin (new_select[i],i);sumfit=sumfit+fit[i]; //种群的适应度总和printf(" %d %f %f\n",new_selec t[i],show[i],fit[i]);}printf("\n第%d代适配总值\n%f\n",count,sumfit);//第1代min1=sumfit;if (min>sumfit){min1=min;min=sumfit;}while(fabs(min-min1)>e&&count<MAX ){//从新一代选择个体交叉printf("\n随机产生交叉个体号");srand( (unsigned)time(NULL) );for(i=0;i<2;i++) //简单起见交叉数设为2{new_T[i]=rand()%N;//0~10的十进制数产生的交叉个体if (i>0)//两个不同个体交叉while(new_T[i]==new_T[i-1])new_T[i]=rand()%N;printf("%d, ",new_T[i]);}srand( (unsigned)time(NULL) );//随机产生交叉位置k=rand()%n2;//0~14的十进制数printf("\n随机产生交叉位置 %d\n",k);printf("\n原编码\n");for(j=n2;j>=0;j--)printf("%c",bitary[new_T[0]][j]);printf("\n");for(j=n2;j>=0;j--)printf("%c",bitary[new_T[1]][j]);printf("\n位置%d后交叉编码\n",k);char temp;for(i=k+1;i<n2+1;i++)//交叉{temp=bitary[new_T[0]][i];bitary[new_T[0]][i]=bitary[new_T[ 1]][i];bitary[new_T[1]][i]=temp;}for(j=n2;j>=0;j--)printf("%c",bitary[new_T[0]][j]);printf("\n");for(j=n2;j>=0;j--)printf("%c",bitary[new_T[1]][j]);//从新一代选择个体变异printf("\n随机产生变异个体号");srand( (unsigned)time(NULL) );for(i=0;i<1;i++) //简单起见变异数设为1个{new_M[i]=rand()%N;//0~9的十进制数产生的变异个体k=rand()%(n2+1);//0~15的十进制数printf("%d\n编码位置 %d\n原编码\n",new_M[i],k);for(j=n2;j>=0;j--)printf("%c",bitary[new_M[i]][j]);if(bitary[new_M[i]][k]=='0')//变异取反bitary[new_M[i]][k]='1';elsebitary[new_M[i]][k]='0';printf("\n位置%d变异后编码\n",k);for(j=n2;j>=0;j--)printf("%c",bitary[new_M[i]][j]);}printf("\n");count++;//新的bitary即产生第二代printf("\n新产生的第%d代\n",count);for(i=0;i<N;i++){for(j=n2;j>=0;j--)printf("%c",bitary[i][j]);printf("\n");}BinToDec ();//二进制转十进制 for(i=0;i<N;i++){new_select[i]=src1[i];show[i]=ShowType(src[i]);//转化成表现型fit[i]=fit_func(show[i]);//计算各个适配值(适应度)sumfit=sumfit+fit[i]; //种群的适应度总和printf("%5d, %f, %f\n",src1[i], show[i],fit[i]);}printf("\n第%d代适配总值\n%f\n",count,sumfit);if (sumfit<min){min1=min;min=sumfit;}}printf("\n\n\n*****************\n over\n*****************\n",sumfit);}//////////////////////////子函数////////////////float ShowType(int a){float temp;temp=(float)(a*200.0/32767-100);/ /(2的15次方减1)=32767return temp;}float fit_func(float a){float temp;temp=a*a;return temp;}void DecToBin (int src,int num){int i;//注意负数的补码if (src<0){src=(int)pow(2,16)-abs(src);}for (i=0;i<=n2;i++){bitary[num][i]='0';bitary0[num][i]='0';if(src){bitary[num][i]=(src%2)+48;bitary0[num][i]=(src%2)+48;src=(int)(src/2);}}}void BinToDec (void){int i,j;for(i=0;i<N;i++){src1[i]=0;for(j=0;j<n2+1;j++){src1[i]=src1[i]+(bitary[i][j]-48) *(int)pow(2,j);}}}int selectT(float a,float b[10]) {int i;for(i=0;i<N;i++){if (a<b[i])return i;}return -1;} 五、实验结果分析：随机性大，精度不高六、实验心得理论指导实践，在实践中得以提高。

一个简单实用的遗传算法c程序一个简单实用的遗传算法c程序（转载） 2009-07-28 23:09:03 阅读418 评论0 字号：大中小这是一个非常简单的遗传算法源代码，是由Denis Cormier (North Carolina State University)开发的，Sita S.Raghavan (University of North Carolina at Charlotte)修正。

代码保证尽可能少，实际上也不必查错。

对一特定的应用修正此代码，用户只需改变常数的定义并且定义“评价函数”即可。

注意代码的设计是求最大值，其中的目标函数只能取正值；且函数值和个体的适应值之间没有区别。

该系统使用比率选择、精华模型、单点杂交和均匀变异。

如果用文件编码（TTU-UITID-GGBKT-POIU-WUUI-0089）Gaussian变异替换均匀变异，可能得到更好的效果。

代码没有任何图形，甚至也没有屏幕输出，主要是保证在平台之间的高可移植性。

读者可以从,目录 coe/evol中的文件prog.c中获得。

要求输入的文件应该命名为‘gadata.txt’；系统产生的输出文件为‘galog.txt’。

输入的文件由几行组成：数目对应于变量数。

且每一行提供次序——对应于变量的上下界。

如第一行为第一个变量提供上下界，第二行为第二个变量提供上下界，等等。

一个简单实用的遗传算法c程序（转载） 2009-07-28 23:09:03 阅读418 评论0 字号：大中小这是一个非常简单的遗传算法源代码，是由Denis Cormier (North Carolina State University)开发的，Sita S.Raghavan (University of North Carolina at Charlotte)修正。

代码保证尽可能少，实际上也不必查错。

对一特定的应用修正此代码，用户只需改变常数的定义并且定义“评价函数”即可。

1.遗传算法简单一元函数优化实例利用遗传算法计算最大值f(x)=x sin(10*pi*x)+2, x in [-1,2]选择二进制编码，种群中个体数目为40，每个种群的长度为20，使用代沟为0.9，最大遗传代数为25。

下面为一元函数优化问题的MATLAB代码figure(1);fplot('variable.*sin(10*pi*variable)+2.0',[-1,2]); %画出函数曲线%定义遗传算法参数NIND=40; %个体数目(Number of individuals)MAXGEN=25; %最大遗传代数(Maximum number of generations)PRECI=20; %变量的二进制位数(Precision of variables)GGAP=0.9; %代沟(Generation gap)trace=zeros(2, MAXGEN); %寻优结果的初始值FieldD=[20;-1;2;1;0;1;1]; %区域描述器(Build field descriptor)Chrom=crtbp(NIND, PRECI); %初始种群gen=0;%代计数器variable=bs2rv(Chrom, FieldD); %计算初始种群的十进制转换ObjV=variable.*sin(10*pi*variable)+2.0; %计算目标函数值while gen<MAXGENFitnV=ranking(-ObjV);%分配适应度值(Assign fitness values)SelCh=select('sus', Chrom, FitnV, GGAP); %选择SelCh=recombin('xovsp', SelCh, 0.7); %重组SelCh=mut(SelCh);%变异variable=bs2rv(SelCh,FieldD); %子代个体的十进制转换ObjVSel=variable.*sin(10*pi*variable)+2.0; %计算子代的目标函数值[Chrom ObjV]=reins(Chrom, SelCh, 1, 1, ObjV, ObjVSel); %重插入子代的新种群variable=bs2rv(Chrom, FieldD);gen=gen+1;%代计数器增加%输出最优解及其序号，并在目标函数图像中标出，Y为最优解,I为种群的序号[Y, I]=max(ObjV);hold on;plot(variable(I), Y, 'bo');trace(1,gen)=max(ObjV); %遗传算法性能跟踪trace(2, gen)=sum(ObjV)/length(ObjV);endvariable=bs2rv(Chrom,FieldD); %最优个体的十进制转换hold on, grid;plot(variable,ObjV,'b*');figure(2);plot(trace(1,:));hold on;plot(trace(2,:),'-.');gridlegend('解的变化','种群均值的变化')基于排序的适应度分配计算由程序段FitnV=ranking(-ObjV)实现，这里的评定算法假设目标函数是最小化的，所以ObjV前加了个负号，使目标函数最大化，适应度值结果由向量FitnV 返回。